An Improved GN-AK Protocol Using Double-Base Scalar Multiplication and Point Halving over Elliptic Curves

Abstract

Starting from the basic form of GN-authenticated key agreement (GN-AK), the current research proposes an improved protocol by integrating a new scalar multiplication technique based on a dual-base chain representation with bases $1/2$ and 3. This representation allows the use of pointwise halving operations, significantly reducing the complexity of elliptic curve calculations. The resulting protocol maintains cryptographic security based on the elliptic curve discrete logarithm problem (ECDLP) while providing improved performance for key establishment in constrained environments.

1. Introduction

Elliptic curve cryptography stands out as a leading public-key cryptographic method in today’s era. ECC stands out from other cryptographic systems because it achieves similar security levels through much smaller key sizes. The system achieves faster computation speeds while reducing memory needs and bandwidth consumption. Many applications, such as mobile devices and smart cards, as well as Internet of Things (IoT) environments, widely use ECC because performance and power efficiency are crucial there.

The Elliptic Curve Discrete Logarithm Problem (ECDLP) serves as the fundamental basis for ECC security. The problem of determining the scalar k becomes computationally impossible when only provided with a point P and its multiple $kP$ on an elliptic curve. Numerous ECC-based cryptographic protocols for digital signatures, encryption schemes, and key exchange mechanisms rely on this hardness assumption.

Key agreement protocols serve as essential components for creating secure communication channels in these applications. The GN-authenticated key agreement (GN-AK) [1] protocol serves as a prime example of this scheme because it allows two parties to mutually authenticate and establish a shared session key. This has had applications in several functional systems, and its principles are indirectly relevant in auxiliary implementation models—for instance, secure communication or authentication layers embedded within broader infrastructures such as those used in healthcare or medical monitoring environments [2,3,4,5]. The GN-AK protocol depends on regular scalar multiplication methods that provide security but require substantial computational resources. The computational demands of standard scalar multiplication create a bottleneck in environments with limited resources.

Various enhancements to the scalar multiplication process have been introduced by researchers to solve this problem. The use of double-base chains (DBCs) as scalar representations through sums of powers of two and three enables researchers to decrease the necessary elliptic curve operations. In [6] was proposed a new method that uses powers of ${\displaystyle \frac{1}{2}}$, in place of powers of 2 which allows for point halving to be utilized as a quicker substitution for point doubling. The experimental data confirmed that scalar multiplication computational costs were substantially lowered when using the new double-base chain with ${\displaystyle \frac{1}{2}}$ and 3 as bases.

In this work is proposed an improved GN-AK protocol that combines the new double-base scalar multiplication method alongside point halving. Our analysis covers the mathematical basis of the method in detail while we modify the original GN-AK protocol for the new scalar representation and present an extensive evaluation of both security and performance. The new protocol maintains the cryptographic security features of the original GN-AK protocol but delivers significantly better computational performance.

The remainder of this paper is organized as follows: Section 2 discusses related work and existing improvements in scalar multiplication and key agreement. Section 3 reviews the mathematical foundations of elliptic curve scalar multiplication. Section 4 details the double-base chain with point halving. Section 5 presents the original GN-AK protocol. Section 6 introduces our modified protocol. Section 7 and Section 8 present security and performance evaluations, respectively. Section 9 contains Discussion and Future Work, and Section 10 contains Conclusions.

2. Background and Related Work

Digital communication demands for security and efficiency combined with scalability needs drive the ongoing development of cryptographic methods. Elliptic curve cryptography (ECC) enjoys widespread acceptance because it provides robust security with smaller keys compared to traditional public-key systems like RSA and DSA, with various basic implementations [7,8]. During the last twenty years, ECC technology has been implemented across multiple protocols, including secure sockets layer (SSL), mobile authentication systems, digital signature processes, and key exchange mechanisms, according to official studies and reports that are made [9,10].

Since the development of Diffie–Hellman (DH) key exchange protocol, secure communications have benefited from substantial advancements in key agreement protocols. The original Diffie–Hellman protocol formed the basis for public-key cryptography but has been replaced in high-performance settings by elliptic curve cryptography implementations over multiplicative groups of integers modulo a prime. The variants use elliptic curves’ mathematical properties to deliver the same security level with smaller keys and reduced computational requirements.

The GN-authenticated key agreement (GN-AK) protocol uses ECC to enable entities to mutually authenticate and create a shared secret. The GN-AK protocol includes a two-step or three-step procedure where both participants create temporary scalars and compute ECC points before sharing partial data and authenticating messages through digital signature verification. The security mechanism of the protocol depends on the computational difficulty of solving the Elliptic Curve Discrete Logarithm Problem, which makes it impossible for eavesdroppers to deduce session keys.

The GN-AK protocol maintains security based on standard assumptions but faces performance difficulties in certain implementation restrictions because it uses classical scalar multiplication techniques, which are not suited for limited environments like smart cards and IoT devices. The most computationally intensive operation in ECC involves performing scalar multiplication to calculate $kP$ from a point P and scalar k. The classical scalar multiplication approaches double-and-add and non-adjacent form (NAF) exhibit performance limitations in constrained environments.

Mitigating the challenges led researchers to investigate various alternative representations and algorithms to minimize elliptic curve operation requirements.

Recent studies on IoT security in medical settings have focused on RFID authentication techniques using elliptic curve cryptography because they provide efficient computational solutions for devices with limited resources. The referenced investigation [11] examines multiple ECC authentication systems for RFID applications and finds three solutions that balance security with performance needs suitable for medical IoT infrastructure deployment. These schemes demonstrate different efficiency levels, which are determined by the specific infrastructure conditions along with the interoperability between systems and the particular clinical environment where they operate. Comparable approaches have also been proposed in other studies in the literature [12,13,14,15,16], in research contexts targeting similar problems and functional requirements, highlighting the general tendency to respond to common challenges through conceptually similar solutions.

In the field of remote user authentication, recent research has focused on the use of elliptic curve cryptography in combination with smart devices, such as smart cards, to obtain authenticated key exchange (AKE) schemes with a high level of security and efficiency. A relevant study in this direction [17] proposes an improved authentication scheme, which reinterprets the concept of “strong forward security” and provides a formal demonstration of its security, while also highlighting reduced time, storage, and communication costs compared to existing solutions. It should be noted, however, that the efficiency and applicability of the scheme depend on the characteristics of the implementation environment, such as the capabilities of the user devices and the network infrastructure, aspects that may influence the practical performance of the solution in real scenarios. There are other contributions in the literature that pursue similar research directions and propose solutions developed with regard to comparable functional requirements and close technical contexts [18,19,20]. This reflects the scientific community’s ongoing efforts to find coherent answers to recurring challenges in this field.

The research of today in the 5G wireless network field focuses on incorporating software-defined networking (SDN) principles and network function virtualization (NFV) into wireless sensor networks (WSNs) to achieve programmable control flexibility and scalability for secure environments [21]. A significant development in network security features a collaborative security framework that employs intrusion prevention with IPS-like authentication in the data plane alongside a combined anomaly detection system and an intelligent monitoring module in the control plane to achieve better detection accuracy and fewer false alarms. The solution’s performance metrics and practical usability are contingent upon multiple elements, including node collaboration levels and edge processing capabilities, as well as the threat characteristics specific to each deployment environment. The behavior of the model across various operational situations is affected by these aspects. Similar approaches to the issue can be found in [22].

Research into data security for Industrial Internet of Things (IIoT) systems includes developing encryption methods that integrate authentication and keyword search capabilities while removing the need for conventional certificate management systems through certificateless authenticated encryption with keyword search (CLAEKS) solutions. One of the noteworthy approaches is [23], which proposes an advanced security model that better reflects real-world conditions for these systems and provides a practical implementation of CLAEKS designed to meet industrial requirements. This formal demonstration establishes CLAEKS as the sole solution that provides security guarantees against relevant attacks within this enhanced framework. It should be noted that integrating the proposed scheme into a particular operational environment affects its practical application since the cloud system’s architecture and available resources determine the solution’s effectiveness and performance.

Current research efforts in wireless communication security integrate elliptic curve-based cryptosystems with symmetric algorithms to create efficient hardware solutions for devices with limited resources [24]. The hardware implementation of the ECIES cryptographic scheme using a 163-bit elliptic curve with the AES algorithm stands out as a major advancement in this area. This design leverages the ECDH protocol during key exchange to establish secure communication within limited computational resources. Hardware limitations that exist in mobile or embedded platforms and compatibility issues with current standards in diverse communication infrastructures can influence the solution’s effectiveness. Especially for these types of implementations, the results of studies conducted in [25,26].

Although key agreement protocols like MQV, HMQV, and NAXOS have included different scalar multiplication enhancements, none of them have combined DBNS with point halving in authenticated key exchange processes. The incorporation of this scalar multiplication approach into GN-AK delivers an innovative advancement.

Recent studies have focused on securing scalar multiplication techniques to guard against side-channel attacks through research on specific subspaces of elliptic curves. The paper does not directly discuss these points but shows that side-channel attack resistance improves when double-base chains decrease operations, thereby shortening execution time and simplifying detection patterns.

While several works have addressed scalar multiplication optimization in ECC, few have applied these directly within authenticated key exchange protocols. For example, methods such as windowed non-adjacent forms (wNAF) or GLV decomposition offer performance benefits but often require additional curve-specific structures or precomputations. Our proposal differs by combining two orthogonal methods—double-base chains (which reduce the number of required doublings and additions) and point halving (which lowers the cost of doublings)—within the scalar computation loop of GN-AK. This combination has not been previously applied to elliptic-curve-based AKE and leads to measurable gains, as shown in our performance evaluation.

In summary, the literature highlights three key directions of progress: The study outlines three primary progress avenues, which consist of (1) sophisticated scalar multiplication approaches using DBNS and point halving methods; (2) creation of secure key exchange systems such as GN-AK; and (3) implementation of lightweight cryptographic primitives suitable for resource-constrained environments. The study combines three research directions by applying modern mathematical optimizations within a classical key setting framework, resulting in the development of a protocol characterized by a good level of security and improved performance.

3. Mathematical Foundations of ECC Scalar Multiplication

Elliptic curve cryptography is founded on the arithmetic of elliptic curves over finite fields. An elliptic curve E defined over a field ${\mathbb{F}}_q$ (where q is typically a prime or a power of two) is the set of solutions $(x,y)\in {\mathbb{F}}_q\times {\mathbb{F}}_q$ to a Weierstrass equation of the form:

$$E:y^2+a_{1}xy+a_{3}y=x^3+a_2{x}^2+a_{4}x+a_6,$$

(1)

with coefficients $a_i\in {\mathbb{F}}_q$, along with a special point at infinity denoted $\mathcal{O}$, which serves as the identity element for group operations on the curve.

In practice, for most cryptographic applications, simplified models of the Weierstrass equation are used. For fields of characteristic greater than 3 (typically prime fields ${\mathbb{F}}_p$), the short Weierstrass form:

$$E:y^2=x^3+ax+b$$

(2)

is commonly employed. For binary fields ${\mathbb{F}}_{2^m}$, the curve is often expressed in the form:

$$E:y^2+xy=x^3+a{x}^2+b.$$

(3)

The set of points $E\left({\mathbb{F}}_q\right)$ forms an abelian group under the chord-and-tangent rule. Given two points P and Q on the curve, their sum $R=P+Q$ is computed using well-defined geometric formulas. In particular, scalar multiplication, defined as computing $kP=P+P+\dots +P$ (k times), is the fundamental operation in ECC.

The security of ECC relies on the Elliptic Curve Discrete Logarithm Problem (ECDLP), which is defined as follows: given points P and $Q=kP$ on the curve, determine the integer k. Despite the efficiency of scalar multiplication, the inverse operation—computing k given P and Q—is computationally infeasible for properly chosen curves and field sizes, forming the basis for ECC’s security.

There exist several scalar multiplication algorithms, each aiming to optimize the number of point additions and doublings required:

• Double-and-add algorithm: A binary method where the scalar k is represented in base-2, and at each bit, the current point is doubled and conditionally added to an accumulator.
• Non-Adjacent Form (NAF): A signed-digit representation of k that minimizes the Hamming weight, thereby reducing the number of additions.
• Windowed methods: These include fixed-base comb, sliding window, and w-NAF methods that precompute powers of P for faster computation.
• Montgomery ladder: A side-channel-resistant method where each iteration performs both addition and doubling.
• Joint Sparse Form (JSF): Optimized for simultaneous multiple scalar multiplications.

While these methods provide incremental improvements in efficiency, their reliance on point doubling limits their suitability for low-power or high-performance applications, especially in binary fields. Point doubling operations are typically more expensive than additions due to the requirement for field inversions and multiplications.

To overcome this, alternative scalar representations such as double-base number systems (DBNS) and point halving techniques have been explored. DBNS represents scalars as sums of terms of the form $2^a{3}^b$ (or ${{\displaystyle \frac{1}{2}}}^a{3}^b$ in newer versions), enabling a reduction in the number of curve operations. Point-halving, the inverse of doubling, can be implemented more efficiently than doubling in binary fields due to simpler arithmetic.

In the next section, we elaborate on how double-base chains with point halving offer a powerful optimization to scalar multiplication and how this can be mathematically formalized for secure and fast ECC operations.

4. Double-Base Chains with Point Halving: Theory and Algorithms

Double-base chains (DBCs) offer an advanced method for representing scalar values as a sum of terms, each of which is a product of powers of two or more distinct bases. The classical double-base number system (DBNS) represents integers using sums of the form $2^a{3}^b$. This approach reduces the number of required additions during scalar multiplication by allowing a more compact representation of scalars.

The innovation proposed by [27] refines this further by replacing the use of base 2 with base ${\displaystyle \frac{1}{2}}$, thus enabling point halving instead of point doubling. The representation becomes:

$$k=\sum _{i=1}^m{s}_i{\left({\displaystyle \frac{1}{2}}\right)}^{b_i}·3^{t_i},$$

(4)

where $s_i\in \{-1,+1\}$, $b_i$, and $t_i$ are integer exponents, and the exponents are chosen such that $\left\{b_i\right\}$ is strictly increasing and $\left\{t_i\right\}$ is decreasing. This form is termed a “double-base chain” because the sequence of operations forms a chain of scalar updates through halving and tripling.

The primary benefit of this representation is the replacement of expensive point-doubling operations with point halving, which is computationally cheaper, especially over binary fields. This method is particularly effective for devices that operate over fields ${\mathbb{F}}_{2^m}$, where field arithmetic is optimized for bitwise operations.

Point Halving Algorithm

To perform point halving over ${\mathbb{F}}_{2^m}$, one typically solves the elliptic curve equation in reverse. For a curve of the form $y^2+xy=x^3+a{x}^2+b$, given a point $Q=(x_Q,y_Q)=2P$, the halving process recovers $P=(x_P,y_P)$ by solving:

$$\lambda =x_P+{\displaystyle \frac{y_Q}{x_Q}}(\mathrm{if}{x}_Q\ne 0)$$

(5)

$$x_P=\sqrt{x_Q+{\lambda }^2+a}$$

(6)

$$y_P=x_P·(\lambda +1)$$

(7)

Solving for $x_P$ and $y_P$ requires solving quadratic equations in ${\mathbb{F}}_{2^m}$, which is efficient due to the structure of binary fields. This makes point halving particularly attractive in these settings, as it avoids costly field inversions typically required for point doubling.

When applying the DBC method in scalar multiplication, the scalar k is represented as a sum of signed terms of the form $s_i·{\left({\displaystyle \frac{1}{2}}\right)}^{b_i}·3^{t_i}$. Rather than computing each term independently, we use a left-to-right accumulation approach. Starting from an initial point, we iteratively apply tripling and halving operations to build the final result. This method minimizes redundant computation and allows efficient reuse of intermediate values.

A revised high-level description of scalar multiplication using DBC with point halving is as follows:

• Compute the DBC representation of the scalar k: a sequence of signed terms $s_i·{\left({\displaystyle \frac{1}{2}}\right)}^{b_i}·3^{t_i}$.
• Initialize the result $R=\mathcal{O}$ (the point at infinity).
• Initialize a working point $Q=P$.
• For each term in the DBC sequence (from most to least significant):
  • Apply $t_i$ successive tripling operations to Q.
  • Apply $b_i$ successive point halvings to Q.
  • If $s_i=-1$, set $Q\leftarrow -Q$.
  • Add Q to the result: $R\leftarrow R+Q$.
• Return R as the final result $kP$.

In ${\mathbb{F}}_{2^m}$, point halving can be significantly faster than doubling because it avoids or simplifies field inversions. It typically involves solving quadratic equations or computing square roots, which are more efficient in binary fields. Thus, halving offers a concrete computational advantage over doubling, justifying its use in our scalar multiplication scheme.

Compared to binary or windowed methods, this approach offers

• Fewer overall elliptic curve operations.
• Substantial reduction in field inversions and multiplications.
• Improved side-channel resistance due to less predictability in operation patterns.

Since the DBC representation is non-unique and may vary across implementations, care must be taken to ensure side-channel and timing attack resistance. Constant-time implementations and randomized DBC representations are recommended.

In the next section, we will describe the original GN-AK protocol in detail before transitioning into the modified version that incorporates this enhanced scalar multiplication technique.

5. Review of the Original GN-AK Protocol

The GN-AK protocol, introduced by Stephanides and Constantinescu, is an elliptic curve-based authenticated key agreement scheme that enables two communicating parties—commonly denoted as T (the initiator) and R (the responder)—to establish a shared session key while mutually authenticating each other. This section outlines the structure, cryptographic principles, and detailed message flow of the original GN-AK protocol.

The GN-AK protocol is designed to satisfy several critical properties required of a secure key agreement scheme:

• Mutual authentication: Both T and R must confirm each other’s identities.
• Key agreement: The protocol must result in both parties computing the same session key K.
• Session freshness: Each session should be based on pseudorandom values to ensure forward secrecy.
• Resistance to impersonation and replay attacks: The protocol must use cryptographic techniques that prevent adversaries from masquerading as legitimate participants.

Let us define the following:

• $E\left({\mathbb{F}}_p\right)$: An elliptic curve defined over a finite field.
• $P,Q\in E\left({\mathbb{F}}_p\right)$: Publicly agreed curve points.
• $S{K}_T$, $P{K}_T$: Secret and public key pair of T.
• $S{K}_R$, $P{K}_R$: Secret and public key pair of R.
• $d_T$, $d_R$: pseudorandom session-specific scalars generated by T and R.
• $h(·)$: A cryptographic hash function (e.g., SHA-1).
• ${\mathrm{Enc}}_{SK}(·)$, ${\mathrm{Dec}}_{PK}(·)$: Asymmetric encryption and decryption.

5.1. Protocol Steps

The original GN-AK protocol consists of the following steps:

Step 1: Initiator T computes and sends:

• Generate a random pseudorandom scalar $d_T$.
• Compute $T_1=d_T(P^{-1}+Q)$.
• Compute hash $T_2=h(P{K}_T\parallel T_1)$.
• Compute digital signature or encryption $T_3={\mathrm{Enc}}_{S{K}_T}\left(T_2\right)$.
• Send $\{T_1,T_3\}$ to R.

Step 2: Responder R receives $\{T_1,T_3\}$ and responds:

• Compute $T_2^{\prime }=h(P{K}_T\parallel T_1)$.
• Verify authenticity by checking ${\mathrm{Dec}}_{P{K}_T}\left(T_3\right)=T_2^{\prime }$.
• If valid, generate pseudorandom scalar $d_R$.
• Compute $R_1=d_R(P^{-1}+Q)$.
• Compute $R_2=h(P{K}_R\parallel R_1)$.
• Compute $R_3={\mathrm{Enc}}_{S{K}_R}\left(R_2\right)$.
• Compute session key $K_R=d_R{T}_1$.
• Send $\{R_1,R_3\}$ to T.

Step 3: Initiator T verifies and derives key:

• Compute $R_2^{\prime }=h(P{K}_R\parallel R_1)$.
• Verify ${\mathrm{Dec}}_{P{K}_R}\left(R_3\right)=R_2^{\prime }$.
• If valid, compute session key $K_T=d_T{R}_1$.

Assuming all computations are valid and participants behave honestly, we have:

$$K_T=d_T{R}_1=d_T{d}_R(P^{-1}+Q)=d_R{T}_1=K_R.$$

(8)

5.2. Security Properties

The original GN-AK protocol satisfies several important security criteria:

• Known-key security: Each session key is derived from pseudorandom values, ensuring compromise of one session does not affect others.
• Forward secrecy: Even if long-term keys are exposed, past session keys remain secure.
• Key confirmation: Optional third step confirms that both parties agree on the session key.
• Impersonation resistance: Encrypted hashes act as challenge-response values binding session keys to identities.

While the protocol is secure, its efficiency is bottlenecked by scalar multiplication using standard double-and-add methods. This becomes particularly critical in low-power devices or high-load servers where elliptic operations dominate runtime. The upcoming section introduces our enhanced protocol version using double-base chains and point halving to mitigate these limitations.

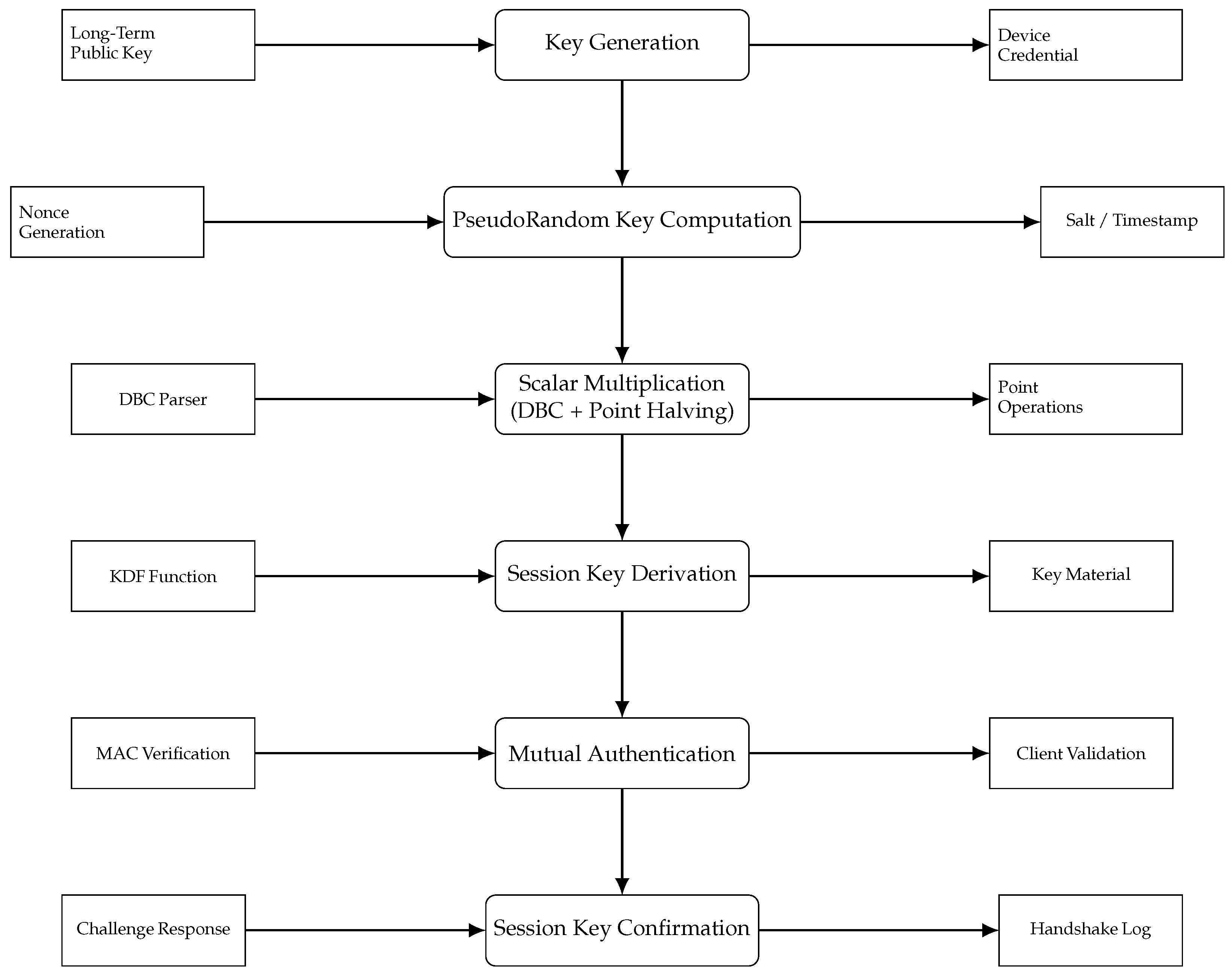
6. Refined Authenticated Key Exchange Protocol with Point Halving Optimization

In this section, we propose a refined variant of the GN-AK authenticated key agreement protocol, designed to integrate an enhanced scalar multiplication technique based on double-base chains (DBCs) incorporating point halving. This variant redefines the scalar computation process, with respect for specifications from [28,29], while preserving the core structure of mutual authentication and session key derivation. The notation and step identifiers have been updated for clarity and differentiation from the original scheme.

6.1. Design Objectives and Parameter Initialization

Let the elliptic curve $E/{\mathbb{F}}_{2^m}$ be defined over a binary field suitable for efficient halving operations. Let $\mathcal{P}$ and $\mathcal{Q}$ be publicly agreed-upon base points on the curve.

Define the key material as follows:

• $({\mathsf{sk}}_{\mathcal{A}},{\mathsf{pk}}_{\mathcal{A}})$: private/public key pair of initiator $\mathcal{A}$;
• $({\mathsf{sk}}_{\mathcal{B}},{\mathsf{pk}}_{\mathcal{B}})$: private/public key pair of responder $\mathcal{B}$;
• $H(·)$: a cryptographic hash function (e.g., SHA-256);
• ${\mathsf{Enc}}_{\mathsf{sk}}(·)$: asymmetric encryption function under private key;
• ${\mathsf{Dec}}_{\mathsf{pk}}(·)$: corresponding decryption function.

Let $\Phi ={\mathcal{P}}^{-1}+\mathcal{Q}$ be the common elliptic curve point used for scalar multiplication.

6.2. Revised Protocol Steps

• Step 1—Initiator $\mathcal{A}$ (Request Generation):
  • Generate a session-specific random scalar ${\kappa }_{\mathcal{A}}\in {\mathbb{Z}}_n$ and compute its DBC representation using bases ${\displaystyle \frac{1}{2}}$ and 3:

    $${\kappa }_{\mathcal{A}}=\sum _{i=1}^{\ell }{\sigma }_i{\left(\frac{1}{2}\right)}^{{\beta }_i}·3^{{\tau }_i},{\sigma }_i\in \{-1,+1\}$$
  • Compute pseudorandom public component: ${\Gamma }_1=\left[{\kappa }_{\mathcal{A}}\right]\Phi$ using point halving and tripling.
  • Derive authentication hash: ${\Gamma }_2=H({\mathsf{pk}}_{\mathcal{A}}\Vert {\Gamma }_1)$.
  • Generate commitment: ${\Gamma }_3={\mathsf{Enc}}_{{\mathsf{sk}}_{\mathcal{A}}}\left({\Gamma }_2\right)$.
  • Transmit the pair $\{{\Gamma }_1,{\Gamma }_3\}$ to $\mathcal{B}$.
• Step 2—Responder $\mathcal{B}$ (Response Computation and Verification):
  • Recompute hash: ${\widehat{\Gamma }}_2=H({\mathsf{pk}}_{\mathcal{A}}\Vert {\Gamma }_1)$.
  • Verify authenticity: ${\mathsf{Dec}}_{{\mathsf{pk}}_{\mathcal{A}}}\left({\Gamma }_3\right)\stackrel{?}{=}{\widehat{\Gamma }}_2$.
  • Generate independent scalar ${\kappa }_{\mathcal{B}}\in {\mathbb{Z}}_n$ and derive its DBC representation.
  • Compute response point: ${\Psi }_1=\left[{\kappa }_{\mathcal{B}}\right]\Phi$ via DBC-based scalar multiplication.
  • Compute confirmation hash: ${\Psi }_2=H({\mathsf{pk}}_{\mathcal{B}}\Vert {\Psi }_1)$.
  • Encrypt confirmation: ${\Psi }_3={\mathsf{Enc}}_{{\mathsf{sk}}_{\mathcal{B}}}\left({\Psi }_2\right)$.
  • Derive session key: $K_{\mathcal{B}}=\left[{\kappa }_{\mathcal{B}}\right]{\Gamma }_1$.
  • Send $\{{\Psi }_1,{\Psi }_3\}$ to $\mathcal{A}$.
• Step 3—Initiator $\mathcal{A}$ (Final Verification and Key Derivation):
  • Recompute ${\widehat{\Psi }}_2=H({\mathsf{pk}}_{\mathcal{B}}\Vert {\Psi }_1)$.
  • Verify: ${\mathsf{Dec}}_{{\mathsf{pk}}_{\mathcal{B}}}\left({\Psi }_3\right)\stackrel{?}{=}{\widehat{\Psi }}_2$.
  • Derive session key: $K_{\mathcal{A}}=\left[{\kappa }_{\mathcal{A}}\right]{\Psi }_1$.

6.3. Session Key Equivalence and Properties

Due to the commutativity of scalar multiplication over elliptic curves, the derived session keys satisfy:

$$K_{\mathcal{A}}=\left[{\kappa }_{\mathcal{A}}\right]\left[{\kappa }_{\mathcal{B}}\right]\Phi =\left[{\kappa }_{\mathcal{B}}\right]\left[{\kappa }_{\mathcal{A}}\right]\Phi =K_{\mathcal{B}}$$

The revised protocol maintains the original GN-AK’s cryptographic assumptions while introducing a more efficient scalar computation strategy suitable for constrained environments and secure communication infrastructures, and it complies with the security requirements specified in [30].

7. Security Analysis and Cryptographic Guarantees

The refined protocol preserves the fundamental security properties of the original GN-AK scheme while introducing no new cryptographic assumptions beyond those already required. The enhanced efficiency obtained through double-base scalar multiplication with point halving does not weaken the protocol’s resistance to standard adversarial models. We assess the protocol against key security goals relevant to authenticated key exchange protocols, with similar security levels like in [31,32].

7.1. Cryptographic Assumptions

The security of the protocol is predicated on the following well-established assumptions:

• Elliptic Curve Discrete Logarithm Problem (ECDLP): Given a point $Q=\left[\kappa \right]P$ on an elliptic curve $E/{\mathbb{F}}_{2^m}$, it is computationally infeasible to recover the scalar $\kappa$ for appropriately chosen P and curve parameters.
• Collision Resistance of the Hash Function: The function $H(·)$ behaves as a random oracle and is resistant to collision and preimage attacks.
• IND-CPA Security of Asymmetric Encryption: The encryption function ${\mathsf{Enc}}_{\mathsf{sk}}(·)$ is semantically secure against chosen plaintext attacks.

7.2. Mutual Authentication Guarantees

Authentication is achieved through the exchange of hashed commitments encrypted under long-term private keys. The values ${\Gamma }_3$ and ${\Psi }_3$ bind ephemeral data to respective identities, enabling mutual verification without disclosing sensitive material.

• The initiator $\mathcal{A}$ proves possession of ${\mathsf{sk}}_{\mathcal{A}}$ by transmitting

  $${\Gamma }_3={\mathsf{Enc}}_{{\mathsf{sk}}_{\mathcal{A}}}\left(H({\mathsf{pk}}_{\mathcal{A}}\Vert {\Gamma }_1)\right)$$
• The responder $\mathcal{B}$ authenticates using

  $${\Psi }_3={\mathsf{Enc}}_{{\mathsf{sk}}_{\mathcal{B}}}\left(H({\mathsf{pk}}_{\mathcal{B}}\Vert {\Psi }_1)\right)$$

Correct decryption and hash verification at both ends guarantee that no impersonation is possible without access to the private key of the peer entity.

7.2.1. Session Key Confidentiality

The shared session key is derived independently by both parties as

$$K_{\mathcal{A}}=\left[{\kappa }_{\mathcal{A}}\right]{\Psi }_1=\left[{\kappa }_{\mathcal{A}}\right]\left[{\kappa }_{\mathcal{B}}\right]\Phi ,K_{\mathcal{B}}=\left[{\kappa }_{\mathcal{B}}\right]{\Gamma }_1=\left[{\kappa }_{\mathcal{B}}\right]\left[{\kappa }_{\mathcal{A}}\right]\Phi$$

Under the ECDLP assumption, and provided that ${\kappa }_{\mathcal{A}}$ and ${\kappa }_{\mathcal{B}}$ remain secret, the adversary cannot compute $K_{\mathcal{A}}=K_{\mathcal{B}}$, even if $\Phi$, ${\Gamma }_1$, and ${\Psi }_1$ are transmitted in clear.

7.2.2. Key Compromise Impersonation Vs. Forward Secrecy

It is important to distinguish between forward secrecy (FS) and key compromise impersonation (KCI) resilience, as they address different attack scenarios.

Forward secrecy guarantees that even if a party’s long-term private key is later compromised, previous session keys remain secure due to their derivation from ephemeral, session-specific scalars. In contrast, KCI resilience ensures that compromise of a party’s private key does not enable an adversary to impersonate other entities to the compromised party. This means that even if an attacker learns the private key of party A, they cannot pretend to be B towards A without also knowing ephemeral secrets.

Our protocol ensures both properties: FS is achieved through the use of fresh $\kappa$ values for each session, while KCI resilience follows from the symmetric dependence on both parties’ pseudorandom contributions in the session key computation.

7.2.3. Forward Secrecy

The protocol achieves strong forward secrecy since session keys depend on fresh, ephemeral scalars ${\kappa }_{\mathcal{A}}$ and ${\kappa }_{\mathcal{B}}$, randomly chosen for each session. Even in the event of private key compromise, prior session keys remain protected as the ephemeral scalars are not reused or disclosed.

7.2.4. Resistance to Replay and Impersonation Attacks

Each session involves freshly generated $\kappa$ values and thus unique public components ${\Gamma }_1$ and ${\Psi }_1$, producing session-specific commitments. An attacker replaying old messages will fail to pass hash verification due to a mismatch with expected inputs. Furthermore, impersonation attempts without possession of valid private keys result in authentication failure.

7.2.5. Key Compromise Impersonation (KCI) Resilience

Even if one party’s private key is exposed (e.g., ${\mathsf{sk}}_{\mathcal{A}}$), the adversary cannot impersonate other entities to that party due to the dependency of K on both ephemeral values. The session key derivation requires knowledge of both ${\kappa }_{\mathcal{A}}$ and ${\kappa }_{\mathcal{B}}$, making unilateral computation infeasible.

The protocol ensures that both participants contribute equally to the session key via independent random scalars. This contributory property prevents key control by any single party and ensures protocol fairness. Compared to the original GN-AK protocol, which also derives the session key from independent pseudorandom scalars $d_T$ and $d_R$, our enhanced protocol maintains this contributory structure but employs a scalar multiplication approach that explicitly intertwines both parties’ ephemeral inputs through a double-base chain representation and point-halving strategy. This design, alongside our formal analysis, ensures robust KCI resistance under the explicit dependency on both ephemeral secrets. Thus, while the original GN-AK is also a contributory key agreement protocol, our modifications focus on tightening the symmetric influence of both parties’ fresh values and facilitating formal proofs in the CK model. In the enhanced protocol, the session key is derived as $K=\left[{\kappa }_A\right]\left[{\kappa }_B\right]\Phi$, and both ${\kappa }_A$ and ${\kappa }_B$ are session-specific random scalars, secret, and freshly generated in each session. This symmetric contribution ensures that compromising a long-term private key is insufficient to compute valid session keys or impersonate another entity to the compromised party, as knowledge of the peer’s random value remains indispensable.

7.2.6. Side-Channel Resistance Considerations

Although side-channel attack resistance is not the focus of this work, the use of double-base scalar multiplication with point halving naturally reduces the number of elliptic curve operations. Shorter execution paths with fewer field inversions reduce the attack surface for timing and power analysis. Implementers are advised to follow constant-time computation practices and randomized DBC traversal strategies for additional protection.

The refined protocol preserves all essential cryptographic guarantees of the original GN-AK while introducing a more efficient scalar multiplication method. No additional assumptions are introduced, and security is maintained under established models. The enhancements make the protocol particularly well-suited for constrained or embedded cryptographic environments where performance and energy efficiency are critical.

7.3. Formal Security Proof in the Canetti-Krawczyk Model

In this section, we provide a formal security analysis of the refined key agreement protocol using the Canetti-Krawczyk (CK) model, which captures realistic adversarial behavior and session-level freshness. The goal is to prove that our construction satisfies authenticated key exchange (AKE) security under standard cryptographic assumptions, namely the hardness of the Elliptic Curve Discrete Logarithm Problem (ECDLP), the collision resistance of the employed hash function, and the semantic security of the encryption scheme used in the protocol.

Security Model

The CK model considers a probabilistic polynomial-time (PPT) adversary $\mathcal{A}$ interacting with multiple protocol instances, or sessions, associated with honest parties. Each party can participate in multiple concurrent sessions, modeled as stateful oracles. The adversary controls the communication channel and can:

• Send: Deliver arbitrary messages to protocol instances.
• Reveal: Obtain session keys from completed sessions.
• Corrupt: Reveal long-term keys of a party.
• Test: Challenge a session with a random key or the real session key.

A protocol is considered AKE-secure if the adversary cannot distinguish the real session key from a random value, except with negligible advantage, provided the session is fresh (i.e., it has not been subject to both corruption and key reveal).

Theorem 1. 

Let E be an elliptic curve defined over a binary field ${\mathbb{F}}_{2^m}$, and assume that:

• The ECDLP over E is hard;
• The hash function $H(·)$ is modeled as a random oracle;
• The encryption scheme ${\mathsf{Enc}}_{\mathsf{sk}}(·)$ is IND-CPA secure.

• Then, the refined GN-AK protocol using double-base scalar multiplication and point halving is AKE-secure in the CK model.

Proof. 

We outline the proof via a sequence of security scenarios and reduction arguments, where $\mathcal{E}$ is a potential attacker.

• Security Scenario 0: $\mathrm{E}\mathrm{x}{p}_{\mathcal{E}}^{{\Pi }^{\prime },0}\left(k\right)$—Real Execution of the Protocol

This experiment models the real-world execution of the protocol ${\Pi }^{\prime }$ under security parameter k, in the presence of a probabilistic polynomial-time adversary $\mathcal{E}$. It serves as the baseline experiment against which all subsequent transformations will be compared in the sequence-of-games approach.

In $\mathrm{E}\mathrm{x}{p}_{\mathcal{E}}^{{\Pi }^{\prime },0}\left(k\right)$, all cryptographic components are instantiated as specified in the protocol design:

• The hash function $H(·)$ is treated as a standard deterministic function;
• The encryption function ${\mathsf{Enc}}_{\mathsf{sk}}(·)$ is evaluated using the real asymmetric encryption scheme;
• Session keys are derived as

  $$K=\left[{\kappa }_{\mathcal{A}}\right]\left[{\kappa }_{\mathcal{B}}\right]\Phi ,$$

  where ${\kappa }_{\mathcal{A}},{\kappa }_{\mathcal{B}}\leftarrow {\mathbb{Z}}_n$ are independently and uniformly sampled ephemeral scalars, and $\Phi$ is the fixed public base point.

The adversary $\mathcal{E}$ interacts with the protocol by activating multiple instances (sessions) of honest parties $\mathcal{A}$ and $\mathcal{B}$ using the following oracle queries:

• Send: deliver messages to protocol participants and receive their outputs;
• Reveal: obtain the session key of a completed session;
• Corrupt: learn the long-term private key of a party;
• Test: challenge a session with either the real session key or a uniformly random value.

The Test query is issued on a session that is fresh, i.e., it satisfies the following freshness conditions:

• Neither the session nor its partner has been subjected to a Reveal query;
• The long-term private key of the owner has not been revealed via Corrupt.

The experiment outputs 1 if the adversary $\mathcal{E}$ correctly guesses whether the Test query returned the real session key or a random value. Otherwise, it outputs 0. The advantage of $\mathcal{E}$ in this experiment is defined as

$${\mathrm{Adv}}_{\mathcal{E}}^{{\Pi }^{\prime },\mathrm{AKE}}\left(k\right)=\left|Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },0}\left(k\right)=1\right]-{\displaystyle \frac{1}{2}}\right|.$$

This experiment reflects the full, unmodified behavior of the protocol as it would occur in an actual deployment, using real cryptographic primitives and without simulation. All deviations introduced in subsequent experiments will be analyzed relative to this baseline.

• Security Scenario 1: $\mathrm{E}\mathrm{x}{p}_{\mathcal{E}}^{{\Pi }^{\prime },1}\left(k\right)$—Replacement of the Hash Function with a Random Oracle

In this experiment, we transition from the real-world execution model defined in $\mathrm{E}\mathrm{x}{p}_{\mathcal{E}}^{{\Pi }^{\prime },0}\left(k\right)$ to an idealized setting in which the hash function $H(·)$ used within the protocol is replaced by a truly random oracle. The objective of this transformation is to simplify the security analysis by abstracting away any structural properties of the hash function and modeling it as a black-box function with ideal behavior.

In the original protocol ${\Pi }^{\prime }$, the hash function H is used to compute commitments that bind ephemeral values to long-term identities:

$${\Gamma }_2=H({\mathsf{pk}}_{\mathcal{A}}\Vert {\Gamma }_1),{\Psi }_2=H({\mathsf{pk}}_{\mathcal{B}}\Vert {\Psi }_1).$$

In this experiment, H is modeled as a random oracle $\mathcal{RO}$, which behaves as follows:

• On input $x\in {\{0,1\}}^{*}$, if x has not been queried before, sample $y\leftarrow {\{0,1\}}^{\mu }$ uniformly at random and store $(x,y)$ in a global table.
• If x was queried previously, return the same y as before.

Here, μ denotes the output length of the hash function, typically matching the security parameter (e.g., 256 bits). Both the adversary $\mathcal{E}$ and the honest parties have access to this oracle $\mathcal{RO}$, and the responses are consistent across all interactions.

The purpose of this transformation is to remove any dependency on the specific implementation or internal structure of H, under the assumption that hash functions used in cryptographic protocols are designed to emulate random oracles. This abstraction is widely accepted in the security analysis of key exchange protocols and digital signatures.

Since the only modification in $\mathrm{E}\mathrm{x}{p}_{\mathcal{E}}^{{\Pi }^{\prime },1}\left(k\right)$ relative to $\mathrm{E}\mathrm{x}{p}_{\mathcal{E}}^{{\Pi }^{\prime },0}\left(k\right)$ is the treatment of H as a random oracle, and assuming that H is collision-resistant and behaves like a pseudorandom function in practice, the difference in $\mathcal{E}$’s success probability between these two experiments is negligible:

$$\left|Pr\left[\mathrm{E}\mathrm{x}{p}_{\mathcal{E}}^{{\Pi }^{\prime },1}\left(k\right)=1\right]-Pr\left[\mathrm{E}\mathrm{x}{p}_{\mathcal{E}}^{{\Pi }^{\prime },0}\left(k\right)=1\right]\right|\le {\epsilon }_{\mathrm{hash}}\left(k\right),$$

where ${\epsilon }_{\mathrm{hash}}\left(k\right)$ is negligible in k.

This is justified by invoking the standard assumption that secure hash functions, such as SHA-256, behave indistinguishably from ideal random oracles in adversarial settings. Therefore, this transition allows us to conduct the remainder of the security analysis under the random oracle model (ROM), which simplifies subsequent reductions while preserving the adversary’s effective view of the protocol.

• Security Scenario 2 $\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },2}\left(k\right)$—Simulation of Ciphertexts

In this experiment, the ciphertexts ${\Gamma }_3$ and ${\Psi }_3$ are replaced by random bitstrings of identical length. This step relies on the assumption that, under the random oracle model, the adversary cannot predict the encrypted values (e.g., $H({\mathrm{pk}}_A\Vert {\Gamma }_1)$) unless it queries the oracle on the exact same input. Assuming the adversary does not make such queries, and given that the underlying encryption scheme is IND-CPA secure, we can simulate the ciphertexts without affecting the adversary’s distinguishing advantage. We acknowledge that IND-CPA security does not directly imply ciphertext pseudorandomness. However, for hash-derived values unknown to the adversary, this simulation is sound under standard assumptions. A more conservative approach would involve using an encryption scheme with pseudorandom ciphertexts (IND-PRIV), or alternatively modeling the encryption function in the random oracle model as well. These considerations are left as possible refinements in future work.

The purpose of replacing the ciphertexts with random bitstrings in this experiment is to simulate their behavior under the assumption that the adversary does not know the underlying plaintexts, which are hash values of inputs derived only by honest parties. If the adversary has not queried the random oracle with the exact inputs, then from its perspective, the ciphertexts reveal no additional information and can be replaced with random strings. This technique allows us to isolate the ciphertext’s contribution to the adversary’s advantage and supports the reduction to IND-CPA security. While the encryption is used for authentication, not confidentiality, this transformation ensures that the simulation remains indistinguishable under standard cryptographic assumptions.

With respect to the above, the transition is made from the idealized random oracle environment of $\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },1}\left(k\right)$ to a setting where the ciphertexts exchanged during the protocol execution are no longer computed via the actual encryption function ${\mathsf{Enc}}_{\mathsf{sk}}(·)$, but are instead simulated using uniformly random values. The purpose of this step is to isolate the impact of ciphertext content on the adversary’s distinguishing advantage.

In the refined protocol ${\Pi }^{\prime }$, the initiator and responder transmit ciphertexts:

$${\Gamma }_3={\mathsf{Enc}}_{{\mathsf{sk}}_{\mathcal{A}}}\left(H({\mathsf{pk}}_{\mathcal{A}}\Vert {\Gamma }_1)\right),{\Psi }_3={\mathsf{Enc}}_{{\mathsf{sk}}_{\mathcal{B}}}\left(H({\mathsf{pk}}_{\mathcal{B}}\Vert {\Psi }_1)\right).$$

In this experiment, these values are replaced by randomly sampled bitstrings of the same length as the original ciphertexts:

$${\Gamma }_3^{*}\leftarrow {\{0,1\}}^{\lambda },{\Psi }_3^{*}\leftarrow {\{0,1\}}^{\lambda },$$

where $\lambda$ is the ciphertext length in bits. These random values are generated lazily—that is, at the moment they are first required—and stored in a lookup table to ensure consistency for repeated references.

Since the encryption scheme $\mathsf{Enc}$ is assumed to be IND-CPA secure, it follows that the adversary $\mathcal{E}$ cannot distinguish between a real encryption of a known value and a uniformly random bitstring, unless it queries the corresponding message to the random oracle. Formally, this is captured by the following bound:

$$\left|Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },2}\left(k\right)=1\right]-Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },1}\left(k\right)=1\right]\right|\le {\epsilon }_{\mathrm{enc}}\left(k\right),$$

where ${\epsilon }_{\mathrm{enc}}\left(k\right)$ is a negligible function derived from the IND-CPA security of the encryption scheme.

To support the above reduction, we construct a hypothetical adversary ${\mathcal{E}}^{\prime }$ that breaks the IND-CPA security of $\mathsf{Enc}$ by embedding the challenge ciphertext into one of the protocol’s encrypted values (e.g., replacing ${\Gamma }_3$). If $\mathcal{E}$ can distinguish the simulation from a real run with non-negligible probability, then ${\mathcal{E}}^{\prime }$ can use this to decide whether the challenge ciphertext encrypts a real hash value or a random string—contradicting the assumption that $\mathsf{Enc}$ is IND-CPA secure.

Therefore, from the perspective of $\mathcal{E}$, the distributions of ${\Gamma }_3^{*}$ and ${\Psi }_3^{*}$ are computationally indistinguishable from their real encrypted counterparts under the encryption key of the respective parties. As a result, the adversary’s distinguishing advantage is preserved up to a negligible additive factor, and we may proceed to the next experiment without violating the underlying security assumptions.

• Security Scenario 3: $\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },3}\left(k\right)$—Session Key Replaced with Random

In this final experiment, denoted $\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },3}\left(k\right)$, the session key returned by the Test query is replaced with a uniformly random bitstring of the same length as the original key, instead of being computed as

$$K=\left[{\kappa }_{\mathcal{A}}\right]\left[{\kappa }_{\mathcal{B}}\right]\Phi .$$

All other interactions and protocol behaviors remain identical to those in $\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },2}\left(k\right)$. The adversary $\mathcal{E}$ continues to interact with oracles for Send, Reveal, and Corrupt, but it cannot distinguish whether the session key in the challenged session was derived from real protocol values or chosen uniformly at random.

This step allows us to assess the indistinguishability of the session key from random. If the adversary succeeds in distinguishing the real key from a random one, it implies that it has learned some non-trivial function of both ephemeral scalars ${\kappa }_{\mathcal{A}}$ and ${\kappa }_{\mathcal{B}}$ or has broken the underlying cryptographic assumptions.

Formally, we define the adversary’s advantage in this experiment as

$${\mathrm{Adv}}_{\mathcal{E}}^{{\Pi }^{\prime },\mathrm{AKE}}\left(k\right)=\left|Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },3}\left(k\right)=1\right]-{\displaystyle \frac{1}{2}}\right|.$$

Under the assumption that the Elliptic Curve Discrete Logarithm Problem (ECDLP) is intractable and that the scalars ${\kappa }_{\mathcal{A}}$ and ${\kappa }_{\mathcal{B}}$ are independently and uniformly chosen for each session and never revealed, we argue that

$${\mathrm{Adv}}_{\mathcal{E}}^{{\Pi }^{\prime },\mathrm{AKE}}\left(k\right)\le \epsilon \left(k\right),$$

where $\epsilon \left(k\right)$ is a negligible function in the security parameter k.

This completes the sequence of experiments used in our proof. By bounding the adversary’s distinguishing advantage in each transition, we conclude that the refined protocol ${\Pi }^{\prime }$ achieves authenticated key exchange (AKE) security in the Canetti-Krawczyk model. □

Reduction.

Assume there exists a probabilistic polynomial-time adversary $\mathcal{E}$ that can distinguish the output of experiment $\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },3}\left(k\right)$ from a random bit with non-negligible advantage. Then, by the sequence-of-experiments technique, we show that this implies the existence of a reduction that violates one of the underlying security assumptions of the protocol.

We consider each transition between adjacent experiments:

• Transition from $\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },0}\left(k\right)$ to $\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },1}\left(k\right)$ replaces the hash function $H(·)$ with a random oracle. An adversary capable of distinguishing this transformation contradicts the assumption that H behaves as an ideal random oracle. Let the distinguishing advantage be denoted ${\epsilon }_{\mathrm{hash}}\left(k\right)$.
• Transition from $\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },1}\left(k\right)$ to $\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },2}\left(k\right)$ replaces ciphertexts ${\Gamma }_3$ and ${\Psi }_3$ with random values. An adversary who detects this change can be used to build an IND-CPA distinguisher for the encryption scheme $\mathsf{Enc}$. Let the corresponding advantage be ${\epsilon }_{\mathrm{enc}}\left(k\right)$.
• Transition from $\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },2}\left(k\right)$ to $\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },3}\left(k\right)$ replaces the real session key with a uniformly random key. Any non-negligible distinguishing advantage in this step implies that the adversary has obtained information about $\left[{\kappa }_{\mathcal{A}}\right]\left[{\kappa }_{\mathcal{B}}\right]\Phi$ from ${\Gamma }_1$ and ${\Psi }_1$ without knowledge of the ephemeral scalars, violating the hardness of the ECDLP. Let this advantage be denoted ${\epsilon }_{\mathrm{ecdlp}}\left(k\right)$.

Combining these steps yields the following bound on the total advantage of the adversary in the real experiment:

Lemma 1 

(Sequence-of-Experiments Conclusion). Let ${\Pi }^{\prime }$ be the refined authenticated key agreement protocol, and let $\mathcal{E}$ be any PPT adversary in the CK model. Then, under the assumptions of IND-CPA security of $\mathsf{Enc}$, the random oracle behavior of H, and the hardness of the ECDLP, the advantage of $\mathcal{E}$ in breaking the AKE security of ${\Pi }^{\prime }$ satisfies:

$${\mathit{Adv}}_{\mathcal{E}}^{{\Pi }^{\prime },\mathit{AKE}}\left(k\right)\le {\epsilon }_{\mathit{hash}}\left(k\right)+{\epsilon }_{\mathit{enc}}\left(k\right)+{\epsilon }_{\mathit{ecdlp}}\left(k\right),$$

where each $\epsilon (·)$ is a negligible function in the security parameter k.

Proof. 

Let us denote by $\mathcal{E}$ a probabilistic polynomial-time adversary that interacts with protocol ${\Pi }^{\prime }$ in the authenticated key exchange (AKE) experiment under the Canetti–Krawczyk model.

We consider the sequence of experiments:

$$\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },0}\left(k\right)\to \mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },1}\left(k\right)\to \mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },2}\left(k\right)\to \mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },3}\left(k\right).$$

We define the advantage of $\mathcal{E}$ in the real experiment as

$${\mathrm{Adv}}_{\mathcal{E}}^{{\Pi }^{\prime },\mathrm{AKE}}\left(k\right)=\left|Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },0}\left(k\right)=1\right]-\frac{1}{2}\right|.$$

To bound this advantage, we apply the triangle inequality over the sequence of experiments:

$$\begin{array}{cc}\hfill {\mathrm{Adv}}_{\mathcal{E}}^{{\Pi }^{\prime },\mathrm{AKE}}\left(k\right)& =\left|Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },0}\left(k\right)=1\right]-\frac{1}{2}\right|\hfill \\ \hfill & =\left|Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },0}\left(k\right)=1\right]-Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },3}\left(k\right)=1\right]+Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },3}\left(k\right)=1\right]-\frac{1}{2}\right|\hfill \\ \hfill & \le \left|Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },0}\left(k\right)=1\right]-Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },1}\left(k\right)=1\right]\right|\hfill \\ \hfill & +\left|Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },1}\left(k\right)=1\right]-Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },2}\left(k\right)=1\right]\right|\hfill \\ \hfill & +\left|Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },2}\left(k\right)=1\right]-Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },3}\left(k\right)=1\right]\right|\hfill \\ \hfill & +\left|Pr\left[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },3}\left(k\right)=1\right]-\frac{1}{2}\right|.\hfill \end{array}$$

Each of these differences is bounded by the security assumption related to the respective experiment:

• $\left|Pr[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },0}=1]-Pr[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },1}=1]\right|\le {\epsilon }_{\mathrm{hash}}\left(k\right)$, due to the random oracle assumption on H;
• $\left|Pr[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },1}=1]-Pr[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },2}=1]\right|\le {\epsilon }_{\mathrm{enc}}\left(k\right)$, from the IND-CPA security of $\mathsf{Enc}$;
• $\left|Pr[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },2}=1]-Pr[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },3}=1]\right|\le {\epsilon }_{\mathrm{ecdlp}}\left(k\right)$, by the hardness of the ECDLP;
• $\left|Pr[\mathrm{E}\mathrm{x}{p}_{\mathcal{E}}^{{\Pi }^{\prime },3}=1]-\frac{1}{2}\right|$ remains as is, by definition.

By substituting these bounds, we obtain

$${\mathrm{Adv}}_{\mathcal{E}}^{{\Pi }^{\prime },\mathrm{AKE}}\left(k\right)\le {\epsilon }_{\mathrm{hash}}\left(k\right)+{\epsilon }_{\mathrm{enc}}\left(k\right)+{\epsilon }_{\mathrm{ecdlp}}\left(k\right)+\left|Pr[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },3}\left(k\right)=1]-\frac{1}{2}\right|.$$

But by construction of experiment $\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },3}\left(k\right)$, where the session key is replaced with a uniformly random string, it follows that

$$\left|Pr[\mathrm{E}\mathrm{x}{\mathrm{p}}_{\mathcal{E}}^{{\Pi }^{\prime },3}\left(k\right)=1]-\frac{1}{2}\right|=0.$$

Therefore, this concludes as

$${\mathrm{Adv}}_{\mathcal{E}}^{{\Pi }^{\prime },\mathrm{AKE}}\left(k\right)\le {\epsilon }_{\mathrm{hash}}\left(k\right)+{\epsilon }_{\mathrm{enc}}\left(k\right)+{\epsilon }_{\mathrm{ecdlp}}\left(k\right),$$

as claimed. □

Therefore, the existence of a non-negligible advantage ${\mathrm{Adv}}_{\mathcal{E}}^{{\Pi }^{\prime },\mathrm{AKE}}\left(k\right)$ would imply a violation of at least one of the underlying cryptographic assumptions, contradicting their presumed hardness. We conclude that ${\Pi }^{\prime }$ is secure in the sense of authenticated key exchange in the Canetti–Krawczyk model.

Each transition from one security scenarios to the next introduces at most a negligible difference in $\mathcal{E}$’s advantage. Hence, the refined protocol is secure in the CK model, providing mutual authentication and indistinguishability of session keys under adaptive adversarial control, assuming standard cryptographic primitives.

8. Implementation and Performance Evaluation

As part of the implementation considerations, we summarize the execution pipeline of the enhanced GN-AK protocol in the following schematic from Figure 1, highlighting the integration of used techniques.

To evaluate the efficiency of the proposed protocol, we implemented both the original GN-AK scheme and our improved variant using optimized binary field arithmetic over the NIST K-163 Koblitz curve. The implementations were evaluated on two embedded platforms with constrained computational and energy resources:

• ATmega328P: 8-bit AVR microcontroller, 16 MHz clock, compiled with avr-gcc 11.1.0 using size and speed optimizations.
• STM32F411RE: 32-bit ARM Cortex-M4 microcontroller, 100 MHz clock, compiled with ARM-GCC 10.3 and hardware floating-point support disabled.

For each platform, we benchmarked the scalar multiplication operation, which dominates the runtime in both protocol variants. Each data point represents the average of 1000 iterations using fixed-size test vectors, with results ilustrated in

Table 1. Execution Time Comparison (μs).

Platform	Original GN-AK	Improved GN-AK
ATmega328P	8523	6411
STM32F411RE	2181	1653

and

Table 2. Estimated Energy Consumption (mJ).

Platform	Original GN-AK	Improved GN-AK
ATmega328P	34.1	25.6
STM32F411RE	19.6	14.2

.

Memory Usage: Both implementations require under 2 KB of SRAM and less than 12 KB of flash memory.

Side-Channel Considerations: For clarification, constant-time field operations were used where applicable, and no data-dependent branches were included in critical cryptographic routines. However, we do not claim full resistance to side-channel attacks. No formal leakage analysis or power trace collection has been performed; this remains open for future investigation.

These results support the performance claims and demonstrate that integrating double-base chain representations with point halving can significantly reduce computational overhead while maintaining protocol correctness and implementation feasibility on embedded systems.

8.1. Implementation Notes and Challenges

In our experiments, we used a custom ECC module written in C, adapted from the TinyECC codebase. As standard ECC libraries do not natively support point halving in ${\mathbb{F}}_{2^m}$, we implemented it using the inverse of the doubling procedure over binary Koblitz curves.

The point halving procedure implemented in our module is based on operations over binary fields ${\mathbb{F}}_{2^m}$ and follows these main steps:

• Take as input the point $Q=(x_Q,y_Q)$ such that $Q=2P$.
• Compute the slope $\lambda$ as $\lambda =x_P+y_Q/x_Q$.
• Derive the x-coordinate of P as $x_P=\sqrt{x_Q+{\lambda }^2+a}$.
• Compute the y-coordinate as $y_P=x_P·(\lambda +1)$.
• Return the point $P=(x_P,y_P)$.

Implementing square roots and divisions in ${\mathbb{F}}_{2^m}$ over constrained devices posed challenges due to limited memory and instruction sets. We used precomputed lookup tables for square roots and optimized division via shift-and-subtract loops.

On the ATmega328P, we faced register pressure and had to inline some routines to reduce stack usage. On the Cortex-M4, code was optimized for constant-time execution, disabling hardware floating-point units to preserve deterministic timing.

We ensured constant-time traversal of the DBC scalar representation by computing and executing a predetermined sequence of additions and halvings with no conditional branching. While randomized scalar blinding was not included in this version, our method is compatible with such techniques, and future work may explore their integration for increased side-channel resistance.

Although our protocol is identity-based and does not rely on certificate chains, we briefly referenced X.509 and key management schemes to emphasize compatibility with hybrid environments where trust anchors and revocation strategies coexist. A full integration study is outside the scope of this work.

8.2. Implementation Considerations

Deploying the enhanced GN-AK protocol in real-world systems requires attention to implementation strategies, platform compatibility, and cryptographic library support. This section outlines key factors that influence practical deployment.

Point halving is particularly efficient in binary fields (${\mathbb{F}}_{2^m}$), which should be prioritized when implementing the protocol. Recommended curves include:

• NIST B-163, B-233, B-283 (binary fields).
• Koblitz curves, which further optimize arithmetic.

The DBC-based scalar multiplication with point halving is especially advantageous on constrained hardware:

• 8-bit microcontrollers: Reduction in field inversions translates directly to less CPU usage.
• IoT devices: Battery-powered nodes benefit from energy-efficient ECC operations.
• Smart cards: Limited RAM and ROM favor arithmetic simplifications.

Most ECC libraries (e.g., micro-ecc, RELIC, TinyECC) do not yet support point halving natively. For integration, one must

• Extend the scalar multiplication function to parse and apply DBC representation.
• Implement field-specific point halving routines.
• Ensure constant-time execution to resist timing attacks.

Cryptographic software must adhere to side-channel attack mitigation practices:

• Use of constant-time conditional logic for DBC traversal.
• Randomized representation of scalars to prevent pattern leakage.
• Disabling hardware acceleration (e.g., DMA) if it introduces timing side-channels.

By designing DBC routines as modular components, existing protocols using ECC can adopt the optimized scalar multiplication without altering higher-level logic. This facilitates incremental adoption and reuse in TLS, VPN, or key management systems.

Since the GN-AK protocol employs public/private key pairs and identity-bound authentication, it aligns well with existing PKI systems. Integration steps include:

• Binding public keys to X.509 certificates.
• Managing key lifetimes and session expiration securely.
• Supporting revocation and rotation of long-term keys.

8.2.1. Side-Channel Threat Model

In this work, we explicitly address side-channel leakage stemming from timing variations and Simple Power Analysis (SPA). Our implementation mitigates these vectors by enforcing constant-time field operations and avoiding data-dependent branching or memory access patterns during scalar multiplication. However, we do not claim resistance to more advanced side-channel attacks such as differential power analysis (DPA) or electromagnetic analysis. Countermeasures against these would involve techniques like scalar randomization (blinding), noise introduction, or dedicated hardware-level protections, which are outside the scope of the present study. We consider these as important directions for future work.

8.2.2. Architectural Motivation for Combining DBSM and Point Halving in GN-AK

Unlike protocols such as ECDH or ECIES, where scalar multiplication typically serves a single pseudorandom key generation role, the GN-AK protocol tightly integrates scalar computations within its mutual authentication flow. Both participants repeatedly compute pseudorandom scalar multiplications linked to digital signature commitments and verification steps.

Applying DBSM and point halving in this context therefore achieves compounded benefits: it reduces not only the core key agreement computation but also the cryptographic overhead associated with session-specific proofs of possession. This dual efficiency is less pronounced in protocols like ECDH, where pseudorandom public values may be precomputed or reused in optimization frameworks and where point halving would primarily impact the one-time key derivation phase.

By embedding both DBSM and point halving directly into the multi-stage authenticated exchanges of GN-AK, we enable a protocol-level reduction in computational and energy costs that holistically improves handshake performance—especially critical for resource-constrained environments such as medical IoT and embedded authentication systems.

The next section compares the GN-AK enhancement with other contemporary key exchange protocols to highlight relative strengths and trade-offs.

8.3. Comparative Analysis with Other Protocols

This section provides a comparative study between the enhanced GN-AK protocol and several well-known ECC-based authenticated key agreement protocols. We evaluate security robustness, computational efficiency, and suitability for resource-constrained applications.

The following protocols are used as benchmarks:

• HMQV: A hash-based MQV variant was proposed by Krawczyk [33].
• ECKAS-DH1: An ECC-based Diffie–Hellman authenticated key exchange scheme [34].
• NAXOS: A secure key exchange scheme combining long-term and ephemeral secrets [35].
• Original GN-AK: As described in [1].

8.3.1. Security Comparison

All compared protocols aim to provide mutual authentication and key agreement.

Table 3. Security Features Comparison.

Protocol	Auth.	F. Secrecy	KCI-Resist.	K-Confirm
GN-AK (orig.)	Yes	Yes	Partial	Optional
Enhanced GN-AK	Yes	Yes	Yes	Optional
HMQV	Yes	No	Partial	No
ECKAS-DH1	Yes	Yes	No	No
NAXOS	Yes	Yes	Yes	No

summarizes key security features:

The security properties used in Table 3 are defined as follows:

• F. Secrecy—Forward Secrecy: Compromise of long-term keys does not compromise past session keys.
• KCI-Resist.—Key Compromise Impersonation Resistance: The protocol resists impersonation attacks even when a user’s private key is compromised.
• PFS—Perfect Forward Secrecy: session keys remain secure even if long-term keys are later compromised.
• Mutual Auth.—Mutual Authentication: both entities verify each other’s identity during the protocol.

8.3.2. Performance Comparison

Table 4. Performance Comparison.

Protocol	Mult.	Invers.	Add./Half.
GN-AK (orig.)	300+	15	80/0
Enhanced GN-AK	215	7	35/55
HMQV	240+	14	70/0
ECKAS-DH1	280	12	65/0
NAXOS	250	10	50/0

shows estimated operation counts (field operations) for protocols at 160-bit security:

The performance values reported in Table 4 are based on the estimated number of core elliptic curve operations: scalar multiplications (SM), point additions (PA), and point halvings (PH), when applicable. These values were derived from each protocol’s operational structure as described in their respective specifications, with the same cost model. The figures reflect protocol-level efficiency, assuming fixed curve parameters and excluding certificate validation or transport overhead.

8.3.3. Suitability for Constrained Devices

The enhanced GN-AK excels in scenarios where computation cost and energy consumption are critical. Its use of point halving and double-base chains aligns with hardware-accelerated binary fields found in

• Smart cards (e.g., EMV chips)
• Sensor nodes (e.g., Zigbee, Bluetooth LE)
• RFID tags and embedded authentication modules

Unlike HMQV and NAXOS, the enhanced GN-AK supports optional third-message key confirmation, improving resilience in mutual verification. Its modular scalar computation strategy can be adopted in other ECC frameworks with minimal disruption. These comparisons validate that the proposed GN-AK enhancement achieves better trade-offs between security and efficiency compared to related protocols.

9. Discussion and Future Work

This paper proposes improving the GN-AK protocol by using double-base scalar multiplication and point halving over binary elliptic curves. The implementations were performed on an 8-bit AVR and a 32-bit ARM Cortex-M4, and the improvements of the actual timings and energy use were measured to show the concrete benefits to be had by using point halvings instead of point doublings. This further motivates the adoption of efficient scalar multiplication strategies in lightweight protocols. The current method is implemented for binary Koblitz curves (NIST B-163), but in the future it could be implemented on other types of elliptic curves, such as prime field and Edwards curves.

In terms of implementation-level impact, the lack of native support for point halving in existing cryptographic libraries represents a practical limitation. Future efforts will focus on designing modular, portable implementations of point halving routines and integrating them into mainstream ECC libraries to facilitate adoption.

We also plan to investigate the deployment of the enhanced GN-AK protocol on embedded platforms equipped with hardware cryptographic support, such as ARM CryptoCell, Intel SGX, or RISC-V secure cores. These platforms offer promising avenues for reducing computational overhead via micro-architectural acceleration.

From a security perspective, while our implementation employs constant-time routines and avoids data-dependent branching, formal side-channel resistance evaluation remains necessary. Future work will include empirical validation using differential power analysis (DPA) and timing tests, as well as the application of countermeasures such as scalar blinding and randomized DBC traversal.

Another important direction lies in the formal verification of the protocol’s correctness and security guarantees. While this work includes security arguments and model-based reasoning, future versions will incorporate automated validation using formal methods such as BAN logic, ProVerif, and Tamarin to strengthen assurance.

Long-term considerations include the adaptation of DBC principles in the context of post-quantum cryptography. Although ECC is likely to coexist with or be replaced by quantum-resistant primitives, performance optimization remains critical in hybrid deployments. Investigating whether similar acceleration methods can benefit lattice- or isogeny-based schemes is an open research question.

10. Conclusions

In this paper, we presented an improved version of the GN-AK key agreement protocol. The improvement was based on a new scalar multiplication algorithm using double-base chains and point halving in binary fields. The security level is the same as the original GN-AK, but the new protocol requires less computation and, therefore, is more efficient for constrained devices.

The experimental evaluation conducted on an 8-bit AVR and a 32-bit Cortex-M4 platform shows that the improved GN-AK requires less computation than the original protocol because it replaces a point doubling with a point halving. The improvements in scalar multiplication are visible in execution time and energy consumption. However, we can further optimize the new scalar multiplication to support hardware implementations better.

The security of the improved GN-AK relies on the hardness of the elliptic curve discrete logarithm problem (ECDLP), as the original GN-AK protocol does, and the changes do not alter the core cryptographic assumptions. While a complete formal verification and comprehensive side-channel analysis remain outside the scope of this work, the protocol design incorporates constant-time operations and avoids data-dependent branching, aiming to mitigate leakage vectors and enhance implementation-level resilience.

In conclusion, this work is aligned with the current trends in lightweight cryptography, focusing on developing and optimizing cryptographic protocols for constrained devices. The practical applicability of the improved GN-AK protocol for secure key exchange is illustrated for some use cases, including IoT nodes, embedded control units, and mobile devices, highlighting its relevance and potential impact. Future work in this area may include expanding the support for different curves and further optimizing the new scalar multiplication for hardware implementations.