Abstract
Anomaly detection methods for industrial control networks using multivariate time series usually adopt deep learning-based prediction models. However, most of the existing anomaly detection research only focuses on evaluating detection performance and rarely explains why data is marked as abnormal and which physical components have been attacked. Yet, in many scenarios, it is necessary to explain the decision-making process of detection. To address this concern, we propose an interpretable method for an anomaly detection model based on gradient optimization, which can perform batch interpretation of data without affecting model performance. Our method transforms the interpretation of anomalous features into solving an optimization problem in a normal “reference” state. In the selection of important features, we adopt the method of multiplying the absolute gradient by the input to measure the independent effects of different dimensions of data. At the same time, we use KSG mutual information estimation and multivariate cross-correlation to evaluate the relationship and mutual influence between different dimensional data within the same sliding window. By accumulating gradient changes, the interpreter can identify the attacked features. Comparative experiments were conducted on the SWAT and WADI datasets, demonstrating that our method can effectively identify the physical components that have experienced anomalies and their changing trends.
1. Introduction
With the widespread application of artificial intelligence, anomaly detection based on deep learning has become an important means of detecting network attacks in industrial control systems (ICSs). However, deep learning models are typically composed of multiple layers, thousands of neurons, and a large number of parameters, and their complexity makes it difficult for people to intuitively understand how these parameters affect the decision results of the model, leading to the emergence of a “black-box” problem. This issue makes the decision-making process of the model opaque, which in turn affects the credibility and usability of the model [1].
The necessity of introducing interpretability in deep learning has been extensively and deeply discussed in both academia and industry. On the one hand, increasing the interpretability of a model usually accompanies more model complexity, which may not only lead to an increase in computing resources [2] and a decrease in inference speed but also inevitably introduce a certain degree of subjectivity, and may even sacrifice the ultimate performance of the model. These factors must be carefully considered when using interpretable models. On the other hand, the current situation urgently requires the emergence of interpretable methods. With the development of deep learning technology, models are becoming increasingly “black”, and the requirements for the credibility, security, and other aspects of deep learning are also increasing. The enhancement of interpretable performance increases trust in these applications. Most of the existing ICS anomaly detection research focuses on evaluating detection accuracy [3] but rarely explains why data is marked as abnormal and which physical components have been attacked. This ’black-box’ decision-making process makes it difficult to gain the trust of operators. In terms of network security, exceptional interpretability helps users to quickly identify attack points or targets and adopt attacking strategies to prevent attacks in a timely manner, ultimately achieving the goal of reducing attack losses [4].
Most of the anomaly interpretable methods based on deep learning are closely related to the original model. These methods perturb input data and use techniques such as reverse gradient and graph neural networks to interpret anomalies based on changes in the internal parameters of the model. This process can help developers to gain a deeper understanding of the decision-making mechanism of the model, effectively identify and fix potential problems, and improve the accuracy and effectiveness of the detection system [5]. This type of explanation is more suitable for developers to use when debugging anomaly detection models. However, these methods may lead to the exposure of the internal structure of the model, thereby increasing the risk of the model being attacked. Some anomaly interpretation methods are independent of the original model and can achieve interpretation without relying on the structure of the original model, which can help operation and maintenance personnel to understand the decision results and attribution interpretation of anomaly detection and accurately locate potential attacks. This type of interpretability does not make the model more reliable or perform better, but it is an important component in building highly reliable systems [6]. Although these methods are flexible, they are designed for supervised tasks [7], while unsupervised methods are commonly used in anomaly detection tasks in ICSs.
Interpretable methods based on gradient optimization are effective means of explaining decision attribution problems in deep learning models. Their theoretical basis mainly comes from the gradient analysis theory in differential calculus, aiming to transform the explanation of anomalous features into solving an optimization problem in a normal “reference” state. Based on this idea, we propose an interpretable method for anomaly detection models based on gradient optimization. The main contributions include the following three aspects.
(1) We propose an interpretable method based on gradient optimization for anomaly dection. Although its interpreter needs to receive the predicted results of the anomaly detection model, it does not rely on the internal structure or parameters of the original model. This method can interpret anomalies in batches without affecting the performance of anomaly detection.
(2) To address the issue of feature independence assumption failure, when selecting important features, we not only use the method of absolute gradient multiplied by input to measure the independent effects of data with different dimensions but also introduce KSG mutual information estimation and multivariate cross-correlation to evaluate the relationships and mutual influences between different dimensions within the same sliding window. This dual method can dig deeper into hidden important features, thereby improving the accuracy and effectiveness of feature selection.
(3) We identify the main features that cause anomalies based on the cumulative gradient and input variation values. Meanwhile, by analyzing the difference between anomalies and optimized values, we can explain the trend of component changes after being attacked. The experimental results validated the effectiveness of the proposed method.
The structure of this paper is arranged as follows: Section 2 will introduce the relevant work and outline the research on interpretable methods based on gradients, Section 3 will elaborate on the design method of the proposed interpreter, and Section 4 will present the results of the experimental research and data analysis. Finally, Section 5 will summarize the entire text and provide a conclusion.
2. Related Works
In order to improve the interpretability of anomaly detection models, researchers have proposed various gradient-based interpretable methods.
Some scholars proposed interpretable methods based on existing anomaly detection models, which directly obtain gradient information from the model through optimization algorithms. Sundararajan et al. [8] attributed the prediction of deep networks to the problem of their input features and proposed the integral gradient method, which effectively avoids the gradient saturation problem of a single input. The integral gradient and its variants are commonly used in model interpretability techniques. For example, Han et al. [9] believed that the integral gradient (IG) relies on baseline input for feature attribution, and therefore further proposed a novel baseline generation algorithm to improve the performance of anomaly event detection. Sipple et al. [10] demonstrated how integral gradients can attribute anomalies to specific dimensions in the anomalous state vector. Yang et al. [11] believe that IG often integrates noise into its explanatory saliency map, which reduces interpretability. The authors proposed an important directional gradient integration framework, which theoretically proves that the true gradient is orthogonal to the noise direction, so the gradient product along the noise direction has no effect on attribution. Nguyen et al. [12] developed a gradient-based framework to explain detected anomalies. The authors believe that, given a trained VAE and an anomaly data point, when the value of a certain feature changes slightly and the reconstruction error changes significantly, it can be considered that the feature is significantly abnormal at the current value because it will force the VAE model to better fit itself through the optimization process. Jiang et al. [13] trained an autoencoder using a loss function containing interpretable perceptual error terms, processed specific features based on the difference between the test image and the average of the training image, and generated an attention map for detecting anomalies. It can be interpreted using GradCAM and also used as part of the training process to improve neural network models. Yang et al. [14] proposed a new graphic anomaly detection method that utilizes interpretability to improve model performance. This method is only trained on normal graph data. Therefore, the trained graph neural network only captures features of normal graphs. When examining the gradient attention map of test data, abnormal samples showed significantly different scores, effectively explaining the decision-making process of the GRAM method.
The advantage of such interpretable methods is that they are simple and easy to implement, and can quickly realize the interpretable method of the model without the need to modify the anomaly detection model. The disadvantage is that, in the process of providing explanations to managers, the internal mechanisms of the model may be inadvertently exposed, thereby increasing the risk of the model being attacked.
Some scholars have proposed interpretable models that use model-independent techniques, such as Kauffmann et al. [15], who proposed a general framework based on the new concept of “neuroticism” and combined it with deep Taylor decomposition to explain the prediction of a large class of kernel one-class SVMs. Han et al. [16] proposed a general unsupervised deep neural network interpretation method (DeepAID). The author provided interpretation methods for tabular data, univariate time-series data, and graph data based on different data types. In addition, they proposed a model-based extended still to improve security systems and facilitate interaction between humans and deep learning models. Based on the DeepAID method, Liu Yuxiao et al. [17] proposed an interpretable anomaly flow detection model based on a sparse autoencoder. The experimental results on the CICIDS2017 dataset and CIRA-CIC Do HBrw-2020 dataset demonstrated that their method can provide interpretability for the model. But, these studies did not consider the correlation between features and only explained anomalies based on the independent effects of features.
3. Interpretable Method Design
3.1. Scheme Framework
In this chapter, we propose an interpretable method based on gradient optimization to address the problem of locating anomalies in anomaly detection in ICSs. The overall framework of this method is shown in Figure 1. Although the explanation module needs to receive the predicted results of the anomaly detection model, it does not rely on the internal structure or parameters of the original model, so there is no need to make any modifications to the original detection model. On the premise of not affecting the performance of anomaly detection, this module only starts when an attack behavior is detected, to determine which input features have a significant impact on the final decision when under attack, thereby helping managers to identify the location of the anomaly occurrence. Inspired by DeepAID [16], we have also reinterpreted the explanation of unsupervised deep anomaly detection models as finding the reasons for abnormal data deviating from normal data. Specifically, the interpretation of anomalies after being attacked is transformed into solving a normal “reference” optimization problem, while the interpretation of anomalies is obtained by the accumulation of gradients and values and the difference between normal “reference values” and anomalies. Initially, DeepAID only addressed the interpretability issue of univariate discrete time series. We further extended the interpreter to handle the problem of multivariate time series. In the case of multivariate time series, the complexity of the optimization problem will significantly increase, which requires us to not only consider the independent effects of different variables but also to simultaneously consider the relationships and mutual influences between variables.
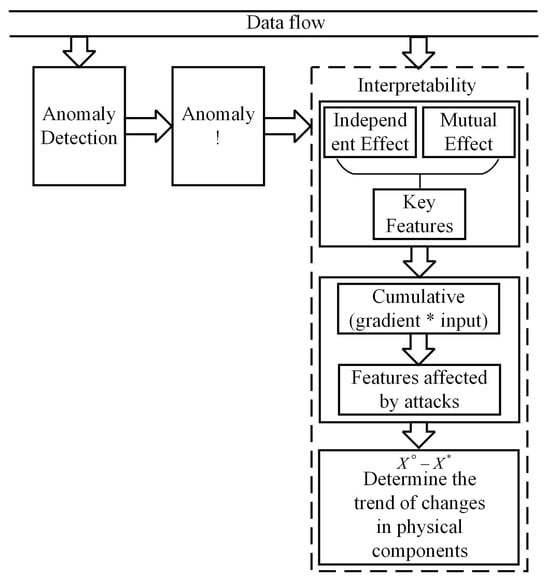
Figure 1.
Overall framework of the proposed interpretable method.
3.2. Detailed Design
Suppose the data we use includes actual abnormal data , consisting of historical sequence of data and a predicted data point . The optimized data is , where and are the length of the historical sequence and the length of the future time series, respectively. represents the anomaly of the lth time step, and represents the optimized “normal value” of the lth time step.
(1) Design of optimization function
When abnormal behavior is detected, the system activates the interpreter and iteratively optimizes the algorithm to find a normal reference value . This also means that, after is trained with a deep learning anomaly detection model, its detection result is judged as a normal value, which satisfies the normal decision boundary of the detection model, as expressed in inequality (1):
where represents the error function, represents the predicted value of the deep learning anomaly detection model, and is the threshold.
However, when searching for the normal value , the value of does not need to be infinitely minimized as long as the predicted value of anomaly detection can reach the decision boundary of anomaly detection. Therefore, can be constrained within the decision boundary range by using the RELU function. To ensure that is on the normal data side of the decision boundary, a small value can be subtracted from , represented by . Meanwhile, we hope that the optimized normal data can be as similar as possible to the predicted data. Therefore, we use the original anomaly detection prediction model to predict abnormal data, calculate the predicted value x, and introduce the Euclidean distance between normal data and predicted data to the optimization function.
The final optimization function is shown in Equation (2). For the convenience of subsequent description, we will abbreviate the objective function as .
(2) Selection of important features
In existing interpretable methods based on gradient optimization, it is often assumed that features are independent of each other. However, in ICS, this assumption is often difficult to establish. The physical component data of industrial control terminals usually includes two categories: data from sensors and data from actuators. A sensor is a device that can detect and respond to physical or chemical changes in the environment, typically used to measure various parameters such as temperature, pressure, flow rate, liquid level, etc. The actuator usually receives signals from the control system (such as PLC and microcontroller) and executes corresponding actions based on these signals.
When attacking these physical components, a significant phenomenon will occur; i.e., the trend of the temporal waveform changes is significantly different from the normal mode. For example, Figure 2 shows the timing waveform diagram of the relevant components during the attack on the liquid level transmitter LIT-101 in the SWAT dataset. The attack caused the water tank to overflow by shutting down pump P-101 and manipulating the value of LIT-101 to remain at 700 millimeters. In the red area, the curve of LIT-101 deviates significantly from the normal state. Another characteristic is that, even if only attacking LIT-101, the consequences of the attack often extend beyond just one physical component. From Figure 2, it can be seen that downstream sensors (such as FIT-201) and actuators (such as MV-201) may be affected by attacks. Therefore, there is a certain correlation between the data changes in these components. These phenomena are not only present in the SWAT dataset but are also very common in other ICS datasets.
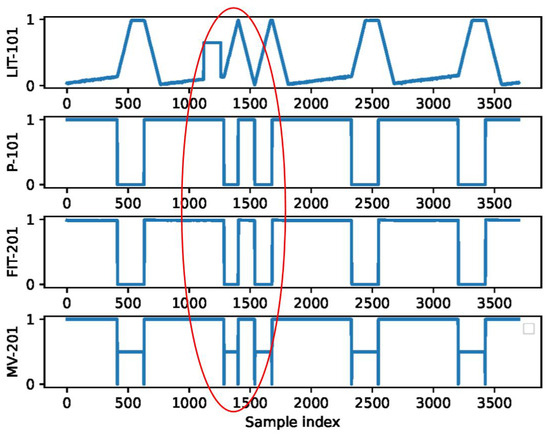
Figure 2.
Time sequence diagram of implementing attacks on LIT101.
Therefore, in the selection of important features, how to balance the independent and interactive effects of features is the key to accurately explaining the location of anomalies.
When assessing the importance of features, we consider two aspects. On the one hand, it is the independent function of a single feature. In multivariate functions, gradients contain the partial derivatives of all independent variables, describing how the function changes with the variation in each independent variable. Introducing eigenvalues based on gradients can measure the contribution of features to model decision-making more accurately. Meanwhile, we only focus on determining the importance of features and do not pay attention to specific directions of influence. Therefore, when quantifying independent effects, Equation (3) is used for calculation. In the t-th iteration, the larger the value of the j-th dimensional feature, the more sensitive the model is to changes in that feature and the higher its importance. Finally, use Equation (4) to calculate the index of the values with the greatest impact in the independent action.
where represents the data of the j-th dimensional feature in the t-th iteration.
On the other hand, it is also necessary to consider the interactions that are affected by the collateral effects after the attack. To comprehensively evaluate the cascading effects caused by attack behavior, we use KSG mutual information estimation [18] combined with multivariate cross-correlation analysis to quantitatively evaluate the interactive effects of multidimensional temporal data within the same sliding window.
KSG mutual information estimation is a non-parametric method based on k-nearest neighbors, which can maintain stable estimation performance in small-sample scenarios and is particularly suitable for revealing nonlinear dependencies between different dimensions of time series. The core calculation formula is shown in Equation (5):
where K is the number of neighbors, and , respectively, represent the number of neighborhood points in the and subspaces, whose distance from the lth sample is less than the k-th nearest neighbor distance in the joint space, N represents the number of samples, and is the digamma function, defined as Equation (6):
Multivariate cross-correlation analysis can capture time delay dependencies by calculating the linear correlation between two time series at different lag orders. The cross-correlation of time delay for time series and is shown in Equation (7):
where , and is the maximum lag order.
We use the maximum absolute value among all time delays as the final correlation, as shown in Equation (8):
Subsequently, we calculate the maximum absolute correlation between all important features of each sample, form a cross-correlation matrix , and then merge the mutual information and cross-correlation matrix with weighted fusion, as shown in Equation (9):
where and are the normalized matrices of and , respectively, and w is the weight.
Then, we sequentially extract the index values , query the upper triangular of the correlation coefficient matrix, select the index values of the maximum correlation dimension that satisfy , and insert them into the corresponding position next to the current position . We take a total of important feature indices . Normally, .
Finally, when searching for the normal reference value , not all normal values are acceptable. We hope to minimize the difference between it and the abnormal input value . In each iteration, features will be filtered based on their importance. For the selected important features, retain their optimized values; for unimportant features, they are replaced with the previous optimized values. Update the optimized value of based on the value of index , as shown in Equation (10).
(3) Feature set affected by attacks
Subsequently, we accumulate the values of in each iteration by feature, and select the values with the greatest impact as the main features affected by the attack, as shown in Equations (11) and (12).
Finally, we calculate the difference between the abnormal value and the “normal value” after iterative optimization, and determine the trend of changes in the physical component after being attacked based on the sign of the difference.
3.3. Iteration Process for the Optimization Algorithm
The iterative training process of the proposed interpretable algorithm is shown in Algorithm 1:
| Algorithm 1: The Proposed Interpretable Algorithm |
Input: Data (containing one or more abnormal input samples ), maximum iteration times Output: Interpretation result, i.e., trend of feature changes affected by attacks
|
4. Experiments
4.1. Parameter Settings
We used SWAT and WADI datasets for testing. In the model interpretation stage, we directly use the complete dataset containing anomalies as the test set for evaluation, where the sample sizes of SWAT and WADI datasets are 449,919 and 172,801, respectively.
The data preprocessing method is the same as in our previous work [19]. The anomaly detection model to be explained adopts the sub-models of Group 1 trained on the SWAT dataset and Group 2 trained on the WADI dataset in [19]. The interpreter uses the Adam optimizer.
We use the random grid search method, combined with three indicators: label flipping rate, successfully identified attack feature rate, and explain success rate, to determine the optimal combination of hyperparameters.
(1) Label Flipping Rate () [16]: It represents the rate at which abnormal data becomes normal after optimization iterations. The higher the value, the more accurate it will be to identify the important features that cause anomalies. The calculation formula is shown in Equation (13).
(2) Successfully Identified Attack Feature Rate (): It represents the ratio of the number of successfully identified attack features to the number of anomalous samples that need to be explained. The higher the value, the greater the probability of locating the anomalies. The calculation formula is shown in Equation (14).
(3) Explain Successful Rate (): It represents the ratio of the number of samples that can accurately predict abnormal trends to the number of abnormal samples that need to be explained. The higher the proportion, the better the interpretation effect. The calculation formula is shown in Equation (15).
In this section, we take the SWAT dataset as an example to illustrate the method of parameter selection. Using the random grid search method, we preliminarily determine that the learning rate is 0.1, is 0.7, the maximum number of iterations is 100, and is 0.005, = 0.001, , , and .
To determine the values of , , and , we conduct the following experiments. When , the values of are 5, 7, and 9, respectively, As the value of gradually decreases to 40%, 30%, 20%, and 10% of the total dimension, respectively, the changes in and are shown in Figure 3a,b. As can be seen from Figure 3a, when the value of is set to be 7, the value of is slightly better than the cases of and . As can be seen from Figure 3b, the value of has little effect on the value of . As the feature dimension is preserved more, the value of becomes slightly higher. At the same time, it can also be observed that, when the value of is 20–40% of the total dimension, the indicator value changes little, and the excessive dimension of may cause greater difficulties for management personnel in identifying attack points. Therefore, after comprehensive consideration, it is recommended to keep the dimension of at around 30% of the total dimension, that is, . As a result, the values of and can be initially set to 7 and 4, respectively. At this time, the and values are 96.73% and 65.05%, respectively. This result is considered a more appropriate choice.
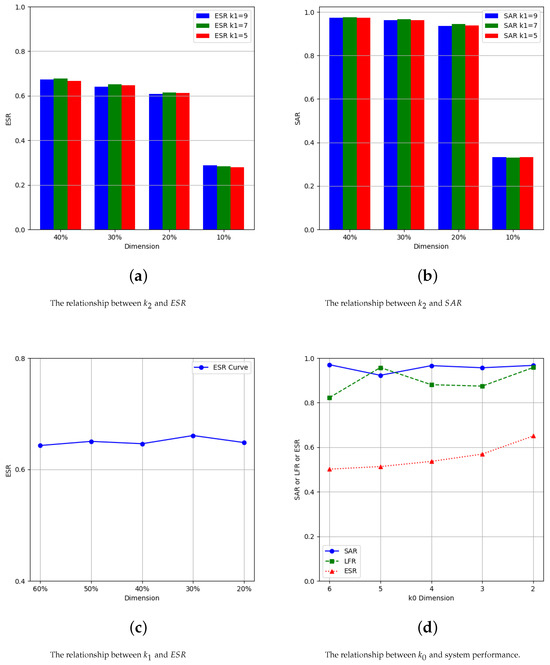
Figure 3.
Relationships between , , and and system performance, respectively.
When is set to 4, the value of decreases to 60%, 50%, 40%, 30%, and 20% of the total dimension, respectively. The relationship between and is shown in Figure 3c. When the value of decreases to 30% of the total dimension, the value of reaches its highest point. is just an intermediate variable, and retaining too few of its dimensions may exclude important features. Therefore, we choose the sub-optimal value of , which is to reduce the value of to 50% of the total dimensions ().
When the value of is between 2 and 6, it can be seen from Figure 3d that, when , the values of , , and are optimal.
The optimal values of the main parameters in SWAT and WADI are shown in Table 1.

Table 1.
Optimal parameters.
From Table 2, it can be seen that the four features most likely to be affected by the attack in the interpretation of sample 1892 are P-203, FIT-201, LIT-101, and MV-101. The actual attack point is MV-101, which was originally in a closed state (state 1) and later changed to an open state (state 2). It can be seen that the value of MV-101 has increased under the attack. This is consistent with the predicted situation. For sample 280322, the actual attack points LIT-101, P-101, and MV-201 show decreasing, increasing, and increasing trends, respectively. Our method predicts that both P-101 and MV-201 have increased in size, which is consistent with the actual situation. LIT-101 did not appear in the explanation table, possibly due to the pumping of water from the first tank to the second stage after P-101 was attacked, resulting in insignificant changes in the water level detected by LIT-101.

Table 2.
Trends of component changes after being attacked.
4.2. Algorithm Performance Comparisons
(1) Baseline methods
In this section, in order to verify the effectiveness of the proposed method, we compared the constructed scheme with several baseline methods. The baseline methods include
Baseline 1: DeepAID [16] is a general unsupervised deep neural network interpretation method. The author provides interpretation methods for tabular data, univariate time-series data, and graph-type data based on different data types. In addition, they proposed a model-based extended still to improve safety systems and facilitate interaction between humans and deep learning models. This method only considers the independent effects of important features when selecting them.
Baseline 2: A method based on attention mechanism, replacing the method of calculating the correlation matrix in this article with an attention mechanism to extract correlations between different dimensions.
Baseline 3: A scheme that uses gradient multiplication input method to select important features. This method assumes that each feature is independent and only considers the independent effects of the features without considering their interrelationships.
Baseline 4: A method based on Pearson correlation coefficient, replacing the method of calculating the correlation matrix in this article with the Pearson correlation coefficient method to extract linear correlations between different dimensions.
SHAP [20]: SHAP is a model interpretation method based on Shapley values in game theory, aimed at fairly allocating the contribution of each feature to model predictions. It provides a consistent and interpretable measure of feature importance by calculating the marginal contributions of all possible feature combinations. SHAP is suitable for various machine learning models and can generate global and local interpretations to help understand the decision-making mechanism of the model.
LIME [21]: LIME is a local model-independent interpretable method that can faithfully interpret the prediction results of any classifier or regressor through local interpretable model approximation and generate easily understandable explanations for individual predictions.
(2) Comparisons
In order to compare the performance of different algorithms, we set experimental conditions such as data processing, models to be explained, and batch interpretation of data to be the same.
From the experimental results in Figure 4a, it can be seen that, when the value of gradually decreases to 40%, 30%, 20%, and 10% of the total dimension, the method proposed in this paper has significant advantages in SAR metrics. Specifically, Figure 4a shows that the SAR value of baseline 1 is significantly lower than other methods, mainly due to its focus on only multiplying the gradient by the positive larger value of the input while ignoring the important influence of negative features. In fact, regardless of the sign of the product of gradients and eigenvalues, as long as their absolute values are large, it indicates that the feature plays an important role in model decision-making. Figure 4b further indicates that the performance of baseline 1 and baseline 3 is poor as these two methods only consider the independent characteristics of features during feature selection and fail to effectively capture the correlation between features, resulting in the omission of some key features. In contrast, the method proposed in this article achieves a more comprehensive feature selection by comprehensively considering the importance and correlation of features, thus successfully identifying attack features.
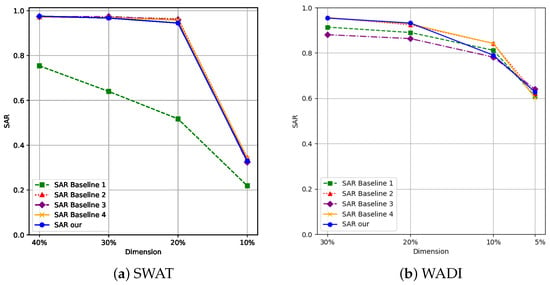
Figure 4.
Comparison of s obtained by different algorithms.
From the experimental results in Figure 5a, it can be seen that, when the value of gradually decreases to 60%-20% of the total dimension, our method overlaps with the baseline 2 and baseline 4 curves and is significantly better than the other two methods in terms of label reversal rate indicators. This result indicates that, in the optimization process of abnormal data, methods that simultaneously consider the interaction between features can more effectively convert abnormal data into normal data, while methods that rely solely on feature independence perform poorly. From Figure 5b, it can be observed that, when the value of decreases to 20% of the total dimension, both our method and the Pearson correlation coefficient method achieve optimal performance. In other dimensions, the index based on the Pearson correlation coefficient method is better. This result indicates that, in the scenario of being attacked, the interrelationships between important features exhibit stronger linear characteristics.
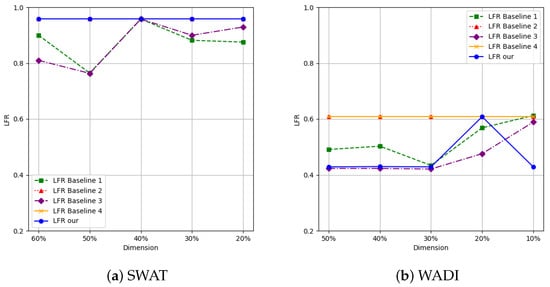
Figure 5.
Comparison of s obtained by different algorithms.
As shown in Figure 6, this method exhibits certain advantages in indicators on the SWAT dataset and is slightly lower than the Pearson correlation coefficient method on the WADI dataset. This result indicates that the method proposed in this paper has good stability in explaining the trend prediction of attack points, especially demonstrating better explanatory power on the SWAT dataset. The performance differences on different datasets may stem from the distribution characteristics of the data, but, overall, this method has certain advantages in specific scenarios while maintaining stability across datasets.
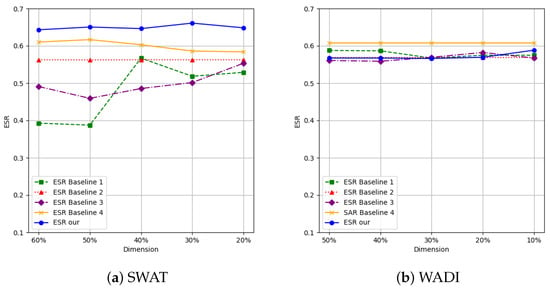
Figure 6.
Comparison of s obtained by different algorithms.
From Table 3 and Table 4, it can be seen that the method proposed in this paper exhibits certain advantages in key evaluation indicators: in Table 3, it simultaneously achieves the optimal values of and , while, in Table 4, it performs the best on . However, LIME only focuses on local areas and may not reflect global behavior or capture the global trend of important features. Although SHAP has global explanatory power, its trend prediction relies on difficult-to-obtain basic data. Therefore, neither of these methods can calculate and indicators. Specifically, the performance of SHAP on the WADI dataset is relatively low, possibly due to limited computer memory and a small number of background data samples, which can lead to lower performance of SHAP on the WADI dataset. Therefore, in situations where memory is limited, our method also has certain advantages.

Table 3.
Performance comparison between our method and baseline methods on SWAT dataset.

Table 4.
Performance comparison between our method and baseline methods on WADI dataset.
5. Summary
In this paper, we propose a gradient-based interpretable method for anomaly detection. When selecting important features, we not only consider the independent effects of different dimensions of data but also extract the mutual influence of different dimensions in the same sliding window, thereby further reducing the number of important features. We identify the main features that cause anomalies by accumulating gradients and input changes. The experiments have been conducted on public datasets, which can effectively explain the changing trend of attack points affected by attacks without affecting the performance of the original anomaly detection system.
Nevertheless, there is still room for improvement in our work. Since the model we explained is based on prediction, additional algorithms need to be introduced to preliminarily determine the trend of the time series if the original interpretable model lacks predictive function.
Author Contributions
Conceptualization, S.T. and Y.D.; methodology, H.W.; software, S.T.; validation, S.T.; formal analysis, Y.D.; investigation, H.W.; resources, H.W.; data curation, S.T.; writing—original draft preparation, S.T.; writing—review and editing, S.T.; visualization, S.T.; supervision, Y.D.; project administration, Y.D.; funding acquisition, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This article is supported in part by the National Key R&D Program of China under project 2023YFB3107301 and the Guangxi Key Laboratory of Digital Infrastructure under project GXDIOP2023006.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The datasets generated and/or analyzed during the current study are available in the (SWAT and WADI) repository, https://itrust.sutd.edu.sg/itrust-labs_datasets/dataset_info/ (accessed on 21 February 2025).
Acknowledgments
During the preparation of this manuscript/study, the authors used the SWAT and WADI datasets for the purposes of the experiments. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hassija, V.; Chamola, V.; Mahapatra, A.; Singal, A.; Goel, D.; Huang, K.; Scardapane, S.; Spinelli, I.; Mahmud, M.; Hussain, A. Interpreting black-box models: A review on explainable artificial intelligence. Cogn. Comput. 2024, 16, 45–74. [Google Scholar] [CrossRef]
- Yu, A.; Yang, Y.B. Learning to explain: A gradient-based attribution method for interpreting super-resolution networks. In Proceedings of the ICASSP 2023-2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greek, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Li, Z.; Zhu, Y.; Van Leeuwen, M. A survey on explainable anomaly detection. Acm Trans. Knowl. Discov. Data 2023, 18, 1–54. [Google Scholar] [CrossRef]
- Xu, L.; Wang, B.; Zhao, D.; Wu, X. DAN: Neural network based on dual attention for anomaly detection in ICS. Expert Syst. Appl. 2025, 263, 125766. [Google Scholar] [CrossRef]
- Moustafa, N.; Koroniotis, N.; Keshk, M.; Zomaya, A.Y.; Tari, Z. Explainable intrusion detection for cyber defences in the internet of things: Opportunities and solutions. IEEE Commun. Surv. Tutor. 2023, 25, 1775–1807. [Google Scholar] [CrossRef]
- Zhang, Y.; Tiňo, P.; Leonardis, A.; Tang, K. A survey on neural network interpretability. IEEE Trans. Emerg. Top. Comput. Intell. 2021, 5, 726–742. [Google Scholar] [CrossRef]
- Carletti, M.; Masiero, C.; Beghi, A.; Susto, G.A. Explainable machine learning in industry 4.0: Evaluating feature importance in anomaly detection to enable root cause analysis. In Proceedings of the 2019 IEEE international conference on systems, man and cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 21–26. [Google Scholar]
- Sundararajan, M.; Taly, A.; Yan, Q. Axiomatic attribution for deep networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6 August 2017; pp. 3319–3328. [Google Scholar]
- Han, X.; Cheng, H.; Xu, D.; Yuan, S. InterpretableSAD: Interpretable Anomaly Detection in Sequential Log Data, Sydney. In Proceedings of the 2021 IEEE International Conference on Big Data, Chengdu, China, 24–26 April 2021; pp. 1183–1192. [Google Scholar]
- Sipple, J. Interpretable, multidimensional, multimodal anomaly detection with negative sampling for detection of device failure. In Proceedings of the International Conference on Machine Learning. International Conference on Machine Learning (PMLR), San Francisco, CA, USA, 7 February 2020; pp. 9016–9025. [Google Scholar]
- Yang, R.; Wang, B.; Bilgic, M. IDGI: A framework to eliminate explanation noise from integrated gradients. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18 June 2023; pp. 23725–23734. [Google Scholar]
- Nguyen, Q.P.; Lim, K.W.; Divakaran, D.M.; Low, K.H.; Chan, M.C. Gee: A gradient-based explainable variational autoencoder for network anomaly detection. In Proceedings of the 2019 IEEE Conference on Communications and Network Security (CNS), Washington, DC, USA, 3–5 June 2019; pp. 91–99. [Google Scholar]
- Jiang, R.Z.; Xue, Y.; Zou, D. Interpretability-aware industrial anomaly detection using autoencoders. IEEE Access 2023, 11, 60490–60500. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, P.; He, X.; Zou, D. GRAM: An interpretable approach for graph anomaly detection using gradient attention maps. Neural Netw. 2024, 178, 106463. [Google Scholar] [CrossRef] [PubMed]
- Kauffmann, J.; Müller, K.R.; Montavon, G. Towards explaining anomalies: A deep Taylor decomposition of one-class models. Pattern Recognit. 2020, 101, 107198. [Google Scholar] [CrossRef]
- Han, D.; Wang, Z.; Chen, W.; Zhong, Y.; Wang, S.; Zhang, H.; Yang, J.; Shi, X.; Yin, X. Deepaid: Interpreting and improving deep learning-based anomaly detection in security applications. In Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security, New York, NY, USA, 15–19 November 2011; pp. 3197–3217. [Google Scholar]
- Liu, Y.; Chen, W.; Zhang, T.; Wu, L. Explainable anomaly traffic detection based on sparse autoencoders. Netinfo Secur. 2023, 23, 74–85. [Google Scholar]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. Stat. Nonlinear Soft Matter Phys. 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- Tang, S.; Ding, Y.; Wang, H. Industrial Control Anomaly Detection Based on Distributed Linear Deep Learning. Comput. Mater. Contin. 2025, 82, 1. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should i trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).