Quantitative Evaluation Method for the Severity of Surface Fuzz Defects in Carbon Fiber Prepreg

Featured Application

The proposed method achieves automated and standardized assessment of the severity of fuzzy defects in carbon fiber prepreg, significantly improving detection efficiency and reducing human subjectivity in quality control of carbon fiber prepreg production.

Abstract

Fuzz defects are prevalent surface imperfections in carbon fiber-reinforced polymer (CFRP) prepregs. Current manual inspection methods or conventional neural network-based approaches face significant limitations in achieving standardized and accurate severity assessment of such defects. In this article, a methodology comprising three key technical innovations is proposed: First, an adaptive thresholding algorithm is implemented, utilizing local average grayscale values to accurately identify fuzz defect pixels. Second, a grayscale histogram analysis is performed on the identified defect regions to quantify severity levels, effectively mitigating the influence of substrate material variations and illumination conditions on assessment accuracy. Third, a quantitative formula is defined based on the detection boxes drawn by the neural network object detection model and the effective area of defects to evaluate the severity of fuzz defects. Experimental validation shows 90% consistency with practical manual assessment in defect severity ranking tasks, proving its industrial applicability.

1. Introduction

Carbon fiber prepreg is a pre-impregnated sheet material fabricated by impregnating a polymer matrix into reinforcing fibers, serving as an essential intermediate for composite materials [1]. As a critical substrate for high-performance composites, defects in the prepreg—often introduced during the production process—can significantly lead to the unreliability of the final product [2]. These defects are usually divided into six categories: fuzz, wrinkles, poor glue, seam separation, foreign objects, and resin-rich areas. They have a substantial adverse effect on the mechanical properties, interfacial bonding, and long-term durability of composite structures. Among these, fuzz defects exhibit considerable morphological variability in the prepreg. Their colors are influenced by different material backgrounds and lighting conditions. Their shapes are affected by the distribution of carbon fibers, manifesting as clustered, strip-shaped, or dispersed patterns. Although deep learning techniques have shown remarkable progress in industrial defect detection, they still face notable technical challenges in accurately evaluating the severity of fuzz defects in carbon fiber prepreg. Traditional machine vision systems are either limited to defect type recognition [3] or lack the ability to grade and assess the severity of defects, which these are two crucial needs for refined quality inspection in industrial production. Consequently, the urgent need for quantitative severity metrics of fuzz defects in prepreg manufacturing has prompted the development of evaluation methods to classify surface imperfection criteria and enable precise inspection systems.

Surface defect detection based on image processing typically encompasses three categories: traditional image processing algorithms, machine learning-based methods, and deep learning approaches [4]. Faced with the demand for defect detection in carbon fiber prepreg, researchers have proposed diverse strategies to address the challenges of defect identification. For instance, Li et al. [5] developed a vision-based automatic recognition system that leverages an artistic conception drawing revert algorithm, exploiting repeated surface pattern features for defect identification, matching, and classification. Similarly, Liu et al. [6] introduced a structural-constrained low-rank decomposition method for fabric defect detection, which constructs a fused image by extracting energy features from both the original and energy images to enhance defect visibility. Houssein [7] proposed a multi-level threshold image segmentation method based on the Black Widow Optimization algorithm, which effectively reduces computational costs by using Otsu or Kapur as the objective function. Versaci et al. [8] proposed a new edge detection method based on fuzzy divergence and fuzzy entropy minimization, and introduced an adaptive S-shaped fuzzy membership function and a new fuzzy degree quantization index, effectively improving the edge detection performance of grayscale images under fuzzy conditions. Shi et al. [9] further combined low-rank decomposition with a structured graph algorithm, segmenting images into defect and defect-free blocks through local feature analysis while incorporating an adaptive threshold mechanism based on cycle counts during block merging.

Neural network-based deep learning models have also been applied to defect detection [10]. Lin et al. [11] introduced the Swin Transformer module into the YOLOv5 framework, significantly improving the detection of small-scale defects on fabric surfaces. Yuan et al. [12] proposed an improved YOLOv5 model, YOLO-HMC, which combines modules such as HorNet, MCBAM, and CARAFE to effectively improve the detection accuracy and efficiency of small defects on PCB surfaces. Building on this, Su et al. [13] optimized the YOLOv8 architecture by introducing Deformable Large Kernel Attention and Global Attention mechanisms, achieving substantial accuracy gains for prepreg surface defect detection. These studies demonstrate the evolving focus from basic defect recognition to more sophisticated feature extraction and model optimization.

Quantification of defects in images typically involves critical steps such as threshold segmentation, histogram analysis, and structural optimization. Zhu et al. [14] proposed an adaptive threshold method based on Adaptive cuckoo search optimization, coupled with genetic algorithms to determine optimal Gabor filter parameters for fabric defect extraction. Palletmulla et al. [15] systematically analyzed how grayscale quantization and window size affect the performance of grayscale co-occurrence matrix features in fabric defect detection. Meanwhile, Wiskin et al. [16] applied threshold segmentation in medical imaging to quantify breast density for cancer risk assessment, while Sun [17] developed a color space-based framework for the quantitative evaluation of flame stability. Wang et al. [18] proposed an acne grading method and severity assessment index based on lesion classification, and constructed a lightweight model called Acne RegNet, which achieved high-precision acne lesion recognition and severity assessment close to the level of dermatologists. Rahman et al. [19] developed an automatic acquisition system and image processing algorithm for rice leaf images, which achieved estimation of leaf infection area percentage based on pixel statistics. These works underscore the importance of accurate quantification for enhancing detection system practicality, though they also reveal inherent limitations in image-based severity assessment due to variations in background-target contrast and lighting conditions.

To address these challenges, researchers have extensively studied image-enhancement techniques [20]. Gray-level histogram equalization has emerged as a pivotal method for improving image quality and analysis reliability. Zhu et al. [21] proposed a threshold segmentation algorithm based on the statistical curve difference method to solve the problem of multi-target image segmentation with a small target area and grayscale close to the background. Uzun et al. [22] optimized adaptive histogram equalization through real-coded genetic algorithms and war strategy optimization, effectively enhancing image clarity. Fan [23] proposed a constrained histogram equalization approach with adjustable contrast parameters to overcome shortcomings in traditional methods. Pang et al. [24] further developed a variable contrast and saturation enhancement model using contrast-limited histogram equalization for local contrast correction. In low-light environments, Oztur et al. [25] introduced a dual-approach enhancement method combining histogram equalization with adaptive gamma correction in HSI color space, effectively resolving brightness inhomogeneity issues. Lv et al. [26] proposed an adaptive high grayscale image enhancement algorithm based on logarithmic mapping and simulated exposure, which effectively improves the visual quality and contrast of high grayscale low contrast images. These advancements in image preprocessing highlight the necessity of robust enhancement strategies to enable accurate detection and evaluation in image detection.

This study proposes a quantitative evaluation metric to assess the severity of surface fuzz defects in carbon fiber prepreg. Most deep learning-based object detectors output rectangular bounding boxes that only indicate the approximate location of defects. These bounding boxes do not provide information about the shape or severity of the defect. To address this limitation, the proposed method incorporates traditional image processing techniques, including adaptive thresholding and histogram normalization, to extract the actual defect region and suppress the background within the detection box. The contributions of this study can be summarized as follows:

• Select pixels of fuzz defects from the detection boxes bounded by the deep learning models;
• Propose a standard for representing the severity of defects per unit area through grayscale histograms of defective pixels and background pixels;
• Calculate the effective area of fuzz defects;
• Obtain an evaluation score that reflects the severity of the fuzz defects.

2. Materials and Methods

2.1. Selection of Defective Pixels

The first step in the proposed method involves converting the color image into a grayscale image, followed by the selection of defective pixels based on the grayscale representation. Due to the inherently uneven surface color distribution in carbon fiber prepreg, global grayscale thresholding proves insufficient for effectively distinguishing defects from the background while suppressing noise and illumination variations. To address this challenge, a localized thresholding strategy is adopted, taking into account the characteristics of the prepreg background—specifically, its irregular horizontal variations and relatively subtle vertical changes. In this approach, the average grayscale value of a local region is utilized as the threshold for segmentation, thereby improving the robustness and accuracy of defect pixel identification under varying background conditions.

To determine whether a given pixel contains a fuzz defect, a local grayscale analysis is performed. Specifically, the average grayscale value of a $(2\times \mathrm{p}+1)\times (2\times \mathrm{p}+1)$ neighborhood centered at the target pixel is calculated. This process is equivalent to applying a mean filter using a square convolution kernel of size $(2\times \mathrm{p}+1)\times (2\times \mathrm{p}+1)$, which helps suppress local noise and smooth intensity variations for more reliable defect detection. The mathematical formulation for the mean grayscale value is given by the following:

$$\mathrm{i}\mathrm{m}{\mathrm{g}}_{\mathrm{mean}}\left(\mathrm{x},\mathrm{y}\right)={\displaystyle \frac{1}{{\left(2\times \mathrm{p}+1\right)}^2}}{\displaystyle \sum }_{\mathrm{i}=\mathrm{x}-\mathrm{p}}^{\mathrm{x}+\mathrm{p}}{\displaystyle \sum }_{\mathrm{j}=\mathrm{y}-\mathrm{p}}^{\mathrm{y}+\mathrm{p}}\mathrm{i}\mathrm{m}\mathrm{g}\left(\mathrm{i},\mathrm{j}\right)$$

(1)

In Equation (1), $\mathrm{m}\times \mathrm{n}$ represents the dimension of the input grayscale image, where m and n represent the number of rows and columns, respectively. The img_mean is generated from the original image by applying a mean filter with convolution kernels of size $(2\times \mathrm{p}+1)\times (2\times \mathrm{p}+1)$, thereby achieving local intensity smoothing and background balance. Average the pixel grayscale values along the row direction of the image to generate an $\mathrm{a}1\times \mathrm{n}$ vector. The method is to repeatedly fill the image and calculate the average grayscale of $\mathrm{m}\times (2\times \mathrm{p}+1)$ pixels centered on the pixel to obtain an $\mathrm{a}1\times \mathrm{n}$ sequence, as follows:

$$\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{y}1\left(\mathrm{y}\right)={\displaystyle \frac{1}{\left(2*\mathrm{p}+1\right)*\mathrm{m}}}{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{m}}{\displaystyle \sum }_{\mathrm{j}=\mathrm{y}-\mathrm{p}}^{\mathrm{y}+\mathrm{p}}\mathrm{i}\mathrm{m}\mathrm{g}\left(\mathrm{i},\mathrm{j}\right)$$

(2)

Here, the i-th element in the summation corresponds to the i-th row, and j spans the $(2\times \mathrm{p}+1)$ pixel window centered at column y. This operation provides a column-wise reference of the average grayscale value, which is used for subsequent thresholding. Based on the results of Equations (1) and (2), a binary mask is constructed to identify the fuzz defect regions. The mask is defined using a threshold criterion that compares the local mean grayscale value img_mean ith mean gray, as follows:

$$\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{k}1\left(\mathrm{x},\mathrm{y}\right)=\left\{\begin{array}{c}1,\mathrm{i}\mathrm{m}{\mathrm{g}}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}\left(\mathrm{x},\mathrm{y}\right)>\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{y}1\left(\mathrm{y}\right)*1.1\\ 0,\mathrm{i}\mathrm{m}{\mathrm{g}}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}\left(\mathrm{x},\mathrm{y}\right)<\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{y}1\left(\mathrm{y}\right)*1.1\end{array}\right.$$

(3)

The resulting image mask1 is the mask of the fuzz region selected through the first threshold. For images with a ratio of m to n greater than 3, using the average grayscale of the pixels as the threshold is too high due to the excessive presence of fuzz areas within the $\mathrm{m}\times (2\times \mathrm{p}+1)$ pixels. The maximum value of m is 4096, and the maximum value of n is 1366. Within the 1366 pixel range, the horizontal variation in the image is relatively small. Therefore, the average grayscale of $(2\times \mathrm{p}+1)\times \mathrm{n}$ pixels centered on the pixel is taken as the grayscale threshold. This is shown as follows:

$$\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{y}1\left(\mathrm{x}\right)={\displaystyle \frac{1}{\left(2*\mathrm{p}+1\right)*\mathrm{n}}}{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{{\displaystyle \int }}_{\mathrm{i}=\mathrm{x}-\mathrm{p}}^{\mathrm{x}+\mathrm{p}}\mathrm{i}\mathrm{m}\mathrm{g}\left(\mathrm{x},\mathrm{y}\right)$$

(4)

$$\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{k}1\left(\mathrm{x},\mathrm{y}\right)=\left\{\begin{array}{c}1,\mathrm{i}\mathrm{m}{\mathrm{g}}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}\left(\mathrm{x},\mathrm{y}\right)>\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{y}1\left(\mathrm{x}\right)*1.1\\ 0,\mathrm{i}\mathrm{m}{\mathrm{g}}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}\left(\mathrm{x},\mathrm{y}\right)<\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{y}1\left(\mathrm{x}\right)*1.1\end{array}\right.$$

(5)

In the computation of the first defect mask, the grayscale threshold is derived by incorporating both the fuzz defect regions and the background. However, since this initial threshold may be biased due to the inclusion of fuzz pixels, a second threshold step is introduced to refine the segmentation. In this step, the background is first cleaned by excluding the previously identified fuzz pixels using the first mask, and a new column-wise grayscale threshold is computed based on the purified background. Specifically, the second column-wise average grayscale value, meangray2, is calculated as follows:

$$\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{y}2\left(\mathrm{y}\right)={\displaystyle \frac{1}{\left(2*\mathrm{p}+1\right)*\mathrm{m}}}{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{m}}{{\displaystyle \int }}_{\mathrm{j}=\mathrm{y}-\mathrm{p}}^{\mathrm{y}+\mathrm{p}}\mathrm{i}\mathrm{m}\mathrm{g}\left(\mathrm{x},\mathrm{y}\right)*\left(1-\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{k}1\right)$$

(6)

Here, mask1 is the binary mask obtained from the first threshold step, where a value of 1 indicates a fuzz defect pixel and 0 indicates a background pixel. Equation (6) computes the average grayscale of the background region after removing the fuzz defect areas, thereby providing a more accurate column-wise threshold for the second segmentation stage. Then, a second defect mask2 is generated by comparing the local average grayscale img_mean with the threshold defined by Equation (6):

$$\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{k}2\left(\mathrm{x},\mathrm{y}\right)=\left\{\begin{array}{c}1,\mathrm{i}\mathrm{m}{\mathrm{g}}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}\left(\mathrm{x},\mathrm{y}\right)>\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{y}2\left(\mathrm{y}\right)*1.1\\ 0,\mathrm{i}\mathrm{m}{\mathrm{g}}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}\left(\mathrm{x},\mathrm{y}\right)<\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{y}2\left(\mathrm{y}\right)*1.1\end{array}\right.$$

(7)

The calculation for images with a ratio of m to n greater than 3 is as follows:

$$\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{y}2\left(\mathrm{x}\right)={\displaystyle \frac{1}{\left(2*\mathrm{p}+1\right)*\mathrm{n}}}{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{{\displaystyle \int }}_{\mathrm{i}=\mathrm{x}-\mathrm{p}}^{\mathrm{x}+\mathrm{p}}\mathrm{i}\mathrm{m}\mathrm{g}\left(\mathrm{x},\mathrm{y}\right)$$

(8)

$$\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{k}2\left(\mathrm{x},\mathrm{y}\right)=\left\{\begin{array}{c}1,\mathrm{i}\mathrm{m}{\mathrm{g}}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}\left(\mathrm{x},\mathrm{y}\right)>\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{y}2\left(\mathrm{x}\right)*1.1\\ 0,\mathrm{i}\mathrm{m}{\mathrm{g}}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}\left(\mathrm{x},\mathrm{y}\right)<\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{y}2\left(\mathrm{x}\right)*1.1\end{array}\right.$$

(9)

To enhance the robustness of the final defect mask and minimize the risk of pixel omission due to improper threshold selection, the mask with the higher number of identified defect pixels among mask1 and mask2 is selected as the final result. This selection is formalized as follows:

$$\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{k}=\max \left(\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{k}1,\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{k}2\right)$$

(10)

In the resulting mask, the value 1 denotes a fuzz defect pixel, while 0 indicates a background pixel. This approach ensures that the threshold process is adaptive to the spatial characteristics of the image, thereby improving the accuracy and reliability of fuzz defect detection in carbon fiber prepreg surfaces.

2.2. Severity of Defects per Unit Area

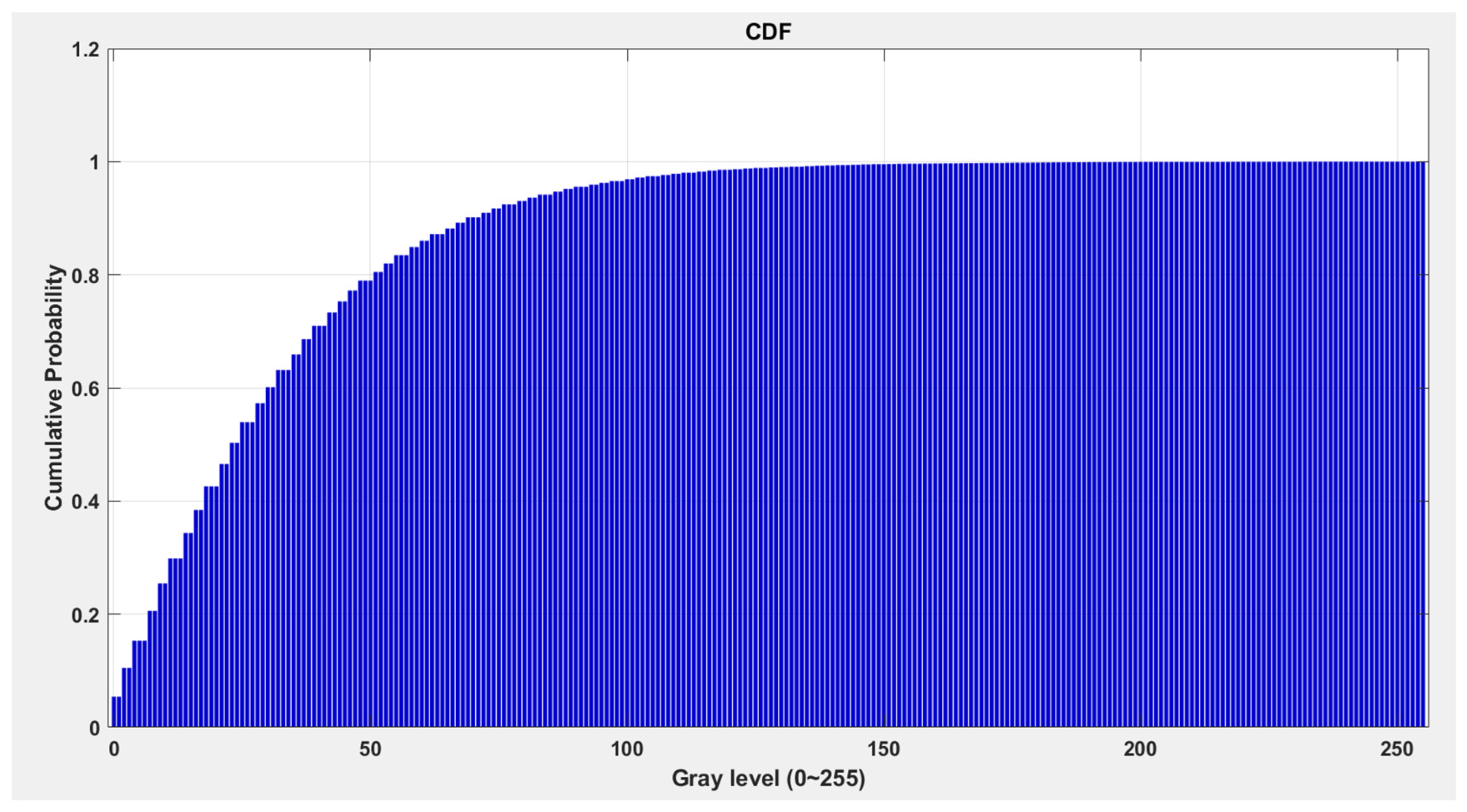
In practical applications, different images may exhibit variations in grayscale values for the same severity of fuzz defects due to differences in lighting conditions and the inherent color properties of the fuzz itself [27]. To eliminate the influence of these external factors on the defect assessment, this study employs a localized grayscale histogram equalization method. This approach is applied specifically to the regions containing fuzz defects, with the lower bound of the local grayscale range defined as the average grayscale value of the fuzz area. The upper bound is determined based on the 80th percentile of the cumulative grayscale probability distribution within the same region. This technique enhances the comparability of images and improves the objectivity and consistency of defect severity evaluation.

Firstly, the grayscale image is normalized from the integer range to the floating-point range, using the following transformation:

$$\mathrm{g}\left(\mathrm{k}\right)={\displaystyle \frac{\mathrm{k}}{255}}$$

(11)

The k represents the grayscale level, ranging from 0 to 255 as an integer. Separate grayscale histograms, denoted as hist_ob and hist_bg, are computed for the fuzz area and the background area as follows:

$$\mathrm{h}\mathrm{i}\mathrm{s}{\mathrm{t}}_{\mathrm{o}\mathrm{b}}\left(\mathrm{k}\right)=\left(\mathrm{h}1\left(0\right),\mathrm{h}1\left(1\right),\dots ,\mathrm{h}1\left(255\right)\right)$$

(12)

$$\mathrm{h}\mathrm{i}\mathrm{s}{\mathrm{t}}_{\mathrm{b}\mathrm{g}}\left(\mathrm{k}\right)=\left(\mathrm{h}2\left(0\right),\mathrm{h}2\left(1\right),\dots ,\mathrm{h}2\left(255\right)\right)$$

(13)

The grayscale probability distributions for the fuzz and background areas are then derived by normalizing the respective histograms:

$${\mathrm{P}}_{\mathrm{o}\mathrm{b}}\left(\mathrm{k}\right)={\displaystyle \frac{\mathrm{h}\mathrm{i}\mathrm{s}{\mathrm{t}}_{\mathrm{o}\mathrm{b}}\left(\mathrm{k}\right)}{{{\displaystyle \sum }}_{\mathrm{i}=0}^{255}\mathrm{h}1\left(\mathrm{k}\right)}}=\left(\mathrm{p}1\left(0\right),\mathrm{p}1\left(1\right),\dots ,\mathrm{p}1\left(255\right)\right)$$

(14)

$${\mathrm{P}}_{\mathrm{b}\mathrm{g}}\left(\mathrm{k}\right)={\displaystyle \frac{\mathrm{h}\mathrm{i}\mathrm{s}{\mathrm{t}}_{\mathrm{b}\mathrm{g}}\left(\mathrm{i}\right)}{{{\displaystyle \sum }}_{\mathrm{i}=0}^{255}\mathrm{h}2\left(\mathrm{i}\right)}}=\left(\mathrm{p}2\left(0\right),\mathrm{p}2\left(1\right),\dots ,\mathrm{p}2\left(255\right)\right)$$

(15)

The ${\mathrm{mean}}_{\mathrm{ob}}$ and ${\mathrm{mean}}_{\mathrm{bg}}$ represent where the average grayscale values of the fuzz area and background area, respectively, as follows:

$$\mathrm{m}\mathrm{e}\mathrm{a}{\mathrm{n}}_{\mathrm{o}\mathrm{b}}={\displaystyle \frac{\sum \mathrm{m}\mathrm{a}\mathrm{s}\mathrm{k}*\mathrm{i}\mathrm{m}\mathrm{g}}{\sum \mathrm{m}\mathrm{a}\mathrm{s}\mathrm{k}}}$$

(16)

$$\mathrm{m}\mathrm{e}\mathrm{a}{\mathrm{n}}_{\mathrm{b}\mathrm{g}}={\displaystyle \frac{\sum \left(1-\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{k}\right)*\mathrm{i}\mathrm{m}\mathrm{g}}{\sum (1-\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{k})}}$$

(17)

To determine the lower threshold of the grayscale range for the fuzz area, the grayscale level g(a) that is closest to mean_ob is identified as follows:

$$\mathrm{g}\left(\mathrm{a}\right)=\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}\left|\mathrm{g}\left(\mathrm{k}\right)-\mathrm{m}\mathrm{e}\mathrm{a}{\mathrm{n}}_{\mathrm{o}\mathrm{b}}\right|,\mathrm{k}\in \left[0,255\right]$$

(18)

The upper threshold b is determined as the 80th percentile of the grayscale probability distribution of the fuzz area. Specifically, b is the smallest grayscale level that satisfies the following conditions:

$${\displaystyle \sum }_{\mathrm{i}=0}^{\mathrm{b}-1}{\mathrm{P}}_{\mathrm{o}\mathrm{b}}\left(\mathrm{i}\right)<0.8$$

(19)

$${\displaystyle \sum }_{\mathrm{i}=0}^{\mathrm{b}}{\mathrm{P}}_{\mathrm{o}\mathrm{b}}\left(\mathrm{i}\right)\ge 0.8$$

(20)

Subsequently, the grayscale histogram and probability distribution for the interval are extracted as follows:

$$\mathrm{h}\mathrm{i}\mathrm{s}{\mathrm{t}}_{\mathrm{a}\mathrm{b}}\left(\mathrm{k}\right)=\left(\mathrm{h}1\left(\mathrm{a}\right),\mathrm{h}1\left(\mathrm{a}+1\right),\dots ,\mathrm{h}1\left(\mathrm{b}\right)\right)$$

(21)

$${\mathrm{P}}_{\mathrm{a}\mathrm{b}}\left(\mathrm{k}\right)={\displaystyle \frac{\mathrm{h}\mathrm{i}\mathrm{s}{\mathrm{t}}_{\mathrm{a}\mathrm{b}}\left(\mathrm{k}\right)}{{{\displaystyle \sum }}_{\mathrm{i}=\mathrm{a}}^{\mathrm{b}}\mathrm{h}1\left(\mathrm{i}\right)}}=\left(\mathrm{p}1\left(\mathrm{a}\right),\mathrm{p}1\left(\mathrm{a}+1\right),\dots ,\mathrm{p}1\left(\mathrm{b}\right)\right)$$

(22)

The cumulative distribution function (CDF) over this interval is then computed as follows:

$$\mathrm{C}\mathrm{D}\mathrm{F}\left(\mathrm{k}\right)={\displaystyle \sum }_{\mathrm{i}=\mathrm{a}}^{\mathrm{k}}{\mathrm{P}}_{\mathrm{a}\mathrm{b}}\left(\mathrm{k}\right)=\left(\mathrm{C}\left(\mathrm{a}\right),\mathrm{C}\left(\mathrm{a}+1\right),\dots ,\mathrm{C}\left(\mathrm{b}\right)\right)$$

(23)

To perform histogram equalization, the grayscale values in the fuzz area are mapped to a new range [28]. The c is the maximum grayscale value of the image. The equalized grayscale value g₁(k) is calculated as follows:

$${\mathrm{g}}_1\left(\mathrm{k}\right)=\mathrm{g}\left(\mathrm{a}\right)+\left(\mathrm{g}\left(\mathrm{c}\right)-\mathrm{g}\left(\mathrm{a}\right)\right)*\mathrm{C}\mathrm{D}\mathrm{F}\left(\mathrm{k}\right)$$

(24)

After mapping, the updated grayscale histogram and probability distribution for the fuzz area are obtained by the following:

$$\mathrm{h}\mathrm{i}\mathrm{s}{\mathrm{t}}_{\mathrm{o}\mathrm{b}}^{\prime }\left(\mathrm{k}\right)=\left(\mathrm{h}{1}^{\prime }\left(0\right),\mathrm{h}{1}^{\prime }\left(1\right),\dots ,\mathrm{h}{1}^{\prime }\left(255\right)\right)$$

(25)

$${\mathrm{P}}_{\mathrm{o}\mathrm{b}}^{\prime }\left(\mathrm{k}\right)==\left(\mathrm{p}{1}^{\prime }\left(0\right),\mathrm{p}{1}^{\prime }\left(1\right),\dots ,\mathrm{p}{1}^{\prime }\left(255\right)\right)$$

(26)

It is worth noting that color variations may exist between different materials or even within different regions of the same material. These variations can lead to differences in the grayscale values of fuzz defects, even when their severity is the same. To mitigate the impact of such color differences on the evaluation process, the focus is shifted from the absolute grayscale values of the fuzz region to the relative difference between the fuzz and background regions.

To achieve this, the grayscale level g(b) that is closest to mean_bg is determined as follows:

$$\mathrm{g}\left(\mathrm{b}\right)=\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}\left|\mathrm{g}\left(\mathrm{k}\right)-\mathrm{m}\mathrm{e}\mathrm{a}{\mathrm{n}}_{\mathrm{b}\mathrm{g}}\right|,\mathrm{k}\in \left[0,255\right]$$

(27)

The relative grayscale difference between the fuzz and background is then calculated by the following:

$${\mathrm{g}}_2\left(\mathrm{k}\right)={\mathrm{g}}_1\left(\mathrm{k}\right)-\mathrm{g}\left(\mathrm{b}\right),\mathrm{k}\in \left[0,255\right]$$

(28)

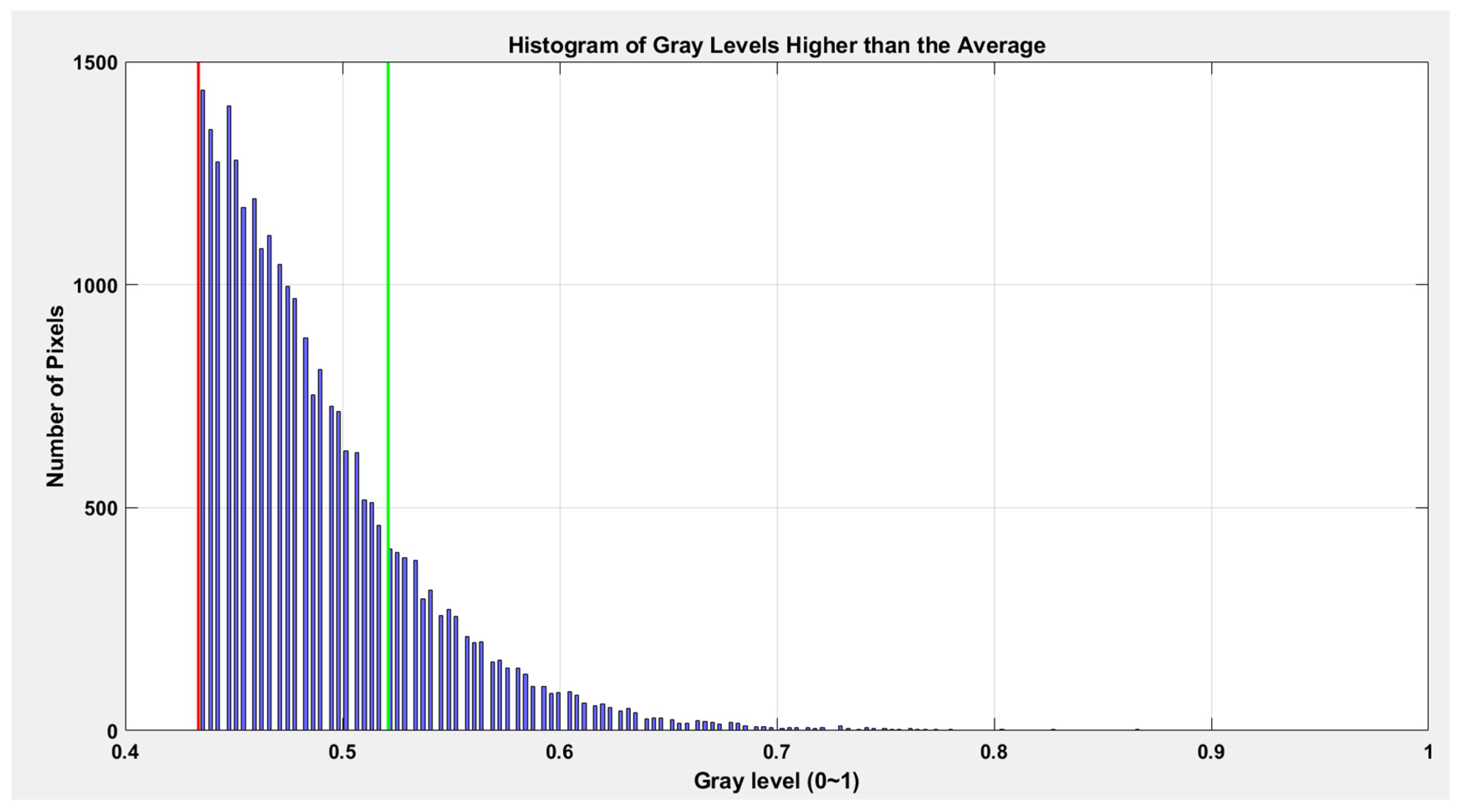
Here, g(b) is the grayscale level closest to the average of the background region. Since the image of fuzz defects is captured on the background material, the grayscale probability distribution derived from the masked area inherently includes contributions from both the fuzz and background regions. To eliminate the background influence on the fuzz severity assessment, the background grayscale probability distribution outside the mask is subtracted from that inside the mask. This operation is defined as follows:

$${\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{f}}={\mathrm{P}}_{\mathrm{o}\mathrm{b}}^{\prime }-{\mathrm{P}}_{\mathrm{b}\mathrm{g}}$$

(29)

Finally, the severity of blurring per unit area is quantified as the absolute sum of weighted grayscale differences above the average grayscale value, as follows:

$$\mathrm{s}=\left|{\displaystyle \sum }_{\mathrm{k}=\mathrm{a}}^{255}{\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{f}}\left(\mathrm{k}\right)*{\mathrm{g}}_2\left(\mathrm{k}\right)\right|$$

(30)

The metric s effectively captures the deviation of the fuzz region from the background in terms of relative grayscale, thereby providing a robust and material-independent measure of defect severity.

2.3. Effective Area

The fuzz defect regions identified in the processed image are further analyzed using a learning approach based on neural networks. In this context, the neural network automatically detects potential fuzz defects and annotates them with rectangular bounding boxes. While these bounding boxes provide a convenient and intuitive representation of the defect region, they may not accurately reflect the true extent of the defect, particularly for irregularly or skewed-distributed defects.

Specifically, when the fuzz defect is not aligned with the axes of the image, the area of the axis-aligned bounding box tends to overestimate the actual defect size. To address this issue and improve the accuracy of area-based severity calculation, the effective area A_eff is defined as the smallest area of the rotated bounding rectangle that tightly encloses the detected fuzz defect. This is achieved by rotating the image and recalculating the bounding rectangle until the minimum enclosing area is found.

The effective area A_eff serves as a more precise geometric descriptor of the fuzz defect, allowing for a more reliable and robust assessment of its severity. By using A_eff instead of the standard axis-aligned bounding box area, the method reduces the impact of spatial misalignment and improves the consistency of quantitative defect evaluation across different orientations and shapes of fuzz regions.

2.4. Quantitative Evaluation Score

To comprehensively evaluate the overall severity of fuzz defects, a composite scoring metric S is introduced, which integrates both the severity per unit area l and the effective area S of the detected defect. This scoring mechanism is formulated as follows:

$$\mathrm{S}=\sqrt[\mathrm{\theta }]{\mathrm{s}}*\mathrm{l}\mathrm{o}{\mathrm{g}}_{\mathrm{\theta }}{\mathrm{A}}_{\mathrm{e}\mathrm{f}\mathrm{f}}$$

(31)

In Equation (31), l represents the normalized grayscale deviation-based severity index defined by (30), while S is the effective area defined in 2.4. The parameter θ is introduced as an adjustable weighting factor that governs the relative contribution of the unit severity and the spatial extent of the defect in the final assessment. The value of θ should be empirically determined according to the specific application requirements and the desired emphasis on either the intensity of the defect or its physical size.

The use of a square root function on the product of θ and s ensures a balanced contribution between the two components, while the logarithmic term with base θ on the effective area A_eff mitigates the overemphasis of large-area defects and enhances the sensitivity to moderate or small defects with high severity. This formulation allows for a more nuanced and application-adaptive quantification of fuzz defect severity, improving the discriminability and interpretability of the final evaluation results.

3. Results

3.1. Image Acquisition

In this study, real-time image acquisition of carbon fiber prepreg was conducted on the production line using a linear array camera. The images had a resolution of 4096 × 4000 pixels and a spatial resolution of 0.06835 mm per pixel, corresponding to a physical field of view of 280 mm × 273.5 mm. The actual prepreg size corresponding to each image with a pixel dimension of 4096 × 4000 is 280 mm × 273.5 mm. The collected prepreg images were analyzed using a deep learning network to detect potential fuzz defects. Specifically, the regions identified within the detection bounding boxes are classified as fuzz defects and used as the examples for severity evaluation in this work.

The minimum image resolution required for the effective application of the method is determined by the pixel dimensions corresponding to the smallest defect size that needs to be detected in the specific industrial context. For example, if the minimum acceptable defect size is $\mathrm{Z}\mathrm{m}\mathrm{m}\times \mathrm{Z}\mathrm{m}\mathrm{m}$ and the spatial resolution is 0.0685 mm/pixel, then the minimum defect size in terms of pixels would be approximately $\mathrm{Z}/0.06835 \mathrm{pixels}\times \mathrm{Z}/0.06835 \mathrm{pixels}$. Figure 1a displays the raw images captured by the camera, while Figure 1b presents the same images with annotations indicating the detected fuzz defects. Each bounding box is labeled with its width, height, threshold, and confidence level, providing a visual reference for the detection performance of deep learning models. In this study, the YOLOv8s architecture was employed as the detection network in the experimental setup. The model was trained on a dataset comprising 1270 annotated samples of fuzz defects. A total of 400 training epochs were conducted to ensure the model’s convergence and robust performance in defect detection.

Figure 2 presents an original image containing a linear object and an enlarged view of the region enclosed in the red box. Fuzzy defects are usually composed of dark linear objects and light flocculent objects. As observed in Figure 2, the average width of a linear object is 3–5 pixels. When the center of the convolution kernel is aligned with the center of this linear object, a small kernel size may result in the kernel covering only the dark linear region. This leads to the average grayscale value being computed based solely on the dark area, even though the corresponding point is judged as a defect-free area. To avoid this misclassification and ensure accurate detection of defect pixels, the width of the convolution kernel must exceed the width of the linear defect. That is, the kernel size (2p + 1) should be greater than five pixels, implying that the minimum value of p should be 3. The effectiveness of different p-values is illustrated in the following figures.

Figure 3a shows the original grayscale image. Figure 3b,c displays the masks obtained for p = 3 and p = 6, respectively. As shown, increasing the value of p leads to a decrease in the accuracy of edge extraction, with more background pixels near the boundary of the defect being incorrectly classified as defect pixels. Therefore, p = 3 is selected as the optimal parameter for subsequent calculations.

3.2. Histogram Equalization

To enhance the consistency of defect evaluation across different lighting conditions, grayscale histogram equalization was applied to the detected fuzz regions. This step is designed to normalize the grayscale distribution within the defect area, reducing the influence of environmental illumination variations.

Figure 4a shows the original grayscale image, and Figure 4b presents the corresponding mask of the fuzz area. Figure 4c displays the cumulative distribution function of grayscale levels within the fuzz region. Figure 5 shows the grayscale histogram of the image above the average grayscale. In this plot, the red line corresponds to point a, which represents the average grayscale value of the fuzz area in the original image. The green line marks point b, indicating the 80th percentile of the cumulative grayscale probability distribution. Figure 6 illustrates the probability density distribution of the grayscale range used for local histogram equalization and the resulting equalized image.

3.3. Effective Area

The effective area of the defect is defined as the minimum rotated bounding rectangle that tightly encloses the fuzz defect region. This definition helps to mitigate the overestimation of defect area caused by skewed or irregularly shaped defects. The angle α, which minimizes the bounding rectangle area, is calculated for each defect.

Figure 7a shows the fuzz area selected using the mask derived from Equation (10). Figure 7b presents the same image rotated by angle α to align the defect region for more accurate effective area computation.

3.4. Quantitative Results of the Severity of Fuzz Defects

The overall severity of fuzz defects is quantified using the composite score, which combines the severity per unit area l and the effective area S. This method allows for a more objective and interpretable assessment of defect severity.

To demonstrate the performance of the proposed method, 10 images with varying severity levels of fuzz defects were selected, as shown in Figure 8b. These images were processed by the neural network to detect defects and generate corresponding cropped regions as shown in Figure 8b. The quantitative severity scores, as calculated using Equation (31) with θ = 2, are summarized in

Table 1. Severity rating of fuzz defects.

Dataset No.	Image Size Within the Box	Quantitative Evaluation Score	Ranking of Methods in This Article	Artificial Ranking
#1	52 × 163	97.2	1	1
#2	68 × 201	105.2	2	2
#3	178 × 1307	108.0	3	3
#4	295 × 749	121.2	4	4
#5	121 × 874	126.4	5	5
#6	156 × 509	128.6	6	6
#7	312 × 2313	136.2	7	7
#8	377 × 3671	143.6	8	8
#9	1280 × 879	161.2	9	9
#10	903 × 4000	200.4	10	10

.

3.5. Impact of Parameter θ on Severity Ranking

To further investigate the impact of parameter θ on the final severity ranking, evaluations were conducted on the three graphs shown in Figure 9 at different θ values (2, 3, and 5). The results demonstrate that the value of θ significantly affects the relative importance of the defect area and the severity per unit area in the final evaluation.

Table 2. Ranking of ratings and severity of three images when θ is 2, 3, and 5.

Dataset No.	Image Size Within the Box	Quantitative Evaluation Score and Ranking
		θ = 2		θ = 3		θ = 5
#11	135 × 163	109.5	1	34.8	1	13.7	2
#12	90 × 298	109.8	2	35.4	3	14.1	3
#13	495 × 131	115.8	3	35.3	2	13.5	1

presents the results for θ = 2, 3, and 5, where the defect area contributes more heavily to the final score. The corresponding quantitative ratings are as follows:

These experimental results confirm that the parameter θ allows for flexible tuning of the evaluation criteria, making the proposed method adaptable to different industrial quality requirements.

3.6. Accuracy

The proposed methods in this paper were applied to rank the severity of defects in a total of twenty cat hairball images. The ranking results generated by the algorithm were compared with those produced by experienced staff through manual evaluation. To quantitatively assess the consistency between the algorithmic rankings and the human rankings, Rank Consistency Scores were employed as the evaluation metrics. These measures focus on the overlap and alignment between the sets of top-ranked items, rather than requiring exact positional matches, making them particularly suitable for evaluating the overall ranking performance in terms of correctness and relevance. As presented in

Table 3. Comparison of manual ranking and method-based ranking with set-based similarity measures at top-k positions.

Image Identifier	Manual Ranking	Algorithm Ranking	Rank Consistency@K
1	1	1	1
2	2	2	1
3	3	3	1
4	4	4	1
5	5	5	1
6	6	7	5/6
7	7	9	6/7
8	8	10	3/4
9	9	11	7/9
10	10	12	4/5
11	11	13	9/11
12	12	8	11/12
13	13	14	12/13
14	14	15	13/14
15	15	16	14/15
16	16	17	15/16
17	17	19	16/17
18	18	18	17/18
19	19	6	1
20	20	20	1

, the first row represents the manual ranking of defect severity by experienced personnel, while the second row corresponds to the rankings generated by the proposed method. The third row provides the Rank Consistency@K scores, as shown in Equation (32), which evaluate the alignment of the top-k ranked images between the two ranking strategies. The accuracy is 92% obtained through Equation (33).

$$\mathrm{Rank} \mathrm{Consistency}@\mathrm{k}={\displaystyle \frac{\left|\mathrm{M}\mathrm{a}\mathrm{n}\mathrm{u}\mathrm{a}\mathrm{l}\mathrm{T}\mathrm{o}\mathrm{p}-\mathrm{k}\cap \mathrm{M}\mathrm{e}\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{d}\mathrm{T}\mathrm{o}\mathrm{p}-\mathrm{k}\right|}{\mathrm{k}}}$$

(32)

$$\mathrm{Rank} \mathrm{Accuracy}={\displaystyle \frac{{\displaystyle \sum _{\mathrm{k}=1}^{20}\mathrm{Rank} \mathrm{Consistency}@\mathrm{k}}}{20}}=0.92$$

(33)

4. Discussion

This article proposes a quantitative evaluation method for the severity of fuzz defects on the surface of carbon fiber prepreg. We selected 20 surface images of prepreg materials exhibiting varying degrees of fuzz defects, as identified and labeled by a neural network-based detection model with bounding box annotations. We have developed an algorithm for separating fuzz areas from detection bounding box selected images, which filters for defective pixels by comparing local grayscale values centered on pixels with a threshold. It can be observed from the experiment that the method used can effectively segment the defect area. Quantitative analysis and calculation were conducted on the defects of the fuzz. Based on the analysis and processing of grayscale histograms, the quantification of defect severity has been achieved, and the quantification results are not affected by different materials, color brightness of different areas, and lighting conditions in the photography environment. Sort the defect images according to the quantified values and match the results determined by human judgment. This quantitative method effectively solves the key problem of existing neural networks being difficult to dynamically adjust judgment criteria according to quality requirements in industrial defect detection. The ranking results obtained using the method proposed in this article have a similarity of 92% with the ranking results artificially obtained by experienced staff. This validates the effectiveness and reliability of the proposed method in assessing the severity of defects and provides an interpretable decision-making basis for automated quality inspection systems.