Abstract
Offshore wind platforms face critical low-frequency vibration challenges requiring advanced isolation solutions. This work develops a quadrilateral-shaped vibration isolation platform (QVIP) with a quasi-zero stiffness property for floating structures, combining negative stiffness elements and optimized damping to achieve high-static-low-dynamic-stiffness. Theoretical modeling establishes the QVIP’s working principle and parametric behavior, while numerical simulations validate its ultra-low frequency (<1 Hz) suppression capabilities with time domain analysis. The design overcomes conventional trade-offs between low-frequency isolation and load-bearing capacity, offering improved stability for offshore applications compared to linear isolators. Results demonstrate effective vibration control through tailored nonlinear stiffness characteristics (e.g., 48.17% isolation efficiency, 39.48% peak amplitude reduction, and 73.14% variance reduction), suggesting practical viability for next-generation floating platforms.
1. Introduction
The global transition toward green energy solutions has driven offshore wind power installations into increasingly deeper and more remote marine environments [1]. While this expansion promises greater energy yields, it introduces significant engineering challenges, particularly concerning low-frequency vibrations induced by extreme wave conditions and complex hydrodynamic interactions [2]. These vibrations not only compromise platform stability and energy conversion efficiency but also pose long-term structural integrity risks through fatigue accumulation [3]. Effective vibration mitigation strategies are therefore critical for ensuring the reliability and longevity of offshore renewable energy infrastructure [1,2,3,4].
Various vibration control approaches have been developed to meet different mitigation requirements, including passive [5], semi-active [6], and active control methods [7]. While semi-active and active strategies can generate substantial control forces and achieve superior performance, they demand significant energy input (e.g., piezoelectric materials or electromagnetic components) and involve costly mechatronic systems with high maintenance requirements. In contrast, passive vibration control offers superior stability and cost-effectiveness, making it particularly attractive for engineering applications [5,8]. The three primary passive methods include dampers for energy dissipation [9,10,11,12], tuned mass dampers for energy transfer [13], and isolation platforms for energy isolation [14]. Among these, vibration isolation systems stand out for their broad effective frequency range and exceptional high-frequency attenuation performance. These advantages have established isolation platforms as the predominant passive control solution in practical offshore applications.
Vibration isolation systems serve dual critical functions in this context, protecting sensitive equipment from environmental vibrations and preventing machinery-induced vibrations from propagating through supporting structures [5]. The fundamental challenge lies in attenuating transmitted forces while maintaining system stability, particularly in the low-frequency range characteristic of ocean wave excitations [2]. Conventional linear isolation systems face inherent limitations in this regard, as achieving sufficient low-frequency attenuation typically requires reducing system stiffness, which in turn compromises static load-bearing capacity. This trade-off has motivated the development of advanced isolation technologies capable of simultaneously providing high static stiffness for structural support and low dynamic stiffness for effective vibration isolation [14].
Recent advances in quasi-zero stiffness (QZS) isolators have demonstrated particular promise for ultra-low frequency vibration isolation in floating platforms [7]. By incorporating negative stiffness elements with carefully tuned linear springs, these systems achieve high-static-low-dynamic stiffness (HSLDS) characteristics that effectively decouple static and dynamic performance requirements [15]. Liu et al. [16] summarized the recent advancements in QZS-based vibration isolators and isolation platforms, while also categorizing and synthesizing the various approaches to achieving QZS characteristics. Theoretical and experimental studies have validated various implementations, including oblique springs or pre-buckled beam configurations that provide tunable negative stiffness [17,18,19,20,21], magnetic arrangements offering contactless stiffness modulation [6,22,23], bio-inspired designs mimicking natural vibration-damping structures [24,25,26,27,28,29,30,31], cam mechanisms [32,33], and metamaterials [34]. The effectiveness of QZS isolators stems from their nonlinear stiffness characteristics, which enable significant extension of the effective isolation bandwidth, maintenance of high static load capacity, and improved stability compared to conventional low-frequency isolators. For instance, building upon the cam-roller spring mechanism, Zhang et al. [33] proposed a nonlinear isolation system based on cam-roller-spring-rod stiffness., Yan et al. [35] successfully implemented an effective nonlinear damping approach to enhance the vibration isolation performance of electromagnetic structures. Liu et al. [36] improved the stability of the three-spring QZS isolator in low-frequency by introducing the inerter element. Jing et al. [14,24,27,31] developed X-shaped and limb-like structures that exhibit beneficial nonlinear stiffness, damping, and inertial characteristics. Their studies revealed that careful parameter tuning could readily achieve a QZS region featuring substantial load capacity, large stroke, broad vibration isolation bandwidth, and superior stability. Similarly, Yan et al. [28] devised an innovative toe-like anti-vibration configuration comprising two rods and a spring, with both theoretical and experimental results confirming effective vibration reduction for excitation frequencies above 3 Hz.
Complementing these stiffness innovations, researchers have developed advanced damping strategies to optimize isolation performance across different frequency regimes. These include velocity-dependent nonlinear damping for resonance control [37], displacement-dependent geometric damping for broadband attenuation [9,38], and hybrid approaches combining multiple damping mechanisms.
In this study, to solve the ultra-low frequency vibrations of the floating platform, a novel quadrilateral-shaped vibration isolation platform (QVIP) is proposed with tunable and enhanced QZS properties. The mechanism of the QVIP for the QZS property based on three-spring element and its dynamic equation are shown in Section 2. Section 3 shows parametric influences on static stiffness force and summarizes the key factors for achieving the QZS property, while Section 4 builds up the simulation model of the QVIP and verifies the vibration control effect on the offshore platform under harmonic excitations and ocean wave conditions. Finally, a conclusion is given in Section 5.
2. Dynamic Modeling of the Proposed QVIP
2.1. Conceptual Design of QVIP
In vibration control systems, a standalone negative stiffness structure may destabilize the platform. Hence, integrating positive stiffness structures is essential to achieve stable and tunable QZS. Addressing this, we propose the QVIP with QZS for vibration control of offshore floating platforms in ultra-low frequencies. Leveraging the foldable parallelogram geometry, the QVIP combines a horizontal spring with two oblique spring sets to realize stable and tunable QZS. Figure 1a illustrates the 3D design of the QVIP. During compression, the vertical component force of horizontal/tensioned springs initially increases then decreases, generating negative stiffness, while compressed springs consistently provide positive stiffness. Adjusting their balance enables QZS design. Figure 1b shows that horizontal/tensioned springs exhibit positive stiffness initially but transition to negative stiffness with larger displacement, risking instability. To extend the QZS range and enhance vibration isolation, this paper analyzes and optimizes the equivalent stiffness of the three-spring system.
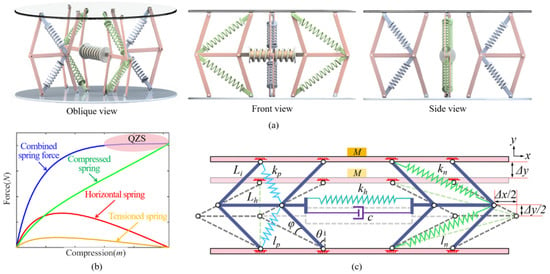
Figure 1.
Modelling and mechanism of the QVIP: (a) 3D design of the QVIP, (b) mechanism of QZS, and (c) simplified mechanical model and the geometric deformation of the QVIP.
2.2. Deformation of the QVIP
The simplified mechanical model of the QVIP is shown in Figure 1c. is the mass, is the length of inclined rods, is the length of horizontal rods, is the initial angle between inclined rods and vertical direction, is the stiffness of horizontal springs, is the stiffness of compression inclined springs, is the stiffness of stretch inclined spring, is the damping coefficient of the horizontal damper, is the total vertical displacement, is the total horizontal displacement, and is the rotation angle of the inclined rod. All the parameters used in the modelling are listed in Table A1 in Appendix A.
Nondimensionalization is performed for , , , , and . The definitions of dimensionless parameters are , , = , , . During compression, the parallelogram mechanism maintains vertical motion. The relationships between motions in different directions are expressed by Equations (1)–(3). The rotation angle and total horizontal displacement are nonlinearly correlated with the total vertical displacement , indicating a nonlinear relationship between horizontal and vertical motions.
Rotation angle of the inclined rod is written as
Total horizontal displacement is obtained as
Total vertical displacement is obtained as
Initial length of compressed inclined spring is obtained as
Length of compressed inclined spring during motion is obtained as
Deformation of compressed inclined spring is obtained as
Initial length of stretch inclined spring is obtained as
Length of stretch inclined spring during motion is obtained as
Deformation of stretch inclined spring is obtained as
2.3. Dynamic Model of the QVIP
The Lagrange principle is employed to establish the dynamic model of the QVIP. The kinetic energy of expressed as
where .
The relative velocity in the horizontal direction of the QVIP, as well as the generalized relative velocities in other directions, can be expressed as
The potential energy is obtained as
Considering the damping effect, the generalized force Q of the QVIP containing the non-constraint force F along the virtual displacement r can be expressed as
where is the viscous damping coefficient of the horizontally placed damper, and is the linear air damping coefficient.
The Lagrange equation incorporating the generalized force Q can be expressed as
The term can be obtained as
Therefore, based on the Lagrange principle, the dynamic equation under the base excitation () can be obtained as
3. QZS Characteristics of QVIP
3.1. Static Stiffness
From Equation (18), the stiffness force of the horizontal spring can be obtained as
The stiffness force of the inclined springs can be obtained as
Thus, the totally combined nonlinear stiffness force of QVIP is defined as
3.2. Parametric Study
The initial model parameters are set as , , , , , , , . At first, using different rod length ratios (), the results are shown in Figure 2a; as gradually increases from 0 (), the equivalent nonlinear stiffness force () significantly increases; when , the QZS range appears; as further increases beyond 1, decreases, and the QZS range shortens. By adjusting , the curves near are shown in Figure 2b. It is observed that an extended QZS range occurs only when . If , negative stiffness appears after reaches its maximum value.
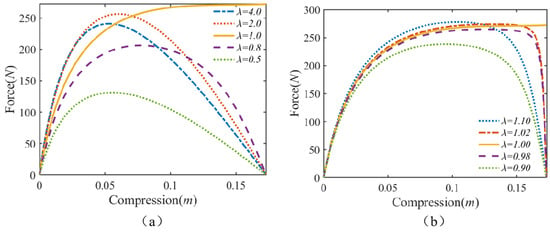
Figure 2.
Parametric influence on static stiffness force (parameters are set as , , , , , k ): (a) using different rod length ratio , and (b) when length ratios near .
To facilitate comparison of QZS state in the QVIP, the system is considered to achieve the QZS state when the slope of the equivalent nonlinear stiffness force curve reaches . is the ratio of the QZS width to the maximum compression displacement. The influence of rod length L is shown in Figure 3. As increases, increases significantly, while the remains invariant.
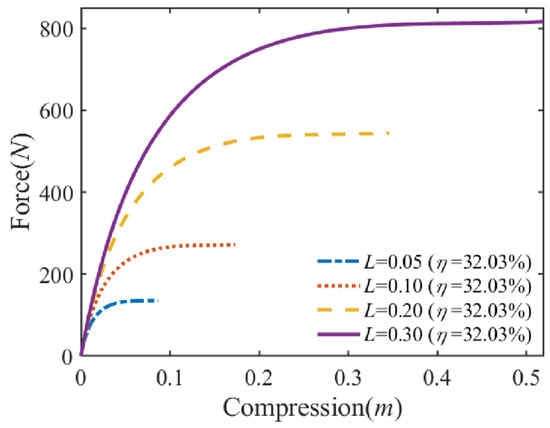
Figure 3.
Different rod length L influence on static stiffness force (parameters are set as , , , , , k ).
The influence of stiffness ratio is shown in Figure 4. As increases, the positive stiffness also increases, it is necessary to increase to a certain value to achieve QZS for QVIP, e.g., . More than this value, the stiffness is always positive as the compression continues and QZS will not appear.
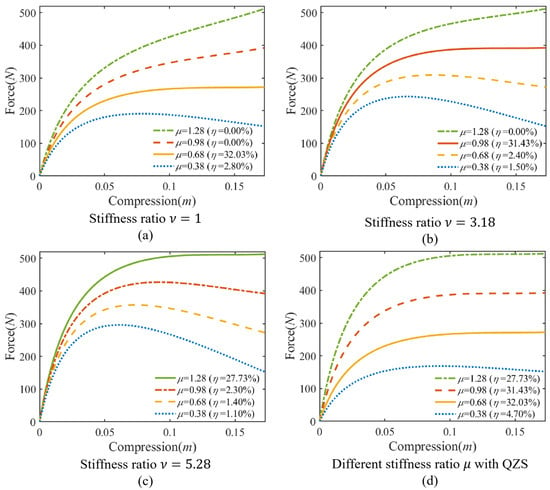
Figure 4.
The influence of stiffness ratios and on static stiffness force (parameters are set as , , , , k ): (a) when stiffness ratio , (b) when stiffness ratio , (c) when stiffness ratio , and (d) comparison of the optimal QZS effect in (a–c).
As shown in Figure 5, the equivalent nonlinear stiffness force of the QVIP is related to the stiffness ratio . Increasing enhances the maximum equivalent nonlinear stiffness force under the same compression while reducing the slope of the equivalent nonlinear stiffness force. By adjusting the ratio between the stiffness of the inclined springs and , a wide QZS range can be achieved for the QVIP under different stiffness ratios . As increases, the required compression for the QIP platform to reach the QZS state also increases, leading to a decrease in the QZS range ratio . Consequently, the QVIP becomes less stable under ultra-low frequency vibrations.
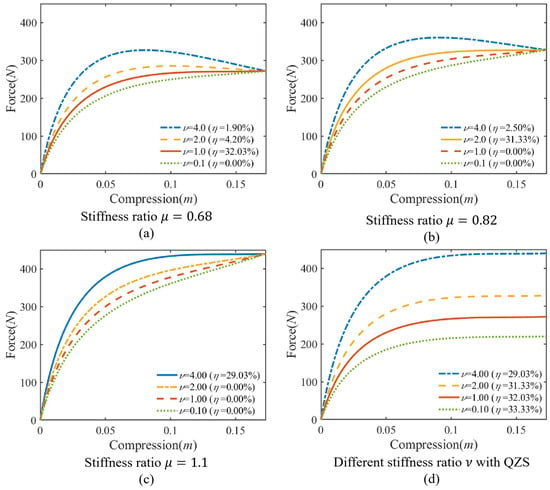
Figure 5.
The influence of stiffness ratios and on static stiffness force (parameters are set as , , , , k ): (a) when stiffness ratio , (b) when stiffness ratio , (c) when stiffness ratio , and (d) comparison of the optimal QZS effect in (a–c).
As can be seen from Figure 6, the equivalent nonlinear stiffness force of the QVIP is related to the initial angle θ. Increasing the initial angle θ will increase the slope of the system’s equivalent nonlinear stiffness force while reducing the maximum equivalent nonlinear stiffness force under the same compression amount. By adjusting the ratio μ between the compressed state inclined spring stiffness and k, as well as the ratio ν between the stretched state inclined spring stiffness and k, a relatively large QZS range of the QVIP can be achieved under different initial angle θ.
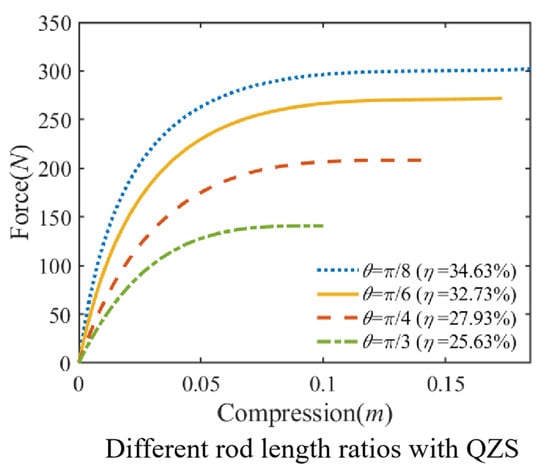
Figure 6.
The influence initial angle on static stiffness force (parameters are set as , , , , , , k ).
It can be observed that only proper values of the structural parameters can lead to the QZS effect, thus, parametric study is important to understand how to tune the structural parameters to achieve the ideal QZS effect. These theoretical analysis results can be used for the simulation experiment of how to choose proper parameters for the desirable QZS effect.
4. Simulation Analysis
4.1. Simulation Model in Adams
To further validate the static performance of the QVIP, the simulation experiment is conducted by using Adams 2023 software. In the simulation, all rods of the QVIP were assumed to be rigid. The bottom plane of the QVIP was fixed, while a translational joint was applied to the upper plane to impose a vertically downward displacement.
The simulation model in Adams software is shown in Figure 7a, and the motion pairs and constraints are shown in Figure 7b. To validate the QZS characteristics of the QVIP, simulation experiments were conducted using the parameters in previous parametric analysis that can generate QZS. With different stiffness ratios and , the simulation results and the theoretically derived equivalent nonlinear stiffness force curves are compared in the Figure 7c,d (parameters are set as: , , , , , k ). The simulation results are consistent with the theoretical results, and the range of quasi-zero stiffness and the variation law of force amplitude are consistent, which verifies the accuracy of both of the theoretical model and simulation model of the QVIP.
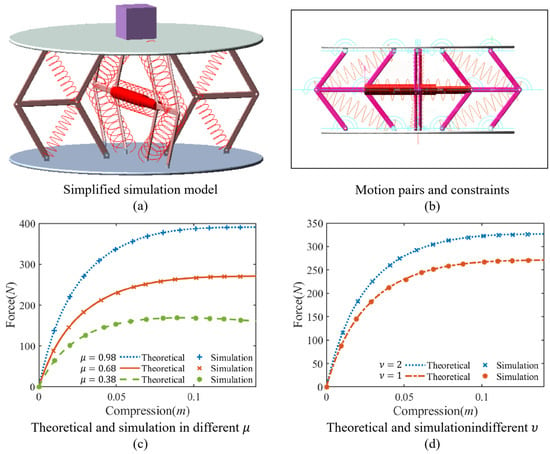
Figure 7.
Comparison of theoretical and simulation results of static stiffness force: (a) simulation model in Adams, (b) setting of motion pairs and constraints, (c) theoretical and simulation results with different , and (d) theoretical and simulation results with different (parameters are set as , , , , , k ).
Floating platforms can be categorized into four main types: barge (30–50 m), tension leg (>50 m), semi-submersible (>50 m), and spar (>100 m) as shown in Figure 8a. Among these four types, the spar platform exhibits significant vibration in the vertical direction, which is suitable for the utilization of the proposed QVIP. According to research by the Xiangshui Yangtze Wind Power Co., Ltd. in Yancheng City of China [39], the spar platform exhibits significant vertical oscillations. Under conditions with wind speed, wave height, and wave period, the vertical excitation amplitude reaches with an excitation angular frequency . The spar platform model was imported into Adams software. Figure 8b illustrates the operational schematic of the QVIP under working conditions.
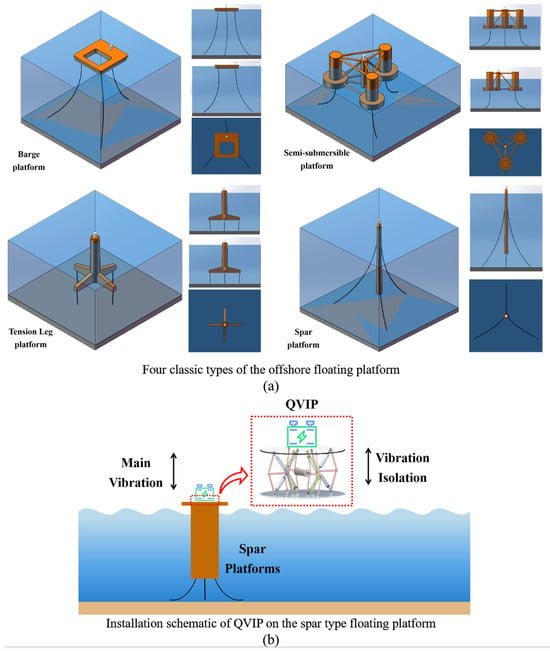
Figure 8.
The types of main floating platforms and the application of the proposed QVIP in the vibration control of the floating platform: (a) four classic types of the offshore floating platform (barge, tension leg, semi-submersible, and spar), and (b) installation schematic of the QVIP on the spar type floating platform.
4.2. Case Study
Using harmonic wave to simulate the working conditions, the damping coefficient of the horizontal damper is set as , the load force is set as 269.5 N, the excitation amplitude is set to , and the excitation angular frequency is set as (), (), and (), respectively. The simulation results of the response displacement are plotted in the Figure 9a–c. As decreases, the isolation efficiency gradually decreases. When reaches , the isolation of QVIP is still effectively.
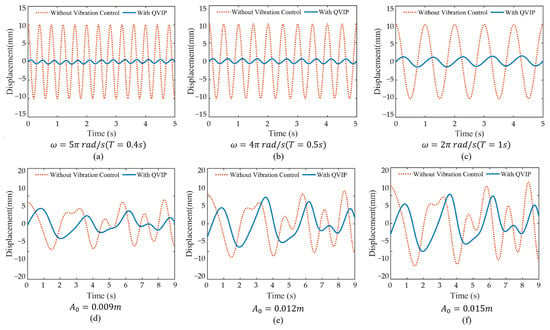
Figure 9.
Responses in time domain with different excitation frequencies and amplitudes: (a) (), (b) (), (c) ( 1 ), (d) , (e) , and (f) .
To realistically simulate ocean wave conditions in Adams simulation environment, we developed a composite vibration excitation profile () comprising (1) a step function representing transient wave impacts, and (2) two superimposed harmonic functions with identical amplitudes but distinct frequencies to mimic characteristic wave frequency variations. This multi-component excitation approach effectively reproduces the complex spectral characteristics of actual offshore wave dynamics while maintaining controlled experimental conditions for precise isolator performance evaluation. The definition of is
The excitation amplitudes were systematically varied at 0.009 m, 0.012 m, and 0.015 m to evaluate the QVIP’s performance under different loading conditions, with the corresponding displacement–time relationships presented in Figure 9d–f. Simulation results demonstrate a positive correlation between excitation amplitude and isolation efficiency within the system’s recoverable deformation range, indicating enhanced vibration isolation performance at larger amplitudes. However, simulation studies reveal an operational threshold beyond which excessive excitation amplitudes (typically >0.015 m in our configuration) prevent the QVIP from achieving steady-state operation, suggesting the existence of a critical amplitude for stable performance.
As vibration frequency decreases, the difficulty of isolation gradually increases. The vibrations in Figure 9a–c are regular cosine waves, which can roughly simulate ocean waves. However, real ocean waves are far more complex than simple cosine waves. Figure 9d–f employs a more realistic wave model that better approximates actual sea conditions, and the wave frequencies used are also lower. Consequently, the vibration attenuation amplitude in Figure 9d–f is smaller than that in Figure 9a–c.
To investigate the influence of the different damping coefficient c on the QVIP, the damping coefficient of the horizontal damper was modified. Based on the dynamic simulation results of the QVIP, the displacement–time curves before and after vibration isolation were plotted, as shown in Figure 10. Under the same excitation conditions, a smaller damping coefficient results in a lower amplitude of the platform after vibration isolation. Simulation results indicate that when the damping coefficient is too small, the platform fails to reach a stable state quickly.
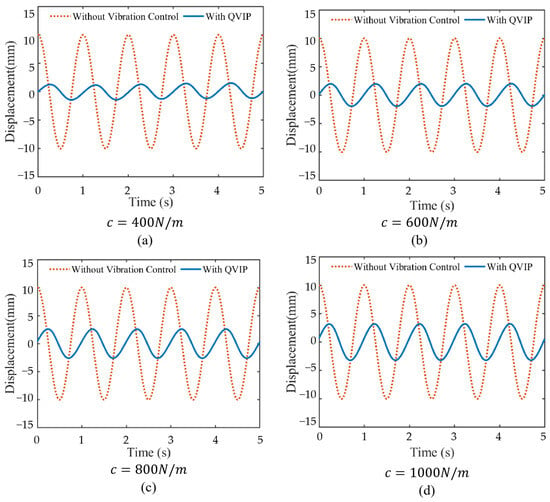
Figure 10.
The influence if damping coefficient c on static stiffness force (parameters are set as , , , , , , , k ): (a) , (b) , (c) , and (d) .
4.3. Vibration Control Effect of Optimally Designed QVIP
Building upon the established theoretical framework, the QVIP’s equilibrium gravity can be effectively tuned through stiffness ratio adjustments (μ and ν), facilitating load-adaptive optimization. The vibration isolation indicators are defined as follows: Maximum Amplitude refers to the maximum amplitude of the object moving at the equilibrium position, Variance refers to the variance of the object’s displacement at the equilibrium position, and Vibration Isolation Efficiency refers to the sum of the percentage reduction in displacement before and after vibration isolation at each moment. Three load cases were investigated: (1) 269.5 N (, ), (2) 325.3 N (, ), and (3) 389.5 N (, ). Figure 11a presents the corresponding theoretical and simulated equivalent nonlinear stiffness forces for these loading conditions. Under a fixed excitation amplitude of 0.009 m, the displacement characteristics are detailed in Figure 11b,c, demonstrating the system’s dynamic response across different parametric configurations. Figure 11d presents the three key performance indicators (i.e., peak amplitude reduction, variance reduction and isolation efficiency) evaluating the QVIP’s vibration isolation effectiveness under these three operational conditions. The detailed comparison results are provided in Table 1. Simulation results confirm that the QVIP maintains effective vibration isolation performance in terms of all three key indicators under different parameter conditions.
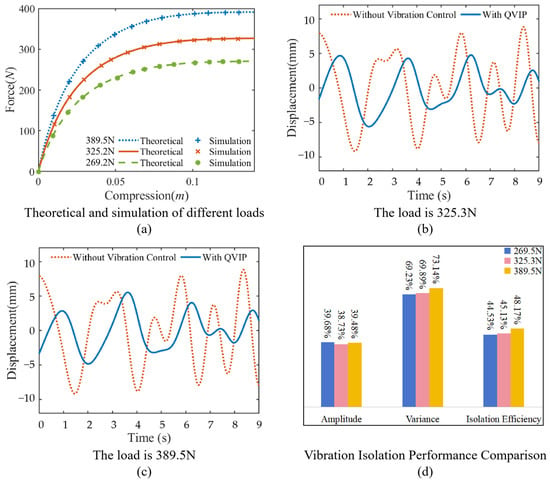
Figure 11.
Vibration control effect of an optimally designed QVIP: (a) theoretical and simulation results of equivalent nonlinear stiffness forces, (b) response when load is 325.3 N, (c) response when the load is 389.5 N, and (d) vibration isolation performance comparison.

Table 1.
The comparison of vibration data without vibration control and with QVIP.
5. Conclusions
This study addresses the critical challenge of low-frequency vibration control in floating platforms by proposing a novel quadrilateral-shaped vibration isolation platform (QVIP) based on a foldable quadrilateral mechanism. Through integrated theoretical modeling, parametric optimization, and dynamic simulations, the research systematically investigates the QVIP’s vibration suppression mechanism and demonstrates its engineering feasibility for offshore applications. The key contributions include the following.
The theoretical modeling and analysis demonstrate that the QVIP can generate an ideal quasi-zero stiffness (QZS) curve when the link length ratio is 1 (forming an equilateral rhombus structure). Parameter analysis further reveals the mechanism behind QZS formation in the QVIP and how to adjust parameters to achieve an extended QZS range. The results indicate that increasing the link length enhances load-bearing capacity while maintaining the QZS range. To validate the theoretical model, a rigid-body dynamics simulation was conducted using Adams software. The numerical simulation results align with the theoretical predictions, confirming the accuracy of the model and verifying that the QVIP can achieve tunable and controllable QZS characteristics.
Numerical simulations were performed to analyze the vibration of a floating platform under wave action. Time-history analysis shows that the QVIP achieves vibration isolation efficiency exceeding 44% under different loads. By adjusting key parameters such as spring stiffness ratio, initial angle, and link length, the QVIP can adapt to varying loads while retaining its QZS vibration suppression properties. For instance, under a 325.3 N load, the isolation efficiency reaches 44.53%, while under a 389.5 N load, it improves to 48.17%, demonstrating excellent vibration isolation performance. Additionally, a systematic parametric study elucidates the influence of key QVIP parameters on the QZS bandwidth, providing practical design guidelines for engineering applications.
In conclusion, this study introduces a QVIP based on a quadrilateral-shaped structure design, combining theoretical analysis and simulation to successfully address the challenge of ultra-low-frequency wave-induced vibrations in offshore floating platforms.
Author Contributions
Conceptualization, Z.G. and J.B.; methodology, Z.G., J.B. and L.L.; software, N.S.; validation, Z.G., J.B. and L.L.; formal analysis, N.S.; investigation, J.B.; resources, Z.G. and J.B.; data curation, L.L.; writing—original draft preparation, Z.G.; writing—review and editing, J.B. and L.L.; visualization, L.L.; supervision, Z.G. and J.B.; project administration, J.B.; funding acquisition, Z.G. and J.B. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge financial support from National Key Research and Development Program of China (Grant No. 2024YFE0208600), the National Natural Science Foundation of China (Grant Nos. 52308144 and 12302124) and the Shenzhen Science and Technology Program (KJZD20230923115402005).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Dataset available on request from the authors. The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Structural parameters of the QVIP used in modeling.
Table A1.
Structural parameters of the QVIP used in modeling.
| Symbol | Structural Parameters | Unit |
|---|---|---|
| Mass | ||
| Stiffness of horizontal spring | ||
| Stiffness of inclined spring under stretch | ||
| Stiffness of inclined spring under compression | ||
| Stiffness of spring | ||
| Ratio of to | ||
| Ratio of to | ||
| Ratio of to | ||
| Damping coefficient of horizontal damper | ||
| Air damping coefficient | ||
| Length of inclined rod | ||
| Length of horizontal rod | ||
| Length | ||
| Ratio of to | ||
| Ratio of to | ||
| Initial length of compressed inclined spring | ||
| Length of compressed inclined spring during motion | ||
| Deformation of compressed inclined spring | ||
| Initial length of stretch inclined spring | ||
| Length of stretch inclined spring during motion | ||
| Deformation of stretch inclined spring | ||
| Initial angle of inclined rod | ||
| Rotation angle of inclined rod | ||
| Total horizontal displacement | ||
| y | Total vertical displacement |
References
- Huang, Z.; Zhang, Y.; Bian, J. Offshore floating platform synergizing internally-installed self-reacting wave energy converters for optimizing vibration control and energy harvesting. Ocean Eng. 2024, 313, 119429. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Han, Q.-L.; Zhang, X.-M. Recent advances in vibration control of offshore platforms. Nonlinear Dyn. 2017, 89, 755–771. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Z.; Bian, J. Multi-dimensional vibration control for offshore floating platform synergizing built-in wave energy converter with decoupled power take-offs. Ocean Eng. 2025, 322, 120450. [Google Scholar] [CrossRef]
- Rahman, M.; Ong, Z.C.; Chong, W.T.; Julai, S.; Khoo, S.Y. Performance enhancement of wind turbine systems with vibration control: A review. Renew. Sustain. Energy Rev. 2015, 51, 43–54. [Google Scholar] [CrossRef]
- Ibrahim, R.A. Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 2008, 314, 371–452. [Google Scholar] [CrossRef]
- Yang, J.; Ning, D.; Sun, S.; Zheng, J.; Lu, H.; Nakano, M.; Zhang, S.; Du, H.; Li, W. A semi-active suspension using a magnetorheological damper with nonlinear negative-stiffness component. Mech. Syst. Signal Process. 2021, 147, 107071. [Google Scholar] [CrossRef]
- Zhang, F.; Shao, S.; Tian, Z.; Xu, M.; Xie, S. Active-passive hybrid vibration isolation with magnetic negative stiffness isolator based on Maxwell normal stress. Mech. Syst. Signal Process. 2019, 123, 244–263. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, Z.; Zhou, Y.; Lu, X. Nonlinear dissipative devices in structural vibration control: A review. J. Sound Vib. 2018, 423, 18–49. [Google Scholar] [CrossRef]
- Bian, J.; Jing, X. Superior nonlinear passive damping characteristics of the bio-inspired limb-like or X-shaped structure. Mech. Syst. Signal Process. 2019, 125, 21–51. [Google Scholar] [CrossRef]
- Liu, C.; Yu, K.; Tang, J. New insights into the damping characteristics of a typical quasi-zero-stiffness vibration isolator. Int. J. Non-Linear Mech. 2020, 124, 103511. [Google Scholar] [CrossRef]
- Hu, X.; Zhou, C. The effect of various damping on the isolation performance of quasi-zero-stiffness system. Mech. Syst. Signal Process. 2022, 171, 108944. [Google Scholar] [CrossRef]
- Donmez, A.; Cigeroglu, E.; Ozgen, G.O. An improved quasi-zero stiffness vibration isolation system utilizing dry friction damping. Nonlinear Dyn. 2020, 101, 107–121. [Google Scholar] [CrossRef]
- Su, N.; Bian, J.; Peng, S.; Chen, Z.; Xia, Y. Analytical optimal design of inerter-based vibration absorbers with negative stiffness balancing static amplification and dynamic reduction effects. Mech. Syst. Signal Process. 2023, 192, 110235. [Google Scholar] [CrossRef]
- Bian, J.; Jing, X. Analysis and design of a novel and compact X-structured vibration isolation mount (X-Mount) with wider quasi-zero-stiffness range. Nonlinear Dyn. 2020, 101, 2195–2222. [Google Scholar] [CrossRef]
- Chai, Y.; Bian, J.; Li, M. A novel quasi-zero-stiffness isolation platform via tunable positive and negative stiffness compensation mechanism. Nonlinear Dyn. 2023, 112, 101–123. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, W.; Yu, K.; Liu, T.; Zheng, Y. Quasi-zero-stiffness vibration isolation: Designs; improvements and applications. Eng. Struct. 2024, 301, 117282. [Google Scholar] [CrossRef]
- Liu, C.; Yu, K. Accurate modeling and analysis of a typical nonlinear vibration isolator with quasi-zero stiffness. Nonlinear Dyn. 2020, 100, 2141–2165. [Google Scholar] [CrossRef]
- Zhao, F.; Ji, J.C.; Ye, K.; Luo, Q. Increase of quasi-zero stiffness region using two pairs of oblique springs. Mech. Syst. Signal Process. 2020, 144, 106975. [Google Scholar] [CrossRef]
- Zhao, F.; Ji, J.; Ye, K.; Luo, Q. An innovative quasi-zero stiffness isolator with three pairs of oblique springs. Int. J. Mech. Sci. 2021, 192, 106093. [Google Scholar] [CrossRef]
- Tian, Y.; Cao, D.; Wang, Y.; Tang, J.; Jiang, B. A Study of a Pendulum-Like Vibration Isolator With Quasi-Zero-Stiffness. J. Comput. Nonlinear Dyn. 2022, 17, 051005. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, R.; Yu, K.; Lee, H.P.; Liao, B. A quasi-zero-stiffness device capable of vibration isolation and energy harvesting using piezoelectric buckled beams. Energy 2021, 233, 121146. [Google Scholar] [CrossRef]
- Yan, B.; Yu, N.; Wang, Z.; Wu, C.; Wang, S.; Zhang, W. Lever-type quasi-zero stiffness vibration isolator with magnetic spring. J. Sound Vib. 2022, 527, 116865. [Google Scholar] [CrossRef]
- Xu, D.; Yu, Q.; Zhou, J.; Bishop, S.R. Theoretical and experimental analyses of a nonlinear magnetic vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vib. 2013, 332, 3377–3389. [Google Scholar] [CrossRef]
- Feng, X.; Jing, X. Human body inspired vibration isolation: Beneficial nonlinear stiffness, nonlinear damping & nonlinear inertia. Mech. Syst. Signal Process. 2019, 117, 786–812. [Google Scholar]
- Deng, T.; Wen, G.; Ding, H.; Lu, Z.-Q.; Chen, L.-Q. A bio-inspired isolator based on characteristics of quasi-zero stiffness and bird multi-layer neck. Mech. Syst. Signal Process. 2020, 145, 106967. [Google Scholar] [CrossRef]
- Ling, P.; Miao, L.; Zhang, W.; Wu, C.; Yan, B. Cockroach-inspired structure for low-frequency vibration isolation. Mech. Syst. Signal Process. 2022, 171, 108955. [Google Scholar] [CrossRef]
- Li, M.; Zhou, J.; Jing, X. Improving low-frequency piezoelectric energy harvesting performance with novel X-structured harvesters. Nonlinear Dyn. 2018, 94, 1409–1428. [Google Scholar] [CrossRef]
- Yan, G.; Zou, H.-X.; Wang, S.; Zhao, L.-C.; Wu, Z.-Y.; Zhang, W.-M. Bio-inspired toe-like structure for low-frequency vibration isolation. Mech. Syst. Signal Process. 2022, 162, 108010. [Google Scholar] [CrossRef]
- Bian, J.; Zhou, X.H.; Ke, K.; Yam, M.C.H.; Wang, Y.H.; Qiu, Y. A passive vibration isolator with bio-inspired structure and inerter nonlinear effects. Struct. Eng. Mech. 2023, 88, 221–238. [Google Scholar]
- Yu, Y.; Yao, G.; Wu, Z. Nonlinear primary responses of a bilateral supported X-shape vibration reduction structure. Mech. Syst. Signal Process. 2020, 140, 106679. [Google Scholar] [CrossRef]
- Chai, Y.; Jing, X.; Chao, X. X-shaped mechanism based enhanced tunable QZS property for passive vibration isolation. Int. J. Mech. Sci. 2022, 218, 107077. [Google Scholar] [CrossRef]
- Li, M.; Cheng, W.; Xie, R. A quasi-zero-stiffness vibration isolator using a cam mechanism with user-defined profile. Int. J. Mech. Sci. 2021, 189, 105938. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, G.; Wen, H.; Jin, D.; Hu, H. Design and analysis of a vibration isolation system with cam–roller–spring–rod mechanism. J. Vib. Control 2021, 28, 1781–1791. [Google Scholar] [CrossRef]
- Cai, C.; Zhou, J.; Wu, L.; Wang, K.; Xu, D.; Ouyang, H. Design and numerical validation of quasi-zero-stiffness metamaterials for very low-frequency band gaps. Compos. Struct. 2020, 236, 111862. [Google Scholar] [CrossRef]
- Yan, B.; Ma, H.; Yu, N.; Zhang, L.; Wu, C. Theoretical modeling and experimental analysis of nonlinear electromagnetic shunt damping. J. Sound Vib. 2020, 471, 115184. [Google Scholar] [CrossRef]
- Liu, C.; Yu, K.; Liao, B.; Hu, R. Enhanced vibration isolation performance of quasi-zero-stiffness isolator by introducing tunable nonlinear inerter. Commun. Nonlinear Sci. Numer. Simul. 2021, 95, 105654. [Google Scholar] [CrossRef]
- Lv, Q.; Yao, Z. Analysis of the effects of nonlinear viscous damping on vibration isolator. Nonlinear Dyn. 2014, 79, 2325–2332. [Google Scholar] [CrossRef]
- Dong, G.; Zhang, Y.; Luo, Y.; Xie, S.; Zhang, X. Enhanced isolation performance of a high-static–low-dynamic stiffness isolator with geometric nonlinear damping. Nonlinear Dyn. 2018, 93, 2339–2356. [Google Scholar] [CrossRef]
- Zhang, J.; He, H.; Zhang, Z. Research Status and Development Prospects of Offshore Wind Turbine Foundation Structures. Nav. Archit. Ocean Eng. 2023, 39, 1–6. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).