1. Introduction
Chip removal machining offers multiple advantages in product manufacturing processes. This technology has played a significant role in the development of societies, playing a key role in developing solutions to diverse problems, such as surface finish control, geometric tolerances, and manufacturing times, among other process advantages. To achieve these advantages, it is necessary to propose technological parameters for the machining process based on process reliability, a task that has not been easy to systematize, given the multiple variables that define the parameters involved during the process.
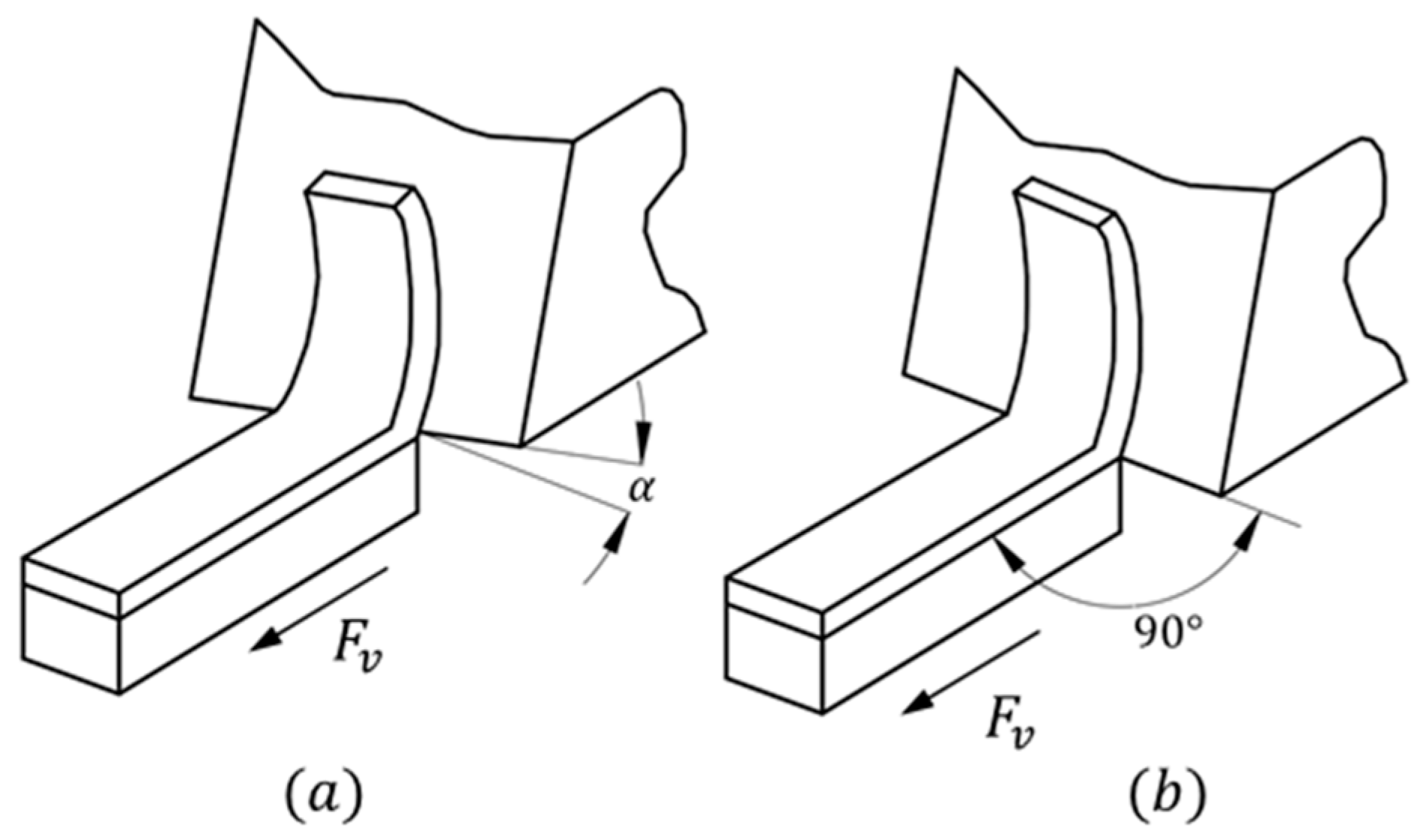
The dynamics of chip removal from the component to be machined are based on the use of a cutting tool, with cutting edges defined by inclination angles. These tools can be used to make straight cuts (perpendicular to the work surface) and oblique cuts (with a tool inclination angle).
Figure 1 illustrates these processes.
Most machined components not only involve a specific configuration during the machining operation but are also subjected to different combinations of these operations: turning, rounding, facing, grooving, and threading, among others. There will most likely be different cutting tools, each with its own lead angles, nose roundings, and material characteristics. All these variations in the workpieces will generate different configurations that involve movements and dynamic loads during the machining process. A detailed study of these configurations is required to fully understand these implications. The objective of this article is to show a method for selecting parameters in cutting speed and dept; variations in the angles of attack of the cutting tool that modify the presence of the applied force are not considered in this analysis. For simplicity, it will be assumed that the cut of interest is oblique and directed along the perpendicular axes shown in
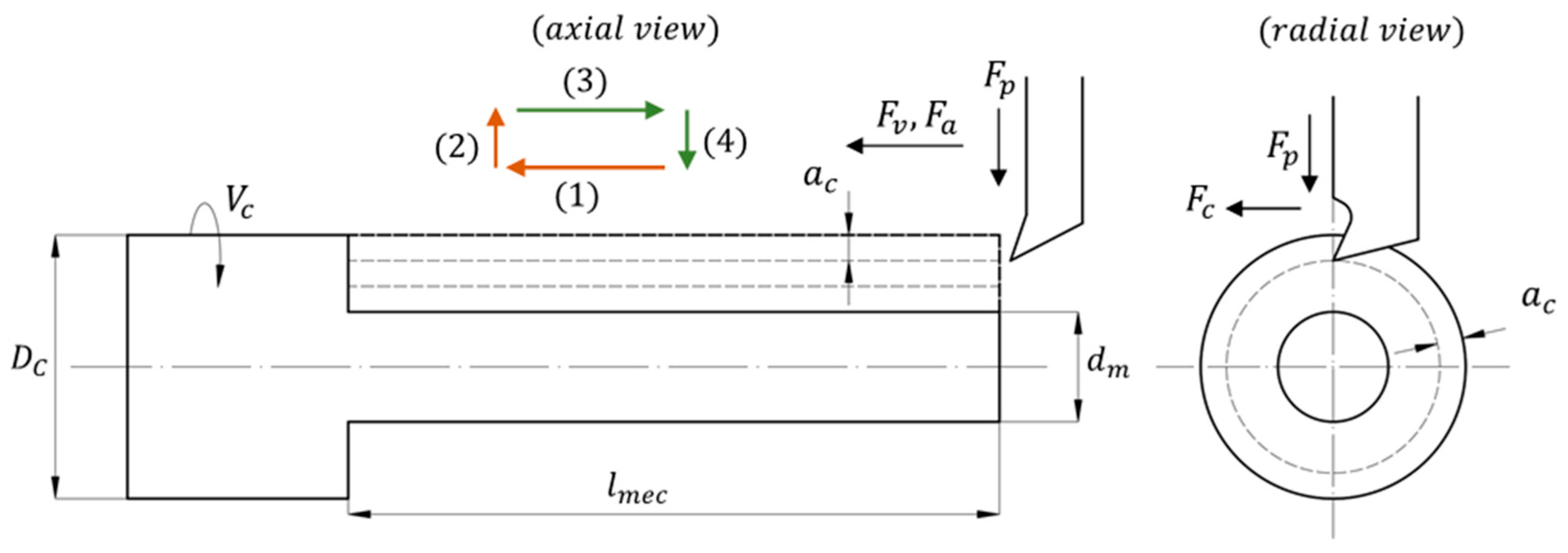
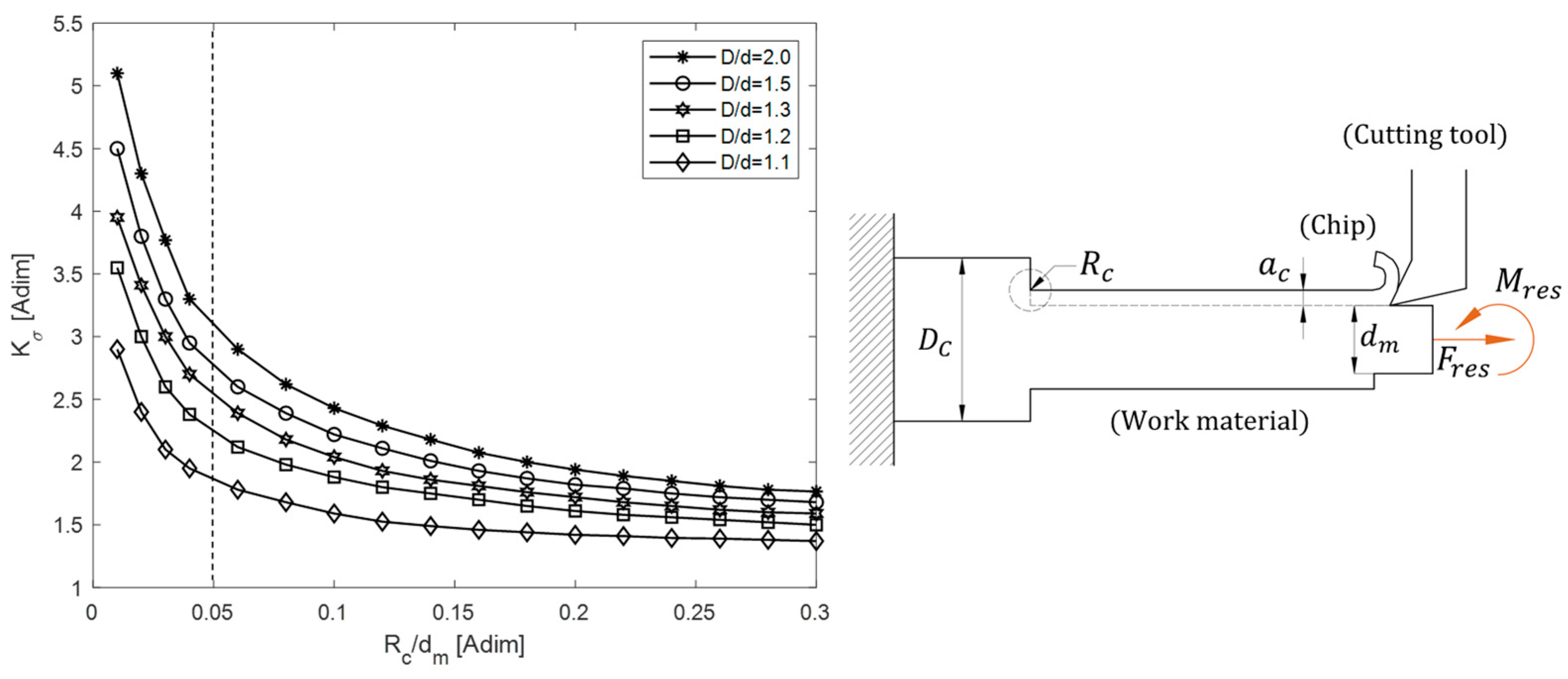
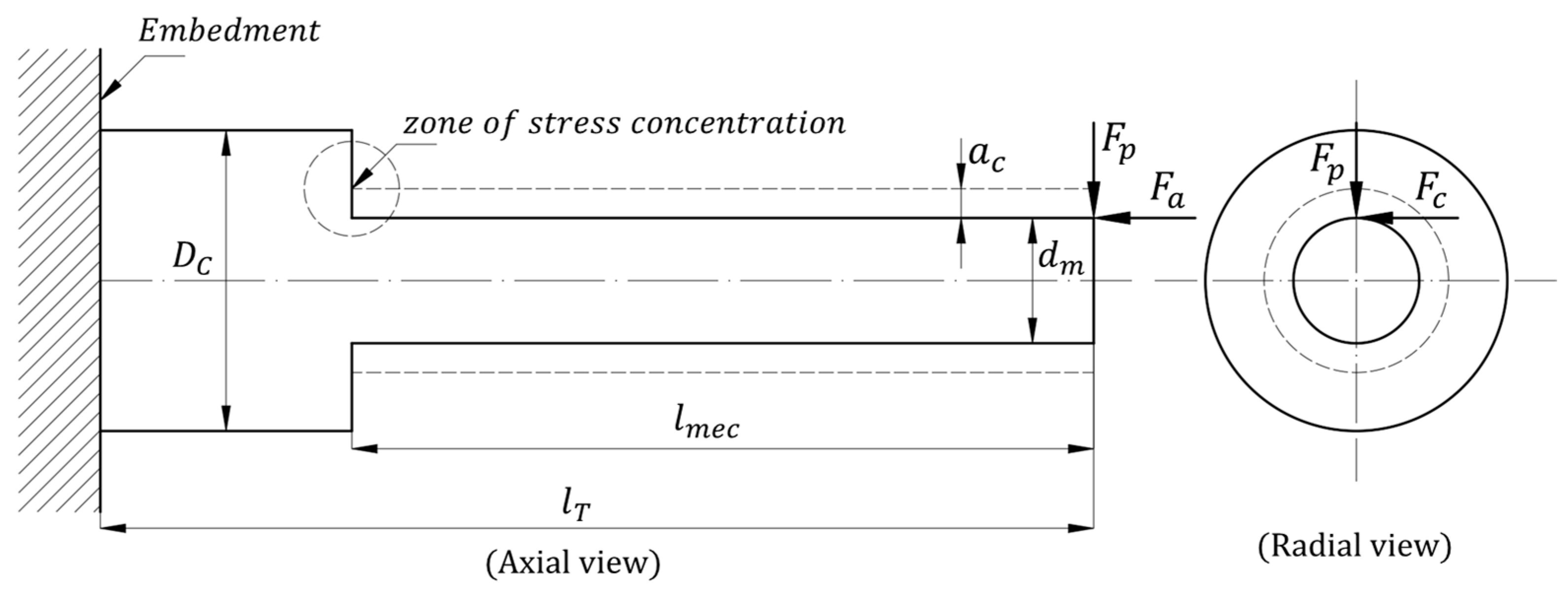
Figure 2, where the expressions for calculating the loads due to contact with the cutting tool and the material are provided by Equation (1), described later.
Cutting is carried out by applying a cutting force at a tool feed rate . The machining process to be considered will be external turning, going from a larger diameter to a smaller final finish diameter , by applying depth cuts over a total machining length and successively applying cutting passes , which are positive integers. The machining process also involves the tangential cutting speed and the process quality conditions, defined as the desired surface roughness of the part .
The arrows numbered (1) to (4) indicate the direction the cutting tool will take during the machining process. Directions (1) and (2) indicate cutting processes, (3) is rapid retraction, and (4) is positioning for a new cut of thickness . The above cycle will be repeated until the requested measurement is reached.
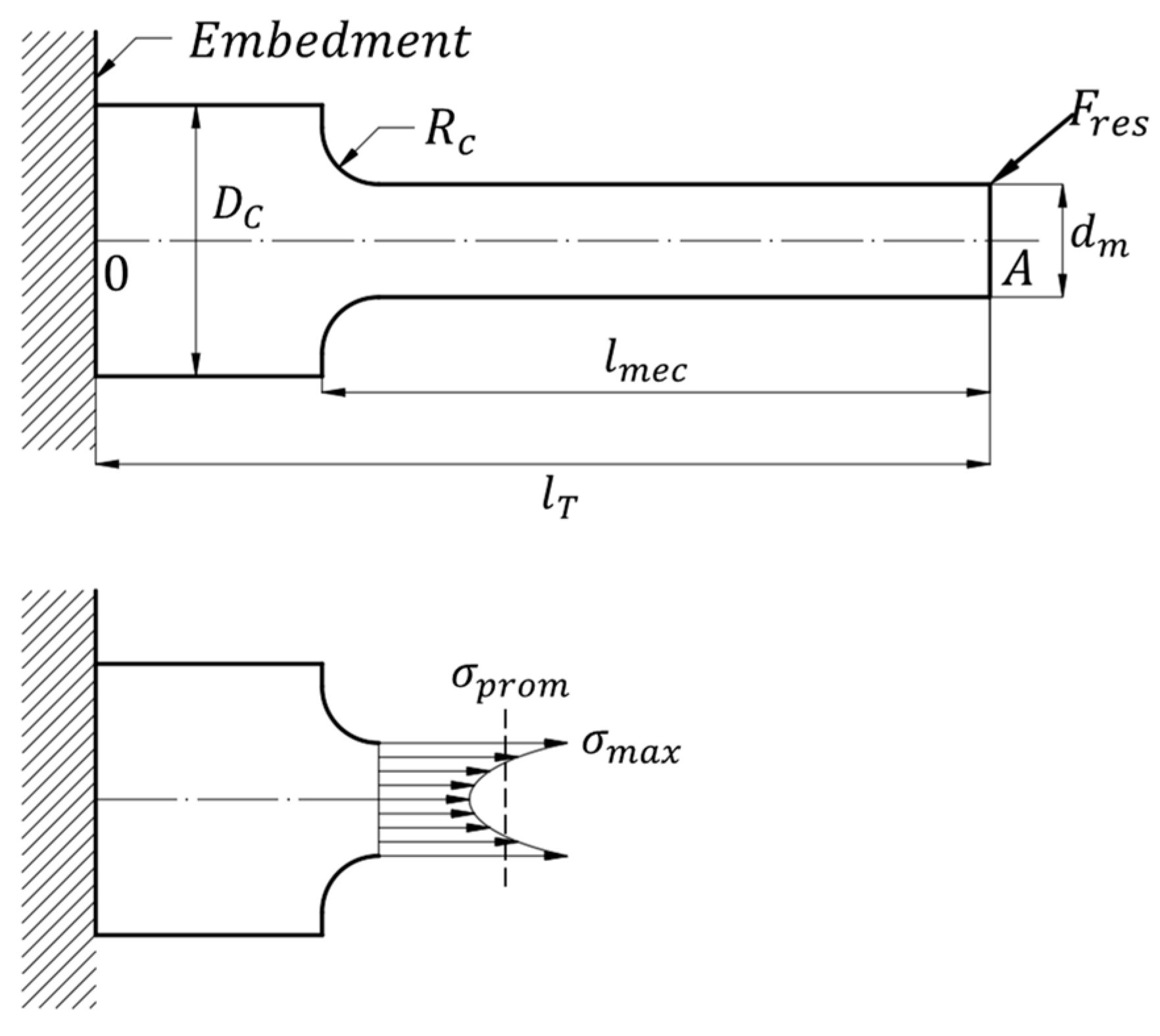
The workpiece to be machined has mechanical properties that, depending on the external loads applied to it during the machining process due to contact with the cutting tool and the desired geometric configuration, may tend to fail during the machining process. The most common failure in the machining process, if proper process design (cutting depth, speed, and feed rate, among others) is not considered, will manifest as the fracture of the workpiece during the machining process.
Another, even more dangerous failure (from the author’s perspective), compromises the structural integrity of the component during the machining process, generating cumulative damage that manifests over time and with the use of the component, which can lead to earlier failure than planned in the component design process, decreasing the reliability of the component and generating losses of variable magnitude.
As can be inferred, it is vitally important, when planning the machining process, to consider the loads applied to the material, since these will result in the prevalence of defects or elements that compromise the long-term quality of the component to be machined.
Due to the importance of the chip removal machining process and the consequences of not properly calculating its parameters, many authors throughout history have tried to find methods, through estimation and analysis or combined methods, to choose the best machining parameters that maximize some benefit criterion. Some examples are the work carried out by the authors in [
1,
2,
3], where, based on specific product cases and through direct and indirect measurements, they seek to obtain the best cutting speeds for the process to maximize some other parameter of interest to the process, such as machining cost.
Other authors use computational systems and evolutionary algorithms in combination with maximization requirements for machining processes to estimate the optimal machining parameters, as in [
4], where swarm algorithms are used to achieve this goal.
Other authors, such as [
5,
6], seek precision in the machining process by monitoring and estimating machine tool conditions. Others, such as [
7], determine the behavior of the machine process through measurement and comparison with accessories such as lubricants in the process or by monitoring cutting tool characteristics and process-related wear, as in [
8,
9,
10]. Authors such as [
11] also seek to define the effect of temperature on the degradation and wear of the process.
Measurement of machining parameters, such as cutting force, is critical for the correct validation of processes. The authors of [
12] use measurement mechanisms to determine the magnitude of the force applied to a machining process, thereby estimating the optimal state of the product.
Other authors study the importance of dynamic analysis to eliminate negative effects in machining processes, such as vibration, through modifications in machining conditions, as is the case in [
13].
This paper aims to contribute to process optimization and reliability methods by proposing parameter estimation based on the geometry of the component to be machined, its mechanical properties, the power delivered by the machine, and the structural integrity derived from the combination of these parameters, formulating a problem within the field of multi-objective optimization. A bibliographic review of multi-objective optimization applied to machining processes was conducted, and the most relevant results for this research are presented.
Regarding the modeling of multi-objective systems, within the field of research of this article, several works of interest were observed, such as [
14] where multi-objective functions are presented, defining the multiple objectives as material removal rate and the rolling factor.
In the article reviewed in [
15], the topic of multi-objective optimization is also addressed by defining the parameters of cutting depth, feed, and speed and defining the multi-objective function, such as tool life and operating time.
In the article reviewed in [
16] multi-objective optimization is worked on by defining a function defined as a desirability function, where the corresponding optimal values of the input parameters are cross feed, cutting speed, and cutting depth.
In the article shown in [
17], a multi-objective optimization mathematical model is presented that considers the spindle speed, cutting tool feed, cutting depth, and process paths as parameters, while the objective function is defined as energy consumption, surface roughness, and machining time.
In the article shown in [
18] a multi-goal optimization model is developed where the cutting speed and feed rate are defined as parameters of the objective functions, which are defined as carbon emissions and machining time.
In the article presented in [
19] the multi-objective function is designed based on Taguchi experimentation, where the objective functions are cutting quality, production speed, and energy consumption reduction.
In the article presented in [
20], a series of advanced multi-objective algorithms for the optimization of turning parameters such as cutting speed, feed, and depth of cut are tested by experimental tests of cutting forces and temperatures, determining material removal rates and surface roughness, and applying four optimization algorithms; values were obtained for the defined functions. This article will be used later to make the comparison with the method of interest.
Table 1 shows the results obtained by various tests carried out and taken into consideration by the author.
In the article shown in [
21] a multi-objective optimization study of the turning process is carried out based on the Taguchi experiment and by modifying the values of five parameters: tool tip radius, tool holder length, spindle speed, feed rate, and cutting depth, from which the objective functions were constructed: surface roughness, roundness deviation, and material removal capacity.
The article defined in [
22] uses neural network-based prediction models to minimize the effect of vibration on the milling process. This article was of interest because the topic it addresses is complementary to that developed in the present article.
The article presented in [
23] proposed a multi-objective optimization model for the parameters involved in CNC turning, considering energy consumption in transient and steady states, as well as tool life.
After reviewing the bibliography described in [
14,
15,
16,
17,
18,
19,
20,
21,
22,
23], it is concluded that the authors do not present a combination of parameters that involve the machine power, surface roughness, and structural integrity as restrictions to building a mathematical optimization model that involves minimizing the machining cycle time.
Based on the argument previously stated, it is concluded that the topic that the authors develop in this paper is innovative, since it will contribute to the optimization and systematization of the machining process, because it is about presenting an integrative method that takes into account not only the requirements for machining the piece but also restrictions of the machine tool and the work material in order to guarantee the structural integrity and reliability of the machining.
5. Discussion
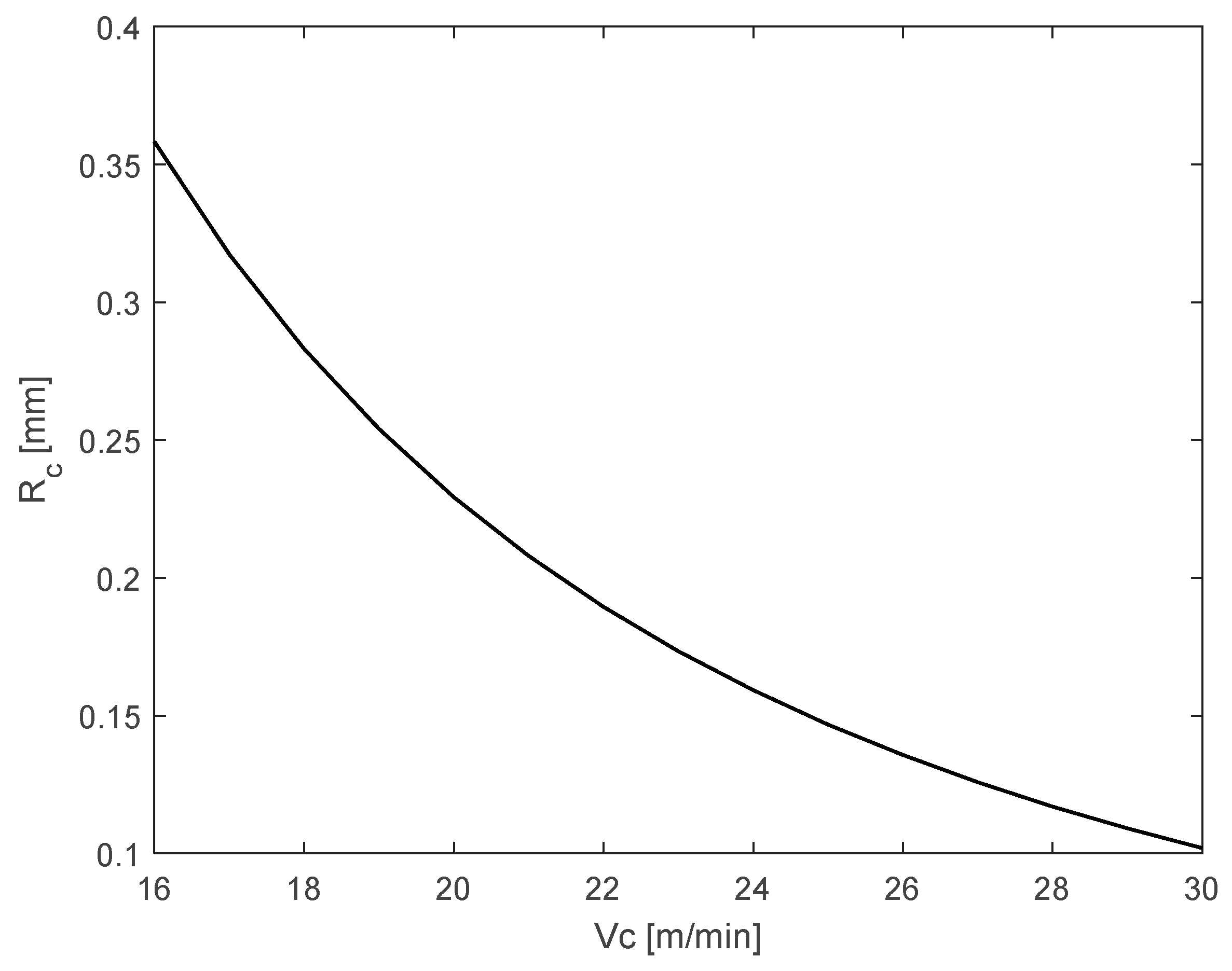
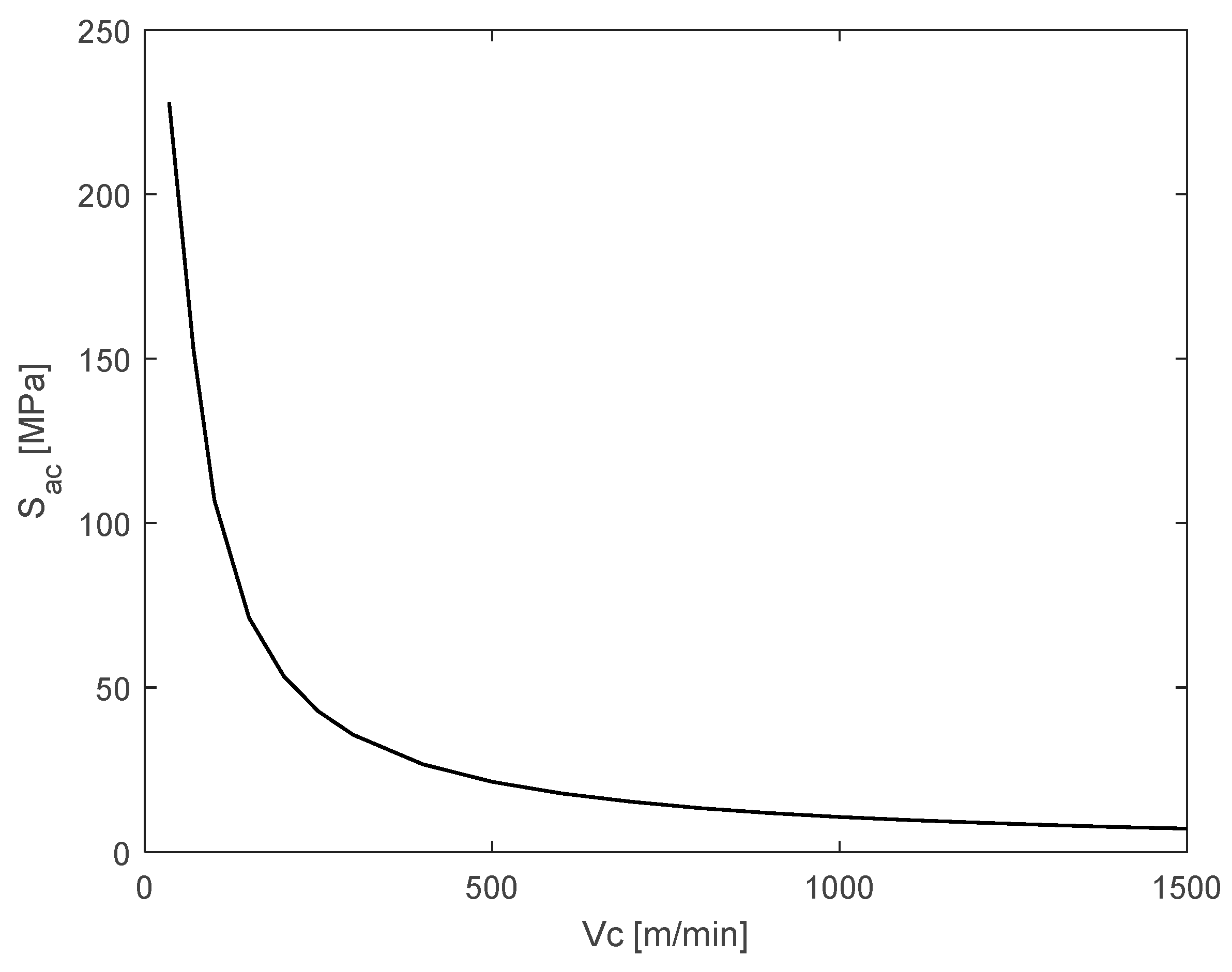
The developed model allows, based on the results obtained in the simulation, exploration of the behavior of the cutting speed
within the ranges recommended by tool manufacturers and its relationship with machining parameters in the study piece, such as the optimal cutting depth
that will guarantee the reliability and structural integrity of the process. The variation of the cutting tool nose radius
and its variation with the cutting speed
can be observed. It is observed that at higher cutting speeds, the cutting tool nose radius is smaller, which meets the requested roughness requirements.
Figure 14 illustrates this process.
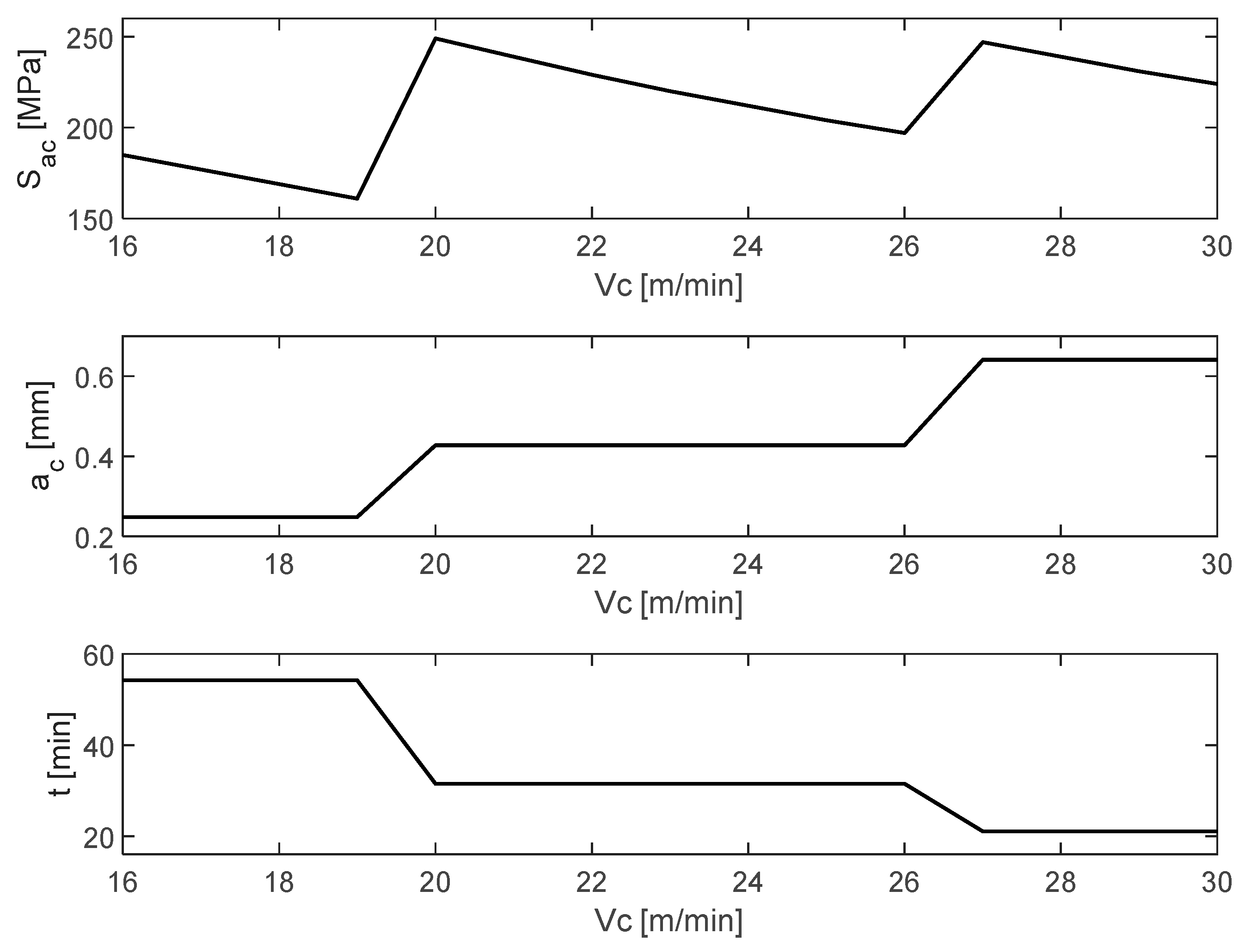
Among the important findings are values that, although permissible by the machining process, should not be selected since they generate the risk of compromising the structural integrity due to the stresses that will be obtained in the cutting process of the material
.
Figure 15 illustrates the behavior of these cutting parameters, crests and valleys, with respect to the stress
generated by the optimal cutting depth
and the time t consumed in the machining process. From this data, the professional will have more information on which values to take according to their technical requirements.
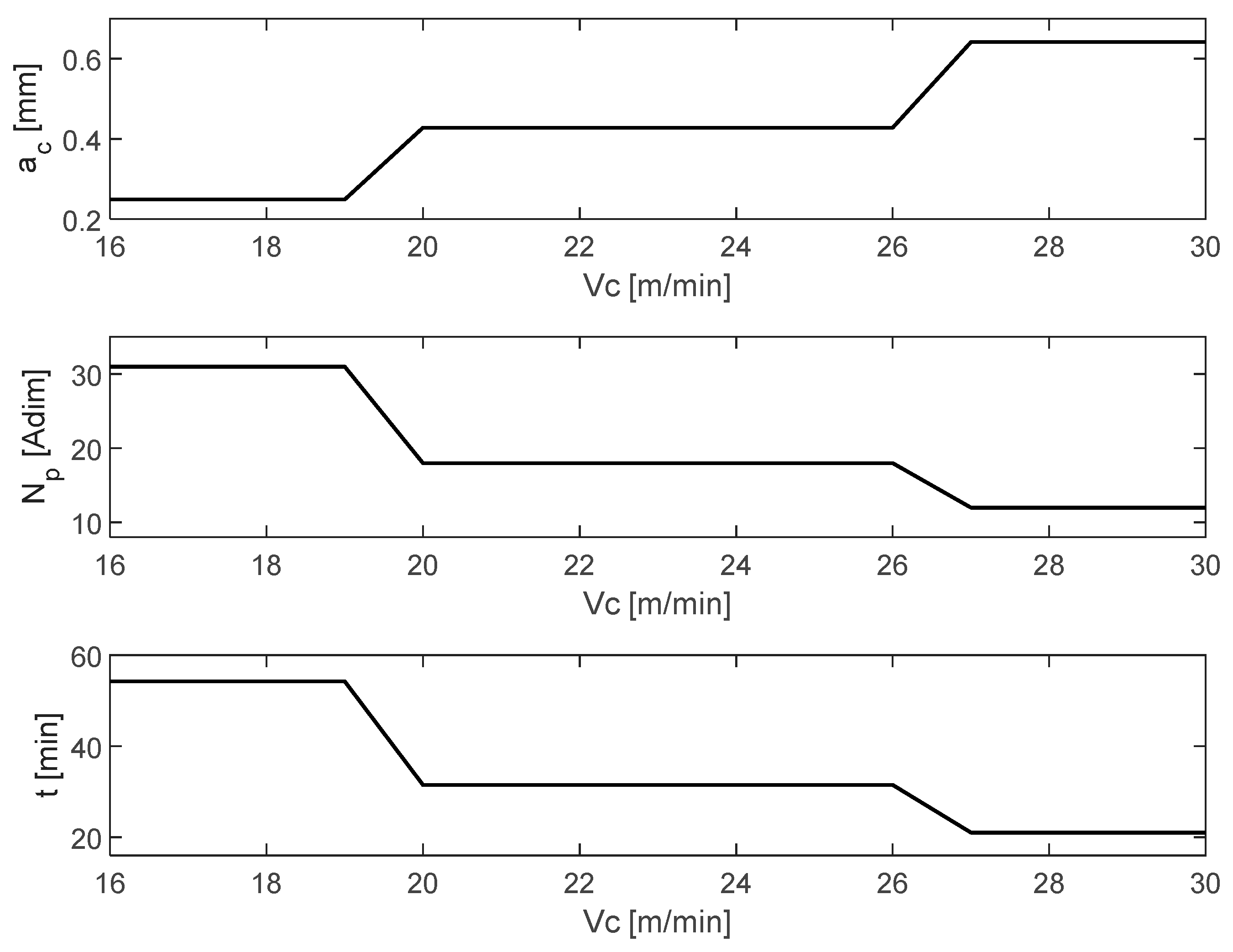
According to the allowable cutting speed
, there will be optimal cutting depth values
in intervals of values in cutting speed
, which will generate the same effect in terms of number of machining cycles
and machining time
.
Figure 16 illustrates this process in such a way that in practice, if only these parameters are involved, it does not matter whether you work at one cutting speed or another that is in the same interval where the machining time
is due to the number of machining cycles
being equal.
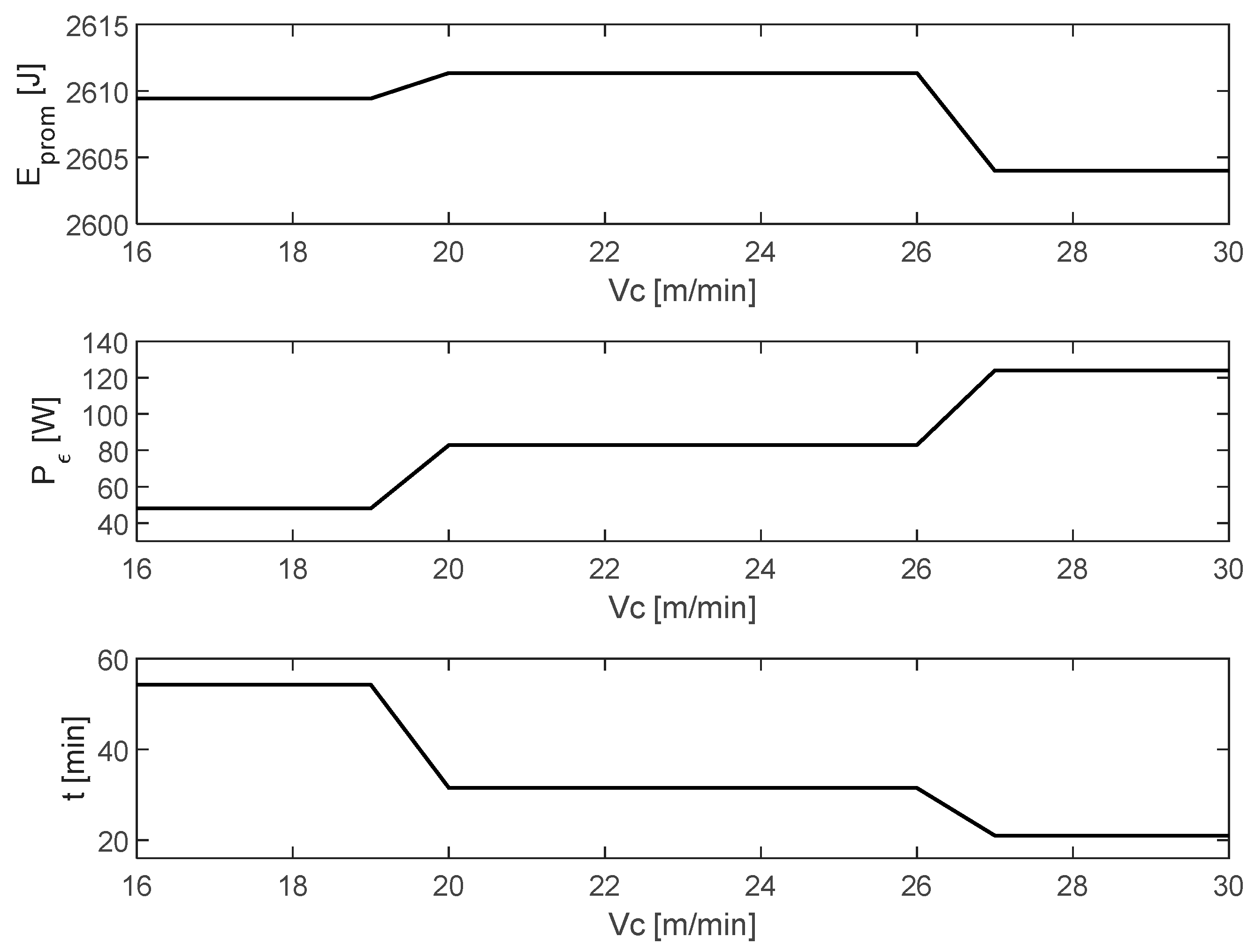
According to the restrictions imposed on the model, the algorithm will always seek to meet viable conditions within the range of allowable cutting speed
and adjusting cutting depth
for the machining process in such a way that the average energy consumed
will try to balance between elapsed time t and consumed power
, showing a quasi-constant behavior as observed in
Figure 17.
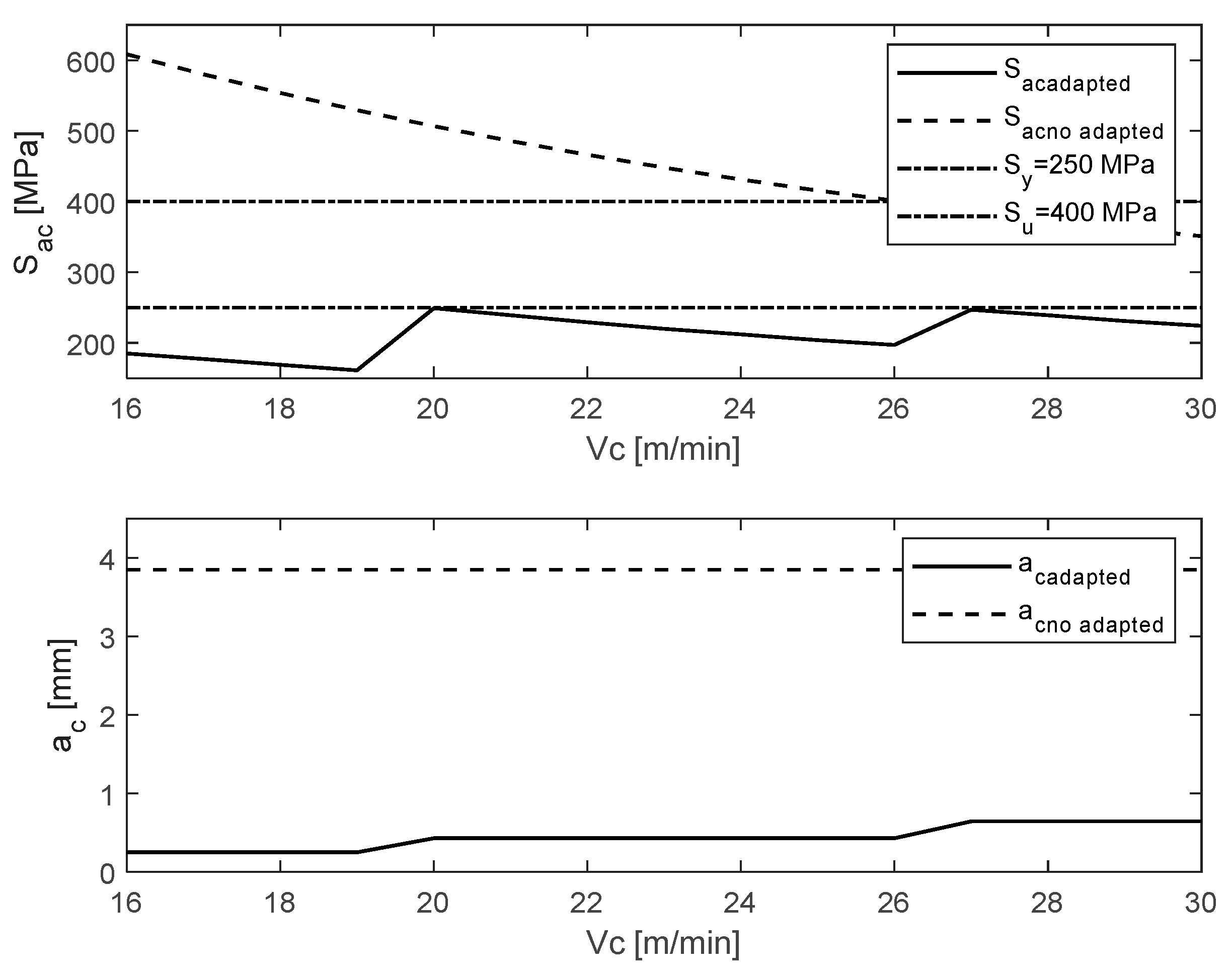
Table 7 summarizes the values obtained by varying the cutting speed within the permissible parameters for the process. Among the values presented in
Table 7, it is important to highlight the column corresponding to the calculation of the maximum stress
, calculated by using the maximum possible cutting depth
due to the cutting power provided by the machine tool motor
. With the calculation of this maximum stress it is possible to justify why, despite the fact that the machine tool allows through the power delivered by it
, it is not advisable to use the maximum cutting thickness
, because this will give rise to a stress
that in most of the cutting speed values used exceeds the ultimate allowable stress
by the test material. Moreover, from that maximum thickness
under the test with all the test cutting speeds
, the estimated maximum stress
exceeds the yield strength
of the test material, which will lead to exceeding the elastic limit of the workpiece, generating, at least, plastic deformations and thereby compromising the machining process.
Figure 18 illustrates the behavior of the stress obtained with respect to the optimal cutting depth
and the initial cutting depth
defined by the characteristics of the electrical power delivered by the machine tool.
The analysis presented in this article is focused on manual machining; however, the presented model can, in theory, provide cutting depth
values for automatic machines operating at higher cutting speed
, from which an analysis of the variation of high cutting speeds for automatic machines is presented, it was observed that, at higher cutting speeds involved in the machining process, the resulting effort of the process is lower, and therefore, the reliability in the process increases significantly, which results in a point to consider when discussing the replacement of equipment or the simulation of the process under other allowed parameters of cutting speed for other types of machinery.
Figure 19 summarizes the theoretical values when varying the speed from
to
and the effort obtained from the process
.
Other parameters, such as cutting depth, are not considered because starting at values of 70 m/min, the minimum required cutting depth is , the power consumed by the electric motor remains at , the number of passes is , and the machining time is .
It should be noted that these simulated high speeds do not consider imbalances, vibration imperfections, or other loading factors, which must be analyzed in greater detail for high-speed analysis. Future work involves strengthening the decision-making model by incorporating more factors from the machining process. For now, the work completed is considered satisfactory.
The method shown is scalable to other types of materials and machines under the same load configuration and geometric configurations; it will be enough to define the parameters of the materials in the proposed model, taking as references the tables recommended by manufacturers of cutting speeds, feeds, and properties of the working materials, exemplified in
Table 2 and
Table 3.
To analyze the characteristics of the developed model, a comparison is made with the model proposed in [
20]. Based on the results presented therein and using the optimal cutting speed defined by the author, the results shown in
Table 6 are obtained.
To draw conclusions from the comparison, some observations must be made:
The model analyzed in [
20] considers the optimization criterion defined as the material removal rate (MRR).
The proposed model uses the final diameter required for the workpiece dm as a necessary measure for calculating structural integrity and process reliability.
The optimization criterion in the proposed model is the machining time and the adjustment of the cutting depth relative to the machining cycle, in conjunction with the available cutting speed Vc.
From which it can be observed that, taking the same criteria of cutting speed
, tool feed
, geometric parameters defined only in roughing operation, there is a variation in the calculation of the cutting force, approximately half of the available. This discrepancy can be explained as a combination of different factors, such as the angular configuration of the tool used in the process described in [
20] and the oblique cutting model proposed in this article, the structural integrity factor, and geometric factors involved in the process. The obtained roughness parameter
is practically the same in both models. These models and subsequent adjustments will be studied in greater depth in future work.
There are several topics to be addressed further under the load analysis framework described above. One of these is dealing with various load configurations, i.e., parts subjected to turning, facing, parting, etc., since these load configurations will give rise to other stress and resistance configurations later.
Another topic of interest is to strengthen the model through a buckling analysis under eccentric loads to determine the vibratory effect of the component to be used. This loading effect is not considered; however, for various load configurations and geometrical characteristics of the part to be machined, will contribute to poor machining.
Following the line of effects due to configuration on mechanical properties, geometry of the part, and dynamics imposed on the system by cutting speed, the vibratory effect of these factors must be analyzed and verified to determine whether together they do not contribute negatively to the machining process, manifesting as imbalances and generating deficiencies in surface machining and machining tolerances.
6. Conclusions
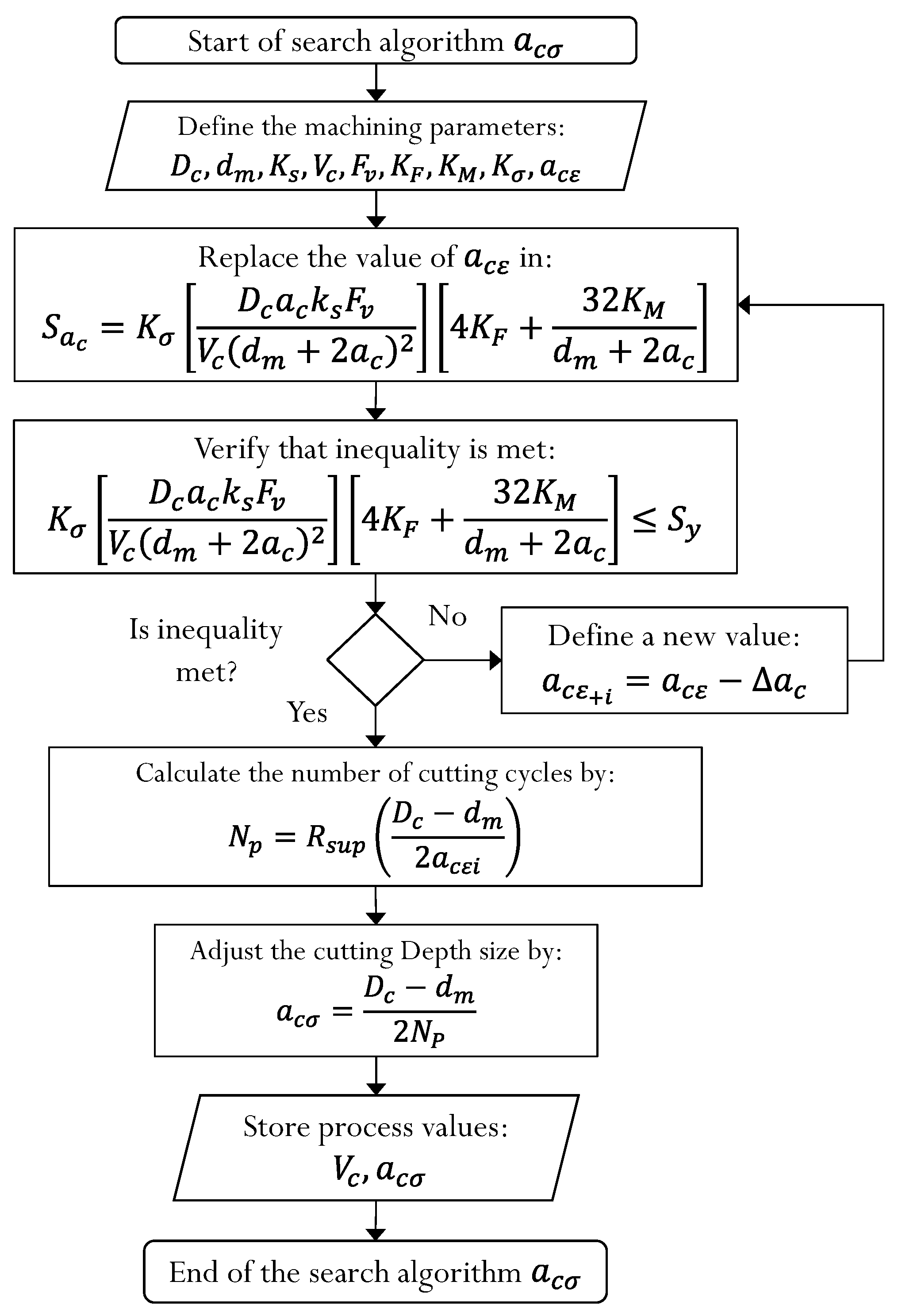
In this paper, a new method is presented for the calculation of the depth of cut and cutting speed focused on machining by chip removal in turning process under roughing operation. This method takes into consideration the loads applied to the workpiece derived from the interaction between cutting tool and work material, as well as the dynamics requested to the machine tool, characterized in the electric power of the motor and the surface finishing conditions required by the surface roughness , integrated in an optimization model that is solved by an iterative search algorithm, which preserves the structural integrity by interpolating parameter values that meet the requested requirements according to the mentioned limitations.
By implementing the parameter search method defined by the iterative algorithm, it is guaranteed that the deflection in the part, as well as the eccentric load due to the cutting, will be within the requested restrictions, thereby ensuring the quality of the surface finish. If a cutting depth greater than estimated is applied, there is a risk of deflection in the part, which could lead to vibratory phenomena that would contribute to the deterioration of the surface roughness , also affecting the dimensional tolerances requested from the workpiece. Under the considerations of defined load analysis, the proposed method is satisfied since it is consistent with the classical theories of structural failure of mechanical components, successfully integrating the optimal machining parameters of interest.
From this article, an analytical methodology is made available to the machining process analyst estimating the optimal cutting depth and cutting speed , according to the optimal machining time , based on structural behavior analysis of the workpiece. With this, it is guaranteed that the workpiece, in an analytical manner, is reliable under the configuration process of the material parameters and the requested geometry. It consumes the minimum electrical power necessary, according to the conditions of the machine tool motor, and that it guarantees to have the minimum surface roughness quality required by the designer of the piece.