Tracking and Registration Technology Based on Panoramic Cameras
Abstract
1. Introduction
- We propose an unsupervised deep learning-based pose estimation model for panoramic cameras, aiming to address the dependence of model training on large-scale panoramic pose-labeled data and to quickly and accurately estimate the pose information of panoramic cameras.
- To reduce the complexity of the model and improve the computational efficiency, we design a lightweight depth estimation sub-network and a pose estimation sub-network.
- To improve the accuracy of the pose estimation, especially to deal with the effect of relative motion, we introduce a learnable occlusion mask module in the pose estimation sub-network.
- To realize the joint training of the two sub-networks, we utilize the constructed panoramic view reconstruction model to extract effective supervised signals from the predicted depth and pose information and the corresponding panoramic images and combine them with the designed spherical photometric consistency loss function to supervise the model training.
2. Related Work
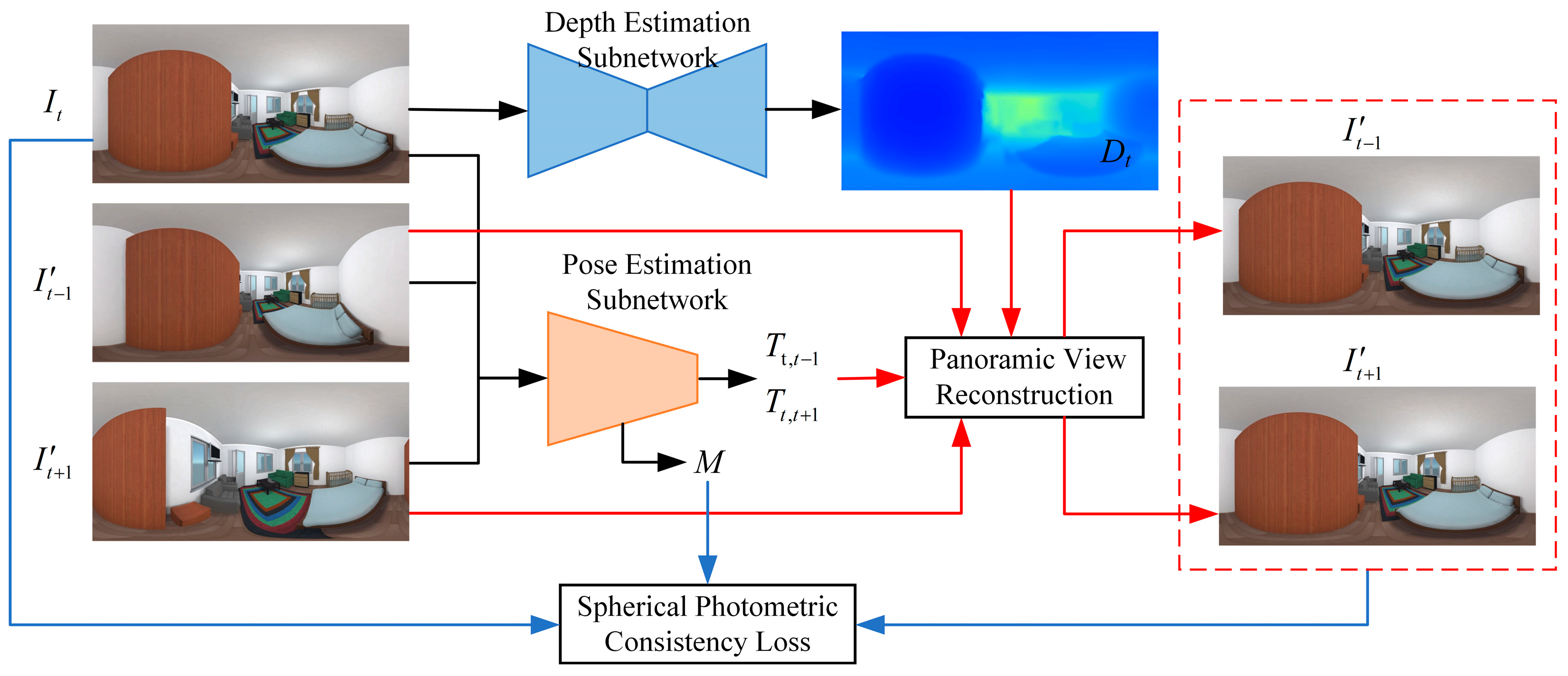
3. Method
3.1. Network Architecture
3.2. Panoramic Depth Estimation Sub-Network
3.3. Panoramic Pose Estimation Sub-Network
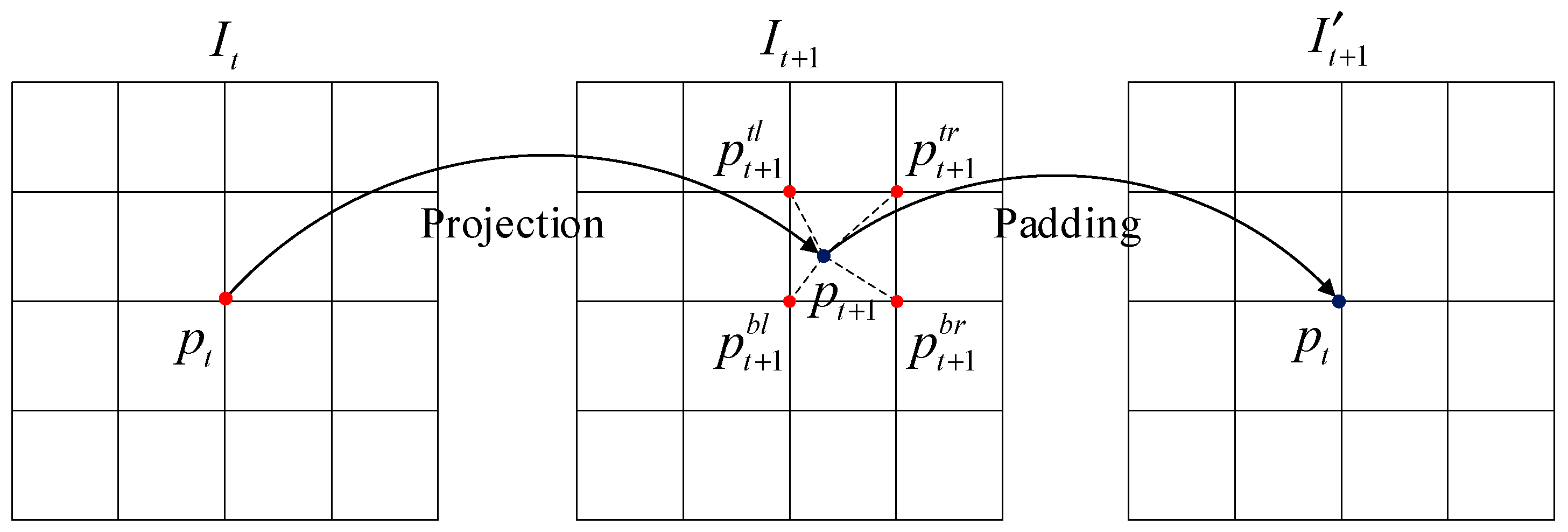
3.4. Panoramic View Reconstruction
3.5. Loss Function
4. Experiments
4.1. Experimental Settings
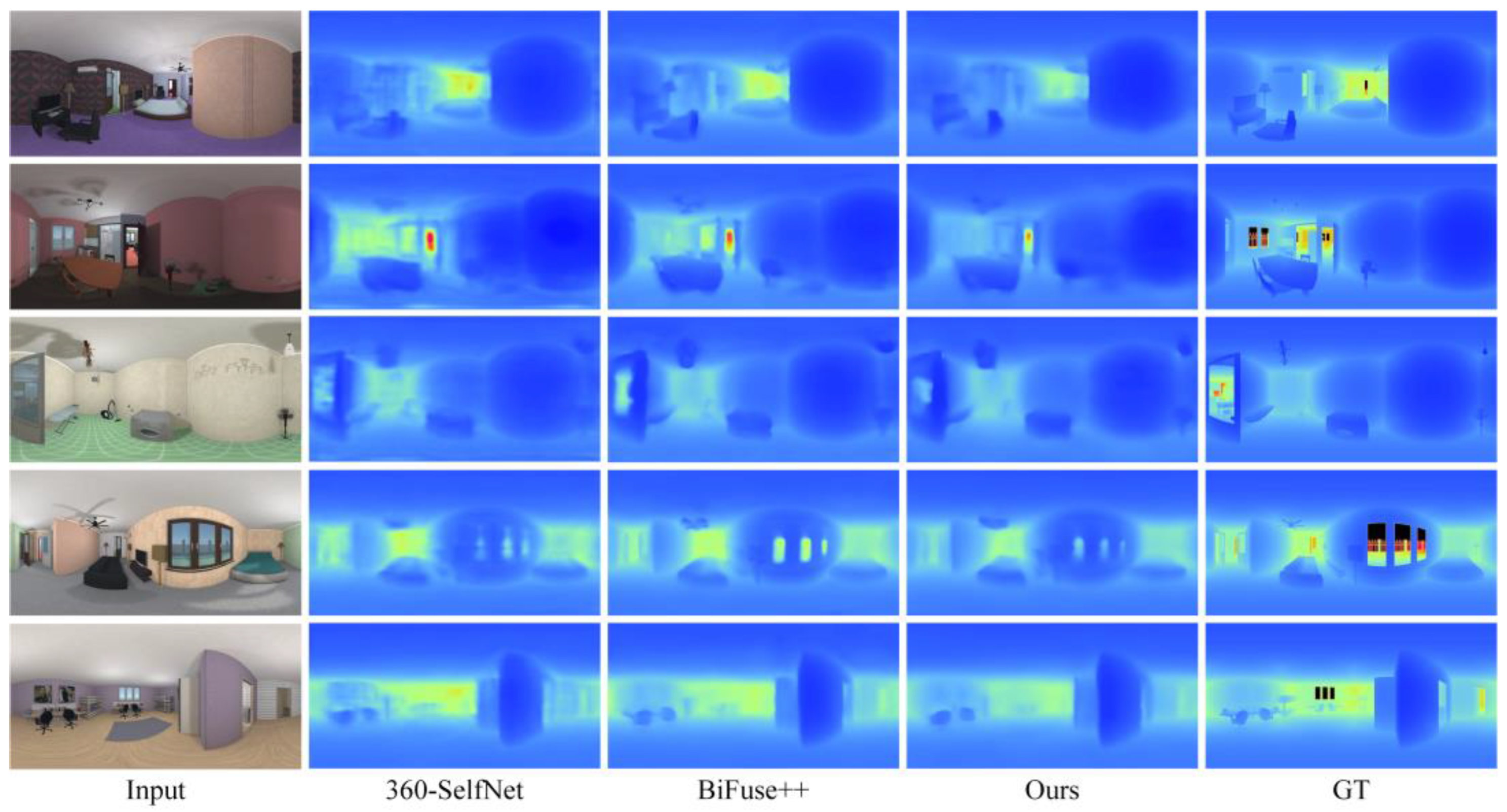
4.2. Comparison Results
4.3. Ablation Study
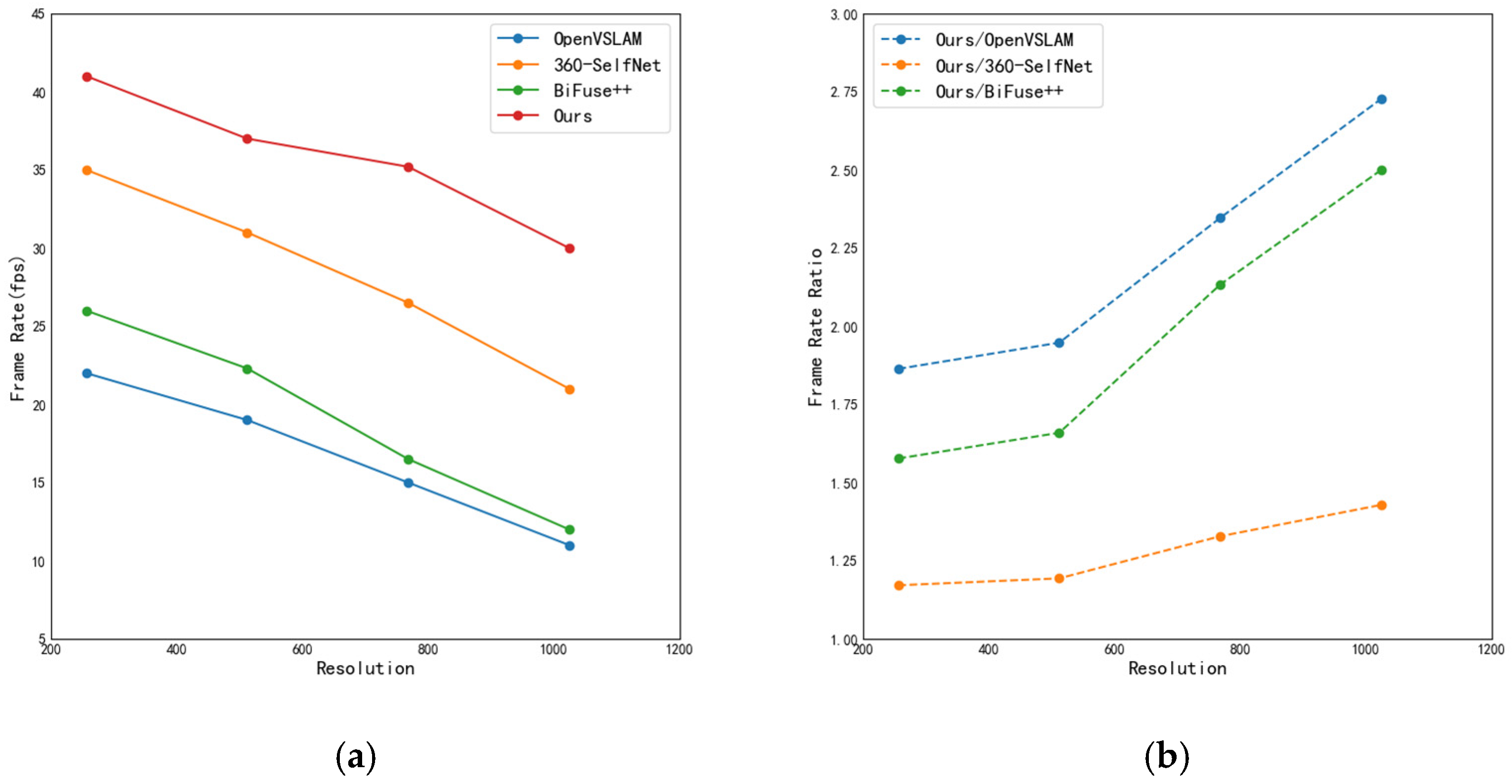
4.4. Complexity Comparison
4.5. Limitations Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kato, H.; Billinghurst, M. Marker Tracking and HMD Calibration for a Video-Based Augmented Reality Conferencing System. In Proceedings of the 2nd IEEE and ACM International Workshop on Augmented Reality (IWAR’99), San Francisco, CA, USA, 20–21 October 1999; IEEE: San Francisco, CA, USA, 1999; pp. 85–94. [Google Scholar]
- Wagner, D.; Schmalstieg, D.; Bischof, H. Multiple target detection and tracking with guaranteed framerates on mobile phones. In Proceedings of the 8th IEEE International Symposium on Mixed and Augmented Reality, Orlando, FL, USA, 19–22 October 2009; pp. 57–64. [Google Scholar]
- Klein, G.; Murray, D. Parallel tracking and mapping for small AR workspaces. In Proceedings of the 6th IEEE and ACM International Symposium on Mixed and Augmented Reality, Nara, Japan, 13–16 November 2007; pp. 225–234. [Google Scholar]
- Mur-Artal, R.; Tardós, J.D. ORB-SLAM2: An open-source SLAM system for monocular, stereo, and RGB-D cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Newcombe, R.A.; Lovegrove, S.J.; Davison, A.J. DTAM: Dense tracking and mapping in real-time. In Proceedings of the 2011 International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 2320–2327. [Google Scholar]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-scale direct monocular SLAM. In Proceedings of the European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014; pp. 834–849. [Google Scholar]
- Engel, J.; Koltun, V.; Cremers, D. Direct sparse odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 611–625. [Google Scholar] [CrossRef] [PubMed]
- Forster, C.; Pizzoli, M.; Scaramuzza, D. SVO: Fast semi-direct monocular visual odometry. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 15–22. [Google Scholar]
- Matsuki, H.; Von Stumberg, L.; Usenko, V.; Stückler, J.; Cremers, D. Omnidirectional DSO: Direct Sparse Odometry with Fisheye Cameras. IEEE Robot. Autom. Lett. 2018, 3, 3693–3700. [Google Scholar] [CrossRef]
- Seok, H.; Lim, J. ROVO: Robust Omnidirectional Visual Odometry for Wide-Baseline Wide-FoV Camera Systems. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 6344–6350. [Google Scholar]
- Ji, S.; Qin, Z.; Shan, J.; Lu, M. Panoramic SLAM from a Multiple Fisheye Camera Rig. ISPRS J. Photogramm. Remote Sens. 2020, 159, 169–183. [Google Scholar] [CrossRef]
- Huang, H.; Yeung, S.-K. 360VO: Visual Odometry Using a Single 360 Camera. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 5594–5600. [Google Scholar]
- Sumikura, S.; Shibuya, M.; Sakurada, K. OpenVSLAM: A Versatile Visual SLAM Framework. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 2292–2295. [Google Scholar]
- Kendall, A.; Grimes, M.; Cipolla, R. Posenet: A Convolutional Network for Real-Time 6-DoF Camera Relocalization. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2938–2946. [Google Scholar]
- Wang, S.; Clark, R.; Wen, H.; Trigoni, N. DeepVO: Towards End-to-End Visual Odometry with Deep Recurrent Convolutional Neural Networks. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2043–2050. [Google Scholar]
- Zhou, T.; Brown, M.; Snavely, N.; Lowe, D.G. Unsupervised Learning of Depth and Ego-Motion from Video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1851–1858. [Google Scholar]
- Yin, Z.; Shi, J. GeoNet: Unsupervised Learning of Dense Depth, Optical Flow and Camera Pose. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 1983–1992. [Google Scholar]
- Wang, F.-E.; Hu, H.-N.; Cheng, H.-T.; Lin, J.-T.; Yang, S.-T.; Shih, M.-L.; Chu, H.-K.; Sun, M. Self-Supervised Learning of Depth and Camera Motion from 360 Videos. In Proceedings of the Asian Conference on Computer Vision, Perth, Australia, 2–6 December 2018; Springer: Cham, Switzerland, 2018; pp. 53–68. [Google Scholar]
- Sharma, A.; Ventura, J. Unsupervised Learning of Depth and Ego-Motion from Cylindrical Panoramic Video. In Proceedings of the 2019 IEEE International Conference on Artificial Intelligence and Virtual Reality (AIVR), San Diego, CA, USA, 9–11 December 2019; p. 139. [Google Scholar]
- Liu, M.; Wang, S.; Guo, Y.; He, Y.; Xue, H. Pano-SfMLearner: Self-Supervised Multi-Task Learning of Depth and Semantics in Panoramic Videos. IEEE Signal Process. Lett. 2021, 28, 832–836. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Ikehata, S.; Aizawa, K. Distortion-Aware Self-Supervised 360° Depth Estimation from a Single Equirectangular Projection Image. arXiv 2022, arXiv:2204.01027. [Google Scholar]
- Wang, F.-E.; Yeh, Y.-H.; Tsai, Y.-H.; Chiu, W.-C.; Sun, M. Bifuse++: Self-Supervised and Efficient Bi-Projection Fusion for 360° Depth Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 5448–5460. [Google Scholar] [CrossRef] [PubMed]
- Hou, S.; Han, J.; Zhang, Y.; Zhu, Z. Survey of Vision-Based Augmented Reality 3D Registration Technology. J. Syst. Simul. 2019, 31, 2206–2215. [Google Scholar]
- Zhi, H.; Yin, C.; Li, H. Review of Visual Odometry Methods Based on Deep Learning. Comput. Eng. Appl. 2022, 58, 1–15. [Google Scholar]
- Zhang, Z.; Rebecq, H.; Forster, C.; Scaramuzza, D. Benefit of Large Field-of-View Cameras for Visual Odometry. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 801–808. [Google Scholar]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual–Inertial, and Multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Caruso, D.; Engel, J.; Cremers, D. Large-Scale Direct SLAM for Omnidirectional Cameras. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 141–148. [Google Scholar]
- Zioulis, N.; Karakottas, A.; Zarpalas, D.; Daras, P. Omnidepth: Dense Depth Estimation for Indoors Spherical Panoramas. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 448–465. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Song, S.; Yu, F.; Zeng, A.; Chang, A.X.; Savva, M.; Funkhouser, T. Semantic Scene Completion from a Single Depth Image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1746–1754. [Google Scholar]
- Kinga, D.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; Volume 5. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the Difficulty of Training Deep Feedforward Neural Networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics (AISTATS), Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Fei-Fei, L. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth Map Prediction from a Single Image Using a Multi-Scale Deep Network. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 8–13 December 2014; Volume 27. [Google Scholar]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A Benchmark for the Evaluation of RGB-D SLAM Systems. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura, Portugal, 7–12 October 2012; pp. 573–580. [Google Scholar]
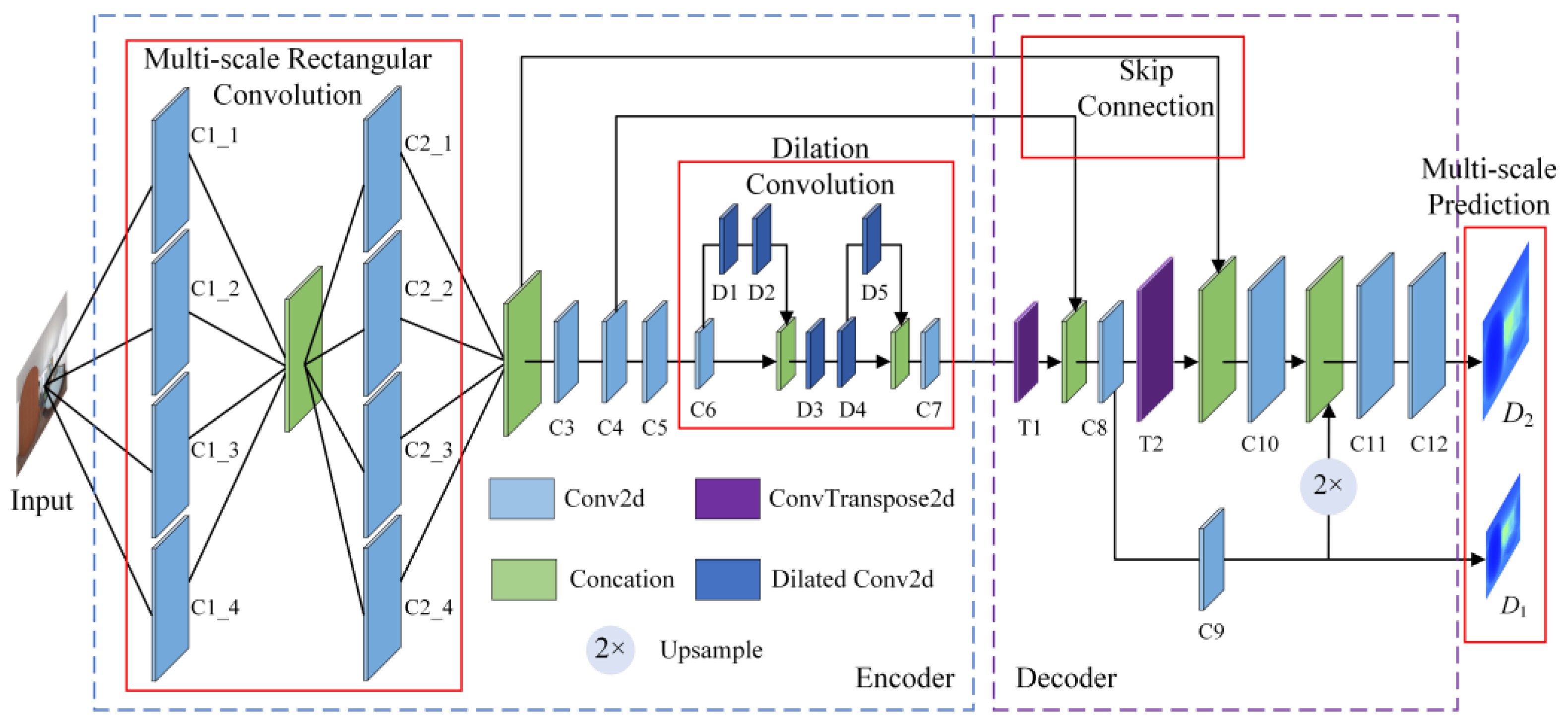

| Name | Operations | Kernel Size | Stride | Padding | Dilation Rate | Output Dimensions |
|---|---|---|---|---|---|---|
| Input | 3 × 256 × 512 | |||||
| C1_1 | Conv2d | 3 × 9 | 1 | 1 × 4 | 1 | 8 × 256 × 512 |
| C1_2 | Conv2d | 5 × 7 | 1 | 2 × 3 | 1 | 8 × 256 × 512 |
| C1_3 | Conv2d | 5 × 11 | 1 | 2 × 5 | 1 | 8 × 256 × 512 |
| C1_4 | Conv2d | 7 × 7 | 1 | 3 × 3 | 1 | 8 × 256 × 512 |
| Concation | 32 × 256 × 512 | |||||
| C2_1 | Conv2d | 3 × 9 | 1 | 1 × 4 | 1 | 16 × 256 × 512 |
| C2_2 | Conv2d | 3 × 7 | 1 | 1 × 3 | 1 | 16 × 256 × 512 |
| C2_3 | Conv2d | 3 × 5 | 1 | 1 × 2 | 1 | 16 × 256 × 512 |
| C2_4 | Conv2d | 3 × 5 | 1 | 2 × 2 | 1 | 16 × 256 × 512 |
| Concation | 64 × 256 × 512 | |||||
| C3 | Conv2d | 3 × 3 | 2 | 1 × 1 | 1 | 128 × 128 × 256 |
| C4 | Conv2d | 3 × 3 | 1 | 1 × 1 | 1 | 128 × 128 × 256 |
| C5 | Conv2d | 3 × 3 | 1 | 1 × 1 | 1 | 128 × 128 × 256 |
| C6 | Conv2d | 3 × 3 | 2 | 1 × 1 | 1 | 256 × 64 × 128 |
| D1 | Conv2d | 3 × 3 | 1 | 2 × 2 | 2 | 256 × 64 × 128 |
| D2 | Conv2d | 3 × 3 | 1 | 4 × 4 | 4 | 256 × 64 × 128 |
| Concation | 512 × 64 × 128 | |||||
| D3 | Conv2d | 1 × 1 | 1 | 4 × 4 | 4 | 256 × 64 × 128 |
| D4 | Conv2d | 3 × 3 | 1 | 8 × 8 | 8 | 512 × 64 × 128 |
| D5 | Conv2d | 3 × 3 | 1 | 16 × 16 | 16 | 512 × 64 × 128 |
| Concation | 1024 × 64 × 128 | |||||
| C7 | Conv2d | 1 × 1 | 1 | 0 × 0 | 1 | 512 × 64 × 128 |
| Name | Operations | Kernel Size | Stride | Padding | Dilation Rate | Output Dimensions |
|---|---|---|---|---|---|---|
| T1 | ConvTranspose2d | 4 × 4 | 2 | 1 × 1 | 1 | 256 × 128 × 256 |
| Concation | 384 × 128 × 256 | |||||
| C8 | Conv2d | 5 × 5 | 1 | 2 × 2 | 1 | 256 × 128 × 256 |
| C9 | Conv2d | 5 × 5 | 1 | 2 × 2 | 1 | 1 × 128 × 256 |
| D1 | 1 × 128 × 256 | |||||
| Upsample | 1 × 256 × 512 | |||||
| T2 | ConvTranspose2d | 4 × 4 | 2 | 1 × 1 | 1 | 128 × 256 × 512 |
| Concation | 192 × 256 × 512 | |||||
| C10 | Conv2d | 5 × 5 | 1 | 2 × 2 | 1 | 128 × 256 × 512 |
| Concation | 129 × 256 × 512 | |||||
| C11 | Conv2d | 1 × 1 | 1 | 0 × 0 | 1 | 64 × 256 × 512 |
| C12 | Conv2d | 3 × 3 | 1 | 1 × 1 | 1 | 1 × 256 × 512 |
| D2 | 1 × 256 × 512 |
| Name | Operations | Kernel Size | Stride | Padding | Dilation Rate | Output Dimensions |
|---|---|---|---|---|---|---|
| Input | 9 × 256 × 512 | |||||
| C1 | Conv2d | 7 × 7 | 2 | 3 × 3 | 1 | 64 × 128 × 256 |
| Maxpool | 64 × 64 × 128 | |||||
| Layer1 | BasicBlock | 3 × 3 | 1 | 1 × 1 | 1 | 64 × 64 × 128 |
| Maxpool | 64 × 32 × 64 | |||||
| Layer2 | BasicBlock | 3 × 3 | 1 | 1 × 1 | 1 | 128 × 32 × 64 |
| Maxpool | 128 × 16 × 32 | |||||
| Layer3 | BasicBlock | 3 × 3 | 1 | 1 × 1 | 1 | 256 × 16 × 32 |
| Maxpool | 256 × 8 × 16 | |||||
| Layer4 | BasicBlock | 3 × 3 | 1 | 1 × 1 | 1 | 512 × 8 × 16 |
| C2 | Conv2d | 3 × 3 | 1 | 1 × 1 | 1 | 256 × 8 × 16 |
| C3 | Conv2d | 3 × 3 | 1 | 1 × 1 | 1 | 12 × 8 × 16 |
| AvgPool2d | 12 × 1 × 1 | |||||
| reshape | 2 × 6 | |||||
| C4 | Conv2d | 3 × 3 | 1 | 1 × 1 | 1 | 2 × 64 × 128 |
| M2 | Upsample | 2 × 256 × 512 | ||||
| C5 | Conv2d | 3 × 3 | 1 | 1 × 1 | 1 | 2 × 32 × 64 |
| M1 | Upsample | 2 × 128 × 256 |
| Approaches | Error Metric ↓ | Accuracy Metric ↑ | |||||
|---|---|---|---|---|---|---|---|
| MRE | MAE | RMSE | RMSElog | δ < 1.25 | δ < 1.252 | δ < 1.253 | |
| 360-SelfNet [18] | 0.1521 | 0.2344 | 0.5121 | 0.0934 | 0.8479 | 0.9420 | 0.9726 |
| BiFuse++ [22] | 0.1176 | 0.1815 | 0.4321 | 0.0790 | 0.8974 | 0.9546 | 0.9773 |
| Ours | 0.1330 | 0.2154 | 0.4730 | 0.0887 | 0.8788 | 0.9480 | 0.9768 |
| Approaches | RPE-R (°) ↓ | RPE-T(m) ↓ |
|---|---|---|
| OpenVSLAM [13] | 5.36 | 0.018 |
| 360-SelfNet [18] | 6.98 | 0.025 |
| Bifuse++ [22] | 6.75 | 0.022 |
| Ours | 6.88 | 0.023 |
| Supervision Types | RPE-R (°) ↓ | RPE-T (m) ↓ |
|---|---|---|
| Fully Unsupervised w/M | 6.88 | 0.023 |
| Fully Unsupervised w/o M | 6.96 | 0.025 |
| Fully Unsupervised w/D1 | 7.02 | 0.028 |
| Supervised w/Pose labels | 4.43 | 0.017 |
| Supervised w/Noisy Pose labels | 5.75 | 0.021 |
| Supervised w/Pose Estimator Only | 3.47 | 0.013 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Li, G.; Bai, Y.; Bai, Y.; Cao, Z.; Han, C. Tracking and Registration Technology Based on Panoramic Cameras. Appl. Sci. 2025, 15, 7397. https://doi.org/10.3390/app15137397
Xu C, Li G, Bai Y, Bai Y, Cao Z, Han C. Tracking and Registration Technology Based on Panoramic Cameras. Applied Sciences. 2025; 15(13):7397. https://doi.org/10.3390/app15137397
Chicago/Turabian StyleXu, Chao, Guoxu Li, Ye Bai, Yuzhuo Bai, Zheng Cao, and Cheng Han. 2025. "Tracking and Registration Technology Based on Panoramic Cameras" Applied Sciences 15, no. 13: 7397. https://doi.org/10.3390/app15137397
APA StyleXu, C., Li, G., Bai, Y., Bai, Y., Cao, Z., & Han, C. (2025). Tracking and Registration Technology Based on Panoramic Cameras. Applied Sciences, 15(13), 7397. https://doi.org/10.3390/app15137397





