Evolution of the Seismic Forecast System Implemented for the Vrancea Area (Romania)
Abstract
1. Introduction
2. Explanation of Relevant Data Analysis Methods
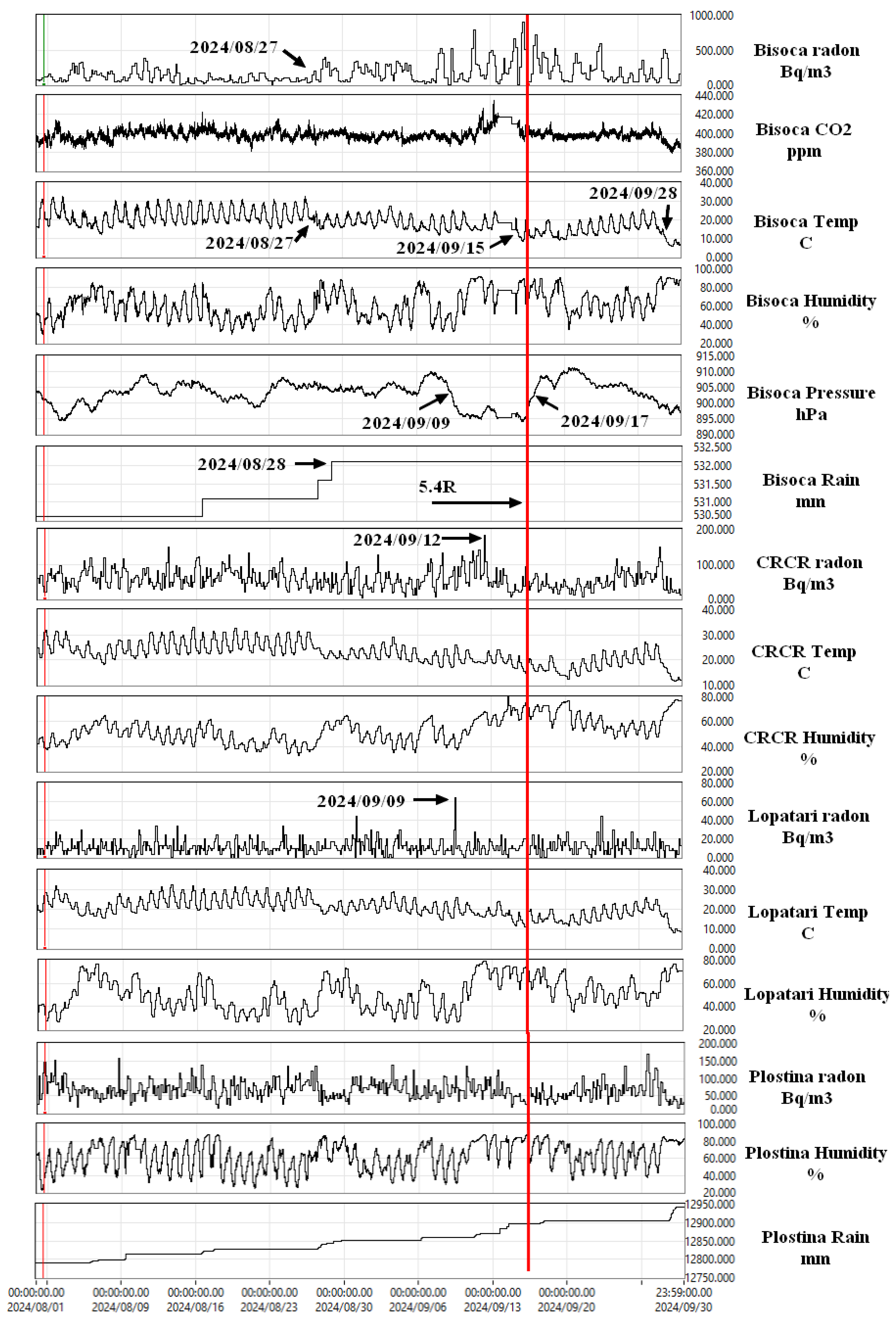
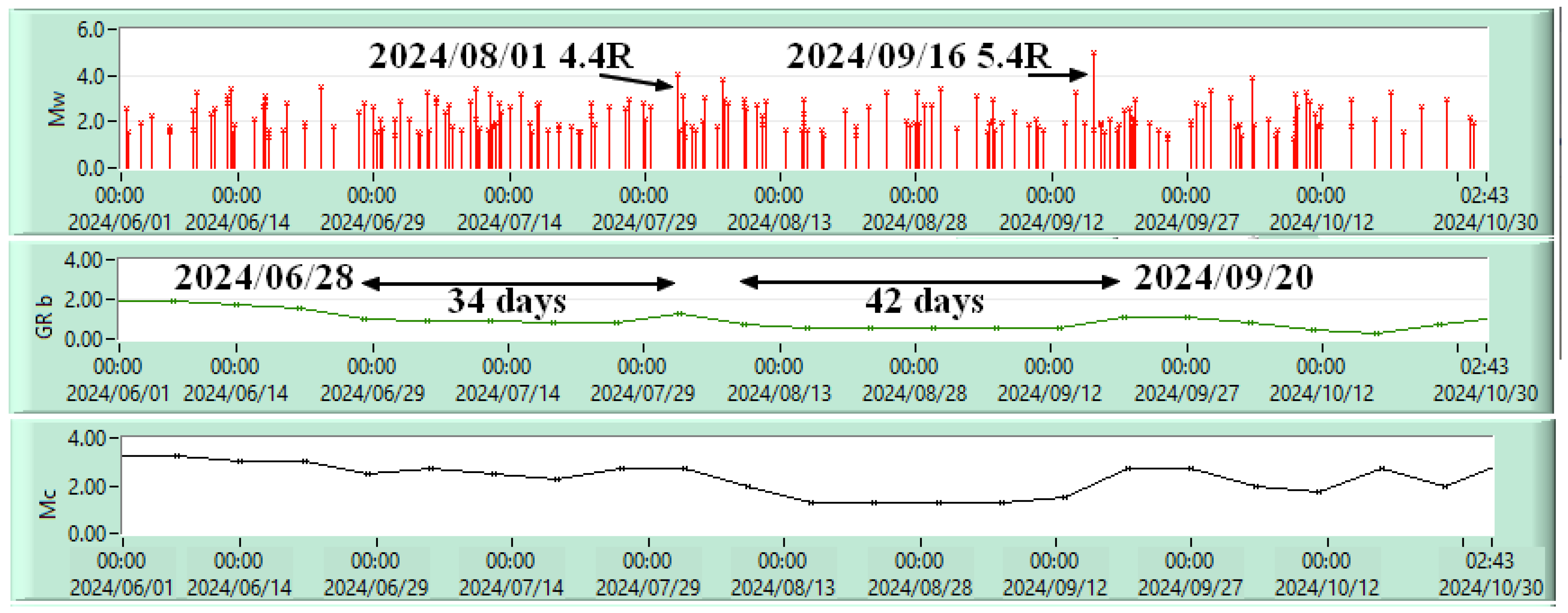
3. Data Collection and Calculation Results, a Case Study
- ▪
- Differentiating radon and CO2 weights;
- ▪
- Modifying weights based on a station’s distance from the hypocenter;
- ▪
- Changing the number of stations;
- ▪
- Altering the maximum number of daily detections per station (set to 4 in this example);
- ▪
- Adjusting the four-day grouping period for detections.
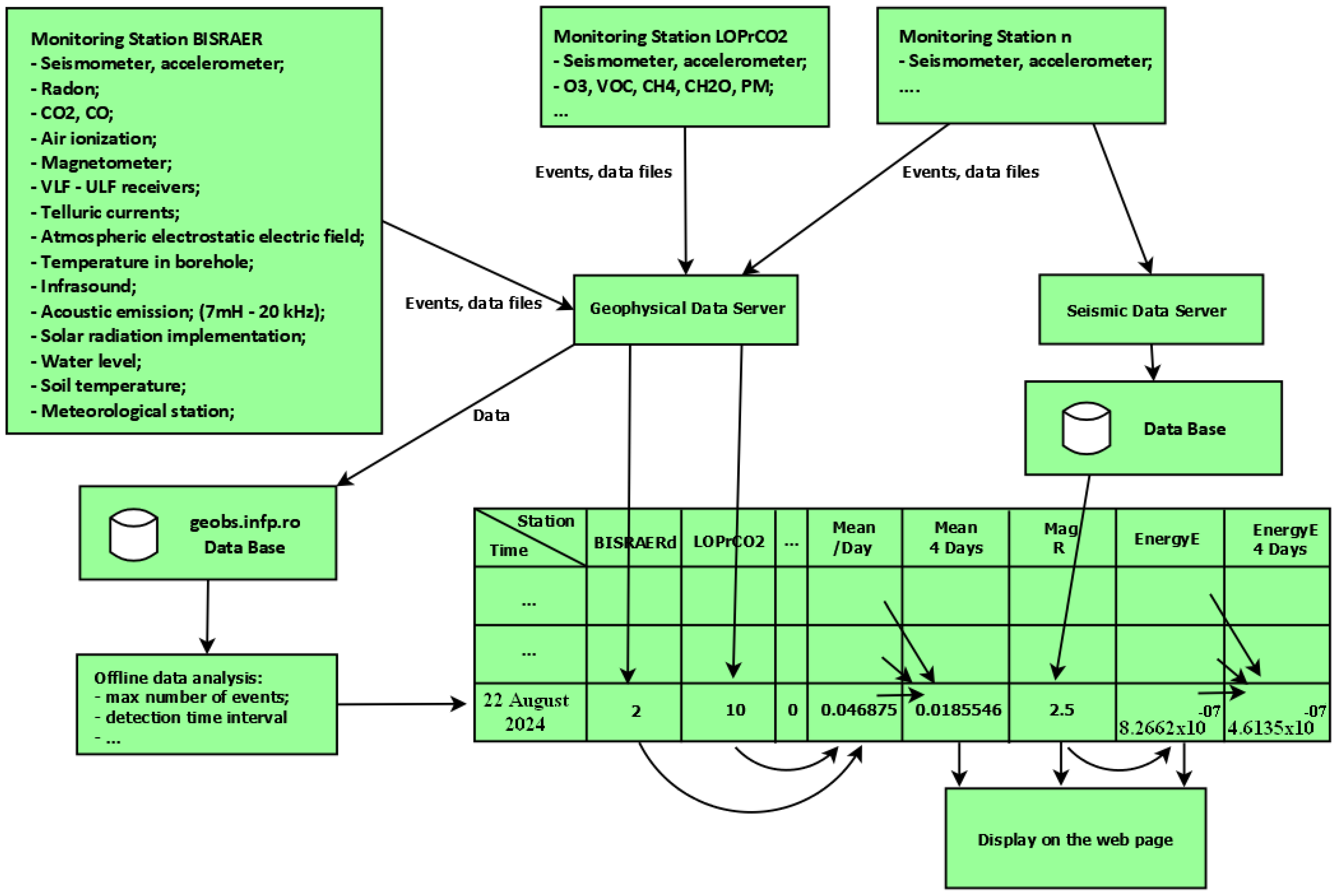
Channel Weightn−1 × eventsn−1/maxim events)/n stations
- -
- The columns represent the Date/Time, BISRAERd, DLMdd, LOPRdd, NEHRdd, PANCdd are radon, and BISRCO2, DLMCO2, LOPrCO2 represent CO2;
- -
- Every day the number of Events for every station is recorded;
- -
- MeanDay for 22 August 2024: 2 Evens for BISRAERd, and 10 for LOPrCO2, relation (1) (0.125 × 2/4 + 0.125 × 0/4 + 0.125 × 0/4 + 0.125 × 0/4 + 0.125 × 10/4 + 0.125 × 10/4 + 0.125 × 10/4 + 0.125 × 10/4)/8 = 0.046875;
- -
- MEAN 4 DAYS = (0.0078125 + 0.0078125 + 0.01171875 + 0.046875)/4 = 0.018554688;
- -
- EnergyE (relation 3) = POWER((1.5 × 2.5 + 11.8),10)/10+18 = 8.26616 × 10−07;
- -
- EnergyE 4 Days = (0 + 6.80297 × 10−07 + 3.38486 × 10−07 + 8.26616 × 10−07)/4 = 4.6135 × 10−07;
4. Discussion
5. Conclusions
- The structure of the OEF-NIEP system is innovative compared to existing approaches. We found no other solutions that utilize real-time event detection—such as threshold exceedance adapted to seasonal variations in gas emissions—directly at monitoring stations within a network and integrate these into a decision-making matrix.
- Experimental results confirmed that the Gutenberg-Richter law (Equation (5)) and gas emissions (radon, CO2) can be used for real-time earthquake forecasting. This enables the possibility of a service where authorities can receive warning information within a time window ranging from several hours to a few days.
- The RTM 1688 radon and thoron monitoring equipment installed at Plostina and Vrancioaia did not improve earthquake forecasting performance compared to the existing Radon Scout Plus equipment. The role of thoron as a precursor at these monitored locations remains unproven, though seismic activity in the area has not exceeded magnitude 4.5.
- Years of experience with real-time monitoring suggest that simple, flexible, and cost-effective solutions (including equipment, maintenance, and analysis software) significantly support the advancement of fundamental research through applied research. However, increasing system complexity presents challenges in terms of implementation, maintenance, and funding. More accurate analyses, such as those based on artificial intelligence algorithms, can be developed and applied offline.
- When developing the OEF system, it is essential to include additional factors beyond radon and CO2, and to increase the number of monitoring stations to allow for more accurate localization of future earthquakes.
- Environmental factors (air pressure, temperature, humidity) can influence gas emissions and may trigger false alarms. Therefore, to mitigate this, sensors should be installed at greater depths.
- Another important conclusion is the need to incorporate the findings of the AFROS project’s fundamental research into the real-time decision matrix, including advanced statistical and machine-learning tools for quantifying spatial and temporal features.
- The article emphasizes decision-making based on real-time data. Anomaly detection was performed using thresholds determined by offline analyses; these thresholds should be further developed and integrated into the OEF system.
- The monitored area should be expanded to include other seismic zones (e.g., Târgu Jiu, Izvoarele-Galați). Some of these regions are characterized by oil and gas extraction, necessitating the analysis of induced seismicity.
- Only a multidisciplinary approach can yield significant results in earthquake prediction. The existence of a platform like AFROS, which presents and analyzes multidisciplinary data in real time, is unprecedented (no comparable systems were identified during our research) and demonstrates the feasibility of implementing an OEF system and providing a complementary service of REWS.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Toader, V.E.; Moldovan, I.-A.; Marmureanu, A.; Dutta, P.K.R.; Partheniu, R.; Nastase, E. Monitoring of radon and air ionization in a seismic area. Rom. Rep. Phys. 2017, 69, 842013. [Google Scholar]
- Toader, V.-E.; Nicolae, V.; Moldovan, I.-A.; Ionescu, C.; Marmureanu, A. Monitoring of Gas Emissions in Light of an OEF Application. Atmosphere 2020, 12, 26. [Google Scholar] [CrossRef]
- Toader, V.-E.; Nicolae, V.; Moldovan, I.-A.; Ionescu, C.; Marmureanu, A.; Lingvay, I. Implementation of a Radon Monitoring Network in a Seismic Area. Atmosphere 2021, 12, 1041. [Google Scholar] [CrossRef]
- Toader, V.-E.; Nicolae, V.; Moldovan, I.-A.; Ionescu, C.; Marmureanu, A. The Results and Developments of the Radon Monitoring Network in Seismic Areas. Atmosphere 2023, 14, 1061. [Google Scholar] [CrossRef]
- Omi, T.; Ogata, Y.; Shiomi, K.; Enescu, B.; Sawazaki, K.; Aihara, K. Implementation of a Real-Time System for Automatic Aftershock Forecasting in Japan. Seismol. Res. Lett. 2019, 90, 242–250. [Google Scholar] [CrossRef]
- Christophersen, A.; Rhoades, D.A.; Gerstenberger, M.C.; Bannister, S.; Becker, J.; Potter, S.H.; McBride, S. Progress and challenges in operational earthquake forecasting in New Zealand. In Proceedings of the 2017 NZSEE Conference, Wellington, New Zealand, 27–29 April 2017; GNS Science: Lower Hutt, New Zealand, 2017; pp. 1–6. [Google Scholar]
- Mizrahi, L.; Dallo, I.; van der Elst, N.J.; Christophersen, A.; Spassiani, I.; Werner, M.J.; Werner, M.J.; Iturrieta, P.; Bayona, J.A.; Iervolino, I.; et al. Developing, Testing, and Communicating Earthquake Forecasts: Current Practices and Future Directions. Rev. Geophys. 2024, 62, e2023RG000823. [Google Scholar] [CrossRef]
- Leet, L.D.; Gutenberg, B.; Richter, C.F. Seismicity of the Earth and Associated Phenomena. Geogr. Rev. 1950, 40, 346. [Google Scholar] [CrossRef]
- Tsuchiya, M.; Nagahama, H.; Muto, J.; Hirano, M.; Yasuoka, Y. Detection of atmospheric radon concentration anomalies and their potential for earthquake prediction using Random Forest analysis. Sci. Rep. 2024, 14, 11626. [Google Scholar] [CrossRef]
- El-Isa, Z.H.; Eaton, D.W. Spatiotemporal variations in the b-value of earthquake magnitude–frequency distributions: Classification and causes. Tectonophysics 2014, 615–616, 1–11. [Google Scholar] [CrossRef]
- Smith, W.D. The b-value as an earthquake precursor. Nature 1981, 289, 136–139. [Google Scholar] [CrossRef]
- Jordan, T.H.; Chen, Y.T.; Gasparini, P.; Madariaga, R.; Main, I.; Marzocchi, W.; Papadopoulos, G.; Sobolev, G.; Yamaoka KZschau, J. Operational Earthquake Forecasting. State of Knowledge and Guidelines for Utilization. Ann. Geophys. 2011, 54, 319–391. [Google Scholar] [CrossRef]
- Zechar, J.D.; Marzocchi, W.; Wiemer, S. Operational earthquake forecasting in Europe: Progress, despite challenges. Bull. Earthq. Eng. 2016, 14, 2459–2469. [Google Scholar] [CrossRef]
- Douglas, J.; Azarbakht, A. Cost–benefit analyses to assess the potential of Operational Earthquake Forecasting prior to a mainshock in Europe. Nat. Hazards 2021, 105, 293–311. [Google Scholar] [CrossRef]
- Vrex, A. Automatic Earthquake Recognition and Timing from Single Traces. Bull. Seismol. Soc. Am. 1978, 68, 1521–1532. [Google Scholar]
- Allen, R. Automatic phase pickers: Their present use and future prospects. Bull. Seismol. Soc. Am. 1982, 72, S225–S242. Available online: https://pubs.geoscienceworld.org/ssa/bssa/article-abstract/72/6B/S225/102172/Automatic-phase-pickers-Their-present-use-and?redirectedFrom=fulltext (accessed on 28 April 2020). [CrossRef]
- Jones, J.P.; van der Baan, M. Adaptive STA–LTA with Outlier Statistics. Bull. Seismol. Soc. Am. 2015, 105, 1606–1618. [Google Scholar] [CrossRef]
- Richter, C.F. Elementary seismology. Geol. J. 1958, 2, 768. [Google Scholar] [CrossRef]
- Båth, M. Earthquake seismology. Earth-Sci. Rev. 1966, 1, 69–86. [Google Scholar] [CrossRef]
- Båth, M. Seismic energy mapping applied to Turkey. Tectonophysics 1982, 82, 69–87. [Google Scholar] [CrossRef]
- Ambrosino, F.; Thinová, L.; Briestenský, M.; Giudicepietro, F.; Roca, V.; Sabbarese, C. Analysis of geophysical and meteorological parameters influencing 222Rn activity concentration in Mladeč caves (Czech Republic) and in soils of Phlegrean Fields caldera (Italy). Appl. Radiat. Isot. 2020, 160, 109140. [Google Scholar] [CrossRef]
- Chasanah, U.; Handoyo, E. Determination the Magnitude of Completeness, b-Value and a-Value for Seismicity Analysis in East Java, Indonesia. J. Phys. Conf. Ser. 2021, 1805, 012009. [Google Scholar] [CrossRef]
- Montiel-López, D.; Molina, S.; Galiana-Merino, J.J.; Gómez, I. On the calculation of smoothing kernels for seismic parameter spatial mapping: Methodology and examples. Nat. Hazards Earth Syst. Sci. 2023, 23, 91–106. [Google Scholar] [CrossRef]
- Dobrovolsky, I.P.; Zubkov, S.I.; Miachkin, V.I. Estimation of the size of earthquake preparation zones. Pure Appl. Geophys. 1979, 117, 1025–1044. [Google Scholar] [CrossRef]
- Tuccimei, P.; Mollo, S.; Soligo, M.; Scarlato, P.; Castelluccio, M. Real-time setup to measure radon emission during rock deformation: Implications for geochemical surveillance. Geosci. Instrum. Methods Data Syst. Discuss. 2015, 4, 111–119. [Google Scholar] [CrossRef]
- Bauer, S.J.; Gardner, W.P.; Lee, H. Real Time Degassing of Rock during Deformation. In Proceedings of the 50th US Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, 26–29 June 2016; pp. 1–7. [Google Scholar]
- Morales-Simfors, N.; Wyss, R.A.; Bundschuh, J. Recent progress in radon-based monitoring as seismic and volcanic precursor: A critical review. Crit. Rev. Environ. Sci. Technol. 2020, 50, 979–1012. [Google Scholar] [CrossRef]
- Reddy, D.V.; Nagabhushanam, P.; Sukhija, B.S.; Reddy, G.R. Continuous radon monitoring in soil gas towards earthquake precursory studies in basaltic region. Radiat. Meas. 2010, 45, 935–942. [Google Scholar] [CrossRef]
- Jilani, Z.; Mehmood, T.; Alam, A.; Awais, M.; Iqbal, T. Monitoring and descriptive analysis of radon in relation to seismic activity of Northern Pakistan. J. Environ. Radioact. 2017, 172, 43–51. [Google Scholar] [CrossRef]
- Barkat, A.; Ali, A.; Hayat, U.; Crowley, Q.G.; Rehman, K.; Siddique, N.; Haidar, T.; Iqbal, T. Time series analysis of soil radon in Northern Pakistan: Implications for earthquake forecasting. Appl. Geochem. 2018, 97, 197–208. [Google Scholar] [CrossRef]
- Saad, O.M.; Chen, Y.; Savvaidis, A.; Fomel, S.; Jiang, X.; Huang, D.; Oboué, Y.A.S.I.; Yong, S.; Wang, X.; Zhang, X.; et al. Earthquake Forecasting Using Big Data and Artificial Intelligence: A 30-Week Real-Time Case Study in China. Bull. Seismol. Soc. Am. 2023, 113, 2461–2478. [Google Scholar] [CrossRef]
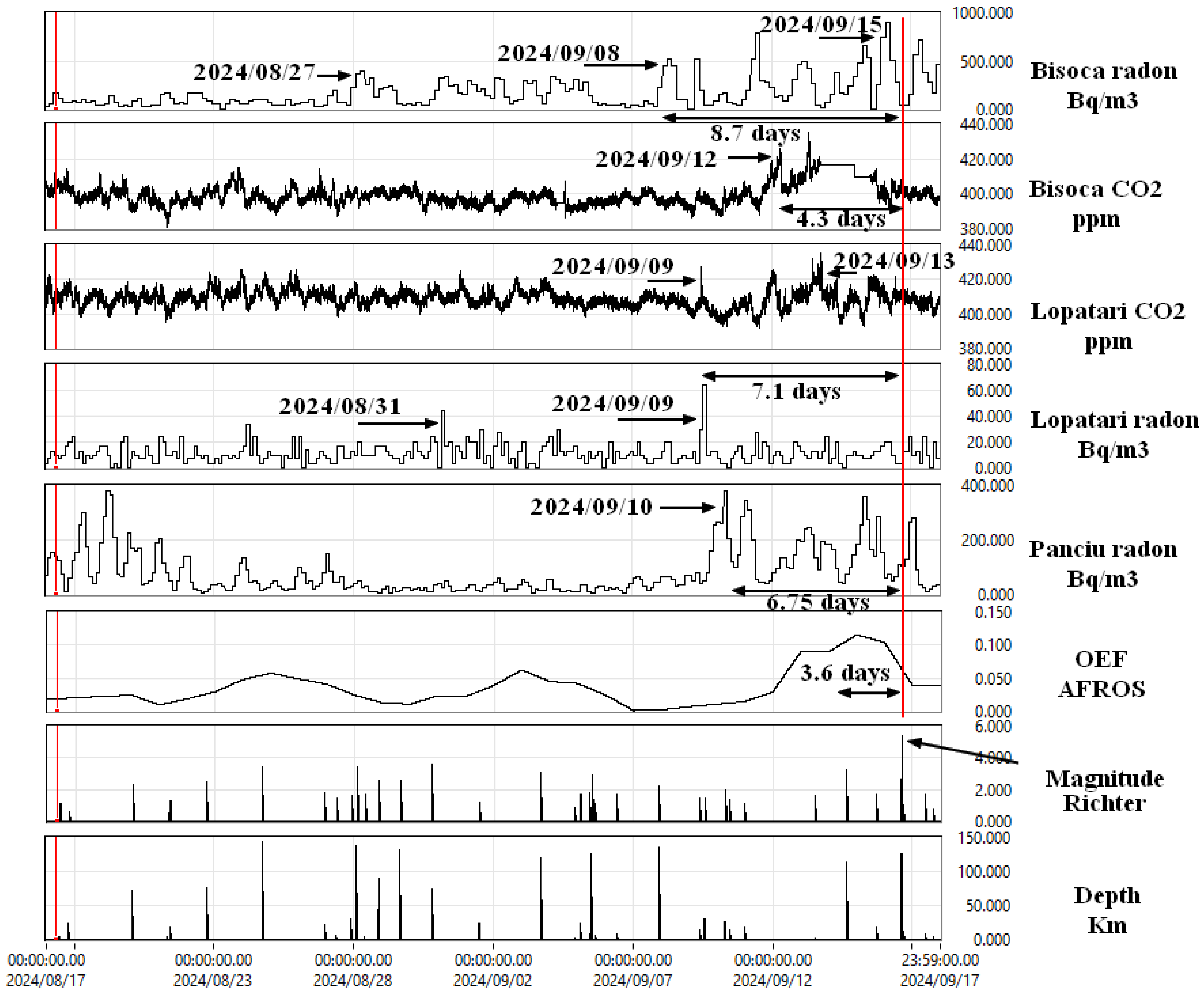



| Channel Weights | 0.125 | 0.125 | 0.125 | 0.125 | 0.125 | 0.125 | 0.125 | 0.125 | 1 | ||||
| Station | BISRAERd | BISRCO2 | DLMCO2 | DLMdd | LOPrCO2 | LOPRdd | NEHRdd | PANCdd | Mean Day | Mean 4 Days OEF AFROS | Mag R | EnergyE × 1018 Erg | EnergyE 4 Days × 1018 Erg |
| 17 August 2024 | 2 | 0 | 0 | 0 | 14 | 0 | 0 | 2 | 0.070312 | 0.0175781 | 1.2; 0.6 | 3.2562 × 10−07 | 8.14048 × 10−08 |
| 18 August 2024 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0.011718 | 0.0205078 | 0 | 8.14048 × 10−08 | |
| 19 August 2024 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0.007812 | 0.0224609 | 0 | 8.14048 × 10−08 | |
| 20 August 2024 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0.007812 | 0.0244140 | 2.3 | 6.803 × 10−07 | 2.51479 × 10−07 |
| 21 August 2024 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0.011718 | 0.0097656 | 0.5; 1.3 | 3.3849 × 10−07 | 2.54696 × 10−07 |
| 22 August 2024 | 2 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0.046875 | 0.0185546 | 2.5 | 8.2662 × 10−07 | 4.6135 × 10−07 |
| 23 August 2024 | 0 | 0 | 0 | 0 | 13 | 0 | 0 | 0 | 0.050781 | 0.0292968 | 0 | 4.6135 × 10−07 | |
| 24 August 2024 | 0 | 0 | 0 | 0 | 21 | 0 | 0 | 0 | 0.082031 | 0.0478515 | 3.4 | 1.9005 × 10−06 | 7.664 × 10−07 |
| 25 August 2024 | 0 | 0 | 0 | 0 | 13 | 0 | 0 | 0 | 0.050781 | 0.0576171 | 0 | 6.81778 × 10−07 | |
| 26 August 2024 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0.011718 | 0.0488281 | 1.8 | 4.1085 × 10−07 | 5.77836 × 10−07 |
| 27 August 2024 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0.019531 | 0.0410156 | 1.5; 1.6 | 6.3309 × 10−07 | 7.36108 × 10−07 |
| 28 August 2024 | 2 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0.015625 | 0.0244140 | 3.4; 1.7; 2.6 | 3.1807 × 10−06 | 1.05615 × 10−06 |
| 29 August 2024 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.003906 | 0.0126953 | 2.6 | 9.0991 × 10−07 | 1.28363 × 10−06 |
| 30 August 2024 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.003906 | 0.0107421 | 3.6 | 2.2661 × 10−06 | 1.74745 × 10−06 |
| 31 August 2024 | 0 | 0 | 0 | 0 | 18 | 0 | 0 | 0 | 0.070312 | 0.0234375 | 0 | 1.58918 × 10−06 | |
| 01 September 2024 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.011718 | 0.0224609 | 1.2 | 2.1647 × 10−07 | 8.48125 × 10−07 |
| 02 September 2024 | 2 | 0 | 0 | 0 | 16 | 0 | 0 | 0 | 0.070312 | 0.0390625 | 0 | 6.20648 × 10−07 | |
| 03 September 2024 | 3 | 0 | 0 | 0 | 22 | 0 | 0 | 0 | 0.097656 | 0.0625 | 3.1 | 1.451 × 10−06 | 4.16859 × 10−07 |
| 04 September 2024 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0449218 | 0.9 | 0 | 4.16859 × 10−07 |
| 05 September 2024 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0419921 | 1.6; 1.7; 1.8; 2.9; 1.1 | 2.5152 × 10−06 | 9.91554 × 10−07 |
| 06 September 2024 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0244140 | 1.7 | 3.7027 × 10−07 | 1.08412 × 10−06 |
| 07 September 2024 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.003906 | 0.0009765 | 2.2 | 6.1627 × 10−07 | 8.75446 × 10−07 |
| 08 September 2024 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0039062 | 0.0019531 | 0 | 8.75446 × 10−07 | |
| 09 September 2024 | 2 | 0 | 0 | 0 | 2 | 0 | 0 | 1 | 0.019531 | 0.0068359 | 1.5; 1.5 | 5.9951 × 10−07 | 3.96511 × 10−07 |
| 10 September 2024 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0.015625 | 0.0107421 | 2; 1.4; 1.1 | 9.672 × 10−07 | 5.45744 × 10−07 |
| 11 September 2024 | 1 | 0 | 0 | 0 | 3 | 0 | 0 | 1 | 0.019531 | 0.0146484 | 0 | 3.91677 × 10−07 | |
| 12 September 2024 | 2 | 4 | 0 | 0 | 9 | 0 | 0 | 1 | 0.0625 | 0.0292968 | 0 | 3.91677 × 10−07 | |
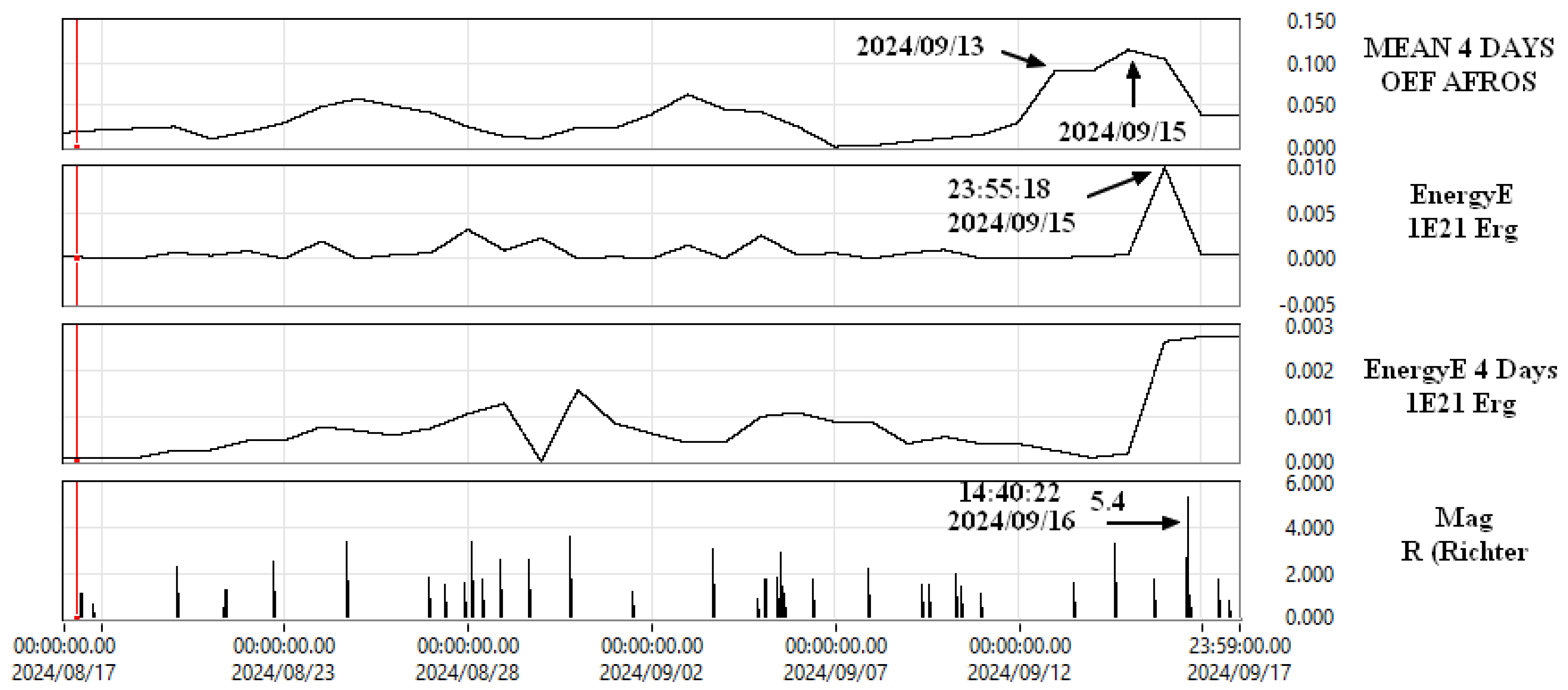
| 13 September 2024 | 1 | 24 | 0 | 0 | 40 | 0 | 0 | 2 | 0.261718 | 0.0898437 | 0 | 2.41801 × 10−07 | |
| 14 September 2024 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 2 | 0.015625 | 0.0898437 | 1.6 | 3.3334 × 10−07 | 8.33342 × 10−08 |
| 15 September 2024 | 1 | 0 | 0 | 0 | 28 | 0 | 0 | 2 | 0.121093 | 0.1152343 | 1.7 | 3.7027 × 10−07 | 1.75902 × 10−07 |
| 16 September 2024 | 2 | 0 | 0 | 0 | 2 | 0 | 0 | 1 | 0.019531 | 0.1044921 | 5.4; 1; | 9.9126 × 10−06 | 2.65404 × 10−06 |
| 17 September 2024 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0390625 | 1.5; 0.8 | 4.3761 × 10−07 | 2.76344 × 10−06 |
| Total | 32 | 30 | 0 | 0 | 218 | 0 | 0 | 24 | |||||
| Station | Location | Equipment | North | East | Description | Start | End |
|---|---|---|---|---|---|---|---|
| BISRAERd | Bisoca | AERC | 45.5481 | 26.7099 | Biscoca, radon | 25 February 2025 | to date |
| BISRCO2 | Bisoca | DL303 | 45.5481 | 26.7099 | Bisoca CO2/CO | 09 July 2019 | to date |
| DLMCO2 | Dalma | DL303 | 45.3629 | 26.5965 | Dalma CO2/CO | 04 July 2022 | to date |
| DLMdd | Dalma | RADONSCOUTp | 45.3629 | 26.5965 | Dalma, radon | 04 July 2022 | to date |
| LOPrCO2 | Lopatari | DL303 | 45.4738 | 26.5680 | Mocearu, CO + CO2 | 26 June 2019 | to date |
| LOPRdd | Lopatari | RADONSCOUTp | 45.4738 | 26.5680 | Mocearu, radon | 06 August 2015 | to date |
| NEHRdd | Nehoiu | RADONSCOUTp | 45.4272 | 26.2952 | NEHR, radon | 06 August 2015 | to date |
| PANCdd | Panciu | RADONSCOUTp | 45.8723 | 27.1477 | PANC, radon | 29 September 2021 | to date |
| Earthquake 5.4 R, 16 September 2024, 45.527600°, 26.352500° | ||
|---|---|---|
| Station | Latitude, Longitude | RE (Km) |
| BISRAERd, BISRCO2, Bisoca | 45.548300°, 26.709740° | 28.30 |
| LOPrdd, LOPRCO2, Lopatari | 45.473715°, 26.568721° | 17.84 |
| PANCdd, Panciu | 45.872272°, 27.147726° | 72.76 |
| PLORCdd, Plostina | 45.851396°, 26.649772° | 34.10 |
| VRICdd, VRI2dd, Vrancioia | 45.865695°, 26.727679° | 39.59 |
| N | Time | ML | Depth | Longitude | Latitude | Mw | PZone |
|---|---|---|---|---|---|---|---|
| Richter | Km | Degrees | Degrees | Km | |||
| 1 | 17 August 2024 11:03:54 | 1.1 | 3.4 | 27.833 | 45.506 | 1.67 | 5.2 |
| 2 | 17 August 2024 19:01:29 | 0.6 | 23.3 | 26.5962 | 45.6352 | 1.43 | 4.1 |
| 3 | 20 August 2024 01:12:21 | 2.3 | 71.6 | 26.9662 | 45.7472 | 2.51 | 12 |
| 4 | 21 August 2024 08:02:42 | 0.5 | 5 | 25.1118 | 45.3059 | 1.38 | 3.9 |
| 5 | 21 August 2024 09:46:06 | 1.3 | 17.6 | 25.3323 | 45.2751 | 1.77 | 5.8 |
| 6 | 22 August 2024 17:15:51 | 2.5 | 75.7 | 26.636 | 45.6211 | 2.66 | 13.9 |
| 7 | 24 August 2024 17:12:46 | 3.4 | 144.6 | 26.5364 | 45.6592 | 3.31 | 26.5 |
| 8 | 26 August 2024 22:43:37 | 1.8 | 22.3 | 26.9137 | 45.3975 | 2.03 | 7.4 |
| 9 | 27 August 2024 08:42:29 | 1.5 | 6.9 | 25.7513 | 46.1202 | 1.87 | 6.4 |
| 10 | 27 August 2024 21:25:54 | 1.6 | 29.4 | 27.177 | 45.8624 | 1.92 | 6.7 |
| 11 | 28 August 2024 02:29:02 | 3.4 | 138.2 | 26.5407 | 45.6608 | 3.31 | 26.5 |
| 12 | 28 August 2024 09:16:36 | 1.7 | 5 | 25.7785 | 46.0638 | 1.97 | 7.1 |
| 13 | 28 August 2024 21:22:12 | 2.6 | 89.3 | 26.7991 | 45.867 | 2.73 | 14.9 |
| 14 | 29 August 2024 15:33:22 | 2.6 | 131.6 | 26.5592 | 45.6529 | 2.73 | 14.9 |
| 15 | 30 August 2024 19:12:55 | 3.6 | 73.4 | 26.6597 | 45.7876 | 3.45 | 30.6 |
| 16 | 01 September 2024 11:43:25 | 1.2 | 23.3 | 26.663 | 45.6164 | 1.72 | 5.5 |
| 17 | 03 September 2024 16:50:43 | 3.1 | 120.5 | 26.4318 | 45.4936 | 3.09 | 21.3 |
| 18 | 04 September 2024 21:39:13 | 0.9 | 3 | 27.7967 | 45.5073 | 1.57 | 4.7 |
| 19 | 05 September 2024 02:43:44 | 1.6 | 13.3 | 27.3125 | 45.7081 | 1.92 | 6.7 |
| 20 | 05 September 2024 02:46:09 | 1.7 | 24.1 | 27.2354 | 45.6858 | 1.97 | 7.1 |
| 21 | 05 September 2024 10:32:28 | 1.8 | 7.5 | 25.3004 | 45.3016 | 2.03 | 7.4 |
| 22 | 05 September 2024 12:11:12 | 2.9 | 126.2 | 26.7778 | 45.7678 | 2.95 | 18.5 |
| 23 | 05 September 2024 15:16:04 | 1.1 | 6.3 | 27.8091 | 45.5281 | 1.67 | 5.2 |
| 24 | 06 September 2024 09:55:21 | 1.7 | 8.9 | 25.7295 | 46.0722 | 1.97 | 7.1 |
| 25 | 07 September 2024 21:57:43 | 2.2 | 135.5 | 26.6322 | 45.7638 | 2.44 | 11.2 |
| 26 | 07 September 2024 21:57:43 | 2.2 | 135 | 26.6167 | 45.7585 | 2.44 | 11.2 |
| 27 | 09 September 2024 09:21:33 | 1.5 | 14.2 | 25.6422 | 46.165 | 1.87 | 6.4 |
| 28 | 09 September 2024 13:25:32 | 1.5 | 30.9 | 27.3081 | 45.8753 | 1.87 | 6.4 |
| 29 | 10 September 2024 06:58:56 | 2 | 26.5 | 27.2948 | 45.7896 | 2.13 | 8.2 |
| 30 | 10 September 2024 10:52:16 | 1.4 | 14.9 | 25.3355 | 45.273 | 1.82 | 6.1 |
| 31 | 10 September 2024 23:36:40 | 1.1 | 18 | 26.5345 | 45.4852 | 1.67 | 5.2 |
| 32 | 14 September 2024 15:06:50 | 1.6 | 114.3 | 26.3026 | 45.4852 | 3.24 | 24.6 |
| 33 | 15 September 2024 17:27:59 | 1.7 | 17.9 | 27.8235 | 45.7048 | 1.97 | 7.1 |
| 34 | 16 September 2024 14:40:22 | 5.4 | 126.8 | 26.3525 | 45.5276 | 5.02 | 144.1 |
| 35 | 16 September 2024 16:08:22 | 1 | 12.2 | 27.8053 | 45.5203 | 1.62 | 5 |
| 36 | 17 September 2024 11:33:18 | 1.5 | 8 | 25.2864 | 45.292 | 1.87 | 6.4 |
| 37 | 17 September 2024 18:15:35 | 0.8 | 5 | 25.3469 | 45.3646 | 1.52 | 4.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toader, V.-E.; Ionescu, C.; Moldovan, I.-A.; Marmureanu, A.; Lıngvay, I.; Mihai, A. Evolution of the Seismic Forecast System Implemented for the Vrancea Area (Romania). Appl. Sci. 2025, 15, 7396. https://doi.org/10.3390/app15137396
Toader V-E, Ionescu C, Moldovan I-A, Marmureanu A, Lıngvay I, Mihai A. Evolution of the Seismic Forecast System Implemented for the Vrancea Area (Romania). Applied Sciences. 2025; 15(13):7396. https://doi.org/10.3390/app15137396
Chicago/Turabian StyleToader, Victorin-Emilian, Constantin Ionescu, Iren-Adelina Moldovan, Alexandru Marmureanu, Iosif Lıngvay, and Andrei Mihai. 2025. "Evolution of the Seismic Forecast System Implemented for the Vrancea Area (Romania)" Applied Sciences 15, no. 13: 7396. https://doi.org/10.3390/app15137396
APA StyleToader, V.-E., Ionescu, C., Moldovan, I.-A., Marmureanu, A., Lıngvay, I., & Mihai, A. (2025). Evolution of the Seismic Forecast System Implemented for the Vrancea Area (Romania). Applied Sciences, 15(13), 7396. https://doi.org/10.3390/app15137396







