Efficient Gamma-Based Zero-Reference Deep Curve Estimation for Low-Light Image Enhancement

Abstract

In recent years, the continuous advancement of deep learning technology and its integration into the domain of low-light image enhancement have led to a steady improvement in enhancement effects. However, this progress has been accompanied by an increase in model complexity, imposing significant constraints on applications that demand high real-time performance. To address this challenge, inspired by the state-of-the-art Zero-DCE approach, we introduce a novel method that transforms the low-light image enhancement task into a curve estimation task tailored to each individual image, utilizing a lightweight shallow neural network. Specifically, we first design a novel curve formula based on Gamma correction, which we call the Gamma-based light-enhancement (GLE) curve. This curve enables outstanding performance in the enhancement task by directly mapping the input low-light image to the enhanced output at the pixel level, thereby eliminating the need for multiple iterative mappings as required in the Zero-DCE algorithm. As a result, our approach significantly improves inference speed. Additionally, we employ a lightweight network architecture to minimize computational complexity and introduce a novel global channel attention (GCA) module to enhance the nonlinear mapping capability of the neural network. The GCA module assigns distinct weights to each channel, allowing the network to focus more on critical features. Consequently, it enhances the effectiveness of low-light image enhancement while incurring a minimal computational cost. Finally, our method is trained using a set of zero-reference loss functions, akin to the Zero-DCE approach, without relying on paired or unpaired data. This ensures the practicality and applicability of our proposed method. The experimental results of both quantitative and qualitative comparisons demonstrate that, despite its lightweight design, the images enhanced using our method not only exhibit perceptual quality, authenticity, and contrast comparable to those of mainstream state-of-the-art (SOTA) methods but in some cases even surpass them. Furthermore, our model demonstrates very fast inference speed, making it suitable for real-time inference in resource-constrained or mobile environments, with broad application prospects.

1. Introduction

In practical scenarios, images acquired under insufficient or constrained lighting conditions frequently manifest characteristics such as low illumination, high noise levels, and poor contrast [1,2,3,4]. These adverse characteristics not only severely impair human visual perception and degrade user experience but also severely hinder the performance of critical computer vision tasks, such as image segmentation, object detection, and face recognition [5,6,7,8]. Consequently, the enhancement of images captured under low-light conditions constitutes a vital research priority. At present, the existing low-light image enhancement techniques can be broadly classified into two categories: traditional methods and deep learning-based approaches.

The traditional methods for low-light image enhancement primarily encompass histogram equalization [9,10,11], Gamma correction [12,13,14], and Retinex theory [15,16,17]. These techniques have been widely utilized due to their simplicity and intuitive principles, yet they suffer from various limitations when applied to complex low-light scenarios. Histogram equalization is a well-established technique that enhances image contrast by redistributing the pixel value distribution. However, it often leads to over-enhancement, noise amplification, and color distortion [18], particularly in images with narrow or skewed histograms. These artifacts can significantly degrade the visual quality of the enhanced images, making histogram equalization less suitable for low-light-enhancement tasks that require fine detail preservation and natural appearance. Retinex theory-based methods decompose images into reflection and illumination components [19], achieving enhancement by adjusting the illumination component. While these methods can effectively enhance the overall brightness and contrast of low-light images, they are computationally intensive due to the complex decomposition and reconstruction processes. Additionally, the parameter tuning required for optimal performance is often non-trivial, making it challenging to adapt these methods to diverse low-light scenarios without extensive manual intervention [20]. Gamma correction is a classical nonlinear transformation method that is computationally simple and efficient. Its nonlinear characteristics align well with the human visual system’s perception of brightness [21], making it suitable for enhancing the overall luminance of low-light images. However, most Gamma correction methods typically employ a fixed Gamma value for the entire image, which cannot adequately adapt to the varying brightness levels within an image. This limitation often results in overexposure in brighter regions or insufficient brightness adjustment in darker areas, thereby failing to achieve balanced enhancement across the entire image. Other traditional approaches, such as those based on wavelet transforms [22,23], fuzzy set theory [24,25], and multi-scale fusion [26], have also been explored for low-light image enhancement. The wavelet transform-based methods excel at effectively separating and processing image information at different scales, enhancing details while suppressing noise, with good edge preservation. For example, the method proposed by Jung et al. [22] in 2017 achieved effective contrast enhancement and noise reduction. However, these methods are often sensitive to the choice in thresholds and basis functions, may lead to artifacts or color distortion if mishandled, and are relatively computationally complex. The fuzzy set theory-based methods can naturally model the fuzziness and uncertainty of image brightness, offering flexible nonlinear mapping rules and strong adaptability. Yet, their performance heavily relies on the design of membership functions and fuzzy rules, and may introduce unnatural appearance or noise if not applied carefully. The multi-scale fusion-based methods can integrate complementary information from different scales or processing results, leveraging the strengths of various techniques to typically achieve more robust and natural enhancement results. For instance, the multi-scale fusion approach proposed by Zhang et al. [26] in 2023 yielded promising results. Nevertheless, these methods are generally computationally intensive, requiring the generation and processing of multiple inputs, the design of fusion weights is crucial and challenging, and improper fusion can easily introduce artifacts or blurring. In summary, while the traditional methods have laid the foundation for low-light image enhancement, their inherent limitations in terms of computational complexity, parameter tuning, and adaptability to diverse scenarios necessitate the development of more advanced and flexible techniques to achieve high-quality enhancement results in complex low-light environments.

In recent years, the field of image enhancement has seen a significant increase in the development of low-illumination enhancement methods based on deep learning. These methods have not only achieved superior performance compared to traditional approaches but also demonstrated promising prospects for further development. The advent of deep learning has fundamentally transformed the landscape of low-light image enhancement by leveraging the powerful representation learning capabilities of neural networks. The pioneering work in this domain can be traced back to 2017, when Lore et al. [27] proposed a deep autoencoder approach for natural low-light image enhancement, known as LLNet, marking the beginning of a new era in low-light enhancement. Their work demonstrated that a variant of a stacked sparse denoising autoencoder trained on synthetic data could effectively enhance low-light and noisy images, thereby highlighting the potential of deep learning in addressing the challenges of low-light imaging. Since then, a plethora of deep learning-based low-light-enhancement methods have been proposed, broadly categorized into supervised and unsupervised approaches. In the realm of supervised learning, Wei et al. [28] introduced Deep Retinex Decomposition (RetinexNet), which leverages deep convolutional neural networks to achieve end-to-end learning of Retinex theory. This method significantly advanced the state of the art by integrating the well-established Retinex model with modern deep learning techniques. Subsequently, Zhang et al. [29] proposed KinD, a simple yet effective network that decomposes the enhancement task into three distinct sub-networks: a layer decomposition net, a reflectance restoration net, and an illumination adjustment net. This modular design enables KinD to effectively address the complexities of low-light enhancement by tackling different aspects of the problem separately. More recently, Cai et al. [6] introduced Retinexformer, the first Transformer-based algorithm for low-light image enhancement. By estimating illumination and directly predicting the illumination enhancement map, Retinexformer avoids the numerical instability issues often encountered in traditional methods that rely on estimating the illumination map. This innovative approach leverages the strengths of Transformer architectures, such as their ability to capture long-range dependencies and contextual information, thereby achieving state-of-the-art performance in low-light-enhancement tasks. However, supervised learning methods, despite their impressive performance, face significant limitations. One of the primary challenges is the requirement for annotated or paired training datasets. Currently, the availability of paired low-light images is limited, which restricts the scalability and applicability of these methods. Moreover, supervised low-light-enhancement methods often exhibit insufficient generalization capabilities when confronted with complex and varied scenes. This limitation is particularly evident when these methods are applied to real-world low-light images with diverse lighting conditions, where they may fail to effectively adapt and produce satisfactory results. In contrast, unsupervised models have emerged as a promising alternative, exhibiting stronger generalization capabilities. In 2021, Jiang et al. [30] proposed EnlightenGAN, a pioneering method that leverages generative adversarial networks (GANs) for deep-light enhancement without paired supervision. This work demonstrated that GANs could be effectively utilized to enhance low-light images by learning the mapping between low-light and normal-light images without requiring paired training data. Building on this foundation, Liang et al. [31] explored the potential of Contrastive Language–Image Pretraining (CLIP) for pixel-level image enhancement and proposed CLIP-LIT, a novel unsupervised backlight image enhancement method. By leveraging the rich semantic information captured by CLIP, CLIP-LIT achieves improved enhancement results while maintaining strong generalization capabilities. In 2024, Chobola et al. [32] introduced CoLIE, a method that redefines the enhancement process by mapping the 2D coordinates of underexposed images to their illumination components. This innovative approach achieves improved results by effectively capturing the spatial relationships and contextual information within the image, thereby providing a more holistic enhancement strategy. In summary, while supervised deep learning methods have achieved remarkable success in low-light image enhancement, their reliance on paired training data and limited generalization capabilities pose significant challenges. In contrast, unsupervised methods, such as EnlightenGAN, CLIP-LIT, and CoLIE, have demonstrated the potential to overcome these limitations by leveraging advanced techniques, such as GANs and CLIP. These developments highlight the ongoing evolution of low-light image enhancement, driven by the continuous integration of deep learning techniques and innovative algorithmic designs.

As mentioned above, it is evident that traditional low-light-enhancement methods often necessitate complex manual prior knowledge or intricate iterative algorithms to achieve satisfactory enhancement results, leading to high computational complexity. On the other hand, while the existing supervised and unsupervised deep learning-based low-light-enhancement models have been continuously improving in terms of enhancement effects, these methods still have certain limitations, particularly regarding inference speed. Most deep learning-based low-light-enhancement methods rely on complex network architectures, resulting in large model parameters and high computational costs, making them challenging to run in real time on resource-constrained devices. In recent years, Guo et al. [33] proposed the Zero-Reference Deep Curve Estimation (Zero-DCE) method for low-light image enhancement, which demonstrates unique advantages with its lightweight design and zero-reference training strategy. This method directly adjusts the original image by learning pixel-level curve mapping functions, circumventing the complex feature extraction process and effectively reducing computational complexity. Zero-DCE does not depend on paired datasets for training, instead, it is guided by zero-reference loss functions such as spatial consistency loss, exposure control loss, and color constancy loss, ensuring the naturalness of the enhancement results. Subsequently, to further improve computational speed and reduce the model size, Li et al. [34] introduced an accelerated and lightweight version of Zero-DCE, called Zero-DCE++. However, despite the partial improvements made by Zero-DCE++, its computational speed is still unsatisfactory, indicating the need for further research and development to enhance the efficiency and practicality of low-light image enhancement methods for real-time applications on resource-limited devices.

As is known, the Zero-DCE and Zero-DCE++ methods design a light-enhancement curve (LE curve), a quadratic function that necessitates eight iterations to achieve satisfactory enhancement results. This iterative process, while effective, presents an opportunity for further improvement in terms of computational efficiency. Drawing from the insights of Zero-DCE, we recognize that the low-light image enhancement task can be reformulated as the estimation of a specific curve, enabling the design of a dedicated curve tailored for low-light image enhancement. Consequently, in this work, our objective is to devise a powerful curve that can directly accomplish the enhancement task—specifically the pixel brightness mapping task—excellently without the need for iterative processing. To this end, we conducted an in-depth analysis of the properties of the LE curve. After continuous efforts, we ultimately designed a completely new curve based on Gamma correction theory, termed the Gamma-based light-enhancement (GLE) curve. Furthermore, to enhance both computational speed and enhancement effects, we redesigned the network architecture and introduced a novel global channel attention (GCA) mechanism for channel reconstruction. This attention mechanism builds upon the SE [35] attention mechanism, simplifying the complex squeeze-and-excitation process and retaining the channel weight allocation strategy. By incorporating the GCA module, our model focuses more on important regions, thereby enhancing its generalization ability and overall enhancement performance. In summary, our contributions are as follows:

(1)

We propose a novel curve formula, the Gamma-based light-enhancement (GLE) curve, specifically tailored for low-light image enhancement tasks, which executes independent pixel-wise transformations and conducts distinct parameter estimation for each of the three RGB channels. This formula achieves pixel brightness mapping with a single application, thereby avoiding the parameter redundancy and computational slowdown associated with multiple iterations. In contrast to Zero-DCE and Zero-DCE++, which require eight iterations for curve application, our GLE curve is applied only once, resulting in a significantly faster computational speed and enhanced efficiency.

(2)

We introduce a new channel attention mechanism, i.e., GCA. The GCA module retains only the essential channel weight allocation process, simplifying the computationally intensive squeeze-and-excitation operations that can impede speed. We redesign the network architecture to fully leverage the GCA module. The proposed model boasts a significantly reduced parameter count of merely 8000, in stark contrast to the 80,000 parameters of the Zero-DCE model. This streamlined architecture, comprising only basic convolutional layers, activation layers, and the GCA module, ensures both effective enhancement and high execution efficiency.

(3)

Our proposed method not only achieves low-light image enhancement results comparable to or even better than those of the state-of-the-art methods in terms of various objective evaluation metrics but also boasts the fastest execution speed. Consequently, our model demonstrates broader application prospects, particularly in scenarios requiring real-time processing and deployment on resource-constrained devices.

2. Related Works

The Zero-DCE [33] method, introduced by Guo et al. in 2020, represents a zero-reference approach for enhancing low-light images. Drawing inspiration from the curve adjustment techniques used in photo editing software to modify image brightness, the authors designed a specific curve for low-light image enhancement, referred to as the LE curve. This innovation effectively transforms the low-light-enhancement task into an image-specific curve estimation problem. The mathematical formulation of the LE curve is given by

$$LE\left(I\right(\mathbf{x});\alpha )=I\left(\mathbf{x}\right)+\alpha I\left(\mathbf{x}\right)(1-I(\mathbf{x}\left)\right),$$

(1)

where $I\left(\mathbf{x}\right)$ denotes the normalized pixel value at position $\mathbf{x}$, constrained within the range [0, 1], and $\alpha$ is a learnable parameter that governs the curvature of the enhancement curve. This pixel-wise adjustment mechanism facilitates spatially varying enhancement, allowing the method to adapt dynamically to different regions within the image.

The network architecture of Zero-DCE, known as DCE-Net, is composed of seven layers, with skip connections incorporated to further preserve image details. This structure is both concise and efficient, utilizing 3 × 3 convolutional kernels and ReLU activation functions in each layer, while the final layer employs a Tanh activation function, ensuring a lightweight design. The output layer generates 24 channels, which are then reshaped into 8 three-channel maps. These maps serve as adjustment parameters for the RGB channels in multiple iterations of the curve mapping function. By iteratively applying the LE curve, the model can gradually optimize the brightness and contrast of the image through progressive refinements. Moreover, Zero-DCE employs a set of carefully designed loss functions to guide the training process, eliminating the need for paired images. These loss functions include spatial consistency loss, exposure control loss, illumination smoothness loss, and color constancy loss. These non-reference losses work in conjunction with the iterative curve mapping process to generate pixel-specific adjustment parameters during training, enabling the model to adaptively enhance each pixel based on its surrounding context and content characteristics. Unlike other supervised learning methods that require a large amount of paired images, the zero-reference learning strategy of Zero-DCE significantly reduces the dependence on training data. This approach not only achieves satisfactory visual quality but also demonstrates clear advantages in computational efficiency and practicality, offering a solution for low-light image enhancement that balances effectiveness and efficiency.

To further lighten the model and accelerate computational speed, Li et al. [34] reintroduced Zero-DCE++, an enhanced version of Zero-DCE. One of the primary improvements is the adoption of depthwise-separable convolutions instead of standard convolutions, which significantly reduces the number of network parameters. Additionally, the number of output channels is decreased from twenty-four to three. Unlike Zero-DCE, which requires 24 different parameter mappings over eight iterations, Zero-DCE++ only needs to reuse three-channel (R, G, and B) maps in each iteration. Furthermore, Zero-DCE++ incorporates downsampling to achieve a better balance between enhancement performance and computational cost.

3. Methodology

In this section, the Gamma-nonlinear enhancement curve is formulated as a specialized mapping operator for low-light image restoration. Its theoretical foundation is derived from adaptive Gamma correction, ensuring pixel-wise adjustments and separate enhancement on the three RGB channels. To preserve critical feature discriminability during illumination transformation, a lightweight convolutional channel attention (GCA) module is strategically incorporated, achieving enhanced perceptual quality within a computationally efficient framework. Subsequent subsections are organized as follows: First, mathematical derivations of the GLE curve are formalized, followed by architectural specifications of the GCA mechanism. The hierarchical neural network topology is then delineated, concluding with an introduction of the hybrid loss function governing model training.

3.1. Basic Idea

While the Zero-DCE method utilizes a simple quadratic light-enhancement curve, achieving satisfactory image enhancement necessitates multiple iterations. However, these iterative applications still leave room for significant improvement in terms of computational efficiency. To address this, we posit that low-light image enhancement can be mathematically formulated as a direct curve mapping process, formally defined through Gamma transformations. Building upon the principles of Gamma correction, we redesign a specialized curve tailored specifically for low-light image enhancement. Consequently, our primary objective is to develop a dedicated curve that is capable of accomplishing the enhancement task through a single-step direct-mapping process.

3.2. Gamma-Based Light-Enhancement (GLE) Curve

Our proposed formula is designed to meet the following critical requirements: (1) Enhanced images should be confined to the [0, 1] normalized range, avoiding information loss from overflow truncation. (2) The curve should possess both brightness enhancement and overexposure suppression capabilities. (3) Akin to the LE curve, our curve must maintain monotonicity within the [0, 1] range to preserve the differences between adjacent pixels. In the subsequent sections, we will detail the step-by-step derivation of our final formula, starting from the standard Gamma correction.

Here, we first introduce the classic Gamma correction formula, which is defined as follows:

$$y=c{x}^{\gamma },x\in [0,1]$$

(2)

where x represents the input intensity, c is the scaling coefficient, y represents the output intensity, and $\gamma$ is the correction parameter.

First, we explore the constraint issue of normalized range of enhanced pixel values. In our work, the parameter c is set to 1, ensuring that, when input pixel values x are within the [0, 1] interval, the corrected pixel values y remain naturally limited to the [0, 1] interval. Based on this property, we decide to retain the design using the original pixel x as the base such that the formula becomes

$$y=x^{\gamma },x\in [0,1].$$

(3)

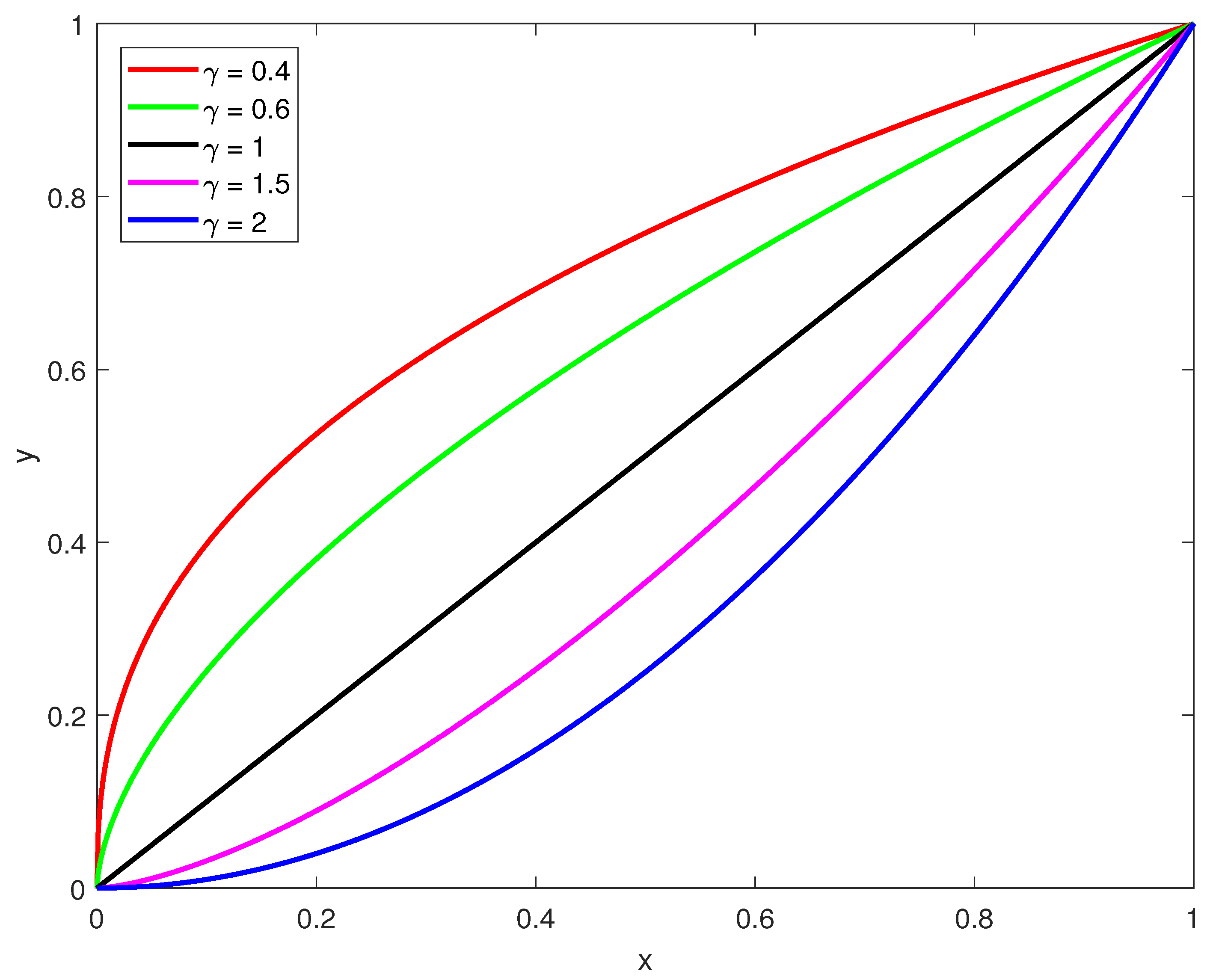
Next, we analyze how the curve can simultaneously possess the dual functions of brightness enhancement and overexposure suppression. As illustrated in Figure 1, it is evident that, when the $\gamma$ value is between 0 and 1, the pixel values after Gamma transformation are increased relative to the original values, thereby achieving image brightness enhancement. Conversely, when the $\gamma$ value exceeds 1, the transformed pixel values decrease, resulting in reduced image brightness and effective suppression of overexposure. To achieve both enhancement of low-illumination regions and suppression of overexposed regions, we modify the formula as follows:

$$y=x^{1+g},x\in [0,1].$$

(4)

In this formula, x still represents the normalized original pixel value, y is the adjusted pixel value, and g represents the trainable curve parameter. Through the Tanh activation function, we strictly limit the range of g to the [−1, 1] interval, with different pixel values x corresponding to different parameters g. This design enables the curve function to simultaneously meet the requirements of enhancing low-light regions and suppressing high-light regions. However, in practical applications, the above formula poses potential problems. As shown in Figure 2a, when the pixel value x is small and g is negative, the adjusted pixel value y undergoes dramatic changes compared to the original value x, leading to unstable model training. Particularly when parameter g approaches $-1$, the function curve becomes abnormally steep, potentially triggering a gradient explosion issue that severely affects the model’s convergence performance. To resolve the stability issue, we need to introduce an adaptive regulation factor into the formula to limit the magnitude of changes during brightness adjustment and avoid excessive enhancement. Based on this idea, we attempt to incorporate the original pixel value x as a regulation factor into the calculation of $\gamma$, forming the following formula:

$$y=x^{1+gx},x\in [0,1].$$

(5)

Unfortunately, experimental results indicate that directly employing x as a regulation factor remains suboptimal. This direct application results in excessive regulation, thereby overly suppressing the model’s ability to enhance dark regions. This can be observed in Figure 2b, where, when the parameter g is set to $-1$, low-pixel-value regions exhibit almost no noticeable changes, which contradicts our original intention of enhancing dark areas. Through in-depth analysis, we discover that the previous regulation factor excessively suppresses the model’s ability to enhance dark regions. This necessitates an optimized design of the regulation factor to provide moderate suppression in dark areas without being overly restrictive. This requirement calls for a nonlinear transformation of the regulation factor. When x is directly used as the regulation factor, its gradient remains constant, resulting in poor enhancement effects in dark regions. The ideal regulation factor should be a function that monotonically increases within the [0, 1] range but with gradually decreasing derivatives. Based on the above analysis, we decide to apply exponential transformation to the regulation factor, adopting the form $x^a$, where a is a hyperparameter. Validated through ablation studies, when a is set to 0.13, it can achieve good enhancement effects in dark regions while maintaining moderate suppression. As such, considering all the above design factors, our GLE curve formula can be defined as

$$y=x^{1+g{x}^a},x\in [0,1].$$

(6)

Theoretical analysis demonstrates that our proposed formula exhibits significant adaptive advantages. When the pixel value x approaches 0, although the regulation factor $x^{0.13}$ also approaches 0, its gradient changes relatively smoothly, ensuring that the formula maintains stable and effective enhancement capabilities in low-light regions. Conversely, when x approaches 1, the regulation factor approaches 1, effectively suppressing excessive enhancement of high-light regions and preventing overexposure distortion. To further enhance performance, we observe that, while using the Tanh activation function limits parameter g to the [−1, 1] range, this constrains the formula’s ability to suppress overexposure. To address this issue, we implement an asymmetric mapping for parameter g after Tanh activation, amplifying its value by a factor of 10 when $g>0$ (used for overexposure suppression) while keeping it unchanged when $g<0$ (used for brightening dark regions). This asymmetric design significantly enhances the model’s control over high-light regions while preserving the fine adjustment capability for dark areas. Figure 3 illustrates the curve characteristics corresponding to different g values under the fixed hyperparameter $a=0.13$. As such, the derivation of the proposed GLE formula and its parameter settings is ultimately complete. The proposed GLE formula satisfies the three objectives we previously established. It requires only a single application to accomplish the mapping of pixel brightness levels, thereby enhancing low-illumination regions while suppressing overexposed areas.

3.3. Global Channel Attention (GCA)

In this section, we introduce a novel channel attention mechanism specifically designed for channel reconstruction. Our approach represents an advancement based on the SE [35] attention mechanism, which enhances feature representation through a two-step process. Initially, the squeeze operation compresses spatial information of each channel into a single descriptor via global average pooling:

$$z_c={\mathbf{F}}_{sq}\left({\mathbf{u}}_c\right)={\displaystyle \frac{1}{H\times W}}\sum _{i=1}^H\sum _{j=1}^W{\mathbf{u}}_c(i,j)$$

(7)

where $z_c$ is the channel descriptor, ${\mathbf{u}}_c$ represents the c-th channel of feature map, H and W denote the height and width of the feature map, and ${\mathbf{F}}_{sq}$ is the squeeze function. Subsequently, the excitation operation captures nonlinear interdependencies between channels through a two-layer fully connected network:

$$\mathbf{s}={\mathbf{F}}_{ex}(\mathbf{z},\mathbf{W})=\sigma \left(g(\mathbf{z},\mathbf{W})\right)=\sigma \left({\mathbf{W}}_2\delta \left({\mathbf{W}}_1\mathbf{z}\right)\right),$$

(8)

where $\mathbf{s}$ represents the channel attention weights, ${\mathbf{F}}_{ex}$ is the excitation function, $\delta$ represents the ReLU activation function, ${\mathbf{W}}_1\in {\mathbb{R}}^{{\displaystyle \frac{C}{r}}\times C}$ and ${\mathbf{W}}_2\in {\mathbb{R}}^{C\times {\displaystyle \frac{C}{r}}}$ denote dimensionality-reduction and dimensionality-increasing parameter matrices, respectively, and $\sigma$ is the sigmoid activation function. The final reconstruction occurs through channel-wise multiplication:

$${\tilde{\mathbf{x}}}_c={\mathbf{F}}_{scale}({\mathbf{u}}_c,s_c)=s_c·{\mathbf{u}}_c,$$

(9)

where ${\tilde{\mathbf{x}}}_c$ is the recalibrated feature, $s_c$ is the attention weight for channel c, and ${\mathbf{F}}_{scale}$ denotes the channel-wise scaling function. Building upon our analysis of SE module, we propose an exceptionally lightweight channel attention mechanism. For a feature map $\mathbf{x}\in {\mathbb{R}}^{C\times H\times W}$, we initially apply global average pooling to acquire channel descriptors:

$$z_c={\displaystyle \frac{1}{H\times W}}\sum _{i=1}^H\sum _{j=1}^W{\mathbf{x}}_c(i,j),$$

(10)

where $z_c$ is the global descriptor for channel c, ${\mathbf{x}}_c$ represents the c-th channel of input feature map, and H and W are the spatial dimensions. Next, we remove the other tedious steps in Equation (8) and directly apply the softmax activation function to these channel descriptors:

$$a_c={\displaystyle \frac{e^{z_c}}{{\sum }_{k=1}^C{e}^{z_k}}},$$

(11)

where $a_c$ is the attention weight for channel c, and the formula represents the softmax activation function that normalizes the exponential values across all channels. Finally, we reconstruct the original features using the generated channel weights:

$${\tilde{\mathbf{x}}}_c={\mathbf{x}}_c\times a_c,$$

(12)

where ${\tilde{\mathbf{x}}}_c$ is the recalibrated output for channel c, ${\mathbf{x}}_c$ is the original feature, and $a_c$ is the computed attention weight. Therefore, our approach only retains the channel weight assignment mechanism in SE attention mechanism, removing modules such as dimensionality-reduction and dimensionality-increasing layers. The proposed attention module can be inserted after any convolutional layer to perform channel reconstruction. Despite its simplicity, our experimental results demonstrate that this channel attention mechanism maintains performance while substantially reducing computational complexity, offering a novel approach for lightweight network architecture design.

3.4. A Lightweight Neural Network

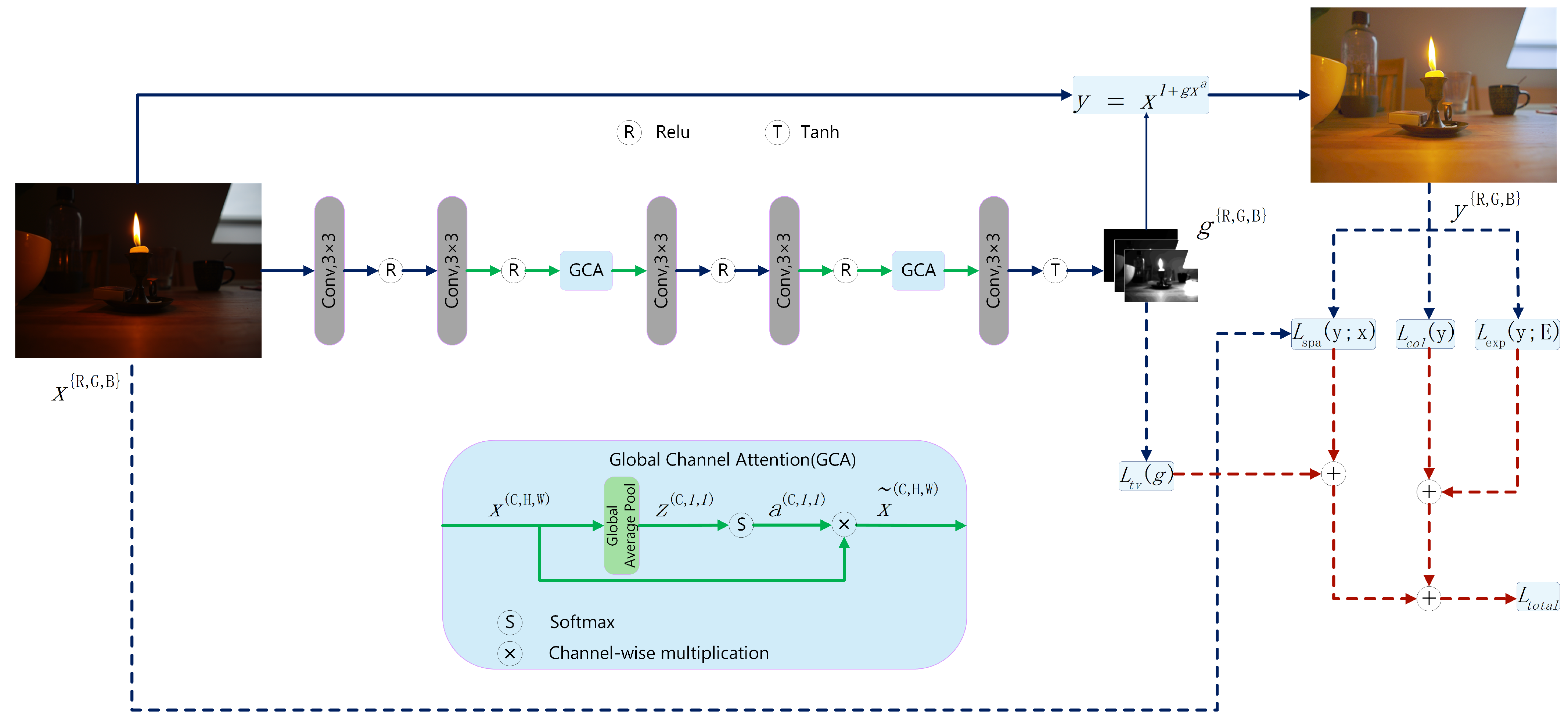
Based on the aforementioned GCA attention mechanism and GLE formula, we design a lightweight neural network for low-light image enhancement. The architecture of our network is depicted in Figure 4, which consists of five convolutional layers integrated with two channel reconstruction modules. Regarding the convolutional layer design, the first four layers employ 3 × 3 convolutional kernels and maintain 16 feature channels to extract comprehensive feature representations. Each of these layers is followed by a ReLU activation function to introduce nonlinear transformations. The final layer utilizes a 3 × 3 convolutional kernel to reduce the feature dimensionality to three output channels, with a Tanh activation function applied to constrain the output range within [−1, 1]. The two channel reconstruction modules are strategically positioned after the second and fourth convolutional layers. These modules implement our GCA channel attention mechanism through global average pooling combined with softmax activation, effectively enhancing the network’s selective capability toward information-rich channels. Subsequently, conditional value amplification is applied, selectively magnifying all positive parameter regions by a factor of 10 while preserving negative value regions unchanged. This asymmetric approach extends the final parameter g output range to [−1, 10], thereby enabling enhanced exposure suppression capabilities. The network ultimately outputs a three-channel mapping g, which is used for pixel adjustment across the R, G, and B channels, resulting in the enhanced image. The proposed model, with a significantly reduced parameter count of merely 8 K compared to the 80 K parameters of the Zero-DCE model, thereby gains a substantial advantage in terms of execution efficiency. The experimental results demonstrate that this network architecture achieves an optimal balance between computational efficiency and parameter estimation accuracy, providing a practical and effective solution for low-light image enhancement.

3.5. Loss Functions

To enable end-to-end training of our network without reference images, we employ a suite of differentiable non-reference loss functions, which facilitate zero-reference training and allow our model to produce enhanced results with optimized visual quality. These loss functions are directly adopted from the Zero-DCE method, and we have retained the original formulations without modification. The total loss function, which integrates four loss items, is expressed as

$$L_{\mathrm{total}}=w_{spa}{L}_{spa}+w_{exp}{L}_{exp}+w_{col}{L}_{col}+w_{tv}{L}_{tv\left(g\right)}$$

(13)

Here, $L_{spa}$, $L_{exp}$, $L_{col}$, and $L_{tv}$ represent the spatial consistency loss, exposure control loss, color constancy loss, and illumination smoothness loss, respectively. $w_{spa}$, $w_{exp}$, $w_{col}$, and $w_{tv}$ represent the weights of these loss functions, which were originally established in the Zero-DCE method. These weights have been meticulously calibrated to balance the contributions of the different loss components. Our empirical evaluations have also confirmed their effectiveness for our task, leading us to use these loss functions and keep the same weights as the Zero-DCE approach throughout our experiments to ensure optimal performance.

4. Results

In this section, we detail our experimental setup, implementation specifics, and comparative results with the existing methods.

4.1. Implementation Details

To comprehensively train the proposed model, enabling it to enhance low-light regions and suppress overexposed areas, we select multi-exposure sequence images from the SICE dataset [36] as our training set, totaling 2002 images. This dataset encompasses scenes under various exposure conditions, providing a rich array of samples for the model to learn image features under different lighting scenarios. All the training images are resized to $512\times 512$ pixels to ensure input consistency and enhance training efficiency. We implement our proposed method using the PyTorch 2.1.0 framework and conduct training and testing on a desktop computer equipped with an NVIDIA RTX 3090 GPU, whose manufacturer is NVIDIA company and was made in Santa Clara, CA, USA. For the training parameter settings, the batch size is set to 8. Network weight initialization employs a standard Gaussian distribution with zero mean and a standard deviation of 0.02, while the bias term is initialized as a constant. The optimization algorithm used is the Adam optimizer with a fixed learning rate of 0.0001. The weight parameters in the loss functions, $w_{spa}$, $w_{exp}$, $w_{col}$, and $w_{tv\left(g\right)}$, are set to values consistent with those provided in the Zero-DCE source code to balance the contribution of different loss components.

We conducted comprehensive evaluations across the following six datasets: LOLv1 [28], LOLv2-Real, LOLv2-Synthetic [37], LSRW-huawei [38], DICM [39], and MEF [40], obtaining extensive experimental data. We adopted a comprehensive evaluation strategy, combining qualitative and quantitative analyses to verify the effectiveness of the proposed method. Qualitative assessment involved analyzing the visual perception of enhanced images in terms of detail preservation, color restoration, and contrast balance. Quantitative evaluation employed two categories of objective evaluation metrics: reference-based metrics, including PSNR (Peak Signal-to-Noise Ratio), SSIM (Structural Similarity Index Measure) [41], and LPIPS (Learned Perceptual Image Patch Similarity) [42], and no-reference metrics, such as NIQE (Natural Image Quality Evaluator) [43]. Note that higher values are preferred for PSNR and SSIM, while lower values indicate better performance for LPIPS and NIQE. The comparison methods included RetinexNet [28], Zero-DCE [33], R2RNet [38], RUAS [44], Zero-DCE++ [34], CLIP-LIT [31], GCP [45], and CoLIE [32]. Comprehensive experimental results demonstrated that our proposed method achieves satisfactory performance in both subjective visual quality and objective evaluation metrics. Particularly, we also conducted a comparison of the execution efficiency of various methods. The experimental data indicates that the proposed model is the most efficient in terms of execution speed, achieving the intended design objectives.

4.2. Ablation Experiment

To validate the optimal value of hyperparameter a and the effectiveness of the GCA attention mechanism, we conducted a series of ablation studies. Through these experiments, we were able to quantitatively assess the impact of these key components on the overall model performance, thereby providing empirical support for our choices.

4.2.1. Hyperparameter a

From the previous analysis and Figure 4, it is evident that hyperparameter a plays a crucial role in controlling the intensity of image enhancement. When a is either too small or too large, achieving the desired enhancement effect becomes challenging. Therefore, it is necessary to investigate the appropriate value of a.

Table 1. Performance comparison of our method with hyperparameter a ranging from 0.1 to 0.16.

	$\mathit{a}=0.10$	$\mathit{a}=0.11$	$\mathit{a}=0.12$	$\mathit{a}=0.13$	$\mathit{a}=0.14$	$\mathit{a}=0.15$	$\mathit{a}=0.16$
PSNR ↑	18.672	18.926	19.063	19.079	18.955	18.790	18.602
SSIM ↑	0.610	0.628	0.629	0.635	0.646	0.644	0.635

presents the variation in PSNR and SSIM metrics across a combined dataset of LOLv1, LOLv2-Real, LOLv2-Synthetic, and LSRW-huawei as a ranges from 0.10 to 0.16. The results demonstrate that the value of a enables the model to achieve the best performance between 0.13 and 0.14. Specifically, the PSNR is higher when a is closer to 0.13, and the SSIM is higher when a is closer to 0.14. Considering that the enhancement of darker regions is more effective when a is set to 0.13 compared to 0.14, we select 0.13 as the value for hyperparameter a. Additionally, these metrics consistently decline when a deviates from 0.13 and 0.14. The possible explanation for this trend is that, when a is smaller, the curve’s enhancement capability becomes excessively strong, leading to images with increased noise or overexposure. Conversely, when a is larger, the enhancement effect on dark regions becomes less pronounced, and the curve’s ability to enhance low-light conditions deteriorates, failing to adequately meet the task requirements.

4.2.2. Channel Attention Mechanism

Channel attention mechanisms enable our model to focus more on important features while suppressing less important ones, thereby better accomplishing the low-light image enhancement task. In our design, to prevent degradation of model generalization capacity caused by using attention at every layer, we strategically implemented attention only after two network layers: specifically following the second and fourth convolutional layers. We now need to conduct comparative validation between implementations with and without our global attention mechanism to demonstrate the effectiveness of our model. We again selected a combined dataset comprising LOLv1, LOLv2-Real, LOLv2-Synthetic, and LSRW-huawei for validation. As shown in

Table 2. Validation of the effectiveness of the GCA module.

GCA	PSNR ↑	SSIM ↑	LPIPS ↓
	18.422	0.585	0.184
✓	19.079	0.635	0.178

, compared to the configuration without the GCA attention mechanism, the model incorporating the GCA module clearly achieved higher scores across the PSNR, SSIM, and LPIPS metrics. This demonstrates that our designed GCA attention module contributes significantly to the image enhancement task. All the subsequent experiments were conducted on the foundation of models incorporating the GCA module.

4.3. Visual and Perceptual Comparisons

In this subsection, we conduct visual comparisons on the LOLv1, LOLv2-Real, LOLv2-Synthetic, LSRW-huawei, DICM, and MEF datasets to gain a more intuitive understanding of the effectiveness of our proposed brightness adjustment method. As illustrated in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, our method achieves superior visual perception in many scenarios. Furthermore, as demonstrated in Figure 7, our proposed method is also effective in scenarios where the input images originally have better lighting conditions. In contrast, methods such as RetinexNet, Zero-DCE, R2RNet, RUAS, and Zero-DCE++ result in varying degrees of overexposure or deviation from the original images.

4.4. Quantitative Comparisons

To further evaluate the effectiveness and advancement of our proposed model, we conducted comprehensive metric assessments on six different datasets, including LOLv1, LOLv2-Real, LOLv2-Synthetic, LSRW-huawei, DICM, and MEF. In all the reference metric evaluations, we highlight the best results in bold and underline, while the second- and third-best results are marked in bold. We measured reference metrics PSNR, SSIM, LPIPS, and the non-reference metric NIQE, as shown in

Table 3. Comparison of reference metrics (PSNR and SSIM) across LOLv1, LOLv2-Real, LOLv2-Synthetic, and LSRW-huawei datasets.

Method	PSNR ↑					SSIM ↑
	LOLv1	LOLv2- Real	LOLv2- Synthetic	LSRW- Huawei		LOLv1	LOLv2- Real	LOLv2- Synthetic	LSRW- Huawei
RetinexNet	16.774	16.097	17.137	16.819		0.546	0.440	0.795	0.556
Zero-DCE	16.752	17.866	18.070	17.956		0.461	0.494	0.538	0.451
R2RNet	18.179	17.949	16.089	17.277		0.605	0.654	0.524	0.554
RUAS	16.405	15.326	13.404	15.690		0.553	0.485	0.549	0.571
Zero-DCE++	15.901	18.352	18.223	17.138		0.433	0.507	0.536	0.418
CLIP-LIT	12.394	15.182	16.190	13.561		0.526	0.563	0.718	0.555
GCP	17.393	16.610	16.620	16.550		0.521	0.436	0.668	0.541
CoLIE	16.310	16.910	17.697	17.249		0.565	0.516	0.751	0.590
Ours	18.065	19.044	19.309	18.940		0.610	0.606	0.673	0.619

,

Table 4. Comparison of reference metric (LPIPS) across LOLv1, LOLv2-Real, LOLv2-Synthetic, and LSRW-huawei datasets.

Method	LPIPS ↓
	LOLv1			LOLv2- Real			LOLv2- Synthetic			LSRW- Huawei
	Mean	Std.		Mean	Std.		Mean	Std.		Mean	Std.
RetinexNet	0.364	0.098		0.425	0.110		0.199	0.062		0.360	0.072
Zero-DCE	0.255	0.075		0.268	0.097		0.140	0.048		0.293	0.072
R2RNet	0.170	0.058		0.183	0.063		0.226	0.078		0.260	0.059
RUAS	0.180	0.088		0.206	0.062		0.281	0.091		0.346	0.102
Zero-DCE++	0.233	0.078		0.228	0.091		0.129	0.053		0.260	0.064
CLIP-LIT	0.274	0.101		0.256	0.117		0.164	0.073		0.285	0.070
GCP	0.331	0.115		0.349	0.143		0.153	0.077		0.308	0.102
CoLIE	0.260	0.107		0.259	0.124		0.140	0.066		0.286	0.087
Ours	0.215	0.084		0.217	0.100		0.111	0.052		0.253	0.072

and

Table 5. Comparison of the non-reference metric (NIQE) across the LOLv1, LOLv2-Real, LOLv2-Synthetic, LSRW-huawei, DICM, and MEF datasets.

Method	NIQE ↓
	LOLv1	LOLv2- Real	LOLv2- Synthetic	LSRW- Huawei	DICM	MEF
RetinexNet	8.734	9.254	5.346	4.063	4.438	4.344
Zero-DCE	7.755	8.079	4.485	3.511	3.807	3.435
R2RNet	4.721	4.984	5.214	5.121	5.203	4.886
RUAS	6.291	6.501	6.530	5.699	6.762	5.369
Zero-DCE++	7.871	8.106	4.522	3.757	3.947	3.537
CLIP-LIT	8.102	8.213	4.553	3.902	3.938	3.461
GCP	9.211	9.156	4.665	4.020	3.880	3.586
CoLIE	8.204	8.283	4.503	3.494	3.761	3.410
Ours	7.600	7.860	4.455	3.716	3.882	3.465

below. Table 3 and Table 4 display the comparative results of the reference metrics. It can be observed that our method demonstrates significant advantages regarding the PSNR, SSIM, and LPIPS metrics. In the PSNR metric comparisons, our method is only slightly inferior to R2RNet on the LOLv1 dataset while achieving the highest metrics on the other three datasets. In terms of the SSIM metric comparisons, our method achieves commendable results, attaining the best performance on the LOLv1 and LSRW-huawei datasets, and securing a position within the top three on the LOLv2-Real dataset. Regarding the LPIPS metric comparison, our approach achieves the best results on both the LOLv2-Synthetic and LSRW-huawei datasets, and also ranks third on the remaining two datasets. Additionally, since the numerical results in the top-performing entries are closely clustered, we introduce a standard deviation column in Table 4 to further demonstrate the stability of the enhancement performance. Overall, judging from the standard deviation indicator in the experimental data, the standard deviation value of the proposed algorithm ranks in the upper-middle level among all the algorithms, showing a certain degree of stability, which basically meets our original design intention of achieving enhancement effects comparable to mainstream algorithms while ensuring optimal computational efficiency. The above results with a reference metric evaluation indicate that our proposed method has a better enhancement effect, and the enhanced image is close to the real image under normal light. Throughout these comparisons, we observed that R2RNet achieved relatively good results across multiple metrics and datasets, possibly because it employs supervised learning with a more complex model, whereas our model is unsupervised with a simpler structure. Furthermore, Table 3 and Table 4 demonstrate that, across all the datasets, our method consistently outperforms Zero-DCE and Zero-DCE++ in the PSNR, SSIM, and LPIPS metrics, validating the superiority of our curve estimation method, which generates enhanced images more closely resembling the real normal-light reference images.

In Table 5, we present a comprehensive comparison of various methods across six datasets using the no-reference indicator NIQE. The results demonstrate that our proposed model achieves good performance in various datasets. Specifically, our model attains the best metric on the LOLv2-Synthetic dataset, outperforming all the other methods. Additionally, on the LOLv1, LOLv2-Real, and LSRW-huawei datasets, our NIQE metrics consistently rank within the top three, further validating the effectiveness of our approach. It should be noted that, although the proposed method does not rank in the top three on the DICM and MEF datasets, the difference in performance metrics compared to the third-ranked algorithm is actually quite small and very close.

4.5. Computation Time

To demonstrate the fast computational capability of our model, we conducted experiments using 100 images on the LOLv2-Real dataset and obtained the average inference time for one image. As illustrated in

Table 6. Comparison of average computation time per image (ms) on the LOLv2-Real dataset.

Method	RetinexNet	R2RNet	RUAS	Zero-DCE++	CLIP-LIT	GCP	CoLIE	Ours
Time (ms)	95.1	1345.0	3.5	1.0	1.9	49.0	1243.0	0.7

, our model achieves remarkable inference speed. It consistently outperforms all the other compared algorithms, securing the top position in terms of computational efficiency. In summary, our approach effectively reconciles the trade-off between rapid inference and superior performance metrics. With a computation time of 0.7 ms, our method is highly suitable for implementation on mobile devices, satisfying the real-time processing requirements. Moreover, the compact model size facilitates deployment on resource-constrained mobile platforms.

5. Conclusions

In this work, we propose a novel lightweight low-light image enhancement method and validate its performance through extensive experiments. The proposed method retains the zero-reference learning strategy of the Zero-DCE method, eliminating the need for paired or unpaired datasets during training, thus making it highly versatile across various application scenarios. The key differentiator between our approach and the Zero-DCE method lies in the significant advancements achieved in both inference speed and image quality. These improvements are primarily attributed to our redesigned GLE curve and a lightweight network architecture that incorporates a GCA mechanism. Specifically, we design a new curve based on Gamma correction principles that requires only a single mapping to complete low-light image enhancement, substantially improving the processing efficiency compared to the Zero-DCE method, which requires eight iterations of the LE curve application to accomplish low-light image enhancement. Additionally, we introduce a GCA mechanism, which enables the model to focus more effectively on key features, thereby significantly enhancing performance in low-light-enhancement tasks. Although our method demonstrates encouraging outcomes, its image quality performance still lags behind certain advanced supervised and unsupervised techniques. Consequently, subsequent research will investigate strategies for boosting generated image quality without compromising the model’s lightweight nature, providing more efficient and robust solutions for practical application scenarios.