Monitoring and Evaluating the Damage to Shear Connectors in Steel–Concrete Composite Beams by Curvature-Based Indicators Through Vibration Tests
Abstract
1. Introduction
2. Theoretical Backgrounds of Damage Detection with Modal Information
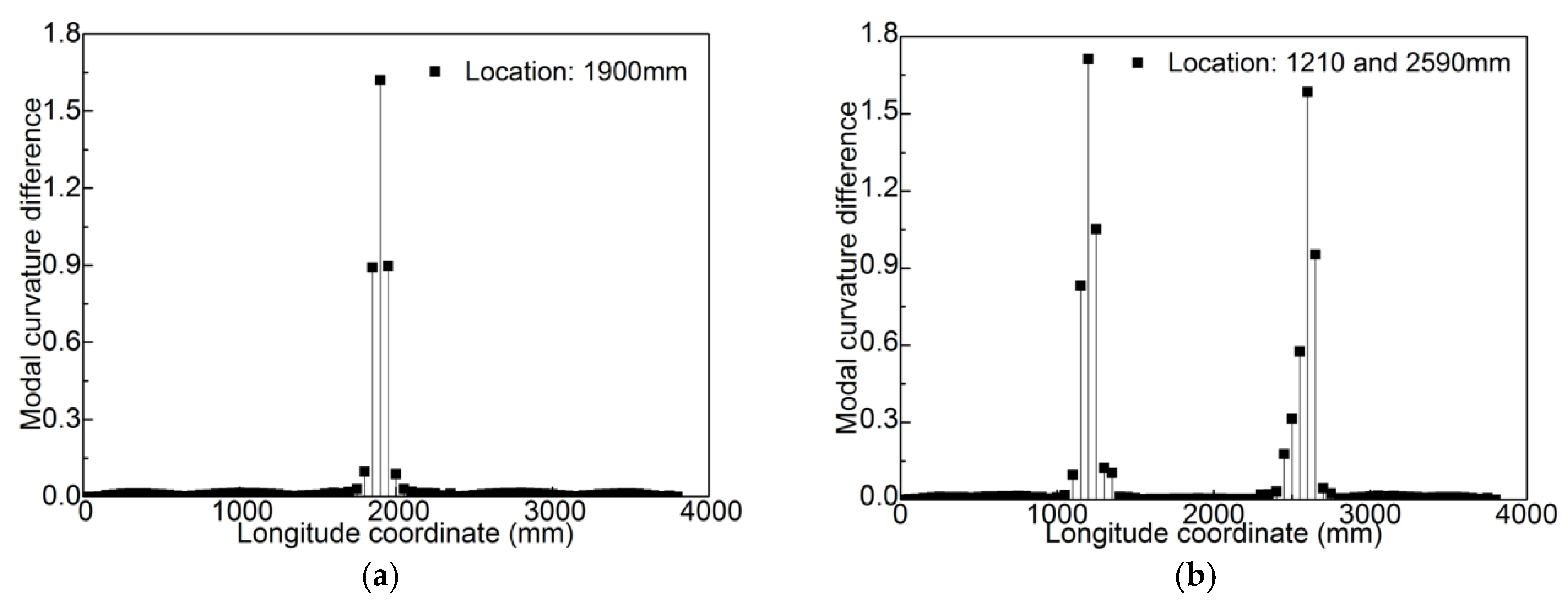
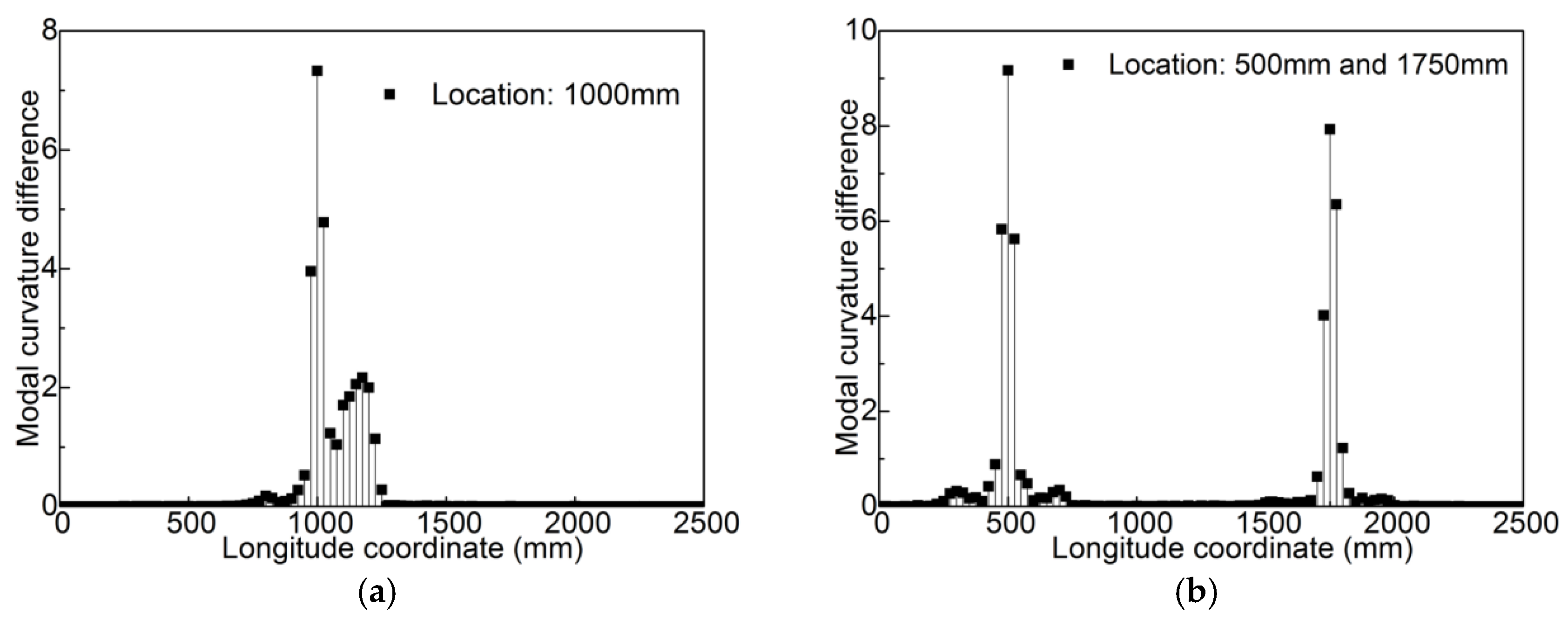
2.1. Modal Curvature Difference
2.2. Modal Flexibility Difference Curvature
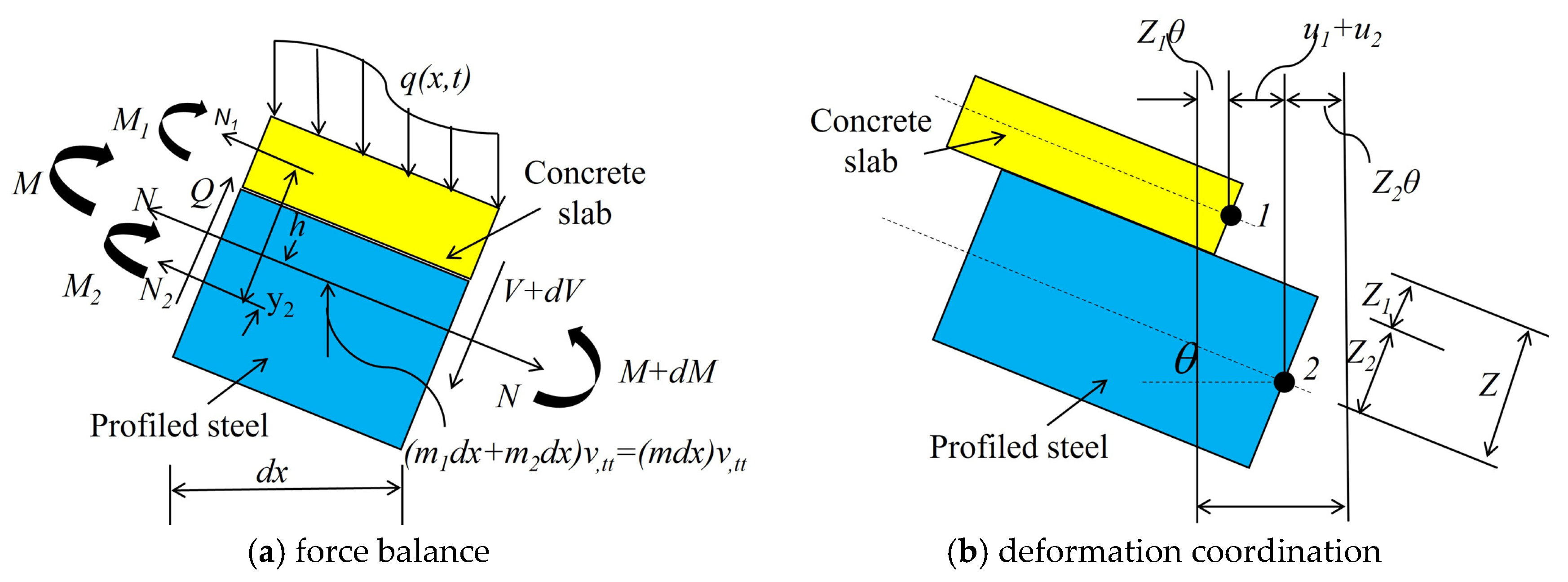
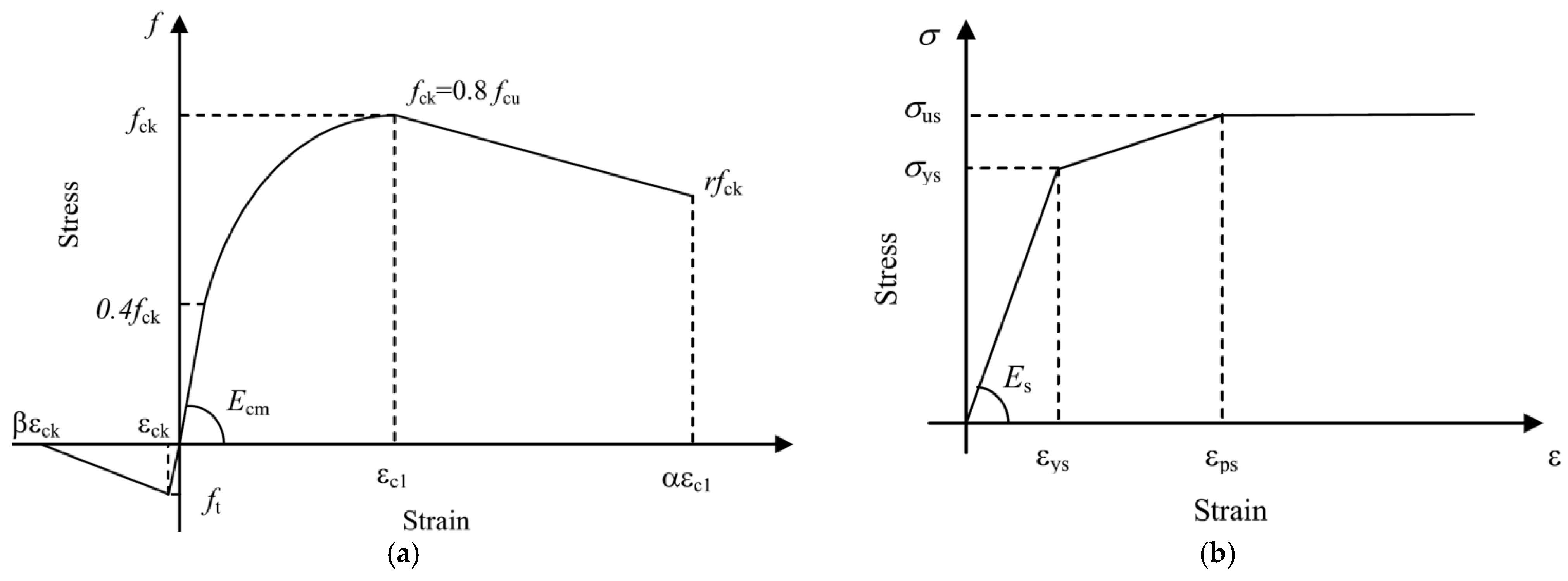
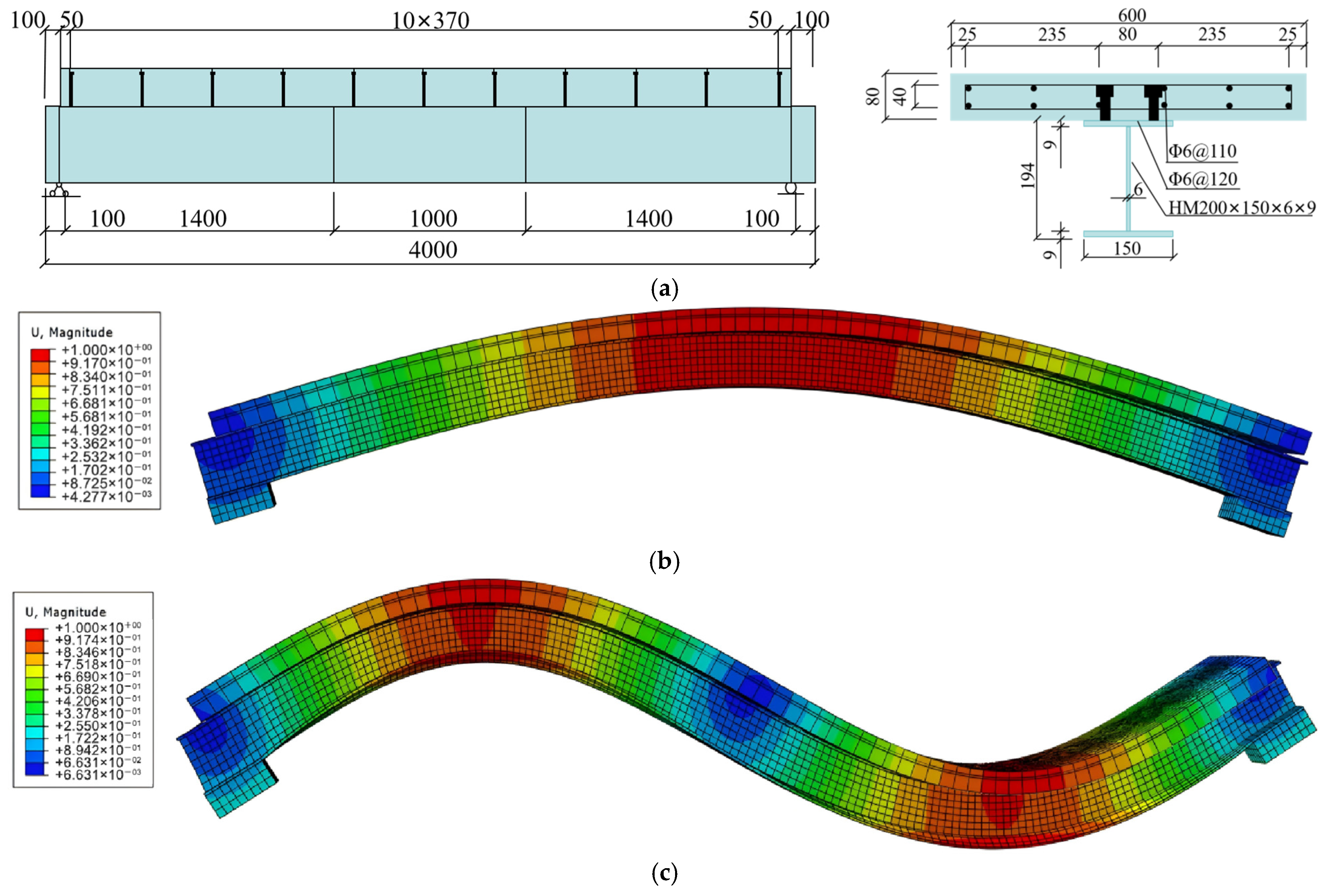
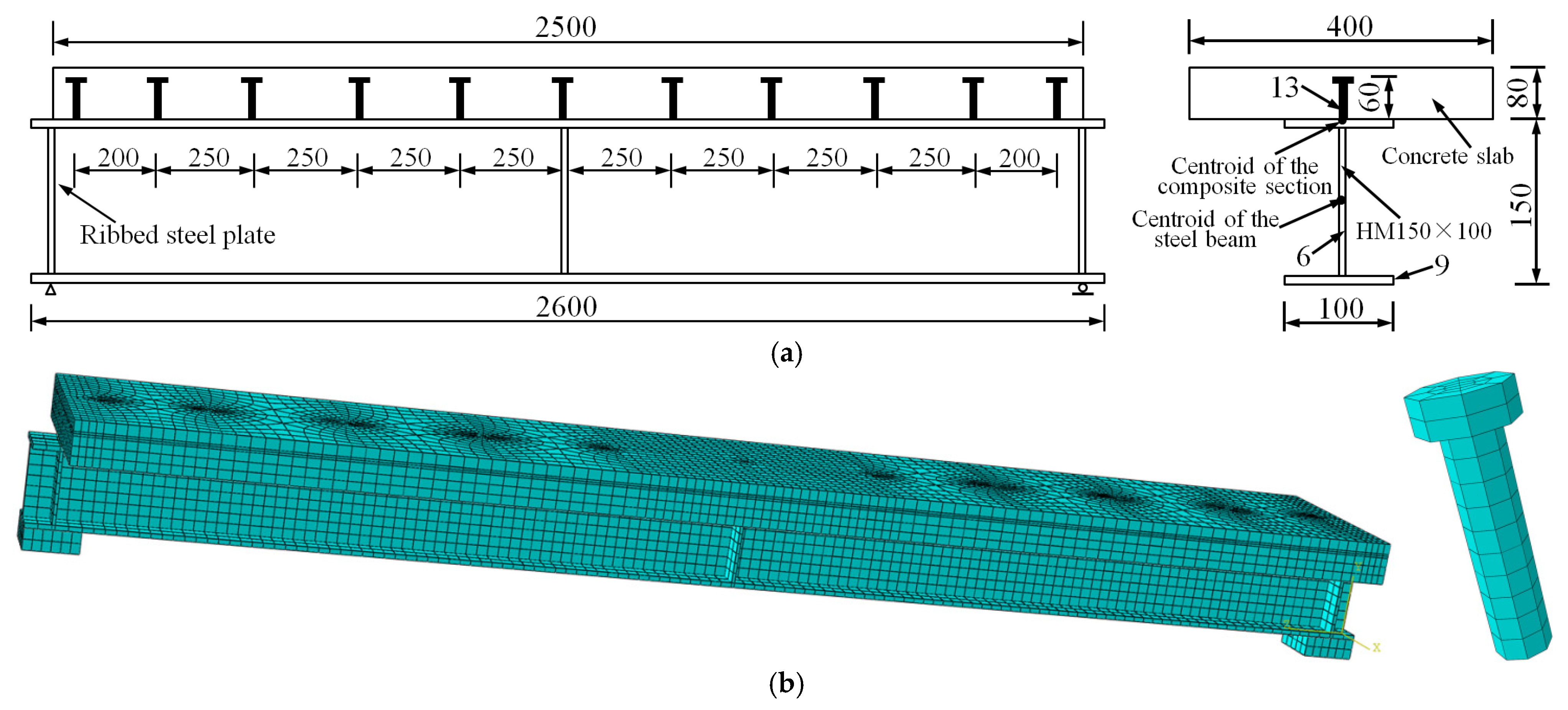
3. Modeling of the Steel–Concrete Composite Beam
3.1. The Solid-Slipping Beam Model
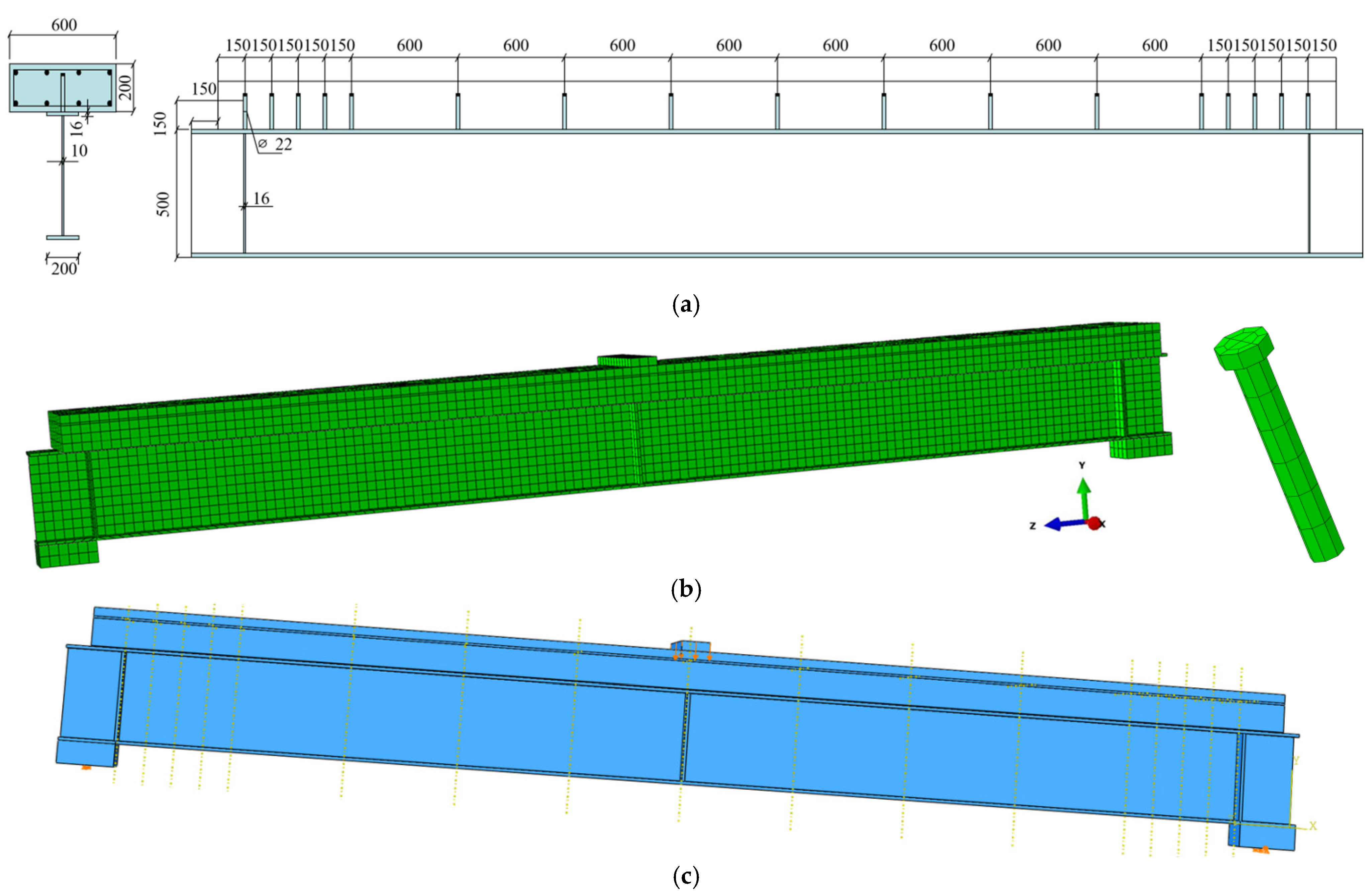
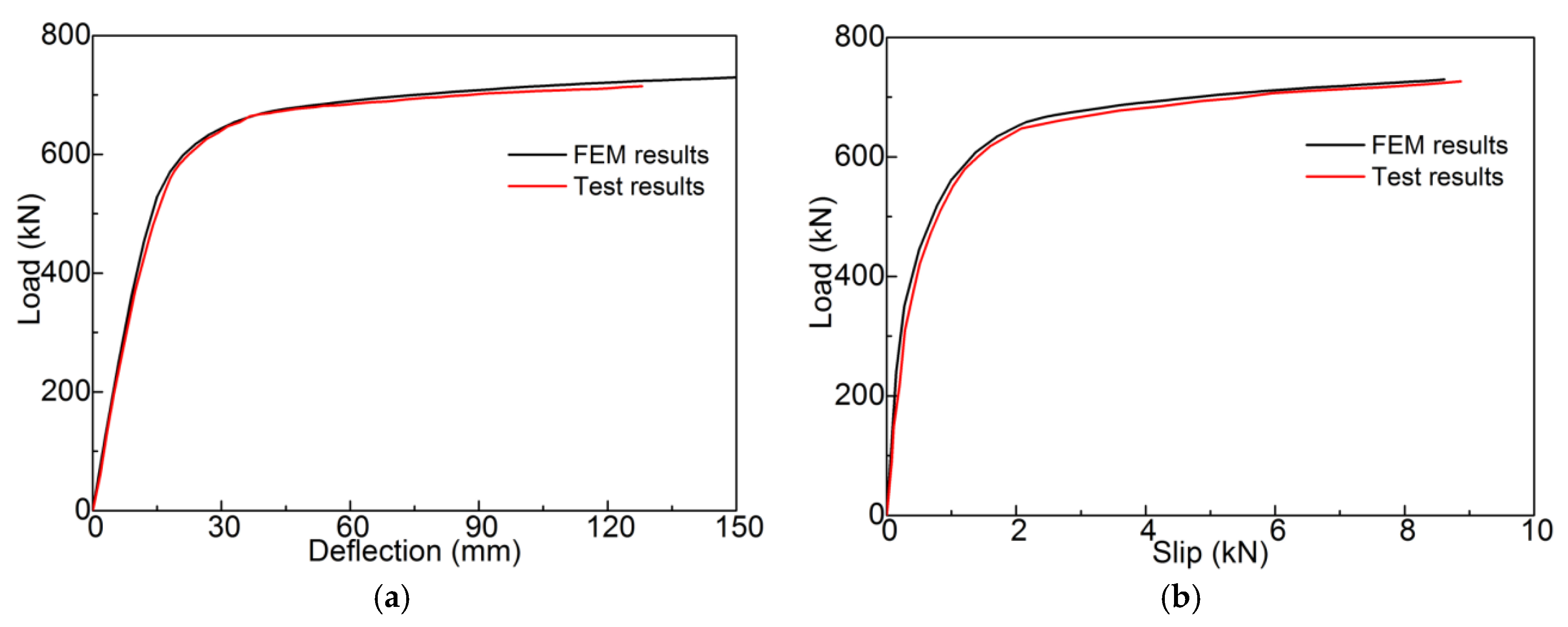
3.2. FE Model Verification 1
3.3. FE Model Verification 2
4. Localization of the Damaged Head Studs
4.1. Damage Localization Based on Modal Curvature Difference
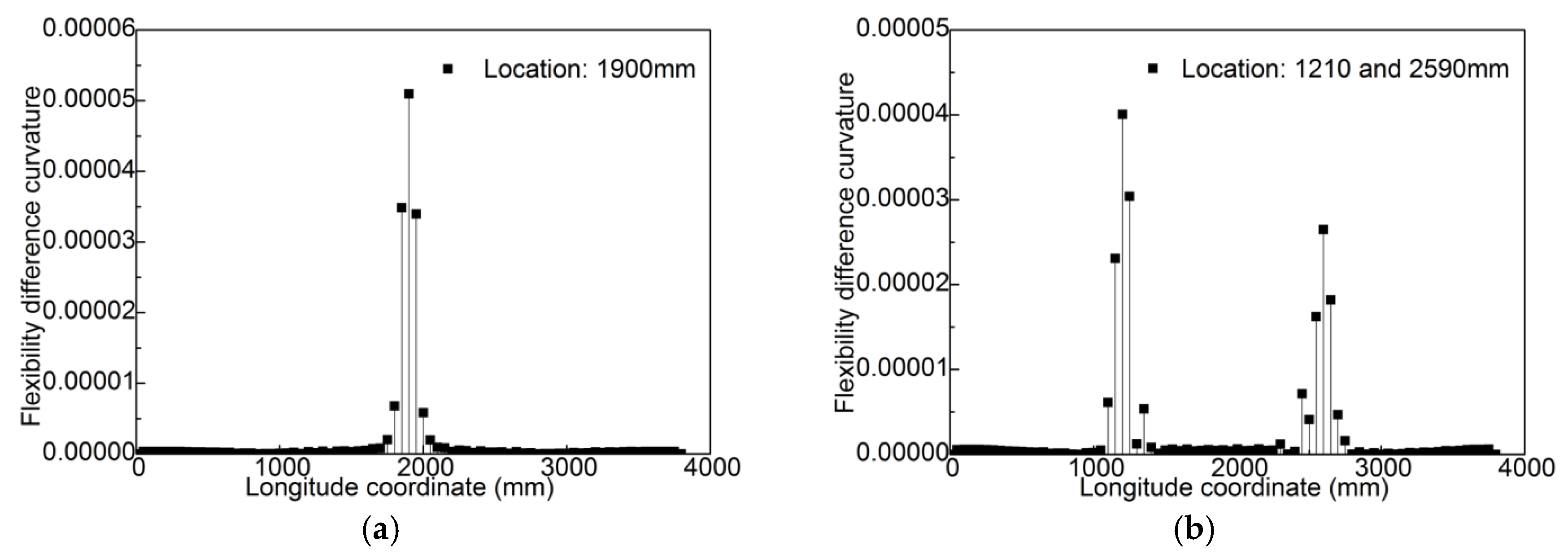
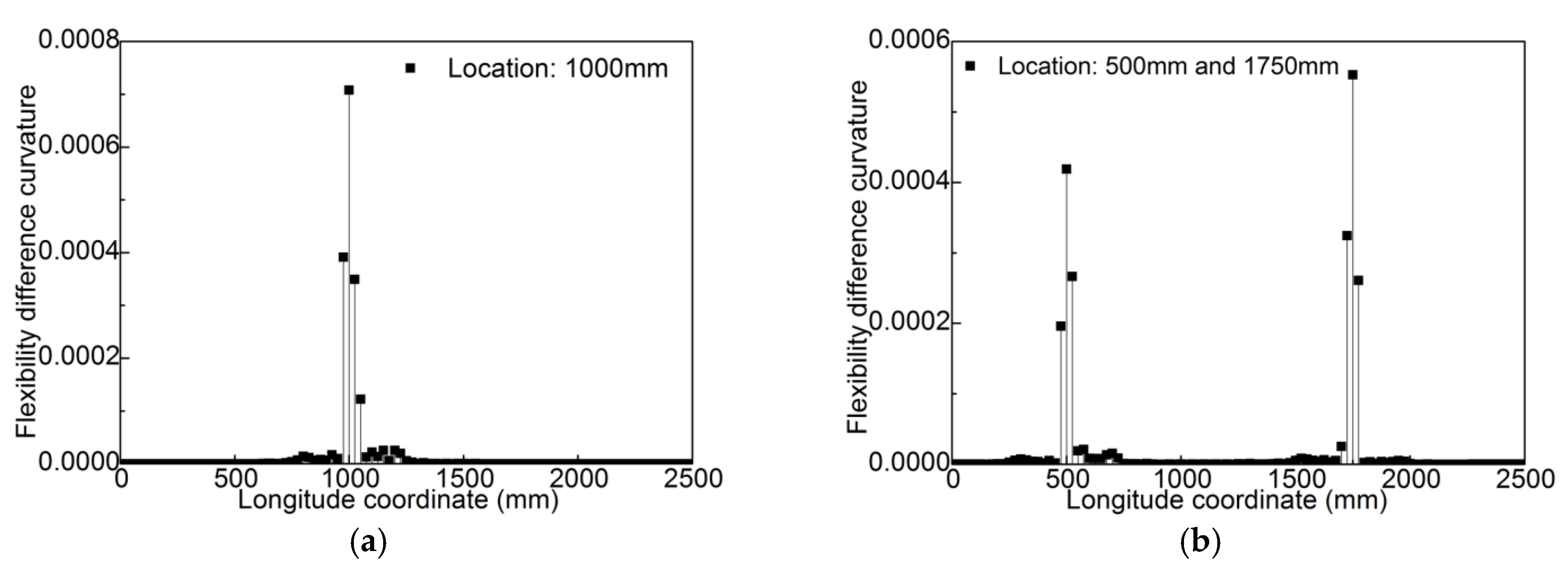
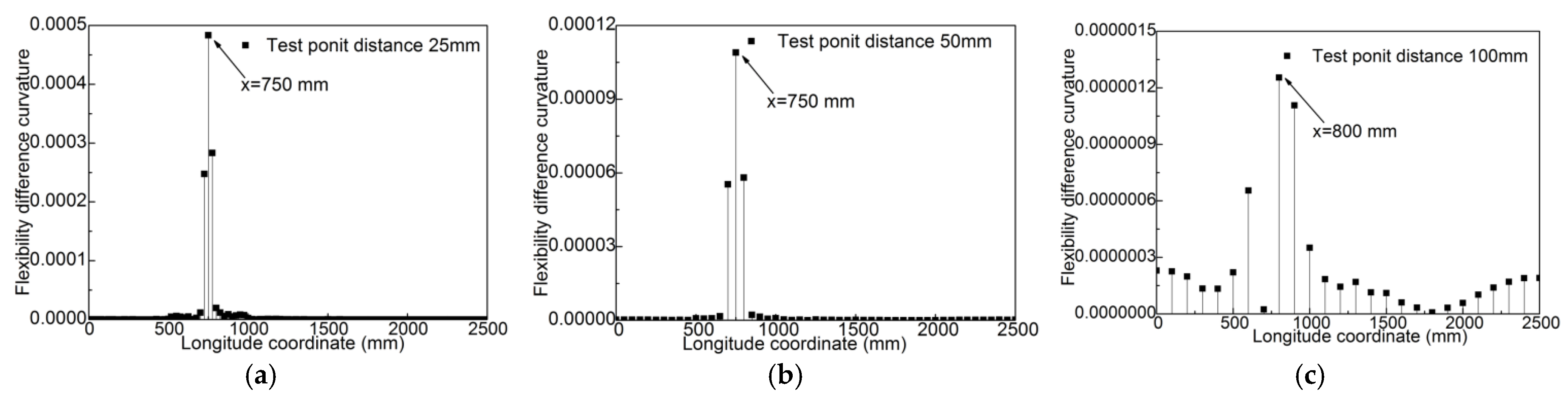
4.2. Damage Localization Based on Modal Flexibility Difference Curvature
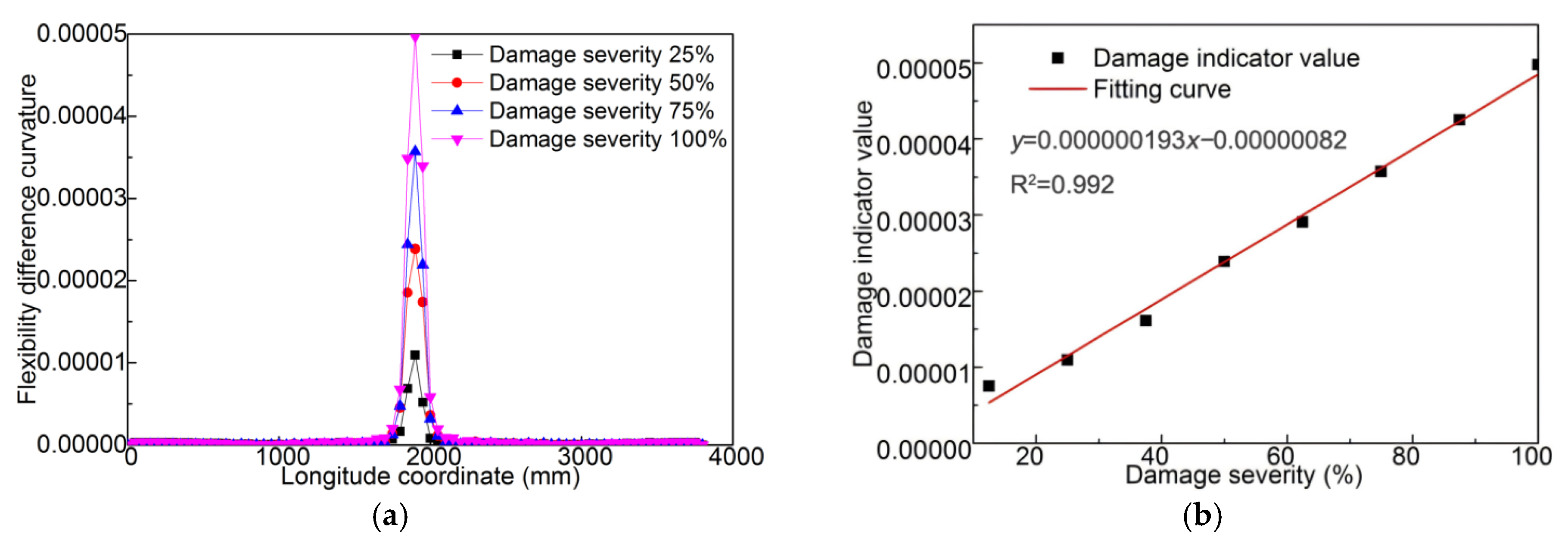
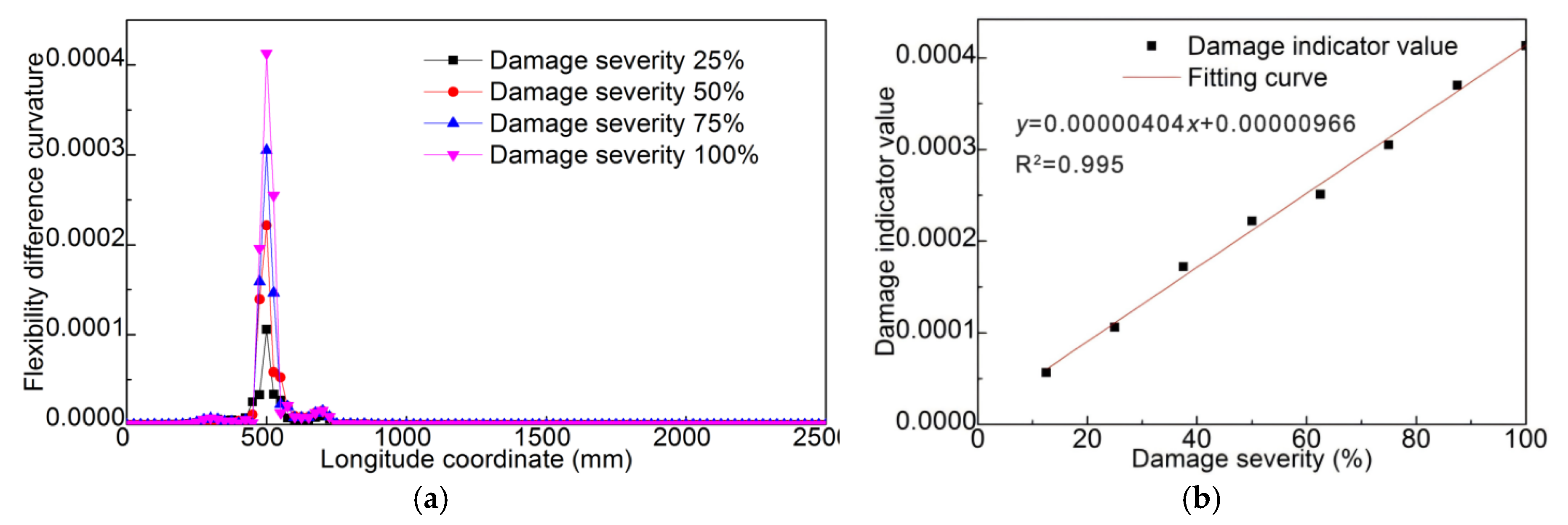
5. Quantification of the Damaged Shear Studs
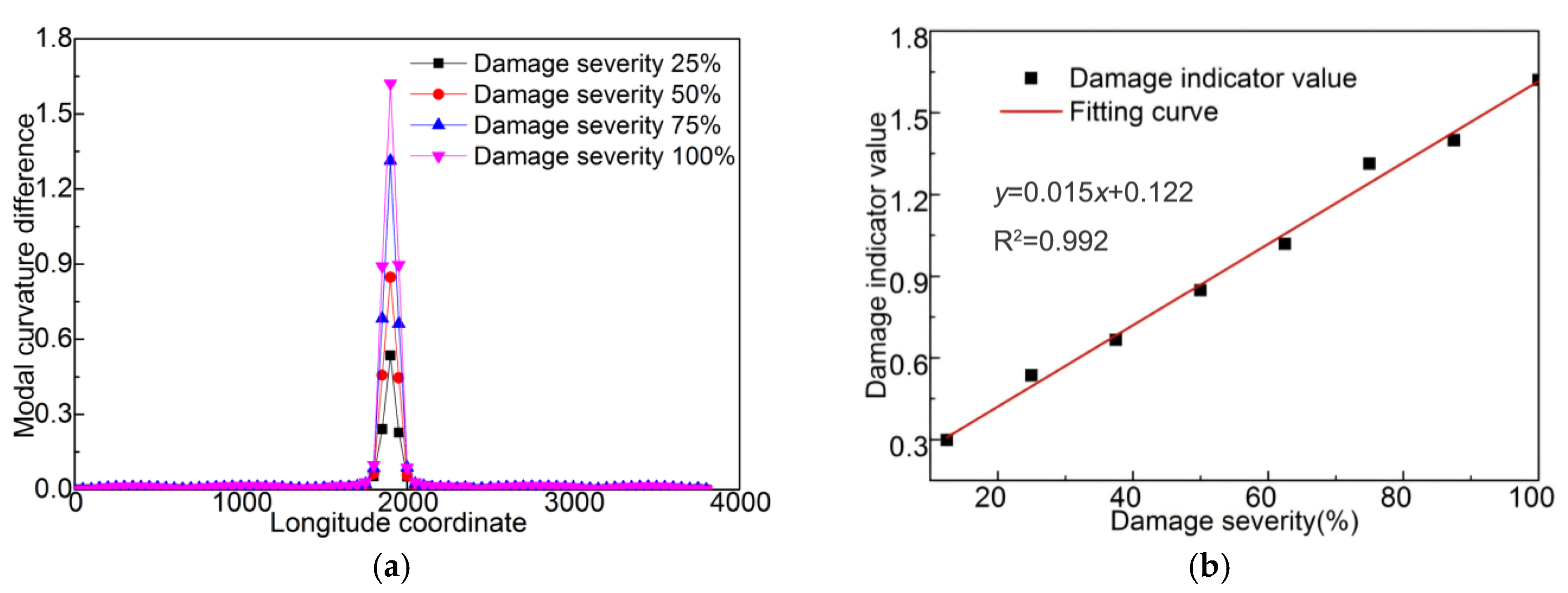
5.1. Damage Quantification Based on Modal Curvature Difference
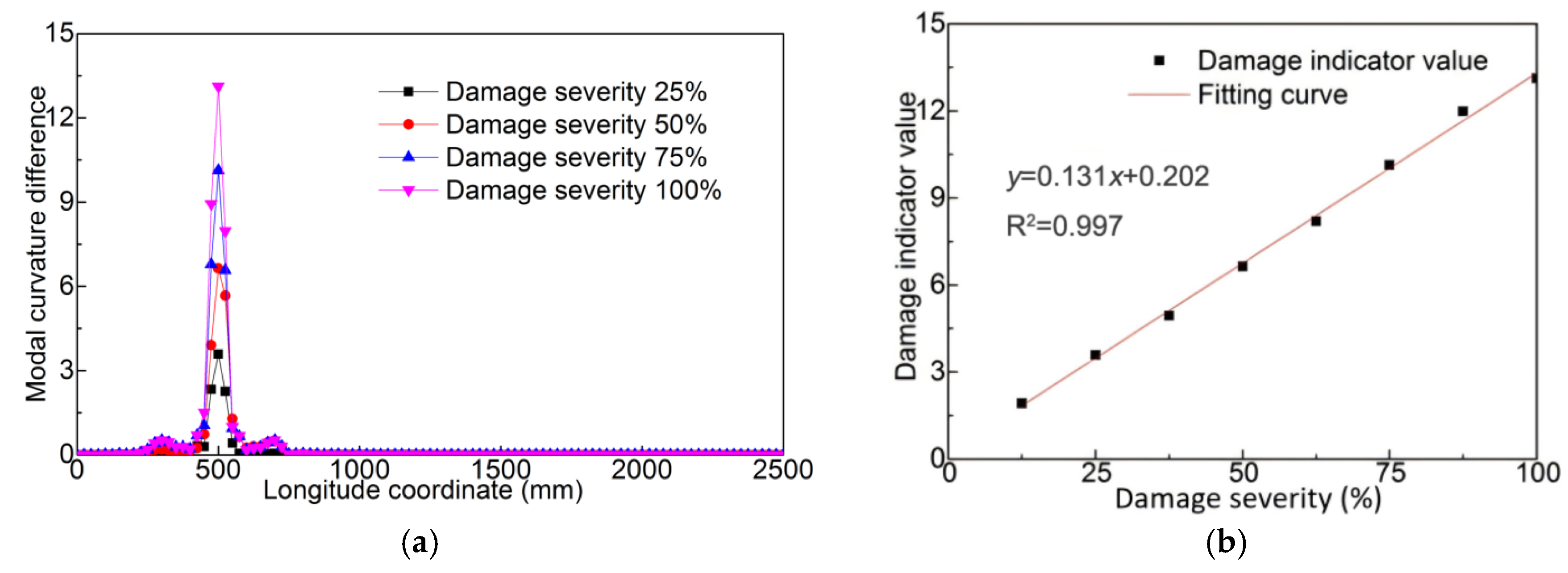
5.2. Damage Quantification Based on Modal Flexibility Difference Curvature
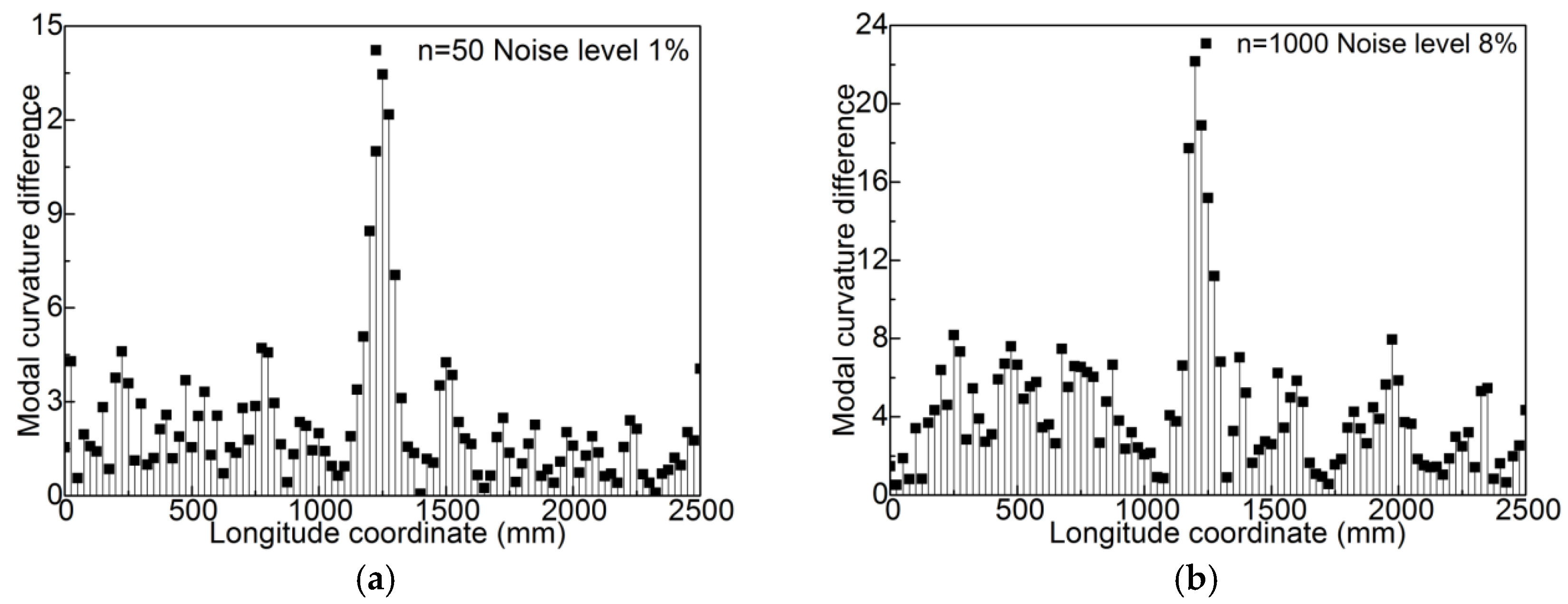
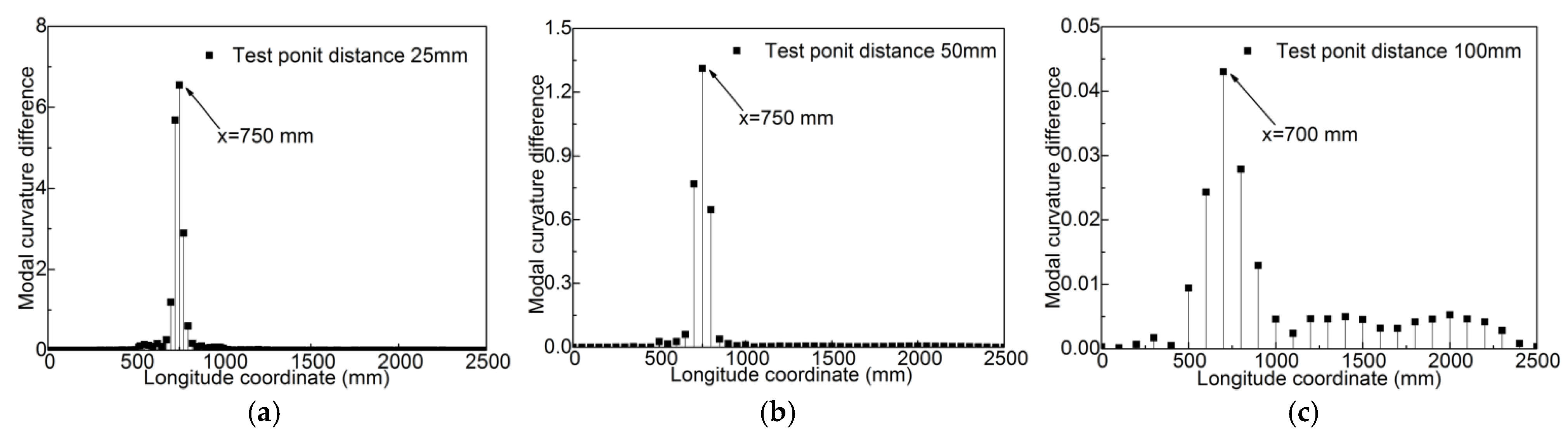
6. Robust Analysis
6.1. The Influence of Ambient Noises
6.2. The Influence of Incomplete Modal Information
7. Conclusions
- (1)
- A solid-slipping nonlinear finite element (FE) model for SCCBs was developed with the supercities of high precision and independent of stiffness-slip function.
- (2)
- Two indicators based on the vibration curvature of SCCB were proposed, which are able to locate the damaged shear studs and quantify the damage degree for both sole damage and multi-damage, having a maximum error of no more than 1%.
- (3)
- Robust analysis proved that the proposed indicators worked well, even though the ambient noise was up to 8% and measurement points decreased by 75%, and the proposed modal curvature difference showed a better robustness to ambient noises than the modal flexibility difference curvature.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Henderson, I.E.J.; Zhu, X.Q.; Uy, B.; Mirza, O. Dynamic Behaviour of Steel-concrete Composite Beams Retrofitted with Various Bolted Shear Connectors. Eng. Struct. 2017, 131, 115–135. [Google Scholar] [CrossRef]
- Lima, J.M.; Berzrrra, L.M.; Bonilla, J.; Mirambell, E. Experimental Study on Full Scale Steel-concrete Composite Beams Using Truss-type Shear Connectors. Eng. Struct. 2024, 303, 117490. [Google Scholar] [CrossRef]
- Dilena, M.; Morassi, A. Vibrations of Steel-Concrete Composite Beams with Partially Degraded Connection and Applications to Damage Detection. J. Sound Vib. 2009, 320, 101–124. [Google Scholar] [CrossRef]
- Hou, Z.M.; Xia, H.; Zhang, Y.L. Dynamic Analysis and Shear Connector Damage Identification of Steel-concrete Composite Beams. Steel Compos. Struct. 2012, 13, 327–341. [Google Scholar] [CrossRef]
- Gu, Y.; Lu, Y. Stiffness Characteristics of Composite Beams and Application in Damage Identification. J. Eng. Mech. 2024, 149, 04023063. [Google Scholar] [CrossRef]
- Cuadrado, M.; Jesús, P.S.; José, A.A.G.; Varas, D. Detection of Barely Visible Multi-impact Damage on Carbon/Epoxy Composite Plates Using Frequency Response Function Correlation Analysis. Measurement 2022, 196, 111–194. [Google Scholar] [CrossRef]
- Dilena, M.; Morassi, A. Experimental Modal Analysis of Steel Concrete Composite Beams with Partially Damaged Connection. J. Vib. Control 2004, 10, 897–913. [Google Scholar] [CrossRef]
- Chellini, G.; De Roeck, G.; Nardini, L.; Salvatore, W. Damage Analysis of a Steel-concrete Composite Frame by Finite Element Model Updating. J. Constr. Steel Res. 2010, 66, 398–411. [Google Scholar] [CrossRef]
- Brigante, D.; Rainieri, C.; Fabbrocino, G. The Role of the Modal Assurance Criterion in the Interpretation and Validation of Models for Seismic Analysis of Architectural Complexes. Procedia Eng. 2017, 199, 3404–3409. [Google Scholar] [CrossRef]
- Gohar, S.; Matsumoto, Y.; Maki, T.; Sakuma, S. Investigation into Vibration—Based Structural Damage Identification and Amplitude—Dependent Damping Ratio of Reinforced Concrete Bridge Deck Slab under Different Loading States. J. Civ. Struct. Health 2023, 13, 133–148. [Google Scholar] [CrossRef]
- Mehboob, S.; Zaman, Q.U. Vibration-based Method for Story-level Damage Detection of the Reinforced Concrete Structure. Comput. Concr. 2021, 21, 29–39. [Google Scholar]
- Yin, T.; Jiang, Q.; Yuen, K. Vibration-based Damage Detection for Structural Connections Using Incomplete Modal Data by Bayesian Approach and Model Reduction Technique. Eng. Struct. 2017, 132, 260–277. [Google Scholar] [CrossRef]
- Xia, Y.; Hao, H.; Deeks, A.J.; Zhu, X. Condition Assessment of Shear Connectors in Slab-girder Ridges Via Vibration Measurements. J. Bridge Eng. 2008, 13, 43–54. [Google Scholar] [CrossRef]
- Li, J.; Hao, H.; Xia, Y.; Zhu, H. Damage Detection of Shear Connection in Bridge Structures with Transmissibility in Frequency Domain. Int. J. Struct. Stab. Dyn. 2013, 14, 634–640. [Google Scholar]
- Dimri, A.; Chakraborty, S. Damage Identification of Reinforced Concrete Slabs Using Experimental Modal Testing and Finite Element Model Updating. Structures 2024, 67, 107–123. [Google Scholar] [CrossRef]
- Li, J.; Hao, H.; Zhu, H.P. Dynamic Assessment of Shear Connectors in Composite Bridges with Ambient Vibration Measurements. Adv. Struct. Eng. 2014, 17, 617–638. [Google Scholar] [CrossRef]
- Zhang, C.; Lai, S.X.; Wang, H.P. Structural modal parameter recognition and related damage identification methods under environmental excitations: A review. SDHM Struct. Durab. Health Monit. 2025, 19, 25–54. [Google Scholar] [CrossRef]
- Huang, Y.; Nie, J.G.; Wei-Jian, Y.I. Stiffness of Steel-concrete Composite Frame Beam with Slip Effect. J. Eng. Mech. 2012, 29, 88–92. [Google Scholar] [CrossRef]
- Liu, X.P.; Bradford, M.A.; Chen, Q.J.; Ban, H.Y. Finite Element Modelling of Steel-concrete Composite Beams with High-strength Friction-grip Bolt Shear Connectors. Finite Elem. Anal. Des. 2016, 180, 54–65. [Google Scholar] [CrossRef]
- Rong, Y.; Ren, H.L.; Xu, X.Z. An Improved Damage-plasticity Material Model for Concrete Subjected to Dynamic Loading Case Studies in Construction Materials. Case Stud. Constr. Mater. 2023, 19, e02568. [Google Scholar]
- Qasem, M.; Hasan, M.; Muhamad, R.; Chin, C.L.; Alanazi, N. Generalised Calibration and Optimization of Concrete Damage Plasticity Model for Finite Element Simulation of Cracked Reinforced Concrete Structures. Results Eng. 2025, 25, 103905. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Kim, S.E. Finite Element Modeling of Push-out Tests for Large Stud Shear Connectors. J. Constr. Steel Res. 2009, 65, 1909–1920. [Google Scholar] [CrossRef]
- Lee, P.G.; Shim, C.S.; Chang, S.P. Static and Fatigue Behavior of Large Stud Shear Connectors for Steel–concrete Composite Bridges. J. Constr. Steel Res. 2005, 61, 1270–1285. [Google Scholar] [CrossRef]
- Wang, J.; Yin, H.; Zhang, S.; Yan, L.; Shuai, L.I. Experimental Investigation on Dynamic Properties of Steel-concrete Composite Beams Considering Effect of Interfacial Slip. J. Bridge Eng. 2016, 37, 142–149. [Google Scholar]
- GB 50017-2017; Standard for Design of Steel Structures. China Architecture & Building Press: Beijing, China, 2017.
- JGJ 99-2015; Technical Specification for Steel Structure of Tall Building. China Architecture & Building Press: Beijing, China, 2015.


| Material | Yield Strength (MPa) | Tensile Strength (MPa) | Elastic Modulus (GPa) | Thickness or Diameter (mm) | Elongation |
|---|---|---|---|---|---|
| Steel beam | 320 | − | 210 | 14 | 34% |
| Rebar | 400 | − | 208 | 16 | − |
| Headed stud | 353 | 426 | 208 | 22 | − |
| Concrete | − | 49.4 | 36.68 | − | − |
| Material | Yield Strength (MPa) | Ultimate Strength (MPa) | Elastic Modulus (GPa) | Thickness or Diameter (mm) | Density (kg/m3) |
|---|---|---|---|---|---|
| Steel beam | 437 | 514 | 211 | 9/6 | 7850 |
| Headed stud | 350 | 467.3 | 208 | 13 | 7850 |
| Concrete | − | 53.67 | 35.13 | − | 2500 |
| Rebar | 270 | − | 208 | 6 | 7850 |
| Flexural Modes | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| FEM frequency (Hz) | 33.08 | 109.20 | 202.22 | 351.52 | 455.50 |
| Test frequency (Hz) | 31.25 | 102.52 | 201.37 | 363.09 | 455.01 |
| Error | 5.52% | 6.12% | 0.42% | 3.29% | 0.11% |
| Material | Yield Strength (MPa) | Ultimate Strength (MPa) | Elastic Modulus (GPa) | Thickness or Diameter (mm) | Density (kg/m3) |
|---|---|---|---|---|---|
| Steel beam | 205 | 300 | 206 | 9/6 | 7850 |
| Headed stud | 320 | 400 | 206 | 13 | 7850 |
| Concrete | − | 26.8(C40) | 31.1 | − | 2450 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Du, F.; Jin, H. Monitoring and Evaluating the Damage to Shear Connectors in Steel–Concrete Composite Beams by Curvature-Based Indicators Through Vibration Tests. Appl. Sci. 2025, 15, 7313. https://doi.org/10.3390/app15137313
Zhang H, Du F, Jin H. Monitoring and Evaluating the Damage to Shear Connectors in Steel–Concrete Composite Beams by Curvature-Based Indicators Through Vibration Tests. Applied Sciences. 2025; 15(13):7313. https://doi.org/10.3390/app15137313
Chicago/Turabian StyleZhang, Haobo, Fangzhu Du, and Haoran Jin. 2025. "Monitoring and Evaluating the Damage to Shear Connectors in Steel–Concrete Composite Beams by Curvature-Based Indicators Through Vibration Tests" Applied Sciences 15, no. 13: 7313. https://doi.org/10.3390/app15137313
APA StyleZhang, H., Du, F., & Jin, H. (2025). Monitoring and Evaluating the Damage to Shear Connectors in Steel–Concrete Composite Beams by Curvature-Based Indicators Through Vibration Tests. Applied Sciences, 15(13), 7313. https://doi.org/10.3390/app15137313






