Time-Resolved Photoacoustic Response of Thin Semiconductors Measured with Minimal Volume Cell: Influence of Photoinduced Charge Carriers
Abstract
1. Introduction
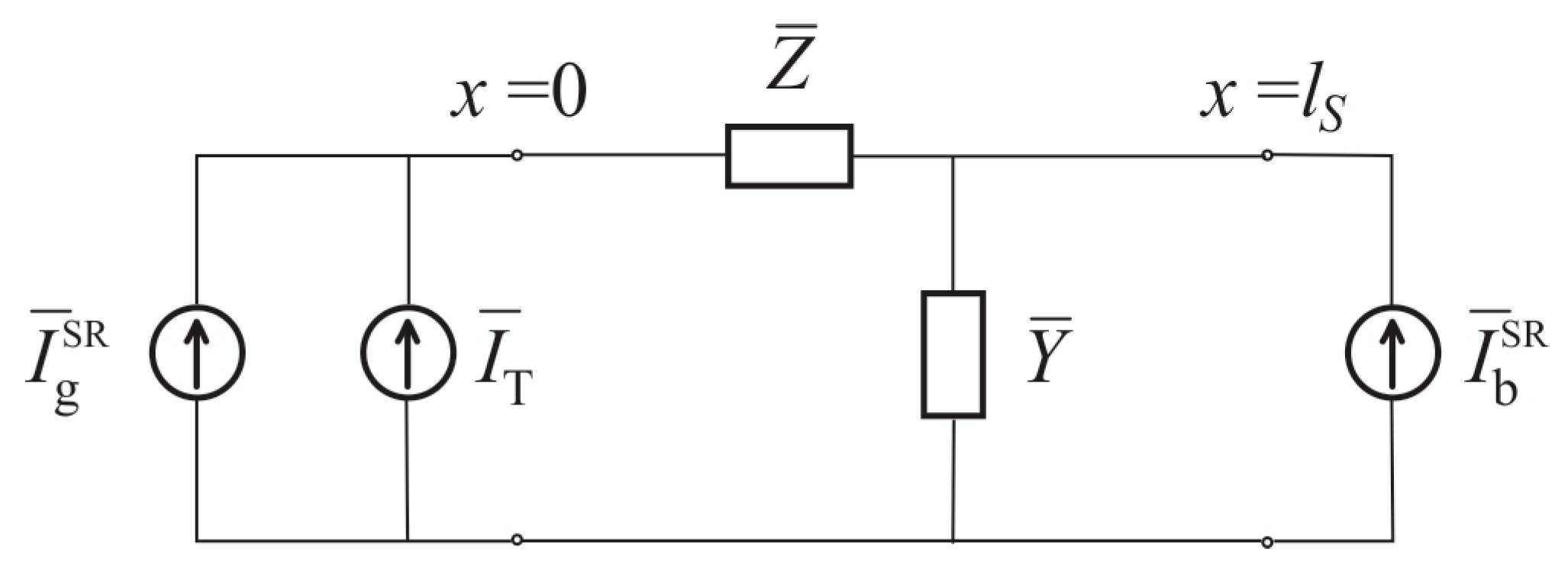
2. Photoinduced Heat Transfer Across Thin Semiconductor: Theoretical Model
- The sample is excited by an optical pulse of irradiance [W/m2], where describes the time dependence of the incident irradiance:where is denoted the Heaviside step function and with T [s] is the pulse duration.
- Before the excitation of optical radiation, the whole structure and its environment are at the same temperature— [K].
- The deexcitation–relaxation processes due to photon–phonon interactions are assumed to be much faster than the rate of change of the rising edge of the optical pulse. Thus, the heat sources formed by these processes follow the temporal shape of the optical pulse [37].
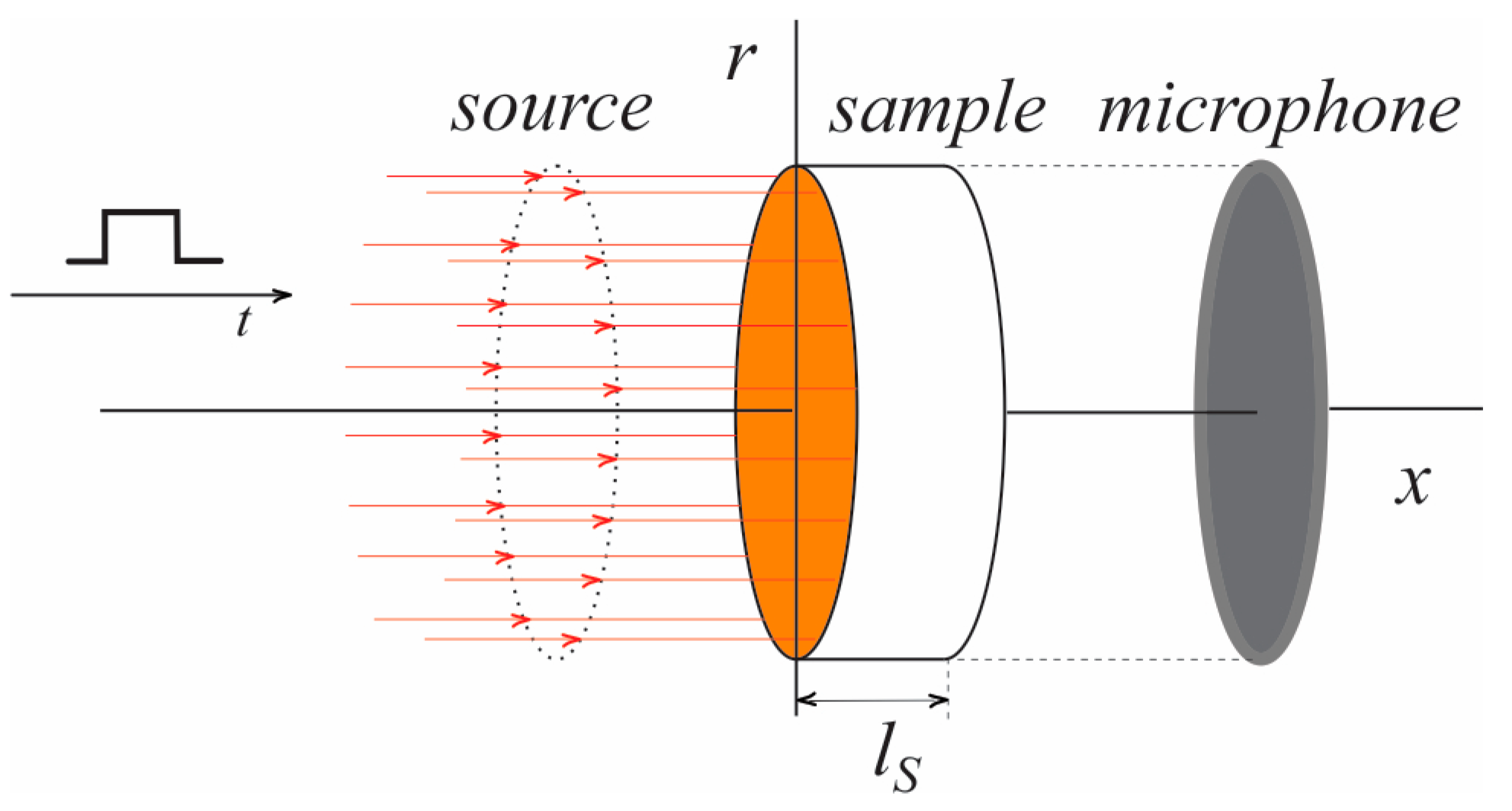
- We consider a semiconductor disk uniformly illuminated across its cross-sectional surface normal to the direction of light propagation (Figure 1), allowing the entire problem of optically generated heat propagation to be analyzed using a one-dimensional approximation.
- It is assumed that the surrounding gas does not absorb the incident radiation. Heat sources are generated solely within the sample; however, the resulting thermal disturbance affects the surrounding area.
- The sample is considered optically opaque, i.e., , where is the optical absorption coefficient [m−1] and [m] is the sample thickness. Thus, the excitation optical beam penetrates only a thin layer of the semiconductor near its illuminated surface. The optically generated heat due to photon–phonon interactions can be described as a surface heat source [38]:where is the sample’s reflectance, is the Dirac delta function, and .
- The semiconductor sample is surrounded by air, which is a much poorer thermal conductor than the semiconductor itself. Therefore, adiabatic boundary conditions for the heat flux are assumed.
- Nonlinear effects in heat conduction, transport of photogenerated charge carriers through the semiconductor, thermal relaxation effects, and effects of dissipation of heat caused by charge carrier recombination are neglected because these effects are not expected to be significant in gas–microphone photoacoustic experiments [18,32,33].
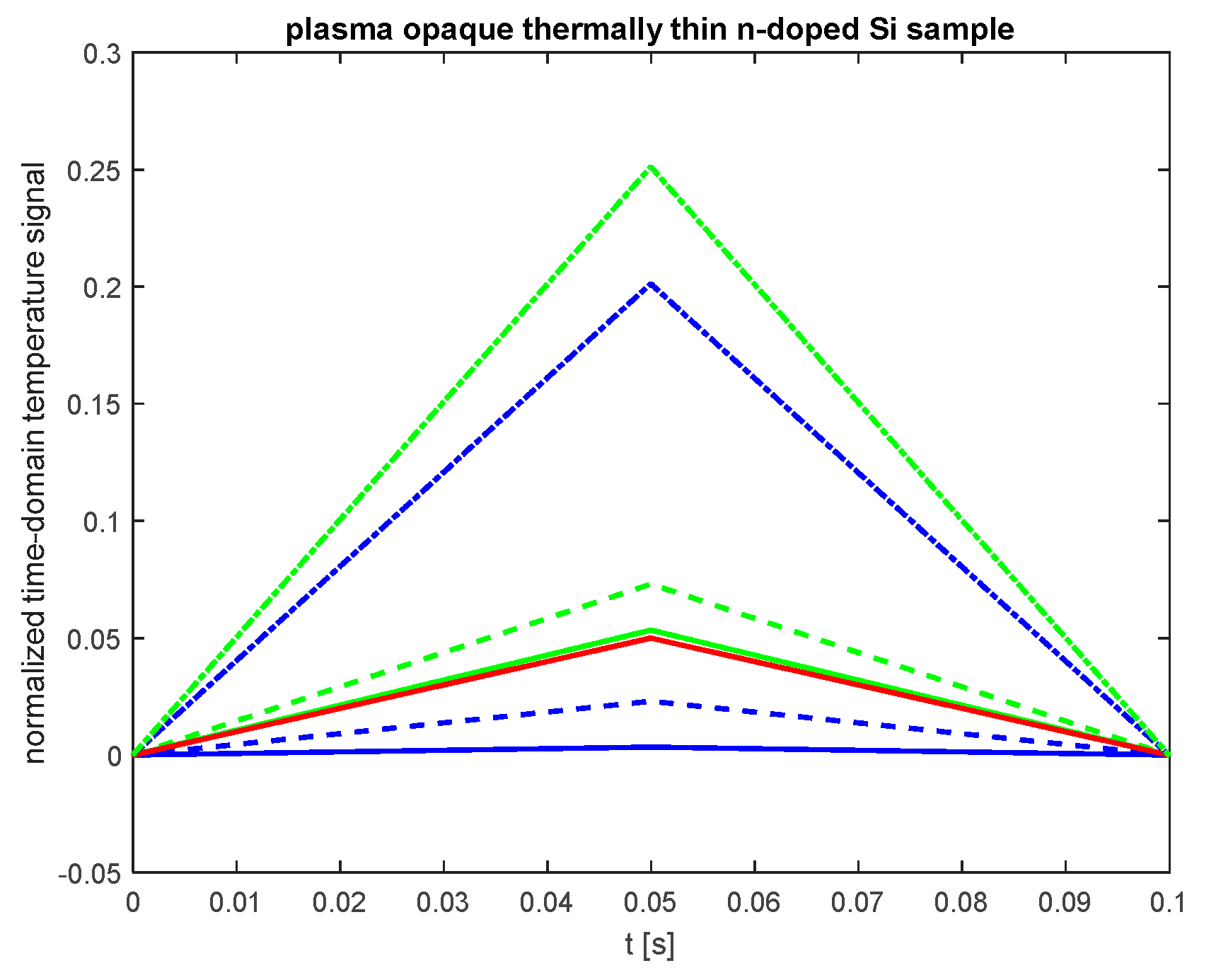
2.1. Surface Temperature Variations in Thermally Thin and Plasma Opaque Semiconductor Samples
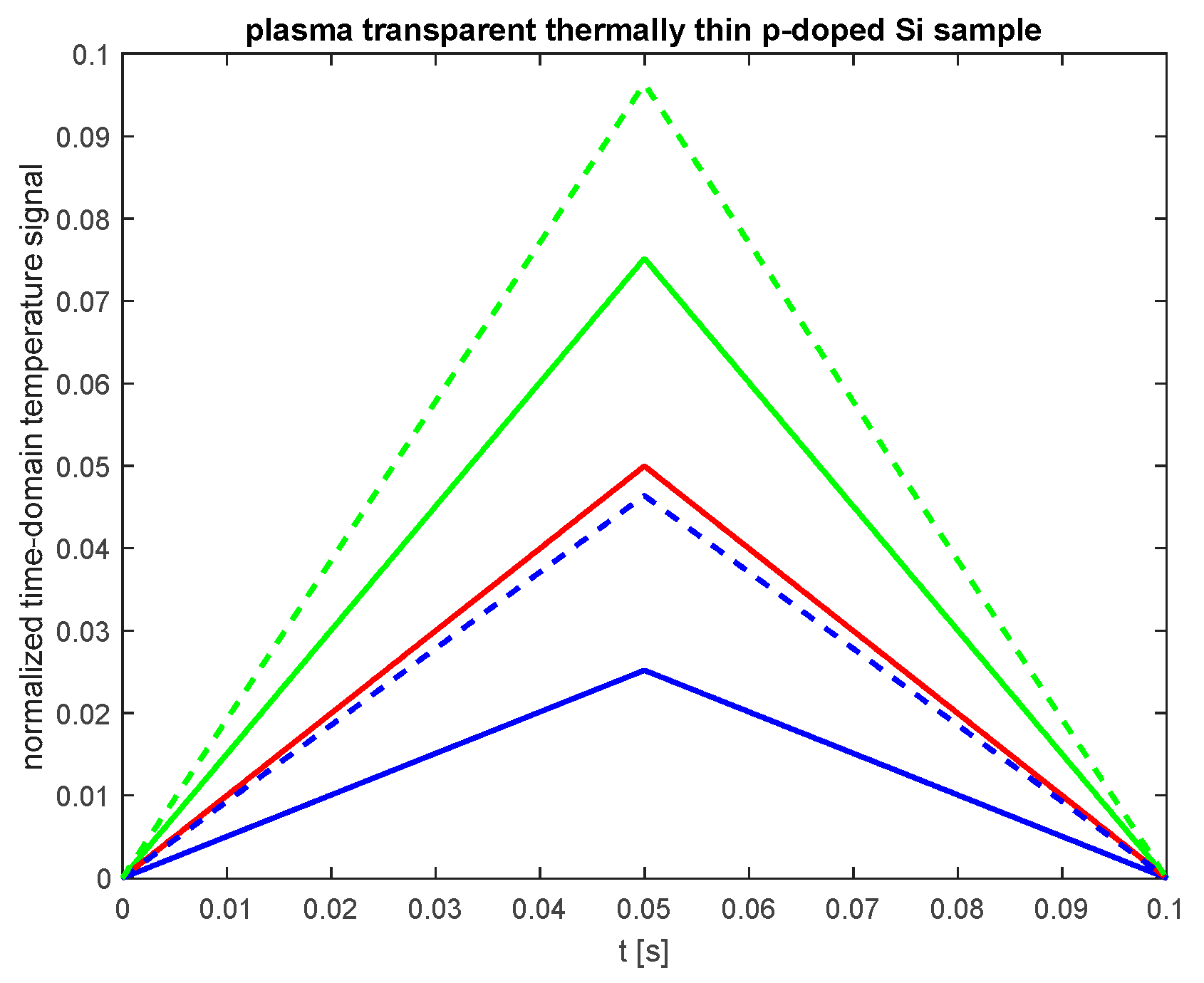
2.2. Surface Temperature Variations in Thermally Thin and Plasma Transparent Semiconductor Samples
3. Analysis and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Photogenerated Diffusion of Charge Carriers in Semiconductor
Appendix B. Inverse Laplace Transform: Method of Partial Fraction and Irrational Function
| Complex Function | Inverse Laplace Transform |
References
- Zakrzewski, J.; Pawlak, M.; Matsuda, O.; Todorovic, D.; Liu, J. Semiconductor physics: Plasma, thermal, elastic, and acoustic phenomena. J. Appl. Phys. 2024, 136, 120401. [Google Scholar] [CrossRef]
- Miranda, L.C.M. Theory of the photoacoustic effect in semiconductors influence of carrier diffusion and recombination. Appl. Opt. 1982, 21, 2923–2928. [Google Scholar] [CrossRef] [PubMed]
- Isaiev, M.; Kuryliuk, V.; Kuzmich, A.; Burbelo, R. Photothermal Transformation In Heterogeneous Semiconductors Structures Under Its Pulse Laser Irradiation: Role of Electron-Hole Diffusion. Arch. Metall. Mater. 2013, 58, 1351–1354. [Google Scholar] [CrossRef]
- Lishchuk, P.; Andrusenko, D.; Isaiev, M.; Lysenko, V.; Burbelo, R. Investigation of Thermal Transport Properties of Porous Silicon by Photoacoustic Technique. Int. J. Thermophys. 2015, 36, 2428–2433. [Google Scholar] [CrossRef]
- Bychto, L.; Maliński, M.; Chrobak, L.; Zakrzewski, J.; Boumhamdi, M. Investigations of optical and thermal properties of surface layers of Cd1−xBexTe samples by the photoacoustic method. Opto-Electron. Rev. 2024, 32, e150186. [Google Scholar] [CrossRef]
- Zakrzewski, J.; Maliński, M.; Bachiri, A.; Strzałkowski, K. Photothermal determination of the optical and thermal parameters of CdxZn1-xSe mixed crystals. J. Mater. Sci. Eng. B 2021, 271, 115305. [Google Scholar] [CrossRef]
- Todorovic, D.M.; Cretin, B.; Song, Y.Q.; Vairac, P. Photothermal elastic vibration method: Investigation of the micro-electro-mechanical-systems. J. Phys. Conf. Ser. 2010, 214, 012105. [Google Scholar] [CrossRef]
- Cyr, B.; Sumaria, V.; Long, Y.; Tadigadapa, S.; Sugawara, T.; Fu, K. How Lasers Exploit Photoacoustic and Photoelectric Phenomena to Inject Signals into MEMS Microphones. Preprint 2024. [Google Scholar] [CrossRef]
- Pawlak, M.; Pal, S.; Ludwig, A.; Wieck, A.D. On the infrared absorption coefficient measurement of thick heavily Zn doped GaAs using spectrally resolved modulated photothermal infrared radiometry. J. Appl. Phys. 2017, 122, 135109. [Google Scholar] [CrossRef]
- Bialkowski, S.E.; Astrath, N.G.C.; Proskurnin, M.A. Photothermal Spectroscopy Methods; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Vargas, H.; Miranda, L.C.M. Photoacoustic and related photothermal techniques. Phys. Rep. 1988, 161, 43–101. [Google Scholar] [CrossRef]
- Escamilla-Herrera, L.F.; Derramadero-Domínguez, J.M.; Medina-Cázares, O.M.; Alba-Rosales, J.E.; García-Rodríguez, F.J.; Gutiérrez-Juárez, G. On the dual-phase-lag thermal response in the pulsed photoacoustic effect: A theoretical and experimental 1D-approach. J. Appl. Phys. 2024, 136, 175105. [Google Scholar] [CrossRef]
- Neprokin, A.; Broadway, C.; Myllyla, T.; Bykov, A.; Meglinski, I. Photoacoustic Imaging in Biomedicine and Life Sciences. Life 2022, 12, 588. [Google Scholar] [CrossRef] [PubMed]
- Park, H.K.; Grigoropoulos, C.P.; Tam, A.C. Optical measurements of thermal diffusivity of a material. Int. J. Thermophys. 1995, 16, 973–995. [Google Scholar] [CrossRef]
- Bertolotti, M.; Li Voti, R. A note on the history of photoacoustic, thermal lensing, and photothermal deflection techniques. J. Appl. Phys. 2020, 128, 230901. [Google Scholar] [CrossRef]
- Skvortsov, L.A. Laser photothermal spectroscopy of light-induced absorption. Quantum Electron. 2013, 43, 1–13. [Google Scholar] [CrossRef]
- Zakrzewski, J.; Maliński, M.; Chrobak, Ł.; Pawlak, M. Comparison of Theoretical Basics of Microphone and Piezoelectric Photothermal Spectroscopy of Semiconductors. Int. J. Thermophys. 2017, 38, 2. [Google Scholar] [CrossRef]
- Todorović, D.M.; Nikolić, P.M. Chapter 9—Carrier Transport Contribution to Thermoelastic and Electronic Deformation in Semiconductors. In Semiconductors and Electronic Materials Progress in Photothermal and Photoacoustic, Science and Technology; Optical Engineering Press: New York, NY, USA, 2000; Volume PM74, pp. 273–318. ISBN 9780819435064. [Google Scholar]
- Sarode, A.P.; Mahajan, O.H. Theoretical Aspects of Photoacoustic Effect with Solids: A Review. Int. J. Sci. Adv. Res. Technol. 2018, 4, 1237–1242. [Google Scholar]
- Telenkov, S.; Mandelis, A. Signal-to-noise analysis of biomedical photoacoustic measurements in time and frequency domains. Rev. Sci. Inst. 2010, 81, 124901. [Google Scholar] [CrossRef]
- Lashkari, B.; Mandelis, A. Comparison between pulsed laser and frequency-domain photoacoustic modalities: Signal-to-noise ratio, contrast, resolution, and maximum depth detectivity. Rev. Sci. Inst. 2011, 82, 094903. [Google Scholar] [CrossRef]
- Galovic, S.P.; Stanimirovic, Z.; Stanimirovic, I.; Djordjevic, K.L.; Milicevic, D.; Suljovrujic, E. Time-resolved photoacoustic response of thin solids measured using minimal volume cell. Int. Commun. Heat Mass Transf. 2024, 155, 107574. [Google Scholar] [CrossRef]
- Djordjevic, K.L.; Galovic, S.P.; Nesic, M.V.; Todorovic, D.M.; Popovic, M.N.; Markushev, D.D.; Markushev, D.K. Transmission pulse photoacoustic set-up for characterization of solids. In Proceedings of the 21st International Symposium INFOTEH-JAHORINA, East Sarajevo, Bosnia and Herzegovina, 16–18 March 2022. [Google Scholar]
- Gärtner, W.W. Photothermal Effect in Semiconductors. Phys. Rev. 1961, 122, 419–424. [Google Scholar] [CrossRef]
- Fournier, D.; Boccara, C.; Skumanich, A.; Amer, N.M. Photothermal investigation of transport in semiconductors: Theory and experiment. J. Appl. Phys. 1986, 59, 787–795. [Google Scholar] [CrossRef]
- Forgot, B.C.; Fournier, D. Photothermal characterization of semiconductors. In Progress in Photothermal and Photoacoustic Science and Technology; Mandelis, A., Hess, P., Eds.; SPIE Press: Washington, DC, USA, 2000; Chapter 7, Volume 4, p. 200. ISBN 9780819435064. [Google Scholar]
- Stanimirović, Z.; Stanimirović, I.; Galović, S.; Djordjević, K.; Suljovrujić, E. Transmission pulse photoacoustic response of thin semiconductor plate. J. Appl. Phys 2023, 133, 195701. [Google Scholar] [CrossRef]
- Titov, O.Y.; Gurevich, Y.G. Recombination and temperature distribution in semiconductors. Semicond. Sci. Technol. 2012, 27, 055014. [Google Scholar] [CrossRef]
- Titov, O.Y.; Gurevich, Y.G. Temperature gradient and transport of heat and charge in a semiconductor structure. J. Low Temp. Phys. 2021, 47, 550–554. [Google Scholar] [CrossRef]
- Sobolev, S.L. Nonlocal two-temperature model: Application to heat transport in metals irradiated by ultrashort laser pulses. Int. J. Heat Mass Transf. 2016, 94, 138–144. [Google Scholar] [CrossRef]
- Sobolev, S.L.; Dai, W. Heat Transport on Ultrashort Time and Space Scales in Nanosized Systems: Diffusive or Wave-like? Materials 2022, 15, 4287. [Google Scholar] [CrossRef]
- Mandelis, A. Laser infrared photothermal radiometry of semiconductors: Principles and applications to solid state elec-tronics. Solid-State Electron. 1998, 42, 1–15. [Google Scholar] [CrossRef]
- Rojas-Trigos, J.B.; Calderón, A.; Marín, E.A. Practical model for the determination of transport parameters in semiconductors. J. Mater. Sci. 2011, 46, 7799–7805. [Google Scholar] [CrossRef]
- Galovic, S.; Djordjevic, K.; Dragas, M.; Milicevic, D.; Suljovrujic, E. Dynamics of Photoinduced Charge Carrier and Photothermal Effect in Pulse-Illuminated Narrow Gap and Moderate Doped Semiconductors. Mathematics 2025, 13, 258. [Google Scholar] [CrossRef]
- Wang, S. Fundamentals of Semiconductor Theory and Device Physics; Prentice Hall, Inc.: Hoboken, NJ, USA, 1989; ISBN 0-13-344425-2. [Google Scholar]
- Galovic, S.P.; Djordjevic, K.L.; Nesic, M.V.; Popovic, M.N.; Markushev, D.D.; Markushev, D.K.; Todorovic, D.M. Time-domain minimum-volume cell photoacoustic of thin semiconductor layer. I. Theory. J. Appl. Phys. 2023, 133, 245701. [Google Scholar] [CrossRef]
- Sablikov, V.A.; Sandomirskii, V.A. The Photoacoustic Effect in Semiconductors. Phys. Status Solidi (b) 1983, 120, 471–480. [Google Scholar] [CrossRef]
- Balderas-Lopez, J.A.; Mandelis, A. Thermal diffusivity measurements in the photoacoustic open-cell configuration using simple signal normalization techniques. J. Appl. Phys. 2001, 90, 2273–2279. [Google Scholar] [CrossRef]
- Stanimirović, I.; Markushev, D.; Stanimirović, Z.; Galović, S.; Djordjević, K. Analysis of plasma-elastic component of time-domain photoacoustic response. J. Appl. Phys. 2023, 133, 235701. [Google Scholar] [CrossRef]
- Aberle, A.G. Surface passivation of crystalline silicon solar cells: A review. Prog. Photovolt. Res. Appl. 2000, 8, 473–487. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Oxford University Press: Oxford, UK, 1959; ISBN 0198533683. [Google Scholar]
- McCord Morse, P.; Feshbach, H. Methods of Theoretical Physics; McGraw-Hill: New York, NY, USA, 1953; ISBN 0070433178/9780070433175. [Google Scholar]
- Galovic, S.; Soskic, Z.; Popovic, M. Analysis of Photothermal Response of Thin Solid Films By Analogy with Passive Linear Electric Networks. Therm. Sci. 2009, 13, 129–142. [Google Scholar] [CrossRef]
- Maillet, D.; André, C.; Batsale, J.-C.; Degiovanni, A.; Moyne, C. Thermal Quadrupoles, Solving the Heat Equation Through Integral Transforms; John Wiley and Sons: Hoboken, NJ, USA, 2000; ISBN 0 471 98320 9. [Google Scholar]
- Suszyński, Z. Thermal model based on the electrical analogy of the thermal processes. In Proceedings of the 10th International Conference on Photoacoustic and Photothermal Phenomena, Rome, Italy, 23–27 August 1998; pp. 197–199. [Google Scholar]
- Chen, G.; Hui, P. Pulsed photothermal modeling of composite samples based on transmission-line theory of heat conduction. Thin Solid Films 1999, 339, 58–67. [Google Scholar] [CrossRef]
- Krapez, J.C.; Dohou, E. Thermal quadrupole approaches applied to improve heat transfer computations in multilayered materials with internal heat sources. Int. J. Therm. Sci. 2014, 81, 38–51. [Google Scholar] [CrossRef]
- Pailhes, J.; Pradere, C.; Battaglia, J.L.; Toutain, J.; Kusiak, A.; Aregba, W.; Batsale, J.C. Thermal quadrupole method with internal heat sources. Int. J. Therm. Sci. 2012, 53, 49–55. [Google Scholar] [CrossRef]
- Salazar, A.; Celorrio, R. Application of the thermal quadrupole method to the propagation of thermal waves in multilayered cylinders. J. Appl. Phys. 2006, 100, 113535. [Google Scholar] [CrossRef]
- Nestoros, M. Photothermal Techniques in Material Characterization. In Materials Science—Advanced Topics; Mastai, Y., Ed.; InTech: London, UK, 2013; Chapter 14. [Google Scholar] [CrossRef][Green Version]
- Pichardo-Molina, J.L.; Alvarado-Gil, J.J. Heat diffusion and thermolastic vibration influence on the signal of an open photoacoustic cell for two layer systems. J. Appl. Phys. 2004, 95, 6450–6456. [Google Scholar] [CrossRef]
- Rousset, G.; Lepoutre, F.; Bertrand, L. Influence of thermoelastic bending on photoacoustic experiments related to measurements of thermal diffusivity of metals. J. Appl. Phys. 1983, 54, 2383–2391. [Google Scholar] [CrossRef]
- Rosencwaig, A.; Gerscho, A. Theory of the photoacoustic effect with solids. J. Appl. Phys. 1976, 47, 64–69. [Google Scholar] [CrossRef]
- McDonald, F.A.; Wetsel, G.C. Generalized theory of the photoacoustic effect. J. Appl. Phys. 1978, 49, 2313–2322. [Google Scholar] [CrossRef]
- Bonno, B.; Zeninari, V.; Joly, L.; Parvitte, B. Study of a Thermophysical System with Two Time Constants Using an Open Photoacoustic Cell. Int. J. Thermophys. 2011, 32, 630–640. [Google Scholar] [CrossRef]
- Tam, A.C. Applications of photoacoustic sensing techniques. Rev. Mod. Phys. 1986, 58, 381–431. [Google Scholar] [CrossRef]
- Bein, B.K.; Pelzl, J. Theory of signal generation in a photoacoustic cell. J. Phys.-Colloq. 1983, 44, C6-27–C6-34. [Google Scholar] [CrossRef]
- Mandelis, A.; Royce, B.S.H. Time-domain photoacoustic spectroscopy of solids. J. Appl. Phys. 1979, 50, 4330–4338. [Google Scholar] [CrossRef]
- Mandelis, A.; Royce, B.S.H. Relaxation time measurements in frequency and time-domain photoacoustic spectroscopy of condensed phases. J. Opt. Soc. Am. 1980, 70, 474–480. [Google Scholar] [CrossRef]
- Domanowska, R.; Bukowski, J. Theoretical Analysis of Pulsed Photoacoustic Effect in Solids. Int. J. Thermophys. 2009, 30, 1536–1556. [Google Scholar] [CrossRef]
- Volovichev, I.N.; Logvinov, G.N.; Titov, O.Y.; Gurevich, Y.G. Recombination and lifetimes of charge carriers in semiconductors. J. Appl. Phys. 2004, 95, 4494–4496. [Google Scholar] [CrossRef]
- Adachi, S. The Handbook on Optical Constants of Semiconductors: In Tables and Figures; World Scientific Publishing: Singapore, 2006; ISBN 978-981-4405-97. [Google Scholar]
- Davies, B.J. Integral Transforms and Their Applications; Springer: Berlin, Germany; New York, NY, USA, 2002; ISBN 978-0-387-95314-4. [Google Scholar]
- Available online: https://eqworld.ipmnet.ru/en/auxiliary/aux-inttrans.htm (accessed on 2 April 2004).
- Chen, Y.Q.; Petras, L.; Vinagre, B.M. A List of Laplace and Inverse Laplace Transforms Related to Fractional Order Calculus. Available online: https://ivopetras.tripod.com/foc_laplace.pdf (accessed on 30 November 2001).
- Oberhettinger, F.; Badii, L. Tables of Laplace Transforms; Springer: Berlin/Heidelberg, Germany, 1973; ISBN 978-3-642-65645-3. [Google Scholar]
- Stojic, M. Continuous System of Automatic Control; Naucna Knjiga-Komerc: Belgrade, Serbia, 1991. (In Serbian) [Google Scholar]
- Lynn, P.A. The Laplace Transform and the z-transform. In Electronic Signals and Systems; Macmillan Education: London, UK, 1986; pp. 225–272. ISBN 978-0-333-39164-8. [Google Scholar] [CrossRef]
- Galovic, S.; Djordjević, A.; Djordjević, K. Analytical Solution of the Inverse Laplace Transform for Combined Shifted Quasi-Rational Radical Functions of Power 1/2 with a Decaying Potential Term. J. Comput. Appl. Math. 2025; under review. [Google Scholar]





| Parameter | Value |
|---|---|
| Coefficient of diffusion of holes Dp | 1.2 ×·10−3 m2s−1 |
| Coefficient of diffusion of electrons De | 3.6 × 10−3 m2s−1 |
| Lifetime of excess charge carriers τ | 5 × 10−6 s |
| Energy gap EG | 1.12 eV |
| Velocity of surface recombination Sg/b | 2–24 ms−1 |
| Coefficient of thermal diffusivity DT | 9 × 10−5 m2s−1 |
| Thermal conductivity k | 150 Wm−1K−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galovic, S.P.; Markushev, D.K.; Markushev, D.D.; Djordjevic, K.L.; Popovic, M.N.; Suljovrujic, E.; Todorovic, D.M. Time-Resolved Photoacoustic Response of Thin Semiconductors Measured with Minimal Volume Cell: Influence of Photoinduced Charge Carriers. Appl. Sci. 2025, 15, 7290. https://doi.org/10.3390/app15137290
Galovic SP, Markushev DK, Markushev DD, Djordjevic KL, Popovic MN, Suljovrujic E, Todorovic DM. Time-Resolved Photoacoustic Response of Thin Semiconductors Measured with Minimal Volume Cell: Influence of Photoinduced Charge Carriers. Applied Sciences. 2025; 15(13):7290. https://doi.org/10.3390/app15137290
Chicago/Turabian StyleGalovic, Slobodanka P., Dragana K. Markushev, Dragan D. Markushev, Katarina Lj. Djordjevic, Marica N. Popovic, Edin Suljovrujic, and Dragan M. Todorovic. 2025. "Time-Resolved Photoacoustic Response of Thin Semiconductors Measured with Minimal Volume Cell: Influence of Photoinduced Charge Carriers" Applied Sciences 15, no. 13: 7290. https://doi.org/10.3390/app15137290
APA StyleGalovic, S. P., Markushev, D. K., Markushev, D. D., Djordjevic, K. L., Popovic, M. N., Suljovrujic, E., & Todorovic, D. M. (2025). Time-Resolved Photoacoustic Response of Thin Semiconductors Measured with Minimal Volume Cell: Influence of Photoinduced Charge Carriers. Applied Sciences, 15(13), 7290. https://doi.org/10.3390/app15137290









