Abstract
When a semiconducting sample is illuminated by an intensity-modulated monochromatic light beam with photon energy exceeding the band gap, part of the absorbed energy is directly converted into heat through photon–lattice interactions. This gives rise to a heat source that closely follows the temporal profile of the optical excitation, known as the fast heat source. Simultaneously, another portion of the absorbed energy is used to generate electron-hole pairs. These charge carriers diffuse together and recombine via electron–electron and electron–hole interactions, transferring their kinetic energy to the lattice and producing additional heating of the sample. This indirect heating mechanism, associated with carrier recombination, is referred to as the slow heat source. In this study, we develop a model describing surface temperature variations on the non-illuminated side of a thermally thin semiconductor exposed to a rectangular optical pulse, explicitly accounting for the contribution of surface charge carrier recombinations. Using this model, we investigate the influence of surface recombination velocity and the material’s plasma properties on the time-domain temperature response for both plasma-opaque and plasma-transparent samples. Our results demonstrate that charge carrier recombinations can significantly affect the transient photoacoustic signal recorded using a minimum volume cell, highlighting the potential of time-resolved photoacoustic techniques for probing the electronic properties of semiconductors.
1. Introduction
Frequency-domain photoacoustic (PA) techniques for semiconductors have been under development for more than four decades. Their primary objective is to enable non-destructive characterization of key material properties—optical, thermal, elastic, and electronic—which are crucial for the design and optimization of microelectronic, photonic, sensor, and biosensor devices, as well as for solar cells and thermal management in VLSI circuits [1,2,3,4,5,6,7,8,9].
Photoacoustic (PA) phenomena arise when a sample is illuminated by an intensity-modulated optical beam, leading to time-dependent heating and subsequent generation of pressure waves (acoustic waves). The resulting acoustic signal can be detected using a variety of techniques: deflection-based photothermal (PT) methods [10,11], ultrasonic detectors [12,13], or gas–microphone configurations, either in reflection or in transmission using a minimum volume cell [14].
The generation of acoustic waves is a consequence of the PT effect, wherein absorbed electromagnetic energy from the excitation beam is converted into heat. In addition to generating acoustic waves, the PT effect also produces other detectable phenomena that do not rely on acoustic sensors [10,11,15,16,17]. For example, it may cause changes in the infrared spectrum of the sample, which can be captured via radiometry; induce gradients in the optical refractive index within the sample (utilized in thermal lens spectroscopy methods) or in the surrounding medium (mirage techniques); or be directly observed as surface temperature changes using calorimetric methods.
This study focuses on the gas–microphone technique implemented using a minimum volume cell. This configuration has been developed in parallel with the more widespread reflection-mode PA techniques [14], and it has proven especially effective for the characterization of metals, semiconductors, and semiconductor devices [1].
In recent years, special attention has been given to developing time-domain PA techniques for real-time electronic characterization of semiconductor structures. However, a critical challenge in this domain is the deconvolution of signal contributions arising from charge carrier dynamics and those due to the detection system. This challenge motivates our current study.
Previous studies have shown that frequency-domain PA spectroscopy [18] can be used to measure the electronic properties of semiconductors. However, these methods are generally not suitable for real-time measurements, which are increasingly important for industrial and biomedical applications [19]. In contrast, time-domain PA methods [20,21,22,23] offer the potential for real-time characterization, but they require more advanced models and signal-processing techniques [22].
There are three main approaches to modeling PT and PA effects in semiconductors. The first approach assumes that photogenerated carriers influence the thermal conductivity, diffusivity, or relaxation times of the semiconductor, thereby affecting the temperature distribution and, ultimately, the generated pressure wave [24,25,26,27]. The second approach utilizes the two-temperature model, treating electrons and lattice as separate thermal systems; this is particularly suited for highly doped or degenerate semiconductors [28,29,30,31]. The third approach, which we adopt in this study, considers two types of heat sources: fast heat sources resulting from immediate photon–lattice interactions and nonradiative relaxation, and slow heat sources resulting from recombination of photogenerated carriers [18,32,33,34]. Among these, the third approach—based on distinguishing fast and slow heat sources—is particularly well-suited for the PA analysis of moderately doped semiconductors. This model forms the theoretical basis of our study.
The first type of heat source, referred to as the fast heat source, is characteristic of all solid-state materials. It originates from the interaction of the excitation electromagnetic radiation with lattice vibrations and non-radiative de-excitation processes. These mechanisms rapidly convert the absorbed photon energy into heat and operate on timescales much shorter than those relevant to photothermal detection. As a result, the temporal profile of this heat generation closely follows that of the incident optical pulse. However, due to the electronic band structure of semiconductors—which includes a filled valence band, a partially empty conduction band, and a band gap in between—photons with energy exceeding the band gap can excite electrons into the conduction band, leaving behind holes in the valence band [35]. These electron-hole pairs (quasi-free charge carriers), bound by Coulomb attraction, diffuse through the material driven by concentration gradients and eventually recombine after a characteristic time known as the carrier lifetime. During recombination, their kinetic energy is transferred to the lattice, generating additional heat. These recombination events are distributed in space and time, and form what is known as the slow heat source. The overall temperature distribution in the semiconductor is therefore a superposition of the contributions from fast and slow heat sources. This dual-source model is especially appropriate for moderately doped, narrow-band gap semiconductors, where the Fermi level remains within the band gap and the photoinduced plasma plays a significant role in thermal dynamics.
From the perspective of PA research and device characterization, this approach provides a physically realistic and experimentally relevant description of how photogenerated carriers influence the PA signal. It links electronic properties, carrier dynamics, and recombination processes to the optically induced heating and the resulting acoustic response detectable in gas–microphone or other PA configurations [18,32,33,34].
Using the third modeling approach, where photogenerated charge carriers contribute to additional heating via recombination (slow heat sources), frequency-domain PA measurements have already enabled the electronic characterization of semiconductors. However, despite having an original time-domain PA setup with gas microphones and validated knowledge from frequency-domain studies, the use of time-domain gas–microphone PA techniques for the electronic characterization of semiconductors remains challenging. The main obstacle lies in the complexity of the system’s transfer characteristics in the time domain—specifically, the transformation of optically induced temperature variations on the non-illuminated surface into acoustic signals, and subsequently into the final electrical signal detected by the microphone. This transformation process is not yet fully understood [22,36], and as a result, it is currently not possible to deconvolve the contributions of charge carrier dynamics from those of the detection system response with sufficient accuracy. Therefore, although our broader research goal is to establish time-domain PA methodologies for the electronic characterization of semiconductor structures, this cannot be realized without first addressing a fundamental intermediate step: quantifying the influence of photogenerated charge carriers on the transient temperature response at the non-illuminated surface.
In this study, we investigate how photo-induced quasi-free carriers affect surface temperature variations in a thin, moderately doped semiconductor when illuminated by square optical pulses. We analyze the transient temperature response at the non-illuminated surface using parameters introduced in our previous work [22,36]: rise time, fall time, settling time, and steady-state value, which are commonly used in system dynamics and signal processing. This provides a quantitative and physically interpretable way to assess the role of photogenerated carriers in shaping the thermal response detectable via time-domain PA measurements.
The paper is structured as follows. Section 2 presents a theoretical model of temperature variations caused by fast and slow heat sources using the Laplace transform and electro-thermal analogies. Section 3 analyzes the impact of thickness, surface recombination velocity, and electronic properties on the time-domain PA signal. Section 4 summarizes our conclusions. Technical details of the calculations are provided in Appendix A and Appendix B.
2. Photoinduced Heat Transfer Across Thin Semiconductor: Theoretical Model
The model of photoinduced heat propagation is derived under the following assumptions:
- The sample is excited by an optical pulse of irradiance [W/m2], where describes the time dependence of the incident irradiance:where is denoted the Heaviside step function and with T [s] is the pulse duration.
- Before the excitation of optical radiation, the whole structure and its environment are at the same temperature— [K].
- The deexcitation–relaxation processes due to photon–phonon interactions are assumed to be much faster than the rate of change of the rising edge of the optical pulse. Thus, the heat sources formed by these processes follow the temporal shape of the optical pulse [37].
- We consider a semiconductor disk uniformly illuminated across its cross-sectional surface normal to the direction of light propagation (Figure 1), allowing the entire problem of optically generated heat propagation to be analyzed using a one-dimensional approximation.
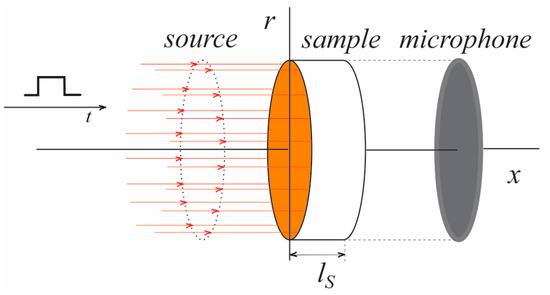 Figure 1. The geometry of the problem of optically excited temperature variations in semiconductors.
Figure 1. The geometry of the problem of optically excited temperature variations in semiconductors.
- It is assumed that the surrounding gas does not absorb the incident radiation. Heat sources are generated solely within the sample; however, the resulting thermal disturbance affects the surrounding area.
- The sample is considered optically opaque, i.e., , where is the optical absorption coefficient [m−1] and [m] is the sample thickness. Thus, the excitation optical beam penetrates only a thin layer of the semiconductor near its illuminated surface. The optically generated heat due to photon–phonon interactions can be described as a surface heat source [38]:where is the sample’s reflectance, is the Dirac delta function, and .
Consequently, the optically generated concentration flux of charge carriers can also be described as surface excitation [39]:
where and signify the energy gap of semiconductor and photon energy, respectively, and [18].
- The slow heat sources generated by charge carrier recombinations, denoted as , , and , can be described by [18,32,33,34]
The surface recombination velocity depends strongly on the surface treatment of the semiconductor. Chemically etched surfaces typically exhibit low recombination velocities due to the removal of surface defects, while untreated or contaminated surfaces can have significantly higher recombination rates. Additional passivation techniques—such as thermal oxidation, hydrogenation, or dielectric layer deposition (e.g., SiO2, Al2O3)—are commonly employed to further reduce surface defect density and electronically stabilize the surface [40]. However, surface recombination velocities are generally higher than volumetric recombination rates, which are intrinsic to the semiconductor and primarily depend on the doping level.
- Due to the significantly lower rates of volumetric recombination compared to surface recombination [39], the intensity of the volumetric heat source described by Equation (6) is much smaller than that of surface-related heat sources [18,34] and can thus be neglected in the thermal analysis
- The semiconductor sample is surrounded by air, which is a much poorer thermal conductor than the semiconductor itself. Therefore, adiabatic boundary conditions for the heat flux are assumed.
- Nonlinear effects in heat conduction, transport of photogenerated charge carriers through the semiconductor, thermal relaxation effects, and effects of dissipation of heat caused by charge carrier recombination are neglected because these effects are not expected to be significant in gas–microphone photoacoustic experiments [18,32,33].
Under these assumptions, the conduction of photogenerated heat through the semiconductor sample can be described by the one-dimensional classical Fourier’s theory of heat conduction [41], leading to the following system of linear partial differential equations:
With the following inhomogeneous boundary conditions [18]:
and zero initial conditions.
In the above equations (Equations (5)–(8)), denotes the temperature variation in relation to the ambient (initial) temperature, , is the heat flux, is the thermal diffusivity of the semiconductor, and is the thermal conductivity.
Since the problem is linear, the temperature distribution in the illuminated semiconductor sample can be obtained by applying the Laplace transform to Equations (7)–(10). In this case, the system of Equations (7)–(10) reduces to a system of ordinary differential equations in the complex domain:
with the following boundary conditions:
In Equations (11)–(14), the variables with an overline denote the Laplace transforms of the temperature, heat flux, the time function describing the modulation of the excitation beam’s amplitude, and the recombination heat sources on the illuminated and non-illuminated surfaces. Here, is denoted the complex frequency and is the imaginary unit (see Appendix B).
The symbols and represent the complex coefficient of heat propagation and thermal impedance, respectively, defined as follows:
As can be seen from Equations (11) and (12), heat propagation through the semiconductor sample is described by equations analogous to those governing the propagation of current and voltage through an electrical transmission line [42,43,44] (see Figure 2), with propagation coefficient and characteristic impedance , defined as
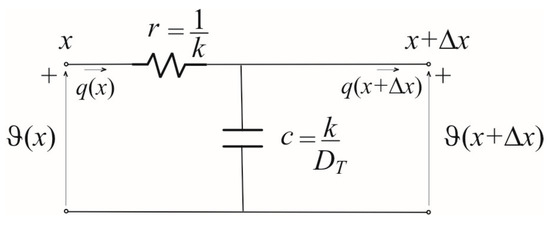
Figure 2.
Equivalent transmission line for the description of heat transfer problem based on classical Fourier heat conduction theory.
With symbols and , we denote complex series impedance and complex parallel admittance of a transmission line segment (Figure 2):
As can be seen from the boundary conditions (Equations (13) and (14)), heat propagation is driven by surface heat fluxes, which is analogous to the excitation of an electrical transmission line by current sources:
To calculate surface temperature variations on the unilluminated side, it is convenient to use the representation of an electrical transmission line via a symmetrical electrical T-network with two ports (quadripole) [43,44,45,46,47,48,49]. The analogous electrical circuit for calculating surface temperature variations on the unilluminated surface is shown in Figure 3.
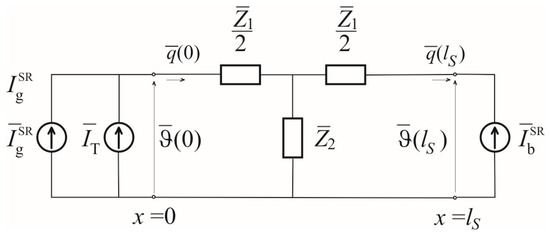
Figure 3.
The equivalent quadripole for the calculation of surface temperature variations in the semiconducting sample.
The impedances of the equivalent electrical circuit shown in Figure 3 are given by the following expressions [43,44]:
where and denote the equivalent longitudinal impedance and the equivalent longitudinal admittance, respectively:
The equivalent current sources are given by the following expression:
The symbols and signify the spectral functions of the concentrations of minority charge carriers at illuminated and non-illuminated surfaces, respectively.
Spectral functions of charge carrier concentrations are obtained by solving the diffusion equation for minority charge carriers [18,34] (see Appendix A):
In the above equations, and represent complex functions given by the following relations (see Appendix A and [18,34]):
for (plasma opaque sample), where
and
for (plasma transparent sample).
In the above relations, the symbol signifies the coefficient of diffusion of minority charge carriers—electrons in p-doped semiconductors (index e) or holes in n-doped semiconductors (index p). The symbol denotes the lifetime of photoinduced charge carriers. The maximum diffusion length of minority carriers is given by [34,50],
By substituting Equations (30) and (31) into Equations (28) and (29), a mathematical description of the spectral functions of recombination heat sources in the illuminated semiconductor is obtained:
As can be seen from Equations (37) and (38), the recombination sources can be described as a convolution of the function that represents the thermalization source and the functions and , which depend on the diffusion of minority carriers in the semiconductor.
By applying the superposition principle in solving the circuit shown in Figure 3, we obtain the spectral functions of the total temperature variations on the unilluminated surface as a sum of temperature variations generated by each of the sources described in Equations (27), (37), and (38):
It is important to note that there are two limiting cases considering the frequency of excitation harmonic: the thermally thin sample () and the thermally thick sample ().
Considering the definition of (Equation (15)) the following relation is obtained:
From the above equation (Equation (40)), it can be easily concluded that for low frequencies, below a certain cutoff frequency (which depends on and ), every sample is thermally thin. Conversely, for high frequencies, above the cutoff frequency , every sample is thermally thick, where is given by:
In further considerations, we assume that the sample is geometrically thin, such that the excitation harmonics span a wide frequency range, and that the sample is thermally thin. In this case, the equivalent circuit from Figure 3 is reduced to the equivalent circuit shown in Figure 4 [43].
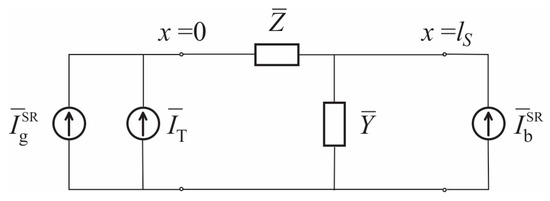
Figure 4.
Equivalent electrical circuit for the calculation of temperature variations in a thermally thin semiconducting sample.
By solving the circuit shown in Figure 4, we obtain the spectral functions of surface temperature variations caused by photon–lattice interactions, as well as the spectral functions of temperature variations resulting from surface recombination of photogenerated excess charge carriers, as follows (Equations (42)–(44)):
By substituting Equations (26) and (27) into Equation (42), the spectral function of surface temperature variations caused by lattice thermalization at the non-illuminated side of the semiconductor sample exposed to the action of a square optical pulse of duration is obtained:
By substituting Equations (26), (30), and (31) into Equations (43) and (44), the spectral function of surface temperature variations due to recombination sources at the surface of the semiconductor, is obtained:
By finding the inverse Laplace transform of Equation (45), we obtain [44,46]:
Considering heat sources generated by recombinations of minority carriers at the sample surfaces depend on the ratio between the sample thickness and the diffusion length of the minority carriers (i.e., plasma transparency (Equations (32)–(36)) [28], we further observe two limiting cases: thermally thin and plasma opaque, and thermally thin and plasma transparent samples.
2.1. Surface Temperature Variations in Thermally Thin and Plasma Opaque Semiconductor Samples
Using Equations (32)–(34), the spectral functions of recombination heat sources in plasma opaque samples can be described as follows [34]:
where
In this case, the temperature variations generated by surface recombination (based on Equation (46)) becomes
By finding the inverse Laplace transform of Equation (52), we obtain (see Appendix B):
where the function is defined by
and
2.2. Surface Temperature Variations in Thermally Thin and Plasma Transparent Semiconductor Samples
Using Equations (35) and (36), the spectral functions of recombination heat sources in plasma-transparent samples are given by [34]
Parameters , , , and are defined by the following expressions:
By substituting Equations (57) and (58) into Equation (46), we obtain the spectral function of temperature variations in a thermally thin and plasma-transparent semiconductor sample, caused by surface recombination heat sources:
with the parameter defined by
By finding the inverse Laplace transform of Equation (63) (see Appendix B), we obtain the following:
where the function is defined by
3. Analysis and Discussion
PA measurements with a minimal volume cell record pressure fluctuations in the gas column located on the non-illuminated side of the sample. The measurement configuration is transmission-based, as the source and the detector are on opposite sides of the sample being examined [51]. The literature indicates that in this type of measurement configuration, the spectral function of the resulting pressure fluctuations in the closed cell can be described by a composite piston model [52]. Specifically, these pressure fluctuations are a consequence of the thermal piston effect, which involves the expansion and contraction of the thin layer of air adjacent to the illuminated surface of the sample [53,54]. Additionally, the bending of the sample surface due to the generation of a thermal moment within the sample [52] acts as a mechanical piston, producing the thermoelastic (TE) component of the PA response.
In semiconductors, due to the photogeneration of charge carriers, there exists a plasma-elastic component resulting from the bending of the sample surface caused by the concentration gradient of excess charge carriers in illuminated semiconductor samples [18,39]. If the sample is thin, both the TE and plasma-elastic components can be neglected [22,55]. In such cases, it can be assumed that the pressure fluctuations are caused solely by the thermal piston effect and are consequently proportional to the surface temperature variations [55,56,57].
However, the thermal piston model is not suitable for time-domain photoacoustics [22,36,58,59,60]. In this case, it is more appropriate to use models derived in [22,36,58,59,60], which indicate that temperature changes at the non-illuminated surface generate pressure variations in a closed PA cell. However, the thermal thickness of the gas column in the closed PA cell [36] and the transfer characteristics of the microphone [22,36] can alter the time profile of the recorded time-resolved electrical signal.
As can be seen from Equations (67) and (68), the recorded photoacoustic signal is a convolution of the temperature variations at the non-illuminated side of the sample and the system’s transfer characteristics, described by and . This implies that a complete understanding of the measured time-domain signal [23] requires the deconvolution of these effects. However, in order to determine the electronic properties of the semiconductor, it is essential to first investigate the influence of photogenerated charge carriers on the surface temperature variations .
In this study, we analyze the evolution of temperature changes at the non-illuminated surface and the influence of photogenerated charge carriers on the magnitude and slope of these changes based on the derived model (hereafter referred to as the time-domain temperature signal). However, modeling the transfer function of the gas column () and the microphone (), which is essential for a complete understanding and accurate processing of the recorded time-resolved PA signal in semiconductors [23], remains the focus of our future research.
In the calculations, it was assumed that the optical source has a nondestructive irradiance, with the power of the employed LED diodes typically below 20 mW and the illuminated surface area approximately 25π mm2 (see Figure 1) [18,22]. Furthermore, the excitation takes place in the visible part of the electromagnetic spectrum, where the photon energy is approximately equal to the energy bandgap of narrow-gap semiconductors such as silicon. Under these conditions, is close to unity [18]. The normalized components were evaluated relative to a constant reference value, .
The time interval was selected to match the excitation pulse duration, which reflects our experimental conditions. This pulse width corresponds to the excitation used in our PA setup and was chosen based on our real measurements on silicon membranes (see Refs. [22,23]). In the analysis, it was assumed that the pulse duration is = 50 ms. The normalized signal was observed over a time interval of .
The values of surface recombination velocity (Table 1) were chosen based on the analysis of frequency-domain PA measurements on semiconductors [18].

Table 1.
Electronic, thermal, and geometrical properties of silicon samples used in the analysis of the model [18,61].
Let us consider the thicknesses of the Si sample for which the assumptions of the derived model are satisfied (the absorption coefficient is significantly larger than the inverse of the sample thickness, justifying the assumption of strong absorption in the thin layer close to the illuminated region—practically surface absorption).
The optical absorption coefficient of silicon is 105 m−1 for light in the visible part of the electromagnetic spectrum [62]. Consequently, the approximation of an optically opaque sample is reasonable for silicon samples thicker than 10 μm.
Since the thermal diffusivity of silicon is 9·10−5 m2s−1 [18], the cutoff frequency between thermally thin and thermally thick regimes for a sample thicker than 10 μm can be calculated from Equation (41). It ranges from approximately 5 kHz for a 90 µm thick sample to 300 kHz for a 10 µm thick sample. For samples with a thickness of about 100 µm, the cutoff frequency varies from 50 Hz for a 900 µm thick sample to 3000 Hz for a 100 µm thick sample. This implies that in the PA measurement range (from 50 Hz to a few kHz), silicon samples with a thickness of 10–150 µm can be considered thermally thin.
Finally, in our model, we considered two cases related to the ratio of the maximum diffusion length of minority carriers to the geometric thickness of the sample. These include the plasma-opaque case, where this ratio is less than one, and the plasma-transparent case, where the ratio is greater than one.
Since the maximum diffusion length of minority carriers is given by the square root of the product of their diffusion coefficient and lifetime (see Appendix B), it can be estimated based on the parameters given in Table 1 that a p-doped silicon sample with a thickness greater than 135 µm is plasma-opaque, while an n-doped silicon sample is plasma-opaque if it is thicker than 75 µm. This means that Si samples, whether p- or n-doped, with a thickness below 75 µm are plasma-transparent, whereas samples thicker than 135 µm are plasma-opaque.
In the further analysis, we considered silicon samples with a thickness of 20 µm as representatives of plasma-transparent, thermally thin, and optically opaque semiconductor samples, and samples with a thickness of 140 µm as representatives of plasma-opaque, thermally thin, and optically opaque semiconductor samples.
Figure 5 shows the normalized time-domain temperature signal (evolution of temperature change on the non-illuminated side) for a thermally thin, plasma-opaque n-doped silicon sample ( = 140 µm, = 1.2 × 10−3 m2s−1). The red line represents the signal originating from lattice thermalization (fast thermal source), while the blue lines correspond to signals influenced by surface recombination for different values of . The green lines depict the total signal resulting from both sources. (Legend: = 6 ms−1 (solid line), = 10 ms−1 (dashed line), = 14 ms−1 (dash-dot line)).
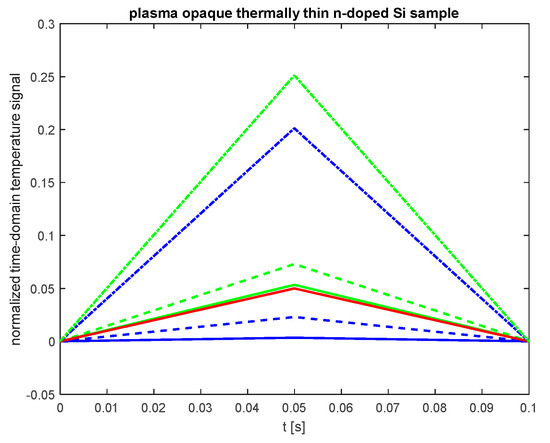
Figure 5.
The normalized time-domain temperature signal for a thermally thin and plasma opaque n-doped silicon sample. The red line represents the signal resulting from lattice thermalization (fast heat source), while the blue lines indicate the signal from surface recombinations at different values. The green lines represent the total signal caused by both sources: = 6 ms−1 (solid line), = 10 ms−1 (dashed line), and = 14 ms−1 (dash-dotted line).
As shown in Figure 5, in plasma-opaque and thermally thin samples, carrier recombination does not alter the shape of the signal but does affect its maximum value (blue and green lines). When the parameter is low (below 6 ms−1), the contribution of recombination sources is negligible, and the signal is primarily determined by lattice thermalization (solid red and green lines). However, as increases, recombination effects become more significant. For = 14 ms−1, recombination sources play a dominant role in temperature change (dash-dot green and blue lines in Figure 5).
From Figure 5, it can also be observed that the time-domain temperature signal for a thermally thin semiconductor sample reaches a steady value of zero after a time equal to . This indicates that the settling time is equal to twice the duration of the optical pulse.
In cases where the signal does not reach a peak during the pulse duration, it is not appropriate to work with parameters such as rising time or falling time; instead, it is much more suitable to consider the slope of the rising or falling curve. Figure 5 shows that the slopes of the rise after the leading edge of the excitation and the slope of the fall after the trailing edge of the pulse are equal and depend on the surface recombination velocities.
To investigate the impact of the charge carrier diffusivity (the semiconductor electronic property) on the shape of the time-domain temperature signal, Figure 6 presents the signal for a thermally thin and plasma-opaque p-doped Si sample ( = 140 µm, = 3.6 × 10−3 m2s−1). The red line represents the signal resulting from lattice thermalization (fast heat source), while the blue lines indicate the signal from surface recombinations at different values. The green lines show the total signal caused by both sources: = 6 ms−1 (solid lines), = 10 ms−1 (dashed lines), and = 14 ms−1 (dash-dotted lines).
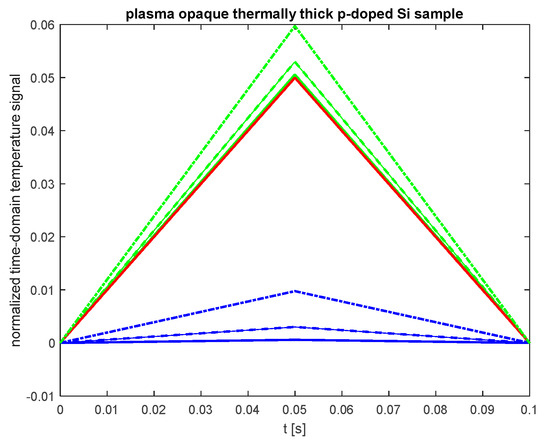
Figure 6.
The normalized time-domain temperature signal for a thermally thin and plasma opaque p-doped silicon sample. The red line represents the signal resulting from lattice thermalization (fast heat source), while the blue lines indicate the signal from surface recombinations at different values. The green lines represent the total signal caused by both sources: = 6 ms−1 (solid line), = 10 ms−1 (dashed line), and = 14 ms−1 (dash-dotted line).
As seen in Figure 6, for the plasma-opaque and thermally thin p-doped sample, the recombination of charge carriers similarly affects the time domain temperature signal as in the n-doped sample (Figure 5). Specifically, it does not influence the shape or settling time, but it does impact the maximum value of the signal in the time domain (indicated by the blue and green lines in Figure 5 and Figure 6) and the slopes of both the rising and falling curves.
However, in the case of the p-doped sample, minority carriers are electrons, which have a diffusion coefficient three times larger (as shown in Table 1). Therefore, at the same surface recombination velocities, the dominance of recombination sources does not occur for the > 10 ms−1 (Figure 6).
Based on this observation, it can be concluded that the slopes of the time-domain temperature signal—both the rising slope following the leading edge of the optical pulse and the falling slope following the trailing edge—are influenced by the electronic properties of the semiconductor, particularly the diffusion coefficient of the minority carriers. An increase in the diffusion coefficient results in a slower rise and fall of the signal and consequently a smaller maximum value for the same surface recombination velocities.
It is interesting to note that the results presented in Figure 5 and Figure 6 indicate that the complex function describing the time-domain temperature signal in thermally thin and plasma-opaque samples (Equation (47)) can, in fact, be approximated by a linear function. The electronic parameters of silicon (such as the minority carrier lifetime and their diffusion coefficient) primarily influence the slope of the linear function.
Figure 7 illustrates the normalized time-domain temperature signal for a thermally thin and plasma-transparent n-doped silicon sample ( = 20 µm, = 1.2 × 10−3 m2s−1). The red line represents the signal originating from the thermalization of the lattice (a fast heat source), while the blue lines show the signal resulting from surface recombinations for = 6 ms−1 and various values. The green lines depict the total signal generated by both sources ( = 6 ms−1 as a solid line and = 14 ms−1 as a dashed line)
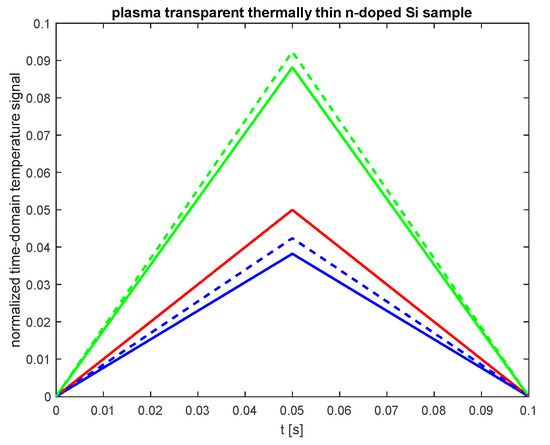
Figure 7.
The normalized time-domain temperature signal for a thermally thin and plasma-transparent n-doped silicon sample ( = 20 µm, = 1.2 × 10−3 m2s−1). The red line represents the signal originating from the thermalization of the lattice (a fast heat source), while the blue lines depict the signal resulting from surface recombinations for = 6 m/s and various values. The green lines illustrate the total signal produced by both sources, with = 6 ms−1 represented by a solid line and = 14 ms−1 by a dashed line.
As seen in Figure 7, the time-domain temperature signal from the plasma-transparent sample behaves similarly to that of the plasma-opaque sample in terms of shape, settling time, and dependence on . However, for the plasma-transparent sample, the slopes of both the rising and falling edges are also affected by the surface recombination velocity . This results in a slower rise of the signal, leading to significantly lower maximum signal values when all other electronic and thermal parameters remain constant.
To further investigate the impact of , Figure 8 presents the time-domain temperature signal for a thermally thin and plasma-transparent n-doped silicon sample ( = 20 µm, = 1.2 × 10−3 ms−1) with a fixed = 2 ms−1. The value of the surface recombination velocity on the unilluminated side, , was varied. The red line indicates the signal resulting from thermalization of the lattice (a fast heat source), while the blue lines show the signal from surface recombinations for = 2 m/s at different values. The green lines represent the total signal caused by both sources, with = 6 ms−1 indicated by a solid line and = 24 ms−1 by a dashed line.
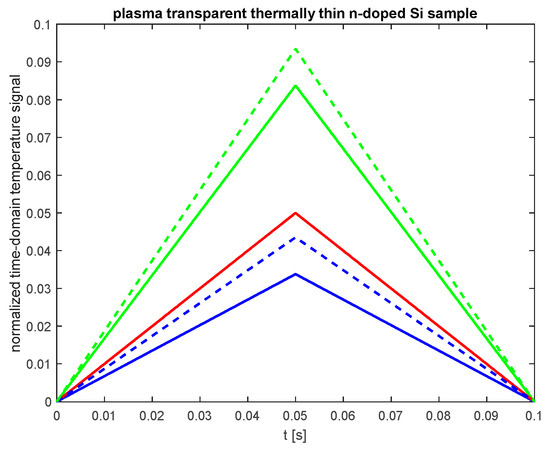
Figure 8.
The normalized time-domain temperature signal for a thermally thin and plasma-transparent n-doped silicon sample ( = 20 µm, = 1.2 × 10−3 m2s−1). The red line represents the signal originating from the thermalization of the lattice (a fast heat source), while the blue lines show the signal from surface recombinations for = 2 ms−1 at different values. The green lines depict the total signal caused by both sources, with = 6 ms−1 indicated by a solid line and = 24 ms−1 by a dashed line.
As seen in Figure 8, the increase in sb influences both the slope of the time-domain temperature signal and the maximum value the signal reaches just before the falling edge of the optical pulse, similar to the effect observed with an increase in .
Finally, Figure 9 presents the normalized time-domain temperature signal for a thermally thin and plasma-transparent p-doped Si sample ( = 20 µm, = 3.6 × 10−3 ms−1) at = 2 ms−1, = 2 ms−1 and = 24 ms−1, = 24 ms−1. This analysis aims to investigate the influence of the electronic properties on the time-domain temperature signal of the thermally thin and plasma transparent semiconductor samples.
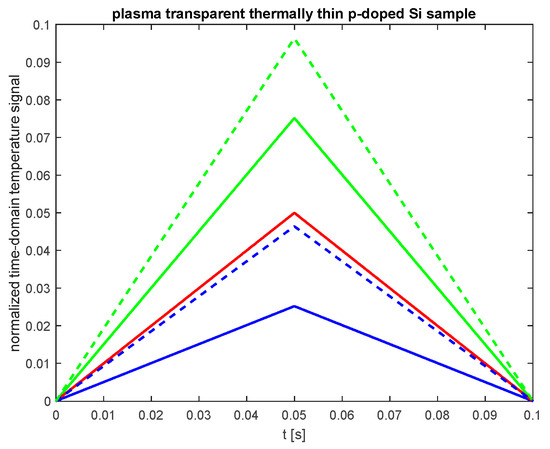
Figure 9.
The normalized time-domain temperature signal for a thermally thin and plasma-transparent p-doped silicon sample. The red line represents the signal originating from the thermalization of the lattice (a fast heat source), while the blue lines denote signals resulting from surface recombinations at various values of and . The green lines indicate the total signal contributed by both sources, with the solid line corresponding to = 2 ms−1 and = 2 ms−1 and the dashed line corresponding to = 24 ms−1 and = 24 ms−1.
By comparing the results shown in Figure 6 and Figure 8, it is evident that an increase in the diffusion coefficient of minority carriers—similar to the case of plasma-opaque samples—influences both the maximum value that the time-domain temperature signal can achieve during the pulse duration and the steepness of the nearly linear rising and falling curves. However, this increase does not affect the settling time.
4. Conclusions
In this paper, we developed a model to describe the temperature variation on the non-illuminated side of thermally thin semiconductor samples exposed to rectangular optical pulses. The model incorporates the effects of surface recombination of photo-generated charge carriers.
Using the derived expressions, we analyzed how recombination heat sources and the electronic properties of semiconductors influence the surface temperature response, with moderately doped n-type and p-type silicon as representative cases.
Our results demonstrate that, depending on the surface recombination velocity—which is strongly influenced by surface treatment methods—recombination heat sources can substantially affect both the amplitude of surface temperature changes and the dynamics of its rise and decay, particularly in plasma-opaque samples with high recombination velocity at the illuminated surface.
At low surface recombination velocities, lattice thermalization remains the dominant heating mechanism, and the contribution of recombination sources becomes negligible in thermally thin and plasma-opaque samples, especially for low recombination rates at the illuminated surface. In contrast, for plasma-transparent samples, recombination remains a non-negligible contributor to heating, regardless of surface recombination velocity.
Additionally, we show that the electronic properties of the semiconductor, particularly the minority carrier diffusion coefficient, affect the slopes of the temperature signal and its maximum value, but have little influence on the overall shape or settling time of the response.
These findings indicate that carrier recombination can significantly influence the thermal response at the non-illuminated surface and, consequently, the time-domain PA signal. The observed dependence of temperature dynamics on sample thickness, surface processing, and electronic transport parameters suggests that this method could be used to extract the electronic properties of semiconductor materials.
The developed model and conclusions of this study may be applied not only to improve the time-domain PA characterization of semiconductors but also in the broader context of non-destructive time-resolved techniques for the electronic characterization of semiconductor materials, nanoelectronic devices, and sensors.
For a complete interpretation and accurate processing of experimentally recorded time-resolved PA signals in thin semiconductor membranes [23], further investigations are needed to fully understand the transformation of transient surface temperature changes into pressure fluctuations, and their subsequent conversion into detectable electrical signals. This remains an open challenge and a subject of our ongoing research.
Author Contributions
Conceptualization, S.P.G.; methodology, S.P.G.; software, S.P.G.; validation, S.P.G., M.N.P. and D.M.T.; formal analysis, S.P.G., D.K.M., D.D.M., K.L.D., M.N.P. and E.S., investigation, S.P.G., D.K.M., D.D.M., K.L.D., M.N.P., E.S. and D.M.T.; resources, S.P.G. and E.S.; data curation, S.P.G. and D.M.T.; writing—original draft preparation, S.P.G.; writing—review and editing, S.P.G., K.L.D., M.N.P. and D.M.T.; visualization, S.P.G. and K.L.D.; supervision, D.M.T. and E.S.; project administration, S.P.G. and E.S.; funding acquisition, S.P.G. and E.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science, Technological Development and Innovations of the Republic of Serbia (Contract No. 451-03-136/2025-03/200017).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
We would like to express our gratitude to ChatGPT with GPT-4o for its assistance in improving the clarity and coherence of the manuscript. However, it is important to emphasize that the authors retain full responsibility for all content, analyses, and conclusions presented in this work. The role of artificial intelligence in this context was limited to providing language enhancement and stylistic suggestions and does not imply that any part of the manuscript was generated by AI.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Photogenerated Diffusion of Charge Carriers in Semiconductor
The equation describing the transport of photogenerated charge carriers in a semiconductor, under the low-level injection approximation, is a linear, one-dimensional spatial diffusion equation for minority carriers. By applying the Laplace transform, this equation is reduced to the second-order differential equation in the complex domain [12].
In the case where optical absorption occurs in a thin layer near the illuminated semiconductor surface (i.e., when the sample is optically opaque and has a high optical absorption coefficient), the transport problem of photogenerated charge carriers is described by the following system of homogeneous differential equations (Equations (A1) and (A2)), with inhomogeneous boundary conditions (Equations (A3) and (A4)) [34]:
In the above equations, denotes the spectral function of the optically generated source of excess carriers, under the assumption that the semiconductor is optically opaque (it is important to note that the model is derived under the assumption of shallow optical penetration depth, meaning that the generation of charge carriers occurs within a spatially confined region near the illuminated surface—practically at the surface itself) [34].
By solving the problem described by Equations (A1)–(A4), the following expression for the spectral function of concentration distribution of photogenerated minority carriers is obtained:
Based on Equation (A5), expressions describing the carrier concentrations at the semiconductor surfaces can be readily derived [34].
In this work, we analyzed two asymptotic cases—the plasma-opaque and the plasma-transparent semiconductor sample—using an analogy with propagation processes. If the complex frequency is written as (stationary propagation), where the symbol denotes the imaginary unit, the real part of the inverse of the complex propagation coefficient (Equation (34)) corresponds to the diffusion length of charge carriers [34,50].
As can be seen from Equation (A8), the carrier diffusion length depends on the frequency of the harmonic excitation. As the frequency increases, the diffusion length decreases to zero, while for a frequency of zero, it reaches its maximum value [34,50]:
If the sample thickness is much greater than the maximum diffusion length , the sample is plasma opaque. Conversely, if the sample thickness is smaller than the maximum diffusion length (), the sample is plasma transparent [34].
Following the results of [34], in the case of optically opaque samples, Equations (A6) and (A7) can be reduced, and the theoretical model of surface recombination heat sources is described by Equations (52) and (63) in the paper.
Appendix B. Inverse Laplace Transform: Method of Partial Fraction and Irrational Function
To obtain the evolution of a function , given its spectral function , one should solve the inverse Laplace transform. The inverse Laplace transform of functions of a complex argument is defined as follows [63,64]:
where is complex plane and is a real number greater than the real part of all singularities of .
The integral formula given by Equation (A10) is called the Bromwich integral, also known as Mellin’s inverse formula or the Fourier–Mellin integral. In many cases, the complex integral can be evaluated using the Cauchy residue theorem.
In practice, it is not necessary to solve the complex integral given by Equation (A10). Instead, existing tables of inverse Laplace transforms can be used [65,66], along with various methods of representing a complex function in forms for which Bromowich integral solutions are known, such as method partial fractions for rational functions of complex argument s [34,65].
For solving the inverse Laplace transform of the irrational function obtained in this study, the known solutions given in table bellow were used [65].
| Complex Function | Inverse Laplace Transform |
Additionally, the following properties of the Laplace transform were used [67,68,69]:
References
- Zakrzewski, J.; Pawlak, M.; Matsuda, O.; Todorovic, D.; Liu, J. Semiconductor physics: Plasma, thermal, elastic, and acoustic phenomena. J. Appl. Phys. 2024, 136, 120401. [Google Scholar] [CrossRef]
- Miranda, L.C.M. Theory of the photoacoustic effect in semiconductors influence of carrier diffusion and recombination. Appl. Opt. 1982, 21, 2923–2928. [Google Scholar] [CrossRef] [PubMed]
- Isaiev, M.; Kuryliuk, V.; Kuzmich, A.; Burbelo, R. Photothermal Transformation In Heterogeneous Semiconductors Structures Under Its Pulse Laser Irradiation: Role of Electron-Hole Diffusion. Arch. Metall. Mater. 2013, 58, 1351–1354. [Google Scholar] [CrossRef]
- Lishchuk, P.; Andrusenko, D.; Isaiev, M.; Lysenko, V.; Burbelo, R. Investigation of Thermal Transport Properties of Porous Silicon by Photoacoustic Technique. Int. J. Thermophys. 2015, 36, 2428–2433. [Google Scholar] [CrossRef]
- Bychto, L.; Maliński, M.; Chrobak, L.; Zakrzewski, J.; Boumhamdi, M. Investigations of optical and thermal properties of surface layers of Cd1−xBexTe samples by the photoacoustic method. Opto-Electron. Rev. 2024, 32, e150186. [Google Scholar] [CrossRef]
- Zakrzewski, J.; Maliński, M.; Bachiri, A.; Strzałkowski, K. Photothermal determination of the optical and thermal parameters of CdxZn1-xSe mixed crystals. J. Mater. Sci. Eng. B 2021, 271, 115305. [Google Scholar] [CrossRef]
- Todorovic, D.M.; Cretin, B.; Song, Y.Q.; Vairac, P. Photothermal elastic vibration method: Investigation of the micro-electro-mechanical-systems. J. Phys. Conf. Ser. 2010, 214, 012105. [Google Scholar] [CrossRef]
- Cyr, B.; Sumaria, V.; Long, Y.; Tadigadapa, S.; Sugawara, T.; Fu, K. How Lasers Exploit Photoacoustic and Photoelectric Phenomena to Inject Signals into MEMS Microphones. Preprint 2024. [Google Scholar] [CrossRef]
- Pawlak, M.; Pal, S.; Ludwig, A.; Wieck, A.D. On the infrared absorption coefficient measurement of thick heavily Zn doped GaAs using spectrally resolved modulated photothermal infrared radiometry. J. Appl. Phys. 2017, 122, 135109. [Google Scholar] [CrossRef]
- Bialkowski, S.E.; Astrath, N.G.C.; Proskurnin, M.A. Photothermal Spectroscopy Methods; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Vargas, H.; Miranda, L.C.M. Photoacoustic and related photothermal techniques. Phys. Rep. 1988, 161, 43–101. [Google Scholar] [CrossRef]
- Escamilla-Herrera, L.F.; Derramadero-Domínguez, J.M.; Medina-Cázares, O.M.; Alba-Rosales, J.E.; García-Rodríguez, F.J.; Gutiérrez-Juárez, G. On the dual-phase-lag thermal response in the pulsed photoacoustic effect: A theoretical and experimental 1D-approach. J. Appl. Phys. 2024, 136, 175105. [Google Scholar] [CrossRef]
- Neprokin, A.; Broadway, C.; Myllyla, T.; Bykov, A.; Meglinski, I. Photoacoustic Imaging in Biomedicine and Life Sciences. Life 2022, 12, 588. [Google Scholar] [CrossRef] [PubMed]
- Park, H.K.; Grigoropoulos, C.P.; Tam, A.C. Optical measurements of thermal diffusivity of a material. Int. J. Thermophys. 1995, 16, 973–995. [Google Scholar] [CrossRef]
- Bertolotti, M.; Li Voti, R. A note on the history of photoacoustic, thermal lensing, and photothermal deflection techniques. J. Appl. Phys. 2020, 128, 230901. [Google Scholar] [CrossRef]
- Skvortsov, L.A. Laser photothermal spectroscopy of light-induced absorption. Quantum Electron. 2013, 43, 1–13. [Google Scholar] [CrossRef]
- Zakrzewski, J.; Maliński, M.; Chrobak, Ł.; Pawlak, M. Comparison of Theoretical Basics of Microphone and Piezoelectric Photothermal Spectroscopy of Semiconductors. Int. J. Thermophys. 2017, 38, 2. [Google Scholar] [CrossRef]
- Todorović, D.M.; Nikolić, P.M. Chapter 9—Carrier Transport Contribution to Thermoelastic and Electronic Deformation in Semiconductors. In Semiconductors and Electronic Materials Progress in Photothermal and Photoacoustic, Science and Technology; Optical Engineering Press: New York, NY, USA, 2000; Volume PM74, pp. 273–318. ISBN 9780819435064. [Google Scholar]
- Sarode, A.P.; Mahajan, O.H. Theoretical Aspects of Photoacoustic Effect with Solids: A Review. Int. J. Sci. Adv. Res. Technol. 2018, 4, 1237–1242. [Google Scholar]
- Telenkov, S.; Mandelis, A. Signal-to-noise analysis of biomedical photoacoustic measurements in time and frequency domains. Rev. Sci. Inst. 2010, 81, 124901. [Google Scholar] [CrossRef]
- Lashkari, B.; Mandelis, A. Comparison between pulsed laser and frequency-domain photoacoustic modalities: Signal-to-noise ratio, contrast, resolution, and maximum depth detectivity. Rev. Sci. Inst. 2011, 82, 094903. [Google Scholar] [CrossRef]
- Galovic, S.P.; Stanimirovic, Z.; Stanimirovic, I.; Djordjevic, K.L.; Milicevic, D.; Suljovrujic, E. Time-resolved photoacoustic response of thin solids measured using minimal volume cell. Int. Commun. Heat Mass Transf. 2024, 155, 107574. [Google Scholar] [CrossRef]
- Djordjevic, K.L.; Galovic, S.P.; Nesic, M.V.; Todorovic, D.M.; Popovic, M.N.; Markushev, D.D.; Markushev, D.K. Transmission pulse photoacoustic set-up for characterization of solids. In Proceedings of the 21st International Symposium INFOTEH-JAHORINA, East Sarajevo, Bosnia and Herzegovina, 16–18 March 2022. [Google Scholar]
- Gärtner, W.W. Photothermal Effect in Semiconductors. Phys. Rev. 1961, 122, 419–424. [Google Scholar] [CrossRef]
- Fournier, D.; Boccara, C.; Skumanich, A.; Amer, N.M. Photothermal investigation of transport in semiconductors: Theory and experiment. J. Appl. Phys. 1986, 59, 787–795. [Google Scholar] [CrossRef]
- Forgot, B.C.; Fournier, D. Photothermal characterization of semiconductors. In Progress in Photothermal and Photoacoustic Science and Technology; Mandelis, A., Hess, P., Eds.; SPIE Press: Washington, DC, USA, 2000; Chapter 7, Volume 4, p. 200. ISBN 9780819435064. [Google Scholar]
- Stanimirović, Z.; Stanimirović, I.; Galović, S.; Djordjević, K.; Suljovrujić, E. Transmission pulse photoacoustic response of thin semiconductor plate. J. Appl. Phys 2023, 133, 195701. [Google Scholar] [CrossRef]
- Titov, O.Y.; Gurevich, Y.G. Recombination and temperature distribution in semiconductors. Semicond. Sci. Technol. 2012, 27, 055014. [Google Scholar] [CrossRef]
- Titov, O.Y.; Gurevich, Y.G. Temperature gradient and transport of heat and charge in a semiconductor structure. J. Low Temp. Phys. 2021, 47, 550–554. [Google Scholar] [CrossRef]
- Sobolev, S.L. Nonlocal two-temperature model: Application to heat transport in metals irradiated by ultrashort laser pulses. Int. J. Heat Mass Transf. 2016, 94, 138–144. [Google Scholar] [CrossRef]
- Sobolev, S.L.; Dai, W. Heat Transport on Ultrashort Time and Space Scales in Nanosized Systems: Diffusive or Wave-like? Materials 2022, 15, 4287. [Google Scholar] [CrossRef]
- Mandelis, A. Laser infrared photothermal radiometry of semiconductors: Principles and applications to solid state elec-tronics. Solid-State Electron. 1998, 42, 1–15. [Google Scholar] [CrossRef]
- Rojas-Trigos, J.B.; Calderón, A.; Marín, E.A. Practical model for the determination of transport parameters in semiconductors. J. Mater. Sci. 2011, 46, 7799–7805. [Google Scholar] [CrossRef]
- Galovic, S.; Djordjevic, K.; Dragas, M.; Milicevic, D.; Suljovrujic, E. Dynamics of Photoinduced Charge Carrier and Photothermal Effect in Pulse-Illuminated Narrow Gap and Moderate Doped Semiconductors. Mathematics 2025, 13, 258. [Google Scholar] [CrossRef]
- Wang, S. Fundamentals of Semiconductor Theory and Device Physics; Prentice Hall, Inc.: Hoboken, NJ, USA, 1989; ISBN 0-13-344425-2. [Google Scholar]
- Galovic, S.P.; Djordjevic, K.L.; Nesic, M.V.; Popovic, M.N.; Markushev, D.D.; Markushev, D.K.; Todorovic, D.M. Time-domain minimum-volume cell photoacoustic of thin semiconductor layer. I. Theory. J. Appl. Phys. 2023, 133, 245701. [Google Scholar] [CrossRef]
- Sablikov, V.A.; Sandomirskii, V.A. The Photoacoustic Effect in Semiconductors. Phys. Status Solidi (b) 1983, 120, 471–480. [Google Scholar] [CrossRef]
- Balderas-Lopez, J.A.; Mandelis, A. Thermal diffusivity measurements in the photoacoustic open-cell configuration using simple signal normalization techniques. J. Appl. Phys. 2001, 90, 2273–2279. [Google Scholar] [CrossRef]
- Stanimirović, I.; Markushev, D.; Stanimirović, Z.; Galović, S.; Djordjević, K. Analysis of plasma-elastic component of time-domain photoacoustic response. J. Appl. Phys. 2023, 133, 235701. [Google Scholar] [CrossRef]
- Aberle, A.G. Surface passivation of crystalline silicon solar cells: A review. Prog. Photovolt. Res. Appl. 2000, 8, 473–487. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Oxford University Press: Oxford, UK, 1959; ISBN 0198533683. [Google Scholar]
- McCord Morse, P.; Feshbach, H. Methods of Theoretical Physics; McGraw-Hill: New York, NY, USA, 1953; ISBN 0070433178/9780070433175. [Google Scholar]
- Galovic, S.; Soskic, Z.; Popovic, M. Analysis of Photothermal Response of Thin Solid Films By Analogy with Passive Linear Electric Networks. Therm. Sci. 2009, 13, 129–142. [Google Scholar] [CrossRef]
- Maillet, D.; André, C.; Batsale, J.-C.; Degiovanni, A.; Moyne, C. Thermal Quadrupoles, Solving the Heat Equation Through Integral Transforms; John Wiley and Sons: Hoboken, NJ, USA, 2000; ISBN 0 471 98320 9. [Google Scholar]
- Suszyński, Z. Thermal model based on the electrical analogy of the thermal processes. In Proceedings of the 10th International Conference on Photoacoustic and Photothermal Phenomena, Rome, Italy, 23–27 August 1998; pp. 197–199. [Google Scholar]
- Chen, G.; Hui, P. Pulsed photothermal modeling of composite samples based on transmission-line theory of heat conduction. Thin Solid Films 1999, 339, 58–67. [Google Scholar] [CrossRef]
- Krapez, J.C.; Dohou, E. Thermal quadrupole approaches applied to improve heat transfer computations in multilayered materials with internal heat sources. Int. J. Therm. Sci. 2014, 81, 38–51. [Google Scholar] [CrossRef]
- Pailhes, J.; Pradere, C.; Battaglia, J.L.; Toutain, J.; Kusiak, A.; Aregba, W.; Batsale, J.C. Thermal quadrupole method with internal heat sources. Int. J. Therm. Sci. 2012, 53, 49–55. [Google Scholar] [CrossRef]
- Salazar, A.; Celorrio, R. Application of the thermal quadrupole method to the propagation of thermal waves in multilayered cylinders. J. Appl. Phys. 2006, 100, 113535. [Google Scholar] [CrossRef]
- Nestoros, M. Photothermal Techniques in Material Characterization. In Materials Science—Advanced Topics; Mastai, Y., Ed.; InTech: London, UK, 2013; Chapter 14. [Google Scholar] [CrossRef][Green Version]
- Pichardo-Molina, J.L.; Alvarado-Gil, J.J. Heat diffusion and thermolastic vibration influence on the signal of an open photoacoustic cell for two layer systems. J. Appl. Phys. 2004, 95, 6450–6456. [Google Scholar] [CrossRef]
- Rousset, G.; Lepoutre, F.; Bertrand, L. Influence of thermoelastic bending on photoacoustic experiments related to measurements of thermal diffusivity of metals. J. Appl. Phys. 1983, 54, 2383–2391. [Google Scholar] [CrossRef]
- Rosencwaig, A.; Gerscho, A. Theory of the photoacoustic effect with solids. J. Appl. Phys. 1976, 47, 64–69. [Google Scholar] [CrossRef]
- McDonald, F.A.; Wetsel, G.C. Generalized theory of the photoacoustic effect. J. Appl. Phys. 1978, 49, 2313–2322. [Google Scholar] [CrossRef]
- Bonno, B.; Zeninari, V.; Joly, L.; Parvitte, B. Study of a Thermophysical System with Two Time Constants Using an Open Photoacoustic Cell. Int. J. Thermophys. 2011, 32, 630–640. [Google Scholar] [CrossRef]
- Tam, A.C. Applications of photoacoustic sensing techniques. Rev. Mod. Phys. 1986, 58, 381–431. [Google Scholar] [CrossRef]
- Bein, B.K.; Pelzl, J. Theory of signal generation in a photoacoustic cell. J. Phys.-Colloq. 1983, 44, C6-27–C6-34. [Google Scholar] [CrossRef]
- Mandelis, A.; Royce, B.S.H. Time-domain photoacoustic spectroscopy of solids. J. Appl. Phys. 1979, 50, 4330–4338. [Google Scholar] [CrossRef]
- Mandelis, A.; Royce, B.S.H. Relaxation time measurements in frequency and time-domain photoacoustic spectroscopy of condensed phases. J. Opt. Soc. Am. 1980, 70, 474–480. [Google Scholar] [CrossRef]
- Domanowska, R.; Bukowski, J. Theoretical Analysis of Pulsed Photoacoustic Effect in Solids. Int. J. Thermophys. 2009, 30, 1536–1556. [Google Scholar] [CrossRef]
- Volovichev, I.N.; Logvinov, G.N.; Titov, O.Y.; Gurevich, Y.G. Recombination and lifetimes of charge carriers in semiconductors. J. Appl. Phys. 2004, 95, 4494–4496. [Google Scholar] [CrossRef]
- Adachi, S. The Handbook on Optical Constants of Semiconductors: In Tables and Figures; World Scientific Publishing: Singapore, 2006; ISBN 978-981-4405-97. [Google Scholar]
- Davies, B.J. Integral Transforms and Their Applications; Springer: Berlin, Germany; New York, NY, USA, 2002; ISBN 978-0-387-95314-4. [Google Scholar]
- Available online: https://eqworld.ipmnet.ru/en/auxiliary/aux-inttrans.htm (accessed on 2 April 2004).
- Chen, Y.Q.; Petras, L.; Vinagre, B.M. A List of Laplace and Inverse Laplace Transforms Related to Fractional Order Calculus. Available online: https://ivopetras.tripod.com/foc_laplace.pdf (accessed on 30 November 2001).
- Oberhettinger, F.; Badii, L. Tables of Laplace Transforms; Springer: Berlin/Heidelberg, Germany, 1973; ISBN 978-3-642-65645-3. [Google Scholar]
- Stojic, M. Continuous System of Automatic Control; Naucna Knjiga-Komerc: Belgrade, Serbia, 1991. (In Serbian) [Google Scholar]
- Lynn, P.A. The Laplace Transform and the z-transform. In Electronic Signals and Systems; Macmillan Education: London, UK, 1986; pp. 225–272. ISBN 978-0-333-39164-8. [Google Scholar] [CrossRef]
- Galovic, S.; Djordjević, A.; Djordjević, K. Analytical Solution of the Inverse Laplace Transform for Combined Shifted Quasi-Rational Radical Functions of Power 1/2 with a Decaying Potential Term. J. Comput. Appl. Math. 2025; under review. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).