GLR: Graph Chain-of-Thought with LoRA Fine-Tuning and Confidence Ranking for Knowledge Graph Completion

Abstract

In knowledge graph construction, missing facts often lead to incomplete structures, thereby limiting the performance of downstream applications. Although recent knowledge graph completion (KGC) methods based on representation learning have achieved notable progress, they still suffer from two fundamental limitations, namely the lack of structured reasoning capabilities and the inability to assess the confidence of their predictions, which often results in unreliable outputs. We propose the GLR framework, which integrates Graph Chain-of-Thought (Graph-CoT) reasoning, LoRA fine-tuning, and the P(True)-based confidence evaluation mechanism. In the KGC task, this approach effectively enhances the reasoning ability and prediction reliability of large language models (LLMs). Specifically, Graph-CoT introduces local subgraph structures to guide LLMs in performing graph-constrained, step-wise reasoning, improving their ability to model multi-hop relational patterns. Complementing this, LoRA-based fine-tuning enables efficient adaptation of LLMs to the KGC scenario with minimal computational overhead, further enhancing the model’s capability for graph-structured reasoning. Moreover, the P(True) mechanism quantifies the reliability of candidate entities, improving the robustness of ranking and the controllability of outputs, thereby enhancing the credibility and interpretability of model predictions in knowledge reasoning tasks. We conducted systematic experiments on the standard KGC datasets FB15K-237, WN18RR, and UMLS, which demonstrate the effectiveness and robustness of the GLR framework. Notably, GLR achieves a Mean Reciprocal Rank (MRR) of 0.507 on FB15K-237, marking a 6.8% improvement over the best recent instruction-tuned method, DIFT combined with CoLE (MRR = 0.439). GLR also maintains significant performance advantages on WN18RR and UMLS, verifying its effectiveness in enhancing both the structured reasoning capabilities and the prediction reliability of LLMs for KGC tasks. These results indicate that GLR offers a unified and scalable solution to enhance structure-aware reasoning and output reliability of LLMs in KGC.

1. Introduction

1.1. Research Motivation

Knowledge graphs (KGs) [1] are structured semantic networks that represent complex relations between entities in the form of triples. They have demonstrated significant utility in domains such as information retrieval [2], recommendation systems [3], and question answering [4]. However, real-world KGs are often incomplete, which substantially impairs their effectiveness and applicability in downstream tasks [5]. To address this limitation, considerable efforts have been devoted to developing methods for inferring missing information, a task commonly referred to as knowledge graph completion (KGC). KGC aims to predict plausible triples that are absent from the KGs by leveraging existing factual knowledge [1]. For example, given a query $(h,r,?)$ consisting of a head entity h and relation r, the goal is to predict the most likely tail entity t that completes the triple.

The mainstream methods for the KGC task are broadly categorized into two groups: embedding-based and LLM-based [6]. The former, including TransE [7] and RotatE [8], model structural patterns in KGs through geometric or algebraic operations, while SimKGC [9] performs KGC by computing semantic similarity between textual entity representations. However, these methods lack the capability for logical reasoning over complex relations or multi-hop inference [10]. On the other hand, LLM-based methods, including models such as GPT-4 [11] and Qwen2.5 [12], are emerging as promising solutions for KGC tasks. Although LLM-based KGC methods exhibit notable advantages in natural language understanding and context modeling, they still face serious challenges regarding generalization and stability. When encountering unseen entity types, rare relations, or domain-shifted knowledge graphs, current models lack explicit structural inductive mechanisms, which limits their ability to generalize. Moreover, due to the absence of systematic modeling for graph-structured constraints and knowledge consistency, LLMs are prone to hallucinations, producing outputs that appear logically coherent but are factually incorrect during tail entity prediction or reasoning path generation. Such hallucinations undermine the credibility of LLMs in KGC tasks and pose potential risks to downstream applications. To address these issues, researchers have explored incorporating external structural information from knowledge graphs, re-ranking candidate entities, and designing structure-aware prompt strategies to guide LLMs toward more robust knowledge reasoning, thereby improving both generalization and output reliability. 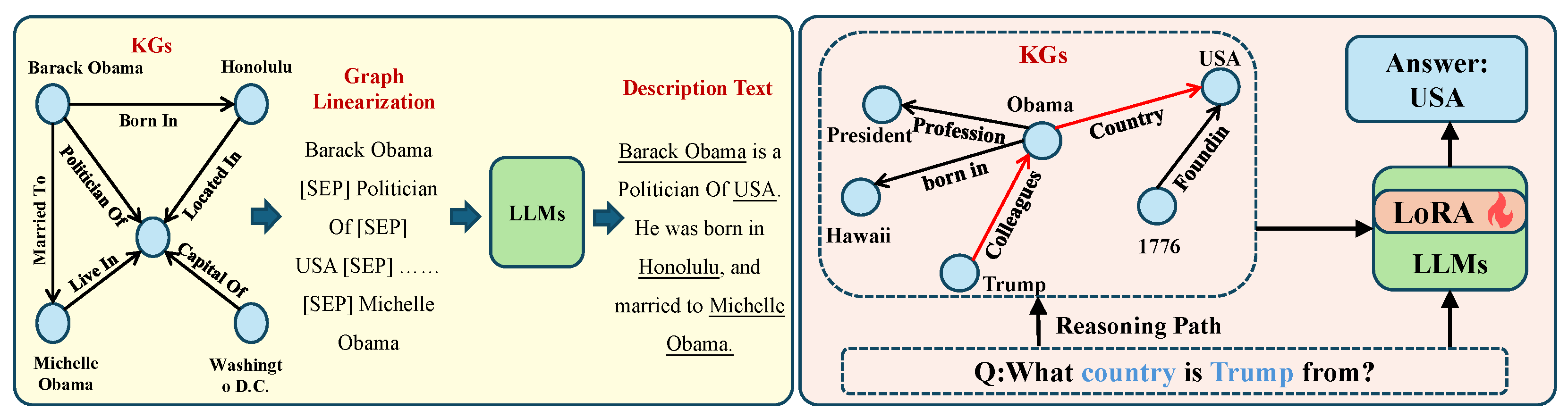As shown in Figure 1, LLM-based prediction methods can be categorized into two main paradigms. The first paradigm involves large language models (LLMs) combined with KG, while the second incorporates both KG and chain-of-thought (CoT) prompting [13]. In the paradigm of LLMs combined with KG, KICGPT proposed by Wei et al. first utilizes a pre-trained knowledge graph embedding (KGE) model to predict the top-m candidate entities [14]. Then, prompts are constructed and multi-turn interactions with ChatGPT (https://openai.com/) are performed, followed by re-ranking of the candidate entities based on ChatGPT’s responses. In contrast, the paradigm of LLMs combined with KG and CoT is represented by the KG-LLM framework proposed by Dong et al. [15], which transforms multi-hop relational paths in the KGs into structured natural language prompt templates. This approach combines CoT [13] reasoning with instruction fine-tuning strategies [16,17], enabling the model to perform multi-hop relation prediction and entity completion. The overall design significantly enhances the model’s ability to capture structural dependencies and improves the controllability of its prediction outputs.

Although the introduction of LLMs into KGC tasks has significantly enhanced the ability of models to complete missing triples, there still exist two major limitations that need to be addressed. On the one hand, existing CoT prompting mechanisms often lack explicit constraints derived from the underlying structure of the knowledge graph. As a result, the generated reasoning chains may deviate from the true topology of the graph, thereby limiting the effective exploitation of structured knowledge. A parallel issue can be observed in the cognitive process of structured knowledge visualization. Spagnolo et al. [18], through eye-tracking experiments, demonstrated that visual representations of structural information significantly enhance learners’ reasoning accuracy in mathematical concept comprehension. This cognitive evidence indirectly highlights the critical role of structural guidance in complex knowledge reasoning and provides theoretical support for the introduction of Graph-CoT prompting in KGC tasks. On the other hand, current LLMs lack a dedicated confidence evaluation mechanism when generating tail entities, making it difficult to quantify the uncertainty of model outputs. This shortcoming adversely affects the stability and controllability of predictions.

To address these challenges, researchers have explored the integration of structured information into CoT-prompted LLMs to enhance reasoning performance. For example, KG-LLM encodes multi-hop paths into natural language prompts to guide LLMs in simulating chain-of-thought reasoning. However, it lacks effective constraints on path selection and entity re-ranking, often resulting in structural drift during the reasoning process. DIFT [19] introduces graph compression and logical control mechanisms to improve output reliability, yet its reasoning chain construction remains relatively simplistic and struggles to model complex structural dependencies accurately. Moreover, most existing LLM-based approaches do not incorporate quantitative evaluation of model outputs.

In light of the above limitations, we propose GLR, a novel framework that integrates Graph Chain-of-Thought (Graph-CoT) [20] prompting with low-overhead adaptation of LLMs through the LoRA technique [21]. In addition, GLR incorporates a confidence evaluation mechanism based on P(True) [22] to effectively constrain the generated results, thereby enhancing the reasoning ability of LLMs and improving the reliability of predictions in KGC tasks. Specifically, GLR first constructs graph structure-aware reasoning prompts by selecting related triples from the KG that have a common head entity or relation with the query triple, forming Graph-CoT [20] prompts that enable the model to perform stepwise reasoning over the candidate entity set under the guidance of graph structure. Then, based on the Graph-CoT prompts, GLR designs an instruction fine-tuning task [16,23] and applies LoRA [21] to enable lightweight adaptation on the base model Qwen2-7B [24], enhancing its adaptability to domain-specific knowledge. Finally, GLR introduces a P(True)-based confidence evaluation mechanism [22], which guides the model to assess the confidence of the predicted triples by appending binary judgment prompts. The confidence scores are then used to rank the candidate entities, improving the reliability of the final predictions [25].

1.2. Contributions of the Study

In summary, our contributions are as follows:

1.

We propose a unified GLR framework that constructs Graph-CoT prompts based on local subgraph structures, guiding LLMs to perform structured chain-of-thought reasoning along the graph paths. This effectively enhances the model’s structural perception capability and its ability to model multi-hop relations.

2.

We design a supervised fine-tuning strategy based on Graph-CoT prompts and apply LoRA to perform parameter-efficient fine-tuning on the base large language model (Qwen2-7B), thereby improving the model’s adaptability to downstream domain-specific tasks.

3.

We introduce a P(True)-based confidence evaluation mechanism to guide the model in quantifying the confidence of candidate entities, enhancing its ability to assess the reliability of prediction results and improving controllability over the output.

1.3. Research Questions

This study aims to enhance the structural reasoning capabilities and output reliability of LLMs in KGC tasks. To this end, we propose the following research questions (RQs):

RQ1: Can the integration of graph structural information improve LLMs’ ability to model structural context?

RQ2: How can LLMs be effectively trained to leverage Graph-CoT reasoning capabilities?

RQ3: How can the reliability of LLM predictions be improved to mitigate hallucination effects?

These questions are further discussed in the discussion section (Section 6).

2. Related Work

Research on knowledge graph completion spans both traditional embedding-based methods and emerging approaches that utilize large language models (LLMs) [17]. In this section, we review representative methods from both lines of research.

2.1. Embedding-Based

Embedding-based approaches estimate prediction probabilities by leveraging vector representations of entities and relations extracted from graph-based or textual characteristics. Recently, graph neural networks (GNNs) [26] have been proposed to better integrate graph structural features into node representations. For example, RUN-GNN [27] introduces query-specific gating units and buffered message updates to address the limitations of previous methods, such as ignoring the order of relation combinations and the delayed propagation of entity information, thereby improving relational rule learning. Neo-GNNs [28] extract structural features of nodes from the adjacency matrix and adopt a neighborhood overlap-aware aggregation strategy to more efficiently capture local structures, significantly enhancing performance on KGC tasks. In addition, MA-GNN [29] integrates graph attention networks (GATs) with Transformers and proposes a “snowball-style” local attention mechanism to strengthen the connection of two-hop neighborhood features, improving the handling of isolated subgraphs and complex relations.

2.2. LLM-Based

With the continuous advancement of LLMs in natural language reasoning tasks [4], researchers have started to explore their potential for KGC [30]. Existing LLM-based methods can be broadly categorized into two groups: prompt-based and fine-tuning-based [31].

Prompt-based methods do not update model parameters but guide LLMs to perform reasoning by constructing examples and context prompts [32,33]. KICGPT [14] proposes a context-enhanced KG reasoning framework, which first generates a top-m candidate entity set using a pre-trained KGE model. It then encodes the query triple and candidate entities into a prompt to guide ChatGPT (gpt-3.5-turbo) in predicting tail entities through multi-turn question answering. The final entity completion is accomplished through re-ranking the candidate entities according to the generated content, thereby eliminating the need for additional fine-tuning and exhibiting strong generalization capabilities in both few-shot [34] and zero-shot prediction settings [35].

Fine-tuning paradigms improve LLMs’ adaptability to KG structures and their structured reasoning ability through parameter updates. KG-LLM [15] models the KGC task as a natural language question-answering task, linearizing multi-hop triple paths into language reasoning chains using CoT prompts [13], guiding the model to predict tail entities within multi-hop relational contexts [36], and leveraging LLMs’ language reasoning capabilities to enhance the integration of multi-hop path information and entity prediction tasks. KoPA [37] focuses on enhancing LLMs’ perception of KG structures by introducing a structural prefix adapter mechanism, which compresses pre-trained KGE information into vector form and injects it into the model input as prefix prompts, helping the model perceive structural patterns and relational distributions among entities, thereby improving its performance on entity completion tasks. DIFT [19] emphasizes controllability and discriminative ability in model outputs, combining discriminative instruction prompt design to guide the model in selecting entities from a pre-filtered candidate set. It employs LoRA [21] for parameter-efficient fine-tuning of LLMs, balancing accuracy and training efficiency, and effectively enhancing the stability of entity prediction. In addition, the recently proposed KnowLA framework [38] further demonstrates the applicability of LoRA in knowledge-enhanced fine-tuning. By introducing a structure-guided adaptation module, it enhances structural alignment and generalization during the fine-tuning process. These findings confirm the feasibility of integrating structural awareness with lightweight adaptation and provide both theoretical and technical foundations for the GLR framework proposed in this study.

Overall, these fine-tuning paradigms have advanced LLMs’ adaptability to KGC tasks from different perspectives, including structure awareness, path modeling, and controlled entity selection, laying the foundation for subsequent research on more fine-grained structure modeling and confidence evaluation mechanisms. In this paper, we propose the GLR framework, which enhances LLMs’ structural perception and output controllability while preserving their general capabilities. By integrating the structured Graph-CoT [20] prompting and the P(True)-based confidence evaluation mechanism [22], GLR further complements and extends existing fine-tuning methods in structured reasoning and result reliability.

3. Methodology

3.1. Problem Definition

A knowledge graph functions as a directed relational structure, characterized by multiple relation types and designed to encode and organize factual information. Formally, it comprises an entity set E and a relation set R, and encodes factual knowledge as a collection of triples $T=\left\{\right(h,r,t)\mid h,t\in E,r\in R\}$, where each triple captures a head entity h linked to a tail entity t via a specific relation r [19].

The objective of KGC is to infer missing facts by leveraging existing triples. Specifically, given an incomplete query $(h,r,?)$ with head h and relation r, the objective is to infer the entity $t\in E$ that best completes the triple while preserving semantic consistency.

3.2. Model Framework

To enhance the predictive accuracy and robustness of LLMs on the KGC task, we propose the GLR framework. This framework fuses Graph-CoT, parameter-efficient LoRA fine-tuning, and a suffix-based P(True) confidence estimation method, to jointly optimize the LLM’s performance in terms of reasoning control, domain adaptation, and result reliability. Figure 2 illustrates the comprehensive architecture of GLR.

3.3. Graph-CoT Prompt Construction

CoT prompting is a method to boost the reasoning ability of LLMs by explicitly breaking down the reasoning process, allowing the model to derive answers step by step. Graph-CoT extends the CoT idea to KGs, enabling LLMs to perform stepwise reasoning with the help of the KG’s entity–relation structure. In this work, we incorporate Graph-CoT into LLM reasoning for KGC by designing a prompt template that infuses multi-hop KG reasoning into LLMs’ thought process. Our Graph-CoT prompt construction is as follows.

The entire prompt consists of three parts, namely the input, the intermediate reasoning process, and the output. The input section explicitly defines the task background and constrains the model to perform reasoning within a predefined set of candidate tail entities, thereby avoiding unreasonable answers that may arise from open-ended generation. Given a descriptive sentence such as “The director of Avatar is James Cameron.”, we can extract the corresponding head entity and relation to construct the query triple to be predicted. Then, combined with the candidate entity set, the task instruction prompt model is constructed to select the most appropriate tail entity in the limited set. The prompt is designed following the structure illustrated in Figure 3.

The intermediate reasoning process provides structured knowledge to facilitate reasoning, which contains two types of supporting information. The first category includes known triples that either have an identical head entity or are linked by an identical relation to the query triple, thereby offering structural context and indicative relational patterns. For example, triples such as (“Avatar”, “producer”, “Jon Landau”) and (“Titanic”, “director”, “James Cameron”) help verify the rationality of candidate tail entities. The second type of supporting information consists of known triples where the head entity of the query appears as the tail entity, offering contextual information about the head entity Avatar in the KG. For instance, (“20th Century Fox”, “produced”, “Avatar”) provides contextual clues to help the model better understand the semantic role of the head entity. With the assistance of these two types of structural information, LLMs can perform more effective structured reasoning, thereby improving the accuracy of their predictions.

In the output section, the model selects the most appropriate tail entity based on the provided structured information and generates an explanation, ensuring the interpretability and rationality of the prediction results. An example of such a prompt construction is illustrated in Figure 3.

Through the design of the Graph-CoT prompt, the model can fully leverage multi-hop contextual information, explicitly presenting the originally implicit reasoning chains in the graph structure within the prompt of LLMs, thereby enhancing the accuracy of the final reasoning results.

3.4. LoRA Fine-Tuning

In Section 3.3, we designed the Graph-CoT prompt to guide LLMs in incorporating the structured information of KGs for reasoning in KGC tasks. However, relying solely on prompt design is still insufficient to guarantee that LLMs can strictly follow the logic of KGs and generate answers that conform to reasoning rules. Therefore, in GLR, we leverage instruction data [23] containing the Graph-CoT reasoning process to perform LoRA-based fine-tuning on LLMs. This enables the model to learn the capability of selecting correct entities under the guidance of Graph-CoT prompts, enhancing its adherence to task instructions and preventing it from generating answers that deviate from the semantics of the KG. Additionally, to overcome the input length limitations of LLMs, we introduce a divide-and-conquer reasoning mechanism for candidate entities. Specifically, the candidate entity set is partitioned into several smaller groups, and separate Graph-CoT prompts are constructed for each group. These prompts are independently fed into the LLM for reasoning, thus improving the model’s prediction capability over large-scale KGs.

During training, we leverage LoRA to facilitate lightweight adaptation of LLMs with minimal parameter updates. Its fundamental principle involves freezing the parameters of the pre-trained model while integrating learnable low-rank matrices A and B [21] into the Transformer layers, optimizing the model to minimize prediction errors. The forward computation of LoRA is formulated as follows:

$$H=W_{0}x+\Delta Wx=W_{0}x+BAx.$$

(1)

where, $\Delta W=BA.$ Here, $W_0\in {\mathbb{R}}^{d\times d}$ represents the frozen pre-trained parameters of the original Transformer layer, $\Delta W$ denotes the newly injected weight matrix, and $A\in {\mathbb{R}}^{r\times d}$ and $B\in {\mathbb{R}}^{d\times r}$ are the trainable low-rank matrices with $r\ll d$ [21], thereby significantly reducing the number of trainable parameters.

3.5. P(True)-Based Confidence Evaluation Mechanism

In this section, we propose a confidence evaluation mechanism that quantifies the reliability of LLMs’ prediction results using the P(True) confidence scoring method, and selects the candidate with the highest score as the final prediction, as illustrated in Figure 4. Compared with traditional uncertainty quantification methods such as Monte Carlo Dropout [39], the P(True)-based confidence scoring mechanism proposed in this study provides a lightweight and interpretable alternative. Conventional approaches typically estimate predictive uncertainty by introducing stochasticity during the forward pass or by constructing multiple models; while these methods offer a degree of stability and theoretical robustness, they often incur substantial computational overhead. In contrast, the P(True) method requires neither architectural modifications nor repeated sampling during inference. It directly derives a normalized confidence score from the LLM’s semantic judgment of whether a candidate triple is true, formulated as a binary classification task. This approach enables both ease of implementation and high inference efficiency. A comparative evaluation between the P(True) method, MC Dropout, and a hybrid approach combining both is presented in Section 5.6.

3.5.1. P(True) Confidence Scoring Method

Building upon the findings of Kadavath et al. [22], we enhance the suffix-based confidence scoring method to enable a more intuitive evaluation of LLMs’ confidence in their own outputs. Specifically, after LLMs generate a candidate tail entity $t^{\ast }$, we append the following prompt to guide the model in performing a binary classification: “The possible correct triple is: (“Avatar”, “director”, “James Cameron”). Is the Possible Triple: (A) True (B) False?” The LLM is then instructed to choose between the two options. We extract the probability assigned to the option True as the confidence score for the candidate tail entity, which is computed as

$$P\left(\mathrm{True}\right)={\displaystyle \frac{e^{s_{\mathrm{True}}}}{e^{s_{\mathrm{True}}}+e^{s_{\mathrm{False}}}}},$$

(2)

where $s_{\mathrm{True}}$ and $s_{\mathrm{False}}$ are the logits output by LLMs for selecting options (A) True and (B) False, respectively. The softmax operation is applied to normalize these logits, resulting in the final confidence score $P\left(\mathrm{True}\right)$.

3.5.2. Confidence Evaluation Mechanism

Confidence Scoring After multi-round structured reasoning, the model produces one candidate tail entity for each sub-group of candidate entities. We collect all these candidate entities and construct the corresponding suffix prompts to calculate their confidence scores $P_i\left(\mathrm{True}\right)$ for the candidate tail entities in the given triple. It is important to note that we do not compute confidence scores for all entities in the candidate sets. Instead, we only evaluate the entities actually generated by the model during the multi-round reasoning process. For example, given the query triple $(“Avatar”,“director”,?)$, the model may generate candidate entities such as James Cameron, Sam Worthington, and Zoe Saldana in different reasoning rounds. We construct suffix prompts for these candidates and compute the corresponding confidence scores $P_i$ using the method presented in Section 3.5.1.

Candidate Ranking The candidate tail entities are ranked in descending order based on their computed confidence scores, and the one with the highest score is selected as the final prediction:

$$t^{\ast }=\underset{t_i\in T_{\mathrm{out}}}{\arg \max } P_i.$$

(3)

where $T_{\mathrm{out}}$ represents the set of candidate entities generated during the reasoning process. Additionally, the model provides an explanation for the selected prediction. This post hoc verification mechanism, when coupled with structure-aware reasoning, improves the model’s ability to differentiate among candidate entities and enhances both interpretability and prediction reliability. In summary, GLR incorporates a confidence evaluation component that ranks candidate tail entities based on their credibility estimates.

Algorithmic 1 provides a unified algorithmic summary that encapsulates both the training and inference procedures of the GLR framework. It delineates the complete pipeline from Graph-CoT prompt construction and LoRA-based instruction tuning to multi-round reasoning and confidence-based prediction. This structured representation offers a clear and reproducible implementation roadmap for applying GLR to knowledge graph completion tasks.

Algorithm 1 Algorithmic workflow of GLR.

Input:  Query triple $q=(h,r,?)$; Knowledge graph $\mathcal{G}$; Large language model M; Instruction tuning set $D_{\mathrm{train}}$ Output: Final predicted tail entity $t^{\ast }$   1: Extract supporting triples $S\subset \mathcal{G}$ satisfying: $S=\{(h^{\prime },r^{\prime },t^{\prime })\in \mathcal{G}\mid h^{\prime }=h\vee r^{\prime }=r\vee t^{\prime }=h\}$   2: Construct Graph-CoT prompt $P_q$ based on S and candidate entity set ${\mathcal{C}}_q$ for query q   3: Construct instruction-tuning dataset: ${\mathcal{D}}_{\mathrm{prompt}}=(P_q^j,t_j)\mid (h_j,r_j,t_j)\in D_{\mathrm{train}}$ by repeating Steps 1–2   4: Fine-tune M on ${\mathcal{D}}_{\mathrm{prompt}}$ using LoRA, resulting in adapted model $M^{\prime }$   5: Partition ${\mathcal{C}}_q$ as ${\mathcal{C}}_q={\bigcup }_{i=1}^k{C}_i$, with $C_i\subseteq {\mathcal{C}}_q$, subject to length constraints   6: for each batch $C_i$ do   7:    Construct prompt $P_q^i$ using S and $C_i$   8:    Predict tail entity: $t_i\leftarrow M^{\prime }\left(P_q^i\right)$   9: end for 10: Collect predictions: $T_{\mathrm{out}}=\{t_1,t_2,\dots ,t_k\}$ 11: Initialize confidence list P 12: for each $t_i\in T_{\mathrm{out}}$ do 13:    Construct binary-choice prompt $B_i$: “The possible correct triple is: $(h,r,t_i)$. Is the Possible Triple: (A) True (B) False?” 14:    Obtain logits from model: $(s_{\mathrm{true}},s_{\mathrm{false}})\leftarrow M^{\prime }\left(B_i\right)$ 15:    Compute confidence score using softmax: $P_i\left(\mathrm{True}\right)={\displaystyle \frac{e^{s_{\mathrm{true}}}}{e^{s_{\mathrm{true}}}+e^{s_{\mathrm{false}}}}}$ 16:    Append $P_i$ to list P 17: end for 18: Rank $T_{\mathrm{out}}$ in descending order of $P_i$ 19: Select final prediction: $t^{\ast }=arg{max}_{t_i\in T_{\mathrm{out}}}{P}_i$ 20: return  $t^{\ast }$

4. Experimental Setup

This section presents a comprehensive set of experiments to assess the performance of the proposed GLR framework across multiple benchmark datasets for KGC. We begin by detailing the experimental configurations and the baseline models used for comparison. Subsequently, we present the main results, followed by ablation studies, comparisons with different LLMs, and further analysis of the effects of training sample size and candidate set size.

4.1. Datasets

We conduct experiments on three standard KGC benchmark datasets, including UMLS [40], FB15K-237 [41], and WN18RR [42]. The descriptions of these datasets are summarized in

Table 1. Descriptions and statistics of benchmark datasets.

Datasets	#Entity	#Relation	#Train	#Valid	#Test
UMLS	135	46	5216	652	661
WN18RR	40,943	11	86,835	3034	3134
FB15K-237	14,541	237	272,115	17,535	20,466

. UMLS serves as a widely adopted structured knowledge resource in the biomedical domain, encompassing medical concepts and their interrelations, and is commonly employed to assess a model’s capability for medical reasoning. FB15K-237 represents a handpicked collection derived from the Freebase knowledge graph, in which inverse relations have been eliminated to increase the complexity of the reasoning task. WN18RR is derived from WordNet and focuses on evaluating the model’s reasoning ability over lexical hierarchies. These datasets cover different domains and reasoning difficulties, providing a comprehensive evaluation of the model’s performance. In this work, we follow the standard dataset splits for KGC tasks and evaluate the model performance on the test set.

4.2. Evaluation Metrics

We adopt Mean Reciprocal Rank (MRR) and Hits@K $(K=1,3,10)$ [1] as the evaluation metrics. MRR measures the average reciprocal rank of the correct entity in the prediction results, while Hits@K indicates whether the correct entity appears within the top-K ranked candidates. A higher MRR score reflects better overall ranking performance of the model, whereas a higher Hits@K value represents a greater probability of covering the correct answer within the top-K candidates [1]. These metrics jointly evaluate the model’s performance in terms of both precision and recall.

4.3. Baselines

To comprehensively evaluate the performance of various KGC approaches, we select a set of representative embedding-based and LLM-based models as baselines across multiple benchmark datasets, with configurations tailored to the characteristics of each dataset. On FB15K-237 and WN18RR, the comparison includes classical embedding models such as TransE [7], TuckER [43], NBFNet [44], and SimKGC [9], alongside mainstream LLM-based methods including zero-shot and one-shot ChatGPT [45], retrieval-augmented KICGPT [14] with in-context prompting, as well as instruction-tuned models such as DIFT [19]. For the UMLS medical knowledge graph, the CP-KGC [46] framework is included as a key baseline. This method integrates structural encoders like KG-BERT [40] and SimKGC [9] with semantic compression through interactions with ChatGPT (GPT-3.5-Turbo), enabling effective zero-shot triple classification with strong adaptability to biomedical domains. These baselines reflect the prevailing paradigms in KGC research and provide a robust foundation for evaluating model adaptability across different architectures and domains.

4.4. Settings

We employ Qwen2-7B [24] as the backbone large language model (LLM) for our experiments. Qwen2-7B, an advanced open-source model containing 7 billion parameters, was selected as the backbone. To improve the model’s adaptability to the specific task, we adopt parameter-efficient fine-tuning using LoRA, with the rank parameter set to $r=8$, the scaling factor $\alpha =32$, and a dropout rate of $0.05$. During training, we use a batch size of 8 with gradient accumulation steps of 2. The maximum input sequence length is set to 4096 tokens, the number of training epochs is 1, and the learning rate is configured as $1\times {10}^{-4}$. This configuration ensures that the model can sufficiently learn task-specific knowledge while maintaining a controllable number of trainable parameters and computational cost, thereby improving the overall training efficiency.

We run our experiments on an NVIDIA L20 GPU (48GB memory, Ada Lovelace architecture), and Ubuntu 20.04 LTS. We apply 4-bit NF4 quantization to Qwen2-7B using the BitsAndBytes library and enable bfloat16 precision to facilitate efficient training. The training pipeline is built upon HuggingFace Transformers and DeepSpeed ZeRO-2, with mixed-precision training enabled throughout.

Owing to the parameter-efficient nature of LoRA, all experiments can be executed within the 48 GB memory of a single GPU, substantially reducing hardware resource requirements and establishing a solid foundation for future deployment on larger-scale knowledge graphs or cross-domain scenarios. To further illustrate the resource efficiency of the GLR framework, we record the training time on different datasets under the specified configuration. Specifically, GLR completes training in approximately 20 min on UMLS, 5 h on WN18RR, and 17 h on FB15K-237. These results demonstrate that, by leveraging LoRA’s efficient parameter adaptation and 4-bit quantization, the proposed framework achieves strong engineering practicality.

5. Results

5.1. Main Results

To evaluate the effectiveness of the proposed GLR method, we compare it against a variety of representative baseline models, including embedding-based methods and LLM-based methods.

Table 2. Performance comparison of different models on FB15K-237 and WN18RR for KGC. The best scores for each metric are shown in underline. The results of SimKGC are adopted from [19], while those of ChatGPT_zero—shot and ChatGPT_zero—shot are taken from [14]. Performance metrics of the remaining baselines were retrieved from the corresponding published sources.

Models	FB15K-237				WN18RR
	MRR	Hits@1	Hits@3	Hits@10	MRR	Hits@1	Hits@3	Hits@10
Embedding-based
TransE	0.279	0.198	0.376	0.441	0.243	0.043	0.441	0.532
TuckER	0.358	0.266	0.394	0.544	0.470	0.443	0.482	0.526
NBFNet	0.415	0.321	0.454	0.599	0.551	0.497	0.573	0.666
SimKGC	0.338	0.252	0.364	0.511	0.671	0.595	0.719	0.802
LLM-based
ChatGPTzero—shot	–	0.237	–	–	–	0.190	–	–
ChatGPTzero—shot	–	0.267	–	–	–	0.212	–	–
KICGPT	0.412	0.327	0.448	0.581	0.564	0.478	0.612	0.677
CP-KGC	0.329	0.243	0.353	0.503	0.648	0.580	0.683	0.773
LLaMA + TransE	0.232	0.080	0.321	0.502	0.202	0.037	0.360	0.516
LLaMA + SimKGC	0.236	0.074	0.335	0.503	0.391	0.065	0.695	0.798
LLaMA + CoLE	0.238	0.033	0.387	0.561	0.374	0.117	0.602	0.697
DIFT + TransE	0.389	0.322	0.408	0.525	0.491	0.462	0.496	0.560
DIFT + CoLE	0.439	0.364	0.468	0.586	0.617	0.569	0.638	0.708
GLR (ours)	0.507±0.018	0.402±0.011	0.511±0.009	0.643±0.008	0.679±0.014	0.621±0.012	0.705±0.007	0.796±0.009

summarizes the KGC performance (MRR and Hits@K) of different models on the FB15K-237 and WN18RR datasets [47], while

Table 3. KGC performance of different models on the UMLS. The notation & indicates that the model is optimized using the CP-KGC framework. The best scores for each metric are shown in underline.

Models	UMLS
	MRR	Hits@1	Hits@3	Hits@10
KG-BERT	0.648±0.021	0.539±0.025	0.714±0.018	0.839±0.015
& CP-KGC	0.798±0.014	0.676±0.016	0.897±0.012	0.980±0.009
SimKGC	0.688±0.018	0.579±0.020	0.748±0.017	0.894±0.014
& CP-KGC	0.780±0.013	0.678±0.015	0.857±0.011	0.951±0.009
GLR (ours)	0.804±0.012	0.715±0.014	0.893±0.010	0.962±0.008

presents the corresponding results on the UMLS dataset, which focuses on the medical knowledge graph domain. The standard deviations are obtained from three runs with different random seeds.

As shown in Table 2, on the more challenging FB15K-237 dataset, GLR achieves a competitive MRR of 0.507, representing a 9.2% improvement over the well-established embedding-based model NBFNet (MRR = 0.415), and a 6.8% gain over the recent LLM-based method DIFT + CoLE. In addition, GLR attains a Hits@10 of 0.643, outperforming competitive baselines such as NBFNet (Hits@10 = 0.599), indicating its improved ability to retrieve correct answers. These results demonstrate that the integration of Graph-CoT reasoning and the candidate filtering strategy effectively enhances the model’s capacity to identify accurate results, contributing to both better ranking quality and higher recall under the Top-K setting.

On the WN18RR dataset, GLR attains a competitive MRR of 0.679, outperforming recent strong baselines such as SimKGC (MRR = 0.671) and DIFT (MRR = 0.617). This represents a relative improvement of 0.8% over SimKGC, the best-performing baseline in this metric. However, it does not obtain the highest scores in Hits@3 and Hits@10, which may be attributed to the characteristics of WN18RR. Specifically, WN18RR has a relatively sparse KG structure with fewer relation types, which is less favorable for methods requiring complex reasoning chains, such as Graph-CoT employed in GLR. In such scenarios, the advantages of multi-hop reasoning approaches may not be fully realized. Nevertheless, GLR maintains leading performance in overall prediction accuracy on WN18RR due to its comprehensive design, demonstrating strong reasoning capability.

It is also worth mentioning that some zero-shot LLM-based methods (e.g., directly using ChatGPT [48] or LLaMA [49] for reasoning) often suffer from outputting invalid entities that are not included in the candidate set due to the lack of task-specific constraints. This typically leads to lower Hits@K performance. In contrast, GLR adopts candidate generation and confidence-based filtering strategies to ensure that the output is always restricted within a reasonable candidate space, thereby significantly improving the valid hit rate and avoiding interference from irrelevant answers.

Table 3 further presents the experimental results on the UMLS dataset, which focuses on the medical domain. It can be observed that all models achieve relatively high performance on this dataset. GLR achieves an MRR of 0.804, representing a new strong baseline in this domain. Compared to the best CP-KGC-based result (MRR = 0.798), GLR achieves a relative improvement of 0.6% in MRR. In addition, GLR reaches a Hits@1 of 0.715, outperforming the strongest baseline (0.678) by 3.7%, which demonstrates the framework’s enhanced ability to accurately identify the top-ranked tail entity. GLR also maintains competitive results on Hits@(3, 10), achieving 0.893 and 0.962, respectively; while not the highest across all metrics, these scores reflect the model’s stable ranking capability and reinforce its overall robustness on the UMLS.

The advantage of GLR lies in its ability to not only leverage the semantic knowledge encoded in pre-trained language models but also explicitly incorporate graph structure information for chain-of-thought reasoning. As a result, GLR is able to achieve subtle yet consistent improvements even when the evaluation metrics on this dataset are close to saturation.

This is primarily attributed to its explicit integration of graph-structured reasoning via Graph-CoT and confidence calibration through the P(True) mechanism, which together enable the model to capture nuanced relational patterns and filter out less reliable candidates, thereby improving the robustness of final predictions.

5.2. Ablation Study

To better understand the role of each major component within the GLR framework, we performed ablation experiments on the FB15K-237 dataset. Specifically, we individually remove three core components of GLR, which are Graph-CoT prompting, LoRA-based parameter-efficient fine-tuning, and P(True)-based confidence re-ranking, while retaining the remaining parts of the framework to retrain or infer the model. We quantitatively assessed the contribution of each component by comparing the complete GLR framework (referred to as Full) with its ablated counterparts, thereby evaluating their respective impact on model effectiveness.

Table 4. Results of the ablation study for GLR on the FB15K-237 dataset.

Models	FB15K-237
	MRR	Hits@1	Hits@3	Hits@10
GLR (Full)	0.507	0.402	0.511	0.643
w/o Graph-CoT	0.454	0.388	0.487	0.602
w/o LoRA	0.374	0.245	0.401	0.493
w/o Confidence Ranking	0.462	0.372	0.483	0.617

illustrates the results of the full GLR framework and its ablated variants on the FB15K-237 dataset in terms of MRR and Hits@K.

As presented in Table 4, the exclusion of any single component from the GLR framework resulted in a noticeable decline in performance, highlighting the critical role of each module. The Graph-CoT module provides LLMs with a reasoning framework constrained by the structure of the knowledge graph, enhancing the model’s ability to handle complex relational chains. Its effectiveness is clearly validated by the ablation study results.

Through LoRA fine-tuning, LLMs are able to learn representations and reasoning patterns specific to the target knowledge graph, bridging the gap between pre-trained language models and the downstream triple prediction task. Furthermore, the P(True)-based confidence evaluation assigns credibility scores to candidate entities generated by LLMs, effectively filtering out misleading entities that may accidentally receive high prediction scores. This mechanism reduces the risk of incorrect predictions caused by the inherent uncertainty of open-ended generation. In summary, the combination of Graph-CoT prompting, LoRA fine-tuning, and P(True)-based confidence evaluation enables GLR to achieve the best overall performance.

5.3. Comparative Study with Different LLMs

To clearly demonstrate and verify the advantages of the GLR framework, we conduct comparative experiments using four representative off-the-shelf LLMs, namely Qwen-7B-Chat with 7 billion parameters [50], its 4-bit quantized version Qwen-7B-Chat-int4 [50], LLaMA2-7B-Chat with 7 billion parameters [51], and GPT-3.5-Turbo with 175 billion parameters [48]. We perform experimental analysis on three public benchmark datasets, which are FB15K-237, WN18RR, and UMLS. The experimental results are presented in Figure 5.

The medium-scale model Qwen2-7B, enhanced by the GLR framework (referred to as GLR-Qwen2-7B), achieves the best performance across all three datasets, with MRR scores of 0.679 on WN18RR, 0.507 on FB15K-237, and 0.804 on UMLS. It significantly outperforms all original LLMs without the GLR framework. These comparative results demonstrate that GLR exhibits strong performance compensatory capabilities, effectively improving downstream task performance. GLR-Qwen2-7B consistently achieves the best results on three datasets with distinct characteristics, namely the general domain (FB15K-237), the lexical domain (WN18RR), and the medical domain (UMLS), indicating the excellent cross-context generalization ability of the GLR framework. By introducing explicit reasoning paths through Graph-CoT, GLR-Qwen2-7B transforms the original LLM from a generative search paradigm to a structure-guided selection paradigm. This transformation significantly reduces generation errors and improves the stability and reliability of predictions. These findings verify that structure-enhanced reasoning is more effective than merely increasing model parameters in improving KGC performance.

Meanwhile, we further compared the differences in runtime efficiency and memory consumption across methods. Under the same hardware environment (NVIDIA L20 GPU), GLR-Qwen2-7B required 20 minutes to complete training on the UMLS dataset, representing an improvement of approximately 39.3% in training efficiency compared to the average training time of 33 minutes observed for other vanilla LLMs. For the WN18RR and FB15K-237 datasets, the training time was reduced by approximately 17.6% and 21.7%, respectively. In addition, since LoRA updates only a small subset of model parameters, the number of trainable parameters in GLR is reduced by approximately 97%, which leads to a substantial decrease in memory usage. These findings further demonstrate that the GLR framework delivers not only significant performance improvements but also superior cost-effectiveness in terms of computational resources.

5.4. Impact of Training Sample Size on GLR Performance

To further investigate the impact of training data size on the prediction performance of the GLR framework, we conduct experiments on the FB15K-237 dataset using different numbers of constructed training examples. Specifically, we select 100, 200, 500, and 1000 Graph-CoT instruction samples to perform LoRA-based fine-tuning, and evaluate the model’s performance on the knowledge graph completion task accordingly. The experimental results are illustrated in Figure 6.

As shown in Figure 6, the performance of the GLR framework steadily improves as the number of training instruction samples increases. In particular, when the number of training samples increases from 200 to 500, the MRR score of the model improves significantly by 9%, indicating that with more structured instruction data, the model can more effectively capture the semantic structure and reasoning patterns of the KG. However, when the number of training samples further increases to 1000, the performance improvement trend becomes relatively flat, suggesting the presence of diminishing marginal returns once a certain data scale is reached. These results demonstrate that the GLR framework can achieve efficient learning even under limited data conditions, leveraging the advantages of parameter-efficient fine-tuning (LoRA) and structure-aware prompting (Graph-CoT). This makes GLR particularly well-suited to low-resource scenarios where labeled data is scarce.

5.5. Impact of Candidate Set Size on GLR Performance

To evaluate the impact of candidate set size on the performance of the GLR framework, and to further verify the robustness of its structure-aware reasoning capability and confidence evaluation mechanism under different constraint conditions, we design a controlled experiment on the UMLS dataset.

Unlike the previous experiments, this experiment focuses solely on exploring the effect of candidate set size on model performance. Therefore, for simplicity, we conduct 10 repeated tests for each group of data. Although the accuracy in this setting may be influenced by randomness, it is sufficient for observing the relationship between candidate set size and model performance. Specifically, a subset of entities was stochastically drawn from the complete entity set containing the ground-truth tail entity, and candidate set sizes were configured as Top-10, Top-20, Top-50, and the full entity set. For the first three candidate set sizes, we randomly select the corresponding number of entities from the entire entity set as candidates and repeat the testing process 10 times. In each test, a different candidate set is input into the model for structured question answering, resulting in 10 different predicted entities. Subsequently, we construct suffix prompts for these 10 candidate entities and calculate their confidence scores using the P(True) mechanism. The entity with the highest confidence score is selected as the final prediction. In the final set of experiments, given the relatively small number of entities in the UMLS dataset, it was feasible to input the entire entity set into the model simultaneously. The experimental results also show that this setting achieves similar performance to our previously proposed batch-wise input strategy designed to handle cases where the number of entities exceeds the maximum token limit of LLMs. This further verifies the effectiveness of our proposed strategy. The experimental results are shown in Figure 7.

As shown in Figure 7, the size of the candidate set has a significant impact on the prediction performance of GLR. The smaller the candidate set, the better the model performance. In particular, under the Top-10 setting, all evaluation metrics achieve their best values, with Hits@10 reaching 100% accuracy. As the candidate set size increases, the reasoning complexity and semantic interference grow substantially. This results in a more dispersed confidence distribution over the candidate entities, reducing the distinguishability of confidence-based ranking.

These experimental results indicate that, under the collaborative mechanism of structure-guided reasoning and confidence evaluation, GLR is more adept at making high-quality decisions within small-scale candidate sets. This not only demonstrates the effectiveness of Graph-CoT prompting in constraining the model’s reasoning path but also further verifies the practicality and discriminative capability of the P(True)-based confidence evaluation mechanism as a post hoc verifier. In future work, combining lightweight candidate filtering techniques to further compress the candidate space may enhance the reasoning efficiency and performance upper bound of GLR in large-scale open-domain entity environments.

5.6. Comparison of Confidence Estimation Strategies

Based on the GLR framework, we replace the confidence evaluation module with alternative methods. In addition to the P(True) approach, the MC Dropout method performs five stochastic forward passes during inference to compute the average confidence. The ensemble method further calculates the arithmetic mean of the confidence scores obtained from both P(True) and MC Dropout for each candidate. Evaluation metrics include MRR, Hits@1, and the average inference time per query (in seconds).

As shown in

Table 5. Performance and efficiency of different confidence estimation methods on the UMLS dataset. The best scores for each metric are shown in underline.

Methods	UMLS
	MRR	Hits@1	Times (s)
Monte Carlo Dropout	0.816	0.724	5.08
Ensemble	0.831	0.736	6.35
P(True)	0.804	0.715	1.17

, the P(True) method achieves competitive accuracy (MRR = 0.804, Hits@1 = 0.715) with an average inference time of 1.17 s. MC Dropout yields slightly higher accuracy (MRR = 0.816, Hits@1 = 0.724) but incurs a significantly longer inference time of 5.08 s per query. The ensemble method attains the highest accuracy (MRR = 0.831, Hits@1 = 0.736), accompanied by the highest latency of 6.35 s. Overall, while MC Dropout and the ensemble approach offer modest improvements in prediction accuracy, they introduce considerable computational overhead. In contrast, P(True) provides a favorable trade-off between accuracy and efficiency, making it a highly practical solution for real-world deployment.

5.7. Evaluation of Overfitting Risk During LoRA Fine-Tuning

This experiment aims to evaluate whether the proposed GLR framework exhibits signs of overfitting during fine-tuning, with particular focus on the performance gap between the validation and test sets. As shown in

Table 6. Evaluation of overfitting risk during LoRA fine-tuning. The Bold indicates the best performance.

Dataset	Set	MRR	Hits@1	Hits@3	Hits@10
UMLS	Valid	0.781	0.688	0.861	0.941
	Test	0.804	0.715	0.893	0.962
FB15K-237	Valid	0.497	0.375	0.488	0.621
	Test	0.507	0.402	0.511	0.643
WN18RR	Valid	0.653	0.598	0.684	0.777
	Test	0.679	0.621	0.705	0.796

, GLR achieves strong performance on the test sets across all three datasets, with MRR scores of 0.804 on UMLS, 0.507 on FB15K-237, and 0.679 on WN18RR. In comparison, slightly lower performance is observed on the corresponding validation sets, where MRR scores are 0.781 on UMLS, 0.479 on FB15K-237, and 0.653 on WN18RR. These results suggest that a mild degree of overfitting occurs during training. Nevertheless, its impact on final reasoning performance remains limited.

In addition, prior studies have suggested that incorporating dropout within the LoRA pathway can effectively mitigate overfitting during fine-tuning [52]. Although the current study does not adopt such a mechanism, future work may consider integrating dropout regularization into the Graph-CoT-based LoRA fine-tuning process to further enhance the generalization capability of the GLR framework.

5.8. Cross-Domain Knowledge Transfer

To evaluate the generalization capability of the GLR framework across different knowledge graph domains, we design a cross-domain transfer experiment. Specifically, models are independently trained on each of the three datasets and subsequently tested on the remaining two knowledge graphs that were not seen during training. This setup simulates the practical challenges of knowledge reasoning under conditions of substantial domain divergence.

The results are presented in Figure 8. It can be observed that the GLR framework achieves the best performance when the training and testing domains are aligned. However, when transferred to other datasets, the model exhibits varying degrees of performance degradation, particularly in transfer scenarios characterized by substantial structural and semantic divergence. These findings indicate that cross-domain knowledge transfer remains a significant challenge. The generalization ability of GLR across heterogeneous knowledge graphs is still limited, with noticeable performance bottlenecks under conditions of entity semantic drift and imbalanced relation distributions.

6. Discussion

This study systematically evaluates the applicability and effectiveness of the proposed GLR framework across multiple KGC tasks, demonstrating significant advantages in structural modeling, reasoning accuracy, and model efficiency. Experimental results show that GLR effectively enhances the predictive capabilities of medium-scale LLMs, particularly exhibiting greater stability and generalization in multi-hop reasoning and structurally complex scenarios.

Ablation studies further verify the synergistic benefits of the framework’s three core components: Graph-CoT prompting, LoRA fine-tuning, and P(True) confidence ranking. Specifically, structural prompts facilitate semantic path alignment, parameter-efficient tuning reduces computational overhead, and the confidence mechanism significantly improves the controllability and trustworthiness of model outputs. Moreover, GLR maintains robust decision-making performance even under conditions of limited training data or constrained candidate sets, indicating its practical potential in low-resource scenarios. Collectively, these findings validate the effectiveness and research value of integrating structure-guided reasoning with confidence modeling to enhance LLM-based KGC performance.

In response to the three research questions (RQs) posed in this study, we provide the following answers:

RQ1: Can structural information be introduced to enhance LLMs’ ability to model contextual structure?

Answer: Our findings suggest that knowledge graphs often contain rich structural information that has been underutilized in prior work, which limits model performance. To address this issue, we design the Graph-CoT prompting mechanism to guide the model in performing structure-aware chain-of-thought reasoning, thereby compensating for the structural modeling limitations of conventional CoT methods.

RQ2: How can large models be trained to leverage Graph-CoT capabilities?

Answer: We integrate Graph-CoT with LoRA-based fine-tuning, utilizing LoRA’s instruction-following capabilities to improve model alignment and performance. This is achieved with only a small number of trainable parameters, making the approach suitable for deployment in resource-constrained environments while minimizing computational cost.

RQ3: How can we improve the reliability of predictions and mitigate hallucination in LLMs?

Answer: We propose the P(True) confidence evaluation mechanism, which estimates confidence scores for candidate entities without requiring additional models. This approach effectively reduces generative errors and improves output consistency. Comparative experiments with other uncertainty estimation methods confirm its advantage in balancing predictive reliability with inference efficiency.

Despite the strong performance of the GLR framework on several mainstream KGC tasks, it faces notable limitations when applied to ultra-large-scale knowledge graphs characterized by highly imbalanced relation distributions or sparse structural connectivity. Specifically, when certain relation types appear infrequently in the training data, the Graph-CoT prompts generated by GLR may lack sufficient structural context. This impairs the model’s ability to construct meaningful reasoning chains and reduces prediction accuracy.

In addition, cross-domain transfer remains a significant challenge. As demonstrated in the experimental results in Section 5.8, the model exhibits considerable performance degradation when applied to domains not encountered during training, particularly when substantial semantic or structural discrepancies exist between knowledge graphs.

Furthermore, in large-scale knowledge graphs such as Wikidata, which contain millions of entities and relations, the sparsity and complexity of multi-hop paths can lead to failures in path retrieval or token length overflow during structured prompt generation. These factors intensify the model’s reliance on graph structure and increase the risk of prediction bias. Although GLR partially alleviates these issues through subgraph extraction and confidence-based evaluation, its generalization and robustness still degrade in the presence of long-tail entity distributions and rare relation types. We will further explore approaches to enabling LLMs to perform more complex forms of reasoning. As reasoning tasks over graphs are not limited to chain-based patterns, more advanced paradigms such as graph-structured reasoning [53] offer promising directions for further enhancing the reasoning capabilities of LLMs.

7. Conclusions

In this work, we have presented GLR, a unified framework for KGC with LLMs, which integrates Graph-CoT-based prompting, parameter-efficient fine-tuning via LoRA, and a confidence assessment mechanism based on P(True) scoring. The proposed framework enables LLMs to perform structured chain-of-thought reasoning under graph structural constraints, thereby enhancing their ability to model knowledge graphs and improving the reliability of reasoning outputs. Extensive experiments conducted on three standard datasets—namely FB15K-237, WN18RR, and UMLS—show that GLR substantially advances the performance boundaries of LLMs in KGC tasks, particularly in terms of structural awareness, multi-hop reasoning, and confidence-based output modeling.

Specifically, the Graph-CoT prompting strategy strengthens the model’s capacity to capture multi-hop structural patterns; the LoRA-based fine-tuning mechanism significantly reduces the cost of parameter updates; and the P(True) confidence evaluation method improves both the controllability and credibility of the predictions. Beyond performance improvements, GLR also contributes a novel framework that unifies structural reasoning, parameter-efficient tuning, and confidence estimation, thereby shifting the paradigm from naive generative querying to structure-guided knowledge selection in LLM-based KGC. This paradigm shift provides a scalable and generalizable foundation for future research on knowledge reasoning with LLMs.

On the aforementioned datasets, GLR achieves MRR scores of 0.679 on WN18RR, 0.507 on FB15K-237, and 0.804 on UMLS, significantly outperforming state-of-the-art baselines. Ablation studies further validate the contribution of each component. For example, removing the Graph-CoT module results in a 10.4% drop in MRR, highlighting its critical role in structural reasoning. Moreover, when comparing GLR-augmented models with their base LLM counterparts, GLR consistently outperforms them across all evaluation metrics, achieving MRR improvements of 28.3% on WN18RR, 24.5% on FB15K-237, and 37.9% on UMLS over the strongest competing baselines. Cross-comparative experiments under different model sizes and training configurations also demonstrate that GLR exhibits favorable sample efficiency, making it suitable for practical deployment in real-world scenarios.

From an application perspective, GLR is particularly well-suited for domains such as healthcare and finance, where structural consistency and knowledge accuracy are essential. It supports tasks including complex entity recognition, relation discovery, and high-reliability knowledge generation. Nevertheless, in ultra-large-scale knowledge graphs such as Wikidata, where relation distributions are severely imbalanced or graph structures are extremely sparse, GLR may face challenges including insufficient graph context, prompt length constraints, and reduced reasoning efficiency, all of which can impair its generalization performance.

In future research, we aim to explore the integration of continuous KG embeddings into the Graph-CoT prompting paradigm, with the objective of unifying symbolic reasoning and vector-based representation learning, as well as investigating how to construct more effective reasoning paradigms. Moreover, extending GLR to support multi-modal KGs and open-domain scenarios presents an exciting direction for future research.