Abstract
Probabilistic analysis of overtopping is an important aspect of dam construction, and the uncertainty in the construction progress complicates the calculation of overtopping probabilities. Construction progress is significantly influenced by human factors, making it difficult to assign an accurate probability distribution. Although the interval non-probabilistic reliability (INPR) method can estimate the likelihood of events with unknown probability distributions, its calculation results for the overtopping probability have significant errors. To improve the rationality of the results, we developed a method that adopted flood frequency of the upstream flood level to correct the traditional INPR calculations, developing an improved model. Taking the Qianping Reservoir as an example, the overtopping probabilities for three construction schedules were calculated, and the results were compared with a flood routing calculation. The results indicated that the improved approach significantly improves the rationality of the calculations, and the results effectively reflected the impact of construction progress uncertainty on overtopping probabilities.
1. Introduction
Dams can generate significant economic and social benefits in flood control, power generation, water supply, irrigation, and other aspects [1,2,3]. Although the construction technology and management level of dams are improving, with increasingly frequent extreme weather conditions, dams around the world are facing unprecedented risks, such as flooding, seepage in the dam foundation [4], and cracks in the dam body [5]. Among many dam types, earth–rock dams have been widely used due to their good economics and strong applicability [6], accounting for approximately 80% of all dams worldwide [7]. However, their ability to resist flood overtopping is relatively low, and overtopping often leads to dam collapse. Therefore, overtopping is the main cause of dam failures for earth–rock dams [8,9]. The various indicators of dams during construction have not yet met the design requirements, further reducing their ability to resist floods. Since 1930, half of the failures of earth–rock dams over 30 m and most of the related deaths have been caused by overtopping during construction [10]. Therefore, establishing an accurate and reasonable probability calculation model for overtopping during the construction period of dams has always been a concern for researchers.
During the construction period, there is a great deal of uncertainty in the factors affecting the overtopping of dams, and uncertainty analysis typically employs probability methods [11]. H. Marengo and M. ASCE considered the probability of dam overtopping during the construction period under the influence of uncertainty in the upstream inflow and discharge capacity and compared the effects of different lining materials in diversion tunnels on the overtopping probability [12]. Humberto Marengo et al. used a first-order second moment approach to calculate the influence of uncertainty in the upstream inflow and discharge capacity on the overtopping probability during the construction period of the dam [13]. Zida Song et al. established a method for calculating the overtopping probability during the construction period of dams considering uncertainty in sediment, hydrology, and hydraulics, particularly for sediment-rich rivers [14]. Lian Liu et al. used the Monte-Carlo method to establish a risk model for diversion during the late stage of dam construction considering hydrological and hydraulic uncertainties and calculated the late-stage diversion overtopping probability for different reservoir operation schemes [15].
The above study focuses on the impact of the uncertainty of upstream inflow (hydrological uncertainty) and discharge capacity (hydraulic uncertainty) on the probability of dam overtopping during the construction period, while the elevation of the top of the dam structures is a fixed value. In actual engineering, the elevation of the top of the dam structures also has uncertainty due to the influence of construction progress uncertainty, which in turn affects the probability of dam overtopping during the construction period. To consider the uncertainty of construction progress, a common method is to assign it a certain probability distribution [16,17]. However, the random parameters of construction progress are subjective, and there are certain difficulties in parameter calculation [18]. The reason for this is that there are many factors influencing construction progress, such as meteorological factors, geological factors, and human factors. Among them, human factors such as construction organization design and construction management have a greater impact on construction progress. Therefore, although construction progress is uncertain, it does not have strict randomness and cannot be simply described by a random probability distribution [19].
In many engineering projects, it is often difficult to obtain precise probability data for uncertain factors [20], but the magnitude or boundaries of uncertainty are easy to determine [21]. Based on this, Professor Ben-Haim proposed a non-probabilistic reliability (NPR) calculation model based on convex set theory in the mid-1990s and systematically established the concept and theoretical system of NPR [22]. The probability distribution of construction progress of dams is difficult to accurately and reasonably describe, but the range of dam crest elevation in a certain period is easy to determine. Therefore, based on the NPR model, this study combined with the characteristics of the construction period of dams to establish a model for the analysis of the probability of dam overtopping during the construction period under the influence of construction progress.
2. Materials and Methods
2.1. Project Overview
The total storage capacity of the Qianping Reservoir is 584 million cubic meters. The main dam is an earth–rock dam. The bottom elevation of the dam is 332.8 m, the top elevation is 423.1 m, and the designed elevation of the cofferdam is 374.4 m. The average annual rainfall in the area where the dam site is located is approximately 761.7 mm. The annual runoff statistics at the dam site are shown in Table 1. Based on the scale of the reservoir, the design flood standard is a return period of 500 years, and the check flood standard is a return period of 5000 years. The construction site is shown in Figure 1.

Table 1.
Statistical results of annual runoff at the dam site.

Figure 1.
The construction site of Qianping Reservoir.
2.2. Definition of Overtopping Probability
During the construction of a dam, upstream water flows into the downstream river through diversion structures. Generally, when the upstream flood level reaches or exceeds the top of the water-retaining building, overtopping will occur, and thus the conditions of overtopping accidents during the construction of dams can be expressed as Equation (1).
where Z is the upstream flood level, and H is the elevation of the top of the water-retaining building.
The use of accident probability to measure the level of flood safety is a common method used in the design and management of dam projects [18]. Therefore, this paper adopts the overtopping probability to quantify the possibility of overtopping during the construction period of dams. The definition of the probability of overtopping during the construction period of dams is shown in Equation (2).
where Pf is the overtopping probability of the dam; Z(t) and H(t) are the upstream flood level and the elevation of the top of the water-retaining building at time t, respectively.
2.3. INPR Theory
2.3.1. Traditional INPR Theory
The convex set model characterizes the uncertainty of parameters by a bounded convex set. NPR models, based on the convex set model, primarily include the interval and ellipsoid models, as shown in Figure 2. Among them, the interval model based on interval mathematics is a general method [23].
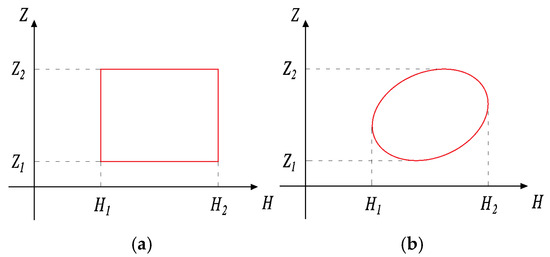
Figure 2.
Interval (a) and ellipsoid (b) models.
Currently, the area method is the primary approach for INPR [24,25,26]. This method represents the interference relationship between stress (upstream flood level Z) and strength (elevation of the top of the water-retaining structure H) on a two-dimensional variable space by using a failure surface to divide the interval variables into a safe domain and a failure domain [27,28], as shown in Figure 3. The limit state function of the overtopping event during the construction period of dams is G = Z − H. When G is less than 0, the system is safe, when G is greater than 0, the system fails, and when G equals 0, the system is in a critical state. Therefore, for the overtopping event during the construction period of dams, when G equals 0, it is the limit state of the system, and at this time Z = H is the failure surface. The area above the failure surface where G is greater than 0 is called the failure area, and the area below the failure surface where G is less than 0 is called the safe area.
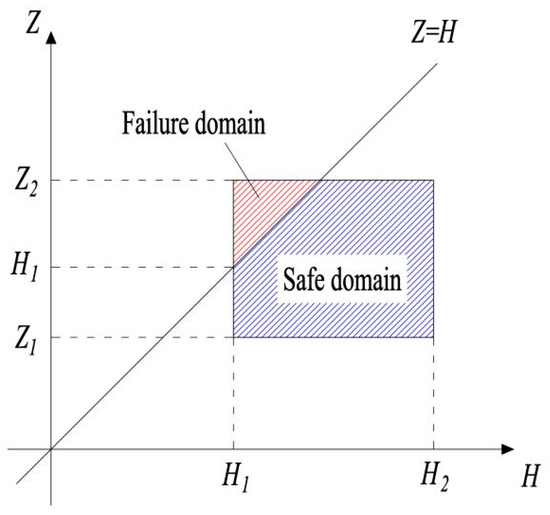
Figure 3.
Spatial schematic diagram of the stress–strength interference model of overtopping accidents.
In Figure 3, [Z1, Z2] is the range of upstream flood level Z, and [H1, H2] is the range of top elevation H of the water-retaining structure. The ratio of the area SF of the failure domain to the total area ST of the basic variable domain is used as the probability of overtopping during the construction period of dams [27,28], as shown in Equation (3).
2.3.2. Improved INPR Calculation Method
If there is probability density information, it should be fully utilized to derive probabilistic reliability [29]. For the overtopping event during the construction period of dams, the probability density of the top elevation of the water-retaining structure under the influence of construction progress is unknown. For the upstream flood level, different flood frequencies (which are the reciprocals of flood return period) correspond to different upstream flood level Z, and there is certain probability density information associated with them. Therefore, it is necessary to make full use of this information to improve the rationality of the calculation results.
To reflect the influence of flood frequency on the probability of overtopping during the construction period of dams, this study couples the upstream flood frequency with the stress–strength interference model. The upstream flood level is differentiated within the range [Z1, Z2], denoted as dz. Then, the flood frequency, failure domain area, and basic variable domain area corresponding to any flood level Z are f(Z), Lf (Z)dz, and (H2 − H1)dz, respectively. Lf (Z) and H2 − H1 represent the failure domain width and the basic variable domain width corresponding to the upstream flood level Z, respectively, as shown in Figure 4.
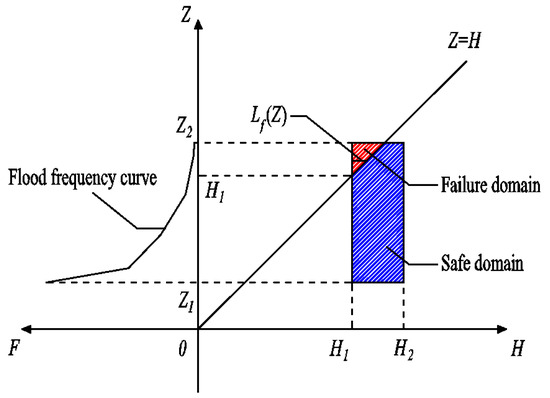
Figure 4.
Schematic diagram of the coupling model of flood frequency and stress–strength interference.
The traditional INPR neglects the differences in flood frequency within the interval [Z1, Z2]. Therefore, flood frequency of the upstream flood level f(Z) is used to modify the failure domain area and the basic variable domain area, and integration is performed over the interval [Z1, Z2]. The improved probability of overtopping during the construction period of dams is shown in Equation (4).
The geometric significance of the frequency of floods and the stress–strength interference coupling model is as follows: in the three-dimensional variable space with H, F, and Z as coordinate axes, the plane Z = H divides the frequency of floods and the stress–strength interference coupling model into the safe domain and the failure domain, as shown in Figure 5a. The ratio of the volume of the failure domain to the total volume of the basic variable domain is used as the probability of overtopping during the construction period of dams. Specifically, when the elevation of the dam’s crest is a constant value, i.e., H1 = H2, the spatial diagram of flood frequency of the upstream flood level and the stress–strength interference coupling model is shown in Figure 5b, where the line represents the flood frequency curve of the upstream flood level. Therefore, the probability of the elevation H1 corresponding to the flashover is the area above elevation H1 in the red region, and the corresponding probability of overtopping is shown in Equation (5).
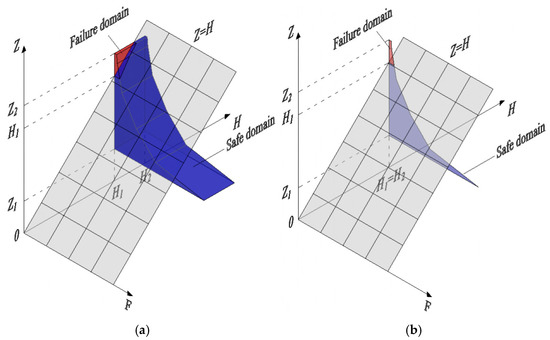
Figure 5.
Spatial schematic diagram of the coupled model of flood frequency and stress–strength interference: (a) H1 ≠ H2; (b) H1 = H2.
3. Results
3.1. Quantitative Analysis of Z and H
3.1.1. Upstream Water Level Range Z
Under current technological conditions, it is difficult to accurately forecast hydrological events exceeding one year [30]. Therefore, the upstream water level range Z needs to be discussed and determined in conjunction with engineering realities and the calculation requirements of INPR models. For the lower limit of the upstream water level range, the minimum value of the annual flood season upstream water level during the construction period is taken, corresponding to the elevation of the once-in-a-year flood in the flood season. Regarding the upper limit of the upstream water level range, in actual engineering, overflow occurs when the upstream water level exceeds the elevation of the top of the damming structure, which constrains the upstream water level. However, INPR methods require knowledge of the maximum height that the upstream water level might reach. Therefore, assuming that the diversion and drainage structures remain consistent with the design, and the elevation of the top of the damming structure is consistently higher than the upstream water level, the upper limit of the range of upstream floodwater levels that can be reached during upstream flooding is denoted as Z.
The “Standard for Rank Classification and Flood Protection Criteria of Water and Hydropower Projects (SL 252-2017)” [31] in China stipulates that the maximum flood standard for the construction period of dams is a 5000 to 10,000-year return period. The corresponding water level of the flood with a return period of 5000 years or 10,000 years is taken as the upper limit of the upstream water level range, with confidence levels of 99.98% and 99.99% for the two intervals. For the interval values of indicators in engineering problems, the Pauta criterion, known as the “3σ” criterion, is commonly used to determine if the observed values exceed the limit [32]. For variables following a normal distribution, the confidence level of the data range satisfying the “3σ” criterion (μ − 3σ, μ + 3σ) is 99.74% [33]. The confidence level of the upper limit of the upstream water level range for the construction period of dams, based on the water level corresponding to the flood with a return period of 5000 or 10,000 years, exceeds 99.74%; hence, it is considered reasonable. In many small and medium-sized basins in China, hydrological stations have relatively short operating periods, limited hydrological data, and a lack of long-term flood observation samples [34]. Therefore, the water level corresponding to the flood with a return period of 5000 years is used as the upper limit of the upstream water level range.
Based on the upstream flood hydrograph of the Qianping Reservoir dam site, the relationship between the reservoir water level and surface area, the discharge capacity of the diversion and spillway structures, and the upstream water level and its flood frequency during the construction period of flood season of the Qianping Reservoir dam are calculated, as shown in Table 2. According to the data in Table 2, the upstream water level range is Z = [344.12, 416.67].

Table 2.
Flood frequency and upstream flood water level of the Qianping reservoir during the construction period.
3.1.2. The Range of Top Elevation of the Water-Retaining Structure H
During the design phase of the Qianping Reservoir, based on the actual engineering conditions and in accordance with relevant requirements such as the “Specifications for Construction Planning of Water Resources and Hydropower Projects (SL 303-2017)” [35] of China, three construction progress plans were formulated for comparison and selection. The planned elevations before each flood season during the construction period are determined. Taking into account factors such as construction intensity, current construction technology, mechanical failure rate, material yard distribution, road traffic, variations in work area, and local precipitation patterns for each schedule, and leveraging expert experience, the interval elevations for each schedule are determined as shown in Figure 6. Among them, schedule 1 in Figure 6a is the conventional one, which conforms to the average advanced level of current construction technology; schedule 2 in Figure 6b is the slower-paced one; and schedule 3 in Figure 6c is the more aggressive one.
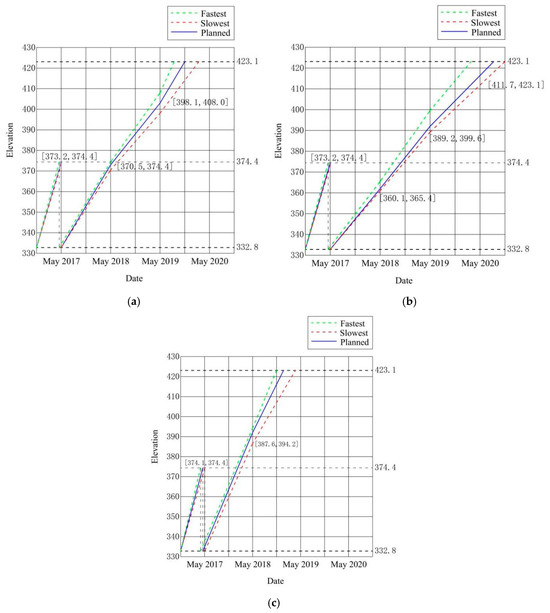
Figure 6.
Construction schedules for Qianping Reservoir: (a) schedule 1; (b) schedule 2; (c) schedule 3.
The flood season of Qianping Reservoir is from May to September each year, with the main flood season occurring from 25 June to 15 August. Therefore, the elevation range (H1, H2) of the water-retaining structure during the flood season is determined based on the elevation range of the dam/weir by the end of May. The three construction schedules all aim to have the top elevation of the cofferdam reach 374.4 m by the end of May 2017 (before the flood season). Therefore, the elevation range of the retaining structure (H1, H2) before the flood season in 2017 is taken as the elevation range of the cofferdam top. In the 2018 flood season, the water-retaining structure elevation range H varied depending on the construction progress. For example, both schedule 1 and schedule 2 were constructed under the protection of cofferdams, and, at this time, the top elevation of the cofferdam had reached 374.4 m, meaning that at this point H1 = H2. However, in schedule 3, the elevation of the dam top exceeded the cofferdam elevation before the 2018 flood season, so the elevation range (H1, H2) for the water-retaining structure is taken as the dam top elevation range.
In order to measure the likelihood of construction progress lagging behind during different construction schedules, the progress risk Rp is defined as shown in Equation (6). The progress risk Rp ranges from 0 to 1. When the value is from 0 to 0.5, there is a greater possibility of construction progress being ahead; when the value is from 0.5 to 1.0, there is a greater possibility of construction progress being behind.
where H0 represents the planned elevation, H1 represents the lower limit of the interval elevation, and H2 represents the upper limit of the interval elevation.
As shown in Figure 6, the elevations of the top of the water-retaining structures for the three construction schemes during each flood season are known, and the corresponding progress risks are calculated using Equation (6), with the results shown in Table 3.

Table 3.
Elevation range H of water-retaining structures and progress risk during the flood season.
3.2. Probability Calculation of Overtopping During the Construction Period
Using the improved INPR model proposed in this study, the probability of overtopping during the construction period of dams considering construction progress uncertainty is calculated and compared with the results of the traditional INPR calculation method, and the flood routing calculation method, as shown in Table 4. In the table, the flood routing calculation method calculates the probability of overtopping at the planned elevation, without considering construction progress uncertainty. The comparison of the results of the improved method and the flood routing calculation is shown in Figure 7.

Table 4.
Overtopping probability of Qianping reservoir.
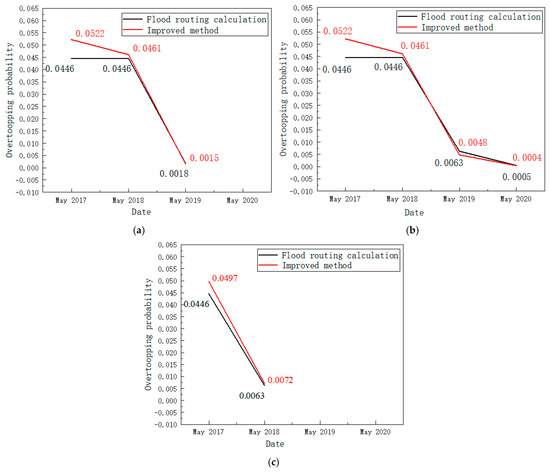
Figure 7.
Overtopping probability of Qianping reservoir: (a) schedule 1; (b) schedule 2; (c) schedule 3.
4. Discussion
- (1)
- According to the data in Table 4, the obtained probabilities are 10 times higher than flood routing calculations, with the highest ratio reaching 104 times, such as in the calculations for schedule 1 of the floods in 2019. This is because the traditional methods assume that the upstream flood levels follow a uniform distribution, neglecting the significant differences in flood frequencies corresponding to different flood levels. From Table 4 and Figure 7, it can be observed that the improved INPR model aligns well with the results obtained from flood routing calculations, demonstrating the rationality and feasibility of the proposed method in this study. Additionally, the improved method in this study considers the uncertainty of construction progress, which is more in line with the actual situation of dam construction progress being influenced by multiple factors and characterized by uncertainty.
- (2)
- There is no fixed relationship between the calculated results of the improved method proposed in this study and the results obtained from flood routing calculations. This is because the uncertainty of the construction progress affects the range of elevation values for flood retaining structures during the flood season. When the construction progress can be easily ensured, the elevation of the flood retaining structures tends to be higher than the planned elevation, and the calculated results of the improved method will be smaller than those of the flood routing calculations. When the construction progress cannot be easily ensured, the calculated results of the improved method will be higher than those of the flood routing calculations. For example, in schedule 2 during the flood season of 2019, the planned elevation for the dam crest is 392.0 m, with an elevation range of [389.2, 399.6], and the progress risk is 0.27. It is evident that the construction progress can be easily ensured; thus, the calculated result of the improved method is 0.0048, which is smaller than the flood simulation result of 0.0063.
- (3)
- Theoretically, a faster construction schedule can reduce the probability of overtopping during the flood season in dam construction. However, considering the uncertainty in the construction progress, excessive construction intensity makes it difficult to guarantee the construction schedule. For example, in schedule 3, the planned elevation during the 2018 flood season is 392.0 m, which is a fast schedule, but it increases the construction intensity. Therefore, the elevation range during the 2018 flood season is [387.6, 394.2], the progress risk is 0.67, and it is difficult to ensure the construction progress. According to the calculation results, the probability of overtopping considering the uncertainty in construction progress for schedule 3 during the 2018 flood season is 0.0072, which is higher than the probability of overtopping corresponding to the planned elevation, which is 0.0063. Therefore, the formulation of construction schedules should be in line with the average advanced level of current construction techniques in order to reduce the difficulty of construction progress control and ensure that the probability of overtopping during the construction period of the dam is not higher than the probability of overtopping corresponding to the planned elevation.
- (4)
- Comparing the calculation results of the two methods in Figure 2, the results of the improved method are not significantly different from those of the flood regulation simulation. For example, the probability calculations of the flood overtopping in 2017 for schedule 1 and schedule 2 using the improved INPR method and the flood regulation simulation method are 0.0522 and 0.0446, respectively. Although the results calculated by the two methods differ slightly, they may lead to significant deviations in the risk assessment results. For instance, assuming that the potential loss of life due to flood overtopping during the 2017 flood season was two people, and considering the dam life risk standard formulated in the “Guidelines for the Classification and Evaluation of Dam Risks” of China [36], it can be known that the two different probability results and the accident with a loss of two lives are of extremely high risk and high risk, respectively. This indicates that a small difference in probability results may lead to a significant difference in risk evaluation results. Therefore, a small change in the probability of flood overtopping should not be ignored.
- (5)
- This paper improves the traditional INPR method to enhance the rationality of the calculation results for the overtopping probability during the construction period of earth–rock dams. The purpose of this is twofold. Firstly, when the probability distribution of the construction progress is difficult to be accurately described, the influence of construction progress uncertainty on the overtopping probability is considered. The improved INPR method is proposed to make the calculation results more accurate and reasonable, providing a reference for subsequent risk decision-making and management. Secondly, this study expands the application scope of non-probabilistic reliability theory. It is not to replace the probabilistic reliability theory but to make it better serve as a supplement to the probabilistic reliability theory.
5. Conclusions
The probability of overtopping during the construction period of a dam is influenced by the uncertainty of construction progress, making it more challenging to calculate. The traditional approach is to assign a certain probability distribution to the construction progress. However, the construction progress, being subject to human factors, is uncertain but lacks strict randomness. Therefore, the conventional probabilistic approach has certain limitations in its applicability. Although the traditional INPR method only requires parameter value ranges without precise probability distributions for the parameters, this method still exhibits significant deviations when applied to the calculation of overtopping probability in dams. This study analyzes the causes of deviations and couples the flood frequency with the stress–strength interference of traditional INPR methods, proposing an improved INPR method.
Taking the Qianping Reservoir as an example, the overtopping probabilities for three construction schedules in different flood seasons were calculated. By comparing the calculation results of different methods, the rationality of the improved method was verified. The calculation results indicated that accelerating the construction progress can reduce the probability of overtopping during the construction period of dam. However, it is difficult to ensure the construction progress, which consequently increases the probability of overtopping. To decrease the probability of overtopping during the construction period to the desired level, two aspects can be considered: (a) develop a faster construction schedule that aligns with the actual engineering conditions, providing more flexibility for the construction progress and (b) strengthen construction progress management and resource supply to reduce uncertainty in the construction progress. This method provides a new approach for the calculation of dam overtopping probability during the construction period of dams and can also be applied in the fields of dam structural design, progress optimization, risk management, and other areas.
Author Contributions
X.G.: Writing—Review and Editing and Methodology. Z.L.: Supervision and Conceptualization. W.G.: Investigation and Funding Acquisition. F.M.: Validation. Y.Z.: Data Curation. H.S.: Formal Analysis. Y.J. and J.W.: Software. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (Grant 52179144, U2243244, and 51679222), China Postdoctoral Science Foundation (Grant No. 2023M731259), Natural Science Foundation of Henan Province (Grant No. 232300421067), and Program for Science & Technology Innovation Talents in Universities of Henan Province (HASTIT) (Grant No. 22HASTIT011).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
Author Wei Ge was employed by the Yellow River Engineering Consulting Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Wang, T.; Li, Z.; Ge, W.; Zhang, Y.; Jiao, Y.; Zhang, H.; Sun, H.; Gelder, P.V. Risk assessment methods of cascade reservoir dams: A review and reflection. Nat. Hazards 2022, 115, 1601–1622. [Google Scholar] [CrossRef]
- Zhang, H.; Ge, W.; Zhang, Y.; Li, Z.; Li, W.; Zhu, J.; Wang, W. Risk Management Decision of Reservoir Dams Based on the Improved Life Quality Index. Water Resour. Manag. 2023, 37, 1223–1239. [Google Scholar] [CrossRef]
- Ge, W.; Qin, Y.; Li, Z.; Zhang, H.; Gao, W.; Guo, X.; Song, Z.; Li, W.; Gelder, P.V. An innovative methodology for establishing societal life risk criteria for dams: A case study to reservoir dam failure events in China. Int. J. Disaster Risk Reduct. 2020, 49, 101663. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Z.; Gu, C.; Li, Y.; Zhang, K.; Xie, M. A Coupled Model for Dam Foundation Seepage Behavior Monitoring and Forecasting Based on Variational Mode Decomposition and Improved Temporal Convolutional Network. Struct. Control Health Monit. 2023, 2023, 3879096. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, H. Automatic Damage Detection and Diagnosis for Hydraulic Structures Using Drones and Artificial Intelligence Techniques. Remote Sens. 2023, 15, 615. [Google Scholar] [CrossRef]
- Chen, Z.; Yin, Y.; Yu, J.; Cheng, X.; Zhang, D.; Li, Q. Internal deformation monitoring for earth-rockfill dam via high-precision flexible pipeline measurements. Autom. Constr. 2022, 136, 104177. [Google Scholar] [CrossRef]
- Taskaya, E.; Bombar, G.; Tayfur, G. Experimental investigation of sediment movement as a result of homogeneous earth-fill dam overtopping break over a simplified urban area. J. Hydrol. 2023, 617, 128924. [Google Scholar] [CrossRef]
- Wang, T.; Li, Z.; Ge, W.; Zhang, H.; Zhang, Y.; Sun, H.; Jiao, Y. Risk consequence assessment of dam breach in cascade reservoirs considering risk transmission and superposition. Energy 2023, 265, 126315. [Google Scholar] [CrossRef]
- Amaral, S.; Caldeira, L.; Viseu, T.; Ferreira, R.M.L. Designing Experiments to Study Dam Breach Hydraulic Phenomena. J. Hydraul. Eng. 2020, 146, 04020014. [Google Scholar] [CrossRef]
- Lempérière, F. Dams and Floods. Engineering 2017, 3, 144–149. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L. A novel interval dynamic topology optimization methodology of piezoelectric structures under reliable active control. Comput. Methods Appl. Mech. Eng. 2024, 421, 116766. [Google Scholar] [CrossRef]
- Hmarengo, M. Case Study: Dam Safety during Construction, Lessons of the Overtopping Diversion Works at Aguamilpa Dam. J. Hydraul. Eng. 2006, 132, 1121–1127. [Google Scholar] [CrossRef]
- Marengo, H.; Arreguin, F.I.; Aldama, A.A.; Morales, V. Case study: Risk analysis by overtopping of diversion works during dam construction: The La Yesca hydroelectric project, Mexico. Struct. Saf. 2013, 42, 26–34. [Google Scholar] [CrossRef]
- Song, Z.; Liu, Q.; Hu, Z.; Li, H.; Xiong, J. Assessment of Sediment Impact on the Risk of River Diversion during Dam Construction: A Simulation-Based Project Study on the Jing River, China. Water 2018, 10, 217. [Google Scholar] [CrossRef]
- Liu, L.; Bricker, J.D.; Hu, C. Late-stage diversion risk assessment for high dams considering early initial impoundment: A case study of Lianghekou Station, China. Front. Earth Sci. 2023, 11, 1232481. [Google Scholar] [CrossRef]
- Hosseinian, S.M.; Arjomand, A.; Li, C.Q.; Zhang, G. Developing a Model for Assessing Project Completion Time Reliability during Construction Using Time-Dependent Reliability Theory. J. Constr. Eng. Manag. 2022, 148, 04022006. [Google Scholar] [CrossRef]
- Li, C.; Zhang, G.; Hosseinian, M. A fast and Accurate Method to Predict Reliability of Project Completion Time. J. Civ. Eng. Manag. 2016, 23, 37–46. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, Z. Risk model of flow diversion in the initial through middle stages for high arch dam construction and its application. Adv. Water Sci. 2019, 30, 102–111. [Google Scholar]
- Beer, M.; Ferson, S.; Kreinovich, V. Imprecise probabilities in engineering analyses. Mech. Syst. Signal Process. 2013, 37, 4–29. [Google Scholar] [CrossRef]
- Jiang, C.; Ni, B.; Han, X.; Tao, Y. Non-probabilistic convex model process: A new method of time-variant uncertainty analysis and its application to structural dynamic reliability problems. Comput. Methods Appl. Mech. Eng. 2014, 268, 656–676. [Google Scholar] [CrossRef]
- Yang, C.; Shi, Q. An interval perturbation method for singular value decomposition (SVD) with unknown-but-bounded (UBB) parameters. J. Comput. Appl. Math. 2024, 436, 115436. [Google Scholar] [CrossRef]
- Yakov, B. A non-probabilistic concept of reliability. Struct. Saf. 1994, 14, 227–245. [Google Scholar]
- Wang, L.; Liu, Y.; Xu, H. Review: Recent Developments in Dynamic Load Identificationfor Aerospace Vehicles Considering Multi-source Uncertainties. Trans. Nanjing Univ. Aeronaut. Astronaut. 2021, 38, 271–287. [Google Scholar]
- Wang, X.; Zhu, J.; Ni, B. Structural reliability-based design optimization with non-probabilistic credibility level. Comput. Methods Appl. Mech. Eng. 2024, 418, 116489. [Google Scholar] [CrossRef]
- Wang, L.; Liu, D.; Yang, Y.; Wang, X.; Qiu, Z. A novel method of non-probabilistic reliability-based topology optimization corresponding to continuum structures with unknown but bounded uncertainties. Comput. Methods Appl. Mech. Eng. 2017, 326, 573–595. [Google Scholar] [CrossRef]
- Xin, T.; Zhao, J.; Cui, C.; Duan, Y. A non-probabilistic time-variant method for structural reliability analysis. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2020, 234, 664–675. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Wang, L.; Fan, W.; Qiu, Z. Non-probabilistic stability reliability measure for active vibration control system with interval parameters. J. Sound Vib. 2017, 387, 1–15. [Google Scholar] [CrossRef]
- Chen, Q.; Ma, H.; Yu, J.; Fei, Q. A modified interval perturbation statistical energy analysis method for structural reliability analysis of vibro-acoustic systems with interval uncertain parameters. Structures 2024, 60, 105902. [Google Scholar] [CrossRef]
- Wang, X.; Qiu, Z.; Elishakoff, I. Non-probabilistic set-theoretic model for structural safety measure. Acta Mech. 2008, 198, 51–64. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, C.; Tian, Y.; Li, Y.; Chen, Z.; Chen, X. Research progresses and prospects of catchment hydrological forecasting driven by global climate forecasts. Adv. Water Sci. 2024, 35, 156–166. [Google Scholar]
- SL 252-2017; Standard for Rank Classification and Flood Protection Criteria of Water and Hydropower Projects. China Water & Power Press: Beijing, China, 2017.
- Gui, Z.; Zhang, H.; Sun, H.; Zhang, F. Research and application of early warning model of vibration deterioration for hydroelectric-generator unit. J. Hydraul. Eng. 2018, 49, 216–222. [Google Scholar]
- Zhang, F.; Pan, L.; An, L. Study on statistical characteristics and maintenance alarm strategy for stability parameters of hydraulic turbine generator unit. J. Hydroelectr. Eng. 2013, 32, 269–272, 293. [Google Scholar]
- Jiang, C.; Xiong, L.; Huang, J.; Yang, S. A derivation method of flood frequency distribution incorporatingrainfall stochastic variable. J. Hydraul. Eng. 2023, 54, 45–53. [Google Scholar]
- SL 303-2017; Specifications for Construction Planning of Water Resources and Hydropower Projects. China Water & Power Press: Beijing, China, 2017.
- SL/T 829-2024; Ministry of Water Resources of the People’s Republic of China. Guidelines for Risk Classification and Assessment of Reservoir Dam. China Water & Electric Press: Beijing, China, 2024.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).