Remaining Useful Life Prediction of Rolling Bearings Based on an Improved U-Net and a Multi-Dimensional Hybrid Gated Attention Mechanism
Abstract
1. Introduction
2. Introduction to Related Methods
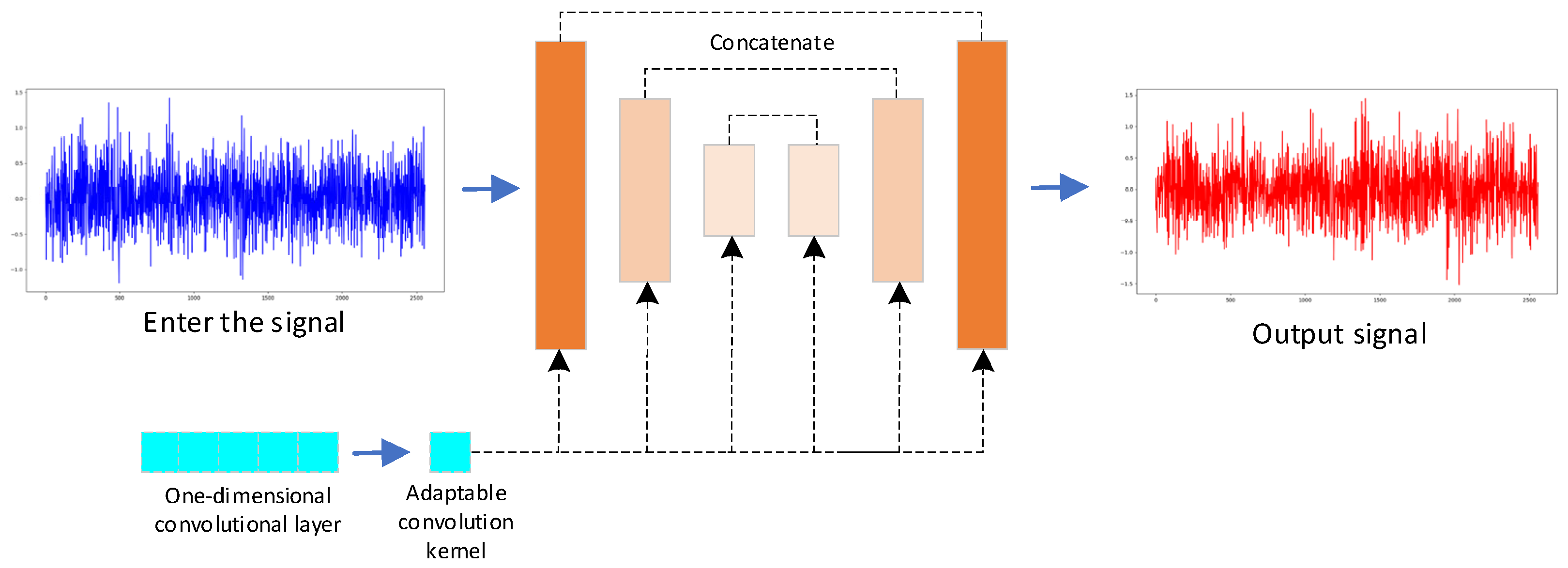
2.1. Improved U-Net Model
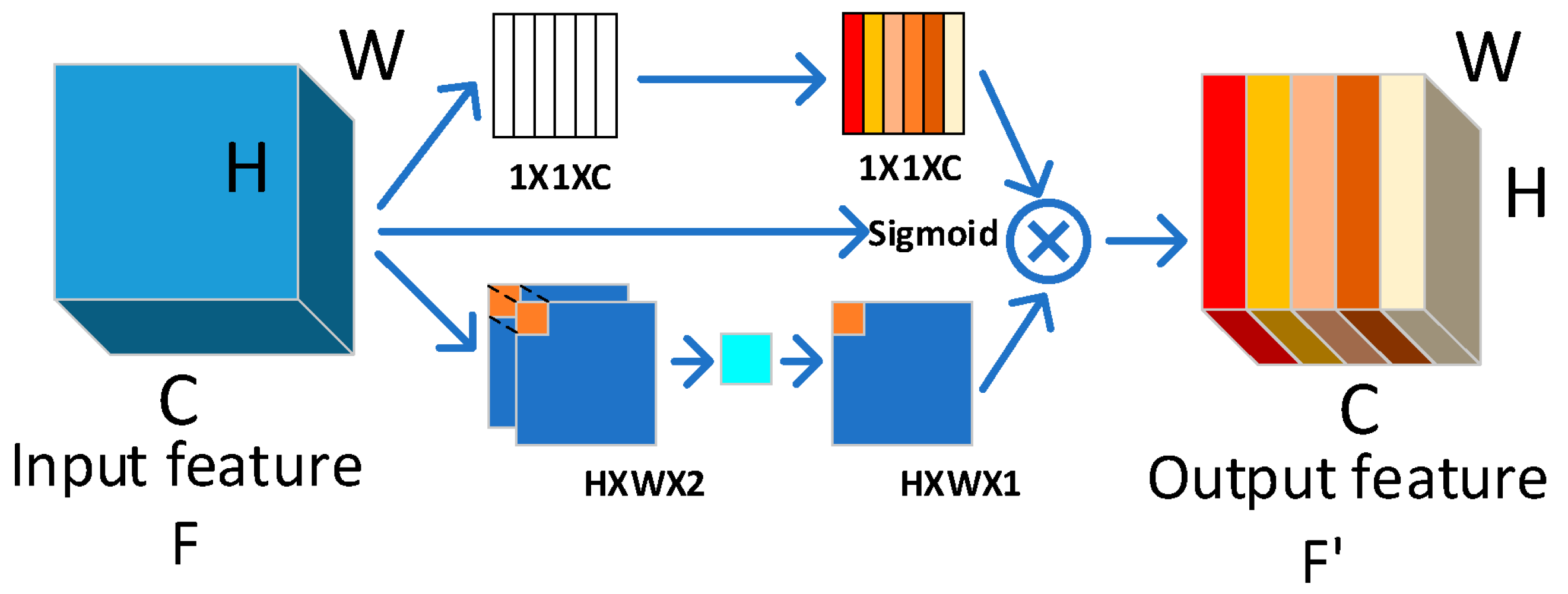
2.2. Multi-Dimensional Hybrid Gated Attention Mechanism
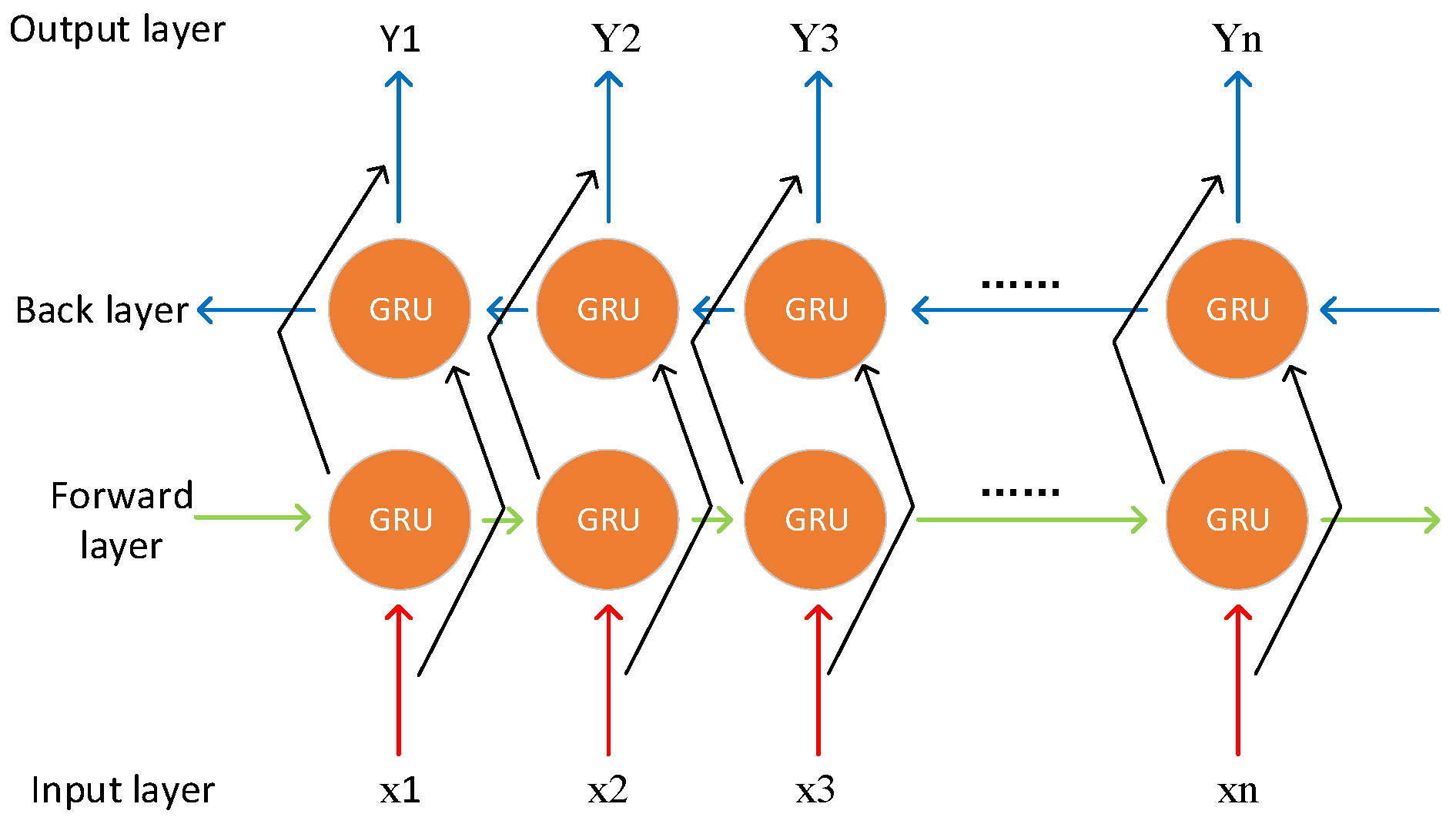
2.3. Bidirectional Gated Recurrent Unit (Bi-GRU)
- The input Xn at time step n is concatenated with the hidden state hn−1 from the previous time step n − 1, followed by a linear transformation. The result is then passed through a sigmoid function to output values within the fixed range of 0 to 1.where Xn is the input, Yn is the output, Wn represents learnable parameters, σ denotes the sigmoid activation function, Zn stands for the update gate, and ht−1 represents the hidden information from the previous time step.
- 2.
- The reset gate primarily determines how much historical information should be forgotten.where rn is the reset gate and Wr is the parameter matrix of the reset gate.
- 3.
- The reset gate is multiplied by the hidden state output Yn−1 from the previous time step n − 1. This product determines how much of the information from the previous step is retained. The result is then passed through the tanh activation function to produce the new output Yn.where Wt is a trainable weight matrix.
- 4.
- The gate value output by the update gate (1 − Zn) is multiplied by the hidden state output from the previous time step (n − 1) to determine the information to be retained. Finally, the result is added to obtain the final hidden state output Yn.The mathematical expressions for the BiGRU network architecture are as follows:where denotes forward propagation and denotes backward propagation.
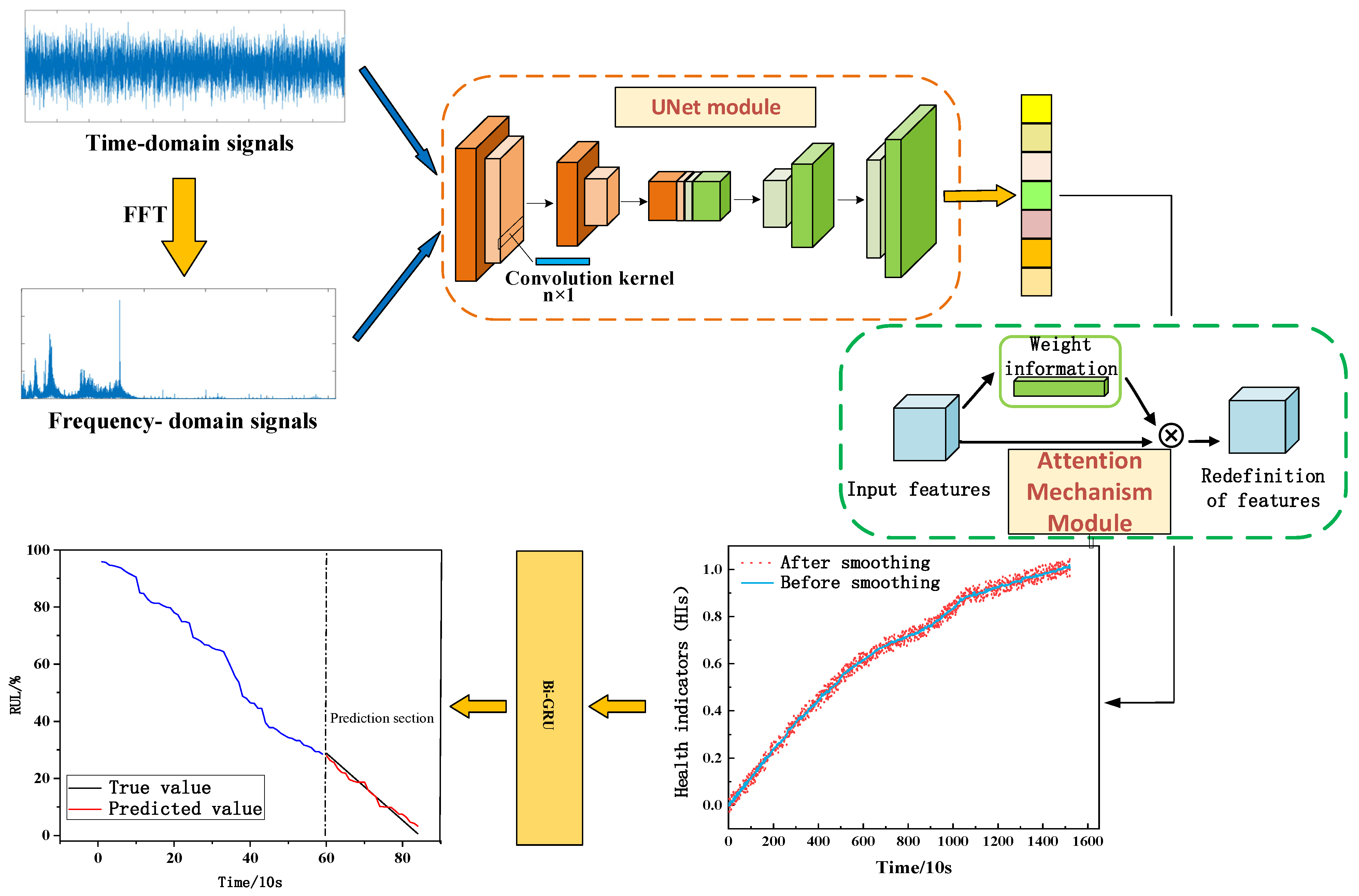
3. Rolling Bearing Remaining Useful Life (RUL) Prediction Method
3.1. Signal Preprocessing
3.2. Overall Method Process
- Data Preprocessing: The IU-Net model is utilized to process and denoise the original time-domain and frequency-domain signals. Multi-scale signal features are extracted using one-dimensional convolution and pooling, followed by deconvolution and concatenation techniques to produce the denoised signals.
- Health Indicator Construction: The processed signals are utilized to compute both time-domain and frequency-domain feature values. A multi-dimensional hybrid gated attention mechanism is implemented to generate multi-dimensional weight information, followed by feature fusion to construct the health indicator.
- RUL Prediction: This section describes the construction of an IU-Net-MHGAM-BiGRU model for predicting the remaining useful life of bearings. The health indicators, which were developed in the previous step, serve as inputs to this model to facilitate accurate RUL predictions.
3.3. Health Indicator Evaluation
3.4. Remaining Useful Life (RUL) Evaluation Metrics
4. Experimental Validation on Public Datasets
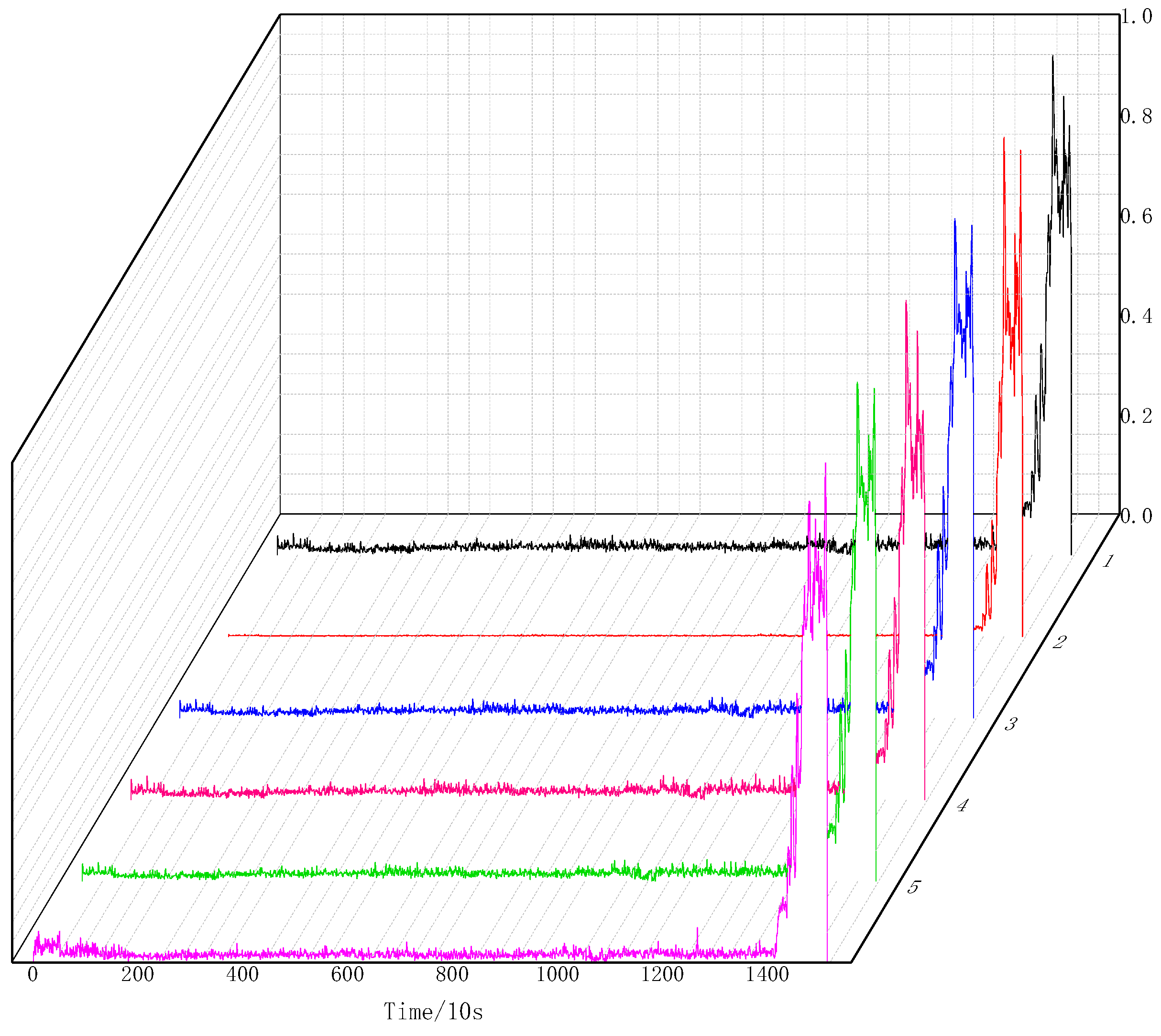
4.1. Dataset Introduction
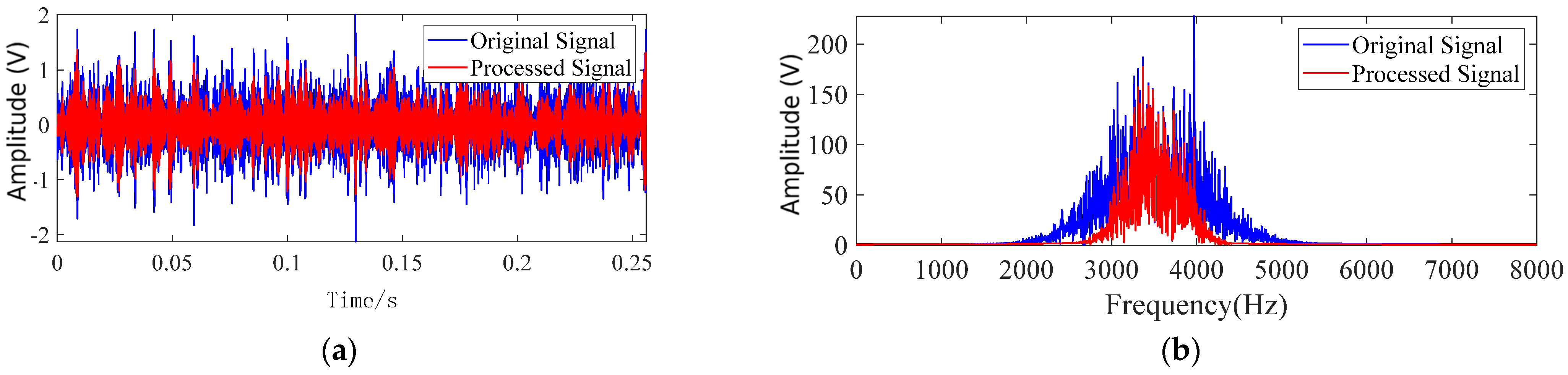
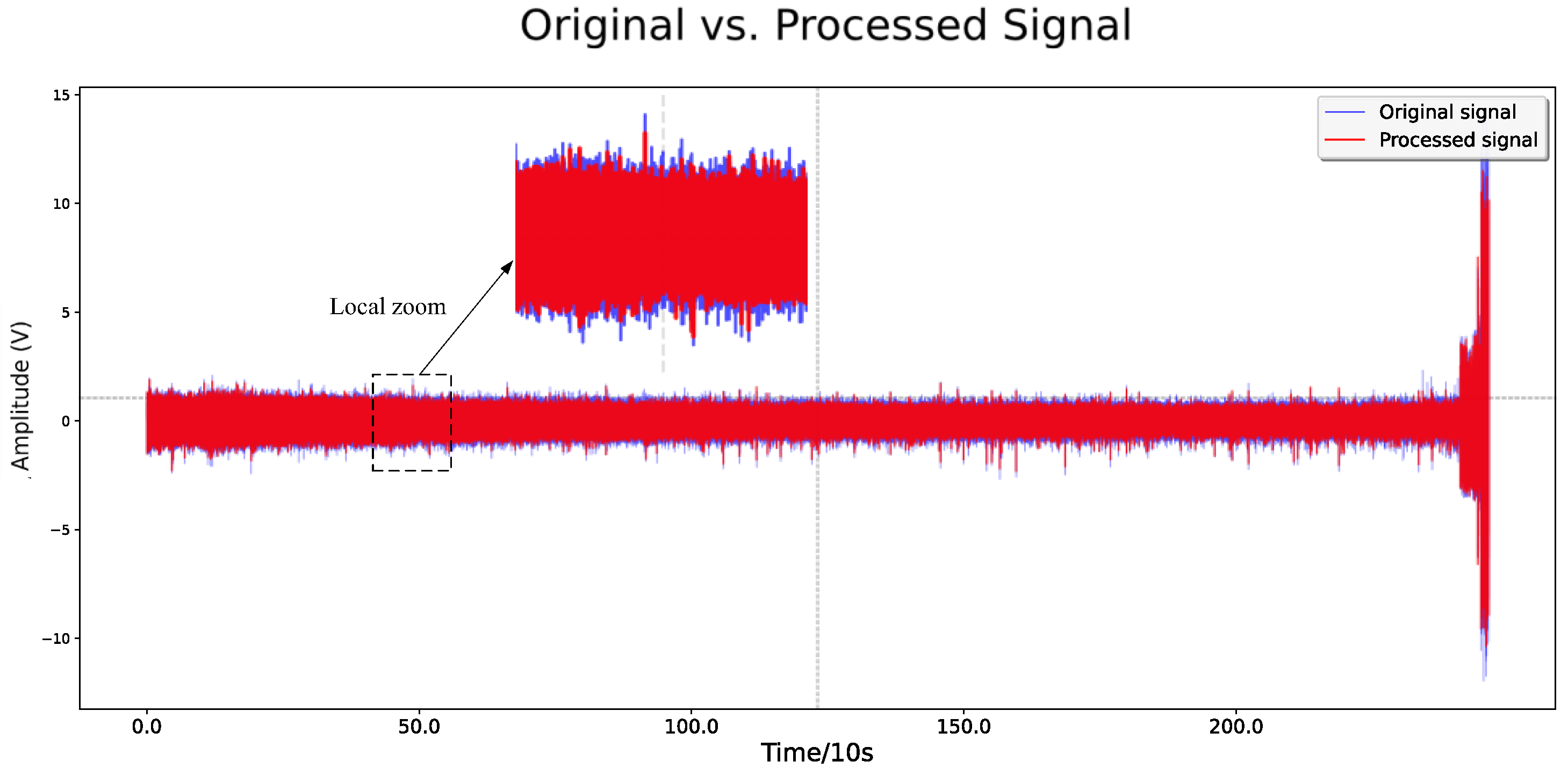
4.2. Raw Data Processing
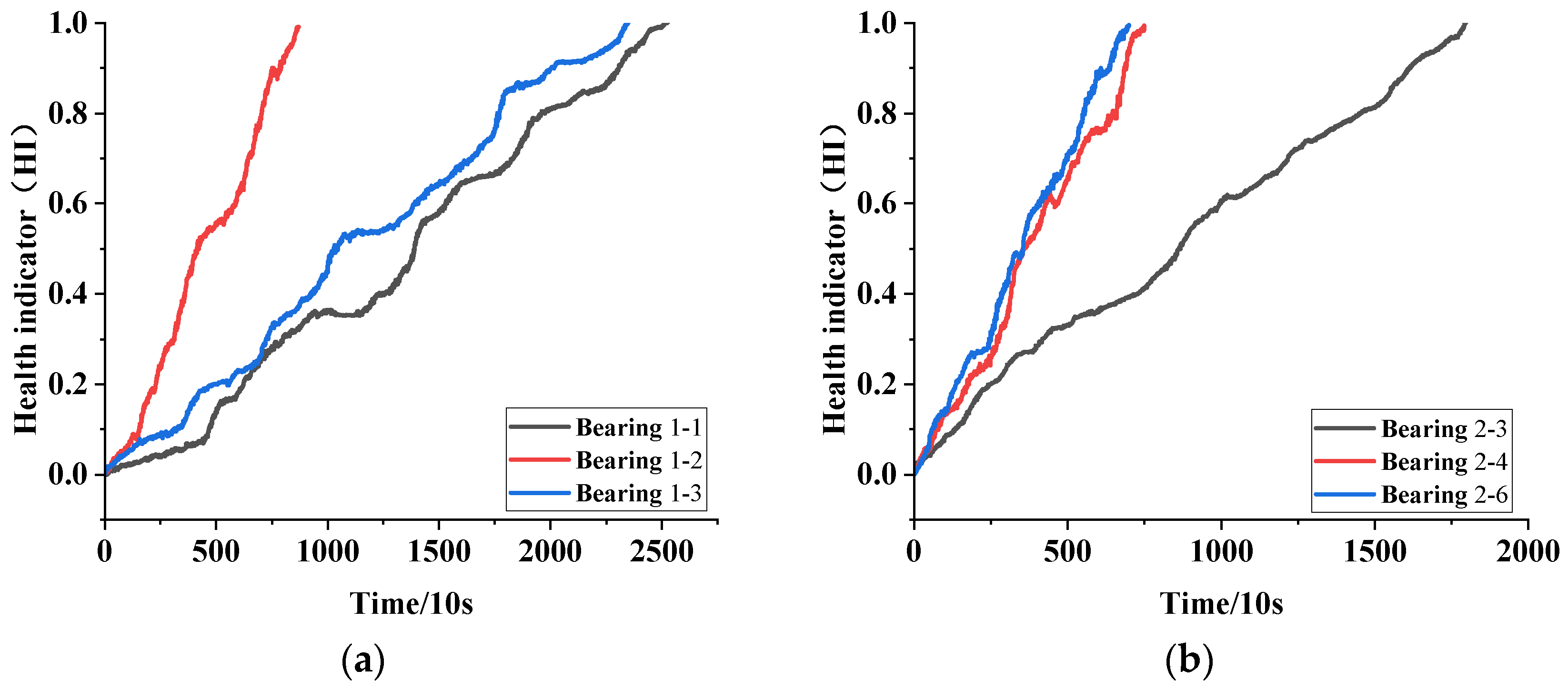
4.3. Health Indicator Construction
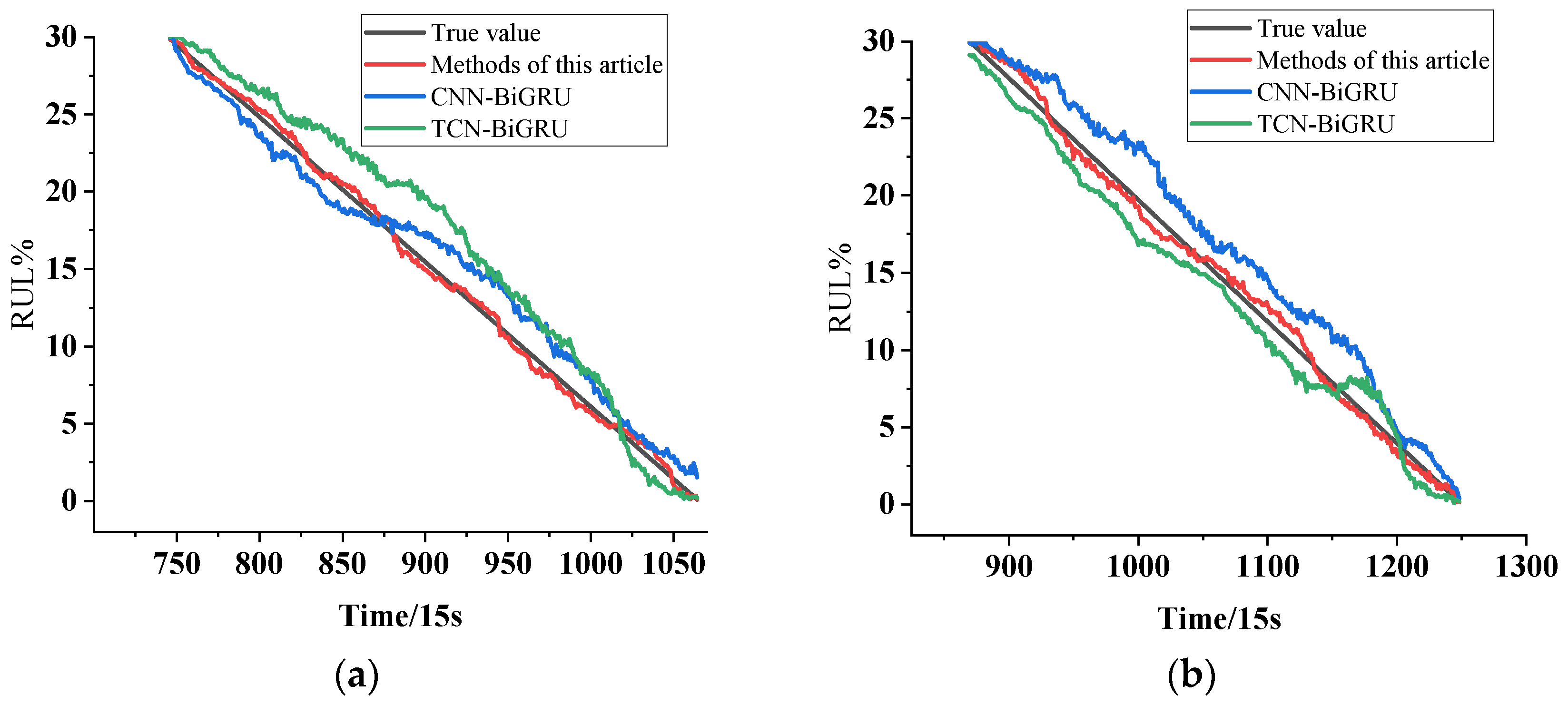
4.4. Remaining Useful Life (RUL) Prediction
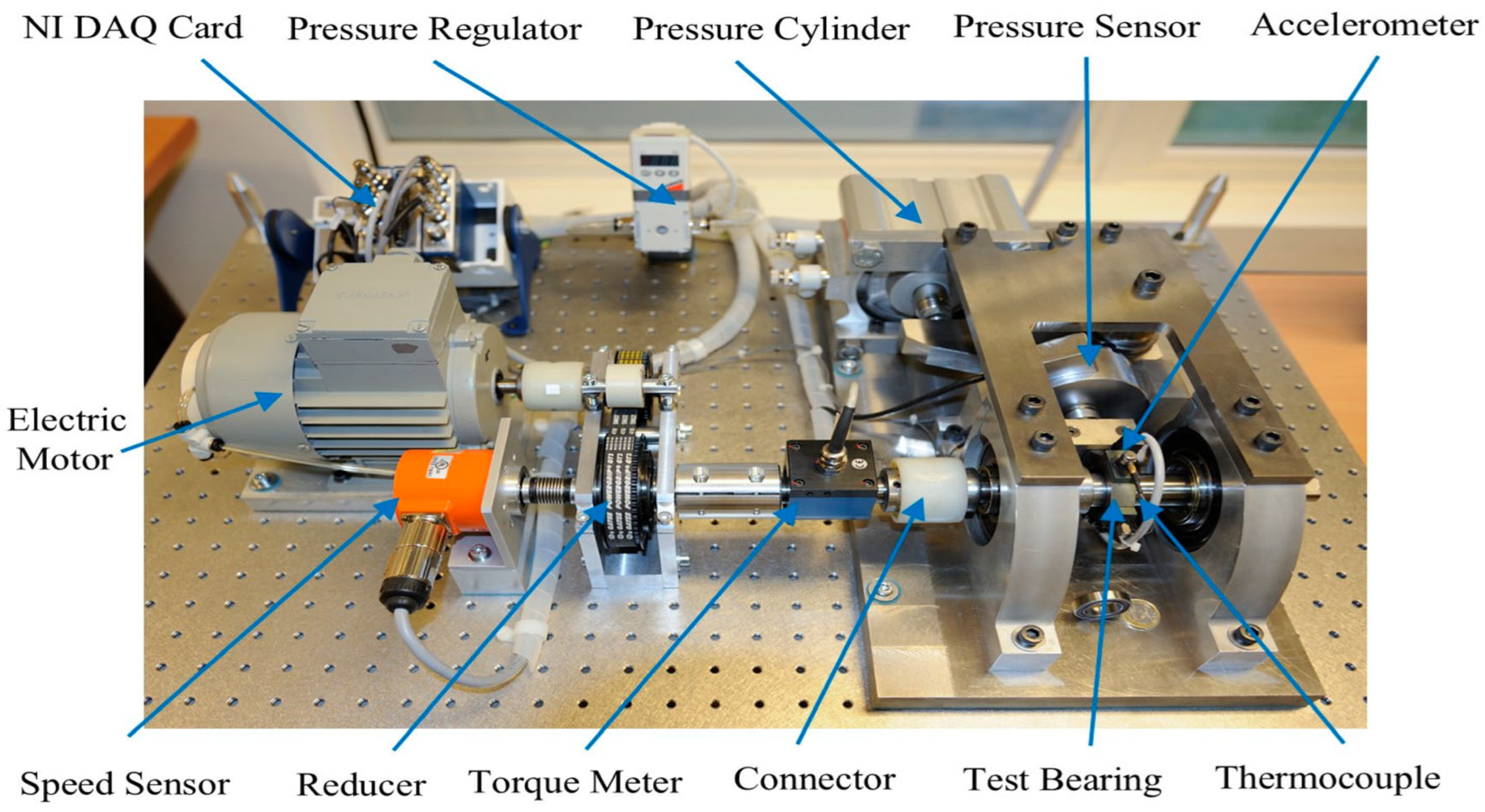
5. Engineering Test Validation
5.1. Introduction to the Test Platform
5.2. Experimental Results Analysis
6. Conclusions
- The improved U-Net model effectively removes noise from vibration signals while preserving essential detail features in the time–frequency domain, utilizing depthwise separable convolutions and residual skip connections. The processed signals demonstrate an average increase in the signal-to-noise ratio (SNR) of 23.69% and a reduction in the root mean square error (RMSE) of 27.53% when compared to the WGAN and DCGAN methods.
- The multi-dimensional hybrid gated attention mechanism (MHGAM) employs a spatial-channel parallel network architecture to dynamically allocate multi-dimensional fusion weights. This approach effectively addresses the information loss commonly encountered in traditional feature dimensionality reduction and fusion processes. The health indices generated by the proposed method show substantial enhancements in correlation, monotonicity, and robustness, thereby exhibiting superior comprehensiveness.
- Experimental validation conducted on the IEEE PHM 2012 Data Challenge dataset demonstrates that the proposed method achieves reductions of 7.8% in RMSE and 14.6% in MAE compared to the CNN-BiGRU and TCN-BiGRU benchmark models, respectively. In terms of overall prediction performance scores, the proposed method exhibits average improvements of 7.8% and 9.3 percentage points, significantly enhancing prediction accuracy.
- Validated by engineering test data, the proposed method demonstrates strong robustness and generalization capabilities under varying operating conditions, thereby providing an innovative technical approach for remaining useful life (RUL) prediction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Structured Nomenclature of the Mathematical Symbols
| Mathematical symbol | Structured nomenclature |
| Input feature tensor | |
| The number of channels for the input feature | |
| The spatial height dimensions of the feature | |
| The spatial width dimensions of the feature | |
| Eigenvectors after global average pooling | |
| Sigmoid activation function | |
| Input eigenvector for time step n | |
| A hidden state vector of the previous time step (n − 1) | |
| The output result vector for time step n | |
| Learnable parameters | |
| Reset door parameter matrix | |
| Trainable weight matrix | |
| Derivative of the feature sequence with respect to the time sequence | |
| Isolated useful signals | |
| Noise signals | |
| The i-th sample value of the real signal | |
| The i-th sample value of the processed signal |
Abbreviations
| Abbreviation | Full Form |
| RUL | remaining useful life |
| MHGAM | multi-dimensional hybrid gated attention mechanism |
| IU-Net | improved U-Net |
| SE | Squeeze-and-Excitation |
| Bi-GRU | Bidirectional Gated Recurrent Unit |
| Corr | correlation |
| Mon | monotonicity |
| Rob | robustness |
| DRSN | Deep Residual Shrinkage Network |
| RMSE | root mean square error |
| MAE | mean absolute error |
| SNR | signal-to-noise ratio |
| WGAN | Wasserstein GAN |
| DCGAN | Deep Convolutional GAN |
References
- Hamadache, M.; Jung, J.H.; Park, J.; Youn, B.D. A comprehensive review of artificial intelligence-based approaches for rolling element bearing PHM: Shallow and deep learning. JMST Adv. 2019, 1, 125–151. [Google Scholar] [CrossRef]
- Wang, J.; Xu, Z.; Liu, W.; Wang, Y.; Liu, L. Review of Research on Rolling Bearing Health Intelligent Monitoring and Fault Diagnosis Mechanism. Comput. Sci. Explor. 2024, 18, 878–898. (In Chinese) [Google Scholar]
- Shao, X.; Cai, B.; Liu, Y.; Kong, X.; Yang, C.; Fam, H.; Sun, X.; Hao, K. A Remaining Useful Life Prediction Method Based on Multi-Stage Correlation Performance Degradation. In Proceedings of the 19th China Ocean (Coastal) Engineering Academic Symposium (Volume 1); 2019-10-11(Upper Volume). Chinese Society of Ocean Engineering: Ningbo, China, 2019; pp. 349–355. [Google Scholar]
- Zeng, D.; Yang, J.; Zou, Y.; Zhang, J.; Song, X. Bearing life prediction method based on parallel mu Iti-channel convolution long short term memory network PMCCNN-LSTM. China Mech. Eng. 2020, 31, 2454–2462, 2471. [Google Scholar]
- Xia, T.; Song, Y.; Zheng, Y.; Pan, E.; Xi, L. An ensemble framework based on convolutional bi-directional LSTM with multiple time windows for remaining useful life estimation. Comput. Ind. 2019, 115, 103182. [Google Scholar] [CrossRef]
- Song, X.; Zhou, Z.; Liu, L.; Chen, K. A method for predicting the remaining service life of rolling bearings based on Transformer model. J. Beijing Univ. Aeronaut. Astronaut. 2023, 49, 430–433. [Google Scholar]
- Luo, X.; Wang, M. Bearing Lifespan Reliability Prediction Method Based on Multiscale Feature Extraction and Dual Attention Mechanism. Appl. Sci. 2025, 15, 3662. [Google Scholar] [CrossRef]
- Sun, B.; Hu, W.; Wang, H.; Wang, L.; Deng, C. Remaining Useful Life Prediction of Rolling Bearings Based on CBAM-CNN-LSTM. Sensors 2025, 25, 554. [Google Scholar] [CrossRef]
- Li, M.; Pan, N.; Duan, Y.; Cao, X. Health Index Construction and Condition Assessment of Coal Mine Rotating Machinery. Ind. Mine Autom. 2022, 48, 33–41. [Google Scholar] [CrossRef]
- Gao, X.; Wang, H.; Zhao, Z.; Tian, J.; Zhang, F.; Wang, C. Prediction of Bearing Remaining Useful Life Based on CNN and Gated Recurrent Unit. In Proceedings of the 2023 Global Reliability and Prognostics and Health Management Conference (PHM-Hangzhou), Hangzhou, China, 12–15 October 2023; IEEE: Los Alamitos, CA, USA, 2023; pp. 1–7. [Google Scholar]
- Yao, D.; Li, B.; Liu, H.; Yao, J.; Pi, Y. Remaining Useful Life Prediction for Rolling Bearings Based on Attention-Based GRU Algorithm. Vib. Shock. 2021, 40, 116–123. [Google Scholar] [CrossRef]
- Qu, Q.; Wei, Q.; Wang, Y.; Liu, Y. Remaining Useful Life Prediction of Rolling Bearings Based on Deep Time–Frequency Synergistic Memory Neural Network. Coatings 2025, 15, 406. [Google Scholar] [CrossRef]
- Mao, W.; Liu, K.; Zhang, Y.; Liang, X.; Wang, Z. Self-supervised deep tensor domain-adversarial regression adaptation for online remaining useful life prediction across machines. IEEE Trans. Instrum. Meas. 2023, 72, 2509916. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Proceedings of the 18th International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Fan, C.; Zhang, Y.; Ma, H.; Yu, K.; Ma, Z. A novel lightweight DDPM-based data augmentation method for rotating machinery fault diagnosis with small sample. Mech. Syst. Signal Process. 2025, 232, 112741. [Google Scholar] [CrossRef]
- Huang, Z.; Zhong, W.; An, R.; Wu, J.; Zhang, Z. A Novel Relay Protection Fault Diagnosis Method for Power Distribution Systems Based on Improved Attention-Gated Recurrent Unit. Tech. Autom. Appl. 2024, 1–9. Available online: http://kns.cnki.net/kcms/detail/23.1474.tp.20241223.1528.147.html (accessed on 17 May 2025).
- Lyu, Y.; Qiu, Q.; Chu, Y.; Zhang, J. An Adaptive BiGRU-ASSA-iTransformer Method for Remaining Useful Life Prediction of Bearing in Aerospace Manufacturing. Actuators 2025, 14, 238. [Google Scholar] [CrossRef]
- Xu, J.; Shen, Y. Bearing Remaining Useful Life Prediction Method Based on ARN and BiLSTM. Noise Vib. Control. 2024, 44, 136–142, 255. [Google Scholar]
- Wang, H.; Chen, P.; Zhang, W.; Wu, S.; Ma, Y. BWO-BiLSTM based staged life prediction method for rolling bearings. Bearing 2025, 1–9. Available online: http://kns.cnki.net/kcms/detail/41.1148.th.20250226.1214.010.html (accessed on 17 May 2025).
- Hodson, T. Root mean square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. Discuss. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Chebel-Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An experimental platform for bearings accelerated degradation tests. In Proceedings of the IEEE International Conference on Prognostics and Health Management, Denver, CO, USA, 18–21 June 2012. [Google Scholar]
- Li, Y.; Zou, W.; Jiang, L. Fault diagnosis of rotating machinery based on combination of Wasserstein generative adversarial networks and long short term memory fully convolutional network. Measurement 2022, 191, 110826. [Google Scholar] [CrossRef]
- Zhou, K.; Diehl, E.; Tang, J. Deep convolutional generative adversarial network with semi-supervised learning enabled physics elucidation for extended gear fault diagnosis under data limitations. Mech. Syst. Signal Process. 2023, 185, 109772. [Google Scholar] [CrossRef]
- Medjaher, K.; Zerhouni, N.; Baklouti, J. Data-driven prognostics based on health indicator construction:application to PRONOSTIA′s data. In Proceedings of the 2013 European Control Conference, Zurich, Switzerland, 17–19 July 2013; pp. 1451–1456. [Google Scholar]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-d transform-domain collaborative filtering. IEEE Trans. Image Process 2007, 16, 2080–2095. [Google Scholar] [CrossRef]
- Niu, Q.; Sui, Z.; Han, J.; Zhao, Y. An Industrial Robot Gearbox Fault Diagnosis Approach Using Multi-Scale Empirical Mode Decomposition and a One-Dimensional Convolutional Neural Network-Bidirectional Gated Recurrent Unit Method. Processes 2025, 13, 1722. [Google Scholar] [CrossRef]
- Cheng, Y.W.; Hu, K.; Wu, J.; Zhu, H.; Shao, X. A convolutional neural network based degradation indicator construction and health prognosis using bidirectional long short-term memory network for rolling bearings. Adv. Eng. Inform. 2021, 48, 101247. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, S.; Liu, J.; Ma, Y. Bearing remaining useful life prediction based on TCN-SA and Bi-GRU. Comput. Integr. Manuf. Syst. 2024, 1–11. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, C.; Li, J.; Xu, L.; Gao, F. Rolling bearing fault diagnosis method based on TCN-BiGRU-Attention. In Proceedings of the 2024 3rd International Conference on Electronics and Information Technology (EIT), Chengdu, China, 20–22 September 2024. [Google Scholar]
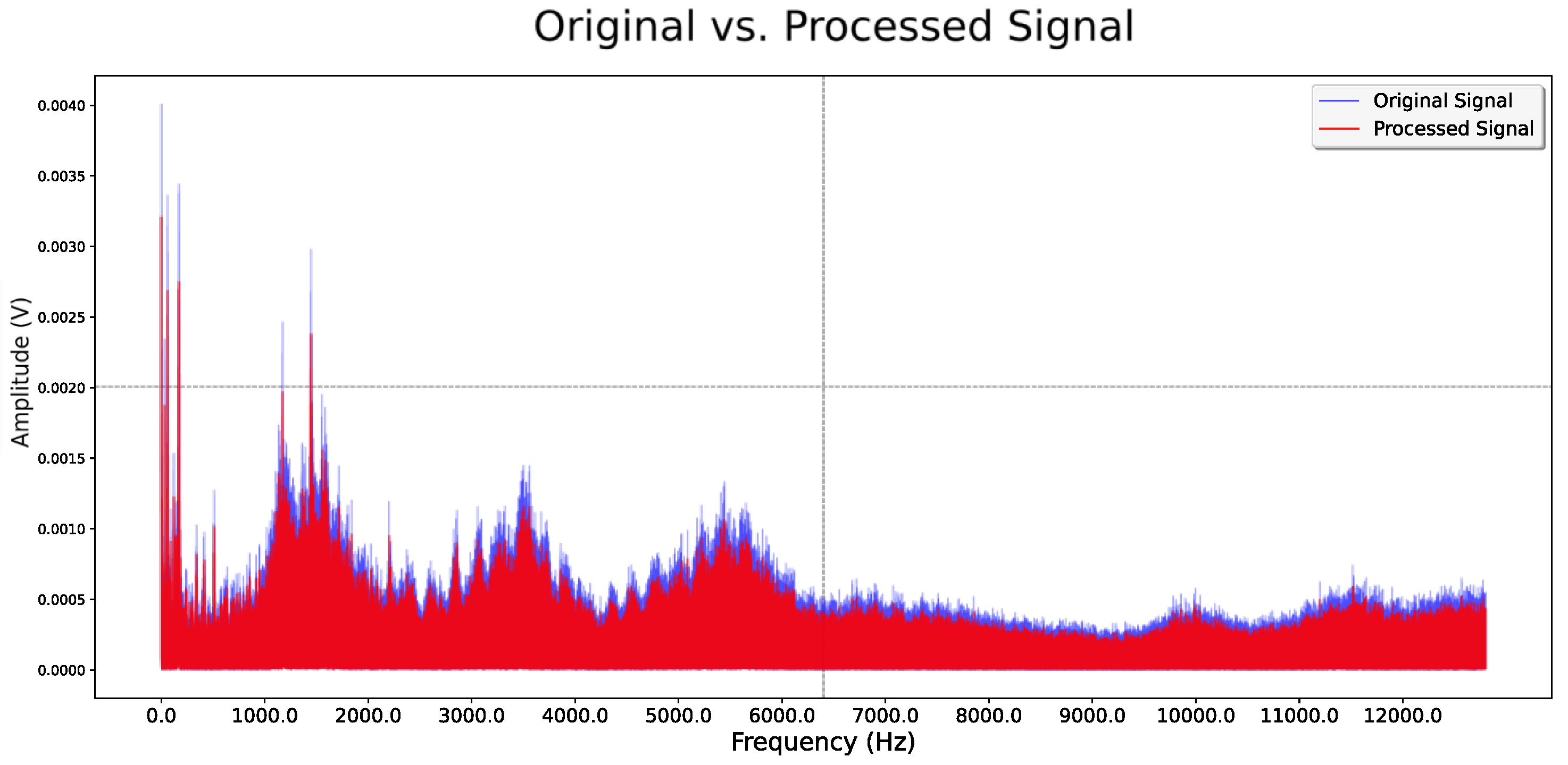
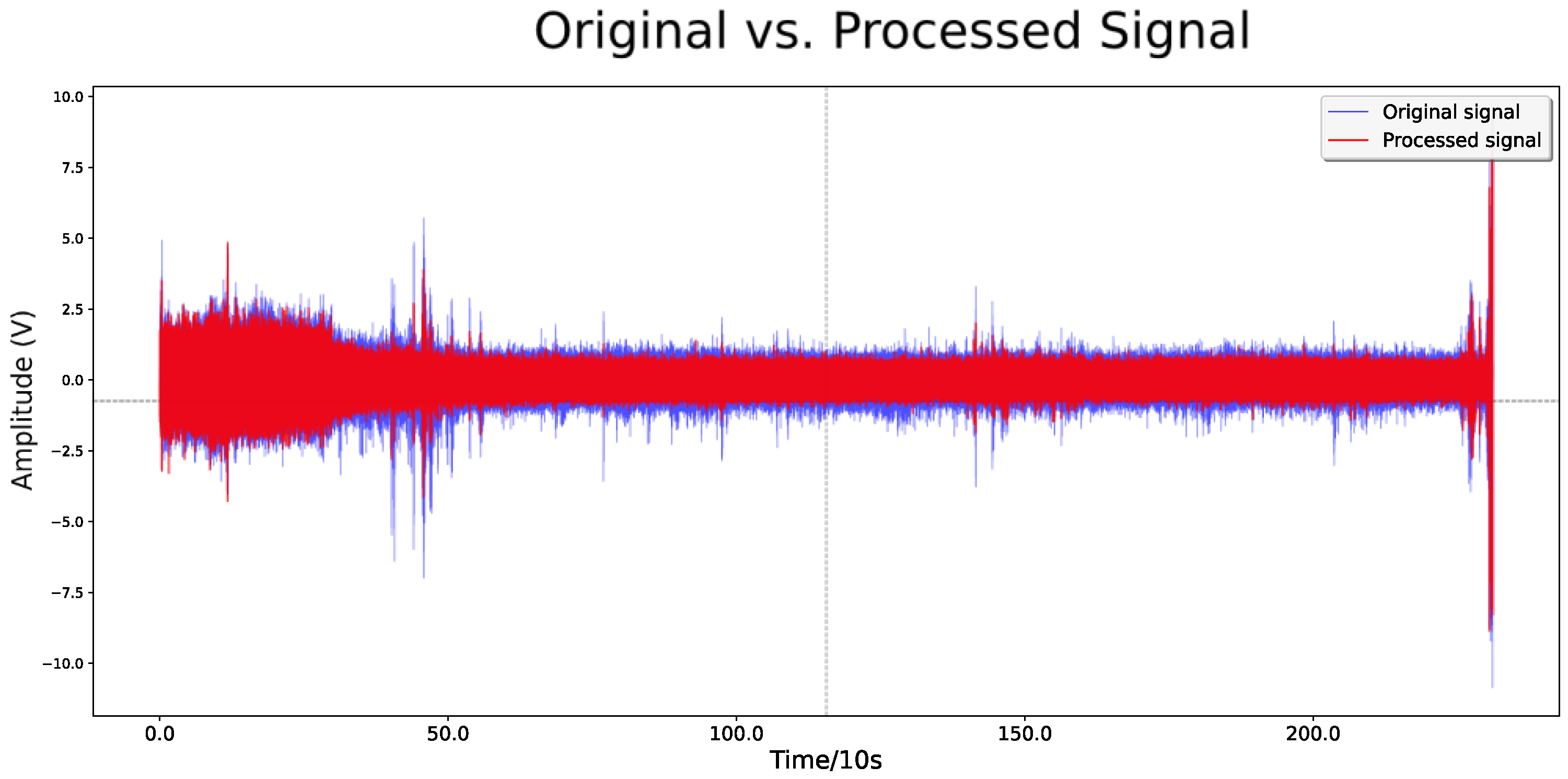
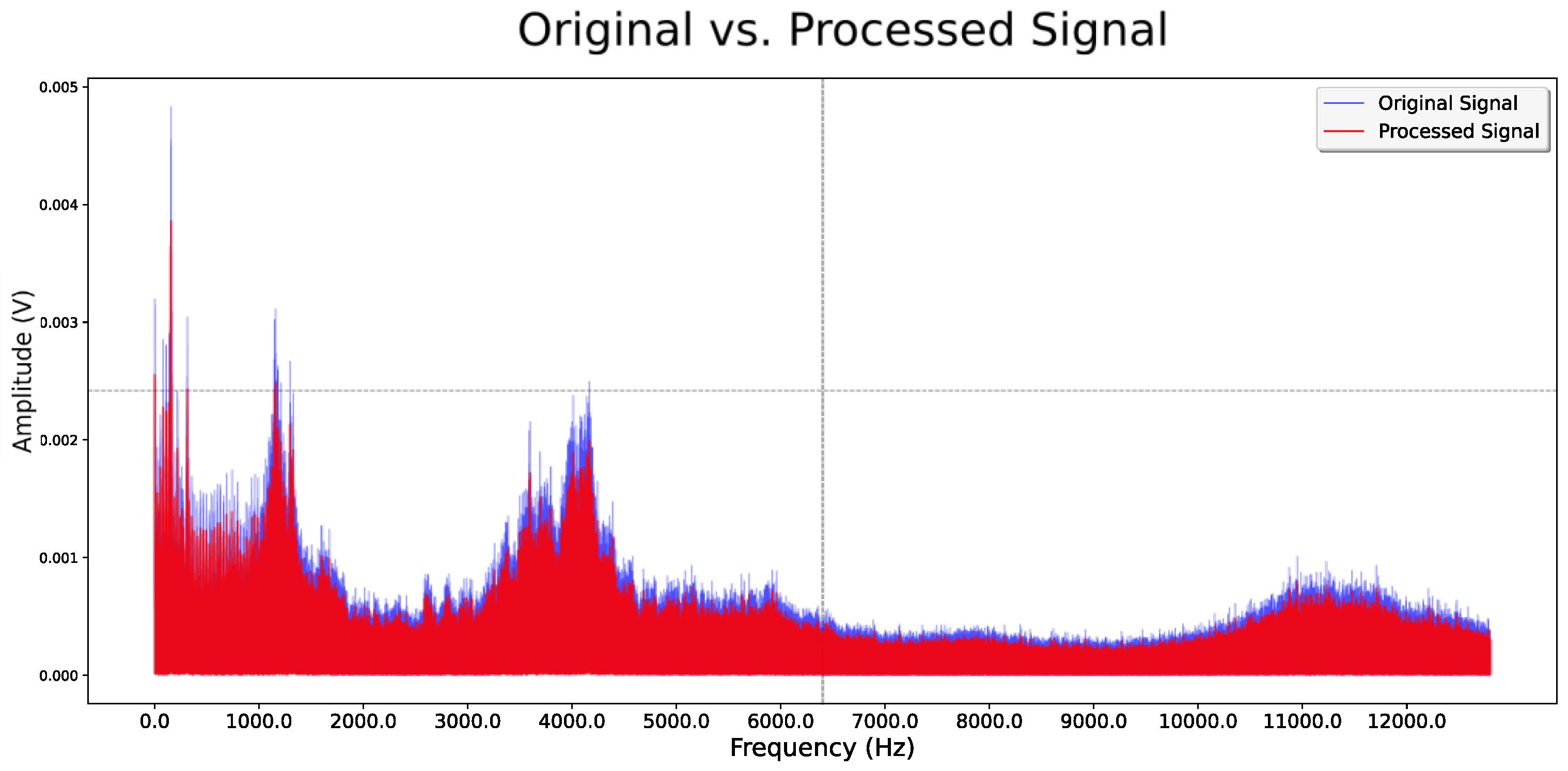
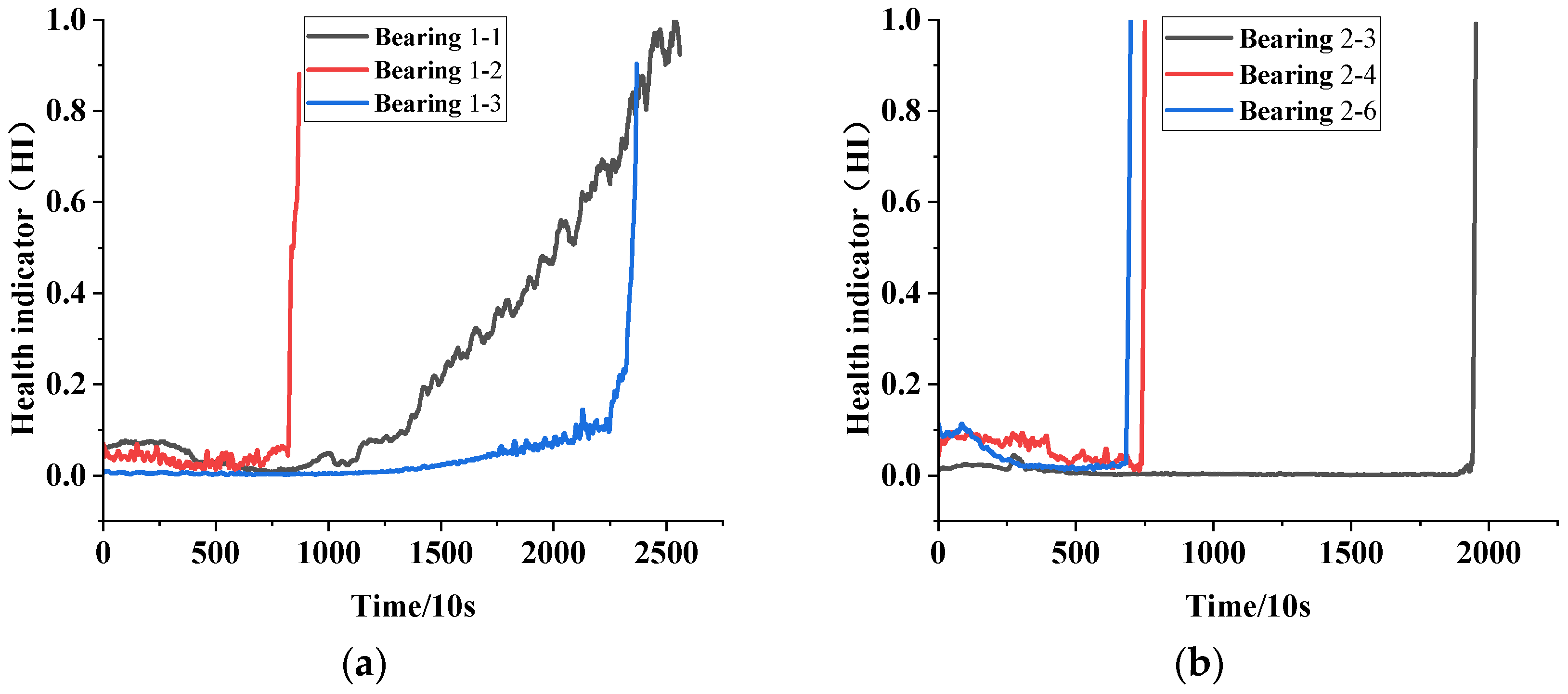
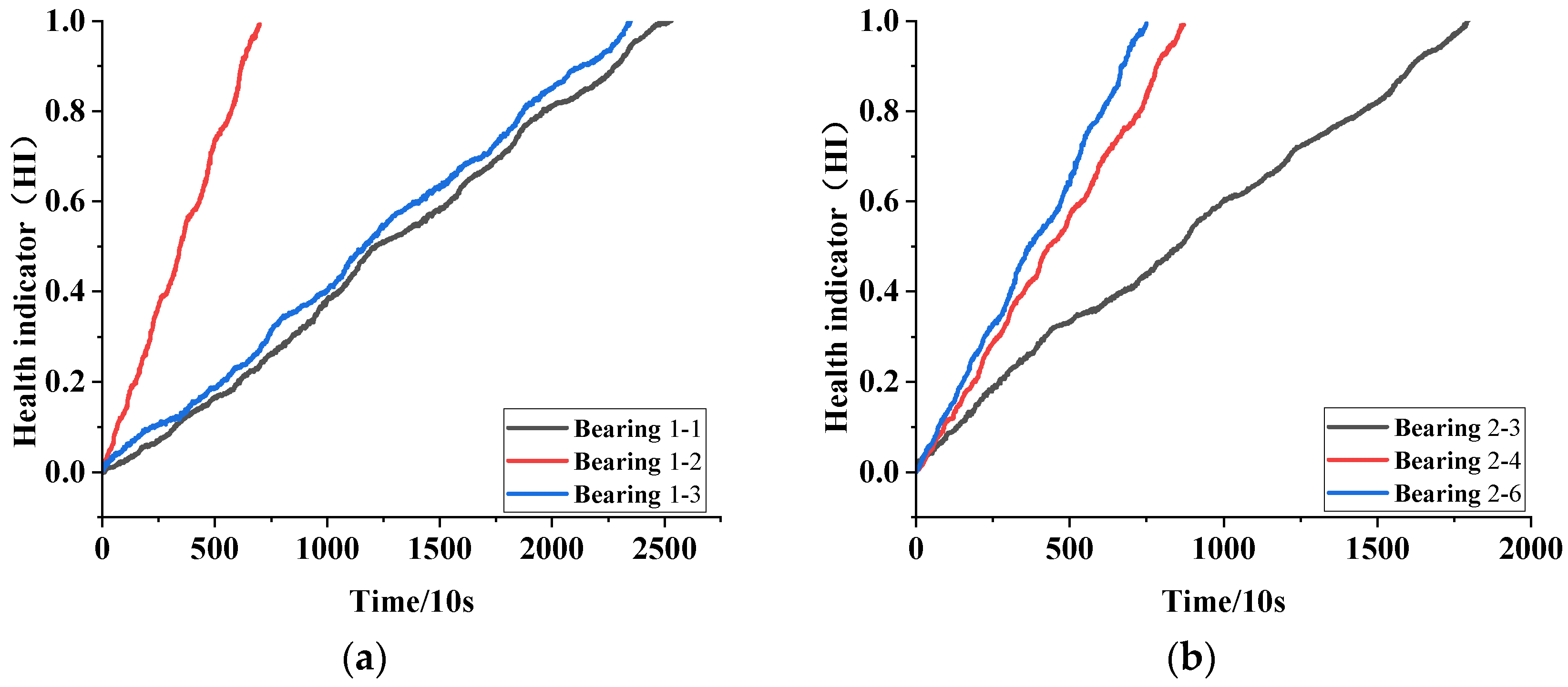
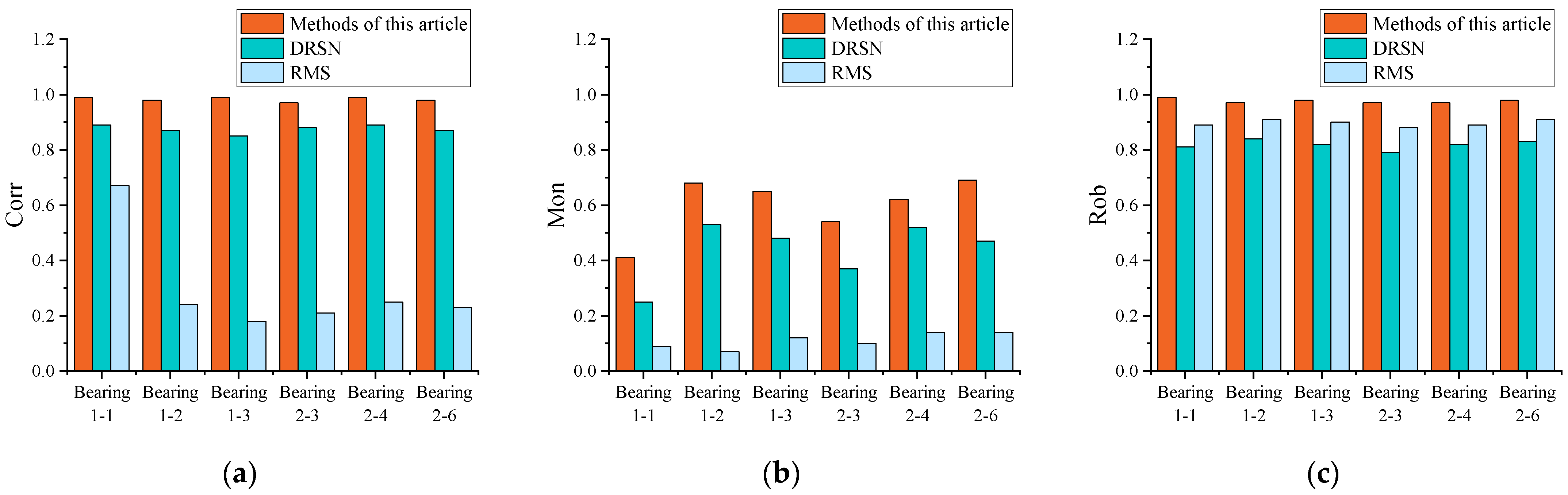
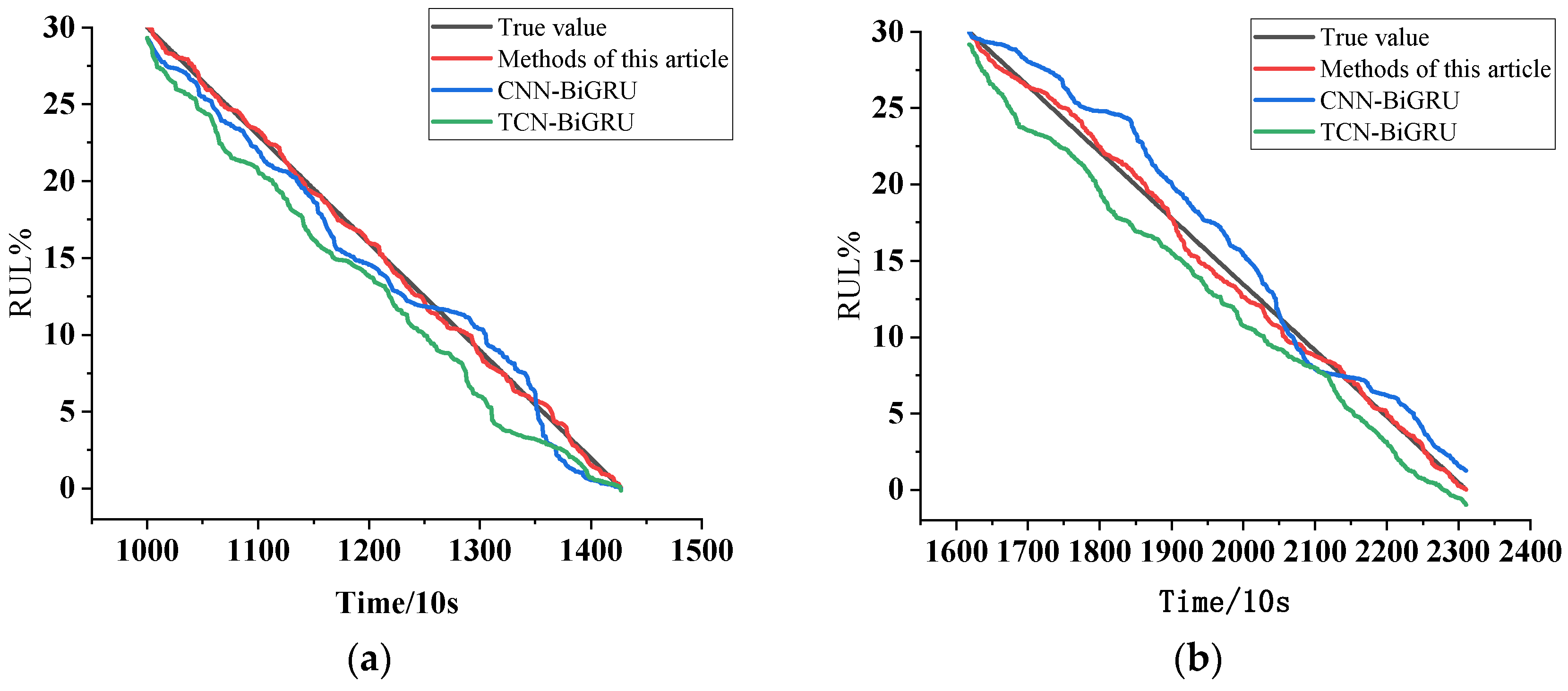

| Operating Condition Number | Rotational Speed (r/min) | Radial Force/N | Bearing Serial Number |
|---|---|---|---|
| 1 | 1800 | 4000 | bearing 1-1~bearing 1-7 |
| 2 | 1650 | 4200 | bearing 2-1~bearing 2-7 |
| 3 | 1500 | 5000 | bearing 3-1~bearing 3-7 |
| Bearing Data Serial Number | Number of Signal Data Points | Sampling Interval | Sampling Frequency | Duration of Each Sampling |
|---|---|---|---|---|
| Bearing 1-4 | 1427 | 10/s | 25.6 kHz | 0.1 s |
| Bearing 2-5 | 2311 | 10/s | 25.6 kHz | 0.1 s |
| Model | RMSE | SNR | |
|---|---|---|---|
| WGAN | Average | 0.2834 | 7.8342 |
| DCGAN | Average | 0.2473 | 9.5436 |
| the method proposed in this paper | Average | 0.1924 | 11.4725 |
| Model | RMSE | SNR | |
|---|---|---|---|
| WGAN | Average | 0.3145 | 9.4523 |
| DCGAN | Average | 0.2585 | 10.4578 |
| the method proposed in this paper | Average | 0.2046 | 11.3258 |
| Model Layer | Parameter | Output Size |
|---|---|---|
| Gated Recurrent Unit | Number of layers: 3; Input dimension: 16; Hidden state size: 64 | 128 × 128 × 128 |
| Self-Attention Mechanism | Input dimension: 128; Number of attention heads: 8 | 128 × 128 |
| Relu | / | 1024 × 128 |
| Dropout | 0.2 | 1024 × 128 |
| Full Connection | / | 1024 × 128 |
| Bearing Number | Number of Samples | Training Data | Validation Data |
|---|---|---|---|
| 1-4 | 1428 | 1000 | 428 |
| 2-5 | 2311 | 1618 | 693 |
| Test Bearings | Methods of This Article | CNN-BiGRU | TCN-BiGRU | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | Score | RMSE | MAE | Score | RMSE | MAE | Score | |
| 1-4 | 0.0479 | 0.0236 | 0.89 | 0.0563 | 0.0345 | 0.82 | 0.0568 | 0.0312 | 0.83 |
| 1-5 | 0.0566 | 0.0245 | 0.81 | 0.0632 | 0.0309 | 0.74 | 0.0712 | 0.0352 | 0.71 |
| 1-6 | 0.0498 | 0.0176 | 0.92 | 0.0664 | 0.0254 | 0.81 | 0.0652 | 0.0218 | 0.79 |
| 2-2 | 0.0408 | 0.0177 | 0.9 | 0.0486 | 0.0189 | 0.86 | 0.0497 | 0.0198 | 0.82 |
| 2-5 | 0.0523 | 0.0281 | 0.83 | 0.0751 | 0.0296 | 0.71 | 0.0634 | 0.0288 | 0.72 |
| 2-7 | 0.055 | 0.0322 | 0.85 | 0.0634 | 0.0421 | 0.74 | 0.0621 | 0.0381 | 0.75 |
| Mean | 0.0504 | 0.0239 | 0.867 | 0.0622 | 0.0302 | 0.78 | 0.0614 | 0.0292 | 0.77 |
| Method | Epoch | Number of Parameters (M) |
|---|---|---|
| CNN-BiGRU | 46 ± 0.8 s | 2.91 |
| TCN-BiGRU | 65 ± 1.3 s | 3.89 |
| Methods of this article | 52 ± 0.7 s | 3.03 |
| Test Bearings | Methods of This Article | CNN-BiGRU | TCN-BiGRU | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | Score | RMSE | MAE | Score | RMSE | MAE | Score | |
| 4-A | 0.0684 | 0.0472 | 0.84 | 0.0745 | 0.0578 | 0.79 | 0.0786 | 0.0564 | 0.77 |
| 4-B | 0.0731 | 0.0554 | 0.82 | 0.0789 | 0.0624 | 0.75 | 0.0767 | 0.0658 | 0.74 |
| Mean | 0.0708 | 0.0513 | 0.83 | 0.0767 | 0.0601 | 0.77 | 0.0777 | 0.0611 | 0.755 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Shi, A. Remaining Useful Life Prediction of Rolling Bearings Based on an Improved U-Net and a Multi-Dimensional Hybrid Gated Attention Mechanism. Appl. Sci. 2025, 15, 7166. https://doi.org/10.3390/app15137166
Wang H, Shi A. Remaining Useful Life Prediction of Rolling Bearings Based on an Improved U-Net and a Multi-Dimensional Hybrid Gated Attention Mechanism. Applied Sciences. 2025; 15(13):7166. https://doi.org/10.3390/app15137166
Chicago/Turabian StyleWang, Hengdi, and Aodi Shi. 2025. "Remaining Useful Life Prediction of Rolling Bearings Based on an Improved U-Net and a Multi-Dimensional Hybrid Gated Attention Mechanism" Applied Sciences 15, no. 13: 7166. https://doi.org/10.3390/app15137166
APA StyleWang, H., & Shi, A. (2025). Remaining Useful Life Prediction of Rolling Bearings Based on an Improved U-Net and a Multi-Dimensional Hybrid Gated Attention Mechanism. Applied Sciences, 15(13), 7166. https://doi.org/10.3390/app15137166





