Pore Pressure Prediction and Fluid Contact Determination: A Case Study of the Cretaceous Sediments in the Bredasdorp Basin, South Africa

Abstract

Pore pressure prediction gives drillers an early warning of potential oil and gas kicks, enabling them to adjust mud weight pre-emptively. A kick causes a delay in drilling practices, blowouts, and jeopardization of the wells. Changes in pore pressure affect the type of fluid contact in the reservoir. This study predicted the pore pressure and determined fluid contacts within the Lower Cretaceous and early Upper Cretaceous (Barremian to early Cenomanian) sandstone reservoirs of the Bredasdorp Basin using well logs and repeat formation test (RFT) data from three wells: E-BK1, E-AJ1, and E-CB1. Eaton’s method of developing a depth-dependent Normal Compact Trend (NCT), using resistivity and sonic wireline logs, as well as other methods including the Mathews and Kelly, Baker and Wood, and Modified Eaton and Bowers methods, were employed for pore pressure prediction. Eaton’s method provided reliable pore pressure results in all the wells when compared to alternative methods in this study. Overburden gradient and predicted pore pressures ranged from 1.84 gm/cc to 2.07 gm/cc and from 3563.74 psi to 4310.06 psi, respectively. Eaton’s resistivity and density/neutron log method results indicated normal pressure in E-BK1 and E-AJ1, as well as overpressured zones in E-AJ1. However, in E-CB1, the results showed only overpressured zones. The E-AJ1 significant overpressures were from 2685 m to 2716 m and from 2716 m to 2735 m in the pores exceeding 7991.54 psi. Gas–water contact (GOC) was encountered at 2967.5 m in E-BK1, while oil–gas contact (OGC) was at 2523 m in E-CB1, and gas–oil and oil–water contacts (GOC and OWC) were at 2699 m and 2723 m, respectively, in E-AJ1. In E-CB1, oil–water contact (OWC) was at 2528.5 m. Fluid contacts observed from the well logs and RFT data were in close agreement in E-AJ1, whereas there was no agreement in E-CB1 because the well log observations showed a shallower depth compared to RFT data with a difference of 5.5 m. This study illustrated the significance of an integrated approach to predicting fluid contacts and pore pressure within the reservoirs by showing that fluid contacts associated with overpressures were gas–water and oil–water contacts. In contrast, gas–oil contact was associated with normal pressure and under pressure.

1. Introduction

The Bredasdorp Basin is widely known as South Africa’s hydrocarbon-producing basin [1]. Exploration and drilling in this basin have revealed the occurrence of active petroleum systems; specifically, the efficient reservoir sandstones, mature source rocks and traps paved the way to the commercial extraction of oil and gas in the basin’s central and northern flanks [2]. Oil and gas are still being explored in this region; thus, the basin’s petroleum system processes are receiving more attention to ensure its economic sustainability [3]. Pore pressure (PP) is the fluid pressure in the pore space and results in an overpressure situation when hydrostatic pressure is exceeded [4]. Reservoir pore pressure is one of the principal concerns for drillers in exploratory areas throughout the primary recovery of hydrocarbons [5]. This is because inaccurate estimation of pore pressure in any reservoir can lead to uncertainties and serious consequences, such as formation damage, wellbore instability, gas kicks, and the worst-case situation of blowouts [6,7,8]. Consequently, this could hinder the attempts to achieve or contribute to the 2030 United Nations’ Sustainable Development Goals (SDGs), including goal numbers 14 ‘Life Below Water’ and 15 ‘Life on Land,’ which aim to protect the ecosystem and environment [9].

Pore pressure prediction is critical in any reservoir for evaluating and accessing fluid contacts for more efficient selection and for safety purposes [8]. In addition, it prevents the kicks and blowout circumstances often triggered by abnormally high pressure (i.e., overpressure) during well drilling activities in the petroleum industry [5,8]. Pore pressure prediction gives drillers an early warning of potential oil and gas kicks, enabling them to adjust mud weight pre-emptively. A kick causes a delay in drilling practices, blowouts, and jeopardization of the wells [5,9,10,11,12]. A comprehensive understanding of reservoir pressure enables the effective design and implementation of casing strategies that maintain a safe and operational mud weight window between pore pressure and the fracture gradient, thereby enhancing wellbore stability and optimizing drilling economics [5,8]. Factors such as compaction, fluid overpressure and tectonic activity can cause pore pressure to deviate significantly from the hydrostatic pressure line [13,14]. Stress-related mechanisms, fluid volume increase mechanisms, and fluid movement mechanisms are classified as overpressure generation categories. All these mechanisms can cause overpressure in the formation if they occur at a rapid rate that exceeds the formation’s ability to expel excess pressure [15]. Compaction disequilibrium is one of the main factors causing high overpressure in the tertiary sediments.

Predrilling data (seismic data) and drilling data (well logging) are the most conventional pore pressure prediction and estimation approaches [16]. Wireline log, which gives extensive and continuous data, is much more affordable than measuring pore pressure directly from the wellbore [15].

Changes in pore pressure affect the type of fluids found in the reservoir. Pore pressure and fluid contacts are significant parameters when locating hydrocarbons in the reservoir. As a result, they necessitate a critical review of regulating factors that may affect both, such as the pressure gradient at which fluid contacts change, mud weight, pore shapes, permeability, pressure type, sediment compaction, overburden, and tectonic stress [8]. The pore pressure and fluid contact changes are induced by reservoir petrophysical anomalies driven by time variation [17].

Determining fluid contacts (gas–water contact—GWC, oil–water contact—OWC, and gas–oil contact—GOC) is imperative for estimating field reserves and formation evaluation [18]. Fluid contacts may differ across a reservoir due to semipermeable barriers, faults, variations in rock quality or reservoir heterogeneity, hydrocarbon filling history, and hydrodynamic processes [19,20,21]. The contact surfaces in the reservoir that separate fluids with different densities (often between gas, oil, and water) result from gravity and capillary pressure [20]. Determining the point (depth and gradient) at which the water and hydrocarbon phases come into contact is intricate yet crucial in analyzing the reservoir because just the slightest change in pore type can cause fluid contacts to be misinterpreted [19]. The Bredasdorp Basin is ideal for this study because it is an active hydrocarbon-producing basin, and this study focuses mainly on the Cretaceous sandstone reservoirs because of their good petrophysical properties. Two separate studies on pore pressure prediction [8] and fluid contact determination [19] have been conducted in the neighbouring offshore basins, Pletmos and Orange Basins, respectively. However, no single published study has been conducted in the Bredasdorp Basin’s Cretaceous sandstone reservoirs to integrate pore pressure prediction and fluid contact determination with the aim of enhancing the predictability of these parameters and investigating their influence on one another. Therefore, a knowledge gap exists concerning the pressure zones in the Cretaceous sandstone reservoirs, the nature of fluid contacts in these reservoirs, and the best pore pressure prediction method. Over the last decades, several studies [8,13,14,15,16,22,23,24,25,26] have predicted pore pressures using wireline log and seismic data. Refs. [18,27,28] determined fluid contacts in the reservoir formation using formation pressure and wireline log.

Several models have been proposed and applied to predict pore pressure using in-process data (drilling data). To select the most suitable pore pressure prediction methods for future studies in the study area, the methods proposed by Eaton, Bowers, Mathews and Kelly, and Baker and Wood were utilized on three wells. All these methods have several strengths and weaknesses; as such, we decided to utilize them to compare the results to see which is more effective in this basin. We also determined fluid contacts within the sandstone reservoirs using well logs and RFT data. Lastly, we attempted to show the relationship between the pore pressure and fluid contacts.

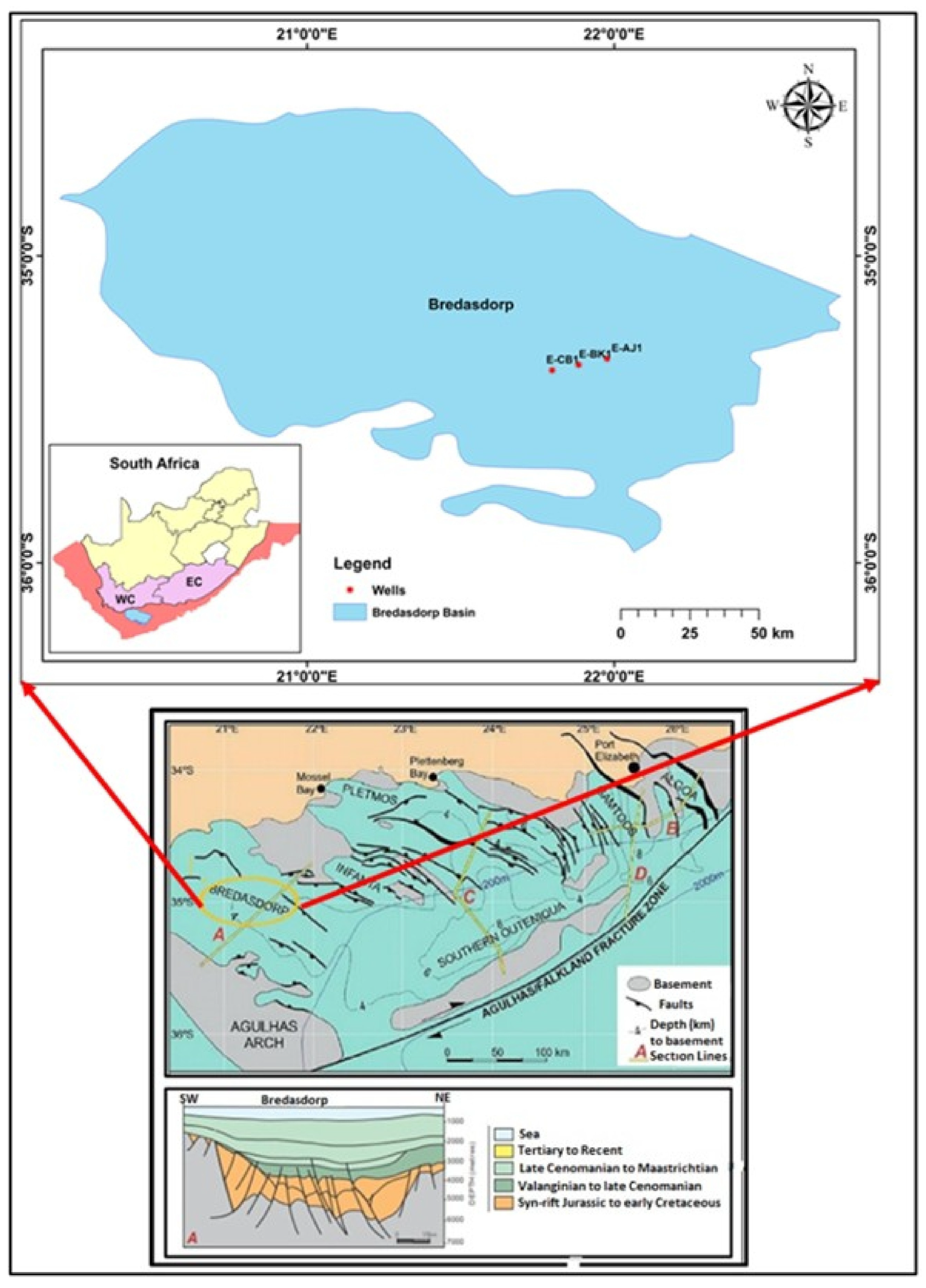
2. Location of the Study Area and the Geological Background

This study focused on three wells (BK1, E-AJ1, and E-CB1) located in the southeast of the Bredasdorp Basin, offshore from South Africa (Figure 1). The Bredasdorp Basin lies on South Africa’s south coast, southeast of Cape Town in the Western Cape (WC) province and west–southwest of Port Elizabeth in the Eastern Cape (EC) province. It is among the four sub-basins of the Outeniqua Basin that is located on the south coast, is surrounded by the Infanta Embayment, Agulhas Arch, and is southwest of Mosselbay [5,29,30,31,32]. It spans approximately 18,000 square kilometers (km²) with sequences of stratigraphy exceeding 5000 m thickness, extending from Cape Town to the Agulhas/Falkland Fracture Zone in the Indian Ocean [33]. The Bredasdorp Basin contains syn-rift continental and marine layers from the Upper Jurassic to Lower Cretaceous periods and divergent rocks formed during the post-Cretaceous and Cenozoic eras [34,35]. This study’s formation of interest lies between the Lower Cretaceous and early Upper Cretaceous period (Barremian to early Cenomanian) between 93 and 112 Ma. The basin’s sediments were derived from the Cape Supergroup and Karoo Supergroup sandstones and shale erosion [36]. The Cape Supergroup sediments are sequences from shallow marine, transitional, and deep-sea environments. The basin is thought to have undergone a sequence of structural deformations (drift and rift activities) during the separation of Gondwanaland and the other southern hemisphere continents [5,37,38,39,40]. The basin’s structural deformation and sediment addition from the coastal zone are adequate to produce an average to good source rock [5,32,41]. It also comprises half grabens (Figure 1) that dip slightly to the south, with geological pinch-outs completing the basin’s hydrocarbon trapping mechanisms [42].

• Tectonic history of the Bredasdorp Basin

South Africa’s offshore basins are classified into three types of tectonostratigraphic regions: the eastern offshore region, southern margins (which include the Outeniqua Basin), and the passive margin encompassing the western border [39,43]. The Bredasdorp Basin is classified as a passive margin basin associated with the early Cretaceous of the South Atlantic opening [44,45]. This basin’s sedimentary filling pulses are associated with distinct contemporaneous tectonic occurrences [37]. The slope and basin system evolved concurrently due to fine-grained density and suspension deposits, leveed slope and basin floor turbidite fans, and fine-grained turbidite systems [38]. This evolution allowed for the classification of the sedimentary history of the Bredasdorp Basin into four tectonostratigraphic stages: pre-rift, syn-rift, transition, and drift (Figure 2) [5,34,46]. Each tectonostratigraphic phase is closely related to a particular unconformity or unconformities.

The pre-rift phase is associated with the basement rocks and sequences deposited before the Valanginian-aged (~139 Ma) 1At1 unconformity.

• Syn-rift Phase

This phase signifies an extensional period during which the continental crust thinned and stretched, leading to faulting in certain places. Sequences associated with an Ordovician to Devonian, approximately 480 Ma to 360 Ma, basement block of Cape Supergroup quartzites and slates characterize this phase, which is topped by the 1At1 unconformity, ~137 Ma (Hauterivian-aged) [36,39]. Rifting ended in the very beginning of the Valanginian (~139 Ma). As migration alongside the Agulhas–Falkland Fracture Zone (AFFZ) began, the 1At1 unconformity formed as a result of a marine retreat after rifting ended in the early Valanginian (~139 Ma) [36,37,44,45].

• Transition Phase

The initial transition phase sediments were deposited after the 1At1 unconformity’s maximum flooding with surface shales (~137 Ma). During this period, fast thermal subsidence along the rift faults and asthenospheric cooling occurred in the Bredasdorp Basin. The central areas of the basin became deeper due to this activity, which decreased water circulation and produced an environment with low oxygen levels [36,47].

• Drift Phase

The drift phase includes the Aptian-aged 13A sequence, which is bound by the 13At1 unconformity (~124 Ma) below. The top of the sequence and the 14At1 unconformity (~108 Ma) below confine the Albian-aged 14A sequence, indicating a surface age of approximately 105.5 Ma [30,41]. The drift stage’s beginning can be marked back to the middle period of the Albian (14At1), when the southwest Columbine–Agulhas arch cleared the 20 Falkland plateau, causing thermal deformation [46]. The last stages of regression occurred within the Tertiary period (Palaeocene age) when significant uplifts took place.

For more information on the tectonic evolution, geological overview, depositional environment and characterization of source and reservoir rocks, several studies such as [3,8,31,32,35,36,37,44,47,48], are recommended for further reading.

3. Materials and Methods

A suite of well logs, including bulk density (RHOB), Gamma-ray (GR), resistivity (LLD), sonic (DT), and caliper (CALI), were loaded into a database in Geoactive Interactive Petrophysics (IP) 2023 software v5.1 Software (Geoactive Limited., Aberdeen, UK) in LAS format. Data quality control techniques, such as environmental corrections, were performed using the Schlumberger parameters before interpretations. Wireline logs were extensively used for pore pressure prediction, and fluid contacts were determined using production data (RFT) and wireline logs.

3.1. Pore Pressure Prediction Methods

Different methods for pore pressure prediction, including methods by Eaton, Bowers, Mathews and Kelly, and Baker and Wood, were used in this study, and their strengths and weaknesses are compared in

Table 1. Strengths and limitations of various pore pressure prediction methods.

Method	Primary Log(s) Used	Strengths	Limitations
Eaton sonic	Sonic (DT)	- Sensitive to compaction trends - Useful for identifying undercompaction	- Results vary significantly compared to others - Sensitive to lithological changes
Eaton (resistivity)	Resistivity	- More stable in shale zones - Simple to apply	- Less sensitive to mechanical compaction changes - May misidentify hydrocarbon zones
Modified Eaton	Resistivity (adjusted formula)	- Improved accuracy over original Eaton - More tailored to formation type	- Still does not account for unloading - Requires calibration
Mathews andKelly	Sonic + density	- Incorporates mechanical rock properties - Can be adapted for resistivity	- Requires multiple logs - Sensitive to data quality
Baker & Wood	Sonic + density (adaptable to resistivity)	- Versatile method with adaptability - Suitable for varying lithologies	- Complex calculation - Depends on accurate NCT definition
Bowers	Sonic (velocity)	- Most precise under unloading conditions - Based on effective stress	- Requires unloading path estimation - May be complex to implement in real-time drilling

. The general approach for all these methods is based on evaluating the measured pore pressure indicators in an abnormal (overpressure zone) compared with a normal pressure zone. The Ben Eaton method is the most widely used and accepted technique in the oil and gas industries [49]. This method uses resistivity and sonic wireline logs to create a depth-dependent Normal Compaction Trend (NCT). Therefore, this study presents detailed Eaton resistivity and sonic method results for pore pressure gradient and pore pressure predictions, as well as Mathews and Kelly and Eaton (both resistivity and sonic) results for fracture pressure and fracture gradient.

3.1.1. Ben Eaton’s Resistivity Method with Depth-Dependent Normal Compaction Trend (NCT) Line

Ben Eaton’s method is an experimental technique that uses resistivity, sonic, and density logs calibrated to reflect pore pressure using drill stem tests (DST) and repeat formation tests (RFT) to envisage pore pressure (RFT) [50]. The Ben Eaton model [50] was established by observing that a well log can predict pore pressure at depth based on deep resistivity measurement. The following equation was used to predict pore pressure gradients in shales using a resistivity log:

$$\mathrm{P}\mathrm{p} = \mathrm{O}\mathrm{B}\mathrm{G} -(\mathrm{O}\mathrm{B}\mathrm{G}- \mathrm{P}\mathrm{n}\mathrm{g}) \times (\mathrm{R}\mathrm{o}/\mathrm{R}\mathrm{n})$$

(1)

where

• $\mathrm{P}\mathrm{p}$ = pore pressure gradient;
• $\mathrm{O}\mathrm{B}\mathrm{G}$ = overburden stress gradient (ppg), (psi/ft);
• $\mathrm{P}\mathrm{n}\mathrm{g}$ = hydrostatic pore pressure gradient, normally 0.45 psi/ft/1.03 MPa/km based on the water salinity of the region;
• $\mathrm{R}\mathrm{o}$ = observed shale resistivity (ohm/m);
• $\mathrm{R}\mathrm{n}$ = normal shale resistivity (hydrostatic pressure).

Finding the state of hydrostatic pore pressure for the shale resistivity when using Equation (1) is challenging; the best solution is to obtain the Normal Compaction Trend line for the prediction of pore pressure. Normal resistivity, or “$\mathrm{R}\mathrm{n}$,” depends on the burial depth, and the most effective method for determining the resistivity of shale conditions of the pore pressure (hydrostatic) is to set up the NCT for pore pressure prediction using the following equation:

$$\mathrm{I}\mathrm{n}\mathrm{R}\mathrm{n} = \mathrm{I}\mathrm{n}\mathrm{R}\mathrm{o} + \mathrm{b}\mathrm{Z}$$

(2)

where

• $\mathrm{R}n$ = shale resistivity in the normal compaction condition;
• $\mathrm{R}\mathrm{o}$ = shale resistivity in a mudline;
• $\mathrm{b}$ = constant number;
• $\mathrm{Z}$ = profundity of mud line below.

The resultant formula from Equations (1) and (2) is called the Eaton resistivity equation and can be presented as follows:

$${\mathrm{P}\mathrm{p}\mathrm{g} = \mathrm{O}\mathrm{B}\mathrm{G} - (\mathrm{O}\mathrm{B}\mathrm{G} - \mathrm{P}\mathrm{n}\mathrm{g}) (\mathrm{R}/{\mathrm{R}\mathrm{o}\mathrm{e}}^{\mathrm{b}\mathrm{z}} )}^{\mathrm{n}}$$

(3)

where

• $R$ = shale resistivity measured at depth $\mathrm{Z}$;
• $\mathrm{b}$ = logarithmic resistivity normal compaction line slope;
• $\mathrm{R}\mathrm{o}$ = mudline normal compaction shale resistivity.

3.1.2. Ben Eaton’s Sonic Velocity Method with Depth-Dependent Normal Compaction Trend (NCT) Line

Ben Eaton’s method for estimating pore pressure sonic log can be presented as follows:

$$\mathrm{P}\mathrm{P} =\mathrm{O}\mathrm{B}\mathrm{G} - (\mathrm{O}\mathrm{B}\mathrm{G} -\mathrm{P}\mathrm{n}\mathrm{g}) \times (∆\mathrm{t}\mathrm{n}/∆\mathrm{t})$$

(4)

where

• $∆\mathrm{t}\mathrm{n}$ = sonic transit travel time/the slowness in shale at normal pressure (μs/ft).

Sayers expanded on Slotnick’s formula as follows [51,52]:

$$\mathrm{V}=\mathrm{V}0 + \mathrm{K}\mathrm{Z}$$

(5)

where

• $\mathrm{V}$ = seismic velocity at depth Z;
• $\mathrm{V}0$ = ground surface velocity;
• $\mathrm{K}$ = a constant.

An exponential relationship between the mean transit time from 17 wells that have normal pressure conditions and a Normal Compaction Trend for shale transit time with depth is given as follows [53]:

$$∆\mathrm{t}\mathrm{n} = 225 + {391\mathrm{e}}^{-0.00103\mathrm{Z}}$$

(6)

where

• $∆tn$ = (µs/m);
• Z = the depth in meters.

Ref. [38] used a similar relationship in their study and presented it as follows:

$$∆\mathrm{t}\mathrm{n} = 176.5 + {461.5\mathrm{e}}^{-0.0007\mathrm{Z}}$$

(7)

The regular compression tendency of the transit time in certain petroleum basins, like Brunei and the deep-water Sabah fold belt, subsequently gave rise to the following relationship:

$$∆\mathrm{t}\mathrm{n} = ∆\mathrm{t}\mathrm{m} + (∆\mathrm{t}\mathrm{m}\mathrm{l} - ∆\mathrm{t}\mathrm{m}){\mathrm{e}}^{-\mathrm{c}\mathrm{z}}$$

(8)

where

• $∆tn$ = compressional transit time in the porosity-free shale matrix;
• $∆tml$ = mudline transit time;
• $c$ = is the constant.

The following is the Eaton’s sonic velocity adjustment method when Equation (7) is substituted into Equation (9):

$$\mathrm{P}\mathrm{p}\mathrm{g} - \mathrm{O}\mathrm{B}\mathrm{G} - (\mathrm{O}\mathrm{B}\mathrm{G} - \mathrm{P}\mathrm{n}\mathrm{g}) (∆\mathrm{t}\mathrm{m} + (∆\mathrm{t}\mathrm{m}\mathrm{l} - ∆\mathrm{t}\mathrm{m}) {\mathrm{e}}^{-\mathrm{c}\mathrm{z}}/∆\mathrm{t}$$

(9)

3.1.3. Application of Eaton’s Method by Developing Normal Compaction Trend (NCT) in Resistivity and Sonic Velocity Log Plots

The normal compact trend (NCT) is the best-fitting linear trend for identifying overpressure and normal pressure formations [4]. To obtain the correct NCT, several factors, such as the regional geology of the study area, pressure data, and comparisons of data from multiple wells, should be taken into account. The geology should reflect the rock types and the nature of compaction. The NCT should be consistent with the pressure data to avoid incorrect pressure zones. Pore pressure was predicted in the studied reservoirs using Eaton’s method by developing a depth-dependent Normal Compaction Trend (Equations (3) and (9)), using resistivity and sonic wireline logs for the required pore pressure attributes such as pore pressure, pore pressure gradient, fracture pressure, fracture gradients, effective stress (ES), and the overburden gradient.

Based on Eaton’s method, the shale resistivity and sonic shale logs can either increase or decrease from the established NCT. This divergence is used to identify the overpressured and normal pressure zones. An overpressured formation is detected when the shale resistivity decreases from the NCT [54,55]. On the other hand, an increase in shale resistivity, as determined by the NCT, indicates a normal pressure formation. However, sonic shale logs show a reverse pattern to shale resistivity logs. A divergence of sonic shale logs (DT) from the established NCT towards the low values scale indicates a normal pressure zone, and a deviation toward the higher values suggests an overpressured zone. The proper selection of the Normal Compaction Trend (NCT) accounts for a sizable amount of uncertainty in predicting pore pressure. As a result, the NCT developed for this study is mostly based on velocity logs obtained from sonic data and resistivity logs [56].

3.2. Different Pore Pressure Prediction Methods

This study utilized the Mathews and Kelly, Modified Eaton, Baker and Wood, and Bowers methods to calculate pore pressure (PP), pore pressure gradient (PPG), fracture pressure (FP), fracture gradients (FG), effective stress (ES) and the overburden gradient (OG) for comparison.

3.2.1. Mathews and Kelly Method

Mathews and Kelly [57] developed the following expression to calculate fracture gradients in sedimentary formations because the matrix stress, which only differs in the degree of compaction, is connected to the rock matrix’s cohesiveness:

$$\mathrm{F} = (\mathrm{P}/\mathrm{D}) + (\mathrm{K}\mathrm{i} \mathrm{S}\mathrm{m}/\mathrm{D}\mathrm{i})$$

(10)

where

• $\mathrm{F}$ = break inclination at the purpose of investment (psi/ft);
• $\mathrm{P}$ = formation pressure (psi);
• $\mathrm{D}$ = depth of interest (ft);
• $\mathrm{S}\mathrm{m}$ = matrix stress (psi);
• $\mathrm{K}\mathrm{i}$ = matrix stress coefficient;
• $\mathrm{D}\mathrm{i}$ = depth at normal matrix.

3.2.2. Bowers Method

The Bowers method employs a similar concept to the Eaton method, which calculates the effective stress reading. Nonetheless, the Bowers equation is superior to Eaton’s due to its greater emphasis on the unloading parameter. The Bowers method is ideal for predicting formations with high pore pressure readings and uses both unloading and loading mechanisms. This approach helps estimate pore pressure in shallow formations that are either poorly consolidated or unconsolidated due to the slow velocity in these formations:

$$\mathrm{V}=5000+\mathrm{A}\mathsf{\sigma }\mathrm{B}$$

(11)

$$\mathrm{V} = 5000 + \mathrm{A}[ \mathsf{\sigma }\mathrm{m}\mathrm{a}\mathrm{x} ( \mathsf{\sigma }/\mathsf{\sigma }\mathrm{m}\mathrm{a}\mathrm{x} ) 1/\mathrm{U}]\mathrm{B}$$

(12)

$$\mathsf{\sigma }\mathrm{m}\mathrm{a}\mathrm{x} = {(\mathrm{V}\mathrm{m}\mathrm{a}\mathrm{x}-5000/\mathrm{A})}^{1/\mathrm{B}}$$

(13)

where

• $V$ = Velocity (Ft/s);
• $\mathsf{\sigma }$ = Effective pressure (Psi);
• $\mathsf{\sigma }max$ = Maximum effective pressure (Psi);
• $A$ and $B$ = Bowers empirical coefficients.

3.2.3. Barker and Wood Method

The Barker and Wood technique is used to predict subsurface conditions below the mud level before drilling. The method assumes that the fracture gradient in the shallow sediments, influenced by the weight of the overlying material, will be equivalent to the overburden gradient. Fracture pressure can be estimated by first finding the average bulk density of the overburden pressure:

$$\mathrm{C}\mathrm{u}\mathrm{m}.\mathrm{A}\mathrm{v}.\mathrm{F}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}.\mathrm{B}\mathrm{u}\mathrm{l}\mathrm{k} \mathrm{D}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{y} \left(\mathrm{p}\mathrm{p}\mathrm{g}\right)= 5.3 \times \left(\mathrm{T}\mathrm{V}\mathrm{D}\mathrm{B}\mathrm{M}\mathrm{L}\right) 0.1356$$

(14)

where

• $\mathrm{T}\mathrm{V}\mathrm{D}\mathrm{B}\mathrm{M}\mathrm{L}$ = True Vertical Depth Below Mud Line

3.2.4. Ben Eaton Modified

Ben Eaton added Poisson’s Ratio to the fracture pressure gradient equation by extending Mathews and Kelly’s formula, with resulting formula given as follows:

$$\mathrm{F}=(\mathrm{S} - \mathrm{P})/\mathrm{D} \times \mathrm{v}/(1 - \mathrm{v}) + \mathrm{P}/\mathrm{D}$$

(15)

where

• $\mathrm{P}$ = pore pressure (psi);
• $\mathrm{S}$ = overburden;
• $F$ = fracture gradient (psi/ft);
• $\mathrm{D}$ = Depth (ft);
• v = Poisson ratio.

3.3. Fluid Contacts Determination

Identifying fluids within rocks and determining possible contacts yield crucial insights for petrophysical analysis. The point at which oil or gas fluids are found in the rock pores is called the water contact. The water gradients and intersection with hydrocarbons are utilized to ascertain the free water level and identify the fluid contact [18,21]. In conditions of very low permeability, mud filtrate invasion can transform formation layers into “supercharges,” creating pressure points that veer off and diverge from the normal pressure gradient line. Supercharged points are often excluded from the pressure versus depth plot due to their lack of reliability [18,21].

In this study, fluid contacts were first determined using a qualitative method by observing the behavior of resistivity and density/neutron porosity logs within the studied reservoirs. Density logs are more reliable for identifying fluid contacts because they are sensitive to the fluids’ densities in the formation and are less impacted by the formation matrix [58,59]. Neutron logs are effective for detecting changes in fluid saturation because they are sensitive to the hydrogen index, which is associated with the presence of fluids in the formation, and they are highly sensitive to porosity [60,61]. Therefore, the density and neutron log combination provides a potent tool for fluid contact identification, providing higher accuracy, reduced uncertainty, and improved interpretation of formation properties.

Secondly, the quantitative method utilized the Repeat Formation Test (RFT) data by constructing pressure versus depth cross-plots. RFT data were used to construct the pressure profiles. Analyzing the gradient provides more information about the type of fluids and the contact between them. Hence, this tool is useful in identifying fluid contacts. The pressure versus depth plots were utilized to determine the fluid densities, fluid contacts, and gradients with respect to the anticipated pore pressures at different depth zones of the selected reservoirs.

The following relationship was used to calculate the fluid densities based on the pressure gradient [21]:

$$\mathrm{F}\mathrm{l}\mathrm{u}\mathrm{i}\mathrm{d} \mathrm{d}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{y} (\mathrm{g}/\mathrm{c}\mathrm{c}) = \mathrm{P}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e} \mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{t} (\mathrm{p}\mathrm{s}\mathrm{i}/\mathrm{f}\mathrm{t}) \times 2.3072$$

(16)

Nevertheless, the psi/m units for pore pressure gradients were expressed as shown below using the comparable connection by modifying Equation (16):

$$1 \mathrm{p}\mathrm{s}\mathrm{i}/\mathrm{m} = 0.7034 \mathrm{g}/\mathrm{c}\mathrm{c}$$

(17)

4. Results

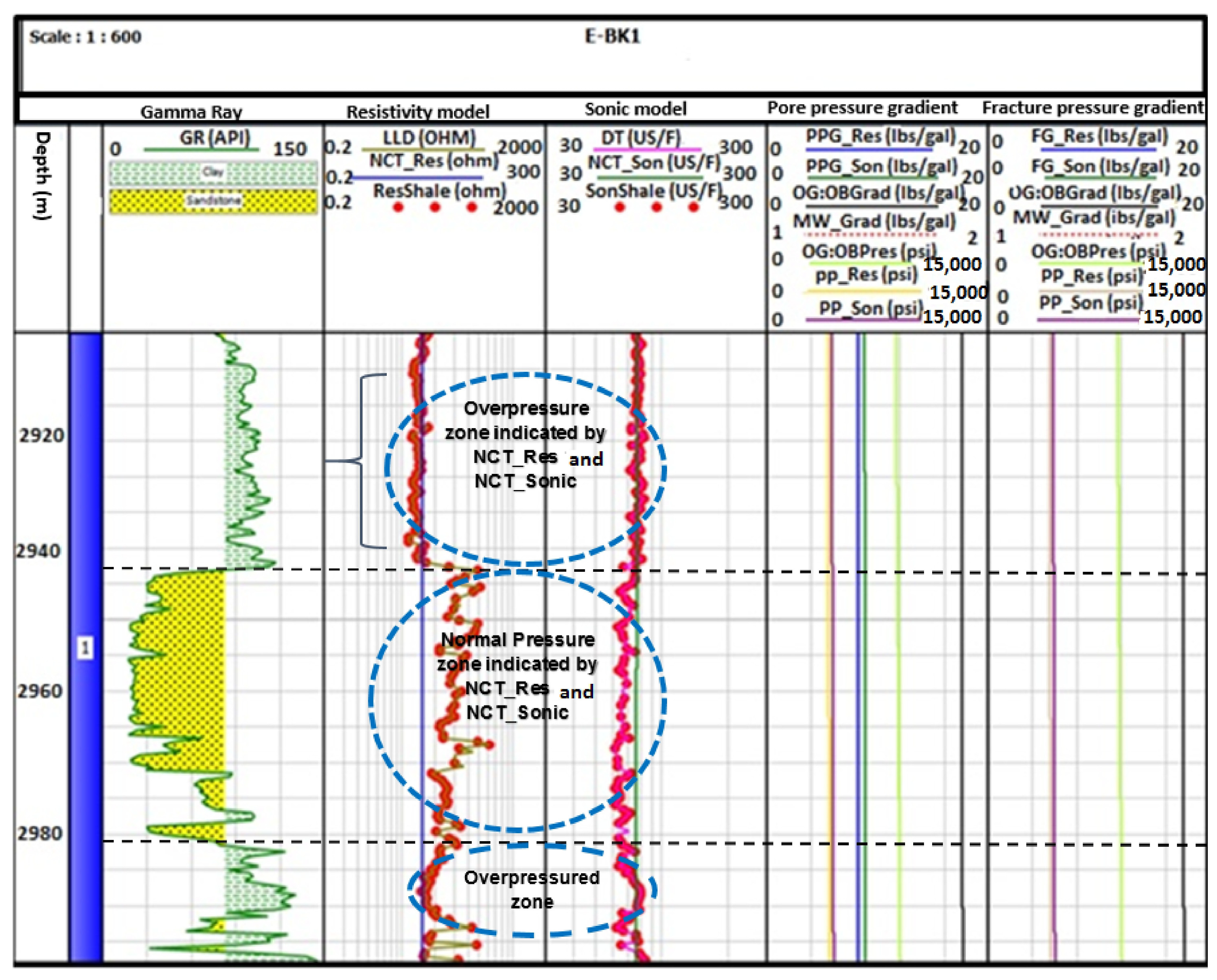
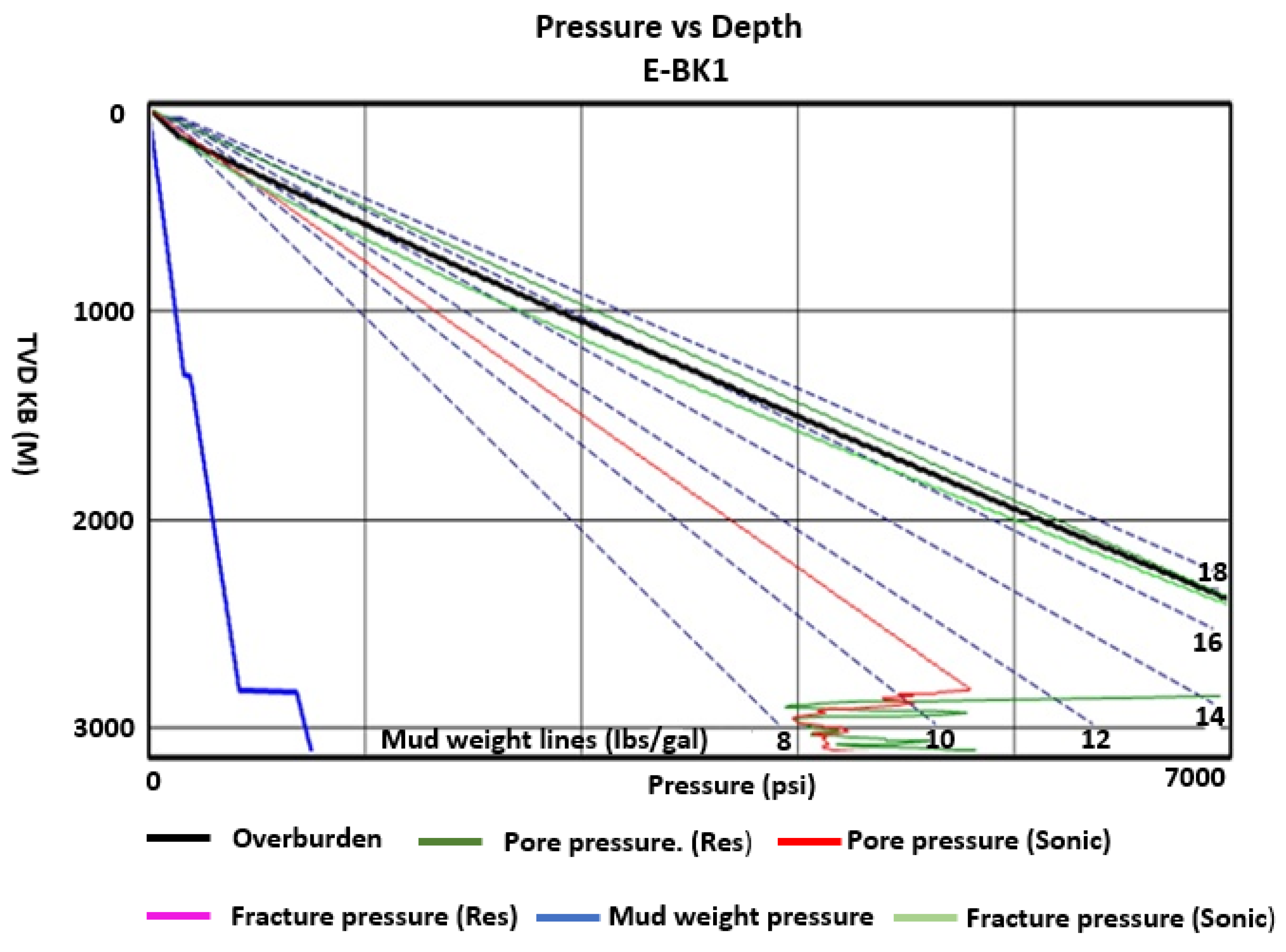
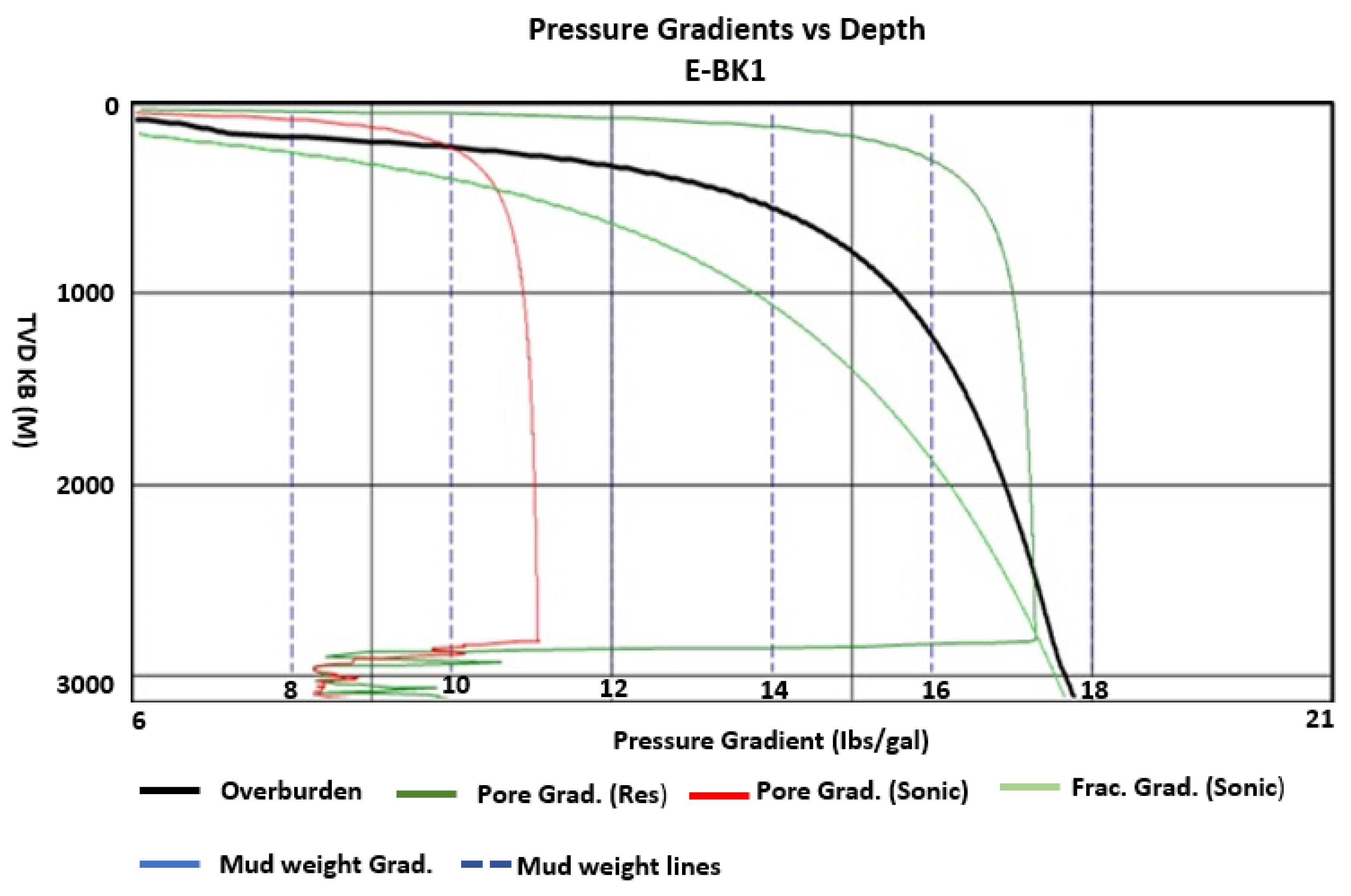
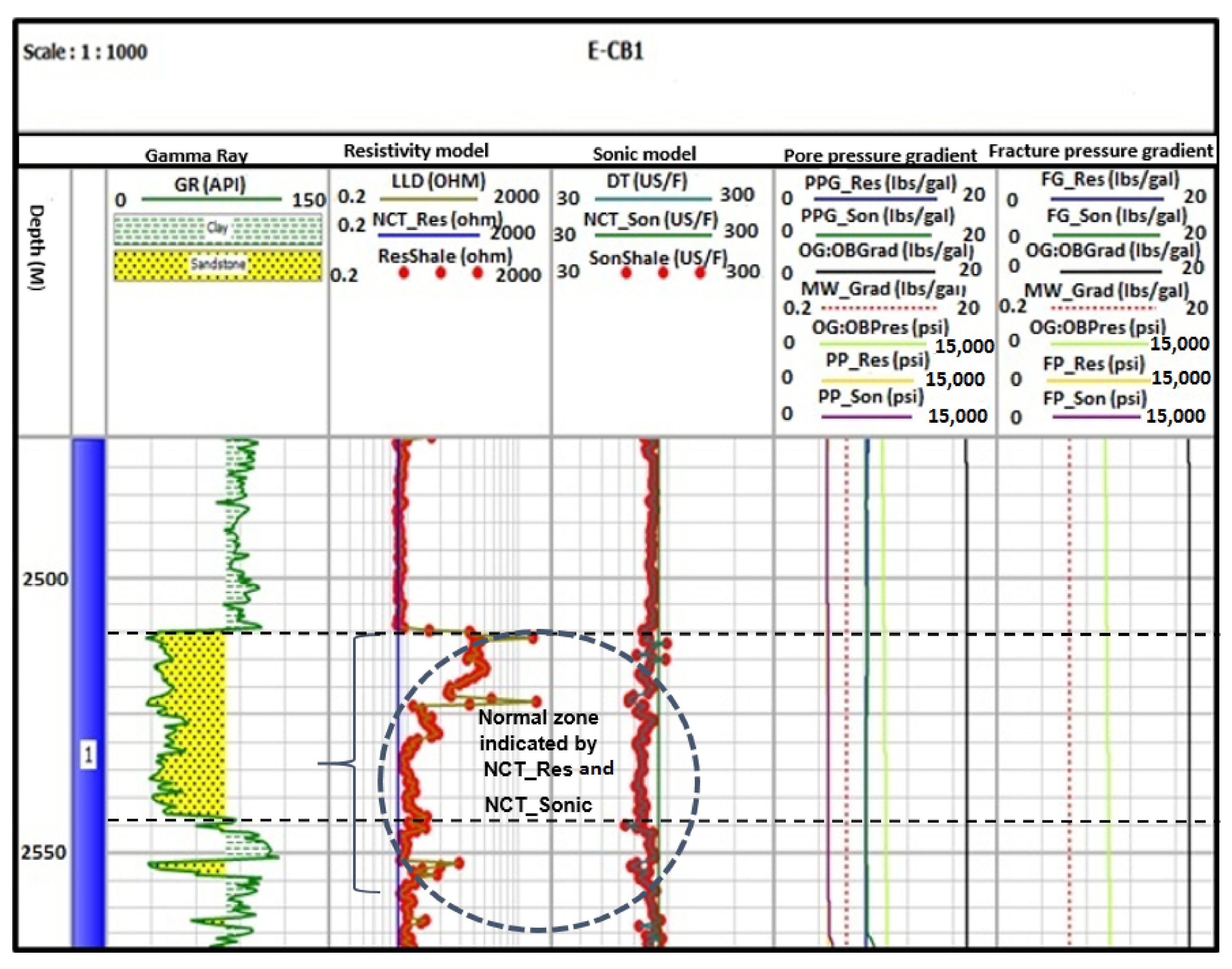
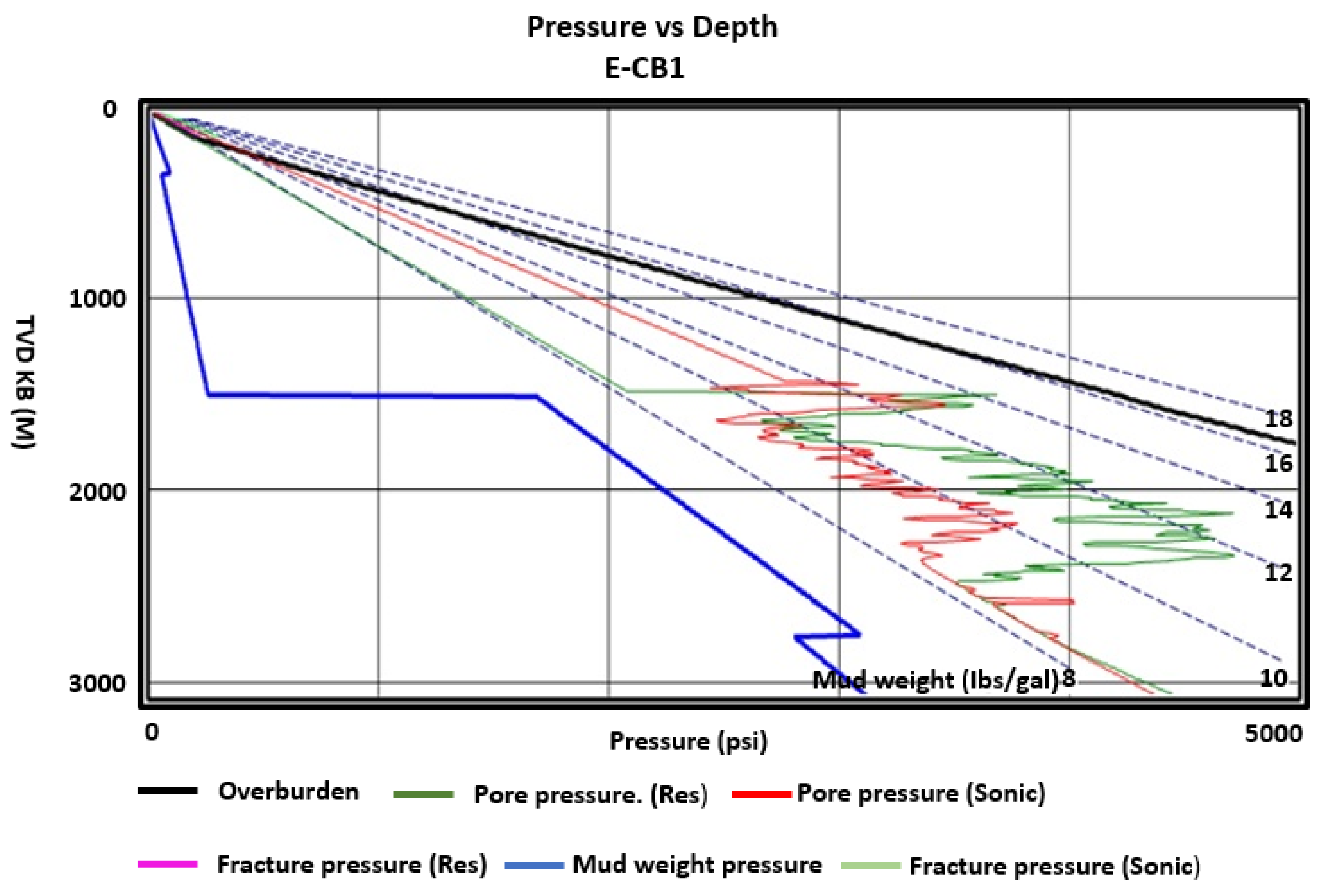
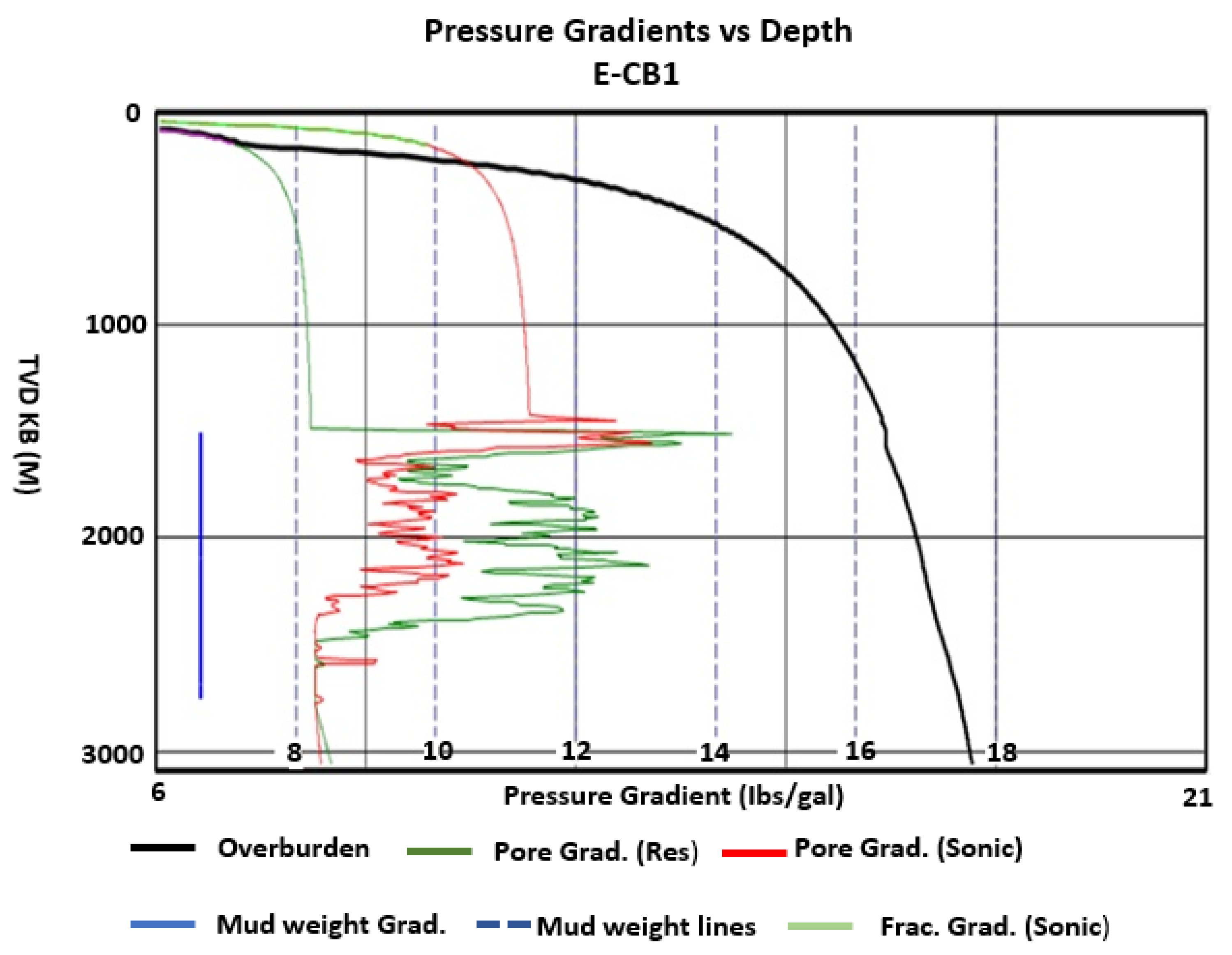
4.1. Pore Pressure Prediction from Resistivity and Sonic Logs

The Eaton [51] resistivity and sonic methods were employed to predict pore pressure gradient and pore pressure. The Mathews and Kelly and Eaton (resistivity and sonic) models were used to calculate fracture pressure and gradient. Similar techniques were applied to all three wells, and therefore, in this section, we present the detailed results for the E-BK1 and E-CB1 wells, and a summary of the results for the E-AJ1 well.

The reservoir zone in E-BK1 (Figure 3) shows a compacted sandstone formation between 2942 m and 2983 m. Normal pressure formation was encountered from 2942 m to 2983 m, as indicated by NCT_Res and NCT_Sonic in tracks 4 and 5. With ResShale and SonShale values of 50.37 ohm/m and 67 µs/f, respectively, the sonic shale deviates to the left of the Normal Compaction Trend (NCT) line, while the shale resistivity deviates to the right. The reservoir zone did not contain any overpressured zones. The overpressures were identified at the top and bottom of the reservoir intervals of the shale formation. In E-AJ1, normal and overpressured formations were observed within the studied interval. The reservoir zone shows an under-compacted sandstone formation and a sequence of intercalated shale intervals within the depths. Normal pressure formations were encountered at depths from 2690 m to 2714 m, and from 2678 m to 2685.

The fracture pressures in E-BK1 (Figure 4) and E-AJ1 were estimated at 280.25 psi (FP_Res) and 17.949 psi (FP_Sonic), and 2110.24 psi (FP_Res) and 22,709.32 psi (FP_Sonic), respectively. Fracture pressure is necessary to fracture the formation at depth to induce mud loss into the fractured zone of the well. The estimated effective stress (ES) within the selected interval depth is −7.98 gm/cc for E-BK1 and −8.02 gm/cc for E-AJ1. These values imply that the ES’s negative effects may result in an overpressure zone when drilling deeper than the selected intervals.

The E-BK1 overburden gradient (OBG) and overburden pressure (OBP) were recorded as 15.35 Ibs/gal (1.84 gm/cc) and 4487.04 psi, respectively. Based on these readings, a low overburden pressure shows that E-BK1 penetrates a low-overburden water column. In E-AJ1, the overburden gradient (OBG) and overburden pressures were recorded at 17.3 Ibs/gal (1.88 gm/cc) and 7991.54 psi, respectively, suggesting that E-AJ1 penetrated under a column with excessive water overburden and thus an increased overburden pressure. Pore pressure gradient (PPG) values during well drilling determine how much mud weight is needed to mitigate the loss of circulation or kick. Pore pressure gradients (PPG) of 8.4 Ibs/gal (1.01 gm/cc) for PPG_Res and 8.3 Ibs/gal (0.99 gm/cc) for PPG_Sonic were determined for E-BK1, whereas E-AJ1 recorded 9.59 Ibs/gal (1.15 gm/cc) for PPG_Res and 8.28 Ibs/gal (0.99 gm/cc) for PPG_Sonic within the overpressured zone.

The sonic and resistivity fracture gradients (FG) were estimated to be 11.55 gm/cc and 7.40 gm/cc, respectively, in E-BK1 (Figure 5). FG serves as the maximum weight of mud needed to drill the formation. A mud weight (MW) of 2 gm/cc was determined to be the required weight to drill through the reservoir interval between 2942 m and 2983 m in E-BK1. The fracture gradients in E-AJ1 were estimated to be 15.52 Ibs/gal (1.86 gm/cc) for FG_Res and 15.23 Ibs/gal (1.86 gm/cc) for FG_Sonic. The mud weight (MW) calculated for this well was 2.02 Ibs/gal (0.26 gm/cc). These values allow determination of the pressures needed to break the formation and cause mud loss.

The predicted pore pressure values for the reservoir interval during drilling in E-BK1 are 4258.03 psi (PP_Res) and 4196.80 psi (PP_Sonic) (Figure 3). Fluids are free to move in this interval, hence the decrease in pore pressure at the wellbore. E-BK1 has with normal pressure formations at the selected reservoir interval (Figure 3, Figure 4 and Figure 5). In E-AJ1, an overpressured zone was identified (2685 m to 2716 m, and 2716 m to 2735 m), showing an increase in pore pressure due to more fluid in the pore spaces and giving the values of 3939.27 psi (PP_Res) and 4334.08 psi (PP_Sonic).

The pore pressures predicted for the studied reservoir interval (2677 m to 2735 m) are psi 4310.06 psi (PP_Res) and 3818.78 psi (PP_Sonic).

In E-CB1, the interval of interest ranges from 2509 to 2544 m in Figure 6. E-CB1 has normal pressure formations, as demonstrated by the Normal Compaction Trend on both NCT-Res and NCT_Sonic on tracks 4 and 5 (Figure 6), which showed a decrease in shale sonic values and an increase in shale resistivity with readings of 93 µs/f and 7.13 ohm/m, respectively. Furthermore, these data suggest the presence of hydrocarbons in the formations.

The overburden gradient (OBG) and overburden pressure showed values of 17.28 Ibs/gal (2.07 gm/cc) and 7442.56 psi, meaning that the well would penetrate through a higher overburden water column, resulting in increased overburden pressure (Figure 7). The pore pressure gradients (PPG) were used to calculate the mud weight of 8.28 Ibs/gal (0.992 gm/cc) for PPG_Res and PPG_Sonic, respectively.

The fracture gradients were estimated at 13.03 Ibs/gal (1.56 gm/cc) for FG_Res and 13.35 Ibs/gal (1.60 gm/cc) for FG_Sonic (Figure 8). The fracture gradient determines the maximum mud weight needed to drill a well. A mud weight (MW) of 6.64 Ibs/gal (0.79 gm/cc) was estimated. According to these estimated data, the fracture gradient (FG) is higher than the mud weight (MW), suggesting that E-CB1 would be stabilized. This stability means that there would be no circulation or mud loss throughout the drilling process. The fracture pressures were estimated to be 2212.41 psi (FP_Res) and 2445.12 psi (FP_Sonic). These fracture pressure values made it possible to determine the pressures needed to break the formation and induce mud loss into the borehole.

Within the targeted reservoir range of 2509 m to 2544 m depth, the effective stress (ES) was −10.17 gm/cc. Because of the adverse effect of effective stress, drilling deeper than the chosen interval may result in an overpressured zone. The pore pressure values of 3563.74 psi (PP_Res) and 3578.75 psi (PP_Sonic) are expected to be encountered during the drilling of the formation (Figure 6, Figure 7 and Figure 8). A comparison of the pore pressure results estimated from different methods is presented in

Table 2. Comparison of the predicted results for pore pressure using different methods.

WELL	Eaton Resistivity (psi)	Eaton Sonic (psi)	Mathews and Kelly (psi)	Modified Eaton (psi)	Baker and Wood (psi)	Bowers
E-BK1	4258.03	4196.80	4258.03	4258.04	4258.03	4258.04
E-AJ1	4310.06	3818.78	4310.06	4310.06	4310.06	4310.06
E-CB1	3563.74	3578.75	3563.73	3563.74	3563.75	3563.74

.

4.2. Fluid Contacts Determination Using Repeat Formation Test (RFT) Data

A total of nineteen RFT pressure tests were carried out within the E-BK1 reservoir (2942 m to 2983 m), and thirty-one in E-AJ1 (2677 to 2735 m) and E-CB1 (2509 to 2544 m), respectively, to determine formation pressures, fluid contacts, fluid gradients, and densities. The pressure versus depth plot for E-BK1 (Figure 9) shows that this reservoir is gas-filled with a calculated gradient of 0.45 psi/m and a density of 0.32 g/cc. A gas pressure of less than 3850 psi was recorded. Fluid contact determination was impossible in this reservoir due to the missing RFT data. In E-AJ1 (Figure 10), two main fluid contacts, oil–water and gas–oil contacts (OWC and GOC), were observed at 2699 m and 2723 m where the pressure gradient lines intersect. The gradients of the gas line, oil line, and water line were 0.33 psi/m, 0.98 psi/m, and 1.44 psi/m, respectively. Pressures below 3928 psi, 3906 psi, and 3920 psi were observed for the oil, gas, and water lines, respectively. The data for E-CB1 (Figure 11) shows that a single oil–water contact (OWC) was encountered at 2528.5 m, with water and oil gradients of 1.37 psi/m and 0.85 psi/m, respectively. Additionally, the densities of water and oil were determined to be 0.97 g/cc and 1.00 g/cc. Within the reservoir interval (2509 m to 2544 m), water and oil pressure lines below 3720 psi and 3690 psi were measured. Since E-CB1’s supercharged points are unreliable, they were ignored in the pressure–depth plot.

Table 3. Summary of pressure gradients and densities for all wells.

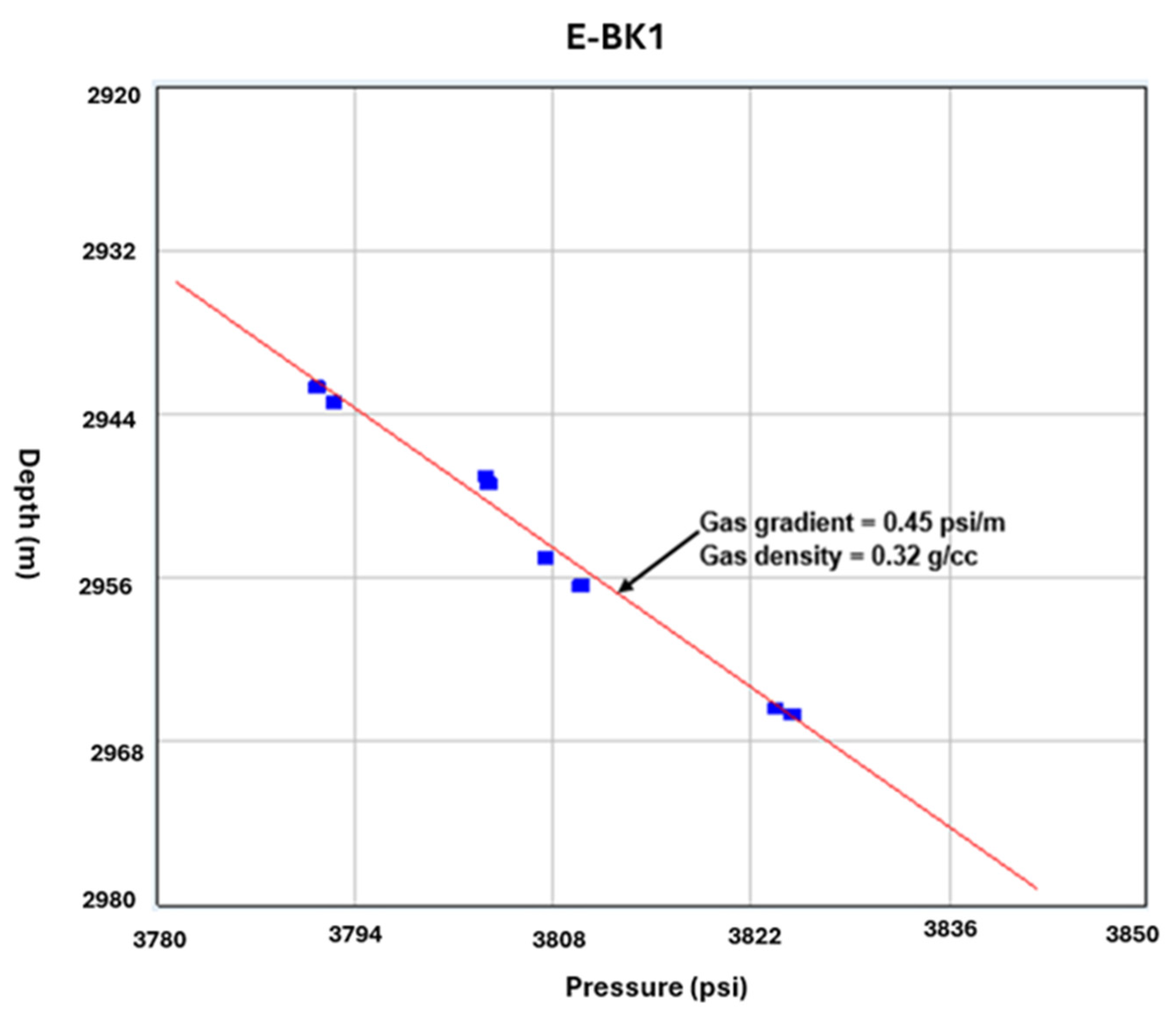
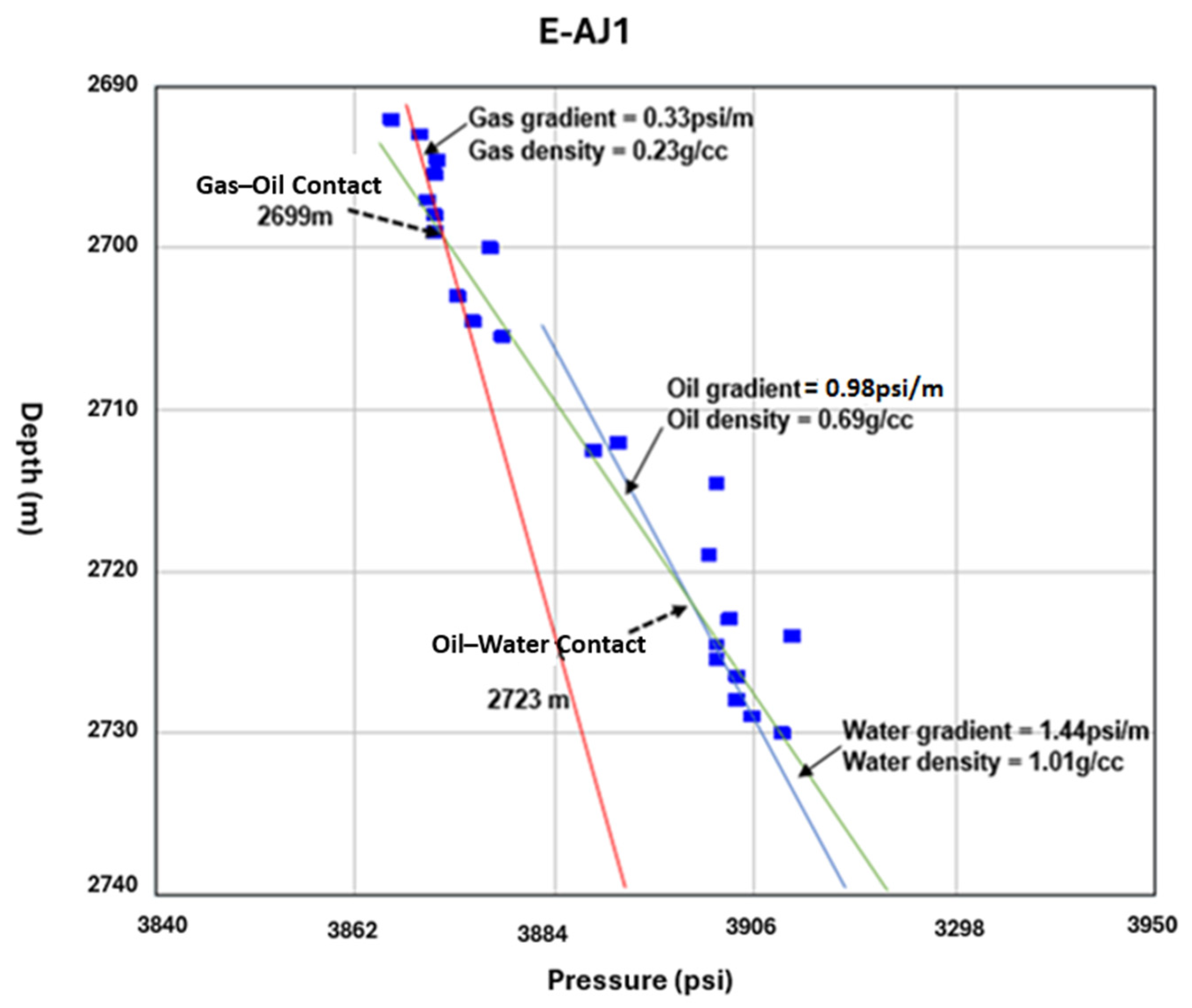
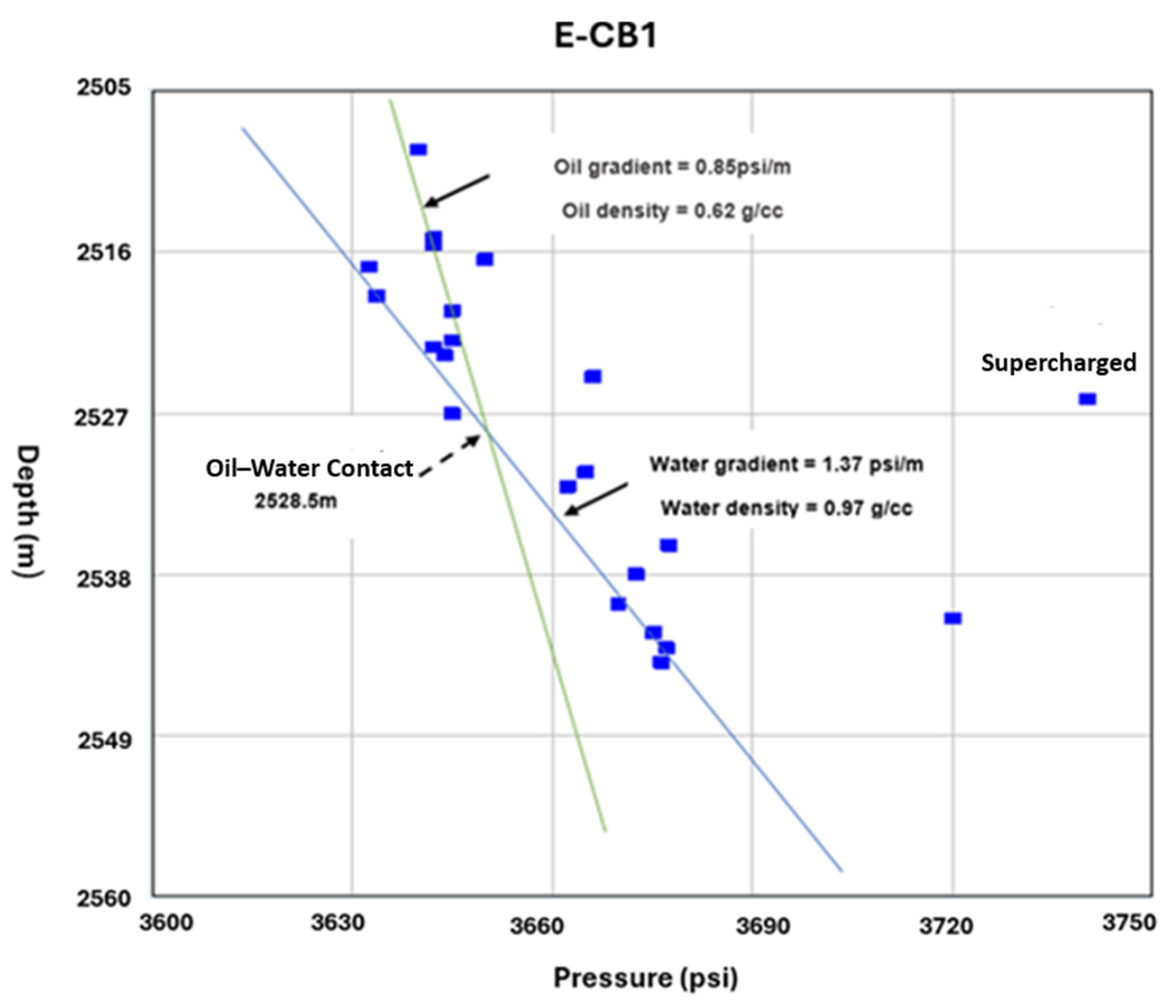
Well	Water Gradient	Density (g/cc)	Oil Gradient	Density (g/cc)	Gas Gradient	Density (g/cc)
E-BK1	–	–	–	–	0.14 psi/ft	0.32
					0.45 psi/m
E-AJ1	0.44 psi/ft	1.01	0.30 psi/ft	0.69	0.1 psi/ft	0.23
	1.44 psi/m		0.98 psi/m		0.33 psi/m
E-CB1	0.42 psi/ft	0.97	0.26 psi/ft	1.00	–	–
	1.37 psi/m		0.85 psi/m
Average	0.43 psi/ft	0.99	0.28 psi/ft	0.85	0.12 psi/ft	0.28
	1.41 psi/m		0.92 psi/m		0.39 psi/m

below summarizes the water, oil, and gas gradients determined from the pressure data of each well. The results show that the water gradient ranges between 1.37 and 1.44 psi/m (0.97 and 1.01 g/cc equivalent). The oil gradient ranges between 0.85 and 0.98 psi/m (1 and 0.69 g/cc), and the gas gradient ranges between 0.33 and 0.45 psi/m (0.23 and 0.32 g/cc).

4.3. Log and RFT Data Fluid Contacts Comparison

The integration and comparison of the log and RFT results were performed to adequately predict/locate the fluid contacts in the studied intervals. The comparison was successfully performed for E-AJ1 and E-CB1. For E-BK1, the resistivity, density, and neutron porosity logs identified a gas–water contact at 2967.5 m with a 25.5 m gas column. However, due to missing RFT data, an adequate comparison could not be achieved. Below, we present a detailed comparison of E-AJ1 and E-CB1.

Figure 12 compares and integrates the results obtained from well logs with RFT within the E-AJ1 studied reservoir. The oil–water contact was identified at 2723 m, while the gas–oil contact was encountered at 2699 m using the well log. The well log and RFT-identified contacts are in agreement with each other. The well logs analysis shows a 6 m gas column, a 24 m high oil production column, and a 12 m water column. A gas–oil contact from 2699 m and 3870 psi formation pressure were observed, while an oil–water contact from 2723 m and 3907 psi formation pressure were also observed.

Figure 13 compares the pressure data and log with the identified oil–water contact for well E-CB1. At a depth of 2523 m, the resistivity curve did, however, show an oil–water contact. The contact occurred at 2528.5 m depth; therefore, it differs from the one determined by the pressure data. The log and pressure data used to establish the oil–water contact do not concur because the well log observations showed a shallower depth compared to RFT data, with a depth difference of 5.5 m. The water and oil gradient results—1.37 psi/m (equivalent to 0.97 g/cc) and 0.85 psi/m (equivalent to 1.00 g/cc)—suggest that the sandstone reservoir seems to be hydraulically connected. The oil–water contact formation pressure observed at 2528.5 m was 3642 psi.

5. Discussion

The application of resistivity and sonic logs, and Eaton’s method of generating a depth-dependent NCT produced relatively similar pore pressure results for all three reservoirs (Figure 3 and Figure 6). The three studied reservoirs’ estimated mud weights (MW) were 2.00 gm/cc, 0.26 gm/cc, and 0.79 gm/cc, respectively. These mud weights are needed to maintain the borehole’s stability during drilling [5,8]. Precisely estimating the mud weight would minimize mud loss or circulation during drilling. However, if excessive mud weight is employed, the will experience fluid circulation loss, meaning that the hydrostatic pressure of mud with an abnormally low mud weight will be less than the pressure of the formation [8,11,62,63]. As a result, pressure fluid from the formation will start to rise to the surface through the wellbore and cause a kick in the formation, resulting in an uncontrollably high blowout should the invasive fluid reach the surface [5,8,11,63,64]. Therefore, to avoid formation fracture as measured by PPG_Res and PPG_Sonic, the MW must be lower than the fracture gradient values to avert circulation loss and kicks during the formation drilling process. This ensures that the wellbore remains stable and that the fracture gradients will be maintained before cementing and installing the well’s casing, preventing the borehole’s fracture during drilling.

The effective stresses (ES) within the studied reservoirs were recorded as −7.98 gm/cc, −8.02 gm/cc, and −10.17 gm/cc, respectively. These values suggest that overpressured formations would be encountered when drilling across the studied interval due to the negative impact of the effective stress. ES enhances the detection of overpressured and normal pressured formations [11,57]. The predicted pore pressures (PPP) likely to be encountered during the drilling of the selected wells were 4258.03 psi (PP_Res) and 4196.80 psi (PP Sonic) in well E-BK1, 4310.06 psi (PP_Res) and 3818.78 psi (PP_Sonic) in well E-AJ1, and 3563.74 psi (PP_Res) and 3578.75 psi (PP_Sonic) in well E-CB1, respectively (Table 3). Notably, normal pore pressures and overpressure zones were identified in all the wells except for E-AJ1. Significant overpressure zones were identified from 2685 m to 2716 m, and from 2716 m to 2735 m in the pores exceeding 7996.43 psi (Figure 6).

The Eaton’s resistivity and density/neutron methods confirmed the normal pressure zones in E-BK1 (Figure 3) and overpressured zones in E-AJ1. However, in E-CB1, the resistivity and density/neutron log methods detected an overpressured zone enhanced by the undercompaction of the formation. These pore pressures were observed from sonic shale and resistivity shale log deviations from the NCT. Overpressured formations were detected by shale resistivity when the log deviated from the NCT towards the lower values, whereas the sonic shale log detected the overpressured formations when it deviated from the designated NCT towards the higher values. Conversely, when shale resistivity deviates from the NCT towards the higher values, it suggests a normal pressure formation, and the deviation towards the lower values suggests a normal pressure zone for sonic shale logs [10,55]. The pore pressure results (Table 2) showed that the Eaton resistivity, Mathews and Kelly, Modified Eaton, and Baker and Wood, and Bowers methods agree with each other, whereas the Eaton sonic method showed varied results. This discrepancy occurs because, when determining the Normal Compaction Trend (NCT) of the formation, which depicts the expected compaction behavior of the formation with increasing depth, the Eaton sonic method detects the abnormal pressure formations by identifying sonic shale log (DT) deviations from the established NCT towards the higher values. Other methods detect abnormal pressure (overpressure) formations by identifying the resistivity of shale deviations from the NCT established closer to the lower values [10].

The wireline logs and RFT data identified fluid contacts within the selected reservoir intervals. The RFT results identified fluid contacts only in two wells, E-AJ1 and E-CB1. The fluid contacts in E-BK1 (Figure 9) could not be determined because of the missing RFT data. In E-AJ1 (Figure 10), oil–water and gas–oil contacts (GOC and OWC) were encountered at 2699 m and 2723 m, with a water density of 1.01 g/cm³, gas density of 0.23 g/cm³ and an oil gradient of 0.69 g/cm³. In E-CB1 (Figure 11), an oil–water contact (OWC) was encountered at a depth of 2528.5 m, with a water density of 0.97 g/cm³ and an oil density of 0.62 g/cm³. The following observations were made from the wireline logs (resistivity, density and neutron): A gas–water contact (GOC) was encountered at 2967.5 m in E-BK1. Gas–oil and oil–water contacts (GOC and OWC) were encountered at 2699 m and 2723 m depths in E-AJ1 (Figure 12), and an oil–gas contact (OGC) was encountered at 2523 m in E-CB1 (Figure 13). Fluid contacts observed from the well logs and RFT pressure data (

Table 4. Log and RFT fluid contacts comparison results summary.

Well	Well Log GWC Depth (m)		RFT GWC Depth (m)
	Resistivity	Neutron/Density	RFT	Observation
EBK-1	2967.5	2967.5	–	-
	Well Log OWC Depth (m)		RFT OWC Depth (m)
	Resistivity	Neutron/Density	RFT	Observation
E-AJ1	2723	2723	2723	Agreement
E-CB1	2523	2523	2528.5	Disagreement
	Well Log GOC Depth (m)		RFT GOC Depth (m)
	Resistivity	Neutron/Density	RFT	Observation
E-AJ1	2699	2699	2699	Agreement

RFT = repeat formation test; GWC = gas–water contact; OWC = oil–water contact; GOC = gas–oil contact; (m) = meters.

) in E-AJ1 were in close agreement as they showed similar depths of encounter. There was no agreement between the well log and RFT fluid contact in E-CB1 (Figure 13), with a discrepancy of 5.5 m. These discrepancies could be attributed to the inaccuracy of the fluid densities estimated from pressure gradients. The estimated fluid densities in the E-CB1 well differ from the actual densities. (The actual density for gas is 0.08 g/cm³, that for water is 1 g/cm³, and that for oil ranges between 0.7 and 0. 9 g/cm³.) The estimated fluid densities for oil (0.62 g/cm³) and water (0.97 g/cm³) were lower than the actual densities. Considering the inaccuracies regarding the fluid densities in E-CB1 estimated from the pressure gradients, the OGC contact from RFT data could be assumed to be inaccurate. This observation agrees with those of [8]. The possible explanation for the differences between the estimated and actual fluid densities in E-CB1 may be due to formation testers not recording pressures from the virgin fluid but from a mixture of water and hydrocarbons [8]. This is usually the case in thicker and high-quality reservoirs [8]. Ref. [19] also observed discrepancies between the RFT and well log contacts in the nearby basin and attributed the discrepancies to the presence of chlorite minerals in the reservoir, leading to the inaccurate reading of the resistivity log in the formation. As previously highlighted by [65], the reservoirs in this basin contain a substantial amount of chlorite. Other factors could be pressure variations, high water production, and supercharging in this well. Changes in pressure affect the fluid contact depth, leading to differences between the well log and RFT data. An increased pressure can cause the fluid contact to move downward, resulting in a deeper RFT-measured depth. High water production in the well, likely due to the dominant clay mineral, leads to low resistivity readings. This can cause the well log data to indicate a shallower fluid contact depth compared to the RFT data. Supercharged pressure points were observed in well E-CB1. Supercharged points often occur in very low permeability environments when the formation is overpressurized [19]. In contrast, the estimated fluid densities from the pressure gradients in E-AJ1 were similar to the actual densities (Table 3); hence, RFT and well logs identified similar fluid contacts.

Putting it all together, we observed that the results (Figure 10, Figure 11, Figure 12 and Figure 13) showed a close correlation between fluid contact and pore pressure. Fluid contacts associated with overpressures were gas–water and oil–water contacts. In contrast, gas–oil contact was associated with underpressure.

Generally, drive mechanisms play an important role in influencing the nature of the fluid contacts and the associated formation pressures. A gas cap drive mechanism influences the low pressure encountered in the GOC. The theory is that the wells are completed across the oil column during drilling operations to avoid producing gas from the cap [66]. The pressure in the reservoir drops quickly when the gas that forms from the gas cap is produced [66], leading to underpressure in the GOC (Figure 10). Contrarily, the gas–water and oil–water contacts are associated with overpressure due to the buoyancy of the hydrocarbons and the fluid density differences. Therefore, an oil and gas column above the water contact leads to high pore pressure (overpressure) in the GWC and OWC contact compared to water alone [66]. Figure 10 and Figure 11 demonstrate the high pore pressure in the GWC and OWC contact. These observations are consistent with those of [15], which demonstrated that hydrocarbon buoyancy may cause an increase in pressure due to the differences in pressure gradients between oil, gas, and water.

6. Conclusions

Understanding the relationship between fluid contacts and pore pressure is crucial for hydrocarbon recovery and drilling operations. Overpressure and normal pressures affect the fluid contacts in the reservoir. The results showed a close correlation between fluid contact and pore pressure. The fluid contacts that are associated with overpressures are gas–water and oil–water contacts. Pore pressure seemed to increase where gas–water and oil–water contacts were detected. An increase in pore pressure can cause a displacement of fluid contacts, either vertically or laterally. Conversely, pore pressures decreased where gas–oil contact was detected. Decreased pore pressure results from gas expansion and increased gas volume.

This study illustrates the significance of an integrated approach to predicting fluid contacts and pore pressure within reservoirs using geophysical well logs and RFT. The RFT and geophysical well logs offered useful information and assisted in improving the accuracy of pore pressure and identifying contacts by assessing their behaviors. Therefore, it can be concluded that integrating RFT and Eaton’s method of developing a depth-dependent NCT using sonic and resistivity logs can aid in predicting pore pressure based on the type of fluid contact.