EKNet: Graph Structure Feature Extraction and Registration for Collaborative 3D Reconstruction in Architectural Scenes
Abstract
1. Introduction
- A point cloud registration framework based on feature metric geometry is introduced. This framework ensures high accuracy while enhancing improving computational efficiency. Compared with the Graph Convolutional Network (GCN) method, the proposed framework achieves a 27.28% improvement computational efficiency.
- A graph-structured, multidimensional feature construction module has been designed. By integrating geometric features with complex network indicators, this module significantly enhances the robustness of the registration results.
- A lightweight graph neural network, EKNet, has been developed. With an overlap rate of 20%, EKNet achieves a registration accuracy that is 80.66% higher than that of the sub-optimal method.
- Open-source GPCR, a geometric point cloud registration dataset for building structures, is now available. This dataset is distinguished by its extensive scale and diversity, providing substantial support for advancing research and development in the field.
2. Related Work
2.1. Registration Methods
2.1.1. Original-Point-Information-Based Methods
2.1.2. Feature Point-Based Methods
2.1.3. Learning-Based Methods
2.2. Graph Feature Extraction Methods
3. Problem Formulation
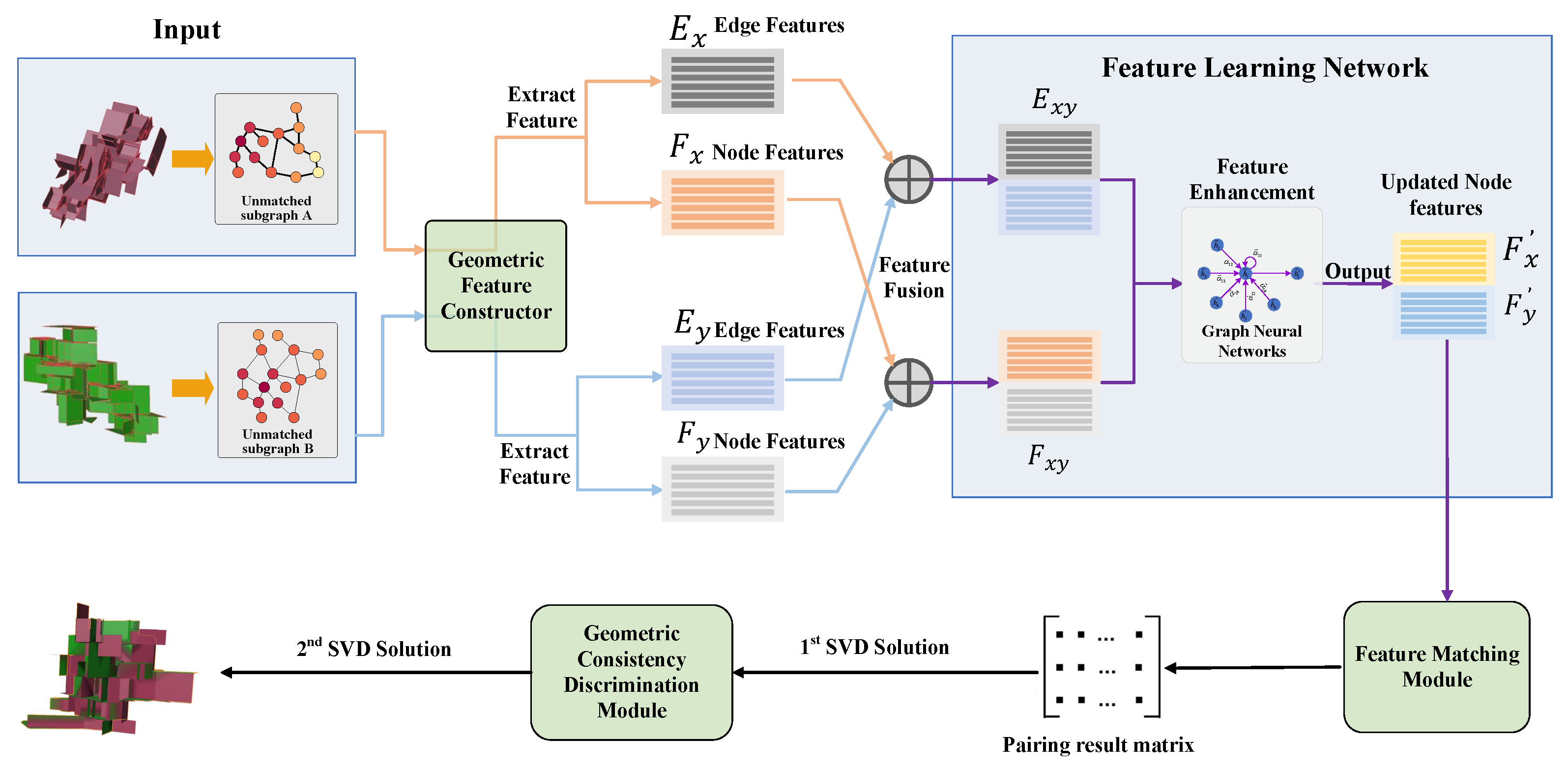
4. Methods
4.1. Feature Construction Module (FCM)
- Edge length: The Euclidean distance between the two endpoints of the edge.
- Edge direction: The normalized direction vector from one endpoint to the other (3 dimensions including xyz).
- Edge loop count: The number of loops occupied by an edge. The meaning of a ring is to characterize the number of connected edges that are connected head to tail to form a closed loop.
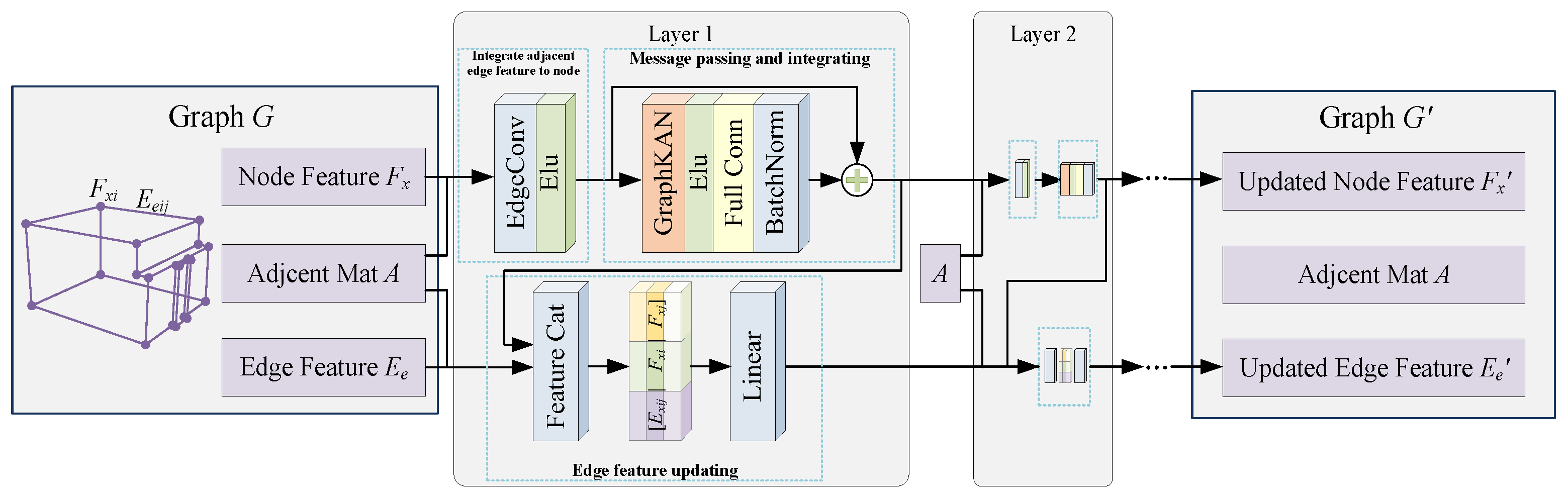
4.2. Feature Learning Network Module (FLNM)
4.2.1. Update of Node Features
4.2.2. Update of Edge Features
- It can obtain non-local structural features of nodes as well as more refined higher-order features.
- It can effectively prevent the problem of feature oversmoothing.
- It can aggregate multidimensional edge features to the central node.
4.3. Loss Function
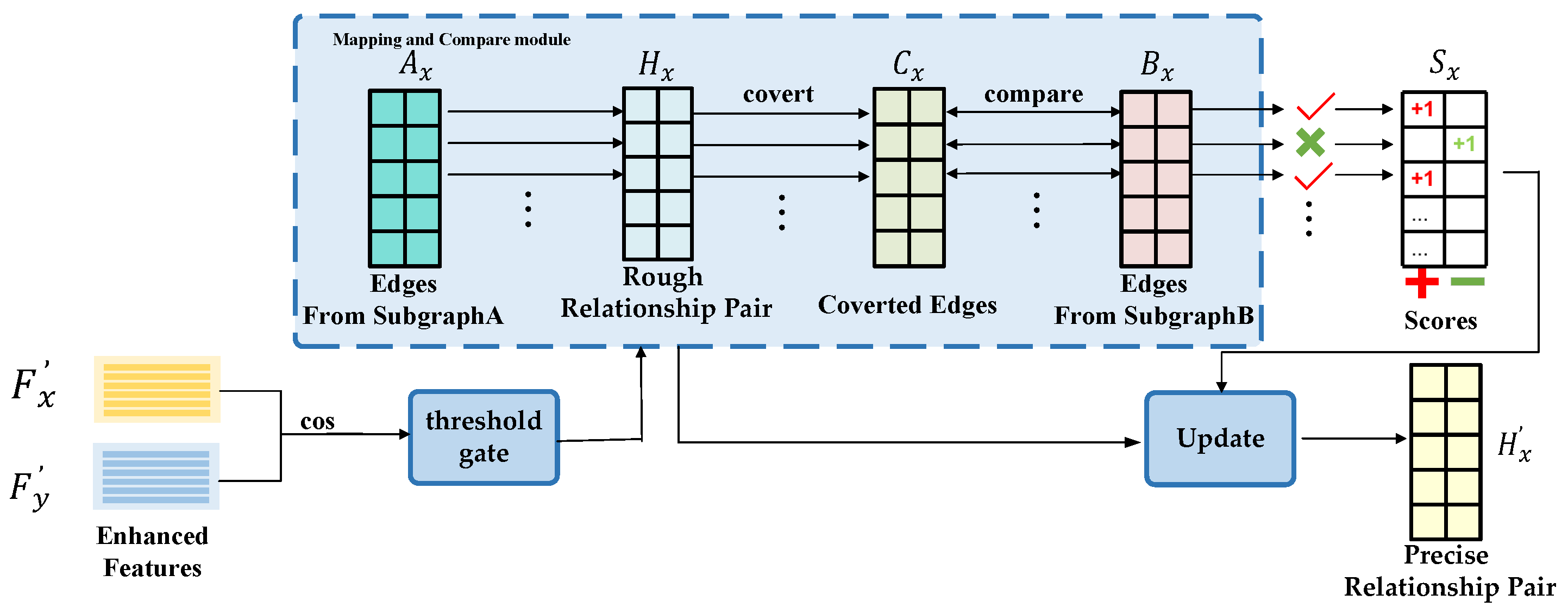
4.4. Node Feature Matching Module (NFMM)
- Threshold Setting: The module begins by computing the cosine similarity matrix from the enhanced node features of the corresponding points in the two images. A threshold filter is then applied, which considers pairs with a cosine similarity below 0.8 as non-matching and excludes them. The pairs with the highest cosine values are selected to form a preliminary coarse correspondence matrix .
- Prediction Matrix Generation: We map each edge from the edge matrix of one of the images to be registered, based on the point correspondence matrix , by scanning row by row. This process results in the predicted point correspondence matrix for the target image.
- Accumulation Matrix Construction: An accumulation matrix is constructed to match the generated edge correspondences. The first column of represents the positive accumulation for each point, while the second column represents the negative accumulation.
- Comparison: Matrix is compared row by row with the edge distance matrix of the corresponding image to be registered. If an edge from is found in , the positive integral for the corresponding points in the integral matrix is incremented by one; otherwise, the negative integral is incremented.
- Updating the Correspondence Matrix: After completing the comparison of all edges, the integral matrix is used to determine the retention of edges. An edge is retained if the absolute value of its positive integral exceeds its negative integral; otherwise, it is discarded. The final output is the feature-matched point cloud correspondence matrix .
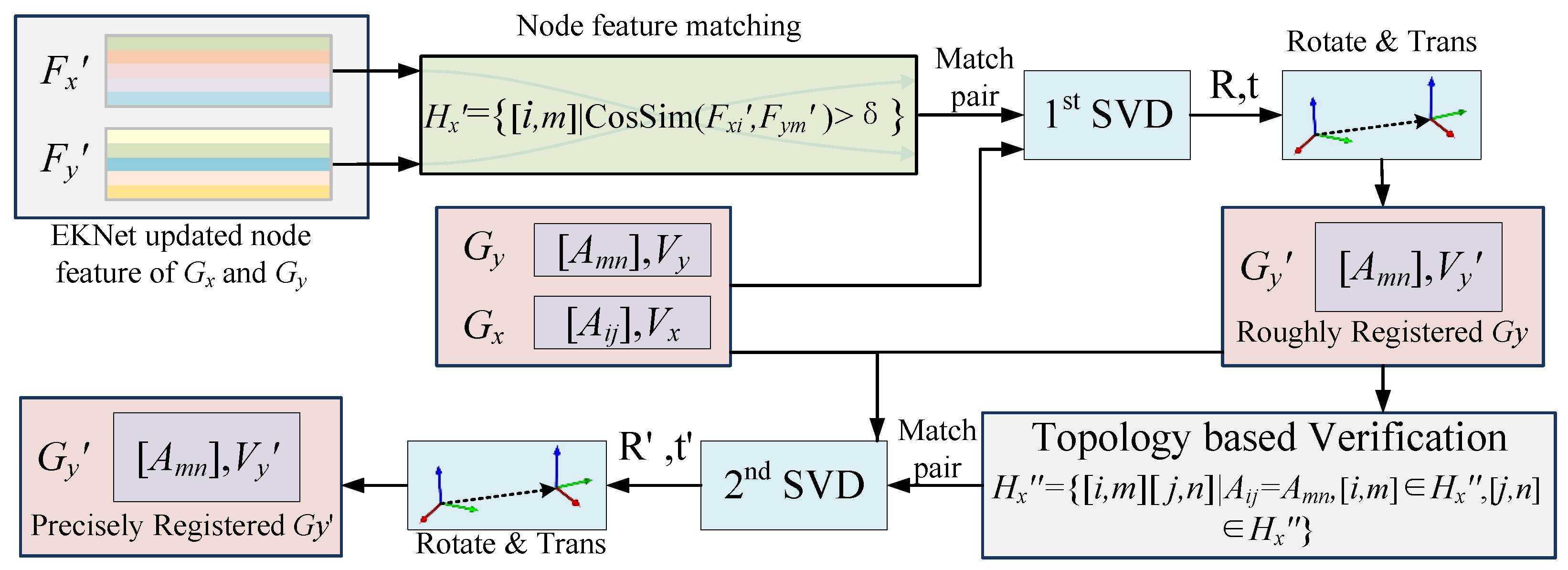
4.5. Geometric Consistency Discrimination Module (GCDM)
5. Experiments
5.1. Dataset Construction
5.2. Evaluation Metrics
5.3. Implementation Details
5.4. Experimental Results
5.4.1. Comparison Experiments with Different Overlap Rates
5.4.2. Comparison Experiments with Noisy Data
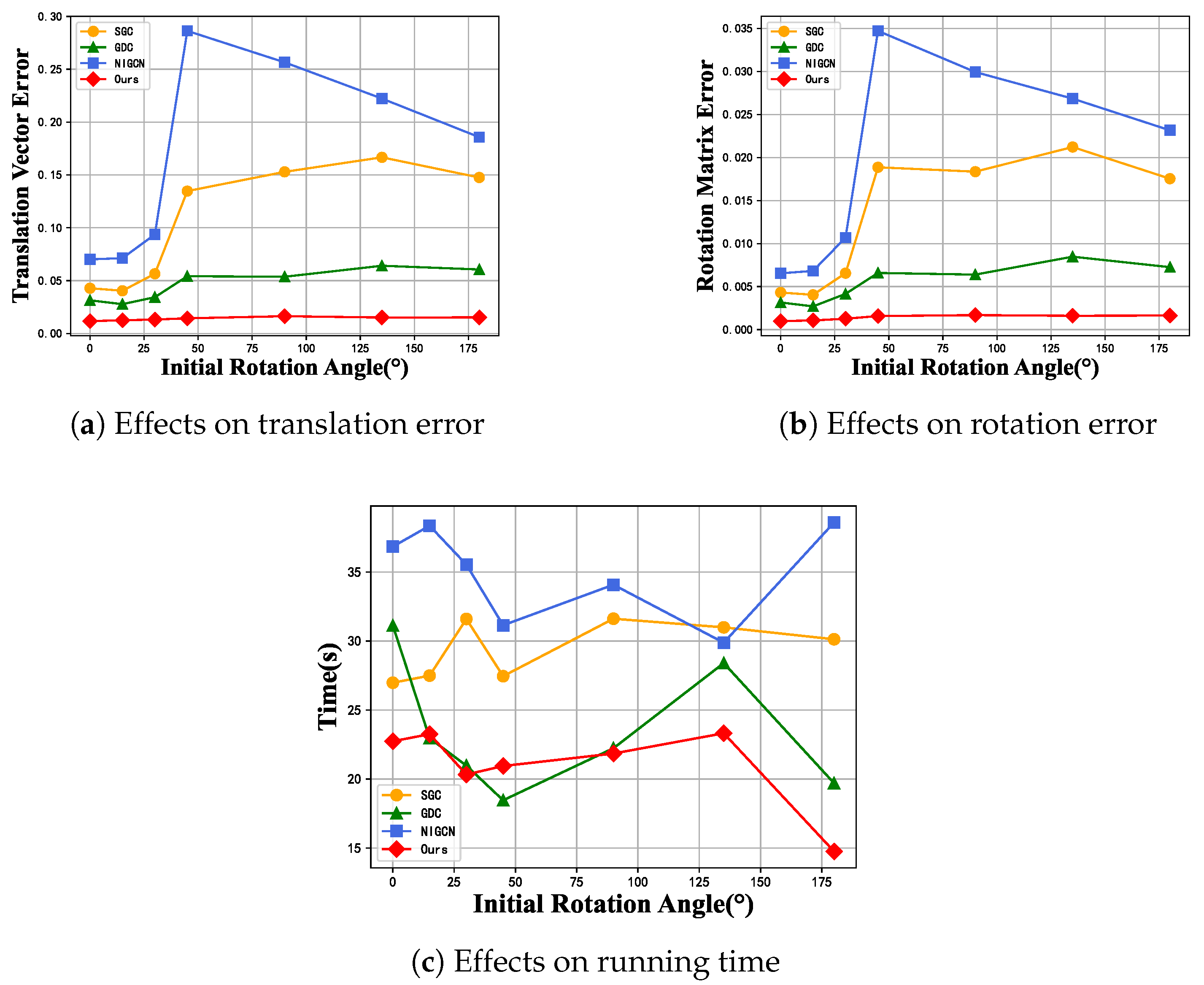
5.4.3. Effect of Initial Rotation Angles on Registration Results
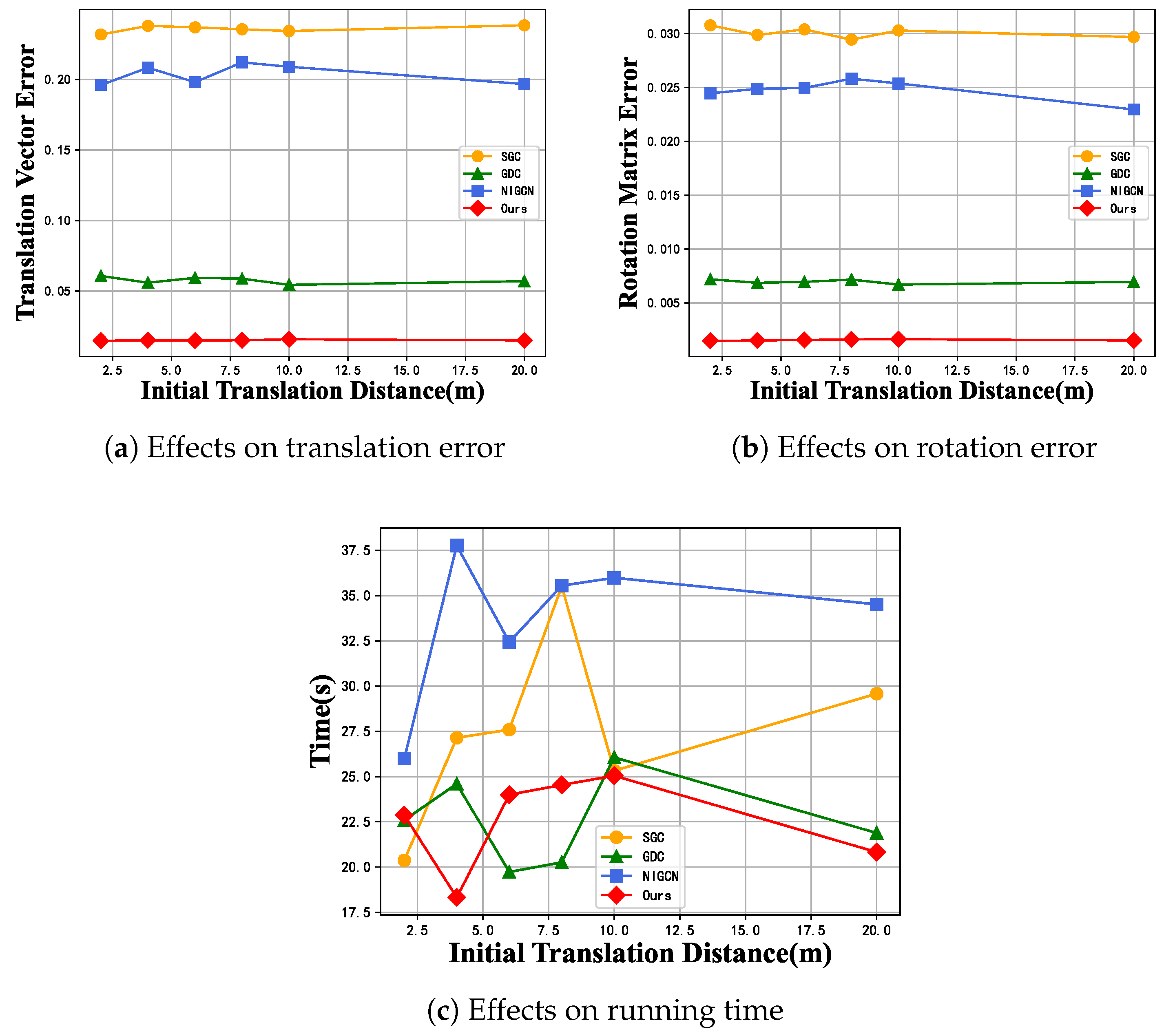
5.4.4. Effect of Initial Translation Distances on Registration Results
5.5. Ablation Studies
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lyu, M.; Yang, J.; Qi, Z.; Xu, R.; Liu, J. Rigid pairwise 3D point cloud registration: A survey. Pattern Recognit. 2024, 151, 110408. [Google Scholar] [CrossRef]
- Pomerleau, F.; Colas, F.; Siegwart, R. A review of point cloud registration algorithms for mobile robotics. Found. Trends® Robot. 2015, 4, 1–104. [Google Scholar] [CrossRef]
- Surmann, H.; Slomma, D.; Grobelny, S.; Grafe, R. Deployment of Aerial Robots after a major fire of an industrial hall with hazardous substances, a report. In Proceedings of the 2021 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), New York, NY, USA, 25–27 October 2021; pp. 40–47. [Google Scholar]
- Paolanti, M.; Pierdicca, R.; Martini, M.; Di Stefano, F.; Morbidoni, C.; Mancini, A.; Malinverni, E.S.; Frontoni, E.; Zingaretti, P. Semantic 3D object maps for everyday robotic retail inspection. In Proceedings of the New Trends in Image Analysis and Processing—ICIAP 2019: ICIAP International Workshops, BioFor, PatReCH, e-BADLE, DeepRetail, and Industrial Session, Trento, Italy, 9–10 September 2019; Revised Selected Papers 20. Springer: Cham, Switzerland, 2019; pp. 263–274. [Google Scholar]
- Peng, F.; Wu, Q.; Fan, L.; Zhang, J.; You, Y.; Lu, J.; Yang, J.Y. Street view cross-sourced point cloud matching and registration. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 2026–2030. [Google Scholar]
- Huang, X.; Zhang, J.; Fan, L.; Wu, Q.; Yuan, C. A systematic approach for cross-source point cloud registration by preserving macro and micro structures. IEEE Trans. Image Process. 2017, 26, 3261–3276. [Google Scholar] [CrossRef]
- Bai, X.; Luo, Z.; Zhou, L.; Fu, H.; Quan, L.; Tai, C.L. D3feat: Joint learning of dense detection and description of 3D local features. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 6359–6367. [Google Scholar]
- Wang, H.; Liu, Y.; Dong, Z.; Guo, Y.; Liu, Y.S.; Wang, W.; Yang, B. Robust multiview point cloud registration with reliable pose graph initialization and history reweighting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 9506–9515. [Google Scholar]
- Choy, C.; Park, J.; Koltun, V. Fully convolutional geometric features. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8958–8966. [Google Scholar]
- Huang, S.; Gojcic, Z.; Usvyatsov, M.; Wieser, A.; Schindler, K. Registration of 3D Point Clouds with Low Overlap. In Proceedings of the Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 1–60. [Google Scholar]
- Qin, Z.; Yu, H.; Wang, C.; Peng, Y.; Xu, K. Deep graph-based spatial consistency for robust non-rigid point cloud registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 5394–5403. [Google Scholar]
- Yu, Z.; Qin, Z.; Zheng, L.; Xu, K. Learning Instance-Aware Correspondences for Robust Multi-Instance Point Cloud Registration in Cluttered Scenes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–21 June 2024; pp. 19605–19614. [Google Scholar]
- Pomerleau, F.; Liu, M.; Colas, F.; Siegwart, R. Challenging data sets for point cloud registration algorithms. Int. J. Robot. Res. 2012, 31, 1705–1711. [Google Scholar] [CrossRef]
- Koide, K.; Yokozuka, M.; Oishi, S.; Banno, A. Voxelized GICP for fast and accurate 3D point cloud registration. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 11054–11059. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Gojcic, Z.; Zhou, C.; Wegner, J.D.; Wieser, A. The perfect match: 3D point cloud matching with smoothed densities. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5545–5554. [Google Scholar]
- Li, J.; Hu, Q.; Ai, M. Point cloud registration based on one-point ransac and scale-annealing biweight estimation. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9716–9729. [Google Scholar] [CrossRef]
- Zhang, J.; Yao, Y.; Deng, B. Fast and robust iterative closest point. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3450–3466. [Google Scholar] [CrossRef]
- Adiyatov, O.; Varol, H.A. A novel RRT*-based algorithm for motion planning in dynamic environments. In Proceedings of the 2017 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 6–9 August 2017; pp. 1416–1421. [Google Scholar]
- Shiarlis, K.; Messias, J.; Whiteson, S. Rapidly exploring learning trees. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1541–1548. [Google Scholar]
- Wang, X.; Zhu, M.; Bo, D.; Cui, P.; Shi, C.; Pei, J. Am-gcn: Adaptive multi-channel graph convolutional networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual, 6–10 July 2020; pp. 1243–1253. [Google Scholar]
- Feng, A.; You, C.; Wang, S.; Tassiulas, L. Kergnns: Interpretable graph neural networks with graph kernels. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022; Volume 36, pp. 6614–6622. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Meng, Y.; Shang, R.; Shang, F.; Jiao, L.; Yang, S.; Stolkin, R. Semi-supervised graph regularized deep NMF with bi-orthogonal constraints for data representation. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 3245–3258. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Sensor Fusion IV: Control Paradigms and Data Structures, Boston, MA, USA, 14–15 November 1991; Volume 1611, pp. 586–606. [Google Scholar]
- Greenspan, M.; Yurick, M. Approximate kd tree search for efficient ICP. In Proceedings of the Fourth International Conference on 3-D Digital Imaging and Modeling, 2003 (3DIM 2003), Proceedings, Banff, AB, Canada, 6–10 October 2003; pp. 442–448. [Google Scholar]
- Min, Z.; Wang, J.; Meng, M.Q.H. Robust generalized point cloud registration using hybrid mixture model. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 4812–4818. [Google Scholar]
- Lo, T.W.R.; Siebert, J.P. Local feature extraction and matching on range images: 2.5 D SIFT. Comput. Vis. Image Underst. 2009, 113, 1235–1250. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Sipiran, I.; Bustos, B. Harris 3D: A robust extension of the Harris operator for interest point detection on 3D meshes. Vis. Comput. 2011, 27, 963–976. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. Visual-lidar odometry and mapping: Low-drift, robust, and fast. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2174–2181. [Google Scholar]
- Prakhya, S.M.; Liu, B.; Lin, W. B-SHOT: A binary feature descriptor for fast and efficient keypoint matching on 3D point clouds. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1929–1934. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Marton, Z.C.; Beetz, M. Aligning point cloud views using persistent feature histograms. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3384–3391. [Google Scholar]
- Chen, C.; Li, G.; Xu, R.; Chen, T.; Wang, M.; Lin, L. Clusternet: Deep hierarchical cluster network with rigorously rotation-invariant representation for point cloud analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4994–5002. [Google Scholar]
- Aoki, Y.; Goforth, H.; Srivatsan, R.A.; Lucey, S. Pointnetlk: Robust & efficient point cloud registration using pointnet. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7163–7172. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3D classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Wang, Y.; Solomon, J.M. Deep closest point: Learning representations for point cloud registration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3523–3532. [Google Scholar]
- Vaswani, A. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Li, J.; Zhang, C.; Xu, Z.; Zhou, H.; Zhang, C. Iterative distance-aware similarity matrix convolution with mutual-supervised point elimination for efficient point cloud registration. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XXIV 16. Springer: Cham, Switzerland, 2020; pp. 378–394. [Google Scholar]
- Wang, Y.; Solomon, J.M. Prnet: Self-supervised learning for partial-to-partial registration. Adv. Neural Inf. Process. Syst. 2019, 32, 8814–8826. [Google Scholar]
- Yuan, W.; Eckart, B.; Kim, K.; Jampani, V.; Fox, D.; Kautz, J. Deepgmr: Learning latent gaussian mixture models for registration. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part V 16. Springer: Cham, Switzerland, 2020; pp. 733–750. [Google Scholar]
- Yew, Z.J.; Lee, G.H. Rpm-net: Robust point matching using learned features. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11824–11833. [Google Scholar]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. stat 2017, 1050, 10–48550. [Google Scholar]
- Xu, B.; Shen, H.; Cao, Q.; Qiu, Y.; Cheng, X. Graph wavelet neural network. arXiv 2019, arXiv:1904.07785. [Google Scholar]
- Wijesinghe, A.; Wang, Q. A new perspective on “How graph neural networks go beyond Weisfeiler-Lehman?”. In Proceedings of the International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Aziz, F.; Ullah, A.; Shah, F. Feature selection and learning for graphlet kernel. Pattern Recognit. Lett. 2020, 136, 63–70. [Google Scholar] [CrossRef]
- Phan, A.V.; Le Nguyen, M.; Nguyen, Y.L.H.; Bui, L.T. Dgcnn: A convolutional neural network over large-scale labeled graphs. Neural Netw. 2018, 108, 533–543. [Google Scholar] [CrossRef]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (elus). arXiv 2015, arXiv:1511.07289. [Google Scholar]
- Zhang, F.; Zhang, X. GraphKAN: Enhancing Feature Extraction with Graph Kolmogorov Arnold Networks. arXiv 2024, arXiv:2406.13597. [Google Scholar]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. Kan: Kolmogorov-arnold networks. arXiv 2024, arXiv:2404.19756. [Google Scholar]
- Zhou, Y.; Huo, H.; Hou, Z.; Bu, L.; Mao, J.; Wang, Y.; Lv, X.; Bu, F. Co-embedding of edges and nodes with deep graph convolutional neural networks. Sci. Rep. 2023, 13, 16966. [Google Scholar] [CrossRef]
- Gasteiger, J.; Weißenberger, S.; Günnemann, S. Diffusion improves graph learning. Adv. Neural Inf. Process. Syst. 2019, 32, 13354–13366. [Google Scholar]
- Wu, F.; Souza, A.; Zhang, T.; Fifty, C.; Yu, T.; Weinberger, K. Simplifying graph convolutional networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 10–15 June 2019; pp. 6861–6871. [Google Scholar]
- Huang, K.; Tang, J.; Liu, J.; Yang, R.; Xiao, X. Node-wise diffusion for scalable graph learning. In Proceedings of the ACM Web Conference 2023, Austin, TX, USA, 30 April–4 May 2023; pp. 1723–1733. [Google Scholar]

| Feature | Formula | Meaning |
|---|---|---|
| Degree | The number of edges connected to vertex . | |
| Average Distance | The average distance of the sum of the lengths of all edges where the point is located. | |
| Average Orientation | The value obtained by normalizing the sum of vectors extending in the direction of all edges where the point is located, starting from that point. | |
| Average Angles | The average degree of angle between the vectors that extend from this point to all the edges where the point is located, measured as the angle between each pair of vectors. |
| Feature | Formula | Meaning |
|---|---|---|
| Clustering Coefficient | The coefficient of the degree of clustering between vertices in a graph. | |
| Degree Centrality | The degree to which a node is connected to all other nodes. | |
| Eigenvector Centrality | Ranking of the likelihood of a node being visited during an infinite-length random walk in the graph. | |
| PageRank | Measures the importance of nodes through random walk models and transition probability matrices. | |
| Load Centrality | Calculates the proportion of all shortest paths in the network that pass through this node. |
| Method | RMSE(R) | RMSE(t) | MAE(R) | MAE(t) | Times(s) |
|---|---|---|---|---|---|
| GDC [53] | 0.158 | 1.080 | 0.085 | 0.554 | 17.8 |
| GAT [44] | 0.245 | 1.673 | 0.144 | 0.937 | 168.3 |
| GCN [21] | 0.176 | 1.238 | 0.092 | 0.610 | 17.4 |
| GraphKan [50] | 0.103 | 0.719 | 0.054 | 0.349 | 20.2 |
| SGC [54] | 0.451 | 3.286 | 0.280 | 1.971 | 21.9 |
| NIGCN [55] | 0.368 | 2.713 | 0.233 | 1.664 | 30.5 |
| Ours | 0.030 | 0.193 | 0.010 | 0.067 | 12.7 |
| Method | RMSE(R) | RMSE(t) | MAE(R) | MAE(t) | Times(s) |
|---|---|---|---|---|---|
| GDC [53] | 0.051 | 0.302 | 0.018 | 0.126 | 17.5 |
| GAT [44] | 0.104 | 0.909 | 0.036 | 0.273 | 168.4 |
| GCN [21] | 0.045 | 0.316 | 0.011 | 0.074 | 21.9 |
| GraphKan [50] | 0.023 | 0.173 | 0.011 | 0.083 | 24.2 |
| SGC [54] | 0.244 | 1.842 | 0.116 | 0.855 | 27.8 |
| NIGCN [55] | 0.126 | 1.043 | 0.066 | 0.513 | 28.1 |
| Ours | 0.005 | 0.037 | 0.002 | 0.017 | 18.8 |
| Method | RMSE(R) | RMSE(t) | MAE(R) | MAE(t) | Times(s) |
|---|---|---|---|---|---|
| GDC [53] | 0.012 | 0.083 | 0.006 | 0.046 | 19.4 |
| GAT [44] | 0.040 | 0.281 | 0.010 | 0.073 | 165.0 |
| GCN [21] | 0.014 | 0.100 | 0.007 | 0.057 | 19.1 |
| GraphKan [50] | 0.005 | 0.046 | 0.003 | 0.023 | 27.2 |
| SGC [54] | 0.086 | 0.592 | 0.031 | 0.237 | 28.6 |
| NIGCN [55] | 0.030 | 0.239 | 0.017 | 0.144 | 33.9 |
| Ours | 0.002 | 0.013 | 0.001 | 0.006 | 19.5 |
| Method | RMSE(R) | RMSE(t) | MAE(R) | MAE(t) | Times(s) |
|---|---|---|---|---|---|
| GDC [53] | 0.013 | 0.105 | 0.007 | 0.059 | 21.2 |
| GAT [44] | 0.051 | 0.451 | 0.012 | 0.092 | 165.5 |
| GCN [21] | 0.017 | 0.133 | 0.009 | 0.075 | 17.7 |
| GraphKan [50] | 0.008 | 0.060 | 0.004 | 0.033 | 23.5 |
| SGC [54] | 0.110 | 0.880 | 0.040 | 0.299 | 21.5 |
| NIGCN [55] | 0.117 | 0.943 | 0.043 | 0.320 | 26.1 |
| Ours | 0.003 | 0.021 | 0.002 | 0.014 | 18.8 |
| Methods | RMSE(R) | RMSE(t) | MAE(R) | MAE(t) | Times(s) | Contribution(%) |
|---|---|---|---|---|---|---|
| Full Models | 0.003 | 0.021 | 0.002 | 0.014 | 18.83 | - |
| w/o FCM | 0.038 | 0.321 | 0.020 | 0.178 | 46.83 | 25.0% |
| w/o FLNM | 0.080 | 0.589 | 0.038 | 0.291 | 31.21 | 48.5% |
| w/o NFMM | 0.015 | 0.128 | 0.009 | 0.083 | 14.25 | 9.4% |
| w/o GCDM | 0.024 | 0.193 | 0.017 | 0.143 | 24.01 | 17.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, C.; Deng, H.; Ni, X.; Wang, D.; Wei, B.; Chen, H.; Huang, J. EKNet: Graph Structure Feature Extraction and Registration for Collaborative 3D Reconstruction in Architectural Scenes. Appl. Sci. 2025, 15, 7133. https://doi.org/10.3390/app15137133
Qian C, Deng H, Ni X, Wang D, Wei B, Chen H, Huang J. EKNet: Graph Structure Feature Extraction and Registration for Collaborative 3D Reconstruction in Architectural Scenes. Applied Sciences. 2025; 15(13):7133. https://doi.org/10.3390/app15137133
Chicago/Turabian StyleQian, Changyu, Hanqiang Deng, Xiangrong Ni, Dong Wang, Bangqi Wei, Hao Chen, and Jian Huang. 2025. "EKNet: Graph Structure Feature Extraction and Registration for Collaborative 3D Reconstruction in Architectural Scenes" Applied Sciences 15, no. 13: 7133. https://doi.org/10.3390/app15137133
APA StyleQian, C., Deng, H., Ni, X., Wang, D., Wei, B., Chen, H., & Huang, J. (2025). EKNet: Graph Structure Feature Extraction and Registration for Collaborative 3D Reconstruction in Architectural Scenes. Applied Sciences, 15(13), 7133. https://doi.org/10.3390/app15137133






