Influence of Degree of Saturation on Soil–Pile Interactions for Piles in Expansive Soils
Abstract
1. Introduction
2. Total Uplift Force on Pile in Expansive Soils
3. Laboratory Testing and Results
- (1)
- Index property tests to classify the samples and determine physical characteristics;
- (2)
- Oedometer tests including the consolidation-swell (CS) test and the constant volume (CV) test to measure vertical swelling pressure under saturated and partially saturated conditions;
- (3)
- Direct shear tests to evaluate the shear strength parameters at varying degrees of saturation;
- (4)
- Pile uplift model tests using a custom-designed setup to simulate soil-pile interaction under wetting conditions.
3.1. Sample Description
3.2. Index Properties
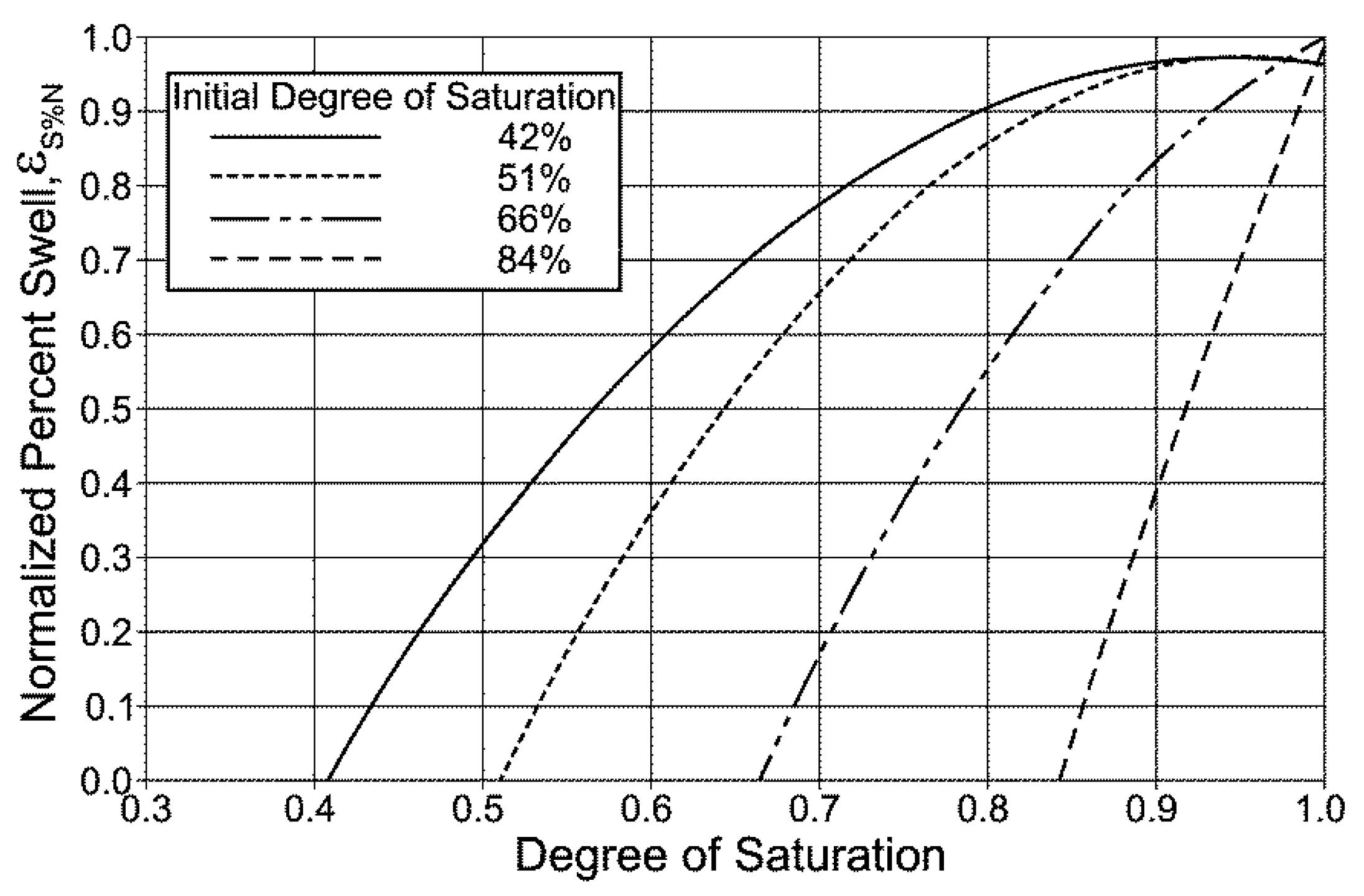
3.3. Oedometer Tests
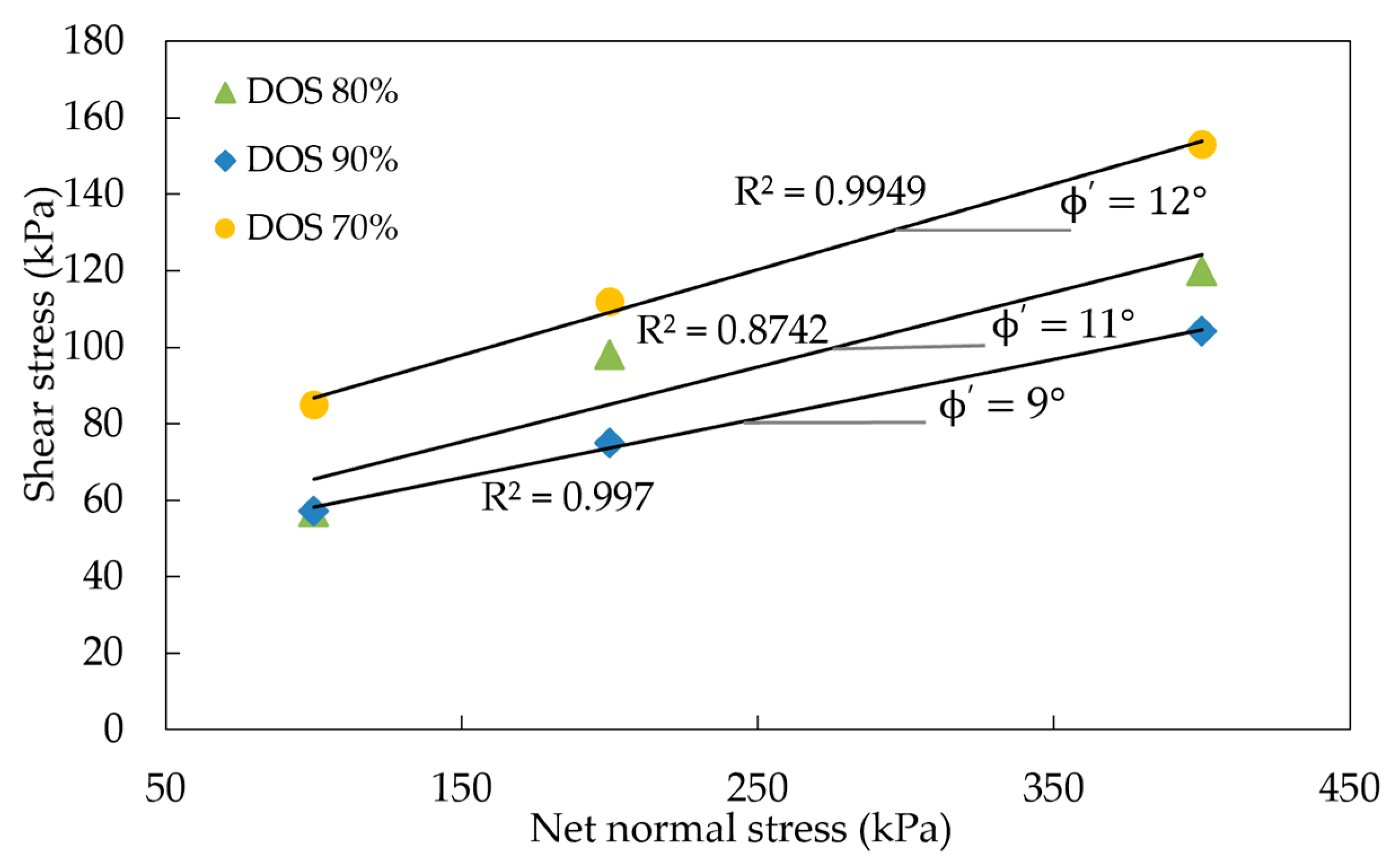
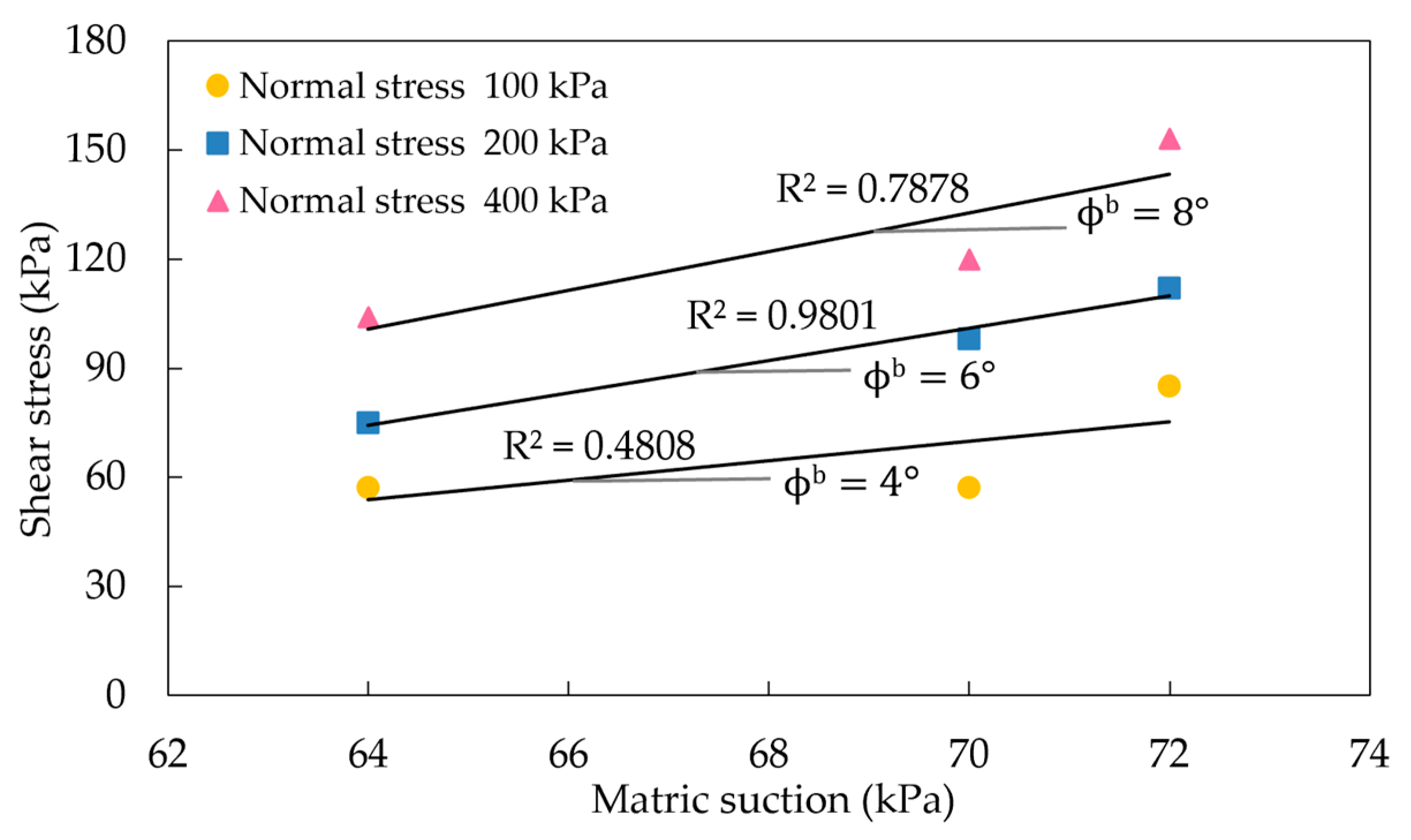
3.4. Direct Shear Tests
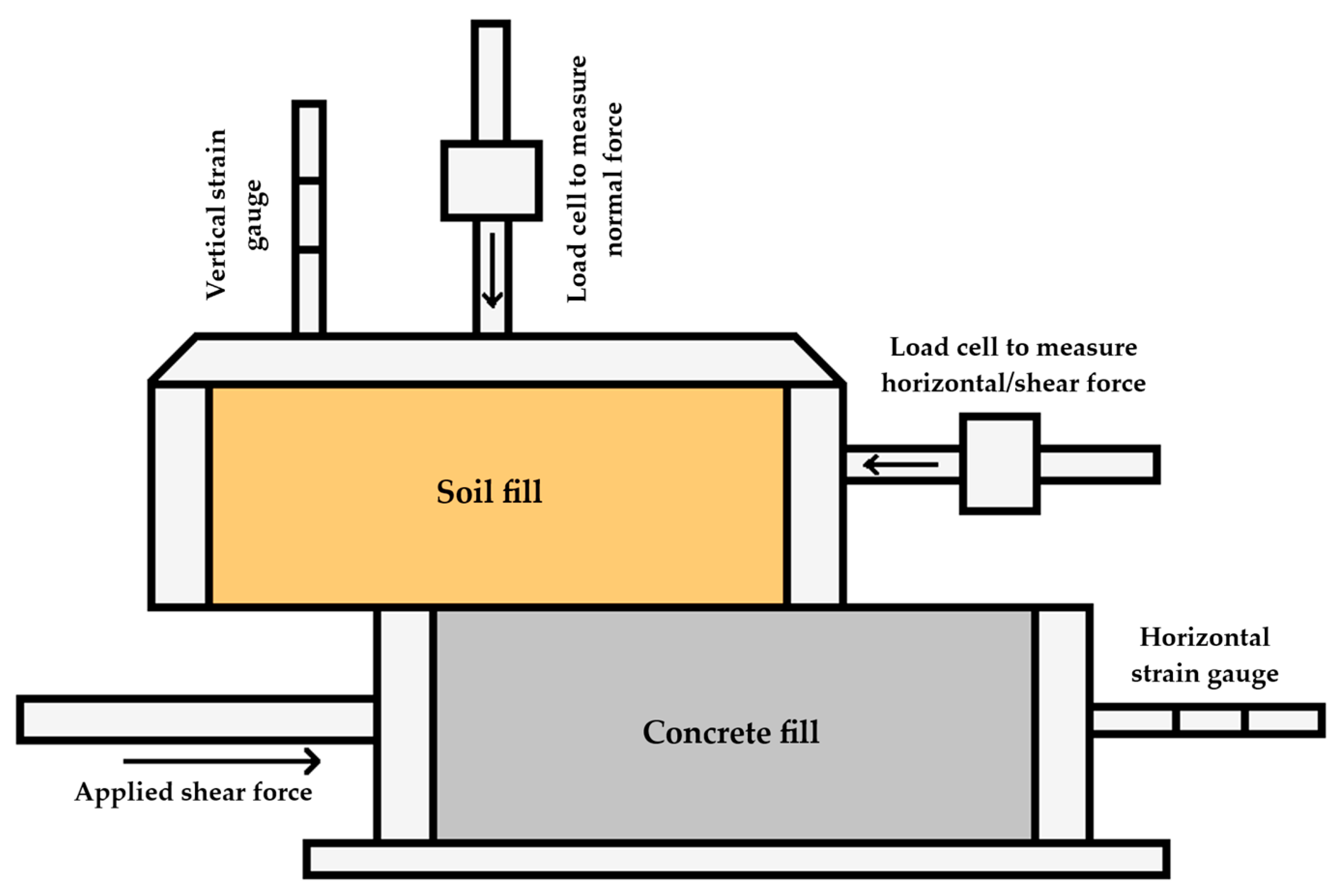
3.5. Pile Uplift Model Tests
4. Evaluation of Pile Uplift Force and Parameters
4.1. Calculation of Pile Uplift Force
4.2. Calculation of α Value
5. Conclusions and Recommendations
- The uplift force developed along the pile shaft during the wetting process exhibited a hyperbolic trend. A significant portion of the uplift force is developed during the early stage of the heaving process. This trend is consistent with the pile heave pattern observed at the TRACON site, and aligns with our observation that the majority of the heave, and thus the associated distress to houses, occurred at the beginning of the construction period.
- The uplift coefficient, α, is a key parameter for computing pile uplift force in pile design for expansive soils. The α value increases as the initial degree of saturation increases, with a change of approximately 9% within the tested saturation range. Based on the experimental investigation, the back-calculated α values were relatively constant across soils with varying initial degrees of saturation, suggesting that a constant α value may be used in design.
- The α values obtained in this study fall within a typically accepted lower to moderate range but are notably lower than some of the higher values reported in the literature. This indicates potential variability depending on site-specific conditions, and therefore, it is recommended that the uplift coefficient be validated through field-scale investigations.
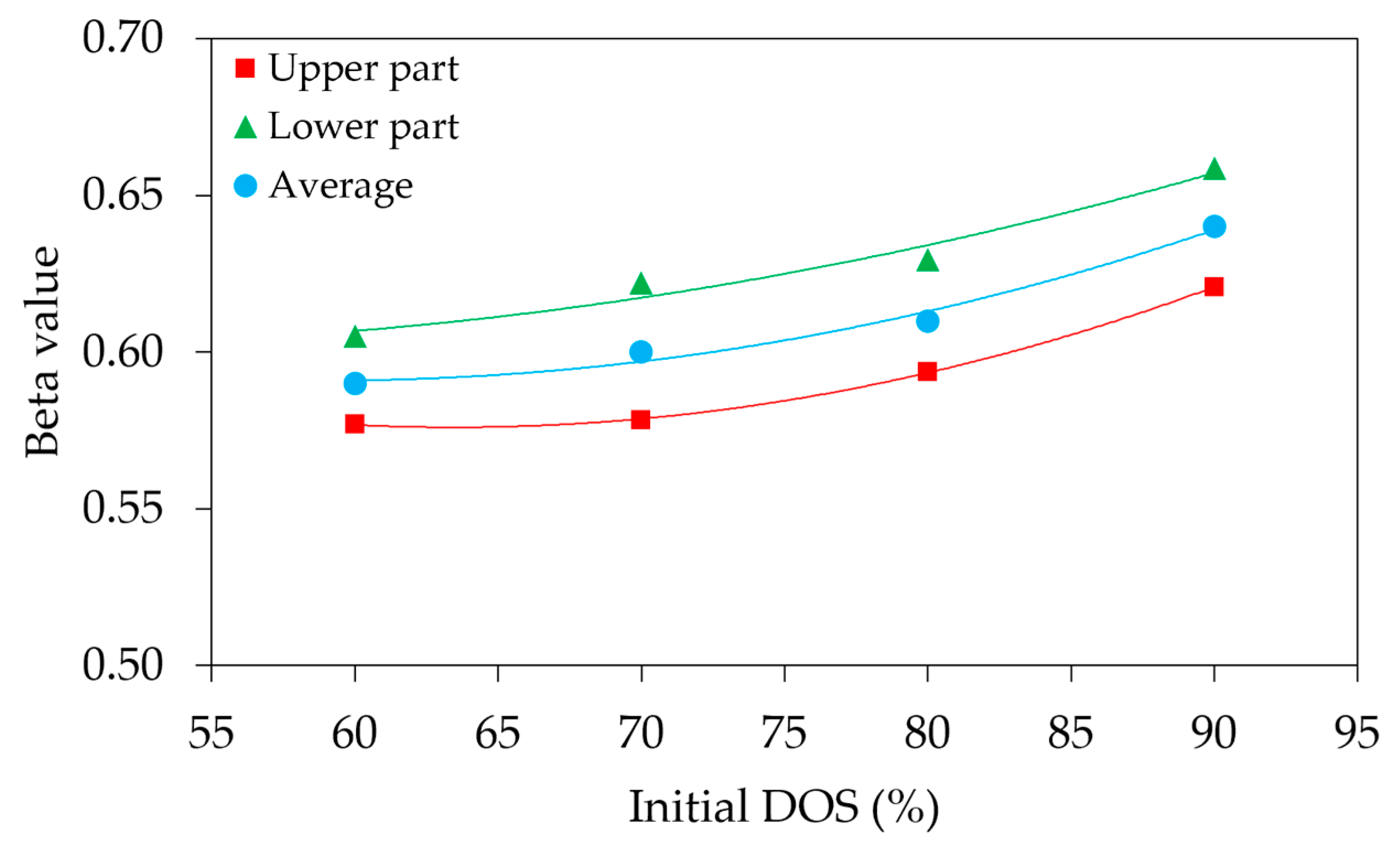
- The swelling pressure ratio, β, was evaluated to understand the difference between horizontal and vertical swelling pressures. The results indicate that β increases with the initial degree of saturation, with an approximate change of 8% within the tested range. This trend is attributed to a greater reduction in vertical swelling pressure compared to lateral swelling pressure as saturation increases, leading to an overall increase in the β value.
- For practical design applications, the use of constant α and β values is considered acceptable within the tested range. However, further research is recommended to explore the influence of pile geometry and soil properties in more detail. Previous studies have examined individual factors such as pile length, diameter, soil type, and group pile orientation. Future investigations could benefit from considering these parameters collectively to better understand their combined impact on the behavior of expansive soils. Additionally, it is suggested that the proposed theoretical equation be validated through comparison with field data and other empirical approaches to ensure its accuracy and reliability in real-world engineering practice.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mitchell, J.K.; Soga, K. Fundamentals of Soil Behavior; John Wiley & Sons, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Muhunthan, B.; Yin, J.H. Behavior of piles in expansive soils: A review. J. Geotech. Geoenviron. Eng. 2003, 129, 207–222. [Google Scholar]
- Das, B.M. Principles of Geotechnical Engineering, 7th ed.; Cengage Learning: Stamford, CT, USA, 2006. [Google Scholar]
- Soundara, B.; Robinson, R.G. Hyperbolic model to evaluate uplift force on pile in expansive soils. KSCE J. Civ. Eng. 2016, 21, 746–751. [Google Scholar] [CrossRef]
- Nelson, J.D.; Chao, K.C.; Overton, D.D.; Nelson, E.J. Foundation Engineering for Expansive Soils; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Mohan, D.; Chandra, S. Frictional resistance of bored piles in expansive clays. Geotechnique 1961, 11, 294–301. [Google Scholar] [CrossRef]
- Johnson, L.D.; Stroman, W.R. Vertical behaviour of two 16-year old drilled shafts in expansive soils. In Analysis and Design of Pile Foundations; ASCE: New York, NY, USA, 1984; pp. 154–173. [Google Scholar]
- Nguyen, H.T.; Bui, Q.B.; Bui, D.T.; Tran, V.Q.; Nguyen, T.T.; Pham, B.T. A Hybrid Artificial Intelligence Approach for Predicting the Load-Bearing Capacity of Driven Piles. Can. Geotech. J. 2022, 59, 878–891. [Google Scholar] [CrossRef]
- Colorado Association of Geotechnical Engineers (CAGE). Commentary on Geotechnical Practices: Drilled Pier Design Criteria for Lightly Loaded Structures in the Denver Metropolitan Area; Colorado Association of Geotechnical Engineers: Denver, CO, USA, 1999. [Google Scholar]
- Poulos, H.G.; Davis, E.H. Pile Foundation Analysis and Design; John Willey and Sons, Inc.: New York, NY, USA, 1980. [Google Scholar]
- Nelson, J.D.; Chao, K.C.; Overton, D.D.; Schaut, R.W. Calculation of heave of deep pier foundations. Geotech. Eng. J. SEAGS AGSSEA 2012, 43, 12–25. [Google Scholar] [CrossRef]
- Crilly, M.S.; Driscoll, R.M.C. Behaviour of lightly loaded piles in swelling ground and implications for their design. Geotech. Eng. 2000, 143, 3–16. [Google Scholar] [CrossRef]
- Chao, K.C.; Nelson, J.D.; Overton, D.D.; Cumbers, J.M. Soil water retention curves for remolded expansive soils. In Proceedings of the 1st European Conference on Unsaturated Soils, Durham, UK, 2–4 July 2008. [Google Scholar]
- Nelson, J.; Miller, D.J. Expansive Soils: Problems and Practice in Foundation and Pavement Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Tadepalli, R.T.; Fredlund, D.G. Predicting the shrinkage properties of expansive soils. Can. Geotech. J. 1991, 28, 310–321. [Google Scholar]
- Pereira, J.M.; Fredlund, D.G. A review of the shear strength of unsaturated expansive soils. Can. Geotech. J. 2000, 37, 1033–1054. [Google Scholar]
- Lim, J.Y.; Miller, G.A. Shear strength characteristics of unsaturated expansive clays. Can. Geotech. J. 2004, 41, 365–378. [Google Scholar]
- Noor, I.M.; Faizal, P.; Saleh, M.M.; Ismail, N.; Zakaria, R. Behavior of lateritic expansive soil as foundation material. Electron. J. Geotech. Eng. 2013, 18, 2313–2323. [Google Scholar]
- Awadalseed, W.; Zhang, X.; Zhang, D.; Ji, Y.; Bai, Y.; Zhao, H. Estimation of Pile Shaft Friction in Expansive Soil upon Water Infiltration. KSCE J. Civ. Eng. 2024, 28, 4832–4843. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H.; Fredlund, M.D. Unsaturated Soil Mechanics in Engineering Practice; John Willey and Sons, Inc.: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Hamid, T.B.; Miller, G.A. Shear strength of unsaturated soil interfaces. Can. Geotech. J. 2009, 46, 595–606. [Google Scholar] [CrossRef]
- Chao, K.C.; Kang, J.B.; Nelson, J.D. Challenges in water migration modeling for expansive soils. In Proceedings of the Geo-Shanghai Conference, Shanghai, China, 26–28 May 2014. [Google Scholar] [CrossRef]
- Chao, K.C.; Nelson, J.D. Validation of Foundation Design Method on Expansive Soils. Geotech. Eng. J. SEAGS AGSSEA 2019, 50, 103–111. [Google Scholar] [CrossRef]
- Chao, K.C.; Overton, D.D.; Nelson, J.D. Design and installation of deep benchmarks in expansive soil. J. Surv. Eng. 2006, 132, 124–131. [Google Scholar] [CrossRef]
- Nelson, J.D.; Chao, K.C.; Overton, D.D. Design of pier foundations on expansive soils. In Proceedings of the 3rd Asian Conference on Unsaturated Soils, Nanjing, China, 20–24 April 2007. [Google Scholar]
- Sapaz, B. Lateral Versus Vertical Swell Pressures in Expansive Soils. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2004. [Google Scholar]
- Katti, R.K.; Katti, D.R.; Katti, A.R. Behaviour of Saturated Expansive Soil and Control Methods, Revised and Enlarged ed.; Balkema: Rotterdam, The Netherlands, 2002. [Google Scholar]
- Chen, F.H. Foundations on Expansive Soils; Elsevier Science Publishing Company Inc.: New York, NY, USA, 1988. [Google Scholar]
- O’Neill, M.W. Adaptive model for drilled shafts in expansive clay. In Special Topics in Foundations; ASCE: Reston, VA, USA, 1988; pp. 1–20. [Google Scholar]
- Benvenga, M.M. Pier-Soil Adhesion Factor for Drilled Shaft Piers in Expansive Soil. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 2005. [Google Scholar]
- Huang, L.; Deng, Q.L.; Wang, H.N. Instability Behavior of Loose Granular Material: A New Perspective via DEM. Granul. Matter 2024, 26, 84. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, L.; Deng, Q.L. Analysis of Factors Affecting the Shear Characteristics of Granular Soils under Increasing Axial Stress in Biaxial Compression Test via DEM. Comput. Part. Mech. 2025. [Google Scholar] [CrossRef]
- ASTM D854-10; Standard Test Methods for Specific Gravity of Soil Solids by Water Pycnometer. ASTM International: West Conshohocken, PA, USA, 2010. [CrossRef]
- ASTM D4318-10; Standard Test Methods for Liquid Limit, Plastic Limit, and Plasticity Index of Soils. ASTM International: West Conshohocken, PA, USA, 2010. [CrossRef]
- ASTM D698-12; Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Standard Effort. ASTM International: West Conshohocken, PA, USA, 2012. [CrossRef]
- Nelson, E.J.; Chao, K.C.; Nelson, J.D.; Overton, D.D. Lessons learned from foundation and slab failures on expansive soils. J. Perform. Constr. Facil. 2017, 31, 3. [Google Scholar] [CrossRef]
- Chao, K.C.; Kang, J.B.; Nelson, J.D. Evaluation of failure of embankment slope constructed with expansive soils. Geotech. Eng. J. SEAGS AGSSEA 2018, 49, 2. [Google Scholar] [CrossRef]
- Nelson, J.D.; Chao, K.C. Relationship Between Swelling Pressures Determined by Constant Volume and Consolidation-Swell Oedometer Tests. In Proceedings of the Sixth International Conference on Unsaturated Soils, Sydney, Australia, 2–4 July 2014. [Google Scholar] [CrossRef]
- Chao, K.C.; Overton, D.D.; Nelson, J.D. The Effects of Site Conditions on the Predicted Time Rate of Heave. In Proceedings of the Unsaturated Soils 2006 Conference, Carefree, AZ, USA, 2–6 April 2006. [Google Scholar] [CrossRef]
- Chao, K.C. Design Principles for Foundations on Expansive Soils. Ph.D. Dissertation, Colorado State University, Fort Collins, CO, USA, 2007. [Google Scholar]
- ASTM D3080-11; Standard Test Method for Direct Shear Test of Soils Under Consolidated Drained Conditions. ASTM International: West Conshohocken, PA, USA, 2011.
- Erol, O.; Ergun, U. Lateral swell pressure in expansive soils. In Proceedings of the 8th International Conference on Soil Mechanics and Foundations Engineering, New Delhi, India, 4–10 January 1994; pp. 1511–1514. [Google Scholar]
- He, D.; Cheng, Y.; Liu, H.; Lin, H. Pile–Soil Interaction and Group Pile Effect in Composite Foundation Under Different Pile Length Conditions. Buildings 2025, 15, 1248. [Google Scholar] [CrossRef]
- Asif, T.H.; Islam, S.; Basak, A.; Shahriar, F.; Rahman, S.M. Application of Numerical Method in Assessing the Variations in Pile Group Efficiency under Different Circumstances. Comput. Eng. Phys. Model. 2022, 5, 50–68. [Google Scholar] [CrossRef]


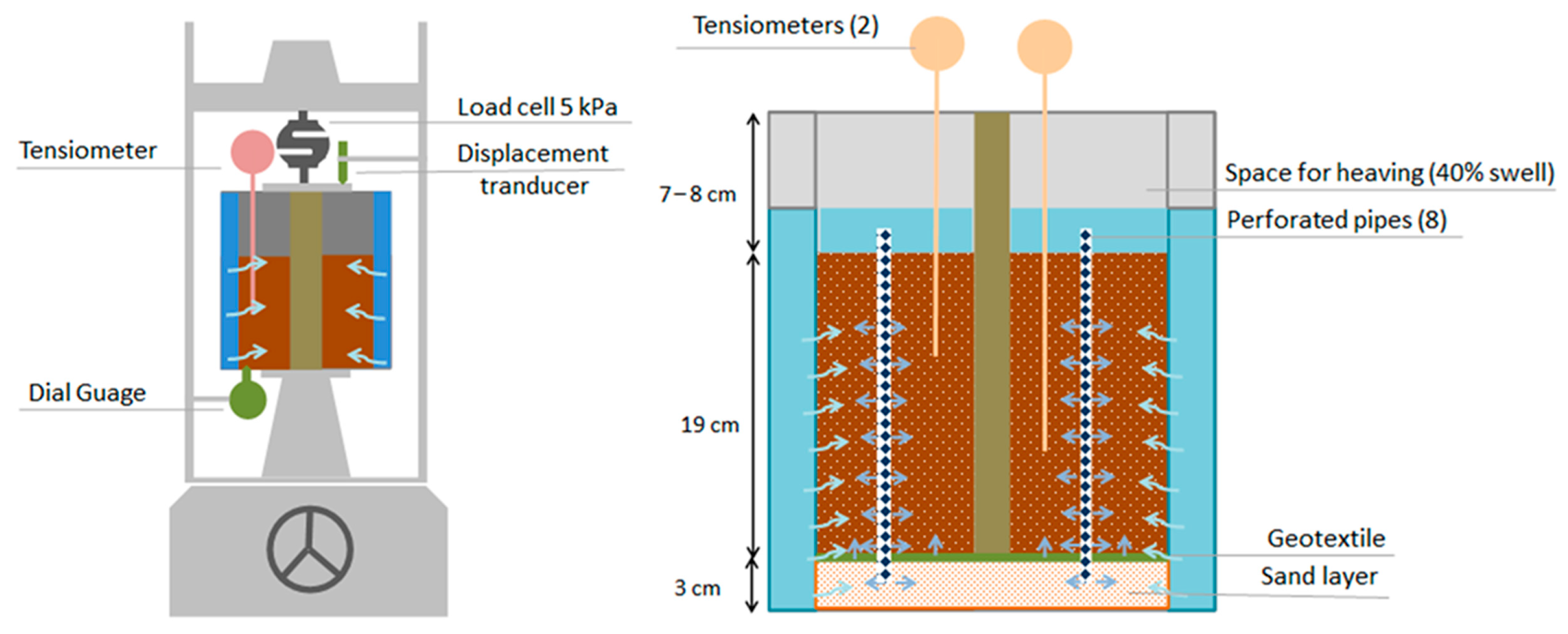
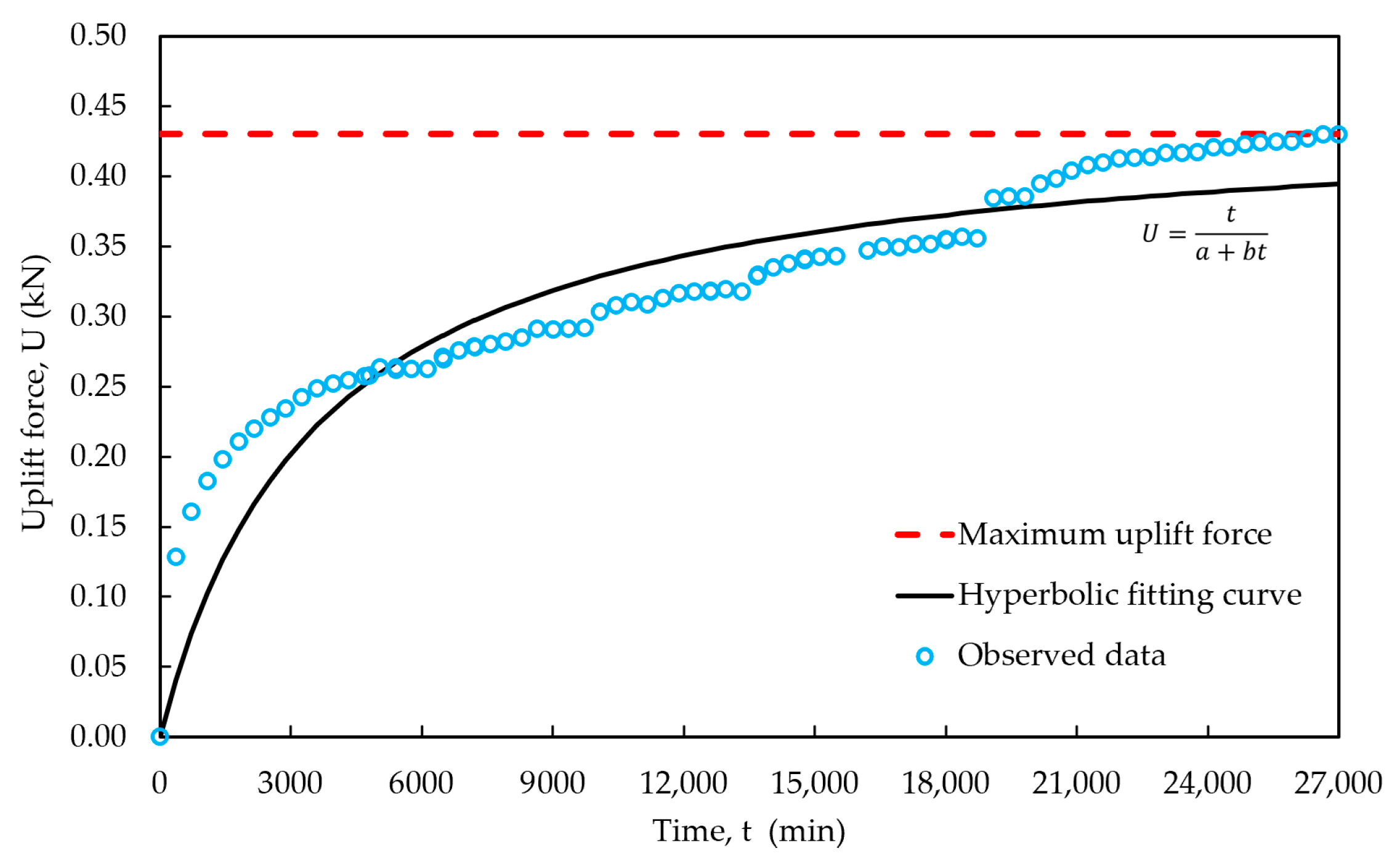
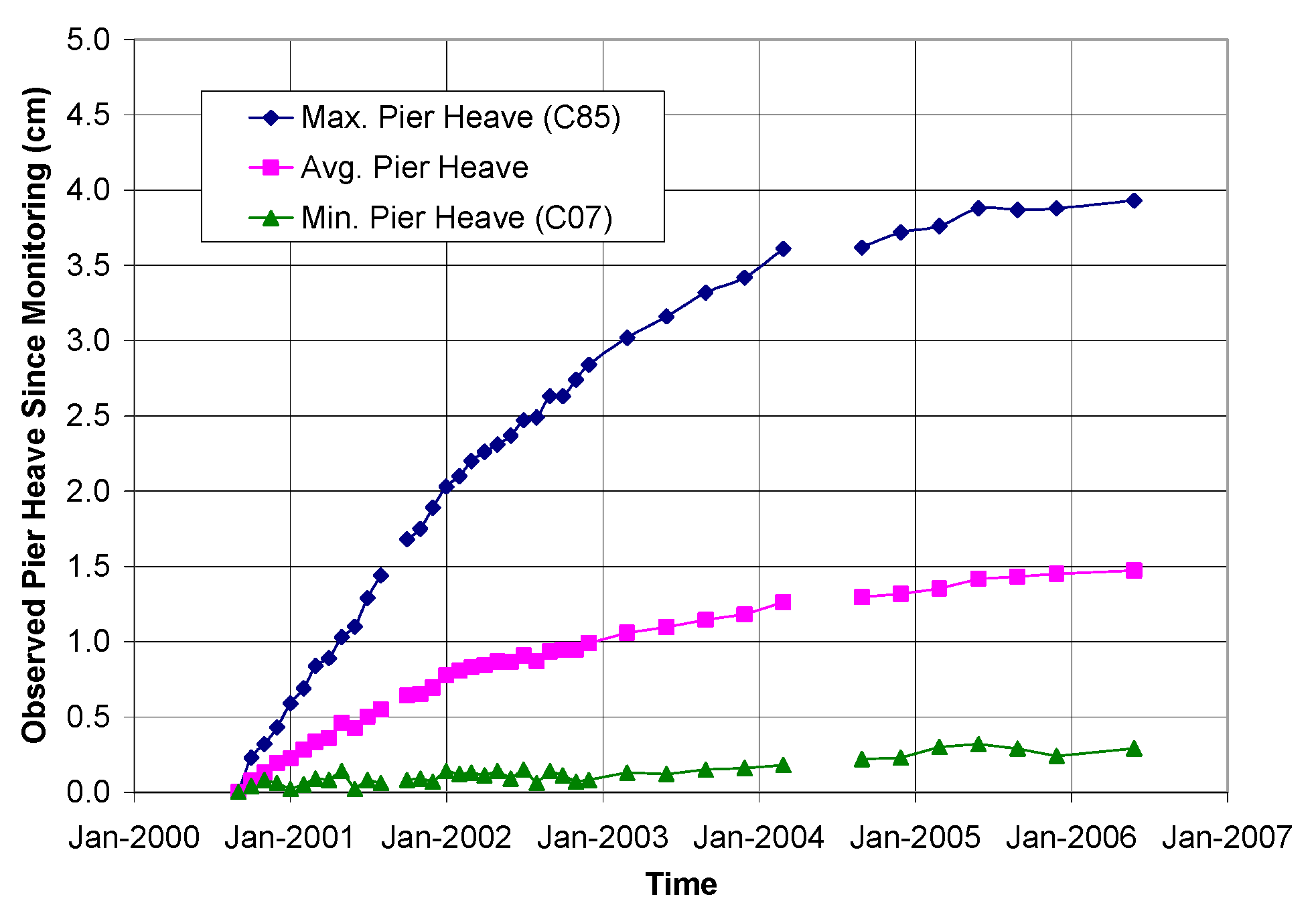
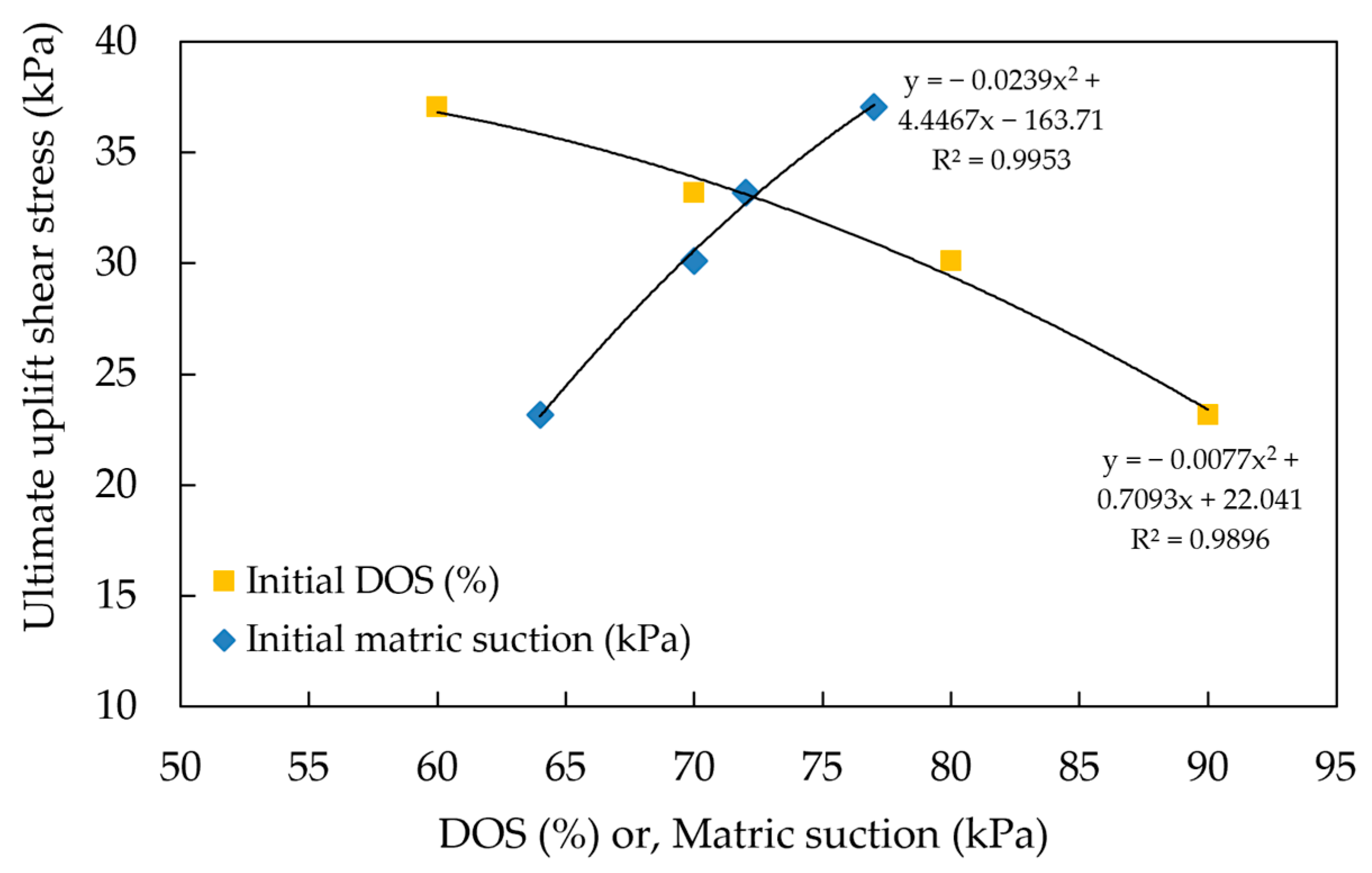

| No. | Test | Standards | Value/Description |
|---|---|---|---|
| 1 | Soil | - | Artificial Clay (sand: sodium bentonite = 45:55) |
| 2 | Specific Gravity (Gs) | ASTM D854-10 [33] | 2.61 |
| 3 | Liquid Limit (%) | ASTM D4318-10 [34] | 315 |
| 4 | Plastic Limit (%) | 47 | |
| 5 | Plastic Index (%) | 268 | |
| 6 | Grain Size Distribution | USCS | - |
| % Gravel | 0 | ||
| %Coarse Sand | 3.2 | ||
| %Medium Sand | 27.2 | ||
| % Fine Sand | 14 | ||
| %Silt and clay | 55.6 | ||
| 7 | Soil Classification | USCS | CH |
| 8 | Color | - | Brown |
| 9 | Maximum Dry Density (kN/m3) | ASTM D698-12 [35] | 14.95 |
| 10 | Optimum Water Content (%) | ASTM D698-12 [35] | 24 |
| Degree of Saturation (%) | Dry Unit Weight (kN/m3) | Water Content (%) | Total Unit Weight (kN/m3) |
|---|---|---|---|
| 60 | 14.20 | 18.45 | 16.82 |
| 70 | 14.20 | 21.53 | 17.26 |
| 80 | 14.20 | 24.61 | 17.70 |
| 90 | 14.20 | 27.68 | 18.13 |
| 100 | 14.20 | 30.76 | 18.57 |
| Initial Degree of Saturation, DOS (%) | Consolidation Swell Pressure at Full Saturation, (kPa) | Constant Volume Swell Pressure at Full Saturation, (kPa) |
|---|---|---|
| 60 | 830 | 260 |
| 70 | 770 | 251 |
| 80 | 710 | 240 |
| 90 | 650 | 231 |
| Description | Symbols and Units | Upper Part | Lower Part | Upper Part | Lower Part | Upper Part | Lower Part | Upper Part | Lower Part |
|---|---|---|---|---|---|---|---|---|---|
| Initial conditions | DOS % | 60 | 60 | 70 | 70 | 80 | 80 | 90 | 90 |
| Suction | 77 | 77 | 72 | 72 | 70 | 70 | 64 | 64 | |
| (kPa) (1) | |||||||||
| w% | 18.5 | 18.5 | 21.5 | 21.5 | 24.6 | 24.6 | 27.7 | 27.7 | |
| ϴ% | 26.8 | 26.8 | 31.2 | 31.2 | 35.7 | 35.7 | 40.1 | 40.1 | |
| Partially wetted conditions | DOS % | 96 | 91 | 97 | 91 | 98 | 93 | 97 | 95 |
| Suction (kPa) | 46 | 60 | 30 | 60 | 26 | 57 | 32 | 52 | |
| w% | 29.5 | 28 | 29.8 | 28 | 30.1 | 28.6 | 29.8 | 29.2 | |
| ϴ% | 42.8 | 40.6 | 43.2 | 40.6 | 43.7 | 41.5 | 43.2 | 42.3 | |
| ε%sn(2) | 0.98 | 0.92 | 0.94 | 0.78 | 0.94 | 0.75 | 0.68 | 0.49 | |
| ()v (3) | 254 | 225 | 245 | 187 | 218 | 162 | 142 | 106 | |
| γ total | 18.4 | 18.2 | 18.4 | 18.2 | 18.5 | 18.3 | 18.4 | 18.4 | |
| PFS | 0.48 | 0.48 | 0.43 | 0.43 | 0.39 | 0.39 | 0.3 | 0.3 | |
| Sat/Unsat | ϕ′ (4) | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 |
| C′ (5) | 65 | 65 | 46 | 46 | 42 | 42 | |||
| α | 0.112 | 0.118 | 0.112 | 0.121 | 0.115 | 0.122 | 0.121 | 0.128 | |
| Average α | 0.115 | 0.117 | 0.119 | 0.124 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chao, K.C.; Chaladthanyakit, A.-N.; Asif, T.H. Influence of Degree of Saturation on Soil–Pile Interactions for Piles in Expansive Soils. Appl. Sci. 2025, 15, 7102. https://doi.org/10.3390/app15137102
Chao KC, Chaladthanyakit A-N, Asif TH. Influence of Degree of Saturation on Soil–Pile Interactions for Piles in Expansive Soils. Applied Sciences. 2025; 15(13):7102. https://doi.org/10.3390/app15137102
Chicago/Turabian StyleChao, Kuo Chieh, A-Nanya Chaladthanyakit, and Taskid Hossain Asif. 2025. "Influence of Degree of Saturation on Soil–Pile Interactions for Piles in Expansive Soils" Applied Sciences 15, no. 13: 7102. https://doi.org/10.3390/app15137102
APA StyleChao, K. C., Chaladthanyakit, A.-N., & Asif, T. H. (2025). Influence of Degree of Saturation on Soil–Pile Interactions for Piles in Expansive Soils. Applied Sciences, 15(13), 7102. https://doi.org/10.3390/app15137102








