Study on Calibration Method of Micromechanical Parameters for Discrete Element Model of Moderately Consolidated Sandstones

Abstract

The study of the mechanical properties of moderately consolidated sandstones is crucial for engineering safety assessments. As an effective research tool, the discrete element method (DEM) encounters challenges during the modeling phase, such as a large number of micromechanical parameters, low modeling efficiency, and unclear coupling mechanisms among multiple parameters. To address these issues, this paper proposes a calibration method for the micromechanical parameters of DEM models for moderately consolidated sandstones. By integrating orthogonal experimental design with a multivariate analysis of variance, the influence of micromechanical parameters on macroscopic mechanical properties is quantified, and a parameter prediction model is constructed using an intelligent dynamic regression selection mechanism, significantly improving the efficiency and accuracy of micromechanical parameter calibration. The results show that the macroscopic elastic modulus E is primarily controlled by the effective modulus ($\overline{E}$), stiffness ratio (k), and particle size ratio (R_max/R_min), following a linear relationship. The influence of the particle size ratio decreases significantly once it exceeds a threshold value. The macroscopic uniaxial compressive strength (UCS) is dominated by cohesion ($\overline{c}$) and tensile strength (${\overline{\mathrm{\sigma }}}_c$), exhibiting a polynomial relationship, where a stronger synergistic effect is generated when both parameters are at higher levels. Poisson’s ratio ($\mu$) is significantly correlated only with the stiffness ratio (k), following a logarithmic relationship. An iterative correction method for micromechanical parameter calibration is proposed. The errors between the three groups of simulation results and laboratory test results are all less than 10%, and the crack distribution patterns show a high degree of consistency. The findings of this study provide a theoretical foundation and technical means for exploring the mechanical behavior and damage mechanism of moderately consolidated sandstones.

1. Introduction

With the rapid development of underground resource extraction and subsurface energy storage infrastructure, studies on the mechanical properties of rocks have become an important foundation for engineering safety assessment [1,2]. As a geological material widely present in oil and gas reservoirs and geotechnical engineering, moderately consolidated sandstone requires in-depth research on its mechanical behavior to ensure engineering safety and resource development [3,4]. Traditional rock mechanics research primarily relies on physical experiments to characterize the macroscopic mechanical properties and failure behavior of rocks. However, this approach encounters several limitations, including the intrinsic heterogeneity of rock specimens, high operational costs, and invisibility of the failure process. The advent and application of numerical simulation techniques have introduced novel approaches for simulating rock failure processes under a wide range of loading and boundary conditions. Although conventional finite element methods can effectively simulate the deformation characteristics of continuous media, they are limited by the discontinuous structure of rocks (composed of particles and cementitious materials), making it difficult to accurately characterize the progressive failure process caused by cementation failure. The discrete element method (DEM), which explicitly simulates particle interactions and discontinuity behavior in rocks, has garnered considerable scholarly attention as a promising tool for investigating rock failure mechanisms. Haeri employed the two-dimensional Particle Flow Code (PFC) to investigate the biaxial failure mechanisms of transversely bedded concrete layers under varying bedding angles and thicknesses [5]. Hashemi utilized DEM simulations to examine borehole stability under in situ stress conditions, exploring the effects of particle bonding variations and confined aquifers on instability within poorly cemented formations [6]. They employed PFC to develop new three-dimensional rock mass strength criteria through polyaxial, triaxial, and biaxial tests on jointed rock blocks containing single or double joint sets, supported by an analysis of 284 numerical simulations [7]. Shemirani integrated laboratory experiments and PFC simulations to evaluate both direct and indirect approaches for determining the mode-I fracture toughness of concrete, including compaction tensile tests, notched Brazilian discs, semi-circular bending specimens, and hollow-centered cracked discs [8]. Among these, the discrete element method has emerged as an effective tool for studying the micromechanical response of sandstone due to its ability to simulate particle bond fracture and energy dissipation mechanisms.

The accurate input of modeling parameters is a fundamental prerequisite for precisely simulating the mechanical behavior of rocks under various working conditions. The micromechanical parameters in discrete element models do not directly correspond to the macroscopic mechanical parameters of rocks. Consequently, the problem of how to quickly and accurately acquire the micromechanical parameters for discrete element models of rocks has attracted extensive attention from researchers. Ajamzadeh employed PFC software to investigate the effects of friction angle, accumulation factor, expansion coefficient, and disc distance on the failure patterns, compressive strength, and tensile strength observed in unconfined compression tests and Brazilian tests [9]. Bahaaddini utilized a trial-and-error approach to inversely calibrate the micromechanical parameters of Hawkesbury sandstone, sequentially adjusting those influencing the elastic modulus (E), Poisson’s ratio (μ), and uniaxial compressive strength (UCS). Due to the combined effects of multiple micromechanical parameters on macroscopic mechanical properties, a single set of micromechanical rock parameters required the completion of ten uniaxial compression tests [10]. Chen used the flat-jointed contact model as the particle contact constitutive model and conducted six trial-and-error experiments to calibrate the micromechanical parameters for the limestone uniaxial compression model [11]. Zhang introduced a calibration procedure for the micromechanical parameters of a discrete element model for gneissic granite, with simulation results demonstrating good agreement with the expected outcomes [12]. Jiang developed a calibration method for the micromechanical parameters of hollow cylindrical gray sandstone using uniaxial and conventional triaxial compression tests based on an iterative approach [13]. Wang proposed two calibration methods for bond strength parameters of ballast particles in discrete element simulation using the GA-BP neural network [14]. Zhong introduced a mesoscopic parameter calibration method for geopolymer concrete based on the analysis of 729 data sets [15]. Miao established fitting relationships between macro- and micromechanical parameters by deriving analytical equations and validating them through extensive numerical simulations [16]. Abierde developed empirical correlations between macro- and micromechanical parameters to characterize the triaxial behavior of marble and validated the findings via case studies [17]. Currently, the calibration of micromechanical parameters in discrete element modeling still primarily depends on trial-and-error approaches, which remain inefficient and are hindered by complex, poorly understood parameter interactions. Furthermore, prior studies have primarily focused on geological materials such as high-strength crystalline rocks and unconsolidated sands, while moderately consolidated sandstones remain underexplored in terms of both modeling strategies and systematic parameter calibration.

To effectively address the current research gap concerning moderately consolidated sandstone, this study proposes a rapid methodology for constructing discrete element models and calibrating their mechanical parameters. Furthermore, this work advances existing approaches by incorporating multiple sets of micromechanical parameters and conducting orthogonal experimental designs across seven critical variables, thereby enhancing the accuracy and efficiency of the modeling process. Through a multivariate analysis of variance and interaction effect analysis, the key micromechanical parameters influencing macroscopic mechanical responses are systematically identified, revealing their coupling mechanisms and influence patterns. A dynamic regression framework is further employed to construct a multi-factor predictive model, thereby proposing an efficient and data-driven parameter calibration approach. Comparison with laboratory test results demonstrates that the relative errors in simulated macroscopic mechanical parameters remain below 10%, validating the accuracy and robustness of the proposed methodology. This work significantly reduces the empirical dependence inherent in conventional calibration techniques and offers a theoretical foundation for investigating the failure mechanisms and constitutive modeling of moderately consolidated sandstones.

2. Model Establishment and Parameter Selection

2.1. Model Composition and Main Principles

In PFC^2D, several constitutive contact models are commonly employed, including the Linear Model (LM), the Linear Contact Bond Model (LCBM), and the Linear Parallel Bond Model (LPBM) [18]. Rock is a heterogeneous composite material, and consists of discrete mineral particles bonded by cementing agents. In contrast to the Linear Model and Linear Contact Bond Model, which are typically used for simulating soil mechanical behavior, the Linear Parallel Bond Model is more commonly adopted to accurately capture the mechanical response and micro-structural evolution of rock materials [19,20,21]. The Linear Parallel Bond Model (LPBM) can transmit both normal and shear contact forces, $F_c$, as well as bending and twisting moments, $M_c$, thereby enabling a more realistic representation of particle interactions and their resultant mechanical behavior (Equation (1)) [22,23]. Therefore, employing the LPBM enables more accurate and reliable simulations of the mechanical response of rocks subjected to external loads.

$$F_c=F^l+F^d+\overline{F},M_c=\overline{M}$$

(1)

(where $F^l$ is the linear force, $F^d$ the damping force, $\overline{F}$ is the parallel bond force, and $\overline{M}$ is the moment generated by the bonding load).

As shown in Figure 1, the Linear Parallel Bond Model (LPBM) comprises a frictional interface and a linear elastic bonding interface. The frictional interface mainly resists frictional forces between particles and transmits external loads. The bonding interface forms a bond between particles, capable of resisting the action of both forces and moments. When the tensile force exceeds the tensile strength or the shear stress exceeds the shear strength, a bond-break callback event is triggered, resetting both the contact force and moment to zero. This results in bond rupture and the formation of mesoscale cracks. With the accumulation of such bond failures, macroscopic cracks eventually develop [24,25].

As illustrated in Figure 1, the Linear Parallel Bond Model (LPBM) was adopted as the contact constitutive model to construct a two-dimensional standard core sample. The numerical model has a height of 100 mm and a diameter of 50 mm, with the minimum particle radius set to 0.2 mm. Particles were randomly generated at a porosity of 20% to simulate the actual structure of the rock. To simulate the compressive stress conditions characteristic of subsurface rock formation, the wall command was utilized to confine and compact the particles.

After shaping and compaction, the CAMT command was employed to assign Linear Parallel Bond Model (LPBM) parameters to particle contacts, thereby achieving particle cementation and completing the rock modeling. To simulate the axial loading conditions of a rock mechanics testing apparatus, the left and right boundary walls were removed, leaving only the top and bottom boundaries. The movement of the top and bottom walls was precisely controlled using a servo mechanism, and a strain-controlled loading mode was applied with a strain rate set to 0.05%. According to these criteria, four types of uniaxial compression specimens with different particle size ratios were generated.

2.2. Main Parameters of the Model

In the numerical simulation of uniaxial compression tests, the macroscopic mechanical behavior of rocks is influenced by geometric parameters and micromechanical parameters. Geometric parameters, such as minimum particle radius (R_min), maximum particle radius (R_max), particle density ($\rho$), and model dimensions (height and width), determine the basic morphology and particle distribution of the model. In the Linear Parallel Bond Model (LPBM), micromechanical parameters are classified into linear micromechanical parameters and parallel bond micromechanical parameters. Linear micromechanical parameters include the effective modulus $\overline{E}$, stiffness ratio $k=k_n/k_s$, and friction coefficient $\mu$, describing the elastic behavior and frictional properties of particles. The parallel bond micromechanical parameters include the radius multiplier ($\overline{\mathrm{\lambda }}$), parallel bond effective modulus $({\overline{E}}^{\mathrm{*}})$, parallel bond stiffness ratio $({\overline{k}}^{\mathrm{*}}={\overline{k}}_n/{\overline{k}}_s)$, tensile strength (${\overline{\mathrm{\sigma }}}_c$), cohesion ($\overline{c}$), shear strength (${\overline{\tau }}_c$), and friction angle ($\overline{\phi }$), which characterize the cementation properties between particles, especially the stiffness and strength of the bonding interface. Due to the large number of model parameters, key parameters must be selected and simplified in practical applications to streamline the calibration process. These parameters should be reasonably chosen and calibrated to ensure the accuracy of simulation results.

In this study, the parameter settings were based on the methodology proposed by Potyondy for Lac du Bonnet granite [26]. Specifically, the effective modulus of particles was set equal to the parallel bond effective modulus, and the stiffness ratio was set equal to the parallel bond stiffness ratio, with the radius multiplier fixed at 1. These settings not only reduce the number of experimental variables, but also ensure that the numerical models accurately reflect the mechanical properties of the rock. The particle density was set to the measured value from actual cores (2140 kg/m³), and the minimum particle radius was set at 0.2 mm. Since shear strength is determined by cohesion and friction angle, it was not treated as an independent variable [22]. Consequently, the principal micromechanical parameters used for calibration in this study were the particle radius ratio (R_max/R_min), effective modulus ($\overline{E}$), stiffness ratio ($k$), friction coefficient ($\mu$), tensile strength (${\overline{\mathrm{\sigma }}}_c$), cohesion ($\overline{c}$), and friction angle ($\overline{\phi }$).

Orthogonal experimental design is a method that enables the systematic investigation of multiple factors while reducing the required number of experimental groups. In this study, parameter levels for experimental investigation were determined by integrating findings from previous research and the material characteristics of moderately consolidated sandstone. Experimental parameters are shown in

Table 1. Levels of micromechanical parameters.

Parameter Levels	Rmax/Rmin	$\overline{\mathit{E}}$ (GPa)	$\mathit{k}$	$\overline{\mathit{c}}$ (MPa)	${\overline{\mathrm{\sigma }}}_{\mathit{c}}$ (MPa)	$\overline{\mathit{\phi }}$ (°)	$\mathit{\mu }$
1	1	3	1	5	10	15	0.3
2	1.5	5	2	10	15	30	0.4
3	2	7	3	15	20	45	0.5
4	2.5	9	4	20	25	60	0.6

.

3. Mechanisms of Macro- and Micro-Parameter Influence and Construction of Multiple Regression Models

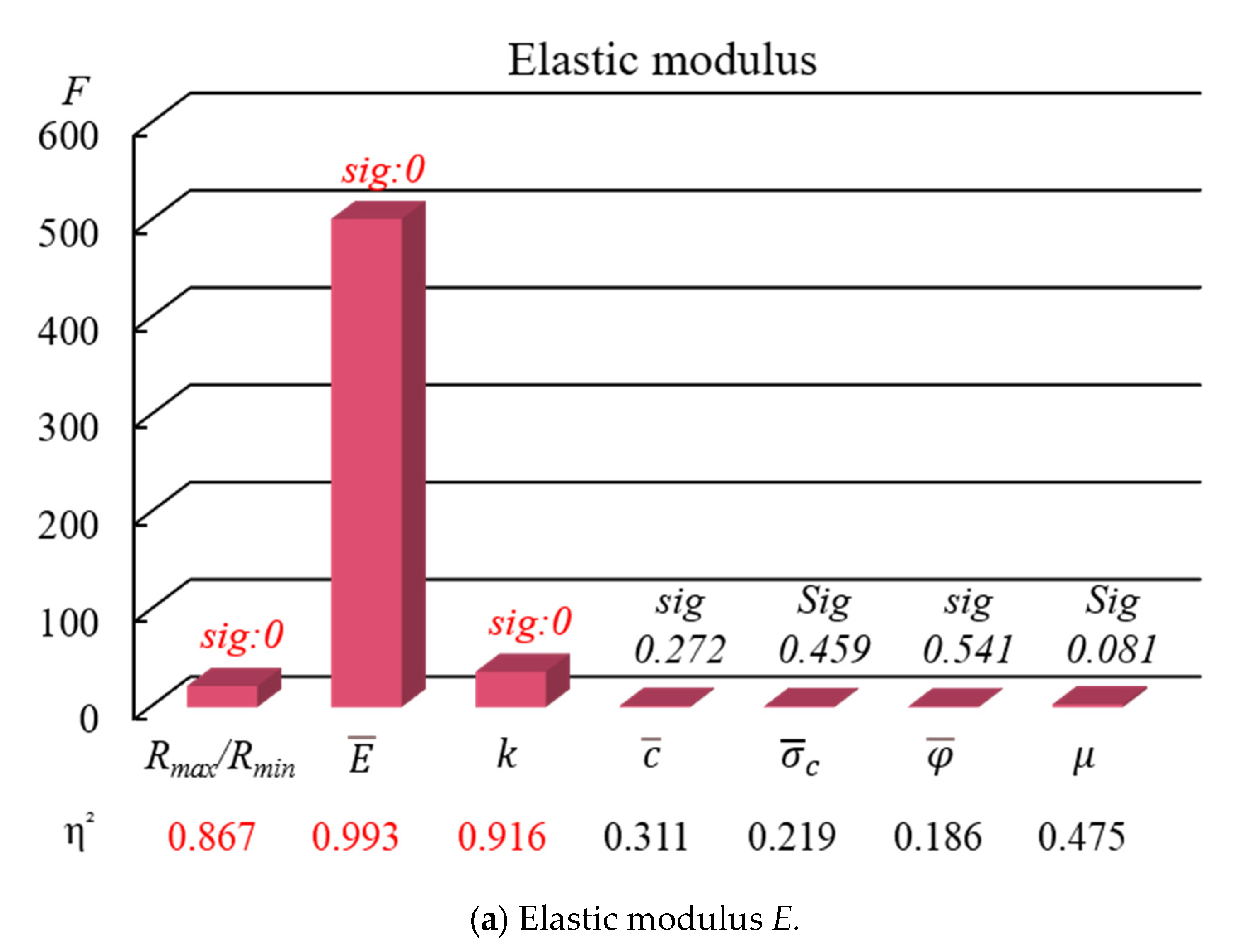
3.1. Analysis of Major Influencing Factors on Macroscopic Mechanical Properties

Based on the experimental parameters in Table 1, a seven-factor, four-level orthogonal experimental design was developed. Macroscopic mechanical properties, including uniaxial compressive strength (UCS), elastic modulus (E), and Poisson’s ratio (υ), were obtained from numerical simulations. The orthogonal experimental scheme and corresponding simulation results are summarized in

Table 2. Orthogonal experimental design and simulation results.

Number	Rmax/Rmin	$\overline{\mathit{E}}$ (GPa)	$\mathit{k}$	$\overline{\mathit{c}}$ (MPa)	${\overline{\mathit{\sigma }}}_{\mathit{c}}$ (MPa)	$\overline{\mathit{\phi }}$ (°)	$\mathit{\mu }$	UCS (MPa)	E (GPa)	$\mathit{\upsilon }$
1	1	7	3	5	20	15	0.5	17.57	12.89	0.273
2	2	5	3	5	15	60	0.3	12.69	7.71	0.292
3	1.5	9	3	10	10	15	0.4	24.8	14.10	0.303
4	1.5	3	2	5	15	30	0.4	14.9	5.29	0.224
5	1.5	7	4	15	10	60	0.5	25.76	10.58	0.346
6	2	3	4	20	15	15	0.6	35.64	4.47	0.35
7	2	9	1	15	10	30	0.6	31.57	17.47	0.066
8	2.5	3	3	10	25	60	0.6	26.28	4.68	0.294
9	1.5	7	4	5	25	30	0.6	18.57	10.60	0.336
10	2.5	7	1	10	15	60	0.4	26.06	13.29	0.086
11	2.5	9	2	15	15	15	0.5	36.38	14.75	0.224
12	1	3	1	5	10	15	0.3	10.57	7.17	0.093
13	2.5	5	4	5	10	45	0.4	14.81	7.19	0.332
14	2	9	1	5	25	60	0.5	14.97	16.97	0.06
15	1	3	1	15	25	45	0.4	35.54	7.47	0.099
16	2.5	7	1	20	20	30	0.3	42.99	13.20	0.107
17	1	9	4	10	15	30	0.3	26.93	16.03	0.337
18	1	9	4	20	20	60	0.4	44.33	16.47	0.348
19	1.5	9	3	20	25	45	0.3	52.35	14.04	0.329
20	2.5	3	3	20	10	30	0.5	25.21	4.64	0.299
21	1	5	2	10	25	30	0.5	27.54	10.71	0.220
22	1.5	5	1	10	20	15	0.6	25.38	11.89	0.245
23	2	7	2	10	10	45	0.3	24.03	11.44	0.238
24	2.5	5	4	15	25	15	0.3	41.01	7.13	0.37
25	2	5	3	15	20	30	0.4	42.85	7.73	0.315
26	1.5	3	2	15	20	60	0.3	35.64	5.18	0.256
27	2	3	4	10	20	45	0.5	28.20	4.45	0.349
28	1	7	3	15	15	45	0.6	38.44	13.61	0.294
29	1.5	5	1	20	15	45	0.5	45.05	10.26	0.084
30	2.5	9	2	5	20	45	0.6	16.53	14.48	0.202
31	2	7	2	20	25	15	0.4	51.27	11.68	0.242
32	1	5	2	20	10	60	0.6	34.57	10.83	0.218

.

Based on the orthogonal experimental results, a multifactor analysis of variance was employed to systematically evaluate the effects of micromechanical parameters on uniaxial compressive strength (UCS), elastic modulus (E), and Poisson’s ratio (υ). As an effective statistical method, a multifactor analysis of variance allows for the quantification of the contributions of multiple independent variables (micromechanical parameters) to dependent variables (macroscopic mechanical properties), while accounting for the potential interaction effects among factors. The F-statistic was used to assess the magnitude of each factor’s effect; higher F-values indicate more pronounced influences. Statistical significance was determined based on the Sig. value as follows: Sig. < 0.01, highly significant; 0.01 < Sig. ≤ 0.05, significant; and Sig. > 0.05, not significant. The analysis results are shown in Figure 2.

According to the results presented in Figure 2a, the factors affecting the elastic modulus (E) are ranked in the following order: effective modulus $\overline{E}$ > stiffness ratio $k$ > particle size ratio R_max/R_min > friction coefficient $\mu$ > cohesion $\overline{c}$ > tensile strength ${\overline{\mathrm{\sigma }}}_c$ > friction angle $\overline{\phi }$. These results indicate that the effective modulus has the strongest influence on the macroscopic elastic modulus, displaying an extremely significant effect. Significance analysis (Sig. values) further confirms that the effective modulus, stiffness ratio, and particle size ratio exhibit highly significant effects on the elastic modulus (with significance levels of zero), while the impact of the remaining parameters is relatively minor. The friction coefficient has a certain effect on the macroscopic elastic modulus, but its effect is not significant. Cohesion, tensile strength, and friction angle have almost no effect on the macroscopic elastic modulus.

According to the results presented in Figure 2b, the factors affecting uniaxial compressive strength (UCS) are ranked as follows: cohesion $\overline{c}$ > tensile strength ${\overline{\mathrm{\sigma }}}_c$ > effective modulus > friction coefficient $\mu$ > friction angle $\overline{\phi }$ > particle size ratio R_max/R_min > stiffness ratio k. The analysis demonstrates that cohesion contributes most significantly to UCS, exhibiting a highly significant effect (significance level = 0). Tensile strength also shows a significant effect, with a Sig. value of 0.002, following closely after cohesion. With the exception of cohesion and tensile strength, the remaining micromechanical parameters have no significant effect on UCS.

According to the results presented in Figure 2c, the factors affecting Poisson’s ratio υ are ranked as follows: stiffness ratio k > particle size ratio R_max/R_min > cohesion $\overline{c}$ > friction angle $\overline{\phi }$ > tensile strength ${\overline{\mathrm{\sigma }}}_c$ > effective modulus $\overline{E}$ > friction coefficient $\mu$. The analysis reveals that only the stiffness ratio has a significant effect on Poisson’s ratio, while the other micromechanical parameters have no significant impact.

3.2. Analysis of the Influence Mechanism of Significant Micromechanical Parameters Interaction

Based on the obtained experimental results and multifactor analysis of variance, the present study analyzes the interaction effects of significant factors on macroscopic elastic modulus and uniaxial compressive strength (UCS). Significant micromechanical parameters identified from the prior analysis were selected as variables. The control variable method was employed to systematically investigate the influence of different significant factors and their interactions on macroscopic mechanical properties.

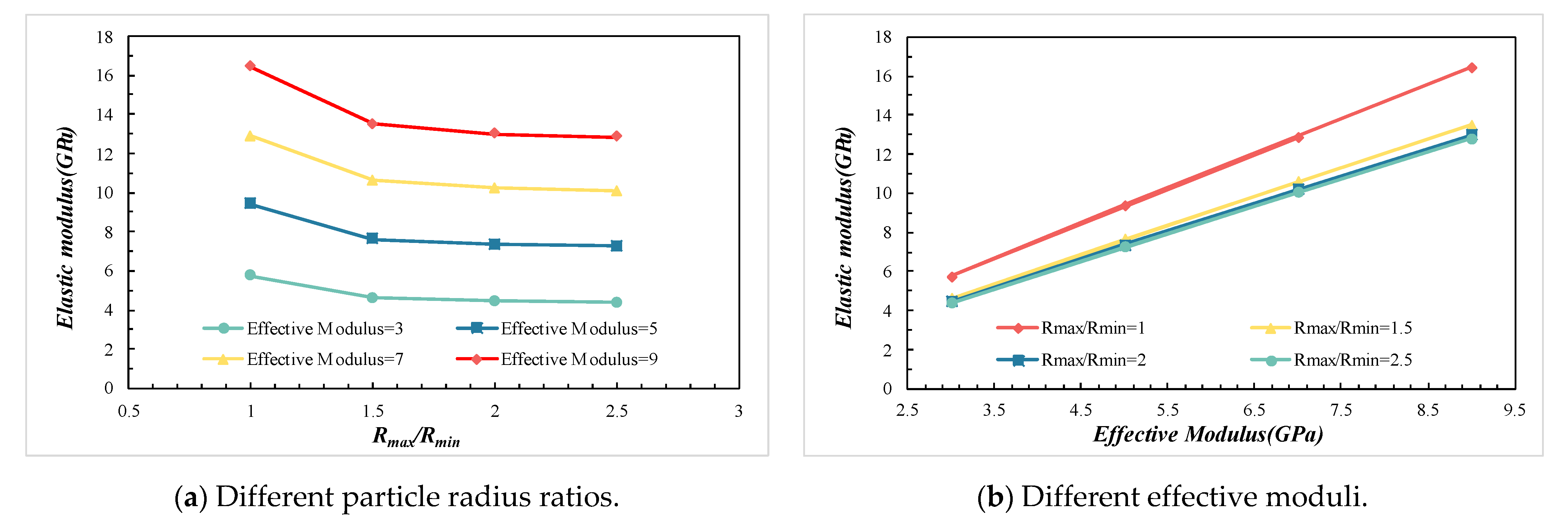
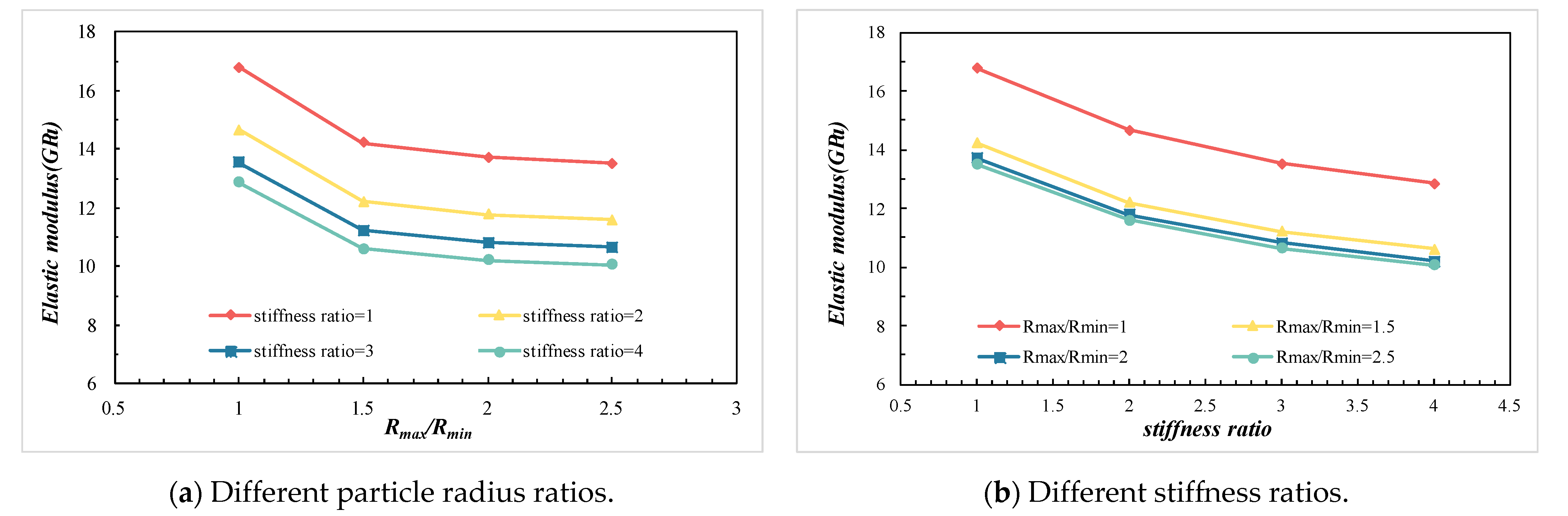
3.2.1. The Effects of R_max/R_min, $\overline{E}$, and k on the E

As shown in Figure 3a, when the effective modulus is fixed, the elastic modulus decreases as the radius ratio (R_max/R_min) increases. When the radius ratio exceeds 1.5, the elastic modulus levels off and exhibits no significant changes. On the other hand, as depicted in Figure 3b, with the radius ratio fixed, the elastic modulus increases linearly with increasing effective modulus. Notably, when the radius ratio is greater than 2.0, the curves corresponding to different radius ratios almost coincide, suggesting that, under these conditions, the elastic modulus is primarily governed by the effective modulus.

As shown in Figure 4a, when the stiffness ratio is held constant, the elastic modulus exhibits a decreasing trend with increasing R_max/R_min, with the most significant change observed when the stiffness ratio equals one. As the stiffness ratio increases, the rate at which the elastic modulus decreases becomes less pronounced. Regardless of the stiffness ratio, when R_max/R_min exceeds 1.5, the downward trend of the elastic modulus levels off. At this stage, the elastic modulus is predominantly influenced by the stiffness ratio. As shown in Figure 4b, under different R_max/R_min conditions, the elastic modulus decreases with increasing stiffness ratio. The R_max/R_min has a significant impact on the elastic modulus at a relatively low level. However, when R_max/R_min exceeds 2.0, the elastic modulus remains nearly unchanged as the stiffness ratio increases, indicating that the influence of R_max/R_min becomes negligible in this range.

A significant interaction effect is observed between the effective modulus and stiffness ratio parameters. As illustrated in Figure 5a, when the effective modulus is held constant, the elastic modulus decreases with increasing stiffness ratio. Notably, when the effective modulus is at a high level, the inhibitory effect of the stiffness ratio on the elastic modulus is significantly enhanced; conversely, when the effective modulus is at a low level, the influence of the stiffness ratio on the elastic modulus weakens. As shown in Figure 5b, with the stiffness ratio held constant, the elastic modulus increases monotonically with increasing effective modulus. With increasing stiffness ratio, its inhibitory influence on the dominant effect of the effective modulus becomes increasingly evident.

As can be seen, the elastic modulus increases with increasing effective modulus and decreases with increasing stiffness ratio. It is worth noting that a threshold exists for the effect of the radius ratio (R_max/R_min) on the elastic modulus. Below this threshold, the radius ratio exerts an inhibitory influence. However, beyond the threshold, its effect becomes negligible, and the elastic modulus is predominantly governed by the effective modulus and stiffness ratio. Based on this characteristic, selecting an appropriate radius ratio can help ensure computational accuracy while enabling dimensionality reduction of the computational model.

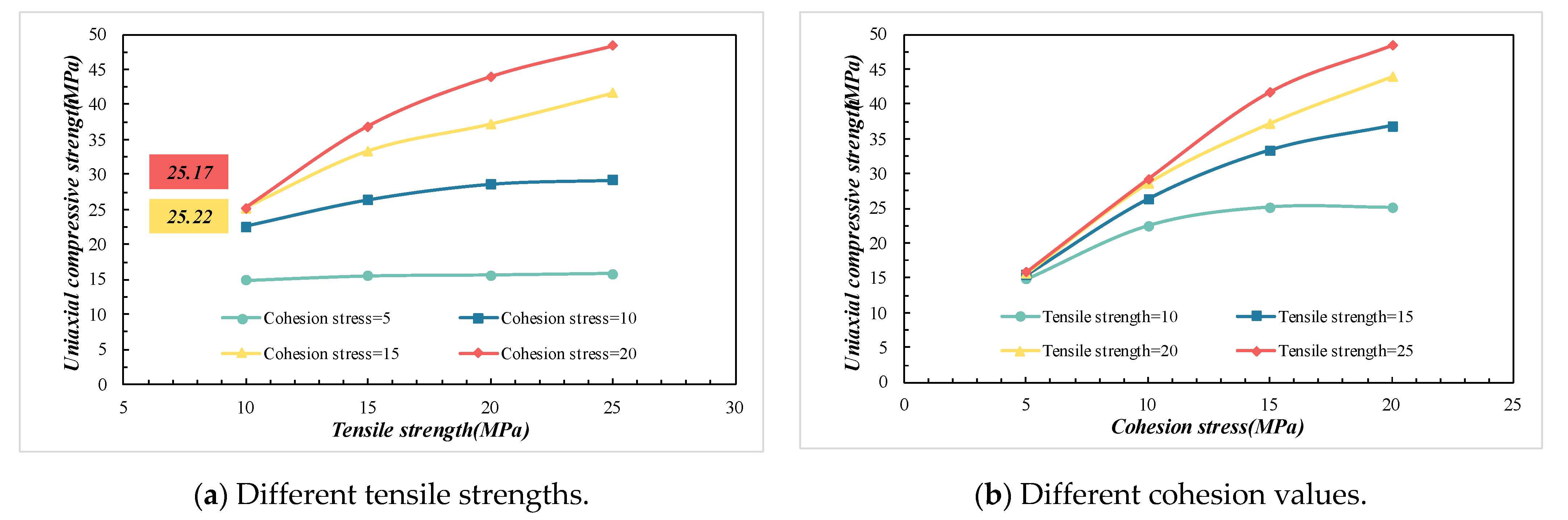
3.2.2. The Effects of ${\overline{\mathrm{\sigma }}}_c$ and $\overline{c}$ on the UCS

The primary influencing factors for uniaxial compressive strength (UCS) are cohesion and tensile strength. As shown in Figure 6a, when cohesion is held constant, UCS exhibits a significant increasing trend with the increase in tensile strength. The higher the cohesion level, the more pronounced the enhancing effect of tensile strength on UCS. In contrast, when cohesion is low, the influence of tensile strength on UCS becomes negligible. As depicted in Figure 6b, with tensile strength held constant, UCS increases with increasing cohesion. The combination of high tensile strength and high cohesion generates a stronger synergistic effect, where their combined contribution exceeds the independent effects of individual parameters.

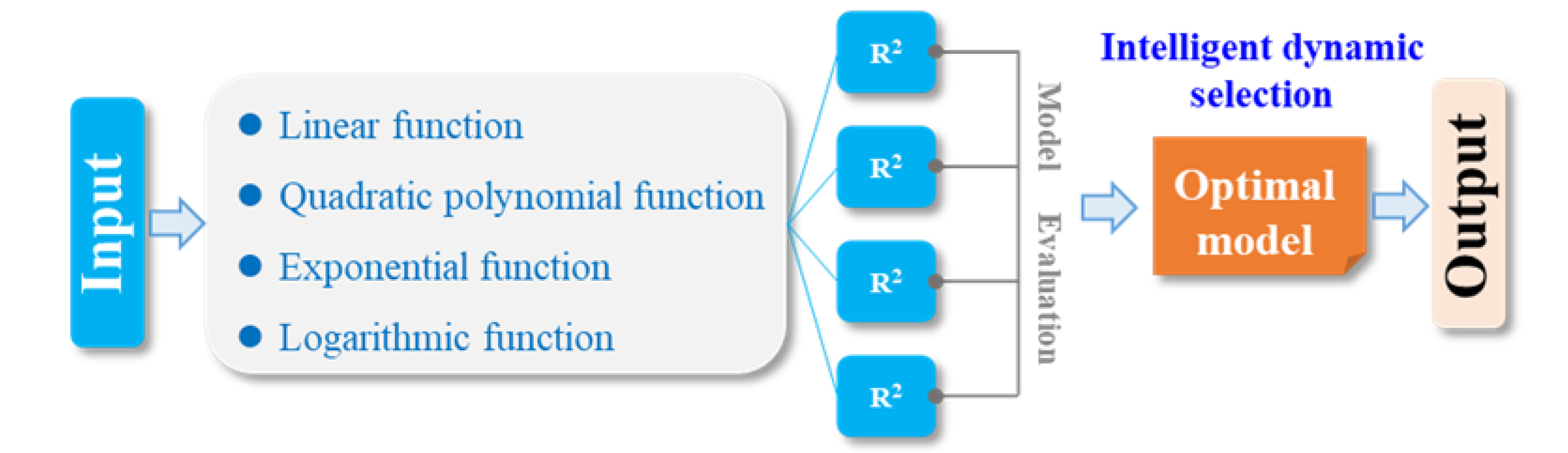
3.3. Regression Analysis of Macroscopic and Micromechanical Parameters Based on an Intelligent Dynamic Regression Selection Mechanism

Based on the results of orthogonal experiments and interaction tests, this study identifies key parameter combinations that significantly influence macroscopic mechanical response parameters to model their complex relationships, and an intelligent dynamic regression selection mechanism is adopted, which is capable of automatically selecting the optimal functional form from multiple candidates, including linear, quadratic, exponential, and logarithmic models. The selection is performed adaptively based on the coefficient of determination (R²), ensuring that the most suitable model is chosen in a data-driven manner. An illustrative framework of this intelligent dynamic selection process is shown in Figure 7, highlighting the automatic evaluation and comparison of multiple functional forms.

The significant influencing factors for the elastic modulus are R_max/R_min, $\overline{E}$, and $k$. Intelligent dynamic regression analysis is then performed to explore their functional relationships, and the corresponding regression models are established accordingly.

$$\begin{array}{cc}\mathrm{Linear}:& E=4.76+1.67\overline{E}-1.19{\displaystyle \frac{R_{\max }}{R_{\min }}}-0.84K (R^2 = 0.96)\end{array}$$

(2)

$$\begin{gathered} \begin{array}{cc}\mathrm{Polynomial}:& E=5.29+3.02\times \overline{E}\cdot {\displaystyle \frac{R_{\max }}{R_{\min }}}-5.50\cdot {\displaystyle \frac{R_{\max }}{R_{\min }}}-1.41k-0.02{\left(\overline{E}\right)}^2-0.34\cdot {\displaystyle \frac{R_{\max }}{R_{\min }}}\cdot \overline{E}-0.20\overline{E}k+ \\ 1.73{\left({\displaystyle \frac{R_{\max }}{R_{\min }}}\right)}^2-0.13\cdot {\displaystyle \frac{R_{\max }}{R_{\min }}}\cdot k+0.34k^2 (R^2 = 0.85)\end{array} \end{gathered}$$

(3)

$$\begin{array}{cc}\mathrm{Exponential}:& E=e^{1.75+0.18\overline{E}-0.16{\displaystyle \frac{R_{\max }}{R_{\min }}}-0.10k} (R^2 = 0.89)\end{array}$$

(4)

$$\begin{array}{cc}\mathrm{Logarithmic}:& E=-2.27+8.99\log \left(\overline{E}\right)-2.06\log \left({\displaystyle \frac{R_{max}}{R_{min}}}\right)-1.91\log \left(k\right) (R^2 = 0.88)\end{array}$$

(5)

By comparing the coefficients of determination, R², Formula (2) was selected to model the effects of R_max/R_min, $\overline{E}$, and k on the E. The resulting model exhibits a high goodness of fit, with a coefficient of determination of R² = 0.96, indicating a satisfactory fitting performance.

The significant influencing factors for the uniaxial compressive strength are ${\overline{\mathrm{\sigma }}}_c$ and $\overline{c}$. Dynamic regression analysis was conducted for the two factors, and their functional relationships are as follows.

$$\begin{array}{cc}\mathrm{Linear}:& UCS=-3.32+1.78\overline{c}+0.62{\overline{\sigma }}_c (R^2 = 0.86)\end{array}$$

(6)

$$\begin{array}{cc}\mathrm{Polynomial}:& UCS=-4.76+1.88\overline{c}+1.04{\overline{\sigma }}_c-0.06{\overline{c}}^2+0.07\overline{c}{\overline{\sigma }}_c-0.04{\overline{\sigma }}_c^2 (R^2 = 0.93)\end{array}$$

(7)

$$\begin{array}{cc}\mathrm{Exponential}:& UCS=e^{2.12+0.07\overline{c}+0.02{\overline{\sigma }}_c} (R^2 = 0.85)\end{array}$$

(8)

$$\begin{array}{cc}\mathrm{Logarithmic}:& UCS=-45.49+19.19\log \overline{c}+10.34{\log \overline{\sigma }}_c (R^2 = 0.88)\end{array}$$

(9)

By comparing the coefficients of determination R², Formula (7) was selected to fit the effects of ${\overline{\mathrm{\sigma }}}_c$ and $\overline{c}$ on the uniaxial compressive strength. With a coefficient of determination of R² = 0.93, the fitting effect is satisfactory.

The only significant influencing factor for Poisson’s ratio is the stiffness ratio k. Dynamic regression analysis was conducted on the experimental results, and the functional relationship is as follows.

$$\begin{array}{cc}\mathrm{Linear}:& \upsilon =0.05+0.08k (R^2 = 0.86)\end{array}$$

(10)

$$\begin{array}{cc}\mathrm{Polynomial}:& \upsilon =-0.05+0.18k-0.02k^2 (R^2 = 0.89)\end{array}$$

(11)

$$\begin{array}{cc}\mathrm{Exponential}:& \upsilon =e^{-2.56+0.41k} (R^2 = 0.73)\end{array}$$

(12)

$$\begin{array}{cc}\mathrm{Logarithmic}:& \upsilon =0.11+0.17\ln k (R^2 = 0.90)\end{array}$$

(13)

By comparing the coefficients of determination, R², Formula (13) was selected to fit the effect of the stiffness ratio on Poisson’s ratio. With a coefficient of determination of R² = 0.90, the fitting effect is satisfactory.

4. Calibration Method for Micromechanical Parameters of Discrete Element Model and Case Application

4.1. Calibration Method for Micromechanical Parameters of Discrete Element Model

Based on the analysis of the significant influencing factors of macroscopic mechanical parameters and the results of interaction among micromechanical parameters, when the R_max/R_min exceeds 2.0, its effect on the elastic modulus becomes negligible. The radius ratio determines the total number and distribution of particles in the model. Considering both computational efficiency and modeling accuracy, calibration with respect to this parameter is prioritized. The detailed calibration procedure is as follows.

• The uniaxial compressive strength, elastic modulus, and Poisson’s ratio of the rock were determined through uniaxial compression tests. A numerical model was established based on the actual dimensions, porosity, and density of the rock.
• Based on the research rules mentioned above and by comprehensively considering computational performance and simulation accuracy, an appropriate radius ratio was selected to determine the number and spatial distribution of particles in the model.
• The experimentally determined Poisson’s ratio is substituted into Equation (13) to obtain the stiffness ratio $k$, which is then set as $k={\overline{k}}^{\mathrm{*}}$. After R_max/R_min and $k$ are determined, the actual elastic modulus is substituted into Equation (2) to calculate the micromechanical parameter, the effective modulus $\overline{E}$, which is then set as $\overline{E}$ = ${\overline{E}}^{\mathrm{*}}.$
• The failure modes of rock under uniaxial compression include shear failure, tensile failure, and conjugate failure. According to the findings of Wu [27], the ratio of tensile strength ${\overline{\mathrm{\sigma }}}_c$ to cohesion $\overline{c}$ determines the failure mode of the rock. Specifically, when ${\overline{\mathrm{\sigma }}}_c/\overline{c}$ < 1.66, the rock exhibits tensile failure; when 1.66 < ${\overline{\mathrm{\sigma }}}_c/\overline{c}$ < 3.0, the rock displays conjugate failure; and when ${\overline{\mathrm{\sigma }}}_c/\overline{c}$ > 3.0, the rock undergoes shear failure. Based on the crack morphology observed in the actual rock mechanics test, the corresponding value of ${\overline{\mathrm{\sigma }}}_c/\overline{c}$ is selected. The experimentally measured uniaxial compressive strength (UCS) and the selected ${\overline{\mathrm{\sigma }}}_c/\overline{c}$ are then substituted into Equation (7) to calculate the micromechanical parameters: tensile strength ${\overline{\mathrm{\sigma }}}_c$ and cohesion $\overline{c}$.
• Since the friction coefficient ($\mu$) and friction angle ($\overline{\phi }$) have negligible effects on macroscopic mechanical properties, initial values of $\mu =0.5$ and $\overline{\phi }=30°$ are adopted based on previous research experience [28]. The above micromechanical parameters are incorporated into the parallel-bond model to establish a particle flow model for moderately consolidated sandstone. By comparing the results of laboratory tests and numerical simulations, if the error is less than or equal to 10%, the calibration of the model’s micromechanical parameters is completed. If the error is greater than or equal to 10%, iterative calibration is performed according to Formula (14).

$$A_{k+1}=A_k+(A_k^{*}-A^{*})\cdot \lambda$$

(14)

$$\lambda =\left\{\begin{array}{l}\begin{array}{ll}1& (A_k^{*}-A^{*})\le 0\end{array}\\ \begin{array}{ll}-1& (A_k^{*}-A^{*})>0\end{array}\end{array}\right.$$

(15)

(where A_k+1 is the simulated input value after No.(k + 1) iteration, $A_k^{*}$ is the simulated result after the No.(k) iteration, and $A^{*}$ is the target value obtained from experiments).

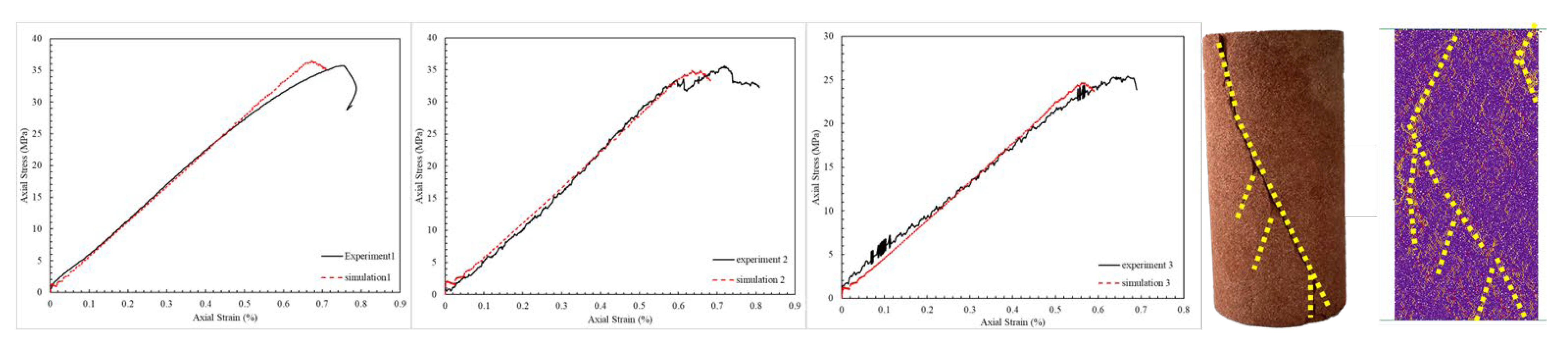
4.2. Case Verification of Moderately Consolidated Sandstone

This study makes red sandstone from the Xinjiang Hutubi Gas Storage into standard cores with a diameter of 50 mm and a height of 100 mm, and conducts uniaxial compression tests on these cores to validate the accuracy of the micromechanical parameter calibration method.

Based on the parameters obtained from experiments, the required parameters are calculated using the micromechanical parameter calibration method described above. The model dimensions are set to a height of 100 mm and a diameter of 50 mm. Adopting a radius ratio of R_max/R_min = 2.0, a particle density of 2.14 g/cm³, and selecting a minimum particle radius of 0.2 mm, particles are randomly generated according to a porosity of 21.6%, resulting in a final particle count of 13,599.

This study conducted three groups of numerical simulations of uniaxial tests on moderately consolidated sandstone. Based on the rock mechanical parameters obtained from the tests, a numerical model consistent with the experimental results was eventually established. The calculated model parameters are presented in

Table 3. Micromechanical parameters for numerical simulation experiments.

Serial No.	$\frac{{\mathit{R}}_{\mathbf{max}}}{{\mathit{R}}_{\mathbf{min}}}$	$\overline{\mathit{E}}$ (MPa)	$\mathit{K}$	$\overline{\mathit{c}}$ (MPa)	${\overline{\mathit{\sigma }}}_{\mathit{c}}$ (MPa)	μ	$\overline{\mathit{\phi }}$
1	2	3.26	1.30	16.44	27.32	0.5	30
2	2	3.48	2.87	14.3	23.74	0.5	30
3	2	2.74	3.58	6.61	10.97	0.5	30

.

As illustrated in Figure 8, the stress–strain curves from laboratory tests and numerical simulations align closely in the elastic stage, and their fracture morphologies are also highly consistent. Due to microcrack development and heterogeneity in real cores, minor fluctuations appear in the experimental curve during axial loading. In contrast, the model’s pre-compression cementation process leads to a denser particle arrangement, resulting in smaller fluctuations. The simulated fracture morphology matches well with that of the failed real core.

Table 4. Results and error comparison of macroscopic mechanical parameters between laboratory tests and numerical simulations.

Serial No.	UCS (MPa)	Error	E (GPa)	Error	λ	Error
experiment 1	35.75	2.06%	6.09	1.98%	0.233	0.85%
simulation 1	36.49		5.97		0.235
experiment 2	35.61	2.02%	5.77	7.79%	0.289	2.42%
simulation 2	34.89		5.32		0.296
experiment 3	25.41	2.71%	4.22	6.39%	0.327	0%
simulation 3	24.72		4.49		0.327

shows that the macroscopic mechanical parameters from experiments and simulations differ by less than 10%, confirming that the constructed model and calibration method are sufficient for experimental requirements.

5. Conclusions

This study employed the linear parallel-bond model as the particle contact constitutive law and developed a numerical model for the uniaxial compression of sandstone. Using orthogonal tests and an interaction analysis of key factors, a functional relationship between micromechanical and macroscopic mechanical parameters of moderately consolidated sandstone was established. This study proposed a micromechanical parameter calibration method for discrete element models of moderately consolidated sandstone. This method is more efficient than the conventional trial-and-error approach.

• The primary micromechanical parameters influencing the macroscopic mechanical properties are the maximum-to-minimum particle size ratio, effective modulus, stiffness ratio, tensile strength, and cohesion. The elastic modulus is mainly determined by the effective modulus, stiffness ratio, and particle size ratio. The uniaxial compressive strength depends on cohesion and tensile strength. Poisson’s ratio is most significantly affected by the stiffness ratio alone.
• Interaction analysis shows that the elastic modulus increases with effective modulus and decreases with stiffness ratio. The effect of the particle size ratio on the elastic modulus exhibits a threshold. When the ratio exceeds 2.0, the elastic modulus is mainly controlled by the effective modulus and stiffness ratio. Uniaxial compressive strength increases with both tensile strength and cohesion, with a pronounced synergistic effect when both parameters are high.
• A multivariate predictive model was developed using an intelligent dynamic regression selection mechanism, achieving a goodness of fit above 90%. An iterative correction method for micromechanical parameter calibration was introduced and validated through three sets of laboratory and numerical simulation tests. The resulting macroscopic mechanical parameters show errors within 10% compared with the experimental results, and the fracture morphology of the numerically simulated rock samples is similar to that of the actual cores. These findings confirm that the proposed calibration method is both accurate and efficient.