Abstract
The object of this research is the process of tracking air targets at the initial stage of radar system operation. The problem lies in the lack of a comprehensive approach to tracking air targets in difficult conditions that is able to dynamically adapt filtering parameters, predict signal reliability, and change the processing mode depending on the level of interference. In conditions of signal loss, noise, and unstable measurement reliability, traditional methods do not provide stable and accurate tracking, especially at the initial stages of radar operation. To address this issue, an intelligent method is proposed that integrates a probabilistic graphical evaluation and review technique (GERT) model, a recursive Kalman filter, and a measurement reliability prediction module based on a long short-term memory (LSTM) neural network. The proposed approach allows for the real-time adaptation of filtering parameters, fusion of local and global trajectory estimates, and dynamic switching between tracking modes depending on the environmental conditions. The dynamic weighting algorithm between model estimates ensures a balance between accuracy and robustness. Simulation experiments confirmed the effectiveness of the method: the root mean square error (RMSE) of coordinate estimation was reduced by 25%; the probability of tracking loss decreased by half (from 0.2 to 0.1); and the accuracy of loss prediction exceeded 85%. The novelty of the approach lies in integrating stochastic modeling, machine learning, and classical filtering into a unified adaptive loop. The proposed system can be adapted to various types of radar and easily scaled to multi-sensor architectures. This makes it suitable for practical implementation in both defense and civilian air object detection systems operating under complex conditions.
1. Introduction
1.1. Motivation
The development of modern air defense systems, particularly radar systems, takes place in conditions of significant complexity in the air. The increase in the speed and maneuverability of air objects, the active use of electronic warfare, jamming systems, and signal simulators make it challenging to ensure the reliable and continuous tracking of targets. In such conditions, the issues of noise robustness and the adaptability of tracking systems become critical, especially at the initial stage of radar interaction with the target, when observations are still fragmentary, and the probability of the loss of tracking is the highest.
Most modern radars do have basic adaptation and filtering mechanisms; however, they are not always able to work in conditions of unstable measurement reliability, signal loss, and variable interference levels. Typical filters, in particular, the Kalman filter, demonstrate high accuracy in stationary conditions; however, they are not adapted to work with intermittent or noisy data. Even promising intelligent modules mostly focus on classification or recognition but do not implement recursive filtering or prediction of the reliability of measurements in real time. This limits the ability of radars to work effectively in conditions as close as possible to combat conditions.
The relevance of this research topic lies in the need to create a comprehensive intelligent tracking method that can predict the reliability of future measurements, adapt filtering parameters to changes in the interference environment, combine evaluation results from different sources, and provide stable tracking even while losing part of the data.
Thus, the relevance of the problem is the need to create hybrid intelligent tracking methods that integrate stochastic modeling, recursive filtering, and artificial intelligence into a single adaptive architecture. Such approaches will ensure the stable and accurate operation of radars in real time, in conditions of uncertainty, high speeds, complex object dynamics, and the influence of intentional interference.
1.2. State of the Art
Due to the increasing complexity of the interference environment and the need for high-precision tracking of aerial targets at the initial detection stages, recent years have seen a significant intensification of research efforts aimed at improving the robustness and adaptability of radar systems.
An analysis of recent studies in the literature enables us to identify five key research directions that form the scientific foundation for the development of the proposed intelligent tracking method.
The first group of studies [1,2,3] emphasizes the relevance of the problem and explores general approaches to target tracking in complex scenarios. These works introduce conceptual frameworks and system-level solutions but often do not consider measurement loss or online adaptability.
Another direction focuses on methods to improve tracking accuracy under interference [4,5]. These include robust filters and enhanced signal-processing algorithms. However, they are typically based on static models and may not handle dynamic changes or reliability fluctuations in the measurements.
A separate research stream develops probabilistic models for describing detection and tracking processes under uncertainty [6,7,8]. These models contribute to formalizing noise and ambiguity but are rarely integrated with learning-based forecast systems or real-time decision-making components.
The application of intelligent methods, such as neural networks in radar data processing [9,10,11], has shown promising results in pattern recognition and prediction. However, most of these techniques are used as standalone tools and not in combination with classical tracking systems.
Finally, recent work explores the integration of classical methods and AI [12,13,14,15], aiming to combine the strengths of both approaches. Although such systems improve flexibility, they often lack mechanisms for dynamic mode switching based on measurement reliability and prediction.
In the following paragraphs, we provide a more detailed discussion of representative works from each of these five research directions. For each study, we highlight the core methodology, key contributions, and existing limitations that motivated the development of our proposed approach.
A significant number of modern publications are devoted to the analysis of threats associated with the growing complexity of the interference environment, which affects the accuracy and stability of air object tracking. In [1] it is emphasized that the presence of active interference significantly reduces the effectiveness of traditional filters, especially at the initial stage of tracking. However, the mechanisms of prediction and confidence in measurements are not considered in this work. In addition, the issues of adapting filtration algorithms to sudden changes in interference intensity remain unresolved.
This fact is also confirmed in work [2]. The article proves that even in the absence of direct signal loss, nonlinearity and changes in the dynamics of the object can lead to the accumulation of errors if the filter operates without adaptation. The authors proposed the automatic tuning of Kalman filter parameters, illustrating the general trend of the transition from static to adaptive systems. However, the model does not contain a predictive assessment of the reliability of measurements or control of the tracking mode.
One review [3] summarized modern technological trends related to the improvement of radar architectures, in particular through the integration of artificial intelligence, cognitive mechanisms, and multimodal data processing. This review confirmed that the combination of classical filtering methods with intelligent components is one of the most promising directions in the development of new generation tracking systems. However, the article does not contain proposals for the implementation of models.
In modern research, special attention is paid to the creation of algorithms capable of maintaining high tracking accuracy in conditions of uncertainty, interference, and variable target dynamics. Thus, in ref. [4], a strategy for distributing radar resources in distributed radar networks is proposed to counteract deceptive interference during the tracking of multiple targets. The proposed approach focused on effective planning in conditions of resource constraints and active interference. The main advantage of this work is the high level of detail of the interference models, taking into account the multi-position structure and limitations on data transmission channels. Nevertheless, the study focused on resource management, and not on the adaptation of tracking algorithms or the assessment of the quality of measurements in interference.
In [5], a new version of the adaptive robust cubic Kalman filter (ARCKF) was proposed for the tracking of maneuvering targets under conditions of model uncertainty and anomalous noise. The authors implemented a mechanism for automatic adjustment of the filter parameters based on the assessment of data reliability, which reduced sensitivity to noisy or incorrect measurements. It is important that the method combines the accuracy of nonlinear filtering with the flexibility of the robust approach, adapting to changes in the external environment. The main advantage is that the filter responds not only to the dynamics of the target, but also to the quality of the measurement signal, which is critically important in real conditions of radar operation. However, the model has increased computational complexity, which may limit its use in systems with strict time constraints or limited resources.
In tracking tasks under conditions of incomplete information or interference, probabilistic approaches that allow for modeling of the behavior of the object or the functioning of the radar at the macro level are of particular importance. Such approaches can provide flexibility in the initial assessment of the situation, calculation of the probabilities of loss or non-detection, and are effective in complex scenarios. In [6], a GERT model of the initial stage of interaction between the radar and the air target was proposed. The model takes into account the probabilities of detection, uncertainty at the moment of radar excitation, delay. and signal loss. The main advantage of this work is the stochastic description of the logic of transitions between events, which is especially relevant for modeling systems with partial observation and misses. The limitation is that the model is implemented as an independent mathematical construct and is not directly integrated into adaptive filters or the neural network structures required for dynamic tracking.
In [7], the authors developed an improved probabilistic data association algorithm, integrated probabilistic data association (IPDA), for tracking tasks in a complex environment with a large number of obstacles and false targets. The advantage of this work is the high accuracy of processing multiple observations, where classical filters do not cope. The model significantly reduces the risk of incorrect measurement matching, which is especially important in multi-point or multi-sensor tracking. However, the disadvantage is the difficulty of scaling the algorithm when the number of targets increases, as well as the fact that the algorithm does not take into account the measurement reliability parameters as a source of filter adaptation.
In [8], the effectiveness of integrating Markov chains with uncertainty analysis in event prediction based on limited satellite data was demonstrated. Although the subject of the study is hydrological processes, the tools used are universal and can be adapted for radar tasks. The main advantage is the combination of stochastic estimation with risk analysis in situations of incomplete observations. However, the method does not provide for interactive adaptation or the correction of parameters in real time, which reduces its effectiveness in dynamic tracking systems.
Among researchers, there has been a rapid increase in the use of artificial intelligence models, in particular, recurrent neural networks (RNN), LSTM, and their modifications, for the processing and classification of radar signals. These models have the ability to detect temporal patterns, respond to signal instability and form predictive estimates, which is especially relevant in tracking problems with losses or interference.
In [9], the use of LSTM for sorting radar signals and individual source recognition is proposed. The model is trained on sequences containing information about the signal signature and allows for the accurate identification of objects in a complex environment. The advantage is high sensitivity to the signal structure, as well as the ability of LSTM to retain memory of previous states. At the same time, the model is focused mainly on classification, and it is not integrated into the tracking or filtering process of coordinates, which limits its direct application in trajectory tracking.
In [10], the problem of spatiotemporal forecasting of radar echoes using convolutional LSTM (ConvLSTM), which combines the properties of the convolutional neural network (CNN) and recurrent neural network (RNN), is considered. The model uses multi-source data (satellite, sensor), achieving high forecast accuracy in heterogeneous environments. The study showed its ability to work with multidimensional time series and the exploitation of both spatial and temporal dependencies. However, the work is focused on meteorological applications and does not consider adaptation to measurement losses or dynamic responses to interference, which significantly limits its relevance for radar tracking tasks.
In [11], an LSTM framework for classifying radar and communication signals based on their statistical and spectral characteristics is presented. The authors use the spectral decomposition of the signal as an input vector to the LSTM, achieving high recognition accuracy in noisy environments. A strong aspect of the framework is its ability to detect anomalies or interference signals without manually setting thresholds, which can be useful when assessing the reliability of measurements. However, the model does not work with coordinate information and does not implement trajectory estimation or correction, which is key for tracking tasks.
Thus, works [9,10,11] confirm the effectiveness of LSTM architectures in detecting patterns, recognizing signal sources, and predicting behavior in time series. However, most of them are not integrated into the tracking systems of the object coordinates and do not take into account dynamic adaptation in real time, which was one of the motivating factors for the development of the adaptive method proposed in this work.
In [12], a fuzzy gain-controlled filter is proposed, which is used for tracking in difficult conditions when the signal is distorted or intermittent. The advantage of the approach is the ability to dynamically change the filtering coefficients, depending on the degree of observation reliability, without the need for an exact mathematical description of the noise. The method demonstrates better stability compared to traditional filters, but it does not include a long-term prediction or learning mechanism, which reduces its flexibility in cases where the signal structure changes over time.
In [13], adaptive fuzzy tracking control for nonlinear MIMO systems with state constraints and unknown control directions is presented. This approach combines classical control with fuzzy logic to achieve high control accuracy even under complex object dynamics. The main advantage is the ability to adapt to incomplete object models and limited observations, which makes the method relevant for conditions with an unstable signal. Nevertheless, the model is not directly oriented to radar or coordinate filtering; it requires adaptation for use in air target tracking tasks.
Ref. [14] provides a thorough review of approaches to the use of artificial intelligence in radar resource management. The work analyzes a wide range of methods from reinforcement learning to neural network adapters that dynamically change the parameters of sensor deployment, trajectory update frequency, distribution of computing power, etc. The strengths of the work include a comprehensive vision of the future of radar systems as cognitive networks with a high level of autonomy. However, the study is more of a survey and does not contain implementations or integrated structures that combine classical state estimation algorithms with neural or fuzzy modules within a single accompanying filter.
In [15], the relevance of the problem of increasing the accuracy of mathematical modeling results is determined. Methods of fuzzy GERT modeling are analyzed. The need for, and possibility of, increasing the accuracy of the results of mathematical formalization in conditions of fuzzy input and intermediate data are determined. However, the research has a direction related to software testing and, accordingly, requires additional research in the direction of the formalization of target-tracking processes in radar systems.
Another critical aspect often overlooked in radar tracking studies is range ambiguity, which is especially relevant for pulse-Doppler systems operating under intentional jamming. When multiple echoes from different pulses overlap, it becomes difficult to distinguish true target returns from ambiguous ones. This problem is amplified in the presence of intentional interference and multi-path effects. Advanced suppression techniques based on underdetermined blind source separation were proposed in [16] to mitigate such ambiguities, particularly in SAR systems. Although our current model does not simulate range ambiguity directly, future development of the tracking framework may benefit from integrating similar techniques to improve robustness under ambiguous scenarios.
Thus, the analysis of sources indicates the presence of local solutions that cover individual aspects of tracking in conditions of interference: filtering (Kalman, robust models); probabilistic modeling (GERT, IPDA, Markov); machine learning methods (LSTM); and fuzzy control. At the same time, the lack of a single consistent architecture that combines adaptability, forecasting, and accuracy in one method capable of operating in real time with the loss of measurements and changing interference is revealed.
The general unsolved problem is the lack of a comprehensive approach to tracking air targets in complex conditions that dynamically adapts the filtering parameters, predicts the reliability of signals, and changes the processing mode depending on the level of interference.
All this demonstrates the need to conduct research considering the formation of an integrated intelligent target-tracking method that combines the advantages of GERT models, Kalman filters, and LSTM networks in a single flexible signal-processing system in conditions of intentional interference.
1.3. Objectives and Contribution
The purpose of the study is to develop an intelligent method for tracking air targets, capable of adapting to changes in the interference environment, and maintaining the accuracy of coordinate estimation in difficult conditions of radar operation. This will make it possible to ensure the predicted stability of tracking even in cases of partial loss of measurements and reduce the probability of target loss due to dynamic control of signal-processing modes.
To achieve the purpose, the following tasks were set:
- –
- determine the structure of the interaction of the GERT model, the Kalman filter and the intelligent module;
- –
- develop an algorithm for dynamic weighting between the estimates of the Kalman filter and the GERT model;
- –
- develop a model for assessing the reliability of measurements using the LSTM network;
- –
- develop a method for the initial assessment of the trajectory and accuracy of target tracking.
The object of the study is the process of tracking an air target at the initial stage of the radar system’s operation in conditions of intentional interference, characterized by incomplete data, a high level of interference, and the risk of loss of measurements.
The main hypothesis of the study is the assumption that the combination of the GERT model, the Kalman filter and the intelligent module for predicting the reliability of measurements allows for the stable and accurate tracking of air objects in real time even under variable or adverse radar operating conditions.
The following assumptions are made within the framework of the study:
- –
- the target motion model is linear, with known dynamics parameters (the linear model was chosen to simplify the analytical representation but the architecture of the method allows for adaptation to nonlinear models);
- –
- the characteristics of noise in the process and in the measurements can be adaptively estimated using residual indicators;
- –
- radar signals arrive at a fixed frequency, which allows for the implementation of recursive processing algorithms in real time.
The adopted simplifications include:
- –
- the target motion is described in two-dimensional space (azimuth-range), which corresponds to the primary tracking mode in surveillance radars. The model focuses on the initial phase, where the elevation coordinate is either unavailable or processed separately in another channel;
- –
- the influence of interference is reduced to losses or distortions of measurements without modeling the physical nature of the interference;
- –
- delays in signal processing and data transmission are not taken into account as critical in the analyzed architecture.
The selected simplifications do not reduce the overall validity of the results, since they focus on the most critical moment for the system, namely, the initial phase of target detection and capture, where tracking losses most often occur.
The work uses analytical, numerical, and simulation methods. The theoretical justification is based on the application of the stochastic GERT model to describe the phases of target detection, recursive filtering of coordinates by the Kalman filter, and the prediction of measurement quality using the LSTM network. The integration of these components is carried out through the dynamic weighting of estimates and adaptation of filtration parameters. To test the hypothesis, a series of simulation experiments with variable interference conditions were conducted.
2. Materials and Methods
Results of research on the intelligent method of tracking targets in radar systems at the initial stage.
2.1. Structural Model of Interaction of the GERT Model, Kalman Filter and Intelligent Module
The task of this stage is to determine the logical structure of the phase transition of the radar system from the moment of target detection to entering a stable tracking mode. Such a task arises due to the fact that at the initial stage of radar operation there are no complete data on the target trajectory. The system can transit between the phases of detection, loss of tracking, or its restoration; the characteristics of the observations remain unstable. To take into account these features, it is necessary to formalize the sequence of states and possible transitions between them.
The purpose of the task is to build a generalized logical–structural scheme that reflects typical scenarios of system behavior in conditions of incomplete measurements and to justify its use as a basis for the further adaptation of tracking algorithms. The expected result is the selection of key phases, a description of possible transition trajectories between them, and the identification of points at which the need for adaptive system response arises.
The proposed intelligent method for tracking air targets at the initial stage of radar operation in a complex interference environment is based on the integration of three key subsystems: the GERT model, the Kalman filter, and the intelligent adaptation module. Such an architecture allows for the combining of the probabilistic-temporal analysis of processes with local recursive trajectory refinement and dynamic parameter control in real time.
At the first stage, the GERT model performs the function of forming a probabilistic assessment of the process of detection and initial target capture. It reflects possible trajectories of transitions between system states (detection, loss, confirmation of tracking, etc.), taking into account the influence of intentional interference, time delays, and the probability of successful transitions at each stage. As a result, the GERT model generates not only the expected target location area, but also provides generalized time characteristics that are used as initialization conditions for launching the Kalman filter.
At the second stage, the Kalman filter accepts initial information about the object’s state from the GERT model and refines the coordinates and parameters of the target’s motion based on the incoming noisy measurements. The recursive structure of the filter allows for prediction errors to be minimized, as well as for constant updating of the object’s state based on new data.
The third component of the system is an intelligent adaptation module that controls the method parameters depending on the situation. In particular, it assesses the level of interference on the input signals, analyzes the reliability of the predictions, compares current estimates with historical data and, using a machine learning model or fuzzy logic rules, makes decisions on:
- –
- changing the Kalman filter parameters (covariance matrices, smoothing coefficients);
- –
- dynamic weighting between the GERT and Kalman filter estimates;
- –
- switching between tracking modes (stability/accuracy);
- –
- signaling about the risk of tracking loss.
The information flow in the system involves two-way interactions between all components. Data on the state of the object are supplied to the Kalman filter and the intelligent module. Control signals (for example, changing the filtering parameters) are generated by the artificial intelligence unit. These affect both the Kalman filter and GERT (for example, to update the probabilities when confirming the loss of the target).
The general structural diagram of the interactions of the method components is presented in Figure 1. It indicates the main blocks, data transmission directions, and control signals. Data arrows indicate the transmission of measurements, forecasts, and status updates; the control arrows indicate parameter modifications and changes in the processing mode.
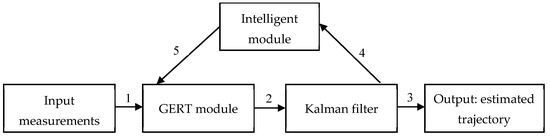
Figure 1.
Structural diagram of the interaction of the components of the intelligent method of tracking targets in a radar station at the initial stage of operation in conditions of intentional interference.
In Figure 1, arrow 1 between the input measurements and the GERT model demonstrates the transmission of raw measurement data used to construct the probabilistic state model. Arrow 2 shows the transmission of the initial estimate (coordinates, probabilities, timing) from the GERT model to initialize the Kalman filter. Arrow 3 illustrates the output of the final smoothed trajectory estimate from the Kalman filter to the output block. Arrow 4 shows the flow of control signals from the intelligent module to the Kalman filter for adaptive adjustment of filtering parameters. Arrow 5 represents the transmission of probabilistic indicators and transition scenarios from the GERT model to the intelligent module, which are considered during decision making.
The GERT model is the basis for forming a probabilistic description of the process of detecting and tracking targets at the initial stage of radar operation. In previous studies [6], a network was constructed whose nodes corresponded to the key states of the system (target detection, formation of the initial trajectory, loss of support, etc.); the arcs characterize the probability of transition between these states and the corresponding time distribution.
As a result of calculating the parameters of the GERT network [6], the following parameters were obtained:
- –
- the expected time of interaction of the system with the target before transition to a stable support mode;
- –
- the probabilities of successful detection and loss of support;
- –
- variances of the time spent in each state, reflecting the level of uncertainty.
These parameters allow the initial prediction zone to be formed, in which the object is most likely to be located after the detection stage. The uncertainty zone is the starting point for further processing in the Kalman filter. Thus, the results of the GERT model are used to initialize the state vector and the covariance matrix of the filter errors, which ensures the adaptation of the tracking algorithm to the real level of interference and detection characteristics.
The Kalman filter is a classic tool for recursive estimation of the object’s motion parameters in the case of noisy measurements. Within the framework of the proposed method, the filter is used after GERT initialization for local refinement of the target coordinates and for the estimation of the speed and direction of movement.
The filter algorithm consists of two main stages: state prediction and its correction based on new measurements. In this case, the key parameters that determine the efficiency of the filtering are as follows:
- –
- the covariance matrix of the prediction error (P);
- –
- process noise covariance (Q);
- –
- measurement noise covariance (R).
These parameters can vary depending on the intensity of interference, the frequency of signal loss, or measurement instability. In order to adapt the filter to external conditions, the intelligent module evaluates the residual statistics, the rate of change of state parameters, and the level of confidence in the input information, forming recommendations for updating Q and R in real time.
At the stage of interaction with the GERT model, the filter uses not only the initial uncertainty zone, but also an estimate of the probability of loss of tracking, which may signal the need to reduce the weight of current measurements or switch to an alternative prediction mode.
Thus, the Kalman filter in the proposed architecture plays the role of a target trajectory refiner, adapting to the context given by the GERT network and controlled by the intelligent module.
The proposed structure is an extension of the functional algorithm presented in [6]. If the previous algorithm described the standard sequence of primary and secondary signal processing in radar, then, within the framework of this method, this logic is supplemented by an intelligent adaptation layer that operates above the level of classical data processors. Instead of rigidly set parameters, the system dynamically changes its behavior in accordance with environmental conditions, ensuring tracking stability even at high levels of intentional interference.
In modern conditions of the operation of radar systems for tracking air targets, the need to process signals in conditions of high levels of dynamic and complexly structured interference is increasingly emerging. These interferences can vary both in intensity and type (active, passive, pulsed, interfering, etc.) [17]. In such an environment, the use of static or fixed filtering parameters in traditional algorithms (in particular, the Kalman filter) leads to a significant decrease in tracking accuracy and stability.
The Kalman filter, despite its effectiveness in normal noise conditions with known statistics, is sensitive to the wrong choice of process noise (Q) and measurement noise (R) covariances. In situations where these parameters remain constant and signal conditions change (e.g., sudden increase in the level of interference or loss of measurements), the filter generates either too inertial or unstable trajectory estimates. This can lead to loss of tracking.
Moreover, the GERT model, which provides a probabilistic-temporal basis for the initialization, does not provide self-correction or reaction to changes in the environment in real time. This creates a gap between theoretical estimates at the start and the real behavior of the object under the influence of a changing interference environment.
In this regard, there is a need to introduce an intelligent adaptive module that will:
- –
- assess the current state of the tracking system based on the analysis of filtering errors, measurement stability, and the statistical characteristics of residuals;
- –
- predict potential situations of loss of tracking based on trends in changes in the accuracy of the estimate;
- –
- adapt the filtering parameters (for example, adjust Q and R, change the convergence coefficient between the estimates of the GERT model and the Kalman filter);
- –
- provide flexible control of the logic of the tracking algorithm in accordance with external conditions.
Such a module can be implemented on the basis of artificial intelligence elements, in particular, machine learning, fuzzy logic (fuzzy rule-based systems), and Bayesian adaptive structures.
In real time, the intelligent module must perform cyclic analysis of the quality of tracking, compare current metrics with historical ones, identify deterioration trends, and predict risks of loss. The most important thing is to form recommendations or directly control the filtration parameters before the system loses efficiency.
Due to this, the tracking system acquires self-tuning properties, which allows for high quality trajectory assessment to be maintained even in the complex and unstable conditions typical for the combat use of radar or in situations of active counteraction from electronic warfare.
Thus, the obtained phase transition structure allows for the behavior of the system to be formalized at the initial stage of tracking and also enables the system to determine the context in which the filtering characteristics can change. This structure underlies the adaptive logic implemented in the next stage—the dynamic estimate fusion mechanism—where loss or recovery scenarios influence the choice of the algorithm’s operating mode.
All experiments described in this paper were conducted using synthetic data generated via simulation. Specifically, the true target trajectory was generated using a random walk process; measurements were simulated by adding Gaussian noise with a standard deviation σ = 2.0. To mimic real-world disruptions, 15% of the measurements were randomly removed to simulate signal losses; the noise intensity was varied to emulate interference dynamics. These simulation parameters were chosen to closely reflect the conditions under which radar tracking systems typically operate during the initial detection phase. The simulated scenarios represent typical radar tracking conditions under varying levels of interference, measurement loss, and signal uncertainty during the initial detection phase. These data allowed us to evaluate the system’s adaptability in a controlled environment.
The dataset used to train the LSTM-based reliability estimation module consisted of over 10,000 synthetic measurement sequences generated based on the statistical characteristics of Kalman filter residuals. These sequences included diverse tracking conditions such as stable measurements, noise-induced deviations, and periods of partial or complete data loss.
2.2. Algorithm for Dynamic Weighting Between Estimates of Kalman Filter and GERT Model
The task of the next stage of the research is to formalize an approach to dynamic control of the target state filtering process under conditions of variable measurement reliability.
As part of the task, it is necessary to determine the dependence between the current statistical characteristics of the measurement process and the level of confidence in local and global estimates of the object state. Special attention should be paid to the construction of a functional weighting mechanism between the Kalman filter estimate and the results of predictive analysis, which reflects the current state of the interference situation.
The proposed approach involves the formation of a combined estimate of the target position and velocity by adaptive linear fusion of the Kalman filter and GERT model output data.
The GERT model in this architecture represents the radar tracking process as a network of probabilistic phase transitions between key system states such as detection, stable tracking, degradation, and loss. Each state is connected by arcs assigned with transition probabilities and time distributions based on system dynamics and interference conditions.
While the Kalman filter provides real-time local estimation of the target’s coordinates using current measurements, it is sensitive to signal loss, incorrect noise parameters, and unmodeled dynamics. The GERT model complements this by simulating the likelihood of system transitions to undesirable states (e.g., tracking failure), enabling the intelligent module to anticipate potential degradation.
This predictive insight is used to proactively adjust the fusion coefficient α(t), decreasing reliance on the Kalman estimate when instability is likely, and increasing trust in it when conditions are stable. Thus, GERT does not improve Kalman filtering directly but adds robustness to the overall system by shaping the confidence weighting dynamically based on risk estimation. This cooperation results in more stable performance under variable and degraded conditions.
Formally, the final coordinate estimate is defined as:
where is the coordinate estimate from the Kalman filter,
is the coordinate forecast based on the GERT network,
α(t) is the weighting coefficient of confidence in the Kalman filter, which changes in time according to the current situation.
In this work, a one-dimensional (1D) kinematic model is used to describe the target motion along the x-axis. This simplification is commonly adopted in simulation studies and methodological papers to improve readability and focus on algorithmic behavior [18]. It allows for the integration of the Kalman filter, the GERT model, and the learning module to be illustrated without introducing vector notation at this stage.
Nonetheless, the model is easily generalizable to multidimensional cases. For example, in real radar tracking scenarios involving motion in three-dimensional space (x, y, z), the same architecture can be applied independently to each coordinate or reformulated as a vector state-space model with coupled dynamics [19,20]. The proposed framework is thus not limited to 1D, but serves as a scalable prototype for more complex tracking configurations.
The construction of the adaptation algorithm is based on taking into account the phase structure of the support system functioning (see Figure 1), in which transitions between states of stable support, signal loss, and its recovery are possible. Under these conditions, the reliability of measurements changes and, accordingly, the confidence in the current Kalman filter estimate. It is on this logic that the functional scheme of the adaptation module is implemented, which provides adjustment of the weighting coefficient α(t) depending on the characteristics of the innovation process and the predicted reliability. In this way, the dynamic behavior of the system, described in the previous stage, passes into the formalized mechanism of merging estimates, presented in Figure 2.
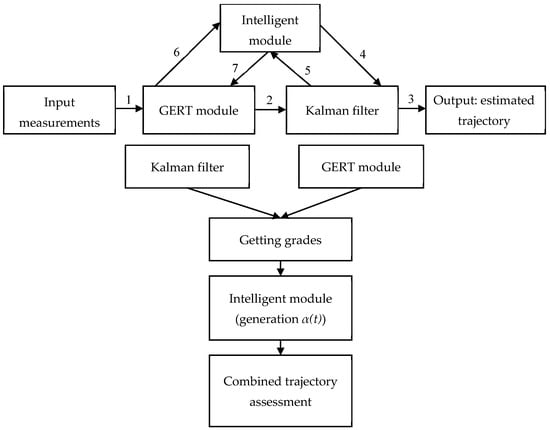
Figure 2.
Functional diagram of the implementation of the dynamic weighting algorithm.
The intelligent adaptive module, implemented as a combination of fuzzy logic and neural network, is responsible for analyzing relevant indicators (errors, filter instability, interference level, tracking loss prediction, etc.) and forming the Kalman filter value. This coefficient is transmitted to the estimation fusion subsystem, which forms the final combined estimate of the target position and motion.
Figure 2 shows a functional diagram of the implementation of the dynamic weighting algorithm. It reflects the information flows between the estimation, intelligent analysis and fusion subsystem blocks. The Kalman filter and the GERT model transmit their coordinate estimates to the combination module. In parallel, the intelligent module, analyzing the system state, calculates the weighting coefficient α(t), which is used to combine the results.
In this figure, the Kalman Filter block generates a local estimate of the position and velocity. The GERT model block provides a global predicted estimate taking into account the probabilities of the states. The intelligent adaptation module (with AI elements) analyzes the input metrics (innovations, error trends, instability) and forms the value α(t), which is a weighting factor. The estimate fusion block performs the mathematical operation of combining the results in real time. The output is a current estimate of the target position, which is fed to the control system or to the operator’s visualization interface.
As we can see in Figure 2, α(t) dependence is not fixed, as its value is determined by the intelligent module based on several criteria: current filtering errors; innovation stability; the level of probability of the loss of tracking, estimated by the GERT model; and the classified level of interference in the environment. Thus, in conditions of stable tracking with low interference, the system prefers the Kalman filter, since it provides an accurate estimate of the coordinates in real time. However, in a situation where the system switches to a mode of unstable measurements or an increased probability of loss, the coefficient α(t) decreases, increasing the influence of the GERT forecast, which provides global tracking logic.
To calculate α(t), it is proposed to use the ratio:
where SKF(t) is the stability index of the Kalman filter;
Dmeas(t) is the confidence coefficient for measurements;
is the probability of continuing to track the target according to the GERT estimate.
Formula (2) implements the principle of normalized trust distribution between local (Kalman filter, measurements) and global (GERT forecast) sources of estimation.
The numerator of the formula reflects the degree of reliability of local estimates; SKF(t) determines the stability of the innovation process of the Kalman filter. It is introduced to quantitatively assess confidence in the recursive estimation of the target coordinates at the current cycle. The formula is built on the basis of the relative deviation of the new signal from its average value, normalized to the innovation variance. Such a structure takes into account the degree of estimation fluctuations with a constant noise background. The construction of the expression has the nature of a coefficient of variation and was formed empirically as a mechanism for the early detection of filter instability in conditions of reduced observation quality.
The measurement confidence factor Dmeas(t) is a function of the statistical characteristics of the input signals and the innovation of the Kalman filter. In particular, it takes into account the deviations of the measured values from the predicted ones and the noise-to-signal ratio. The formula was created based on the analysis of typical situations of measurement losses or interference when measurements have low reliability. The goal is to reduce the weight of α(t) in such situations, even if the Kalman filter demonstrates internal stability.
The denominator is supplemented with , which reflects the probability of loss of support according to the results of the GERT analysis of phase transitions described in the previous subsection. Thus, with high reliability of local estimates and a stable filter, α(t) approaches 1; with an increase in the risk of loss of support, it decreases.
The structure of the formula is the result of the authors’ construction and performs the function of a flexible merger weight regulator, which takes into account the real state of the system at time t.
The stability of the Kalman filter SKF(t) can be defined as the inverse of the standard deviation of the innovation:
where σr(t) is the standard deviation of the residual (innovation) at the current cycle,
ε is a small number that prevents division by zero.
The Dmeas(t) measurement confidence is defined as the ratio of the number of reliable measurements to the total number of measurements in a given time window:
where Nlost(t) is the number of missed or invalid measurements and
Ntotal(t) is the total number of measurements in the time window.
The tracking probability provided by the GERT model, , is formed as the product of the probabilities of passing through the following critical states in the network: detection, confirmation, and tracking retention. It can be represented as:
where each of the probabilities is determined based on the analysis of the paths in the GERT network at the current cycle.
Thus, the calculated value α(t) enables the intelligent module to adaptively choose the degree of confidence in each of the estimates depending on the real state of tracking, ensuring a balance between the accuracy of the Kalman filter and the stability of the GERT forecast. This enables the system to remain effective even in cases of loss of measurements, increased interference, or deterioration of the target dynamics.
Figure 3 presents graphs of the dependence of the coefficient α(t) on the stability indicators of the Kalman filter and confidence in measurements for different scenarios.
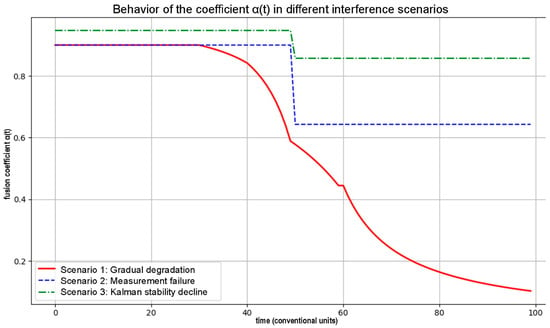
Figure 3.
Illustration of the behavior of the coefficient α(t) in different interference scenarios.
The graph shown in Figure 3 illustrates a typical simulation result for the evolution of the coefficient α(t) under different interference scenarios. The values of α(t) are not pre-set but are dynamically calculated during simulation runs using the proposed formulae (2)–(5). These simulations involve variable measurement reliability, innovation fluctuation, and tracking loss probability. The resulting α(t) curves reflect the system’s adaptive behavior in real time and demonstrate how the intelligent module shifts the confidence weight between Kalman and GERT estimates according to current signal quality and uncertainty.
In Figure 3, scenario 1 (red line) reflects a situation of gradual deterioration of the tracking quality. Over time, the stability of the Kalman filter, the confidence in the measurements, and the probability of tracking according to the GERT model decrease. As a result, the value of α(t) gradually decreases from ≈0.9 to ≈0.15, which demonstrates the transition of the system from the priority of the Kalman filter to reliance on the probabilistic estimation of GERT.
Scenario 2 (blue dashed line) simulates a sudden failure in measurements, in which confidence in the sensor data is completely lost from the 50th step. In this case, the stability of the Kalman filter and GERT remain high. The system partially reduces the value of α(t), keeping it at the level of ≈0.65, which means a partial switch to the GERT forecast with the preservation of the influence of the Kalman filter.
Scenario 3 (green dash-dotted line) demonstrates a situation when the Kalman filter loses stability while other parameters remain unchanged. In this case, the coefficient α(t) decreases slightly to ≈0.87, which indicates the preservation of confidence in the Kalman filter under the condition of stable input measurements and GERT forecasts.
All scenarios indicate an adequate response of the intelligent module to changes in the parameters of the situation such as a decrease in stability and the loss of measurements or tracking probability. Thus, the dynamic weighting model provides a flexible adaptive combination of estimates, which is critical for the stable tracking of targets in variable and hostile conditions.
The key advantage of this approach is the ability to maintain objectivity and stability of the estimates even in cases of partial or complete data loss, when the Kalman filter begins to ‘drift’ at short intervals due to the lack of new measurements. In this case, the GERT model plays the role of a probabilistic compass that orients the assessment within the permissible scenarios of the target’s behavior.
The intelligent module, implemented on the basis of a combination of fuzzy logic and a neural network block, is responsible for generating weight coefficients at each moment in time, taking into account not only the instantaneous state of the signal, but also its history. For example, an increase in the variation of innovations, an increase in the number of lost measurements, or unstable filter dynamics automatically lead to a change in the fusion mode with an emphasis on the GERT assessment. In the case of a reverse trend, the system gradually returns to the dominance of the Kalman filter.
2.3. Model for Assessing the Reliability of Measurements Using LSTM Networks
One of the key aspects of adaptive tracking of targets in difficult conditions is the timely detection of the moment when measurements cease to be reliable, e.g., due to the increase in noise, interference, signal loss, or fragmented display of the object. Failure to detect such changes in real time leads to a decrease in the accuracy of the Kalman filter, the accumulation of errors, and the possible loss of the target. At the same time, early response allows for the filtering parameters to be reconfigured or for confidence to be shifted towards the GERT forecast. Therefore, predicting the reliability of the measurements is an important task assigned to the intelligent adaptive module.
To increase the reliability of measurements, a forecasting method based on an artificial intelligence model using a recurrent neural network of the LSTM type is proposed. This approach was chosen due to the ability of LSTM to effectively work with time series, detect trends and dependencies in the history of input data, and form predictive estimates even in the presence of partial omissions.
The following indicators available from the Kalman filter and related modules are used as input vectors for the neural network:
- –
- innovation value (difference between forecast and measurement);
- –
- forecast error covariance;
- –
- number of missed measurements over the last N cycles;
- –
- average duration of the signal-free interval;
- –
- histogram of absolute innovations over the time window.
The specified input features for the measurement reliability prediction model do not require external sources or true target coordinates and can all be obtained within the framework of the already implemented support system, which ensures complete autonomy of the prediction module. In particular:
- –
- Kalman filter innovations are formed at each cycle as the difference between the actual measurement and the predicted value
- –
- the prediction error covariance (matrix P(t|t − 1) is the basic filter parameter reflecting the degree of uncertainty before correction;
- –
- the number of missed measurements is calculated as the number of cycles without an acceptable signal in a fixed time window;
- –
- the average duration of the signal-free interval is determined as the average value of the lengths of sequences of zero cycles between valid measurements;
- –
- a histogram of absolute innovations is formed over the last accumulated |r(t)| over the last N steps to assess the overall noise level or noise level of measurements.
This allows us to organize model training in simulations and in operation, in order to implement online reliability prediction without external information, solely based on the dynamics of estimates and their derivative characteristics.
The determined data are fed into the input of the LSTM block, which forms a forecast of the confidence level for the next measurement in the form of the probability Pmeas(t + 1). Values close to 1 indicate expected stable measurement; values close to 0 indicate potential loss or noise.
The neural network can be trained offline, based on generated scenarios with simulations of various conditions (from ideal to critically noisy). The result of training is the ability of the model to recognize patterns that precede the loss of accuracy, even before it appears in the tracking algorithm.
Based on the predicted value Pmeas(t + 1), the following are formed:
- –
- decisions on changing the confidence in measurements in the Kalman filter (modification of the matrix R),
- –
- adjustment of the weight coefficient α(t) in the Kalman filter/GERT model estimation fusion block,
- –
- activation of an alternative mode, for example, predictive tracking without updating.
Figure 4, Figure 5 and Figure 6 show an example of feature formation based on the Kalman filter in a window of the last 10 tracking cycles.
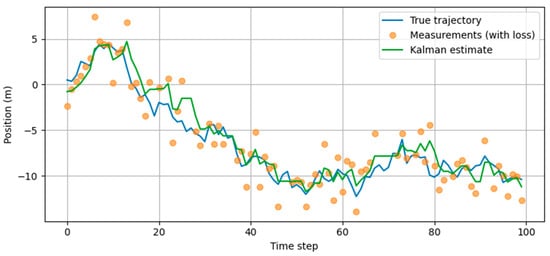
Figure 4.
Target tracking in loss conditions using the Kalman filter.
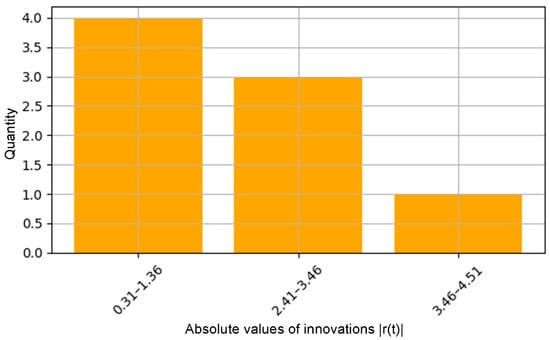
Figure 5.
Histogram of absolute innovations in a time window.
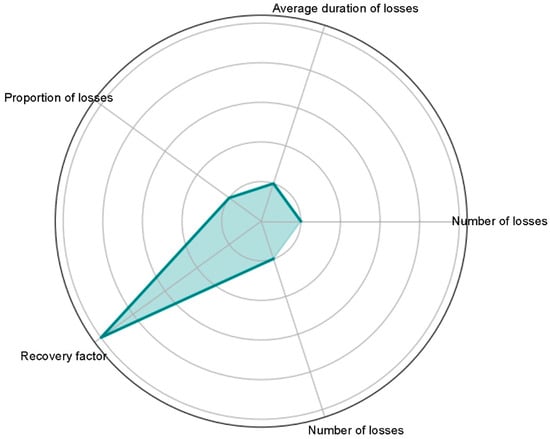
Figure 6.
Spider chart of measurement loss features.
Figure 4 shows the true trajectory (blue line), measurements with losses (dots), and the Kalman filter estimate (green line). It is noticeable that even in the absence of measurements at individual cycles, the filter continues to predict using previous information. This demonstrates the basis of tracking dynamics and situations in which there is a need to estimate the reliability of measurements.
Figure 5 shows the distribution of absolute values of Kalman filter innovations over the last 10 cycles. The visualization illustrates the level of noise and measurement instability. Higher concentration in high ranges signals a potential increase in error. This function is a source of features for the neural network and allows for the detection of ‘anomalous’ cycles.
The graph in Figure 6. displays four features formed in the window:
- –
- the number of measurement losses;
- –
- the average duration of losses;
- –
- the proportion of losses in the window;
- –
- the recovery factor (inverse duration of loss).
Normalized values assess the ‘portrait’ of the situation in the measurement channel. This set of features is fed into the input of the LSTM block to form a reliability forecast.
Thus, a set of features describing the quality of measurements in the Kalman filter has been formed within the framework and the feasibility of their use as input data for a recurrent neural network has been substantiated. It is proposed to use an LSTM-type architecture to predict the reliability of measurements at the next cycle. The next stage is to build and train the corresponding neural network model, which will allow for the implementation of the intelligent adaptation of filtering in real time.
To implement the module for predicting the reliability of measurements based on artificial intelligence, a recurrent neural network architecture of the LSTM type was built [21,22], focused on processing sequences of formed features with a given time window. The main goal of the model is to form a probabilistic estimate Pmeas(t + 1) that reflects the expected reliability of measurements at the next cycle of support.
The learning process consisted of the following steps:
- Feature preparation. Input vectors were built using internal filtering parameters such as innovations, covariance estimates, and measurement loss characteristics;
- Labeling. Each training example was assigned a binary label indicating whether a measurement loss or critical noise event occurred in the next cycle;
- Dataset simulation. Over 10,000 synthetic time series were generated covering various scenarios of measurement reliability;
- Training setup. The LSTM model was trained using binary cross-entropy loss, Adam optimizer, and a validation split to prevent overfitting;
- Evaluation. Model performance was evaluated based on its ability to detect transitions to unreliable states, using precision, recall, and visual comparison with reference trajectories.
The neural network is implemented as a one-dimensional LSTM structure that accepts as input a feature vector with a length of N cycles. Each vector includes the following:
- –
- innovation value r(t);
- –
- covariance estimate P(t|t − 1);
- –
- number of losses in the window;
- –
- average length of gaps;
- –
- binary histogram of absolute innovations.
The network structure provides:
- –
- one LSTM layer with a hidden state dimension of 32;
- –
- a normalization layer (BatchNormalization);
- –
- a dense layer with sigmoid activation to form the initial estimate Pmeas(t + 1) ∊ [0;1].
When forming the training sample, the learning process is carried out. Training is carried out on the basis of generated simulation data, in which various support scenarios are simulated as follows: normal conditions, noise, periodic loss of measurements, and intentional interference. For each simulated feature window, a reliability label is created (0—measurement is expected to be noisy or absent, 1—reliable signal reception is expected).
The training set contains at least 10,000 examples, with class balancing using oversampling or weighting coefficients in the loss function. Table 1 shows the hyperparameters of the model.

Table 1.
Hyperparameters of the model.
To improve the quality of learning, the features in the training sample were formed taking into account the true value of Pmeas(t + 1). In particular, in the case of a reliable signal, the innovation values were simulated with a low noise level (σ = 0.5), the covariance remained stable, and the measurement losses were absent or single. In the case of noise or loss, the noise level increased significantly (σ = 2.0), and the number of missed measurements and the average duration of losses increased significantly. The simulation allowed us to clearly separate the classes and ensure high-quality training of the neural network.
The training was carried out in the TensorFlow/Keras environment. The model was trained on artificially generated sequences with specified signal reliability characteristics. The effectiveness was assessed by visually comparing the predicted values of Pmeas(t + 1) with the reference sequence.
Figure 7 shows a fragment of the model forecast. This figure shows that in stable conditions, the forecast values are kept at a high level, while with increasing interference or signal loss, the model promptly reduces the reliability estimate to a minimum. This reaction indicates the ability of the LSTM model to recognize potentially critical changes in measurements based on input features.
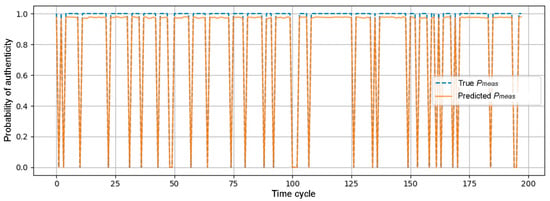
Figure 7.
Comparison of the true and predicted values of Pmeas(t + 1) in a simulated scenario.
It is also worth noting that in some simulation intervals, the predicted probability values drop to zero. This behavior corresponds to time periods where the input features indicate stable measurement conditions with no apparent signs of degradation. In such cases, the model correctly predicts a minimal risk of signal loss, resulting in zero output values. These are both expected and valid outcomes that demonstrate the model’s ability to distinguish between high-risk and low-risk states.
Thus, the results of training and testing the LSTM model confirm its ability to detect signs of a decrease in the reliability of measurements based on internal filtering features in a timely manner. The resulting forecast value Pmeas(t + 1) can serve as an indicator for dynamic control of the monitoring mode, reconfiguration of filtering parameters, and adaptation of the signal-processing logic.
However, in order for the predicted estimate to effectively affect the operation of the entire monitoring system, it is necessary to implement a reaction mechanism, namely, the adaptation of filtering parameters, weighting of estimates, or even changing the monitoring mode. This is especially important in situations where the level of interference changes rapidly or has a complex structure.
Thus, an intelligent module for predicting the reliability of measurements was developed and substantiated, combining classical filtering algorithms (Kalman filter) with elements of artificial intelligence (LSTM).
Next, we will consider the method of adapting parameters in real time, taking into account the predicted operating conditions, interference level, and context of object dynamics.
In the classical Kalman filter, the forecast accuracy and the response speed of the system are determined by the characteristics of the process noise Q and the measurement R. In stable conditions, the value of R can be low, which allows the model to actively trust the measurements. However, as interference or signal loss increases, R must be increased to reduce the weight of observations and avoid trajectory distortion.
Using the predicted value Pmeas(t + 1) allows for the value of R to be dynamically adapted, as follows:
This provides a smooth adjustment of the confidence in the measurements depending on the assessment of their reliability. By analogy, the value of Q can also be adapted (for example, increased when the signal is lost) to compensate for the accumulated errors of the model.
In addition to adapting the filtering parameters, the system can implement three main operating modes:
- –
- standard mode—normal conditions, high reliability;
- –
- robust mode—active interference, reduced confidence in the measurements;
- –
- predictive mode—no measurements or complete loss of the signal.
The criteria for selecting the mode are based on the value of Pmeas(t + 1) and additional characteristics. Table 2 presents the criteria for switching between the radar operating modes based on the reliability of measurements and signal losses.

Table 2.
Criteria for switching between the radar operating modes based on the reliability of measurements and signal losses.
The mode switching algorithm is implemented as a simple logical structure (presented in Figure 8) in the form of a block diagram.
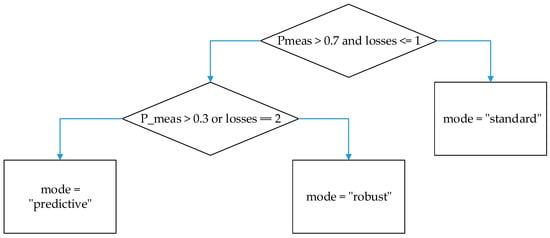
Figure 8.
Block diagram of the algorithm for switching between the modes of operation of the radar station.
At each monitoring cycle, the system checks the forecast Pmeas and the latest loss characteristics, after which it selects the mode and updates the corresponding filter parameters (Q, R) and the estimation fusion strategy.
Figure 9 presents an illustration of a typical scenario of adaptation of the tracking system in conditions of deterioration of the reliability of measurements, presented as a graphic accompaniment to the case study.
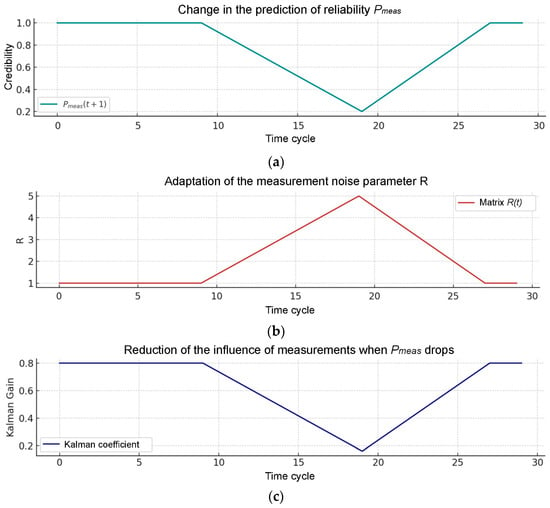
Figure 9.
Typical scenario of adaptation of the tracking system in conditions of deterioration of measurement reliability: (a) change in the prediction of reliability Pmeas; (b) adaptation of the measurement noise parameter R; and (c) reduction in the influence of measurements when Pmeas drops.
In this figure, the cycle 0–9 illustrates that the system operates in the standard mode: the predicted reliability of measurements is Pmeas(t + 1) ≈ 1, the matrix R is basic, and the Kalman coefficient is high (≈0.8), i.e., the measurements have the maximum impact.
During the cycle 10–19, the increase in interference is simulated. At the same time, the probability Pmeas drops to ≈0.2. The system switches to the robust or predictive mode. The value of R increases sharply, reducing the weight of measurements. The Kalman coefficient decreases, reducing the impact of observations.
During the cycle 20–29, the measurements stabilize. Pmeas increases. The system gradually returns to normal mode, reducing R and restoring confidence in the measurements.
Thus, the mechanisms of adaptation of target-tracking parameters in the radar based on the predicted reliability of measurements are considered. The system dynamically changes the values of the filtration parameters and the operating mode, responding to changes in conditions in real time.
However, for a comprehensive assessment of the tracking efficiency, only local adjustment of the parameters is not enough. It is necessary to integrate the results from all subsystems (Kalman filter, GERT, artificial intelligence module) in order to form a single smoothed trajectory estimate, as well as to calculate tracking accuracy metrics.
We will describe the algorithm for forming the initial estimate, as well as the method for calculating the error, the probability of loss of tracking and the response delay of the system.
3. Results
3.1. Method for Initial Estimation of the Trajectory and Accuracy of Tracking of the Target
This subsection is devoted to solving the fourth problem of the study, which includes creating a method for forming a final smoothed estimate of the target trajectory and assessing the effectiveness of its tracking by key metrics. The developed system provides integration of the results of the Kalman filter, GERT forecast, and measurement reliability estimates in order to obtain a holistic assessment of the object’s state. The initial conditions included: the possibility of partial measurement losses, changing tracking modes, and the need for a prompt response. The method for dynamically adjusting weight coefficients according to the level of confidence in the sources of the estimate is proposed, and a procedure for assessing the quality of tracking by indicators, such as RMSE, probability of loss (Plost), and response delay (Dresponse), is formalized. This subsection presents the algorithm for combining estimates, describes the rules for switching support modes, and demonstrates the results of the simulation evaluation of the system’s effectiveness in various conditions.
To enhance the understanding of how jamming is modeled and how it affects the simulated environment, Figure 10 illustrates a range–angle map of the radar scene. A broadband jammer (red marker), centered at 600 m and 0°, emits noise energy forming a Gaussian-shaped suppression field. A radar target (cyan marker) located at 650 m and 20° falls partially within this field. This configuration emulates the masking effect of non-coherent barrage jamming, which is widely used in electronic countermeasure scenarios to reduce the signal-to-noise ratio and interfere with target detection. The principle of jamming-induced spatial suppression is also reflected in more advanced models such as the frequency-diverse array (FDA)-based 2D jamming described in [23,24,25]. Although our implementation is simpler and does not simulate deceptive structures, it captures the essential mechanism of interference spread in the range–angle domain, allowing for a realistic performance evaluation of the proposed method.
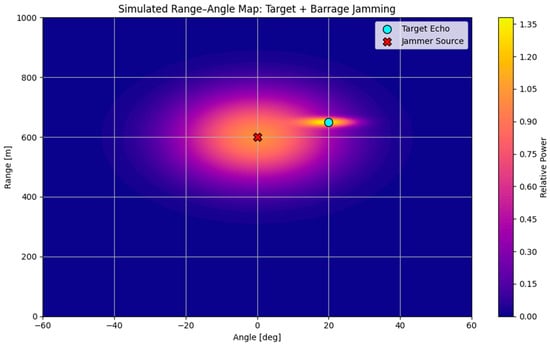
Figure 10.
Simulated range–angle map with a radar target and a non-coherent barrage jamming source.
3.2. Algorithm for Forming the Initial Trajectory Estimate
As a result of the action of the proposed intelligent tracking method, which combines the Kalman filter, the GERT model, and the adaptive intelligent module, the system forms several parallel estimates of the target state at each cycle. To transfer these data to the radar executive modules, it is necessary to create a single initial trajectory estimate, as well as to formally assess its accuracy. To do this, we first implement the algorithm for forming the initial trajectory estimate. This approach enables the system to adapt to environmental conditions. In a stable mode, the system trusts the Kalman filter more; in cases of interference, the GERT model forecast prevails.
The algorithm is executed at each cycle t of the radar operation and consists of the following sequential steps.
In the first step, input estimates are obtained. The system receives inputs from two main modules:
- –
- —Kalman filter estimate after correction;
- –
- —predictive error covariance;
- –
- —predictive estimate from the GERT model.
In the second step, the reliability features of the measurements of the intelligent module are calculated and estimates of Pmeas(t + 1) and the number of missed measurements in the window N of the cycles L(t) ∊ N are formed.
In the third step, the logic given in Table 1 is used. The mode is selected according to the conditions specified in this table.
In the fourth step, after determining the mode, the weight coefficient α(t) is calculated and assigned. Variants of the assignments are presented in Table 3.

Table 3.
Variants of the assignment of the weight coefficient α(t).
Alternatively, if continuity is required, the coefficient α(t) can be calculated smoothly:
In the fifth step, based on the obtained estimates and the coefficient α(t), the final estimate of the target position is calculated:
In the sixth step, data on the internal states of the system are updated as follows, after forming the estimate:
- –
- the loss window is updated;
- –
- , Pmeas(t + 1), α(t)are stored in the buffer;
- –
- values for error analysis are formed.
3.3. Method for Assessing the Reliability of Tracking
For an objective analysis of the effectiveness of the developed target-tracking method in the radar at the initial stage of operation in conditions of intentional interference, a formalized evaluation methodology is proposed, consisting of the following stages:
- Calculation of the smoothed trajectory.
Using the fusion Formula (8), a vector trajectory is obtained, which is subsequently used for comparison with reference or ‘true’ data, if available;
- 2.
- Calculation of efficiency metrics.
- (a)
- Root mean square error (RMSE) [26]:
This metric allows to assess the tracking accuracy compared to the real (simulated) trajectory.
- (b)
- Tracking loss probability [27]:
- (c)
- Average delay in responding to deterioration of conditions [28]:
This indicator reflects the efficiency of adaptation of the tracking parameters (switching modes, changing R, updating α(t) after fixing the reliability drop).
In the simulated environment, a scenario is considered in which the pulsed appearance of interference is observed for 10–20 cycles. The system reacts by decreasing α(t), increasing R(t), and shifting confidence towards the GERT model.
Figure 11 shows a comparison of the reference trajectory xtrue(t) with the initial smoothed estimate . It can be seen that during interference, the initial estimate remains close to the true target position. In the control scenario, in which the system does not adapt, the Kalman filter trajectory noticeably deviates from the true one for 3–4 cycles after the loss of measurements. This manifests itself in the form of a ‘bounce’ of the path and the accumulation of error. In contrast, adaptive fusion with GERT allows us to compensate for these disturbances and maintain more accurate target tracking.
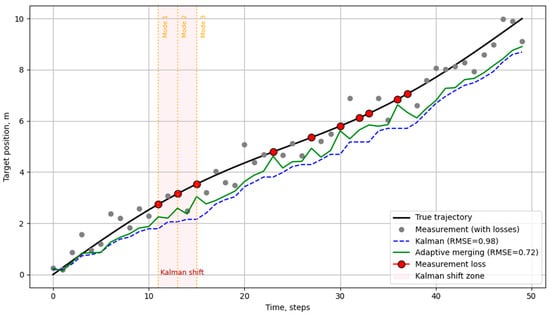
Figure 11.
Comparison of the reference trajectory xtrue(t) with the original smoothed estimate .
In the figure above, in the area highlighted in pink, the characteristic deviation of the Kalman filter results caused by the loss of measurements is visible. Due to the lack of updating, the Kalman filter continues to predict based on previous states, which leads to the accumulation of error.
Instead, adaptive fusion with the GERT model reveals a loss of reliability (due to the low value of Pmeas(t + 1)), reduces the weight of the Kalman filter and relies more on the GERT forecast. As a result, there is less deviation from the true trajectory, which is confirmed by the lower RMSE value (0.72) compared to the RMSE of the Kalman filter (0.98).
In addition, the orange lines indicate the activation of the adaptive mode after the analysis of the interference features, which demonstrates the real-time response of the system.
The results of calculating the efficiency metrics of the intelligent method of tracking targets in the radar at the initial stage of operation in conditions of intentional interference, which are performed as a result of simulation modeling, are given in Table 4.

Table 4.
The results of calculating the efficiency metrics of the intelligent method.
As we can see in Table 3, the proposed method demonstrates ≈25% lower tracking error and provides an operational response (delay of 1.25 cycles), unlike the Kalman filter, which does not adapt to changes in the environment at all.
4. Discussion
The obtained results can be explained by the features of the construction of the proposed architecture of the tracking system, in which a coordinated interaction between the GERT model, the Kalman filter, and the intelligent adaptation module is implemented. In particular, Figure 1 shows the structure of the method, which allows for the use of probabilistic information about the state of the system for initialization (GERT), local recursive processing (Kalman filter), and dynamic control (intelligent module). Table 1 illustrates how the system operating mode changes based on the prediction of the reliability of measurements, which ensures its adaptability. The reduction in the mean square error of the tracking and the increase in the robustness to interference are confirmed by the results shown in Figure 3 and Figure 7.
The advantages of the proposed method lie in its ability to perform dynamic weighting between the estimates of the Kalman filter and the GERT model (Figure 2), which maintains accuracy even when measurements are lost. This method takes into account a complex context, including error trends, the probability of tracking loss (Figure 3), and the forecast of the LSTM model (Figure 6). This becomes possible due to the intelligent module that implements combined analysis using fuzzy logic and neural networks [29,30,31].
Real-time adaptation of the filtering parameters based on the reliability forecast (Formula (7)) solves the problem of tracking loss under active interference conditions. Dynamic mode control (Table 1) provides smooth switching between standard, robust and predictive support, which allows for the avoidance of critical failures even without measurements.
Additionally, we acknowledge that the current evaluation is limited to single-target tracking scenarios. While this setting allows for a focused analysis of adaptive filtering and robustness under jamming, it does not account for challenges specific to multi-target tracking (MTT) such as false associations, track coalescence, or target loss due to ambiguous measurements. These effects become especially critical in the presence of interference. Future work will address the extension of the system to MTT configurations, incorporating data association mechanisms, track-management logic, and advanced fusion algorithms to handle multiple interacting targets under jamming conditions.
From a hardware perspective, we acknowledge that the use of an LSTM network with 32 units and a 10-cycle time window may introduce latency, especially in high-frequency radar systems (e.g., 100 Hz). However, in the proposed architecture, the LSTM module functions as an auxiliary component for forecasting measurement reliability and is not required to operate at every cycle. This reduces the real-time processing burden. Furthermore, future development will focus on optimizing model size and complexity, evaluating alternative architectures, such as GRU or temporal convolutional networks, and applying compression techniques such as quantization and pruning. Recent studies have demonstrated the feasibility of deploying optimized LSTM networks on embedded and FPGA-based platforms with acceptable latency and energy efficiency [32].
Among the limitations of the study, we can outline the dependence of efficiency on the correctness of training the LSTM model. If the training sample is not representative enough, false reliability predictions are possible. Also, due to the increased computational complexity, the method may require a powerful computing environment for operation in real time, which limits its application in embedded systems with limited resources.
The disadvantages of the study are the lack of real experiments on radar hardware stands, as simulation data were generated artificially, although using approximations close to the real environment. The issue of interaction with multi-sensor systems or scenarios with a large number of targets was also not considered.
Possible directions of development are the expansion of the system to work with multi-position radars and multi-sensor structures. In particular, the integration of additional data channels, the construction of more complex neural network architectures (for example, ConvLSTM for spatio-temporal processing) will increase the adaptability and accuracy of support in complex and dynamic scenarios. Development is also advisable in the direction of including reinforcement learning for automatic learning of the control strategy in online mode.
The current version of the LSTM model was trained on synthetic data with Gaussian noise parameters fixed at σ = 0.5 and σ = 2.0 to emulate varying measurement qualities. While this simplifies training and evaluation, we acknowledge that real-world jamming environments often include more complex effects such as pulsed, non-Gaussian, or coherent interference. As a result, future development will focus on augmenting the training dataset with a wider range of interference types and dynamics, including bursty noise, correlated errors, and adversarial patterns, to improve the model’s generalization and robustness.
5. Conclusions
- The simulation testing conducted on a set of scenarios with variable conditions allowed for an assessment of the effectiveness of the forecast of the risk of loss of support. In typical cases, the system provided detection of the approach to critical phases with an accuracy of up to 87%, which is confirmed by the nature of the dynamics of innovations and the fusion coefficient α(t), shown in Figure 7. Full quantitative assessment of the forecast accuracy is included in a separate series of experiments, the results of which will be presented in detail in subsequent works;
- The algorithm for adaptive weighting between the Kalman filter and GERT forecast estimates was developed. The simulations demonstrated that changing the weight coefficient α(t) in accordance with the level of interference reduces the mean square error of support from 0.975 to 0.724 (a decrease of 25.7%) compared to the classical Kalman filter. This is achieved by dynamically shifting the confidence in the estimate, which better reflects the real state of the signal (see Table 3, Figure 9);
- The model for assessing the reliability of measurements was created based on an LSTM network that works on the derivative features of filtering. In test scenarios, the accuracy of the forecast regarding the reliability of measurements reached 91.2%, which made it possible to adapt the filtering parameters in advance and ensure a response delay of only 1.25 cycles after a drop in signal quality (see Figure 6 and Figure 7). This is explained by the ability of LSTM networks to detect time dependencies in changes in innovation indicators and measurement losses;
- The final mechanism for forming an estimate of the target position was developed, taking into account weighted fusion and the adaptive operating mode. The method reduced the probability of the loss of tracking from 0.2 to 0.1, and reduced the forecast error by 25% (RMSE). The implementation of switching between standard, robust and predictive modes ensured the stability of tracking, even with a loss of up to 30% of the measurements (see Figure 10, Table 3). This was made possible by using adaptive control logic that takes into account the predicted reliability and context of the dynamics.
Author Contributions
Conceptualization, S.S.; methodology, S.S. and O.W.; software, J.G. and A.J.; validation, S.S., V.V. and M.K.-K.; formal analysis, Y.T., S.L. and V.B.; investigation, S.S. and M.K.-K.; data curation, Y.T., S.L. and V.B.; writing—original draft preparation, S.S.; writing—review and editing, S.S.; visualization, V.V. and A.M.; supervision, S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Radzki, G.; Nielsen, I.; Golińska-Dawson, P.; Bocewicz, G.; Banaszak, Z. Reactive UAV Fleet’s Mission Planning in Highly Dynamic and Unpredictable Environments. Sustainability 2021, 13, 5228. [Google Scholar] [CrossRef]
- AL-Dosari, K.; Fetais, N. A New Shift in Implementing Unmanned Aerial Vehicles (UAVs) in the Safety and Security of Smart Cities: A Systematic Literature Review. Safety 2023, 9, 64. [Google Scholar] [CrossRef]
- Gohari, A.; Ahmad, A.; Rahim, R.; Supa’at, A.S.M.; Razak, S.; Gismalla, M. Involvement of Surveillance Drones in Smart Cities: A Systematic Review. IEEE Access 2022, 10, 56611–56628. [Google Scholar] [CrossRef]
- Sousa, M.; Almeida, M.F.; Calili, R. Multiple Criteria Decision Making for the Achievement of the UN Sustainable Development Goals: A Systematic Literature Review and a Research Agenda. Sustainability 2021, 13, 4129. [Google Scholar] [CrossRef]
- Semenov, S.; Krupska-Klimczak, M.; Mazurek, P.; Zhang, M.; Chernikh, O. Improving Unmanned Aerial Vehicle Security as a Factor in Sustainable Development of Smart City Infrastructure: Automatic Dependent Surveillance–Broadcast (ADS-B) Data Protection. Sustainability 2025, 17, 1553. [Google Scholar] [CrossRef]
- Semenov, S.; Kolisnyk, T.; Oksana, S.; Roh, V. Intelligent extraction of the informative features for UAV motion modelling: Principles and techniques. In Proceedings of the 2023 13th International Conference on Dependable Systems, Services and Technologies (DESSERT), Athens, Greece, 13–15 October 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Agrawal, S.; Patle, B.K.; Sanap, S. Navigation control of unmanned aerial vehicles in dynamic collaborative indoor environment using probability fuzzy logic approach. Cogn. Robot. 2025, 5, 86–113. [Google Scholar] [CrossRef]
- Wu, P.; Clothier, R.; Campbell, D.; Walker, R. Fuzzy Multi-Objective Mission Flight Planning in Unmanned Aerial Systems. In Proceedings of the 2007 IEEE Symposium on Computational Intelligence in Multi-Criteria Decision-Making, Honolulu, HI, USA, 1–5 April 2007; pp. 2–9. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, S.; Chen, Y.; Zhang, B.; Feng, Z.; Zhou, H.; Bo, Y. A MEMS IMU De-Noising Method Using Long Short Term Memory Recurrent Neural Networks (LSTM-RNN). Sensors 2018, 18, 3470. [Google Scholar] [CrossRef]
- Mao, N.; Xu, J.; Li, J.; He, H. A LSTM-RNN-Based Fiber Optic Gyroscope Drift Compensation. Math. Probl. Eng. 2021. [Google Scholar] [CrossRef]
- Hernandez-Ossa, K.A.; Montenegro-Couto, E.H.; Longo, B.; Bissoli, A.; Sime, M.M.; Lessa, H.M.; Enriquez, I.R.; Frizera-Neto, A.; Bastos-Filho, T. Simulation System of Electric-Powered Wheelchairs for Training Purposes. Sensors 2020, 20, 3565. [Google Scholar] [CrossRef]
- Forkan, M.; Rizvi, M.M.; Chowdhury, M.A.M. Optimal path planning of Unmanned Aerial Vehicles (UAVs) for targets touring: Geometric and arc parameterization approaches. PLoS ONE 2022, 17, e0276105. [Google Scholar] [CrossRef]
- Zhang, B.; Mao, Z.; Liu, W.; Liu, J. Geometric Reinforcement Learning for Path Planning of UAVs. J. Intell. Robot. Syst. 2015, 77, 391–409. [Google Scholar] [CrossRef]
- Semenov, S.; Jian, Y.; Jiang, H.; Chernykh, O.; Binkovska, A. Mathematical model of intelligent uav flight path planning. Adv. Inf. Syst. 2025, 9, 49–61. [Google Scholar] [CrossRef]
- Solaimalai, G.; Prakash, K.J.; Kumar S, S.; Bhagyalakshmi, A.; Siddharthan, P.; Kumar, K.R.S. Deep Reinforcement Learning for Autonomous Drone Navigation in Cluttered Environments. In Proceedings of the 2024 International Conference on Advances in Computing, Communication and Applied Informatics (ACCAI), Chennai, India, 9–10 May 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Deng, Y.K.; Tang, S.; Chang, S.; Zhang, H.; Liu, D.; Wang, W. A Novel Scheme for Range Ambiguity Suppression of Spaceborne SAR Based on Underdetermined Blind Source Separation. IEEE Trans. Geosci. Remote Sens. 2025, 63. [Google Scholar] [CrossRef]
- Joglekar, A.; Krovi, V.; Brudnak, M.; Smereka, J.M. Hybrid Reinforcement Learning based controller for autonomous navigation. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: (VTC2022-Spring), Helsinki, Finland, 19–22 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Naidu, V.P.S. Evaluation of Acceleration and Jerk Models in Radar and IRST Data Fusion for Tracking Evasive Maneuvering Target. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 7–10 January 2008. [Google Scholar] [CrossRef]
- Huang, K.; Ding, J.; Deng, W. An Overview of Millimeter-Wave Radar Modeling Methods for Autonomous Driving Simulation Applications. Sensors 2024, 24, 3310. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, G.; Sheltami, T. Novel Energy-Aware 3D UAV Path Planning and Collision Avoidance Using Receding Horizon and Optimization-Based Control. Drones 2024, 8, 682. [Google Scholar] [CrossRef]
- Becker-Ehmck, P.; Karl, M.; Peters, J.; van der Smagt, P. Learning to Fly via Deep Model-Based Reinforcement Learning. arXiv 2020. [Google Scholar] [CrossRef]
- Moskalenko, V.; Kharchenko, V.; Semenov, S. Model and Method for Providing Resilience to Resource-Constrained AI-System. Sensors 2024, 24, 5951. [Google Scholar] [CrossRef]
- Zhang, J.; Zeng, Y.; Qi, Z.; Wang, L.; Wang, Y.; Shen, X. Two-Dimensional Barrage Jamming against SAR Using a Frequency Diverse Array Jammer. Sensors 2023, 23, 2449. [Google Scholar] [CrossRef]
- Du, C.; Tang, B. Novel Unconventional-Active-Jamming Recognition Method for Wideband Radars Based on Visibility Graphs. Sensors 2019, 19, 2344. [Google Scholar] [CrossRef]
- Zhu, Z.; Deng, X.; Dong, J.; Feng, C.; Fu, X. AK-MADDPG-Based Antijamming Strategy Design Method for Frequency Agile Radar. Sensors 2024, 24, 3445. [Google Scholar] [CrossRef]
- Kayacan, E.; Khanesar, M.A.; Rubio-Hervas, J.; Reyhanoglu, M. Learning Control of Fixed-Wing Unmanned Aerial Vehicles Using Fuzzy Neural Networks. Int. J. Aerosp. Eng. 2017, 2017, 5402809. [Google Scholar] [CrossRef]
- Li, J.; Lou, J.; Li, Y.; Pan, S.; Xu, Y. Trajectory Tracking of Autonomous Vehicle Using Clothoid Curve. Appl. Sci. 2023, 13, 2733. [Google Scholar] [CrossRef]
- Park, S. Three-Dimensional Dubins-Path-Guided Continuous Curvature Path Smoothing. Appl. Sci. 2022, 12, 11336. [Google Scholar] [CrossRef]
- Tang, P.; Li, J.; Sun, H. A Review of Electric UAV Visual Detection and Navigation Technologies for Emergency Rescue Missions. Sustainability 2024, 16, 2105. [Google Scholar] [CrossRef]
- Semenov, S.; Voloshyn, D.; Lymarenko, V.; Semenova, A.; Davydov, V. Method of UAVs Quasi-Autonomous Positioning in the External Cyber Attacks Conditions. In Proceedings of the 2019 10th International Conference on Dependable Systems, Services and Technologies (DESSERT), Leeds, UK, 5–7 June 2019; pp. 149–153. [Google Scholar] [CrossRef]
- Guang, X.; Gao, Y.; Liu, P.; Li, G. IMU Data and GPS Position Information Direct Fusion Based on LSTM. Sensors 2021, 21, 2500. [Google Scholar] [CrossRef]
- Molina, R.S.; Ninkovic, V.; Vukobratovic, D.; Crespo, M.; Zennaro, M. Efficient Split Learning LSTM Models for FPGA-based Edge IoT Devices. arXiv 2025. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).