Formal Analysis of Ratchet Protocols Based on Logic of Events

Abstract

Ratchet protocols are a class of secure protocols based on ratcheting encryption mechanisms, widely employed in instant messaging. Against the backdrop of frequent incidents of communication privacy breaches, ratchet protocols have become a vital technology for ensuring secure end-to-end communication. This paper presents a formal analysis framework for ratchet protocols grounded in Logic of Events theory (LoET). We further extend LoET by introducing dedicated Diffie–Hellman (DH) and ratchet event classes, along with tailored axioms and inference rules, to support precise modeling of ratcheted encryption. Using the Signal protocol as a case study, we construct a bidirectional authentication model and rigorously prove that both its symmetric and asymmetric ratchet phases satisfy strong authentication properties. Compared with existing formal approaches, our method enables more expressive modeling of key update sequences and supports structured reasoning over causality and authentication flows. The proposed framework lays a theoretical foundation for analyzing the security of modern ratcheted protocols and holds potential for future automated verification.

1. Introduction

Ratchet protocols are a class of security protocols designed to enhance communication security [1]. The core principle of the ratchet mechanism lies in dynamically updating keys to achieve forward secrecy [2,3] and backward secrecy [4]. It is widely adopted in instant messaging [5] (for example, Signal protocol, WhatsApp [6]), end-to-end encryption (E2EE) [7,8], and key exchange [9], among other domains. For example, Signal [10] provides E2EE for numerous instant messaging platforms such as WhatsApp, Wire, and Facebook Messenger, serving over 1 billion active users. In the midst of growing concerns about communication privacy breaches [11], the Signal protocol leverages X3DH (Extended Triple Diffie–Hellman) [12] and the double ratchet encryption technique [13] to provide robust security properties. These mechanisms ensure that even if a key is compromised, past and future messages remain protected.

Off-the-Record (OTR) [14] was one of the earliest secure messaging protocols. It employs a Diffie–Hellman ratchet, generating a new ephemeral shared key with each message exchange. Since past messages cannot be decrypted from subsequent states, this technique is referred to as a ratchet mechanism. Ratchet protocols are broadly categorized into unidirectional (single) and bidirectional (double) ratchets [15]. A unidirectional ratchet—such as the KDF-based ratchet [16]—updates keys in only one direction. In contrast, a bidirectional ratchet combines a KDF ratchet and a Diffie–Hellman ratchet to achieve both forward and backward secrecy, thereby offering stronger security guarantees.The evolution of ratchet structures has been complex. For instance, TextSecure [17], the predecessor of Signal, was the first to formalize the double ratchet mechanism by integrating both a symmetric-key ratchet and an asymmetric Diffie–Hellman ratchet. a In recent years, the security of ratchet protocols and their associated mechanisms has been extensively studied. Frosch et al. [18] conducted a security analysis of TextSecure v3, demonstrating that, in their model, the long-term symmetric keys used to initialize the ratchet mechanism form a secure one-round key exchange protocol. However, their analysis did not address the security properties of the ratchet mechanism itself. Cohn-Gordon et al. [19] proposed a formal security analysis framework capable of capturing ratchet structures. Building on this, they introduced the asynchronous ratcheting tree (ART) design method to achieve stronger security guarantees. Meanwhile, Bellare et al. [20] formally defined security properties for ratchet mechanisms and presented a provably secure ratcheted key exchange protocol, demonstrating how to model the characteristics of ratchet encryption.Further advancing the field, Beguinet et al. [21] employed the Tamarin prover to formally model and verify the Signal protocol, including its ratchet-based components. Additionally, Li et al. [22] developed a formal security analysis of the Signal protocol using Logic of Events theory, providing rigorous proofs for the security of its ratchet mechanism.

These studies have provided in-depth analyses and improvements of ratchet protocols and their associated mechanisms from various angles, including key exchange, ratchet operations, and formal verification [23,24]. Collectively, they have laid a solid theoretical foundation for ensuring the security and robustness of ratchet-based communication protocols.

Logic of Events theory (LoET) [25,26] is a theorem-proving approach frequently employed for analyzing the security of distributed systems. In response to the limitations of Protocol Composition Logic (PCL) [27], Xiao et al. made significant theoretical advancements by applying LoET to security protocol analysis. Their work substantially expanded the theoretical framework of LoET, enabling it to support the formal verification of security protocols across multiple domains. These innovations have reinforced LoET’s influence in formal methods research while providing a powerful analytical tool for verifying the security of complex systems.

LoET employs events to characterize system behaviors and security properties. By formally modeling protocol executions or specifying desired security goals, LoET enables rigorous verification of whether these properties hold within the protocol model. This approach offers unique advantages in detecting subtle vulnerabilities that may be overlooked by other analysis methods.

In this study, we conduct a formal analysis of the ratchet mechanism in the Signal protocol to identify potential vulnerabilities and ensure the security of Signal message exchanges. Our principal contributions are as follows:

• A formal analysis framework for ratchet protocols based on LoET. We extend the LoET event class system by introducing DH (Diffie–Hellman) and ratchet event classes and by developing dedicated axioms and inference rules tailored to the characteristics of ratchet protocols. This framework addresses the limitations of conventional formal methods in accurately modeling ratchet-based encryption mechanisms.
• Construction of a bidirectional authentication formal model for the Signal protocol. To capture the dynamic nature of ratchet encryption, we abstract its key negotiation and update processes. By integrating LoET, we formally define the security properties of protocol interactions, precisely characterizing the requirements for bidirectional authentication.
• Formal verification of strong authentication properties in the Signal protocol. Leveraging our extended LoET rules, we rigorously prove the strong authentication properties of the ratchet mechanism in message exchange scenarios. This work also extends the applicability of LoET to the analysis of ratchet protocols.

The remainder of this paper is organized as follows: Section 2 introduces the Logic of Events theory (LoET) and its extensions developed for the formal analysis of ratchet protocols. Section 3 presents a formal analysis of the Signal protocol, including an overview of the protocol and its formal verification framework, followed by a detailed exposition and proof of its strong authentication properties based on LoET. Section 4 presents a comparison between our approach and existing methods. Section 5 summarizes the main conclusions of this study and offers suggestions for future research directions.

In addition, several studies have conducted formal verification of the Signal protocol in depth. Tools such as CryptoVerif [28] and Verifpal [29], provide automated protocol analysis capabilities, enabling the modeling of complex cryptographic mechanisms and potential attack vectors. These tools are particularly well-suited for evaluating the security of ratchet-based protocols like Signal. Furthermore, closely related to our work, OSM [30] proposes a model-checking framework based on structured event tracing, which allows for dynamic observation of protocol behavior in aspect-oriented programming systems. This approach aligns well with the event-driven modeling strategy employed by LoET. Additionally, BlockASP [31] extends model-checking techniques for security protocols by emphasizing semantic cleanliness, which plays a critical role in verifying the security of key materials and the integrity of protocol state transitions. These frameworks complement our approach and highlight the broader applicability of event-based formal verification.

2. Logic of Events Theory

The Logic of Events theory (LoET) is a formal verification method that models protocols or specifies their required properties to determine whether these properties hold within the protocol model. It helps identify security vulnerabilities that are difficult to detect using other approaches. LoET defines core elements such as identifiers, atoms, and unpredictable data (e.g., nonce, signature, ciphertext, and encryption key), as well as event, event class, and event structure. These components support the construction of authentication theories used to prove strong authentication properties in security protocols.

2.1. Notation

The basic notations and semantics used throughout our formal model are summarized in

Table 1. Basic notations and semantics in Logic of Events theory (LoET).

Notation	Semantics	Example
ID	Identifier of protocol participant	A, B
Atom	Unpredictable information	nonce, key, signature
Data	Message content or plaintext	“Hello”, session key
e	An individual event	Encrypt(e)
E	A set of events	E = {e1, e2, e3}
nonce	Random number generated in protocol	r = New(e)
has	Predicate indicating data is contained in event	e has a
bs	Basic event sequence for a participant	I1, R2
<	Causal ordering of events	e1 < e2
loc(e)	Principal executing event e	loc(e) = A
key(e)	Cryptographic key used in event e	key(e) = PrivKey(A)
New(e)	Random atom introduced by event e	New(e) = r
Send(e)	Sending message event	Send(e) = “msg”
Rcv(e)	Receiving message event	Rcv(e) = “msg”
Encrypt(e)	Encryption event with message, key, atom	Encrypt(e) = $\langle m,k,a\rangle$
Decrypt(e)	Decryption event corresponding to Encrypt(e)	Decrypt(e) = $\langle m,k,a\rangle$

, including representative examples to aid clarity.

2.2. Fundamental Concepts

In the Logic of Events Theory (LoET), protocol interactions are modeled as threads—ordered sequences of actions performed by protocol participants—and matching relations that capture both message consistency and causal dependencies. The definitions that follow formalize these concepts using set theory and first-order logic, with relevant terms introduced below.

• Act List: $thr$ is an action list (Act List), representing a sequence of protocol actions (such as Send, Receive, Encrypt, etc.) executed by a single participant. The condition $\forall i:\mathrm{thr}\left[i\right]{<}_{\mathrm{loc}}\mathrm{thr}[i+1]$ indicates that the events in this list are arranged in order, i.e., local causal ordering holds: each preceding event occurs before the next one and all events belong to the same participant’s thread.
• Thread (Thread): An ordered sequence of events executed by a single principal, satisfying intra-participant causal ordering $e_i{<}_{\mathit{loc}}{e}_{i+1}$.
• Weak Match ($\mathit{s}\sim \mathit{r}$): The send and receive events contain identical message content ($\mathrm{Send}\left(s\right)=\mathrm{Rcv}\left(r\right)$), without requiring causal order.
• Strong Match ($\mathit{s}\mapsto \mathit{r}$): A weak match that additionally satisfies causal precedence ($s<r$), ensuring the chronological execution of the events.

2.2.1. Threads and Matching Sessions

Equation (1) formally defines a thread (thr) as an Act List—an ordered list of protocol actions such as Send, Receive, and Encrypt—executed sequentially by a single protocol participant, preserving local causal ordering.

$$\mathit{Thread}{\equiv }_{\mathit{def}}\left\{\mathit{thr}:\mathit{Act}\mathit{List}|\forall i:\mathit{thr}\left[i\right]{<}_{\mathit{loc}}\mathit{thr}[i+1]\right\}$$

(1)

If there exist two messages s and r, such that the first message s is a message on a send event and the second message r is a message on a receive event with consistent information, then s and r are considered to be weakly matched and denoted as $s\sim r$. If s precedes r and there is a direct causal relationship, a strong match $s\mapsto r$ is formed.The concepts of weak match and strong match are formally captured in Equation (2).

$$\left\{\begin{array}{c}s\sim r{\equiv }_{\mathit{def}}s\in E\left(\mathit{Send}\right)\wedge r\in E\left(\mathit{Rcv}\right)\wedge \mathit{Send}\left(s\right)=\mathit{Rcv}\left(r\right)\\ s\mapsto r{\equiv }_{\mathit{def}}s\sim r\wedge s<r\end{array}\right\}$$

(2)

If two threads ${\mathit{th}}_1$ and ${\mathit{th}}_2$ each contain at least n messages, and the first n messages of the two threads match each other such that each message pair $\langle m_1,m_2\rangle$ satisfies $m_1\mapsto m_2\vee m_2\mapsto m_1$, then threads ${\mathit{thr}}_1$ and ${\mathit{thr}}_2$ constitute a matching session of length n. Moreover, if this matching session can be further subdivided into a strong matching session, it is denoted as ${\mathit{thr}}_1\stackrel{n}{\approx }{\mathit{thr}}_2$.

2.2.2. Strong Authentication Properties of Protocols

Principals Alice and Bob (hereafter referred to as A and B) are both honest participants who abide by the agreement. Principal A initiates a sequence of conversations, and Principal B responds with a corresponding sequence of replies, forming a legally matching session. If Principal B completes an instance of the full reply sequence, then a matching session exists with Principal A—meaning the content of the received messages matches the corresponding sent messages. Both parties complete identity authentication, ensuring that no attacker can launch a camouflage session attack using previously intercepted messages. The matching session process satisfies the strong matching property. The basic sequence $bs$ in protocol $Pr$ authenticates n messages, and the authentication process satisfies the Equation (3)

$$\begin{array}{c}\forall Pr\vDash \mathit{auth}(bs,n){\equiv }_{\mathit{def}}\forall A,B.\forall {\mathit{thr}}_1.\\ \left(\begin{array}{c}\mathit{Honest}\left(A\right)\wedge \mathit{Honest}\left(B\right)\wedge \forall Pr\left(A\right)\wedge \forall Pr\left(B\right)\\ \wedge A\ne B\wedge loc\left({\mathit{thr}}_1\right)=A\wedge bs(A,B,{\mathit{thr}}_1)\end{array}\right)\\ \Rightarrow \exists {\mathit{thr}}_2.loc\left({\mathit{thr}}_2\right)=B\wedge {\mathit{thr}}_1\stackrel{n}{\approx }{\mathit{thr}}_2\end{array}$$

(3)

2.2.3. Axioms of the Logic of Events Theory

Key Axiom: The Key Axiom (AxiomK) is symmetric, the symmetric key corresponds uniquely to the principal that holds it. The key material is unique to each principal; different principals cannot share the same private key. Moreover, the private key held by principal A can only correspond to its own public key, as shown below

$$\left\{\begin{array}{c}\mathit{AxiomK}:\forall A,B:\mathit{Id}.\forall k,k^{\prime }:\mathit{Key}.\forall a:\mathit{Atom}.\\ MatchingKeys(k,k^{\prime })\iff MatchingKeys(k^{\prime },k)\wedge \\ MatchingKeys\left(\mathit{Symm}\right(a),k)\iff k=\mathit{Symm}\left(a\right)\wedge \\ MatchingKeys\left(\mathit{PrivKey}\right(A),k)\iff k=A\wedge \\ MatchingKeys(A,k)\iff k=\mathit{PrivKey}\left(A\right)\wedge \\ \mathit{Privkey}\left(A\right)=\mathit{Privkey}\left(B\right)\iff A=B\end{array}\right\}$$

(4)

Honest Axiom: LoET includes the Honest function to assert the honesty of a principal. An honest principal does not disclose its private key during protocol interactions. Furthermore, all encryption, decryption, and signature events are assumed to occur on honest principals. The Honest Axiom (AxiomS) characterizes the behavior of trustworthy signers as follows:

$$\left\{\begin{array}{c}\mathit{AxiomS}:\forall A:\mathit{Id}.\forall s:E\left(\mathit{sign}\right).\forall e:E\left(\mathit{Encrypt}\right).\forall d:E\left(\mathit{Decrypt}\right).\\ \mathit{Honest}\left(A\right)\Rightarrow \mathit{signer}\left(s\right)=A\Rightarrow \left(\mathit{loc}\right(s)=A)\wedge \\ \mathit{key}\left(e\right)=\mathit{PrivateKey}\left(A\right)\Rightarrow \left(\mathit{loc}\right(e)=A)\wedge \\ \mathit{key}\left(d\right)=\mathit{PrivateKey}\left(A\right)\Rightarrow \left(\mathit{loc}\right(d)=A)\end{array}\right\}$$

(5)

Flow Relation Axiom: Flow Relation is a correlation between events in a causal order of a random number. The flow of atom a from action $e_1$ to action $e_2$ is described $e_1\stackrel{a}{\to }{e}_2$, there are three scenarios. The first case is that atom a from $e_1$ and $e_2$ are located in the same body; the second case is when there are send and receive events, and a is sent in clear text; in the third case, a is located in the plaintext of the encryption event and flows with the ciphertext to the matching decryption event. Streaming relational recursion is defined as follows:

$$\left\{\begin{array}{c}{e}_1\stackrel{a}{\to }{e}_2{\equiv }_{\mathit{def}}\\ \left(e_{1}hasa\wedge e_{2}hasa\wedge e_1{\le }_{\mathit{loc}}{e}_2\right)\vee \\ \left(\begin{array}{c}\exists s:E\left(\mathit{Send}\right).\exists r:E\left(\mathit{Rcv}\right).e_1\le s<r\le e_2\wedge Send\left(s\right)=\mathit{Rcv}\left(r\right)\\ \wedge e_1\stackrel{a}{\to }s\wedge r\stackrel{a}{\to }{e}_2\end{array}\right)\vee \\ \left(\begin{array}{c}\exists e:E\left(\mathit{Encrypt}\right).\exists d:E\left(\mathit{Decrypt}\right).e_1\le e<d\le e_2\wedge \mathit{DEMatch}(d,e)\\ \wedge \mathit{key}\left(d\right)\ne \mathit{Symm}\left(a\right)\wedge e_1\stackrel{a}{\to }e\stackrel{\mathit{ciphertext}}{\to }d\wedge d\stackrel{a}{\to }{e}_2\end{array}\right)\end{array}\right\}$$

(6)

The Flow Relation is the association between random number causal events, and the axiom of random numbers is denoted as $\mathit{AxiomF}$, which contains three parts, namely, ${\mathit{AxiomF}}_1$, ${\mathit{AxiomF}}_2$, and ${\mathit{AxiomF}}_3$, which are defined as follows:

$$\left\{\begin{array}{c}{e}_1\stackrel{a}{\to }{e}_2\Rightarrow e_1\le e_2\wedge e_2\mathit{has}a\wedge \mathit{release}(a,e_1,e_2)\hfill \\ {\mathit{AxiomF}}_1:\forall e_1:E\left(\mathit{new}\right).\forall e_2:E.\mathit{has}\mathit{New}\left(e_1\right)\Rightarrow e_1\stackrel{\mathit{New}\left(e_1\right)}{\to }{e}_2\hfill \\ {\mathit{AxiomF}}_2:\forall e_1:E\left(\mathit{Sign}\right).\forall e_2:E.e_2\mathit{has}\mathit{signature}\left(e_1\right)\Rightarrow \hfill \\ \exists e^{\prime }:E\left(\mathit{Sign}\right).\mathit{Sign}\left(e^{\prime }\right)=\mathit{Sign}\left(e_1\right)\wedge e^{\prime }\stackrel{\mathit{signature}\left(e_1\right)}{\to }{e}_2\hfill \\ {\mathit{AxiomF}}_3:\forall e_1:E\left(\mathit{Encrypt}\right).\forall e_2:E.e_2\mathit{has}\mathit{signature}\left(e_1\right)\Rightarrow \hfill \\ \exists e^{\prime }:E\left(\mathit{Encrypt}\right).\mathit{Encrypt}\left(e^{\prime }\right)=\mathit{Encrypt}\left(e_1\right)\wedge e^{\prime }\stackrel{\mathit{signature}\left(e_1\right)}{\to }{e}_2\hfill \end{array}\right\}$$

(7)

Axiom F₁ is about the nature of streams, and Axiom F₂ and Axiom F₃ introduce signature, ciphertext, and the relationship between the two types of events, and if an action contains a signature or ciphertext, some signatures or encryption actions with the same information can be inferred.

2.3. Logic of Event Theory Extensions

Overview of X3DH in the Signal Protocol [10]. To help readers better understand the following extensions of the Logic of Events theory (LoET), we briefly introduce the communication mechanism adopted by the Signal protocol, especially the Extended Triple Diffie–Hellman (X3DH) key agreement scheme. X3DH allows two communicating parties (typically an initiator and a responder) to establish a shared root key in an asynchronous setting. The initiator combines three types of public keys from the responder—an identity key, a signed prekey, and a one-time prekey—along with its own ephemeral key to perform a series of Diffie–Hellman operations, thereby generating a shared secret. This shared secret is then used to initialize the double ratchet mechanism, which drives subsequent encrypted communications. By incorporating both long-term and ephemeral keys, X3DH achieves forward secrecy and authentication, laying the theoretical foundation for modeling key evolution using LoET. For a complete description of the Signal protocol’s interaction flow and ratchet mechanism, please refer to Section 3.

2.3.1. Event Class Extension

LoET classifies protocols through events. The authentication protocol involves seven types of events: the generation of challenge numbers, message sending, receiving, signing, verification, encryption, and decryption. The formal definition based on these seven event types is as follows:

$$\left\{\begin{array}{c}\mathit{New}:EClass\left(\mathit{Atom}\right)\hfill \\ \mathit{Send},\mathit{Rcv}:EClass\left(\mathit{Data}\right)\hfill \\ \mathit{Encrypt},\mathit{Decrypt}:EClass(\mathit{Data}\times \mathit{key}\times \mathit{Atom})\hfill \\ \mathit{Sign},\mathit{Verify}:EClass(\mathit{Data}\times \mathit{Id}\times \mathit{Atom})\hfill \end{array}\right.$$

(8)

However, these events do not cover all protocol operations, including those involved in the ratchet encryption mechanism. We extend the event class by introducing new types—DH and ratchet—to more effectively model ratchet encryption. These extensions provide an abstract and precise formal description of ratchet protocols, defined as follows:

$$\left\{\begin{array}{c}\mathit{DH}:EClass(\mathit{Data}\times \mathit{Key}\times \mathit{Atom})\hfill \\ \mathit{Ratchet}:EClass(\mathit{Data}\times \mathit{Key}\times \mathit{Atom})\hfill \end{array}\right.$$

(9)

If there exists an event $e_1\in E\left(\mathit{DH}\right)$, then the principal A performs a series of computations within $e_1$ to generate an initial symmetric encryption key for future long-term message sessions. If there exists an event $e_2\in E\left(\mathit{Ratchet}\right)$, then the principal B updates the ratchet key to generate a new temporary ratchet key.

2.3.2. Related Axiomatic Extension

In the Logic of Events, the causal axioms include the Receive Axiom ($\mathit{AxiomR}$), the Verify Axiom ($\mathit{AxiomV}$), and the Decrypt Axiom ($\mathit{AxiomD}$). These three axioms associate the event classes $\mathit{Rcv}$, $\mathit{Verify}$, and $\mathit{Decrypt}$ with their causally related counterparts $\mathit{Send}$, $\mathit{Sign}$, and $\mathit{Encrypt}$, respectively. Among them, AxiomR and AxiomV are structurally similar, both describing the matchability of protocol behaviors—that is, any receive event or signature verification event must be preceded by a corresponding send or signing event, with identical message content. AxiomD introduces the element of the key, asserting that the decryption event corresponds to an encryption event with both matching content and matching key. The formal definitions are as follows:

$$\left\{\begin{array}{c}\mathit{AxiomR}:\forall e:E\left(\mathit{Rcv}\right)\exists e^{\prime }:E\left(\mathit{Send}\right).(e^{\prime }<e)\wedge \mathit{Rcv}\left(e\right)=\mathit{Send}\left(e^{\prime }\right)\\ \mathit{AxiomV}:\forall e:E\left(\mathit{Verify}\right)\exists e^{\prime }:E\left(\mathit{Sign}\right).(e^{\prime }<e)\wedge \mathit{Verify}\left(e\right)=\mathit{Sign}\left(e^{\prime }\right)\\ \mathit{AxiomD}:\forall e:E\left(\mathit{Decrypt}\right)\exists e^{\prime }:E\left(\mathit{Encrypt}\right).e^{\prime }<e\wedge \mathit{DEMatch}(e,e^{\prime })\\ \mathit{DEMatch}(e,e^{\prime }){\equiv }_{\mathit{def}}\mathit{plaintext}\left(e\right)=\mathit{plaintext}\left(e^{\prime }\right)\wedge \\ \mathit{ciphertext}\left(e\right)=\mathit{ciphertext}\left(e^{\prime }\right)\wedge \mathit{MatchingKeys}(\mathit{key}\left(e\right),\mathit{key}\left(e^{\prime }\right))\end{array}\right\}$$

(10)

To introduce DH and ratchet events, the causal axiom needs to be extended. The extended axiom is denoted as AxiomE. It stipulates that, in the sequence of these two types of events, a corresponding DH event must occur before the ratchet event. The two events are causally related and share relevant information content. In addition, the keys involved must also be match-associated. The formal definition of AxiomE is given as follows:

$$\left\{\begin{array}{c}\mathit{AxiomE}:\forall e:E\left(\mathit{Ratchet}\right)\exists e^{\prime }:E\left(\mathit{DH}\right).(e^{\prime }<e)\wedge \mathit{Ratchet}\left(e\right)=\mathit{DH}\left(e^{\prime }\right)\wedge \\ \mathit{RDMatch}(e,e^{\prime }){\equiv }_{\mathit{def}}\mathit{plaintext}\left(e\right)=\mathit{plaintext}\left(e^{\prime }\right)\wedge \\ \mathit{ciphertext}\left(e\right)=\mathit{ciphertext}\left(e^{\prime }\right)\wedge \mathit{MatchingKeys}(\mathit{key}\left(e\right),\mathit{key}\left(e^{\prime }\right))\end{array}\right\}$$

(11)

To ensure the soundness of AxiomE, we clarify that the relation RDMatch(e, e’)—which links a ratchet event to a prior DH event—is assumed to be injective. That is, for every ratchet event, there exists at most one DH event such that RDMatch holds. This uniqueness is guaranteed by the local causal ordering in LoET and the protocol design of Signal, where each DH operation generates a fresh ephemeral key used exactly once. Therefore, ambiguity is avoided even in long sessions.

In asynchronous environments such as message delay, loss, or replay, RDMatch remains valid based on symbolic causality. A ratchet event must be causally linked to a verifiable prior DH event. Messages that lack this linkage are considered invalid and excluded from the protocol trace, thus ensuring the correctness of AxiomE even under adversarial or unreliable conditions.

2.3.3. Rule Extension

In LoET, the definition of has appears in the stream relationship. The Act class contains seven basic events, which are referred to as actions. The expression $e\mathit{has}a$ is true only if the action e contains the atom a. Therefore, it should be expanded after introducing new events DH and ratchet, and the formally defined Rule after the expansion is as follows:

$$\left\{\begin{array}{c}\mathit{Rule}:e\mathit{has}a{\equiv }_{\mathit{def}}(e\in E\left(\mathit{New}\right)\wedge \mathit{New}\left(e\right)\mathit{has}a)\vee \\ (e\in E(\mathit{Send})\wedge \mathit{Send}(e\left)\mathit{has}a\right)\vee \\ (e\in E(\mathit{Rcv})\wedge \mathit{Rcv}(e\left)\mathit{has}a\right)\vee \\ (e\in E(\mathit{Encrypt})\wedge \mathit{Encrypt}(e\left)\mathit{has}a\right)\vee \\ (e\in E(\mathit{Decrypt})\wedge \mathit{Decrypt}(e\left)\mathit{has}a\right)\vee \\ (e\in E(\mathit{Sign})\wedge \mathit{Sign}(e\left)\mathit{has}a\right)\vee \\ (e\in E(\mathit{Verify})\wedge \mathit{Verify}(e\left)\mathit{has}a\right)\vee \\ (e\in E(\mathit{DH})\wedge \mathit{DH}(e\left)\mathit{has}a\right)\vee \\ (e\in E(\mathit{Ratchet})\wedge \mathit{Ratchet}(e\left)\mathit{has}a\right)\end{array}\right\}$$

(12)

The Equation (12) only describes the protocol actions or the ownership of all atoms in a single operation, without distinguishing specific types of information. During the proof process, distinguishing information content—such as differentiating between plaintext and keys—can help more accurately verify causal relationships between events. Therefore, we propose extending ${\mathit{Rule}}_1$, ${\mathit{Rule}}_2$, and ${\mathit{Rule}}_3$ to account for these cases.

As shown in Equation (13), Rule1 can combine and split information—including plaintext, ciphertext, and keys—which facilitates the distinction, transmission, and reception of information.

$$\left\{\begin{array}{c}\mathit{Rule}1:\forall e:E\left(\mathit{New}\right)\vee E\left(\mathit{Send}\right)\vee E\left(\mathit{Rcv}\right)\vee E\left(\mathit{Encrypt}\right)\vee \hfill \\ E\left(\mathit{Decrypt}\right)\vee E\left(\mathit{Sign}\right)\vee E\left(\mathit{Verify}\right)\vee E\left(\mathit{DH}\right)\vee E\left(\mathit{Ratchet}\right).\hfill \\ \left(\right(e\mathit{has}\left(\mathit{plaintext}\right(e),K))\iff (e\mathit{has}\mathit{plaintext}\left(e\right))\wedge (e\mathit{has}K\left)\right)\vee \hfill \\ \left(\right(e\mathit{has}\left(\mathit{ciphertext}\right(e),K))\Rightarrow (e\mathit{has}\mathit{ciphertext}\left(e\right))\wedge (e\mathit{has}K\left)\right)\hfill \end{array}\right\}$$

(13)

As shown in Equation (14), Rule2 operates under the assumption that event e possesses both the plaintext and the corresponding key K, and that K is valid and usable at e, which allows encrypting plaintext or decrypting ciphertext when the corresponding key is held, thereby obtaining the information content and ensuring that the information is clearer and more accurate.

$$\left\{\begin{array}{c}\mathit{Rule}2:\forall e:E\left(\mathit{Encrypt}\right)\vee E\left(\mathit{Decrypt}\right)\vee E\left(\mathit{DH}\right)\vee E\left(\mathit{Ratchet}\right)\\ \left(\right(e\mathit{has}\mathit{plaintext}\left(e\right),K)\Rightarrow e\mathit{has}\mathit{ciphertext}(e\left)\right)\vee \\ \left(\right(e\mathit{has}\mathit{ciphertext}\left(e\right),K)\Rightarrow e\mathit{has}\mathit{plaintext}(e\left)\right)\end{array}\right\}$$

(14)

As shown in Equation (15), Rule3 introduces the concept of $\mathit{Clean}$, based on the $\mathit{has}$ rule. The $\mathit{Clean}$ predicate provides a formal method for accurately describing the security conditions of keys. Incorporating $\mathit{Clean}$ predicates into the Logic of Events theory ($\mathit{LoET}$) can enhance its ability to describe and reason about security protocols, especially those involving key management.

$$\left\{\begin{array}{c}\mathit{Rule}\mathit{3}\left(\mathit{definition}\mathit{of}\mathit{Clean}\right):\\ ((\mathit{DH}\left(e_0\right)=a\Rightarrow \mathit{Clean}(e_0,a))\vee \\ (\mathit{Ratchet}\left(e_1\right)=a\Rightarrow \mathit{Clean}(e_1,a))\vee \\ (\forall A:\mathit{Id}.\exists e_2:\exists E\left(\mathit{DH}\right)\vee E\left(\mathit{Ratchet}\right).\forall e_3:E_1,\exists e_4:E_2.\\ \mathit{loc}\left(e_2\right)=\mathit{loc}\left(e_3\right)=\mathit{loc}\left(e_4\right)=A\wedge e_2<e_3<e_4\wedge \\ E_2\left(e_4\right)\mathit{has}a\wedge \left(\neg \left(\mathit{send}\left(e_3\right)\mathit{has}a\right)\vee \neg (e_3=E\left(\mathit{send}\right))\right)\\ \Rightarrow \mathit{Clean}(e_4,a))\end{array}\right\}$$

(15)

The predicate Clean(e, a) indicates that the atom a has not been exposed before event e, thereby ensuring its security within the symbolic event sequence. Specifically, Clean(e, a) holds if the following two conditions are satisfied:

• Prior to event e, all events executed by the same participant (loc(e)) must not include atom a in any attacker-observable operation, such as Send, Rcv, or unprotected Encrypt. This condition can be verified using the extended has rule in combination with the local order relation (${<}_{\mathit{loc}}$).
• The occurrence of a in event e must originate from secure events (e.g., DH or ratchet) and must not be derivable from any previously exposed message. This corresponds to the flow relation defined in AxiomF.

Therefore, verifying Clean(e, a) essentially involves checking whether atom a has already been transmitted or leaked through any symbolic path before event e.

3. Formal Analysis of the Signal Protocol

3.1. Overview of the Signal Protocol

The ratchet mechanism is widely used in the field of instant messaging encryption, and the Signal protocol—which incorporates the ratchet mechanism—is one of its most representative examples. The Signal protocol can be roughly divided into three main phases:

1. X3DH Protocol: This phase combines long-term, medium-term, and ephemeral Diffie–Hellman keys to generate a shared root key. 2. Asymmetric Ratchet Phase: In this phase, users alternately exchange new ephemeral Diffie–Hellman keys and combine them with the previously generated root key to produce a forward-secret chain key. 3. Symmetric Ratchet Phase: In this phase, no additional randomness is introduced. Instead, a key derivation function (KDF) is used to stretch the chain key forward to derive symmetric encryption keys.

Throughout this process, each message is encrypted using a newly generated ephemeral key, which significantly enhances the protocol’s forward secrecy and post-compromise security. The main steps of the Signal protocol can be summarized in four parts, as illustrated in Figure 1.

Figure 1 illustrates the message exchange procedure of the Signal protocol between an initiator A and a responder B through a server S. The process can be broken down into the following four stages:

• Registration. Initiator A and Responder B respectively register their identity and prekey bundles with the server. Each prekey bundle contains the party’s respective public keys.
• Session setup. A requests B’s prekey bundle from the server and establishes a secure communication channel with B. Using these public keys, A generates an initial symmetric encryption key, encrypts a message, and sends it to B. This process is known as the Triple Diffie–Hellman (3DH) handshake. Upon receiving the message, B fetches A’s prekey bundle from the server and derives the shared secret.
• Symmetric Ratchet Phase. If A needs to send another message to B before receiving a reply, A derives a new symmetric encryption key via the ratchet mechanism, generates a temporary ratchet public key, attaches it to the message, and sends it to B for use in the response.
• Asymmetric Ratchet Phase. When B receives A’s message and needs to reply, B generates a new temporary ratchet public key, encrypts the message, and sends it to A. When A replies in turn, A generates another temporary ratchet public key based on the received message, encrypts the response, and sends it back to B—thus completing the asymmetric ratchet process.

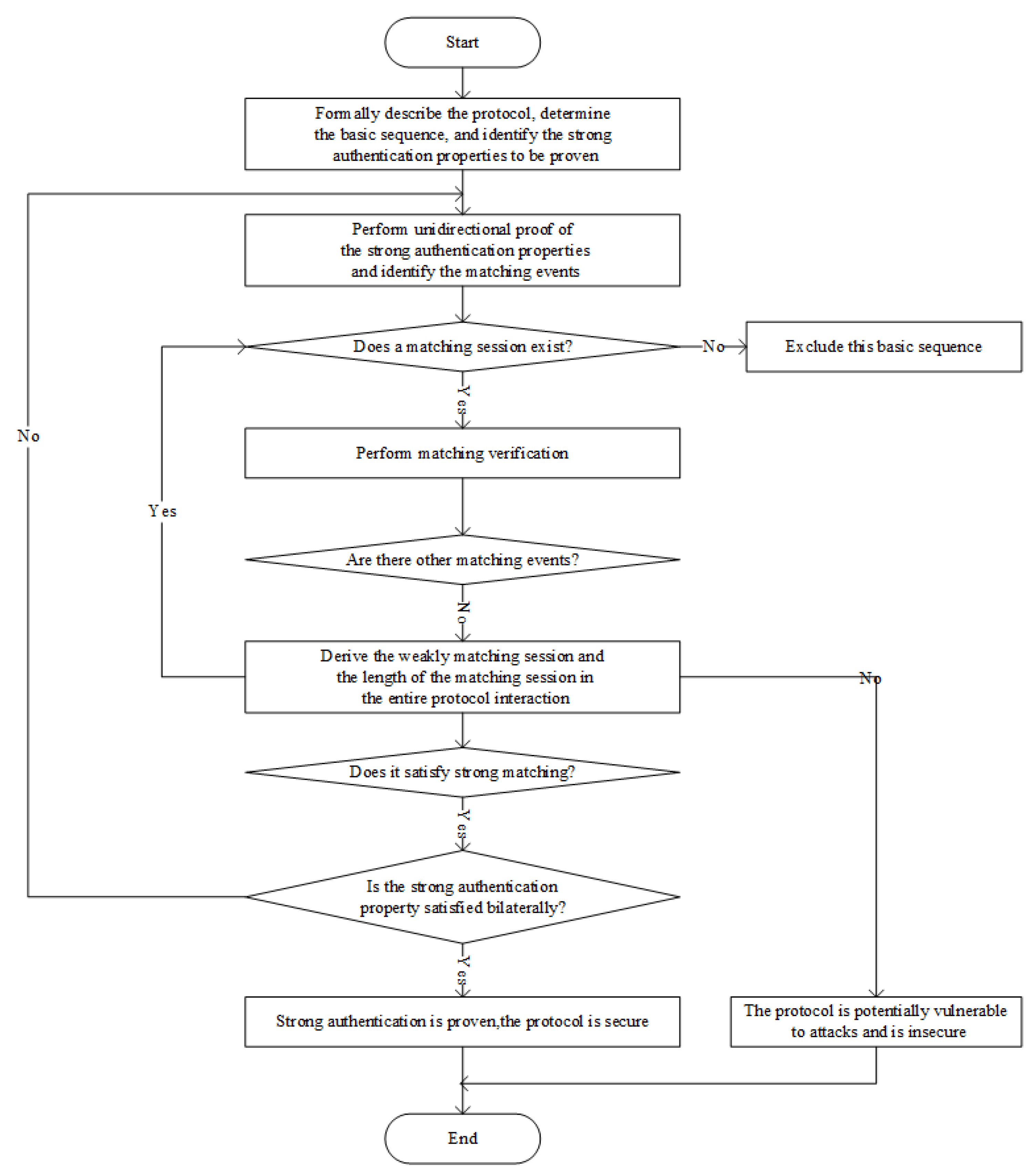
3.2. Formal Verification Framework

The formal verification process for the Signal protocol’s strong authentication properties, as illustrated in Figure 2.

Figure 2 presents the logical flowchart of the verification process based on the extended Logic of Events theory (LoET). It outlines a stepwise framework: modeling the ratchet phases with LoET, proving unidirectional and bidirectional strong authentication, and determining matching session validity through axiomatic rules and causal consistency. This framework is then translated into a concrete procedural logic, as detailed in the following steps.

• Use LoET and its extensions to formally describe the ratcheting mechanism of the Signal protocol. Define the actions between initiator A and responder B, specify the basic sequence, and identify the strong authentication properties to be verified.
• Prove the unidirectional strong authentication property. Assume both A and B are honest. For any instance of the basic sequence, identify matching events and exclude non-matching ones.
• Check whether the matching events satisfy the session conditions. If so, prove the matching session; otherwise, continue filtering. If only weak matching is found, analyze the sequence length and verify strong matching based on the axioms.
• After completing the unidirectional proof, verify the bidirectional property. The protocol is secure only if both directions hold. If any event fails even weak matching, the protocol lacks strong authentication and is vulnerable to impersonation.

3.3. Formal Verification of Strong Authentication Properties

In this formal analysis, we adopt the widely accepted Dolev–Yao adversary model, which is particularly well-suited for symbolic verification frameworks such as LoET. Under this model, the adversary is assumed to have full control over the communication channel, including the ability to intercept, modify, replay, delay, and inject arbitrary messages. However, the adversary is considered computationally bounded, and thus incapable of breaking cryptographic primitives—such as encryption schemes, digital signatures, or key derivation functions—unless the corresponding keys have already been compromised.

This model is chosen for its ability to provide a rigorous yet tractable abstraction of real-world adversaries. It enables us to concentrate on the logical structure and causal relationships within the protocol, without relying on the underlying algebraic properties of cryptographic algorithms. The Dolev–Yao model represents a widely accepted assumption in symbolic protocol analysis and provides a solid theoretical foundation for verifying strong authentication guarantees in the Signal protocol under ideal cryptographic conditions.

3.3.1. Formal Description of Basic Sequences

In the Signal protocol, apart from the registration phase—during which A and B register their identities and public keys with the server and request each other’s pre-key bundles—the server does not participate in the conversation. Therefore, we focus only on the interaction between the two communicating parties. The asymmetric and symmetric ratchet phases of the Signal protocol are described using basic sequences. We define Initiator A and Responder B to represent both parties in the interaction. Specifically, $I_1,I_2,I_3$ are the basic sequences of Initiator A, while $R_1,R_2,R_3$ are the basic sequences of Responder B, as illustrated in Figure 3 and  Figure 4. The notations is explained in

Table 2. Notation descriptions.

Notations	Description
PKB-X	Prekey bundle of X
${\mathit{rchpk}}_x^y$	The x-th ratchet key generated by party y
$m_x$	The x-th ciphertext of the sender
$s_x$	The x-th message

.

Figure 3 illustrates the formalized basic event sequences $I_1,I_2$, and $I_3$ of the initiator A during the asymmetric ratchet phase of the Signal protocol. Each sequence represents a distinct round in the message exchange:

• ${\mathit{I}}_{\mathbf{1}}$ captures the initial message transmission from A to B, where A uses Diffie–Hellman (DH) to generate an ephemeral key and encrypts the message;
• ${\mathit{I}}_{\mathbf{2}}$ models the reception of B’s response, including decryption using A’s previous key and updating A’s ratchet key for forward secrecy;
• ${\mathit{I}}_{\mathbf{3}}$ reflects A’s subsequent message to B, built upon the updated ratchet state.

These sequences collectively represent the progression of ratcheted state transitions at the initiator’s side, and form the basis for verifying the strong authentication property $SP\vDash \mathit{auth}(I_3,2)$.

Figure 4 illustrates the formalized basic event sequences $R_1,R_2$, and $R_3$ of the responder B during the symmetric ratchet phase of the Signal protocol. Each sequence models a message processing step by B after receiving messages from A:

• ${\mathit{R}}_{\mathbf{1}}$ depicts the initial decryption of the received ciphertext from A using the ratcheted key, enabling B to retrieve the plaintext message;
• ${\mathit{R}}_{\mathbf{2}}$ represents the generation of a new ratchet key by B and the encryption of a response message to A, establishing a new ratcheted state;
• ${\mathit{R}}_{\mathbf{3}}$ shows the reception and decryption of a subsequent message from A using the updated ratchet key.

These sequences collectively capture the symmetric ratcheting process on the responder’s side, where key updates are driven by key derivation functions (KDFs) rather than new Diffie–Hellman exchanges. They form the basis for verifying the strong authentication property $SP\vDash \mathit{auth}(R_3,1)$.

Whether in the asymmetric or symmetric ratchet interaction phase, if the Signal protocol can ensure that two threads at different states establish a strongly matching session, then it satisfies the properties of strong authentication. Therefore, we define the Signal authentication protocol as $\mathit{Protocol}(I_1,I_2,I_3,R_1,R_2,R_3)$, abbreviated as $\mathit{SP}$. Next, we analyze the dual ratchet processes separately.

3.3.2. Analysis of the Asymmetric Ratchet

As Figure 1 shows, in the asymmetric ratchet phase, after obtaining B’s prekey bundle, A sends the generated keys and messages to B. Upon receiving the message, B responds to A. The two parties then repeat this process to communicate. According to the description in Section 2, in the asymmetric ratchet phase of the Signal protocol, the strong authentication property to be verified is given by $\mathit{SP}\vDash \mathit{auth}(I_3,2)\wedge \mathit{SP}\vDash \mathit{auth}(R_3,3)$.

As Figure 3 shows, we assume that the honest principals $A\ne B$ both behave according to the honest principle (Equation (5)). According to the definition of the basic sequence, each thread of A and B is an instance of the basic sequence. Let ${\mathit{thr}}_1$ be an instance on $I_3$, and for Atom-typed parameters $\mathit{PKB-B},{\mathit{rchpk}}_1^A,{\mathit{rchpk}}_2^B,{\mathit{Rchpk}}_3^A,m_1,m_2,m_3,s_1,s_2,s_3$, there exists an event sequence $e_0{<}_{\mathrm{loc}}{e}_1{<}_{\mathrm{loc}}\cdots {<}_{\mathrm{loc}}{e}_8$, and the event instance of ${\mathit{thr}}_1$ is as follows:

$$\left\{\begin{array}{c}\mathit{New}\left(e_0\right)=\langle \mathit{PKB}-B\rangle \wedge \hfill \\ \mathit{DH}\left(e_1\right)=\langle {\mathit{rchpk}}_1^A\rangle \wedge \hfill \\ \mathit{Encrypt}\left(e_2\right)=\langle m_1,{\mathit{rchpk}}_1^A,s_1\rangle \wedge \hfill \\ \mathit{Send}\left(e_3\right)=\langle s_1\rangle \wedge \hfill \\ \mathit{Rcv}\left(e_4\right)=\langle s_2\rangle \wedge \hfill \\ \mathit{Decrypt}\left(e_5\right)=\langle m_2,\langle {\mathit{rchpk}}_1^A,{\mathit{rchpk}}_2^B\rangle ,S_2\rangle \wedge \hfill \\ \mathit{DH}\left(e_6\right)=\langle {\mathit{rchpk}}_2^B,{\mathit{rchpk}}_3^A\rangle \wedge \hfill \\ \mathit{Encrypt}\left(e_7\right)=\langle m_3,\langle {\mathit{rchpk}}_2^B,{\mathit{rchpk}}_3^A\rangle ,s_3\rangle \wedge \hfill \\ \mathit{Send}\left(e_8\right)=\langle s_3\rangle \hfill \end{array}\right\}$$

(16)

According to AxiomD (Equation (10)) and AxiomS (Equation (5)), there exists an event $e^{\prime }$ such that $e^{\prime }<e_5\wedge \mathit{DEMatch}(e^{\prime },e_5)\wedge \mathit{loc}\left(e^{\prime }\right)=A\vee \mathit{loc}\left(e^{\prime }\right)=B$. In the basic sequence, actions containing Encrpt() are included in $I_1,I_3,R_2$. Since it is based on the current event, all future events are not considered, thus $I_3$ is excluded. This implies that in $I_1$ or $R_2$, there exists a basic sequence that could potentially match with $I_3$. Assume $e^{\prime }$ is an instance in $R_2$, then for Atom-typed values $\mathit{PKB}-{\mathit{A}}^{\prime }$, ${\mathit{rchpk}}_1^{A^{\prime }}$, ${\mathit{rchpk}}_2^{B^{\prime }}$, $m_1^{\prime },m_2^{\prime },s_2^{\prime }$, there exists a sequence of events $e_0^{\prime },e_1^{\prime },e_2^{\prime },e^{\prime },e_3^{\prime },e_4^{\prime }$ on principal B as follows:

$$\left\{\begin{array}{c}{e}_0^{\prime }{<}_{\mathit{loc}}{e}_1^{\prime }{<}_{\mathit{loc}}{e}_2^{\prime }{<}_{\mathit{loc}}{e}_3^{\prime }{<}_{\mathit{loc}}{e}^{\prime }{<}_{\mathit{loc}}{e}_4^{\prime }\hfill \\ \mathit{Rcv}\left(e_0^{\prime }\right)=\langle s_1^{\prime }\rangle \wedge \mathit{New}\left(e_1^{\prime }\right)=\langle \mathit{PKB}-A^{\prime }\rangle \wedge \hfill \\ \mathit{Decrypt}\left(e_2^{\prime }\right)=\langle m^{\prime },{\mathit{rchpk}}_1^{A^{\prime }},s_1^{\prime }\rangle \wedge \mathit{Ratchet}\left(e_3^{\prime }\right)=\langle {\mathit{rchpk}}_1^{A^{\prime }},{\mathit{rchpk}}_2^{B^{\prime }}\rangle \wedge \hfill \\ \mathit{Encrypt}\left(e^{\prime }\right)=\langle m^{\prime },\langle {\mathit{rchpk}}_1^{A^{\prime }},{\mathit{rchpk}}_2^{B^{\prime }}\rangle ,s_2^{\prime }\rangle \wedge \mathit{Send}\left(e_4^{\prime }\right)=\langle s_2^{\prime }\rangle \hfill \end{array}\right\}$$

(17)

$\mathit{DEMatch}(e^{\prime },e_5)$ holds by AxiomD (Equation (10)) and AxiomE (Equation (11))

$$\left\{\begin{array}{c}\mathit{Plaintext}\left(e^{\prime }\right)=\mathit{Plaintext}\left(e_5\right)\wedge \\ \mathit{ciphertext}\left(e^{\prime }\right)=\mathit{ciphertext}\left(e_5\right)\wedge \\ \mathit{MatchingKeys}(\mathit{key}\left(e^{\prime }\right),\mathit{key}\left(e_5\right))\Rightarrow \\ {\mathit{rchpk}}_1^{A^{\prime }}={\mathit{rchpk}}_1^A\wedge {\mathit{rchpk}}_2^{B^{\prime }}={\mathit{rchpk}}_2^B\wedge \\ s_2^{\prime }=s_2\wedge m_2^{\prime }=m_2\end{array}\right\}$$

(18)

From the Equations (16)–(18), it can be derived that

$$\left\{\begin{array}{c}{e}_0^{\prime }{<}_{\mathit{loc}}{e}_1^{\prime }{<}_{\mathit{loc}}{e}_2^{\prime }{<}_{\mathit{loc}}{e}^{\prime }{<}_{\mathit{loc}}{e}_4^{\prime }\hfill \\ \mathit{Rcv}\left(e_0^{\prime }\right)=\langle s_1\rangle \wedge \hfill \\ \mathit{New}\left(e_1^{\prime }\right)=\langle \mathit{PKB}-A\rangle \wedge \hfill \\ \mathit{Decrypt}\left(e_2^{\prime }\right)=\langle m_1,{\mathit{rchpk}}_1^A\rangle \wedge \hfill \\ \mathit{Ratchet}\left(e_3^{\prime }\right)=\langle {\mathit{rchpk}}_1^A,{\mathit{rchpk}}_2^B\rangle \wedge \hfill \\ \mathit{Encrypt}\left(e^{\prime }\right)=\langle m_2,\langle {\mathit{rchpk}}_1^A,{\mathit{rchpk}}_2^B\rangle ,s_2\rangle \wedge \hfill \\ \mathit{Send}\left(e_4^{\prime }\right)=\langle s_2\rangle \hfill \end{array}\right\}$$

(19)

The Equation (19) shows that $e^{\prime }$ is an instance of $R_2$. At this point, $e^{\prime }$ matches $e_5$, so it can be excluded from $I_1$. Similarly, analyzing the $\mathit{Decrypt}\left(\right)$ event in $R_2$, it must exist in an event $e^{″}$, such that $e^{″}\in \mathit{DEMatch}(e^{″},e_2)\wedge \mathit{loc}\left(e^{″}\right)=A\vee \mathrm{loc}\left(e^{″}\right)=B$, thus making $\mathit{Encrypt}\left(e^{″}\right)=\langle m_1,{\mathit{rchpk}}_1^A,s_1\rangle$. Assuming that $e^{″}$ is an instance on $I_1$, for the $\mathit{Atom}$ type of $\mathit{PKB}-\mathit{B},{\mathit{rchpk}}_1^A,m_1,s_1$, the event on the main body A would be as follows:

$$\left\{\begin{array}{c}{e}_0^{″}{<}_{\mathit{loc}}{e}_1^{″}{<}_{\mathit{loc}}{e}^{″}{<}_{\mathit{loc}}{e}_2^{″}\hfill \\ \mathit{New}\left(e_0^{″}\right)=\langle \mathit{PKB}-B^{″}\rangle \wedge \hfill \\ \mathit{DH}\left(e_1^{″}\right)=\langle {\mathit{rchpk}}_1^{A^{″}}\rangle \wedge \hfill \\ \mathit{Encrypt}\left(e^{″}\right)=\langle m_1^{″},{\mathit{rchpk}}_1^{A^{″}},s_1^{″}\rangle \wedge \hfill \\ \mathit{Send}\left(e_2^{″}\right)=\langle s_1^{″}\rangle \hfill \end{array}\right\}$$

(20)

$\mathit{DEMatch}(e^{″},e_2^{\prime })$ holds by AxiomD (Equation (10)) and AxiomE (Equation (11))

$$\left\{\begin{array}{c}\mathit{Plaintext}\left(e^{″}\right)=\mathit{Plaintext}\left(e_2^{\prime }\right)\wedge \hfill \\ \mathit{ciphertext}\left(e^{″}\right)=\mathit{ciphertext}\left(e_2^{\prime }\right)\wedge \hfill \\ \mathit{MatchingKeys}(\mathit{key}\left(e^{″}\right),\mathit{key}\left(e_2^{\prime }\right))\Rightarrow \hfill \\ {\mathit{rchpk}}_1^{A^{″}}={\mathit{rchpk}}_1^A\wedge s_1^{″}=s_1\wedge m_1^{″}=m_1\hfill \end{array}\right\}$$

(21)

From the Equations (19)–(21), it can be derived that

$$\left\{\begin{array}{c}\mathit{New}\left(e_0^{″}\right)=\langle \mathit{PKB}-B\rangle \wedge \hfill \\ \mathit{DH}\left(e_1^{″}\right)=\langle {\mathit{rchpk}}_1^A\rangle \wedge \hfill \\ \mathit{Encrypt}\left(e^{″}\right)=\langle m_1,{\mathit{rchpk}}_1^A,s_1\rangle \wedge \hfill \\ \mathit{Send}\left(e_2^{″}\right)=\langle s_1\rangle \hfill \end{array}\right\}$$

(22)

The Equation (22) shows that $e^{″}$ is an instance on $I_1$, and it matches $e_2^{\prime }$. From the above proof, we can deduce that $\mathit{Send}\left(e_3\right)=\mathit{Rcv}\left(e_4\right)$ and $\mathit{Send}\left(e_4^{\prime }\right)=\mathit{Rcv}\left(e_4\right)$, which forms two weak matching pairs, $\mathit{Send},\mathit{Rcv}$. Next, we need to confirm the event order, $e_3<e_0$ and $e_4^{\prime }<e_4$, to prove the strong matching property.

From the extension of Axiom F (Equation (7)) and the has rule (Equations (12)–(15)). It is known that there exists a sending event s between $e_3$ and $e_0^{\prime }$ that releases a random number m. If $e_3\le s$, we can obtain $e_3<e_0^{\prime }$. otherwise, If $e_0^{\prime }\le s$, then must exist $e_0^{\prime }<\mathit{loc}\left(j\right)<e_3$. In this case, s must be the result of a process on the main thread $t{h}_1$ of B. According to Axiom F (Equation (7)), it is known that $e_3$ and $e_0$ do not exist in the sending event, which implies that the random number m will not be released before $e_3$. Therefore, we can conclude that $e_3<e_0^{\prime }$, and similarly, it can be proven that $e_4<e_4^{\prime }$. Thus, $\mathit{SP}\vDash$$\mathit{auth}\mathit{1}(l_3,2)$ is established.

Similarly, it can be verified that $\mathit{SP}=\mathit{auth}(I_3,2)$. Let ${\mathit{thr}}_2$ be a basic sequence on $R_3$. Define a sequence of events on thread ${\mathit{thr}}_2$ as $e_0{<}_{\mathit{loc}}{e}_1{<}_{\mathit{loc}}\dots {<}_{\mathit{loc}}{e}_7$. For some information of type Atom, including $s_1,s_2,s_3,m_1,m_2,m_3,{\mathit{rchpk}}_1^A,{\mathit{rchpk}}_2^B,{\mathit{rchpk}}_3^A$, we have $\mathit{Decrypt}\left(e_7\right)=\langle m_3,\langle {\mathit{rchpk}}_2^B,{\mathit{rchpk}}_3^A\rangle ,s_3\rangle$. According to AxiomD and AxiomS, there exists some event $e^{\prime }$ such that $e^{\prime }<e_7\wedge \mathit{DEMatch}(e^{\prime },e_7)\wedge (\mathit{loc}\left(e^{\prime }\right)=A\vee \mathit{loc}\left(e^{\prime }\right)=B)$. Since principal B follows the honesty axiom and mutual authentication protocol, $e^{\prime }$ must be a valid instance in the basic sequence, which includes Encrypt() events from $I_3,I_1,R_2$. Assume that $e^{\prime }$ is one such instance from $I_3$; then for Atom-type data ${\mathit{rchpk}}_1^A,{\mathit{rchpk}}_2^B,{\mathit{rchpk}}_3^A,m_2^{\prime },m_3^{\prime },s_2^{\prime },s_3$, the following events exist in principal: A: $e_0,e_1,e_2,e^{\prime },e_3$, and we have $\mathit{Encrypt}\left(e^{\prime }\right)=\langle m_3^{\prime },\langle {\mathit{rchpk}}_2^B,{\mathit{rchpk}}_3^A\rangle ,s_3^{\prime }\rangle$.

Therefore, $\mathrm{DEMatch}(e^{\prime },e_7)$ holds. According to Axiom D and Axiom E, we know that there exists an event $e^{\prime }$ in $I_3$ such that $\mathit{Send}\left(e_3^{\prime }\right)=s_3=\mathit{Rcv}\left(e_6\right)$, forming a weakly matching pair. Similarly, $I_1$ and $R_2$ can be excluded. Since it has been proven that $e^{\prime }$ is an event from $I_3$, there must exist another event $e^{″}$ such that $e^{″}<e_1^{\prime }\wedge \mathit{DEMatch}(e^{″},e_1^{\prime })\wedge (\mathrm{loc}\left(e^{″}\right)=A\vee \mathit{loc}\left(e^{″}\right)=B)$. The proof process can reference $\mathit{auth}(I_3,2)$. We then have $\mathit{Rcv}\left(e_0^{\prime }\right)=s_2=\mathit{Send}\left(e_5\right)$. Likewise, it can be derived that $e^{‴}<e_2\wedge \mathrm{DEMatch}(e^{‴},e_2)\wedge (\mathrm{loc}\left(e^{‴}\right)=A\vee \mathrm{loc}\left(e^{‴}\right)=B)$, which yields $\mathit{send}\left(e_3\right)=\mathit{rcv}\left(e_0^{\prime }\right)$. This completes the proof of three weakly matching pairs.

Next, we need to prove that $e_3^{\prime }<e_6,e_5<e_0^{\prime },e_3<e_0^{\prime }$, thereby completing the proof of strong authentication. According to extension of Axiom F and the has rule, we can deduce as follows: Suppose a sending event s releases random number m and occurs between $e_3$ and $e_6$. If $e_3\le s$, we get $e_3<e_6$. Otherwise, if $e_6\le s$, then $e_6<\mathit{loc}\left(j\right)<e_3^{\prime }$. In this case, s must be a member on thread $t{h}_2$ of principal B. According to Axiom F₁, we know that $e_6$ and $e_3$ are not part of the send event, m will not be released before $e_3$. Therefore, we conclude that $e_3<e_6$. Similarly, it can be proven that $e_5<e_0^{\prime }$ and $e_3<e_0^{\prime }$. Thus, $\mathit{SP}=\mathit{auth}(R_3,3)$ is established.

3.3.3. Analysis of the Symmetric Ratchet

As Figure 4 shows, unlike the asymmetric ratchet phase, in the symmetric ratchet phase, after principal A sends the encryption key and message to B, if B has not received the message or does not respond to A in time upon receiving it, A can continue sending new keys and messages until a response is received from B. Once B responds to A, both parties resume normal communication, alternating between ratchet and non-ratchet steps. Therefore, it is sufficient to prove that the symmetric ratchet phase satisfies the strong authentication properties. According to the description in Section 2, the strong authentication properties that need to be verified in the symmetric ratchet phase of the Signal protocol are $\mathit{SP}\vDash \mathit{auth}(I_3,2)\wedge \mathit{SP}\vDash \mathit{auth}(R_3,1)$.

In the asymmetric ratchet phase, assume that honest principals $A\ne B$, and both parties follow the honest principal rule (Equation (5)). According to the definition of the basic sequence, each thread of A and B is an instance of a basic sequence. Let ${\mathit{thr}}_1$ be an instance on $I_3$ and define $e_0{<}_{\mathit{loc}}{e}_1{<}_{\mathit{loc}}\cdots {<}_{\mathit{loc}}{e}_8$, where the following events exist:

$$\left\{\begin{array}{c}\mathit{New}\left(e_0\right)=\langle \mathit{PKB}-B\rangle \wedge \mathit{DH}\left(e_1\right)=\langle {\mathit{rchpk}}_1^A\rangle \wedge \hfill \\ \mathit{Encrypt}\left(e_2\right)=\langle m_1,{\mathit{rchpk}}_1^A,s_1\rangle \wedge \hfill \\ \mathit{Send}\left(e_3\right)=\langle s_1\rangle \wedge \mathit{DH}\left(e_4\right)=\langle {\mathit{rchpk}}_2^A\rangle \wedge \hfill \\ \mathit{Decrypt}\left(e_5\right)=\langle m_2,{\mathit{rchpk}}_2^A,s_2\rangle \wedge \hfill \\ \mathit{Send}\left(e_6\right)=\langle s_2\rangle \wedge \mathit{Rcv}\left(e_7\right)=\langle s_3\rangle \hfill \\ \mathit{Encrypt}\left(e_8\right)=\langle m_3,\langle {\mathit{rchpk}}_2^A,{\mathit{rchpk}}_3^B\rangle ,s_3\rangle \hfill \end{array}\right\}$$

(23)

According to Axiom D (Equation (10)) and Axiom S (Equation (5)), there exists some event $e^{\prime }$ such that $e^{\prime }<e_8\wedge \mathit{DEMatch}(e^{\prime },e_8)\wedge (\mathit{loc}\left(e^{\prime }\right)=A\vee \mathit{loc}\left(e^{\prime }\right)=B)$. In the basic sequence, the Encrypt() action may appear in $I_1,I_2,\mathit{or}{R}_3$. To ensure the availability of event occurrences, the event types involving initiator A and responder B must involve both or multiple parties. Therefore, $I_1$ and $I_2$ can be excluded. Assuming $e^{\prime }$ is an instance from $R_3$, then for Atom-type values $s_2^{\prime },s_3^{\prime },m_2^{\prime },m_3^{\prime },{\mathit{rchpk}}_2^A,{\mathit{rchpk}}_3^B$, there exist events $e_0^{\prime },e_1^{\prime },e_2^{\prime },e^{\prime },e_3^{\prime }$ on principal B.

$$\left\{\begin{array}{c}{e}_0^{\prime }{<}_{\mathit{loc}}{e}_1^{\prime }{<}_{\mathit{loc}}{e}_2^{\prime }{<}_{\mathit{loc}}{e}^{\prime }{<}_{\mathit{loc}}{e}_3^{\prime }\hfill \\ \mathit{Rcv}\left(e_0^{\prime }\right)=\langle s_2^{\prime }\rangle \wedge \mathit{Decrypt}\left(e_1^{\prime }\right)=\langle m_2^{\prime },{\mathit{rchpk}}_2^{A^{\prime }},s_2^{\prime }\rangle \wedge \hfill \\ \mathit{Ratchet}\left(e_2^{\prime }\right)=\langle {\mathit{rchpk}}_2^{A^{\prime }},{\mathit{rchpk}}_3^{B^{\prime }}\rangle \wedge \hfill \\ \mathit{Encrypt}\left(e^{\prime }\right)=\langle m_3^{\prime },\langle {\mathit{rchpk}}_2^{A^{\prime }},{\mathit{rchpk}}_3^{B^{\prime }}\rangle s_3^{\prime }\rangle \wedge \hfill \\ \mathit{Send}\left(e_3^{\prime }\right)=\langle s_3^{\prime }\rangle \hfill \end{array}\right\}$$

(24)

$\mathit{DEMatch}(e^{\prime },e_8)$ holds by AxiomD (Equation (10)) and AxiomE (Equation (11))

$$\left\{\begin{array}{c}\mathit{Plaintext}\left(e^{\prime }\right)=\mathit{Plaintext}\left(e_8\right)\wedge \hfill \\ \mathit{ciphertext}\left(e^{\prime }\right)=\mathit{ciphertext}\left(e_8\right)\wedge \hfill \\ \mathit{MatchingKeys}(\mathit{key}\left(e^{\prime }\right),\mathit{key}\left(e_8\right))\Rightarrow \hfill \\ {\mathit{rchpk}}_2^{A^{\prime }}={\mathit{rchpk}}_2^A\wedge {\mathit{rchpk}}_3^{B^{\prime }}={\mathit{rchpk}}_3^B\wedge \hfill \\ s_2^{\prime }=s_2\wedge s_3^{\prime }=s_3\wedge m_3^{\prime }=m_3\hfill \end{array}\right\}$$

(25)

From the Equations (23)–(25), it can be derived that

$$\left\{\begin{array}{c}{e}_0^{\prime }{<}_{\mathit{loc}}{e}_1^{\prime }{<}_{\mathit{loc}}{e}_2^{\prime }{<}_{\mathit{loc}}{e}^{\prime }{<}_{\mathit{loc}}{e}_3^{\prime }\hfill \\ \mathit{Rcv}\left(e_0^{\prime }\right)=\langle s_2\rangle \wedge \hfill \\ \mathit{Decrypt}\left(e_1^{\prime }\right)=\langle m_2,{\mathit{rchpk}}_2^A,s_2\rangle \wedge \hfill \\ \mathit{Ratchet}\left(e_2^{\prime }\right)=\langle {\mathit{rchpk}}_2^A,{\mathit{rchpk}}_3^B\rangle \wedge \hfill \\ \mathit{Encrypt}\left(e^{\prime }\right)=\langle m_3,\langle {\mathit{rchpk}}_2^A,{\mathit{rchpk}}_3^B\rangle ,s_3\rangle \wedge \hfill \\ \mathit{Send}\left(e_3^{\prime }\right)=\langle s_3\rangle \hfill \end{array}\right\}$$

(26)

The Equation (26) shows that $e^{\prime }$ is an instance from $R_3$. At this point, $e^{\prime }$ matches with $e_8$, so we obtain a weakly matching pair $\mathit{Send}\left(e_3^{\prime }\right)=\langle s_3\rangle =\mathit{Rcv}\left(e_7\right)$. Similarly, analyzing the Decrypt() event in $R_3$, there must exist another event $e^{″}$ such that $e^{″}<e_1^{\prime }\wedge \mathit{DEMatch}(e^{″},e_1^{\prime })\wedge (\mathit{loc}\left(e^{″}\right)=A\vee \mathit{loc}\left(e^{″}\right)=B)$, which implies that $\mathit{Encrypt}\left(e^{″}\right)=\langle m_2,{\mathit{rchpk}}_2^A,s_2\rangle$ holds. At this point, the Encrypt() action exists in either $I_1$ or $I_2$. Assuming $e^{″}$ exists in $I_2$, then for Atom-type values ${\mathit{rchpk}}_2^{A^{\prime \prime }},m_2^{″},s_2^{″}$, there exist events $e_0^{″},e^{″},e_1^{″}$.

$$\left\{\begin{array}{c}{e}_0^{″}{<}_{\mathit{loc}}{e}^{″}{<}_{\mathit{loc}}{e}_1^{″}\hfill \\ \mathit{DH}\left(e_0^{″}\right)=\langle {\mathit{rchpk}}_2^{A^{″}}\rangle \wedge \hfill \\ \mathit{Encrypt}\left(e^{″}\right)=\langle m_2^{″},{\mathit{rchpk}}_2^{A^{″}},s_2^{″}\rangle \wedge \hfill \\ \mathit{Send}\left(e_1^{″}\right)=\langle s_2^{″}\rangle \hfill \end{array}\right\}$$

(27)

$\mathit{DEMatch}(e^{″},e_1^{\prime })$ holds by AxiomD (Equation (10)) and AxiomE (Equation (11))   

$$\left\{\begin{array}{c}\mathit{Plaintext}\left(e^{″}\right)=\mathit{Plaintext}\left(e_1^{\prime }\right)\wedge \hfill \\ \mathit{ciphertext}\left(e^{″}\right)=\mathit{ciphertext}\left(e_1^{\prime }\right)\wedge \hfill \\ \mathit{MatchingKeys}(\mathit{key}\left(e^{″}\right),\mathit{key}\left(e_1^{\prime }\right))\Rightarrow \hfill \\ {\mathit{rchpk}}_2^{A^{″}}={\mathit{rchpk}}_2^A\wedge s_2^{″}=s_2\wedge m_2^{″}=m_2\hfill \end{array}\right\}$$

(28)

From Equations (26)–(28), it can be derived that

$$\left\{\begin{array}{c}{e}_0^{″}{<}_{\mathit{loc}}{e}^{″}{<}_{\mathit{loc}}{e}_1^{″}\hfill \\ \mathit{DH}\left(e_0^{″}\right)=\langle {\mathit{rchpk}}_2^A\rangle \wedge \hfill \\ \mathit{Encrypt}\left(e^{″}\right)=\langle m_2,{\mathit{rchpk}}_2^A,s_2\rangle \wedge \hfill \\ \mathit{Send}\left(e_1^{″}\right)=\langle s_2\rangle \hfill \end{array}\right\}$$

(29)

Therefore, it can be concluded that $e^{″}$ is an instance from $I_2$. At this point, $e^{″}$ matches with $e^{\prime }$, forming a weakly matching pair $\mathit{Send}\left(e_1^{″}\right)=\langle s_2\rangle =\mathit{Rcv}\left(e_0^{\prime }\right)$. Similarly, $I_1$ can be excluded.

Next, we only need to prove $e_1^{″}<e_0^{\prime }$ and $e_3^{\prime }<e_7$ to verify the property of strong matching. According to the extension of AxiomF (Equation (7)) and the has Rule (Equations (12)–(15)), if a sending event s that releases a random number m exists between $e_1^{″}$ and $e_0^{\prime }$, then if $e_1^{″}\le s$, it follows that $e_1^{″}<e_0^{\prime }$; if $e_0^{\prime }\le s$, then $e_0^{\prime }{<}_{\mathit{loc}}\left(j\right)<e_1^{″}$. In this case, s must be on thread $t{h}_1$ of principal B, and based on Axiom F₁, since there is no sending event between $e_1^{″}$ and $e_0^{\prime }$, the random number m could not have been released before $e_1^{″}$. Therefore, we conclude that $e_1^{″}<e_0^{\prime }$. Similarly, we can also prove that $e_3^{\prime }<e_7$, and hence $\mathit{SP}\vDash \mathit{auth}(I_3,2)$ is established.

Based on the proof of $\mathit{SP}\vDash \mathit{auth}(I_3,2)$, we now provide a separate proof for $\mathit{SP}\vDash \mathit{auth}(R_3,1)$. Let ${\mathit{thr}}_2$ be a basic sequence on $R_3$. Define the thread ${\mathit{thr}}_2$ as having events $e_0{<}_{\mathrm{loc}}{e}_1{<}_{\mathit{loc}}\dots {<}_{\mathit{loc}}{e}_4$. For some Atom-type values $s_2,s_3,m_2,m_3,{\mathit{rchpk}}_2^A,{\mathit{rchpk}}_3^B$, suppose $\mathit{Decrypt}\left(e_1\right)=\langle m_2,{\mathit{rchpk}}_2^A,s_2\rangle$. According to Axiom D and Axiom S, there exists an event $e^{\prime }$ such that $e^{\prime }<e_1\wedge \mathit{DEMatch}(e^{\prime },e_1)\wedge (\mathit{loc}\left(e^{\prime }\right)=A\vee \mathit{loc}\left(e^{\prime }\right)=B)$. Since principal B follows the honesty axiom and mutual authentication protocol, $e^{\prime }$ must be a valid instance of a basic sequence. The Encrypt() action can appear in either $I_1$ or $I_2$. Assuming $e^{\prime }\in I_2$, then for Atom-type values ${\mathit{rchpk}}_2^{A^{\prime }},m_2^{\prime },s_2^{\prime }$, the following must exist on principal A: $\mathit{Encrypt}\left(e^{\prime }\right)=\langle m_2^{\prime },{\mathit{rchpk}}_2^{A^{\prime }},s_2^{\prime }\rangle$. Thus, from $\mathit{DEMatch}(e^{\prime },e_1)$, we obtain ${\mathit{rchpk}}_2^{A^{\prime }}={\mathit{rchpk}}_2^A\wedge s_2^{\prime }=s_2\wedge m_2^{\prime }=m_2$, which leads to $\mathit{Send}\left(e_1^{\prime }\right)=\langle s_2\rangle$. Hence, $e^{\prime }$ is an instance from $I_2$, and matches with $e_1$, forming a weakly matching pair $\mathit{Send}\left(e_1^{\prime }\right)=\langle s_2\rangle =\mathit{Rcv}\left(e_0\right)$. Similarly, $I_1$ can be excluded through analogous reasoning.

Next, it suffices to confirm the event order $e_1^{\prime }<e_0$. Based on axioms such as AxiomF, we can reason that if there exists a sending event s that releases a random number m between $e_1^{\prime }$ and $e_0$, then if $e_1^{\prime }\le s$, it follows that $e_1^{\prime }<e_0$; if $e_0\le s$, then there exists j such that $e_0{<}_{\mathit{loc}}\left(j\right)<e_1^{\prime }$. At this point, s must be on thread ${\mathit{th}}_2$ of principal B. According to AxiomF₁, there exists no sending event between $e_0$ and $e_1^{\prime }$, hence random number m could not have been released before $e_1^{\prime }$. From this reasoning, we conclude $e_1^{\prime }<e_6$. Therefore, $\mathit{SP}\vDash \mathit{auth}(R_3,1)$ holds.

In conclusion, based on the above proof, we arrive at the result that both the asymmetric and symmetric ratchet phases in the Signal protocol satisfy strong mutual authentication properties. This can be written as $\mathit{SP}\vDash \mathit{auth}(I_3,2)\wedge \mathit{auth}(R_3,3)$ and $\mathit{SP}\vDash \mathit{auth}(I_3,2)\wedge \mathit{auth}(R_3,1)$.

In addition, we construct a symbolic model of the Signal protocol’s ratchet mechanism using the Tamarin prover to verify the strong authentication property between the I3 and R3 stages. The verification result is consistent with our theoretical analysis based on LoET. Further details can be found in Appendix B.

3.3.4. Computational Complexity and Scalability

LoET has strong expressive power, but its current verification process requires manual reasoning steps. When applied to protocols with high state complexity or multiple participants, it may become operationally burdensome. We estimate that the verification of event sequences during each ratchet update round remains linearly tractable, assuming the number of events per round is bounded.

Time Complexity. A typical ratchet round includes one Diffie–Hellman key exchange (two events), one symmetric key derivation (one event), one encryption (one event), and one send/receive pair (two events), totaling approximately six events. Given R ratchet rounds and M messages per round, the number of causal relations to be verified is approximately $\mathcal{O}(R\times M)$. Since each verification step (based on key and message matching) is a constant-time operation, the overall time complexity is $\mathcal{O}(R\times M)$.

Space Complexity. The LoET framework must store each event along with its metadata (e.g., position, message content, associated keys). If the total number of events is $N=R\times M$, and each event occupies constant space, then the overall space complexity is $\mathcal{O}\left(N\right)$. When constructing the flow relation (i.e., the causal graph among events), the worst-case complexity may reach $\mathcal{O}(NlogN)$, depending on the branching structure of the protocol.

Scalability. The current LoET framework is mainly designed for two-party interaction modeling but can be extended to multi-party protocols (e.g., group messaging). Preliminary analysis suggests that with P participants and R rounds of group communication, the total number of events could reach $\mathcal{O}(P\times R\times M)$, and the size of the causal graph may grow to $\mathcal{O}(P^2\times R\times M)$. In such cases, identity binding and message routing ambiguity significantly increase, placing greater demands on the modeling of the Clean predicate and AxiomE rule.

These scalability constraints further underscore the importance of understanding how LoET captures core security guarantees such as forward and backward secrecy across diverse communication scenarios.

Forward secrecy is ensured by the unidirectional flow from DH to Ratchet events, making prior keys irrecoverable even if a later key is compromised. This is formally modeled in LoET by the causal dependency chain DH → Ratchet → Encrypt. The Clean predicate ensures that any decryption event is based only on fresh keys derived through legitimate DH and ratchet steps, preventing key reuse or rollback attacks. Backward secrecy is achieved through periodic DH key refresh and use of ephemeral keys. In LoET, this is captured via the New event (nonce/fresh key generation), which is causally linked to each ratchet event. Even if a previous key is compromised, it does not allow the decryption of future messages due to the causal isolation enforced by AxiomE and Rule3. Practically, this allows protocol designers to assess the temporal granularity of key update strategies and understand the trade-off between security and performance. Our model thus offers both formal guarantees and actionable design insights for protocol hardening.

4. Comparison

Frosch et al. [18] proved that the ratchet module of the TextSecure protocol is secure by analyzing the source code of TextSecure v3. However, the composite security of interactions between modules remains unverified. Cohn-Gordon et al. [19] proposed ART (asynchronous ratcheting trees) to achieve stronger security properties, constructing a game-based computational security model to analyze the protocol. Their performance evaluation showed that while ART introduces innovative ratcheting for asynchronous group messaging, it suffers from limitations in computational complexity, synchronization issues, and dynamic group support, which affect the protocol’s performance and scalability. Bellare et al. [20] demonstrated how to formalize ratchet encryption by defining syntax for ratcheted encryption and key exchange, although their model only captures unidirectional ratcheting (sender-side key updates) and does not extend to bidirectional mechanisms such as Signal’s double ratchet algorithm. Beguinet et al. [21] employed the Tamarin tool for formal modeling and verification of Signal’s ratchet protocol, where automated verification relies on explicit security assumptions. However, Tamarin faces limitations in formalizing ratchet processes and integrating them into broader verification procedures.

Compared with the prior works [19,22], this paper introduces several key innovations. In contrast to [19], which proposes the Asynchronous Ratcheting Tree (ART) model focusing on group messaging, our method focuses on formal verification of pairwise ratchet-based protocols, specifically the double ratchet mechanism used in Signal. Rather than employing game-based computational models, we construct a logical model in the Logic of Events (LoET) framework, allowing for deductive proofs of authentication properties. Compared with [22], our work is the first to extend LoET by introducing two new event classes: DH (Diffie–Hellman operations) and ratchet (state update operations). We also add new causal axioms and matching rules (e.g., AxiomE, Rule1–3), enabling modeling of dynamic key evolution. While our primary demonstration uses the Signal protocol, the extended LoET framework is designed to be protocol-agnostic. It can potentially analyze other ratcheting protocols like MLS, but current limitations include lack of automation and scalability for large protocol families.

Unlike Tamarin [21], which supports automated security analysis, it relies on complex user-defined lemmas and does not naturally express bidirectional authentication constraints or temporally structured event matching. In contrast, our approach based on LoET employs explicit causal semantics, enabling clear modeling of the evolution of keys and messages, as well as the logical binding between authentication properties and their cryptographic dependencies. To demonstrate the advantages and necessity of our model, we provide a vulnerability scenario. If AxiomE—the rule that links Diffie–Hellman (DH) and ratchet event chains—is disabled or bypassed, an attacker can inject a forged public key into the communication sequence. This breaks the causal continuity between key derivation steps. Under a false assumption, the receiver may derive an incorrect session key, which ultimately results in impersonation. In this case, the protocol loses its strong authentication guarantees. Our model can formally detect such violations through the failure of the Clean predicate. In Appendix A, we provide a simplified attack example to illustrate how the omission of a critical logical rule can directly lead to protocol failure. Meanwhile, we further compare the Tamarin and ART frameworks through a systematic evaluation. The results demonstrate that LoET offers clear advantages in terms of modeling clarity, expressiveness of authentication properties, and verification efficiency.

Compared with the above methods, LoET offers distinct advantages in verifying the security of ratchet protocols. It accurately expresses security properties using higher-order logic and supports inductive proofs to cover all possible scenarios. Based on LoET, we constructed a bidirectional authentication model that effectively captures the security features of the double ratchet encryption mechanism, ensuring protocol security and improving scalability. With its theoretical depth and formal reasoning capability, LoET serves as a powerful approach for provable security. A summary of the comparison is shown in

Table 3. Comparison of ratchet protocol analysis methods and their verification efficiency.

Reference	Research Method	Analysis of Ratchet	Verification Efficiency
This paper	LoET (Extended)	Models bidirectional authentication; introduces DH and ratchet event types, AxiomE, and Clean predicate; supports full ratchet evolution.	✓ Structured logic; supports over three strong matching events; short reasoning paths; modular logic; suitable for pre-integration with automated tools; the time complexity is $O\left(RM\right)$.
Ref. [18]	TextSecure source analysis	Only validates modules; lacks formal modeling and global security reasoning.	×   No formal reasoning structure; depends on source code details; verification cannot be generalized
Ref. [19]	ART	Supports asynchronous group ratchet; suffers from complexity, sync issues, and weak verification support.	×   Complex state transitions; cannot support systematic authentication; low verification efficiency
Ref. [20]	Syntax for ratcheted encryption	Models unidirectional ratchet; does not capture Signal’s double ratchet logic.	×   Cannot construct complete authentication chains; lacks modeling for complex causal event dependencies; limited verification
Ref. [21]	Tamarin	Automates partial proofs; lacks native support for causality or bidirectional authentication semantics.	×   Automated but requires model rewriting; lacks efficient matching for structured events; leads to long and fragmented verification;the time complexity is $O\left(2^n\right)$.
Ref. [22]	Original LoET	Early LoET use; no AxiomE/Clean support; only basic match rules used.	×   Coarse-grained modeling; fewer verification steps and weak completeness; lacks Clean and AxiomE support; incomplete reasoning paths

.

5. Conclusions

This paper proposes a formal analysis framework for ratchet protocols based on LoET, introducing dedicated axioms and rules tailored to the characteristics of ratchet protocols. It addresses the modeling limitations of traditional formal methods in capturing ratchet encryption mechanisms. Using the Signal protocol as a case study, we construct a bidirectional authentication model for ratchet encryption that precisely captures the security properties required for mutual authentication. We also complete a formal verification of Signal’s strong authentication properties, thereby extending the applicability of LoET to the analysis of ratchet protocols. This work not only provides a theoretical security guarantee for the Signal protocol at a foundational level but also establishes a reusable methodology for the formal verification of similar secure communication protocols.

Building upon the formal security guarantees established in our current model, future work will focus on bridging the gap between theoretical verification and real-world deployment, aiming to promote the practical adoption of formal protocol models in engineering contexts. To further enhance protocol security under real operational conditions, we plan to conduct in-depth research on implementation-level formal verification, including security property validation at the code level, consistency checking between implementations and formal specifications, and security evaluation within execution environments. These efforts aim to establish a complete verification chain spanning from theoretical modeling to engineering practice. Specifically, our planned directions include: (1) developing a prototype tool capable of parsing protocol communication logs and automatically generating corresponding LoET event models; (2) extending the LoET framework to support group communication and dynamic participant management, while exploring integration with the ART model for hybrid verification; (3) enhancing the framework’s ability to capture asynchronous communication scenarios, such as message loss and reordering; and (4) extracting event traces from real-world protocol logs (e.g., Wire, WhatsApp) and validating their conformance to the formal model’s causal dependencies and authentication semantics. Collectively, these efforts will further advance the applicability of the LoET framework in diverse communication protocols and provide systematic support for the verifiable design and implementation of secure protocols.