Transfer Learning Model for Crack Detection in Side SlopesBased on Crack-Net
Abstract
1. Introduction
- (1)
- We propose a frequency-domain nonlinear mapping module to better capture the characteristics of small cracks using fast Fourier transform and enhancing the amplitude and phase information;
- (2)
- A bidirectional attention module is designed to enable the model to pay more attention to the key features of the crack and better suppress irrelevant features;
- (3)
- We propose the Crack-Net model combined with the transfer learning strategy to overcome the challenge of insufficient datasets of slope cracks.
2. Related Works
2.1. Crack Detection Method
2.2. Transfer Learning Method
3. Materials and Methods
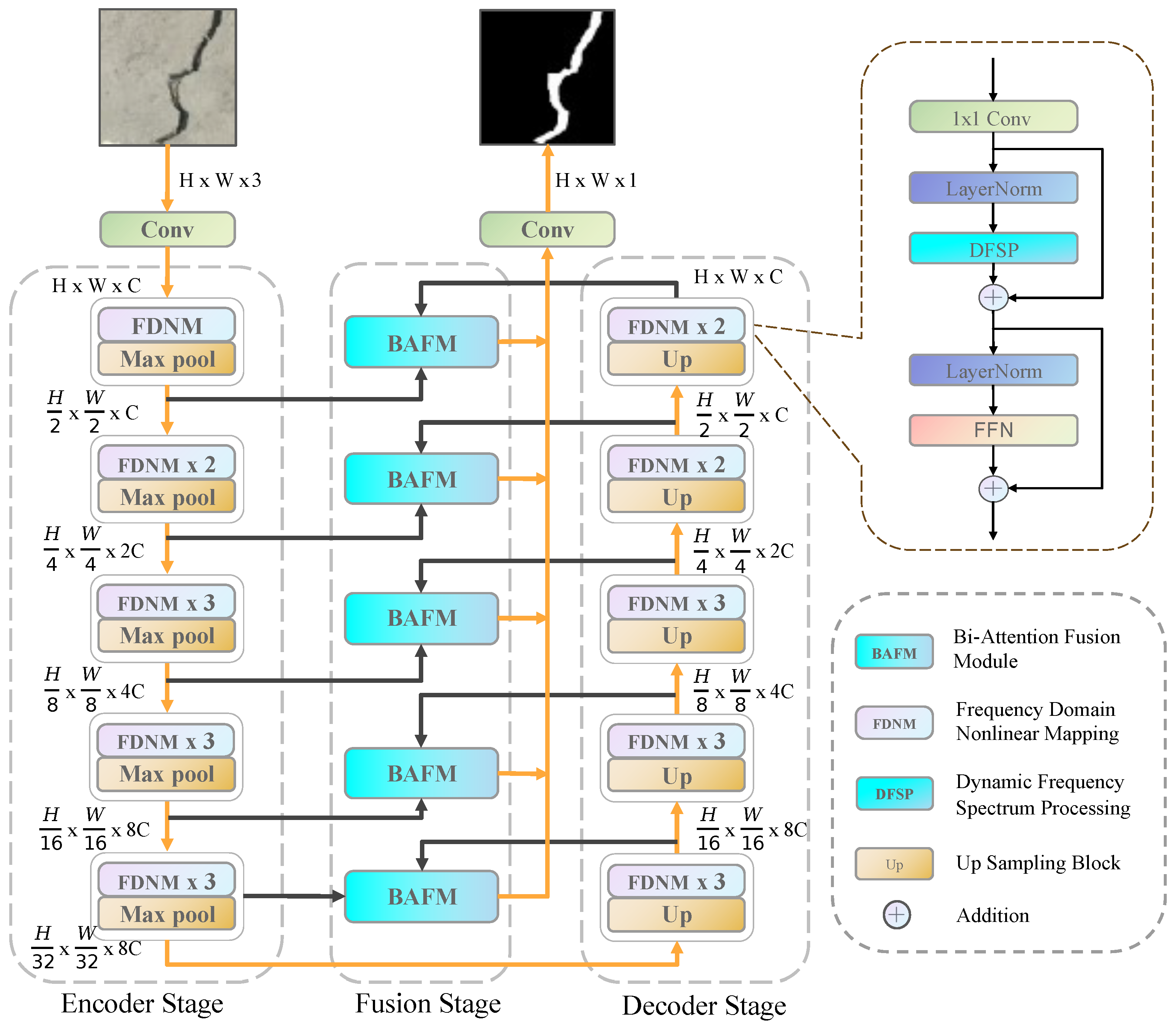
3.1. Detection Model with Crack-Net
3.1.1. Overall Structure
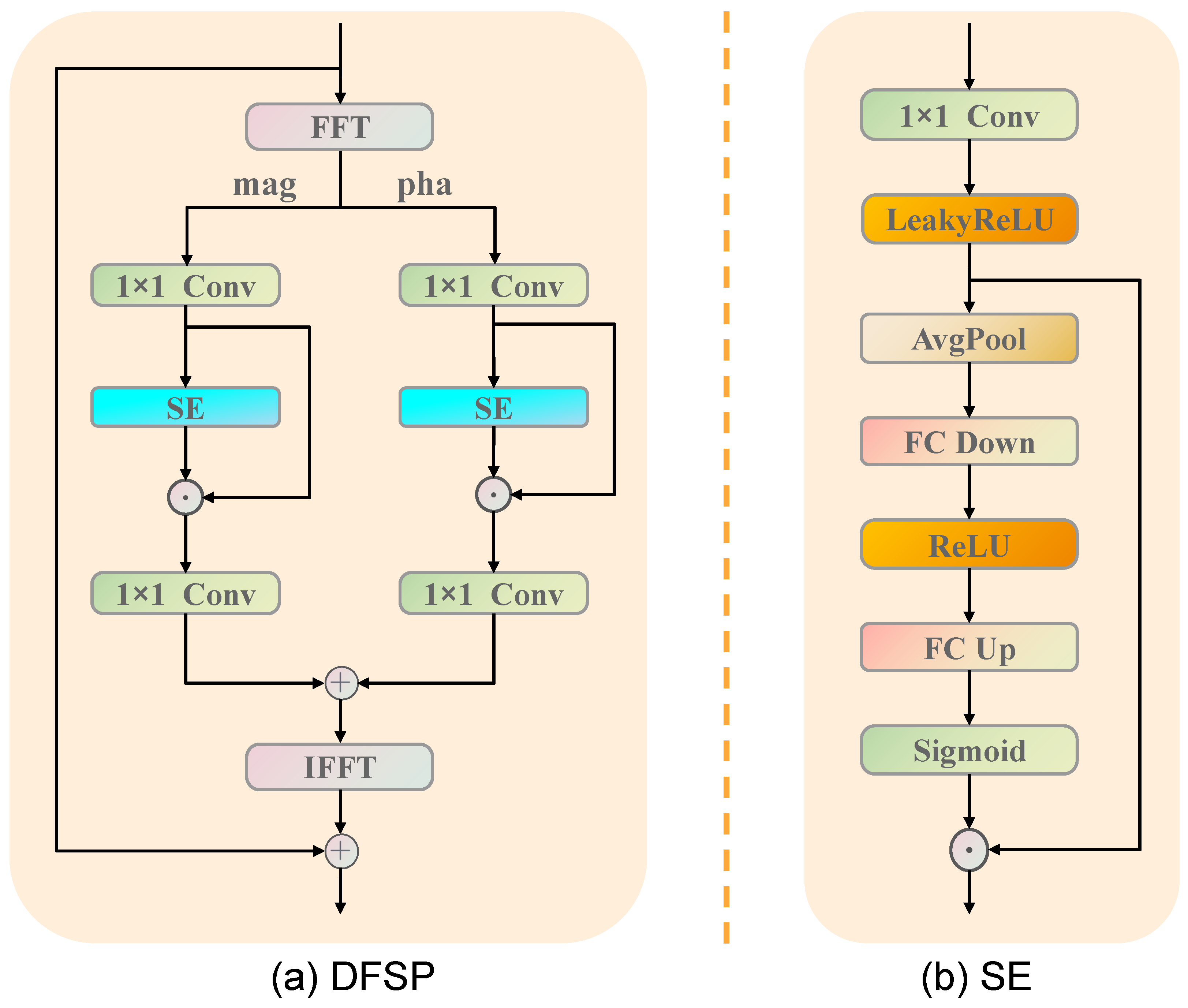
3.1.2. Frequency-Domain Nonlinear Mapping Module
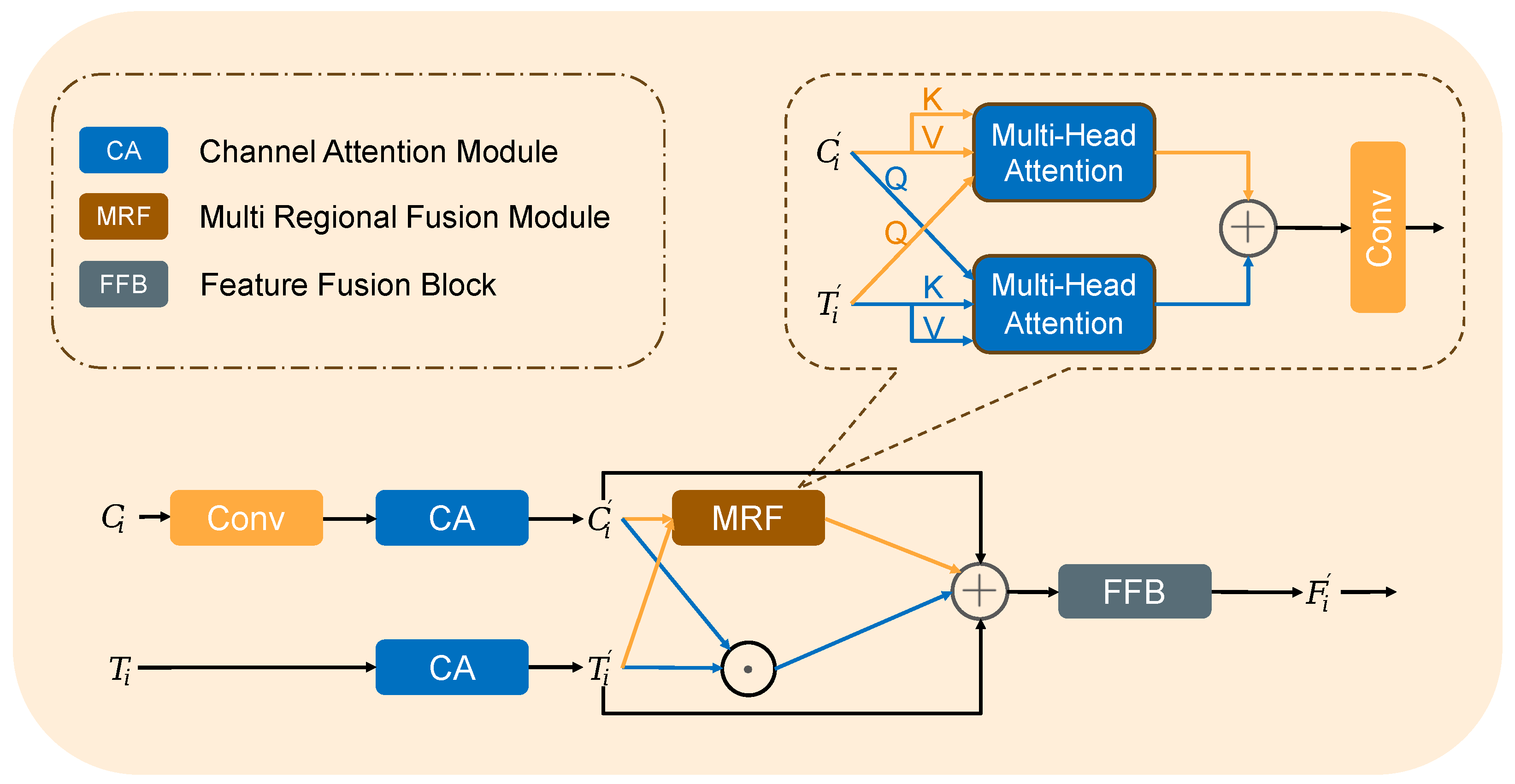
3.1.3. Bi-Attention Fusion Module
3.1.4. Loss Function
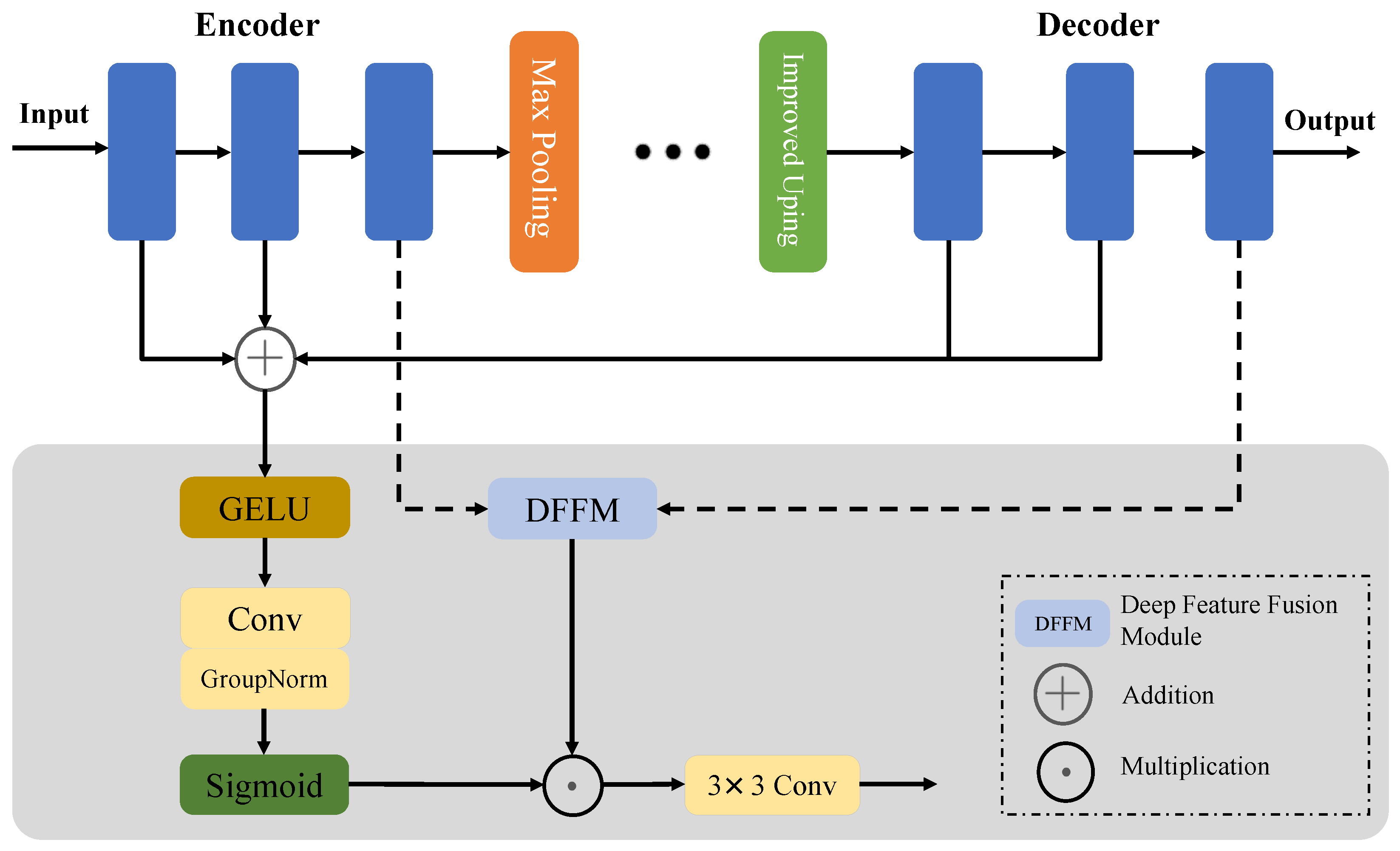
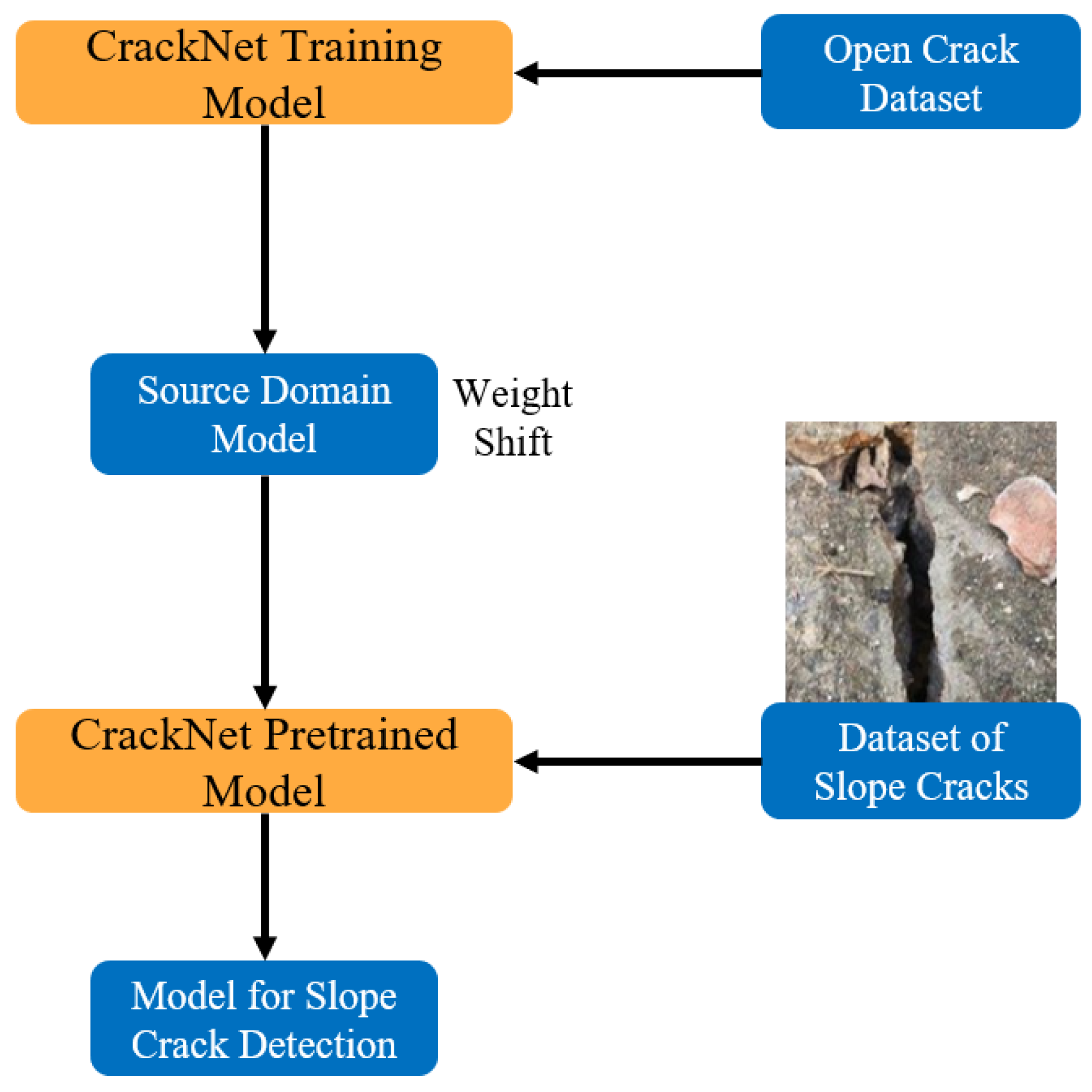
3.2. Transfer Learning Strategy
4. Experiment
4.1. Implementation Details
4.2. Experimental Settings
- (1)
- Datasets
- (2)
- Evaluation Metrics
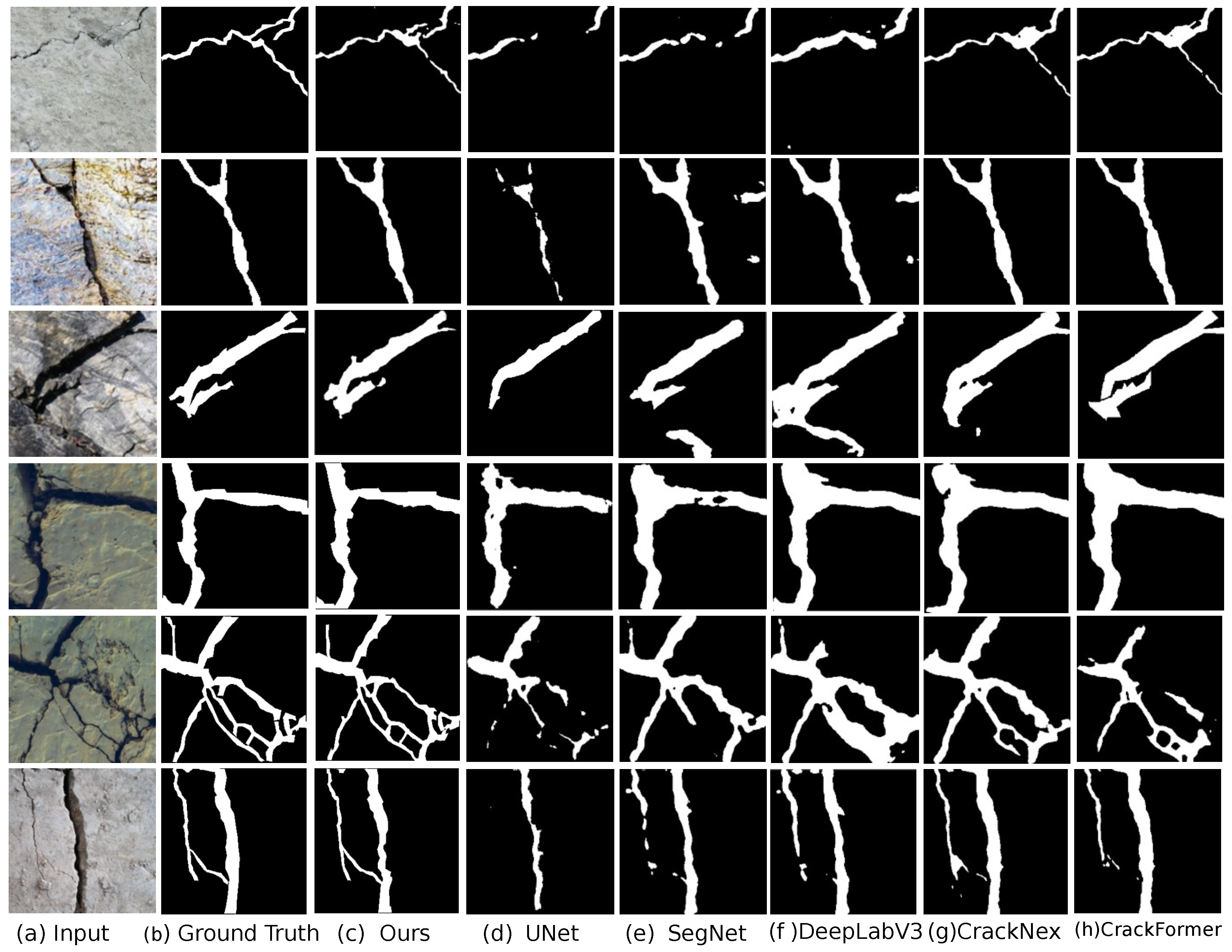
4.3. Comparative Analysis
4.4. Extreme Sample Visualization Analysis
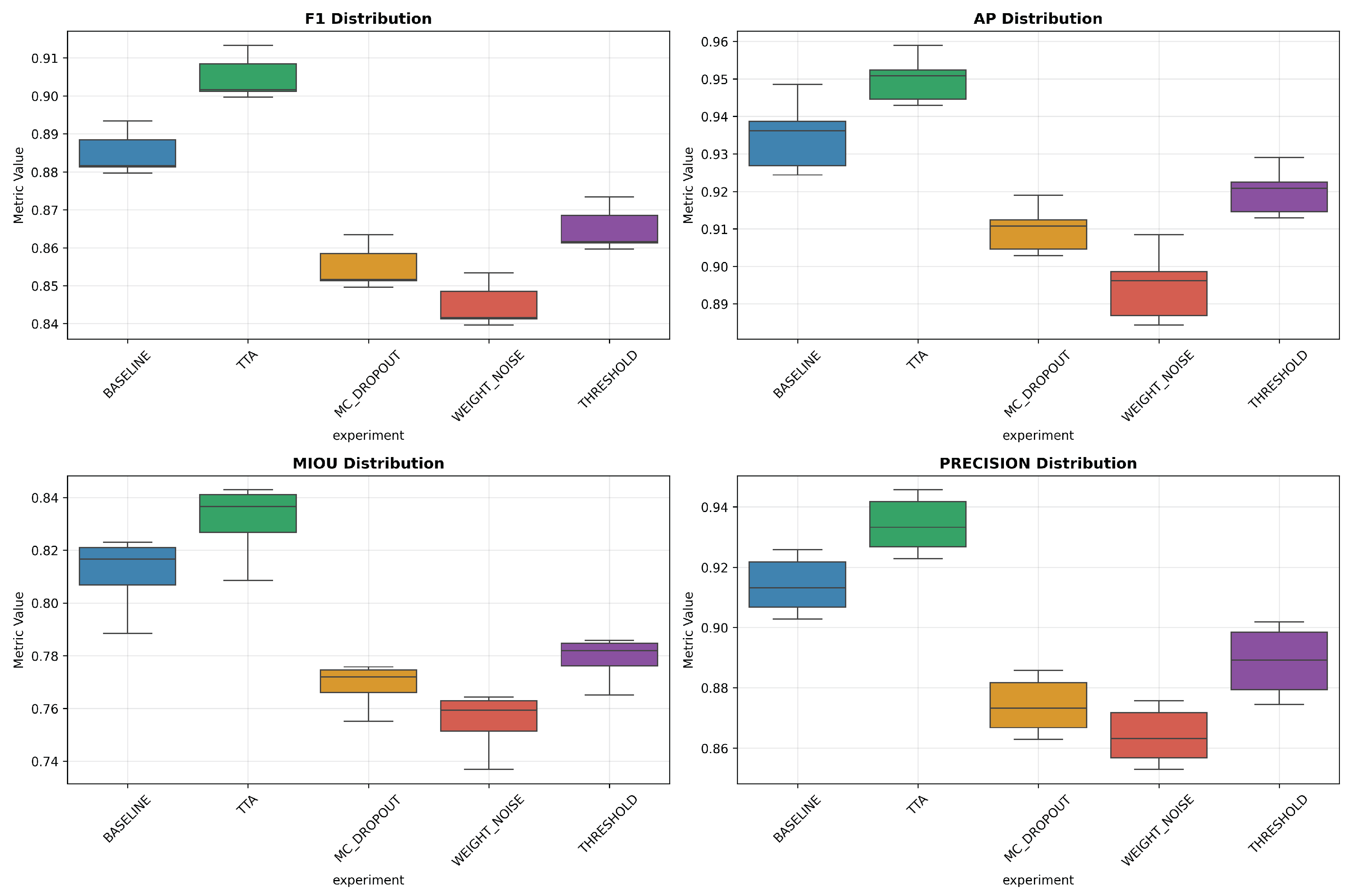
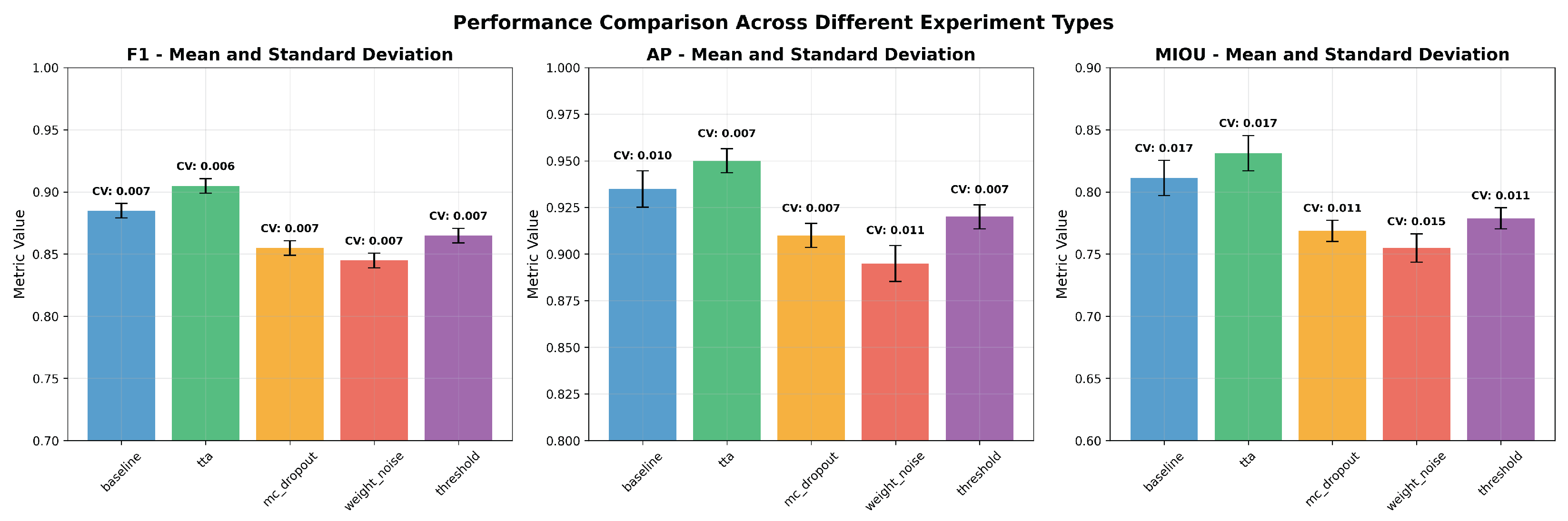
4.5. Model Stability and Reproducibility Analysis
4.6. Ablation Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Azarafza, M.; Akgün, H.; Ghazifard, A.; Asghari-Kaljahi, E.; Rahnamarad, J.; Derakhshani, R. Discontinuous rock slope stability analysis by limit equilibrium approaches—A review. Int. J. Digit. Earth 2021, 14, 1918–1941. [Google Scholar] [CrossRef]
- Zhang, R.; Tang, P.; Lan, T.; Liu, Z.; Ling, S. Resilient and sustainability analysis of flexible supporting structure of expansive soil slope. Sustainability 2022, 14, 12813. [Google Scholar] [CrossRef]
- Xiao, S.; Dai, T.; Li, S. Review and comparative analysis of factor of safety definitions in slope stability. Geotech. Geol. Eng. 2024, 42, 4263–4283. [Google Scholar] [CrossRef]
- Chen, X.; Jing, X.; Li, X.; Chen, J.; Ma, Q.; Liu, X. Slope crack propagation law and numerical simulation of expansive soil under Wetting–Drying cycles. Sustainability 2023, 15, 5655. [Google Scholar] [CrossRef]
- Gao, Q.F.; Zeng, L.; Shi, Z.N. Effects of desiccation cracks and vegetation on the shallow stability of a red clay cut slope under rainfall infiltration. Comput. Geotech. 2021, 140, 104436. [Google Scholar] [CrossRef]
- Yuan, Q.; Shi, Y.; Li, M. A review of computer vision-based crack detection methods in civil infrastructure: Progress and challenges. Remote Sens. 2024, 16, 2910. [Google Scholar] [CrossRef]
- Neyestani, A.; Ahmed, I.; Daponte, P.; De Vito, L. Concrete Crack Detection and Segmentation in Civil Infrastructures Using UAVs and Deep Learning. In Proceedings of the 2023 7th International Conference on Internet of Things and Applications (IoT), Athens, Greece, 18–20 September 2023; pp. 1–6. [Google Scholar]
- Zhuang, H.; Cheng, Y.; Zhou, M.; Yang, Z. Deep learning for surface crack detection in civil engineering: A comprehensive review. Measurement 2025, 248, 116908. [Google Scholar] [CrossRef]
- Mohammed, M.A.; Han, Z.; Li, Y. Exploring the detection accuracy of concrete cracks using various CNN models. Adv. Mater. Sci. Eng. 2021, 2021, 9923704. [Google Scholar] [CrossRef]
- Wu, Q.; Song, Z.; Chen, H.; Lu, Y.; Zhou, L. A highway pavement crack identification method based on an improved U-Net model. Appl. Sci. 2023, 13, 7227. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, N. A novel road crack detection and identification method using digital image processing techniques. In Proceedings of the 2012 7th International Conference on Computing and Convergence Technology (ICCCT), Daejeon, Republic of Korea, 29–31 October 2012; pp. 397–400. [Google Scholar]
- Cao, X.; Li, T.; Bai, J.; Wei, Z. Identification and Classification of Surface Cracks on Concrete Members Based on Image Processing. Trait. Du Signal 2020, 37, 519–525. [Google Scholar] [CrossRef]
- Safaei, N.; Smadi, O.; Masoud, A.; Safaei, B. An automatic image processing algorithm based on crack pixel density for pavement crack detection and classification. Int. J. Pavement Res. Technol. 2022, 15, 159–172. [Google Scholar] [CrossRef]
- Kheradmandi, N.; Mehranfar, V. A critical review and comparative study on image segmentation-based techniques for pavement crack detection. Constr. Build. Mater. 2022, 321, 126162. [Google Scholar] [CrossRef]
- Müller, A.; Karathanasopoulos, N.; Roth, C.C.; Mohr, D. Machine learning classifiers for surface crack detection in fracture experiments. Int. J. Mech. Sci. 2021, 209, 106698. [Google Scholar] [CrossRef]
- Loverdos, D.; Sarhosis, V. Automatic image-based brick segmentation and crack detection of masonry walls using machine learning. Autom. Constr. 2022, 140, 104389. [Google Scholar] [CrossRef]
- Aravind, N.; Nagajothi, S.; Elavenil, S. Machine learning model for predicting the crack detection and pattern recognition of geopolymer concrete beams. Constr. Build. Mater. 2021, 297, 123785. [Google Scholar] [CrossRef]
- Ahmadi, A.; Khalesi, S.; Golroo, A. An integrated machine learning model for automatic road crack detection and classification in urban areas. Int. J. Pavement Eng. 2022, 23, 3536–3552. [Google Scholar] [CrossRef]
- Jiang, X.; Mao, S.; Li, M.; Liu, H.; Zhang, H.; Fang, S.; Yuan, M.; Zhang, C. MFPA-Net: An efficient deep learning network for automatic ground fissures extraction in UAV images of the coal mining area. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103039. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, F.; Zhang, Y.D.; Zhu, Y.J. Road crack detection using deep convolutional neural network. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Atlanta, GA, USA, 25–28 September 2016; pp. 3708–3712. [Google Scholar]
- Yang, X.; Li, H.; Yu, Y.; Luo, X.; Huang, T.; Yang, X. Automatic pixel-level crack detection and measurement using fully convolutional network. Comput.-Aided Civ. Infrastruct. Eng. 2018, 33, 1090–1109. [Google Scholar] [CrossRef]
- Gao, Y.; Cao, H.; Cai, W.; Zhou, G. Pixel-level road crack detection in UAV remote sensing images based on ARD-Unet. Measurement 2023, 219, 113252. [Google Scholar] [CrossRef]
- Laxman, K.; Tabassum, N.; Ai, L.; Cole, C.; Ziehl, P. Automated crack detection and crack depth prediction for reinforced concrete structures using deep learning. Constr. Build. Mater. 2023, 370, 130709. [Google Scholar] [CrossRef]
- Ali, R.; Chuah, J.H.; Talip, M.S.A.; Mokhtar, N.; Shoaib, M.A. Structural crack detection using deep convolutional neural networks. Autom. Constr. 2022, 133, 103989. [Google Scholar] [CrossRef]
- Su, P.; Han, H.; Liu, M.; Yang, T.; Liu, S. MOD-YOLO: Rethinking the YOLO architecture at the level of feature information and applying it to crack detection. Expert Syst. Appl. 2024, 237, 121346. [Google Scholar] [CrossRef]
- Saberironaghi, A.; Ren, J. DepthCrackNet: A Deep Learning Model for Automatic Pavement Crack Detection. J. Imaging 2024, 10, 100. [Google Scholar] [CrossRef]
- Zhang, K.; Cheng, H.D.; Zhang, B. Unified approach to pavement crack and sealed crack detection using preclassification based on transfer learning. J. Comput. Civ. Eng. 2018, 32, 04018001. [Google Scholar] [CrossRef]
- Jin, X.; Bu, J.; Yu, Z.; Zhang, H.; Wang, Y. FedCrack: Federated transfer learning with unsupervised representation for crack detection. IEEE Trans. Intell. Transp. Syst. 2023, 24, 11171–11184. [Google Scholar] [CrossRef]
- Qingyi, W.; Bo, C. A novel transfer learning model for the real-time concrete crack detection. Knowl.-Based Syst. 2024, 301, 112313. [Google Scholar] [CrossRef]
- Katsigiannis, S.; Seyedzadeh, S.; Agapiou, A.; Ramzan, N. Deep learning for crack detection on masonry façades using limited data and transfer learning. J. Build. Eng. 2023, 76, 107105. [Google Scholar] [CrossRef]
- Wu, L.; Lin, X.; Chen, Z.; Lin, P.; Cheng, S. Surface crack detection based on image stitching and transfer learning with pretrained convolutional neural network. Struct. Control Health Monit. 2021, 28, e2766. [Google Scholar] [CrossRef]
- Zheng, Z.; Qi, H.; Zhuang, L.; Zhang, Z. Automated rail surface crack analytics using deep data-driven models and transfer learning. Sustain. Cities Soc. 2021, 70, 102898. [Google Scholar] [CrossRef]
- Su, C.; Wang, W. Concrete cracks detection using convolutional neuralnetwork based on transfer learning. Math. Probl. Eng. 2020, 2020, 7240129. [Google Scholar] [CrossRef]
- Vinodhini, K.A.; Sidhaarth, K.R.A. Pothole detection in bituminous road using CNN with transfer learning. Meas. Sens. 2024, 31, 100940. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Voon, Z.C.; Chaw, J.K. Crack Segmentation Using DeepLab. Ph.D. Thesis, Tunku Abdul Rahman University College, Kuala Lumpur, Malaysia, 2020. [Google Scholar]
- Li, Y.; Ma, R.; Liu, H.; Cheng, G. Real-time high-resolution neural network with semantic guidance for crack segmentation. Autom. Constr. 2023, 156, 105112. [Google Scholar] [CrossRef]
- Yao, Z.; Xu, J.; Hou, S.; Chuah, M.C. Cracknex: A few-shot low-light crack segmentation model based on retinex theory for uav inspections. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 11155–11162. [Google Scholar]
- Liu, H.; Miao, X.; Mertz, C.; Xu, C.; Kong, H. Crackformer: Transformer network for fine-grained crack detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 3783–3792. [Google Scholar]




| Method | Typical Scenario | Advantages | Limitations | Applicability to Slopes |
|---|---|---|---|---|
| Image Processing | Roads/Concrete surfaces | Simple and fast | Sensitive to lighting; background interference; poor for fine cracks | Low |
| Machine Learning | Buildings/Pavements | Learns complex features | Requires feature engineering; limited generalization | Moderate to low |
| Deep Learning | General structures | Automatic feature extraction; high accuracy | Requires large datasets; high computational cost | High potential |
| Transfer Learning | Pavements/Slopes | Efficient with small samples; strong generalization | Sensitive to domain differences; few studies on slopes | High |
| Model | P | R | AP | ODS | OIS | F1 | mIoU | Params (M) |
|---|---|---|---|---|---|---|---|---|
| U-Net | 0.681 | 0.716 | 0.762 | 0.665 | 0.684 | 0.698 | 0.761 | 31.0 |
| SegNet | 0.674 | 0.806 | 0.771 | 0.689 | 0.704 | 0.734 | 0.758 | 29.5 |
| DeepLab | 0.694 | 0.802 | 0.793 | 0.697 | 0.714 | 0.744 | 0.772 | 26.6 |
| DeepLabV3 | 0.712 | 0.810 | 0.827 | 0.715 | 0.735 | 0.758 | 0.785 | 11.38 |
| HrSegNet-B16 | 0.748 | 0.813 | 0.844 | 0.734 | 0.757 | 0.779 | 0.784 | 9.51 |
| CrackNex | 0.776 | 0.808 | 0.853 | 0.757 | 0.789 | 0.792 | 0.801 | 28.3 |
| CrackFormer | 0.780 | 0.818 | 0.869 | 0.764 | 0.797 | 0.799 | 0.843 | 25.4 |
| Ours | 0.823 | 0.844 | 0.921 | 0.817 | 0.841 | 0.833 | 0.865 | 22.3 |
| Experimental Group | P | R | AP | ODS | OIS | Convergence Epochs | Training Time (h) |
|---|---|---|---|---|---|---|---|
| No transfer learning | 0.823 | 0.844 | 0.921 | 0.817 | 0.841 | 126 | 8.7 |
| With transfer learning | 0.854 | 0.847 | 0.937 | 0.821 | 0.845 | 73 | 4.2 |
| Model | FDNM | DFFM | P | R | AP | ODS | OIS | FPS |
|---|---|---|---|---|---|---|---|---|
| Original | × | × | 0.741 | 0.819 | 0.851 | 0.731 | 0.762 | 22.9 |
| Only FDNM | ✓ | × | 0.789 | 0.835 | 0.884 | 0.779 | 0.811 | 25.5 |
| Only DFFM | × | ✓ | 0.816 | 0.821 | 0.892 | 0.774 | 0.815 | 26.7 |
| Full model | ✓ | ✓ | 0.834 | 0.846 | 0.912 | 0.808 | 0.830 | 27.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Zhang, Y.; Zhang, Q.; Zhu, S. Transfer Learning Model for Crack Detection in Side SlopesBased on Crack-Net. Appl. Sci. 2025, 15, 6951. https://doi.org/10.3390/app15136951
Li N, Zhang Y, Zhang Q, Zhu S. Transfer Learning Model for Crack Detection in Side SlopesBased on Crack-Net. Applied Sciences. 2025; 15(13):6951. https://doi.org/10.3390/app15136951
Chicago/Turabian StyleLi, Na, Yilong Zhang, Qing Zhang, and Shaoguang Zhu. 2025. "Transfer Learning Model for Crack Detection in Side SlopesBased on Crack-Net" Applied Sciences 15, no. 13: 6951. https://doi.org/10.3390/app15136951
APA StyleLi, N., Zhang, Y., Zhang, Q., & Zhu, S. (2025). Transfer Learning Model for Crack Detection in Side SlopesBased on Crack-Net. Applied Sciences, 15(13), 6951. https://doi.org/10.3390/app15136951







