Radiodosiomics Prediction of Treatment Failures Prior to Chemoradiotherapy in Head-and-Neck Squamous Cell Carcinoma
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview
2.2. Patients
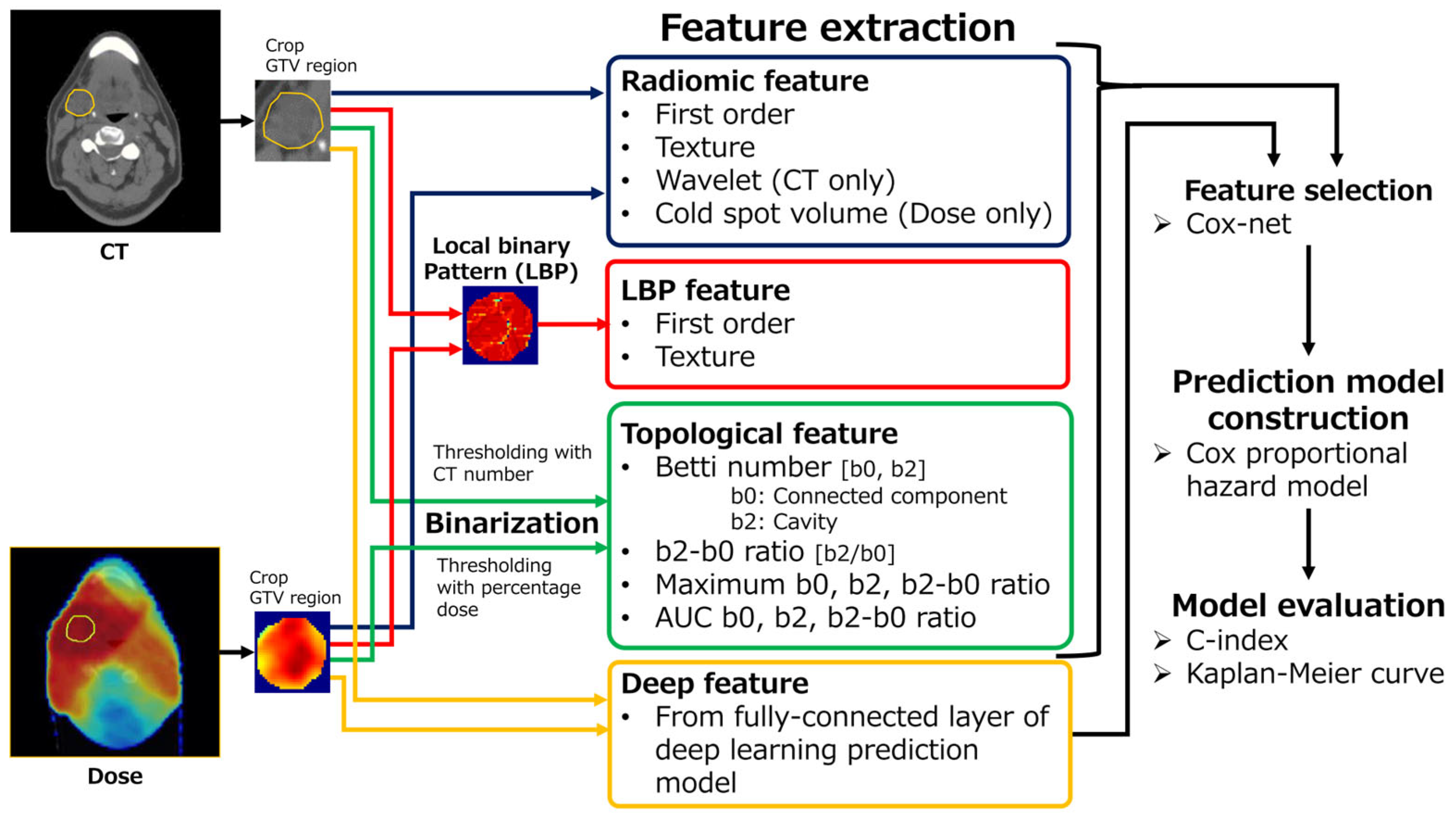
2.3. Feature Extraction
2.3.1. Radiomics (R) Feature
2.3.2. Local Binary Pattern (L) Feature
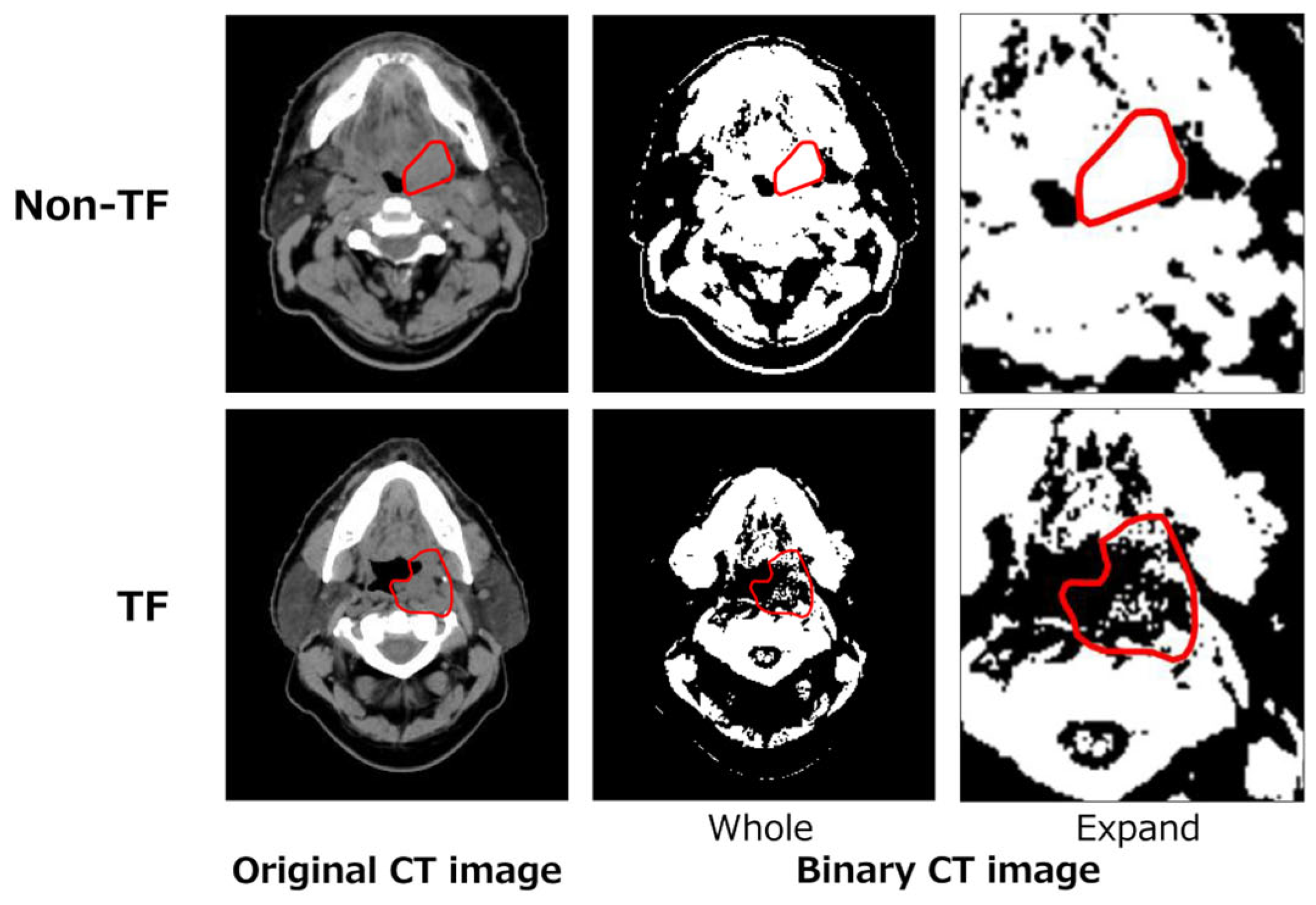
2.3.3. Topological (T) Feature
2.3.4. Deep (D) Feature
2.4. Prediction Model Construction and Performance Evaluation
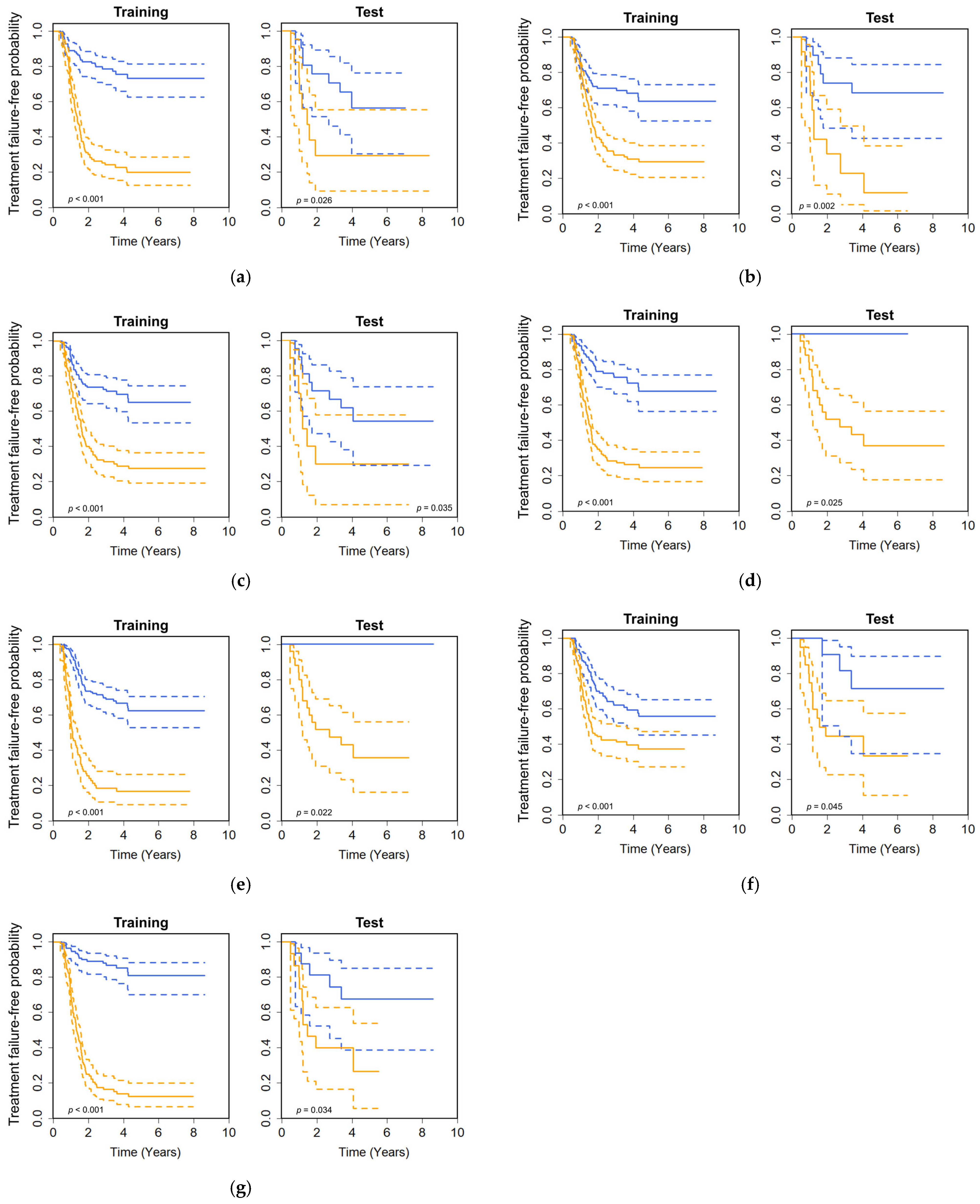
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AUBC | Area under the Betti number curve |
| AUC | Area under the receiver operator characteristic curve |
| CD | Computed tomography and dose distribution |
| C-index | Concordance index |
| CPH | Cox proportional hazard |
| CRT | Chemoradiotherapy |
| CT | Computed tomography |
| DD | Dose distributions |
| DL | Deep learning |
| DM | Distant metastasis |
| GLCM | Gray-level cooccurrence matrix |
| GLRLM | Gray-level run length matrix |
| GLSZM | Gray-level size zone matrix |
| GTV | Gross tumor volume |
| HNSCC | Head-and-neck squamous cell carcinoma |
| HU | Hounsfield unit |
| LASSO | Least absolute shrinkage and selection operator |
| LBP | Local binary pattern |
| LR | Local recurrence |
| LRR | Locoregional recurrence |
| NGTDM | Neighborhood gray-tone matrix |
| PET | Positron emission tomography |
| PS | Patch size |
| Rad-score | Radiomics score |
| ResNet | Residual network |
| RT | Radiotherapy |
| SF | Selected feature |
| SMOTE | Synthetic minority oversampling technique |
| TF | Treatment failure |
| TNM | Tumor, lymph node, metastasis |
| TRIPOD | Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis |
| WD | Wavelet decomposition |
References
- Kono, M.; Ishihara, R.; Kato, Y.; Miyake, M.; Shoji, A.; Inoue, T.; Matsueda, K.; Waki, K.; Fukuda, H.; Shimamoto, Y.; et al. Diagnosis of pharyngeal cancer on endoscopic video images by Mask region-based convolutional neural network. Dig. Endosc. 2021, 33, 569–576. [Google Scholar] [CrossRef] [PubMed]
- Petit, C.; Lacas, B.; Pignon, J.-P.; Le, Q.T.; Grégoire, V.; Grau, C.; Hackshaw, A.; Zackrisson, B.; Parmar, M.K.B.; Lee, J.-W.; et al. Chemotherapy and radiotherapy in locally advanced head and neck cancer: An individual patient data network meta-analysis. Lancet Oncol. 2021, 22, 727–736. [Google Scholar] [CrossRef] [PubMed]
- Forastiere, A.A.; Zhang, Q.; Weber, R.S.; Maor, M.H.; Goepfert, H.; Pajak, T.F.; Morrison, W.; Glisson, B.; Trotti, A.; Ridge, J.A.; et al. Long-term results of RTOG 91-11: A comparison of three nonsurgical treatment strategies to preserve the larynx in patients with locally advanced larynx cancer. J. Clin. Oncol. 2013, 31, 845–852. [Google Scholar] [CrossRef] [PubMed]
- Cooper, J.S.; Zhang, Q.; Pajak, T.F.; Forastiere, A.A.; Jacobs, J.; Saxman, S.B.; Kish, J.A.; Kim, H.E.; Cmelak, A.J.; Rotman, M.; et al. Long-term follow-up of the RTOG 9501/intergroup phase III trial: Postoperative concurrent radiation therapy and chemotherapy in high-risk squamous cell carcinoma of the head and neck. Int. J. Radiat. Oncol. Biol. Phys. 2012, 84, 1198–1205. [Google Scholar] [CrossRef]
- Bernier, J.; Domenge, C.; Ozsahin, M.; Matuszewska, K.; Lefèbvre, J.-L.; Greiner, R.H.; Giralt, J.; Maingon, P.; Rolland, F.; Bolla, M.; et al. European Organization for Research and Treatment of Cancer Trial 22931. Postoperative irradiation with or without concomitant chemotherapy for locally advanced head and neck cancer. N. Engl. J. Med. 2004, 350, 1945–1952. [Google Scholar] [CrossRef]
- Brockstein, B.; Haraf, D.J.; Rademaker, A.W.; Kies, M.S.; Stenson, K.M.; Rosen, F.; Mittal, B.B.; Pelzer, H.; Fung, B.B.; Witt, M.-E.; et al. Patterns of failure, prognostic factors and survival in locoregionally advanced head and neck cancer treated with concomitant chemoradiotherapy: A 9-year, 337-patient, multi-institutional experience. Ann. Oncol. 2004, 15, 1179–1186. [Google Scholar] [CrossRef]
- Denis, F.; Garaud, P.; Bardet, E.; Alfonsi, M.; Sire, C.; Germain, T.; Bergerot, P.; Rhein, B.; Tortochaux, J.; Calais, G. Final results of the 94-01 French Head and Neck Oncology and Radiotherapy Group randomized trial comparing radiotherapy alone with concomitant radiochemotherapy in advanced-stage oropharynx carcinoma. J. Clin. Oncol. 2004, 22, 69–76. [Google Scholar] [CrossRef]
- Keek, S.; Sanduleanu, S.; Wesseling, F.; de Roest, R.; Brekel, M.; van der Heijden, M.; Vens, C.; Giuseppina, C.; Licitra, L.; Scheckenbach, K.; et al. Computed tomography-derived radiomic signature of head and neck squamous cell carcinoma (peri)tumoral tissue for the prediction of locoregional recurrence and distant metastasis after concurrent chemo-radiotherapy. PLoS ONE 2020, 15, e0232639, Erratum in PLoS ONE 2020, 15, e0237048. [Google Scholar] [CrossRef]
- Wu, A.; Li, Y.; Qi, M.; Lu, X.; Jia, Q.; Guo, F.; Dai, Z.; Liu, Y.; Chen, C.; Zhou, L.; et al. Dosiomics improves prediction of locoregional recurrence for intensity modulated radiotherapy treated head and neck cancer cases. Oral Oncol. 2020, 104, 104625. [Google Scholar] [CrossRef]
- Kamezawa, H.; Arimura, H. Recurrence prediction with local binary pattern-based dosiomics in patients with head and neck squamous cell carcinoma. Phys. Eng. Sci. Med. 2023, 46, 99–107. [Google Scholar] [CrossRef]
- Kamezawa, H.; Arimura, H.; Yasumatsu, R.; Ninomiya, K.; Haseai, S. Preoperative and non-invasive approach for radiomic biomarker-based prediction of malignancy grades in patients with parotid gland cancer in magnetic resonance images. Med. Imaging Inf. Sci. 2020, 37, 66–74. [Google Scholar] [CrossRef]
- Ikushima, K.; Arimura, H.; Yasumatsu, R.; Kamezawa, H.; Ninomiya, K. Topology-based radiomic features for prediction of parotid gland cancer malignancy grade in magnetic resonance images. Magn. Reson. Mater. Phys. Biol. Med. 2023, 36, 767–777. [Google Scholar] [CrossRef]
- Le, Q.C.; Arimura, H.; Ninomiya, K.; Kodama, T.; Moriyama, T. Can Persistent Homology Features Capture More Intrinsic Information about Tumors from 18F-Fluorodeoxyglucose Positron Emission Tomography/Computed Tomography Images of Head and Neck Cancer Patients? Metabolites 2022, 12, 972. [Google Scholar] [CrossRef]
- Huynh, B.N.; Groendahl, A.R.; Tomic, O.; Liland, K.H.; Knudtsen, I.S.; Hoebers, F.; van Elmpt, W.; Malinen, E.; Dale, E.; Futsaether, C.M. Head and neck cancer treatment outcome prediction: A comparison between machine learning with conventional radiomics features and deep learning radiomics. Front. Med. 2023, 10, 1217037. [Google Scholar] [CrossRef]
- Mossinelli, C.; Tagliabue, M.; Ruju, F.; Cammarata, G.; Volpe, S.; Raimondi, S.; Zaffaroni, M.; Isaksson, J.L.; Garibaldi, C.; Cremonesi, M.; et al. The role of radiomics in tongue cancer: A new tool for prognosis prediction. Head Neck 2023, 45, 849–861. [Google Scholar] [CrossRef]
- Nakane, K.; Tsuchihashi, Y.; Matsuura, N. A simple mathematical model utilizing topological invariants for automatic detection of tumor areas in digital tissue images. Diagn. Pathol. 2013, 8, S27. [Google Scholar] [CrossRef]
- Nakane, K.; Takiyama, A.; Mori, S.; Matsuura, N. Homology-based method for detecting regions of interest in colonic digital images. Diagn. Pathol. 2015, 10, 36. [Google Scholar] [CrossRef]
- Pranav, P.; van de Weygaert, R.; Vegter, G.; Jones, B.J.T.; Adler, R.J.; Feldbrugge, J.; Park, C.; Buchert, T.; Kerber, M. Topology and geometry of Gaussian random fields I: On Betti numbers, Euler characteristic, and Minkowski functionals. Mon. Not. R. Astron. Soc. 2019, 485, 4167–4208. [Google Scholar] [CrossRef]
- Grossberg, A.; Elhalawani, H.; Mohamed, A.; Mulder, S.; Williams, B.; White, A.L.; Zafereo, J.; Wong, A.J.; Berends, J.E.; AboHashem, S.; et al. HNSCC [Dataset]. The Cancer Imaging Archive. 2020. Available online: https://www.cancerimagingarchive.net/collection/hnscc/ (accessed on 16 June 2025). [CrossRef]
- Grossberg, A.J.; Mohamed, A.S.R.; Elhalawani, H.; Bennett, W.C.; Smith, K.E.; Nolan, T.S.; Williams, B.; Chamchod, S.; Heukelom, J.; Kantor, M.E.; et al. Imaging and Clinical Data Archive for Head and Neck Squamous Cell Carcinoma Patients Treated with Radiotherapy. Sci. Data 2018, 5, 180173. [Google Scholar] [CrossRef]
- Elhalawani, H.; Mohamed, A.S.R.; White, A.L.; Zafereo, J.; Wong, A.J.; Berends, J.E.; AboHashem, S.; Williams, B.; Aymard, J.M.; Kanwar, A. Matched computed tomography segmentation and demographic data for oropharyngeal cancer radiomics challenges. Sci. Data 2017, 4, 170077. [Google Scholar] [CrossRef]
- Vallières, M.; Kay-Rivest, E.; Perrin, L.J.; Liem, X.; Furstoss, C.; Khaouam, N.; Nguyen-Tan, P.F.; Wang, C.S.; Sultanem, K. Head-Neck-PET-CT [Dataset]. The Cancer Imaging Archive. 2017. Available online: https://www.cancerimagingarchive.net/collection/head-neck-pet-ct/ (accessed on 16 June 2025). [CrossRef]
- Vallières, M.; Kay-Rivest, E.; Perrin, L.J.; Liem, X.; Furstoss, C.; Aerts, H.J.W.L.; Khaouam, N.; Nguyen-Tan, P.F.; Wang, C.-S.; Sultanem, K.; et al. Radiomics strategies for risk assessment of tumour failure in head-and-neck cancer. Sci. Rep. 2017, 7, 10117. [Google Scholar] [CrossRef] [PubMed]
- Clark, K.; Vendt, B.; Smith, K.; Freymann, J.; Kirby, J.; Koppel, P.; Moore, S.; Phillips, S.; Maffitt, D.; Pringle, M.; et al. The Cancer Imaging Archive (TCIA): Maintaining and Operating a Public Information Repository. J. Digit. Imaging 2013, 26, 1045–1057. [Google Scholar] [CrossRef] [PubMed]
- Moons, K.G.M.; Altman, D.G.; Reitsma, J.B.; Ioannidis, J.P.A.; Macaskill, P.; Steyerberg, E.W.; Vickers, A.J.; Ransohoff, D.F.; Collins, G.S. Transparent Reporting of a multivariable prediction model for Individual Prognosis or Diagnosis (TRIPOD): Explanation and elaboration. Ann. Intern. Med. 2015, 162, W1–W73. [Google Scholar] [CrossRef] [PubMed]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Gillison, M.L.; Trotti, A.M.; Harris, J.; Eisbruch, A.; Harari, P.M.; Adelstein, D.J.; Jordan, R.C.K.; Zhao, W.; Sturgis, E.M.; Burtness, B.; et al. Radiotherapy plus cetuximab or cisplatin in human papillomavirus-positive oropharyngeal cancer (NRG Oncology RTOG 1016): A randomised, multicentre, non-inferiority trial. Lancet 2019, 393, 40–50. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural Features for Image Classification. IEEE Trans. Syst. Man. Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Galloway, M.M. Texture classification using gray level run length. Comput. Graph. Image Process. 1975, 4, 172–179. [Google Scholar] [CrossRef]
- Thibault, G.; Fertil, B.; Navarro, C.; Pereira, F.; Cau, P.; Levy, N.; Sequeira, J.; Mari, J.L. Texture indexes and gray level size zone matrix application to cell nuclei classification. In Proceedings of the Pattern Recognition and Information Processing, Minsk, Belarus, 19–21 May 2009; pp. 140–145. [Google Scholar]
- Amadasun, M.; King, R. Textural features corresponding to textural properties. IEEE Trans. Syst. Man Cybern. 1989, 19, 1264–1274. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31, pp. 4278–4284. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Tanaka, S.; Kadoya, N.; Sugai, Y.; Umeda, M.; Ishizawa, M.; Katsuta, Y.; Ito, K.; Takeda, K.; Jingu, K. A deep learning-based radiomics approach to predict head and neck tumor regression for adaptive radiotherapy. Sci. Rep. 2022, 12, 8899. [Google Scholar] [CrossRef] [PubMed]
- Arimura, H.; Soufi, M.; Ninomiya, K.; Kamezawa, H.; Yamada, M. Potentials of radiomics for cancer diagnosis and treatment in comparison with computer-aided diagnosis. Radiol. Phys. Technol. 2018, 11, 365–374. [Google Scholar] [CrossRef] [PubMed]
- Karabacak, M.; Patil, S.; Feng, R.; Shrivastava, R.K.; Margetis, K. A large scale multi institutional study for radiomics driven machine learning for meningioma grading. Sci. Rep. 2024, 14, 26191. [Google Scholar] [CrossRef]
- Zhai, T.-T.; Langendijk, J.A.; van Dijk, L.V.; Halmos, G.B.; Witjes, M.J.; Oosting, S.F.; Noordzij, W.; Sijtsema, N.M.; Steenbakkers, R.J. The prognostic value of CT-based image-biomarkers for head and neck cancer patients treated with definitive (chemo-)radiation. Oral Oncol. 2019, 95, 178–186. [Google Scholar] [CrossRef]
- Jiang, L.; Xu, C.; Bai, Y.; Liu, A.; Gong, Y.; Wang, Y.-P.; Deng, H.-W. Autosurv: Interpretable deep learning framework for cancer survival analysis incorporating clinical and multi-omics data. npj Precis. Oncol. 2024, 8, 4. [Google Scholar] [CrossRef]
- Moon, C.; Li, Q.; Xiao, G. Using persistent homology topological features to characterize medical images: Case studies on lung and brain cancers. Ann. Appl. Stat. 2023, 17, 2192–2211. [Google Scholar] [CrossRef]
- Morgan, H.E.; Sher, D.J. Adaptive radiotherapy for head and neck cancer. Cancers Head Neck 2020, 5, 1. [Google Scholar] [CrossRef]
- Pavic, M.; Bogowicz, M.; Würms, X.; Glatz, S.; Finazzi, T.; Riesterer, O.; Roesch, J.; Rudofsky, L.; Friess, M.; Veit-Haibach, P.; et al. Influence of inter-observer delineation variability on radiomics stability in different tumor sites. Acta Oncol. 2018, 57, 1070–1074. [Google Scholar] [CrossRef]
- Bufacchi, A.; Caspiani, O.; Rambaldi, G.; Marmiroli, L.; Giovinazzo, G.; Polsoni, M. Clinical implication in the use of the AAA algorithm versus the AXB in nasopharyngeal carcinomas by comparison of TCP and NTCP values. Radiat. Oncol. 2020, 15, 150. [Google Scholar] [CrossRef]

| Training | Test | p-Value | |
|---|---|---|---|
| Total number of cases | 140 | 32 | |
| Age [y, min–max (median)] | 29–91 (62) | 49–82 (64) | 0.23 * |
| Sex | 0.28 + | ||
| Male | 111 | 24 | |
| Female | 29 | 8 | |
| Stage | 0.75 + | ||
| III | 18 | 6 | |
| IV | 122 | 26 | |
| Tumor site | 0.50 + | ||
| Nasopharynx | 5 | 2 | |
| Oropharynx | 125 | 28 | |
| Hypopharynx | 10 | 2 | |
| Tumor status after CRT | 1.00 + | ||
| Treatment failure | 28 (112 †) | 16 | |
| Complete response | 112 | 16 | |
| Treatment failure-free survival time [y, min–max (median)] | 0.39–8.64 (3.80) | 0.46–8.62 (3.08) | 0.08 * |
| Category | Data | Feature | No. of Features |
|---|---|---|---|
| R | CT | First-order features | 14 |
| Texture features (GLCM, GLRLM, GLSZM, and NGTDM) | 40 | ||
| Wavelet decomposition features | 432 | ||
| DD | First-order features | 14 | |
| Texture features (GLCM, GLRLM, GLSZM, and NGTDM) | 40 | ||
| Cold spot volume | 1 | ||
| L | CT | First-order features | 14 |
| Texture features (GLCM, GLRLM, GLSZM, and NGTDM) | 40 | ||
| DD | First-order features | 14 | |
| Texture features (GLCM, GLRLM, GLSZM, and NGTDM) | 40 | ||
| T | CT | Betti number (b0, b2, and b2/b0) | 303 |
| Area under the Betti number curve | 3 | ||
| Maximum Betti number | 3 | ||
| DD | Betti number (b0, b2, and b2/b0) | 63 | |
| Area under the Betti number curve | 3 | ||
| Maximum Betti number | 3 | ||
| Total | 1027 |
| Model | Optimal Number of Features | C-Index | Balanced C-Index | Statistically Significant Differences | ||
|---|---|---|---|---|---|---|
| Training | Test | Training | Test | |||
| CT-R | 3 | 0.726 | 0.641 | 0.684 | *** | * |
| CT-L | 3 | 0.635 | 0.745 | 0.690 | *** | ** |
| CT-T | 12 | 0.688 | 0.647 | 0.668 | *** | n.s. |
| CT-RL | 2 | 0.705 | 0.614 | 0.660 | *** | n.s. |
| CT-RT | 4 | 0.704 | 0.616 | 0.660 | *** | n.s. |
| CT-LT | 14 | 0.753 | 0.595 | 0.674 | *** | n.s. |
| CT-RLT | 5 | 0.747 | 0.597 | 0.672 | *** | n.s. |
| DD-R | 2 | 0.572 | 0.622 | 0.597 | ** | n.s. |
| DD-L | 5 | 0.670 | 0.641 | 0.656 | *** | * |
| DD-T | 9 | 0.743 | 0.760 | 0.752 | *** | * |
| DD-RL | 8 | 0.596 | 0.553 | 0.575 | ** | n.s. |
| DD-RT | 7 | 0.730 | 0.747 | 0.739 | *** | * |
| DD-LT | 21 | 0.679 | 0.756 | 0.718 | *** | * |
| DD-RLT | 18 | 0.764 | 0.619 | 0.692 | *** | n.s. |
| CD-R | 2 | 0.704 | 0.625 | 0.665 | *** | n.s. |
| CD-L | 13 | 0.694 | 0.592 | 0.643 | *** | n.s. |
| CD-T | 6 | 0.601 | 0.734 | 0.668 | ** | n.s. |
| CD-RL | 2 | 0.702 | 0.630 | 0.666 | *** | n.s. |
| CD-RT | 5 | 0.648 | 0.630 | 0.639 | *** | n.s. |
| CD-LT | 18 | 0.780 | 0.611 | 0.696 | *** | n.s. |
| CD-RLT | 22 | 0.834 | 0.644 | 0.739 | *** | * |
| DL | 17 | 0.776 | 0.710 | 0.743 | *** | n.s. |
| Model | Balanced C-Index | |
|---|---|---|
| Without Clinical Variables | With Clinical Variables | |
| CT-R | 0.684 | 0.650 |
| CT-L | 0.690 | 0.627 |
| DD-L | 0.656 | 0.521 |
| DD-T | 0.752 | 0.751 |
| DD-RT | 0.739 | 0.728 |
| DD-LT | 0.718 | 0.683 |
| CD-RLT | 0.739 | 0.541 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamezawa, H.; Arimura, H. Radiodosiomics Prediction of Treatment Failures Prior to Chemoradiotherapy in Head-and-Neck Squamous Cell Carcinoma. Appl. Sci. 2025, 15, 6941. https://doi.org/10.3390/app15126941
Kamezawa H, Arimura H. Radiodosiomics Prediction of Treatment Failures Prior to Chemoradiotherapy in Head-and-Neck Squamous Cell Carcinoma. Applied Sciences. 2025; 15(12):6941. https://doi.org/10.3390/app15126941
Chicago/Turabian StyleKamezawa, Hidemi, and Hidetaka Arimura. 2025. "Radiodosiomics Prediction of Treatment Failures Prior to Chemoradiotherapy in Head-and-Neck Squamous Cell Carcinoma" Applied Sciences 15, no. 12: 6941. https://doi.org/10.3390/app15126941
APA StyleKamezawa, H., & Arimura, H. (2025). Radiodosiomics Prediction of Treatment Failures Prior to Chemoradiotherapy in Head-and-Neck Squamous Cell Carcinoma. Applied Sciences, 15(12), 6941. https://doi.org/10.3390/app15126941







