Chemometrics-Assisted Calibration of a Handheld LIBS Device for the Quantitative Determination of Major and Minor Elements in Artifacts from the Archaeological Park of Tindari (Italy)
Abstract
1. Introduction
2. Experimental Section
2.1. Materials and Methods
2.1.1. Standard Samples
2.1.2. Archaeological Samples
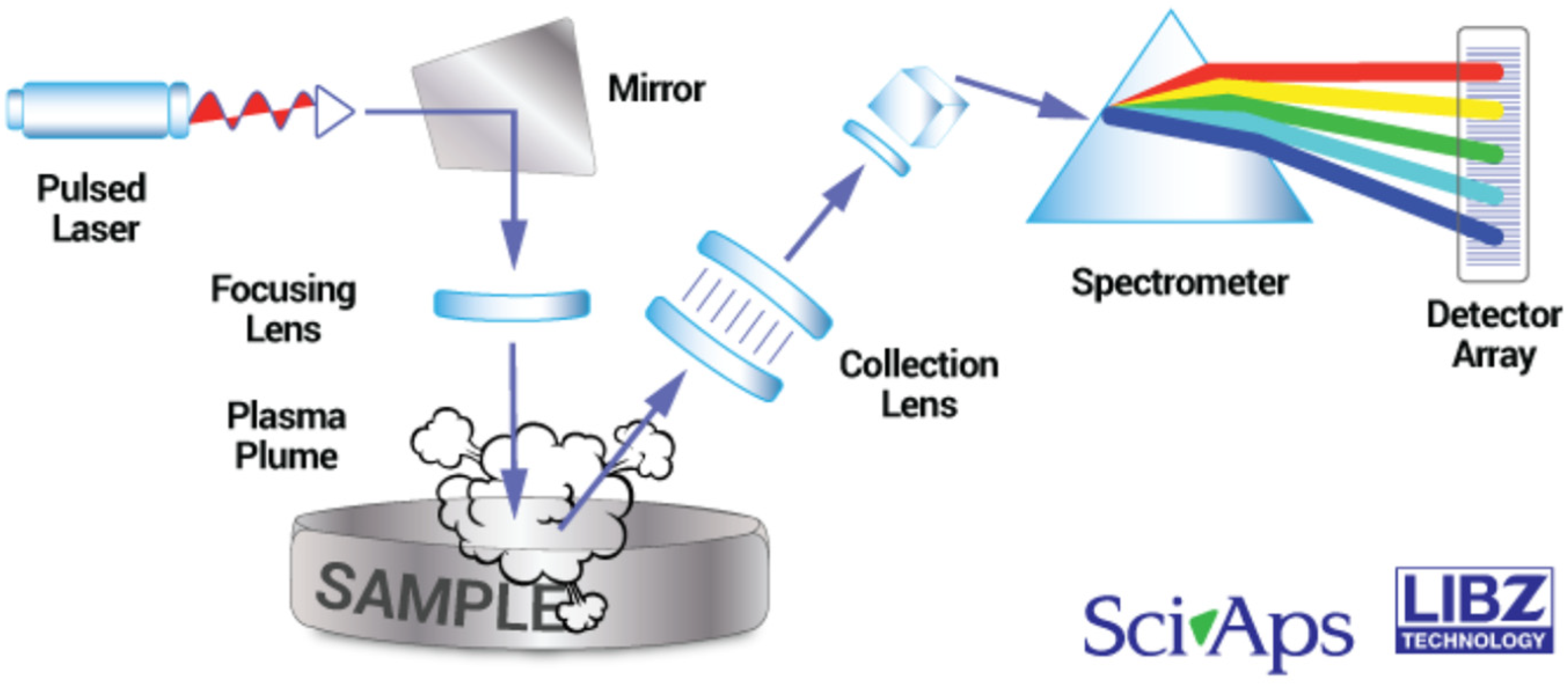
2.1.3. Data Collection with the h-LIBS Device
- X17,23401, containing 17 spectra collected from standard samples (i.e., one for each standard sample) for model calibration and validation;
- A23,23401, consisting of the 23 spectra collected from 9 archaeological samples (being some spectra collected in replicates, see Table 1) with unknown elemental concentration.
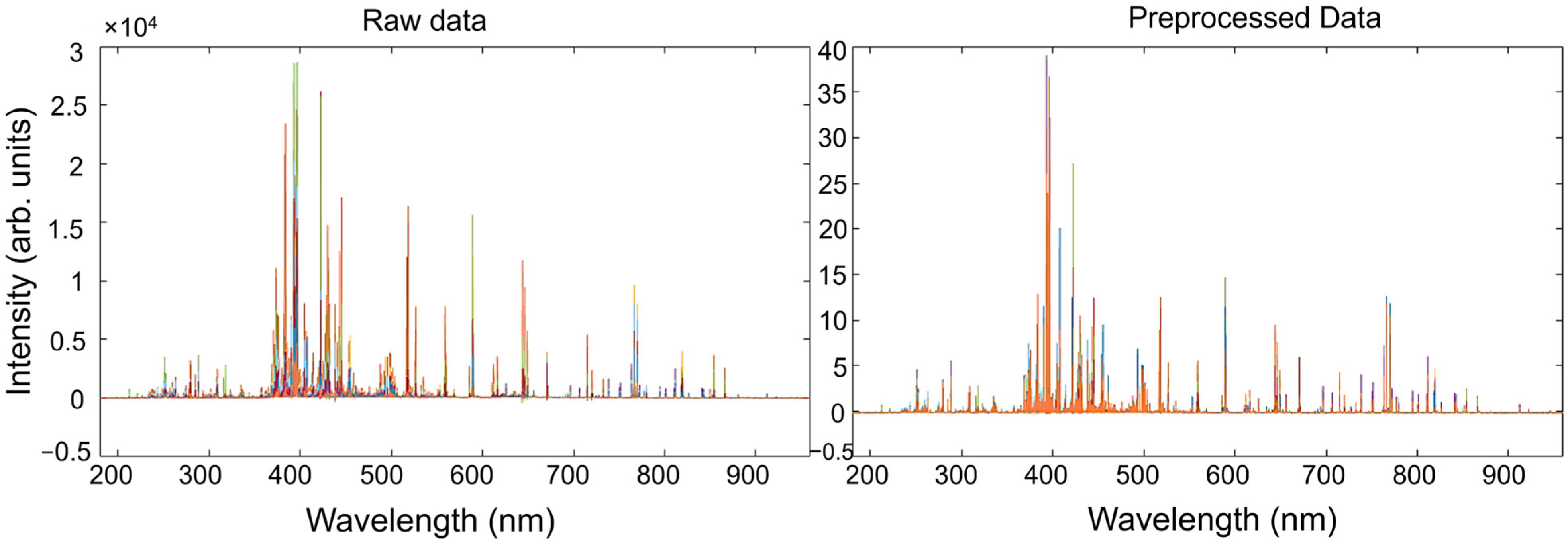
2.1.4. Data Processing
3. Results and Discussion
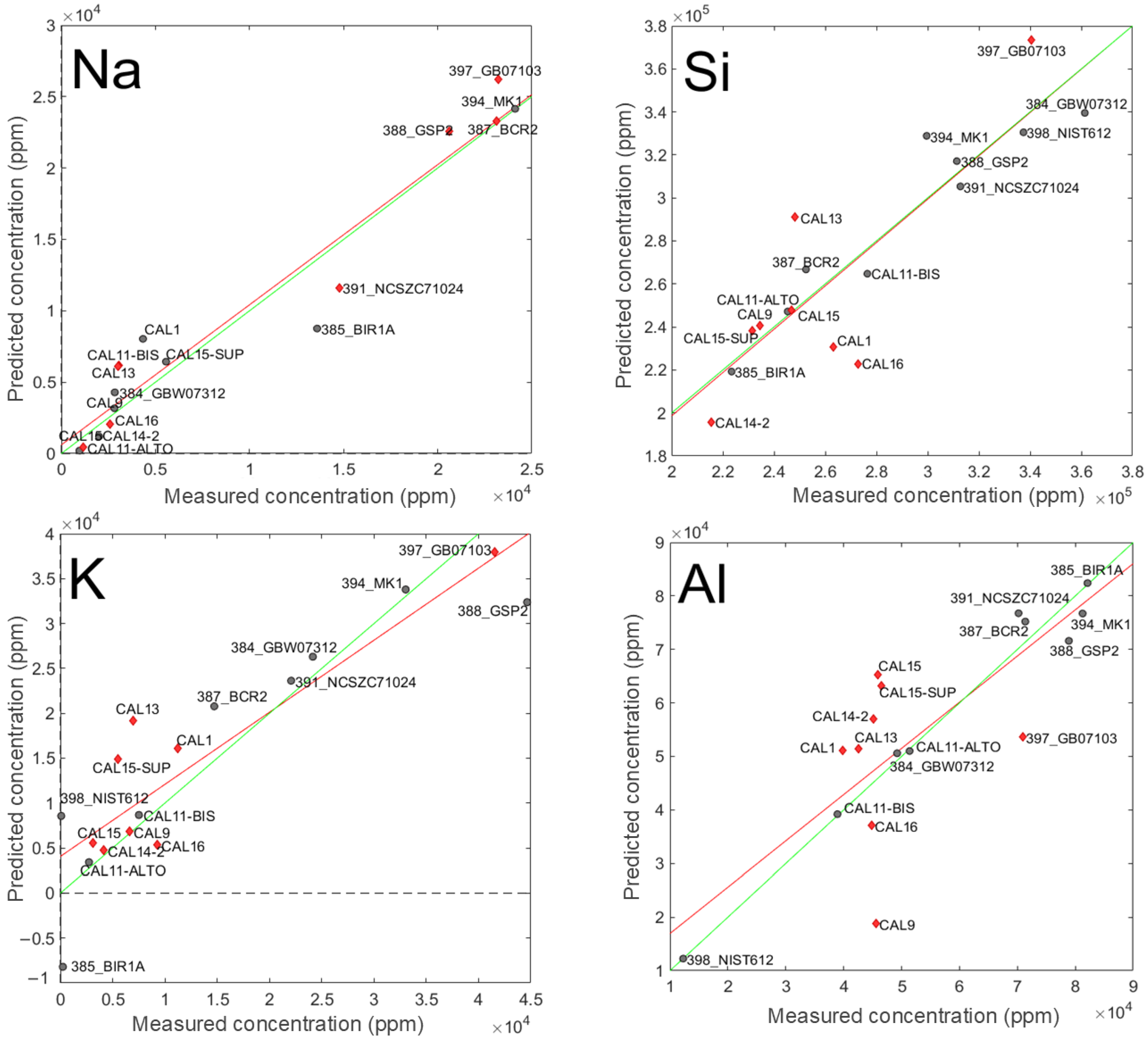
3.1. Calibration and Validation
3.2. Archaeological Samples
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rousaki, A.; Moens, L.; Vandenabeele, P. Archaeological Investigations (Archaeometry). Phys. Sci. Rev. 2018, 3, 20170048. [Google Scholar] [CrossRef]
- Artioli, G. Scientific Methods and Cultural Heritage: An Introduction to the Application of Materials Science to Archaeometry and Conservation Science; Oxford Academic: Oxford, UK, 2010. [Google Scholar]
- Mazzeo, R. Analytical Chemistry for Cultural Heritage, 1st ed.; Topics in Current Chemistry Collections (TCCC); Springer International Publishing: Cham, Switzerland, 2017; ISBN 978-3-319-52802-1. [Google Scholar]
- Pollard, A.M.; Heron, C.; Armitage, A.M. Archaeological Chemistry, 3rd ed.; The Royal Society of Chemistry: London, UK, 2016; ISBN 978-1-78262-426-4. [Google Scholar]
- Pollard, A.M.; Armitage, R.A.; Makarewicz, C.A. Handbook of Archaeological Sciences; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2023. [Google Scholar]
- Gomez-Laserna, O.; Irto, A.; Irizar, P.; Lando, G.; Bretti, C.; Martinez-Arkarazo, I.; Campagna, L.; Cardiano, P. Non-Invasive Approach to Investigate the Mineralogy and Production Technology of the Mosaic Tesserae from the Roman Domus of Villa San Pancrazio (Taormina, Italy). Crystals 2021, 11, 1423. [Google Scholar] [CrossRef]
- Cardiano, P.; Sergi, S.; De Stefano, C.; Ioppolo, S.; Piraino, P. Investigations on Ancient Mortars from the Basilian Monastery of Fragalà. J. Therm. Anal. Calorim. 2008, 91, 477–485. [Google Scholar] [CrossRef]
- Yogurtcu, B.; Cebi, N.; Koçer, A.T.; Erarslan, A. A Review of Non-Destructive Raman Spectroscopy and Chemometric Techniques in the Analysis of Cultural Heritage. Molecules 2024, 29, 5324. [Google Scholar] [CrossRef]
- Carter, S.; Clough, R.; Fisher, A.; Gibson, B.; Russell, B.; Waack, J. Atomic Spectrometry Update: Review of Advances in the Analysis of Metals, Chemicals and Materials. J. Anal. At. Spectrom. 2019, 34, 2159–2216. [Google Scholar] [CrossRef]
- Vandenabeele, P.; Donais, M.K. Mobile Spectroscopic Instrumentation in Archaeometry Research. Appl. Spectrosc. 2016, 70, 27–41. [Google Scholar] [CrossRef]
- Bardelli, F.; Barone, G.; Crupi, V.; Longo, F.; Majolino, D.; Mazzoleni, P.; Venuti, V. Combined Non-Destructive XRF and SR-XAS Study of Archaeological Artefacts. Anal. Bioanal. Chem. 2011, 399, 3147–3153. [Google Scholar] [CrossRef]
- Vandenabeele, P.; Edwards, H.G.M.; Jehlička, J. The Role of Mobile Instrumentation in Novel Applications of Raman Spectroscopy: Archaeometry, Geosciences, and Forensics. Chem. Soc. Rev. 2014, 43, 2628. [Google Scholar] [CrossRef]
- Gómez-Laserna, O.; Arrizabalaga, I.; Prieto-Taboada, N.; Olazabal, M.Á.; Arana, G.; Madariaga, J.M. In Situ DRIFT, Raman, and XRF Implementation in a Multianalytical Methodology to Diagnose the Impact Suffered by Built Heritage in Urban Atmospheres. Anal. Bioanal. Chem. 2015, 407, 5635–5647. [Google Scholar] [CrossRef]
- Venuti, V.; Fazzari, B.; Crupi, V.; Majolino, D.; Paladini, G.; Morabito, G.; Certo, G.; Lamberto, S.; Giacobbe, L. In Situ Diagnostic Analysis of the XVIII Century Madonna Della Lettera Panel Painting (Messina, Italy). Spectrochim. Acta A 2020, 228, 117822. [Google Scholar] [CrossRef]
- Spoto, S.E.; Paladini, G.; Caridi, F.; Crupi, V.; D’Amico, S.; Majolino, D.; Venuti, V. Multi-Technique Diagnostic Analysis of Plasters and Mortars from the Church of the Annunciation (Tortorici, Sicily). Materials 2022, 15, 958. [Google Scholar] [CrossRef] [PubMed]
- Jehlička, J.; Culka, A. Critical Evaluation of Portable Raman Spectrometers: From Rock Outcrops and Planetary Analogs to Cultural Heritage—A Review. Anal. Chim. Acta 2022, 1209, 339027. [Google Scholar] [CrossRef]
- Briani, F.; Caridi, F.; Ferella, F.; Gueli, A.M.; Marchegiani, F.; Nisi, S.; Paladini, G.; Pecchioni, E.; Politi, G.; Santo, A.P.; et al. Multi-Technique Characterization of Painting Drawings of the Pictorial Cycle at the San Panfilo Church in Tornimparte (AQ). Appl. Sci. 2023, 13, 6492. [Google Scholar] [CrossRef]
- Frahm, E. Protocols, Pitfalls, and Publishing for pXRF Analyses: From “Know How” to “Best Practices”. J. Archaeol. Sci. 2024, 60, 104831. [Google Scholar] [CrossRef]
- Harmon, R.S.; DeLucia, F.C.; McManus, C.E.; McMillan, N.J.; Jenkins, T.F.; Walsh, M.E.; Miziolek, A. Laser-Induced Breakdown Spectroscopy—An Emerging Chemical Sensor Technology for Real-Time Field-Portable, Geochemical, Mineralogical, and Environmental Applications. Appl. Geochem. 2006, 21, 730–747. [Google Scholar] [CrossRef]
- Giakoumaki, A.; Melessanaki, K.; Anglos, D. Laser-Induced Breakdown Spectroscopy (LIBS) in Archaeological Science—Applications and Prospects. Anal. Bioanal. Chem. 2007, 387, 749–760. [Google Scholar] [CrossRef]
- Fortes, F.J.; Laserna, J.J. The Development of Fieldable Laser-Induced Breakdown Spectrometer: No Limits on the Horizon. Spectrochim. Acta B 2010, 65, 975–990. [Google Scholar] [CrossRef]
- Botto, A.; Campanella, B.; Legnaioli, S.; Lezzerini, M.; Lorenzetti, G.; Pagnotta, S.; Poggialini, F.; Palleschi, V. Applications of Laser-Induced Breakdown Spectroscopy in Cultural Heritage and Archaeology: A Critical Review. J. Anal. At. Spectrom. 2019, 34, 81–103. [Google Scholar] [CrossRef]
- García-Escárzaga, A.; Martínez-Minchero, M.; Cobo, A.; Gutiérrez-Zugasti, I.; Arrizabalaga, A.; Roberts, P. Using Mg/Ca Ratios from the Limpet Patella Depressa Pennant, 1777 Measured by Laser-Induced Breakdown Spectroscopy (Libs) to Reconstruct Paleoclimate. Appl. Sci. 2021, 11, 2959. [Google Scholar] [CrossRef]
- Kuzmanovic, M.; Stancalie, A.; Milovanovic, D.; Staicu, A.; Damjanovic-Vasilic, L.; Rankovic, D.; Savovic, J. Analysis of Lead-Based Archaeological Pottery Glazes by Laser Induced Breakdown Spectroscopy. Opt. Laser Technol. 2021, 134, 106599. [Google Scholar] [CrossRef]
- Siozos, P.; Hausmann, N.; Holst, M.; Anglos, D. Application of Laser-Induced Breakdown Spectroscopy and Neural Networks on Archaeological Human Bones for the Discrimination of Distinct Individuals. J. Archaeol. Sci. 2021, 35, 102769. [Google Scholar] [CrossRef]
- Živković, S.; Botto, A.; Campanella, B.; Lezzerini, M.; Momčilović, M.; Pagnotta, S.; Palleschi, V.; Poggialini, F.; Legnaioli, S. Laser-Induced Breakdown Spectroscopy Elemental Mapping of the Construction Material from the Smederevo Fortress (Republic of Serbia). Spectrochim. Acta B 2021, 181, 106219. [Google Scholar] [CrossRef]
- Richiero, S.; Sandoval, C.; Oberlin, C.; Schmitt, A.; Lefevre, J.-C.; Bensalah-Ledoux, A.; Prigent, D.; Coquidé, C.; Valois, A.; Giletti, F.; et al. Archaeological Mortar Characterization Using Laser-Induced Breakdown Spectroscopy (LIBS) Imaging Microscopy. Appl. Spectrosc. 2022, 76, 978–987. [Google Scholar] [CrossRef]
- Sun, D.; Zhang, Y.; Yin, Y.; Zhang, Z.; Qian, H.; Wang, Y.; Yu, Z.; Su, B.; Dong, C.; Su, M. A Comparative Study of the Method to Rapid Identification of the Mural Pigments by Combining LIBS-Based Dataset and Machine Learning Methods. Chemosensors 2022, 10, 389. [Google Scholar] [CrossRef]
- Senesi, G.S.; Allegretta, I.; Marangoni, B.S.; Ribeiro, M.C.S.; Porfido, C.; Terzano, R.; De Pascale, O.; Eramo, G. Geochemical Identification and Classification of Cherts Using Handheld Laser Induced Breakdown Spectroscopy (LIBS) Supported by Supervised Machine Learning Algorithms. Appl. Geochem. 2023, 151, 105625. [Google Scholar] [CrossRef]
- Harmon, R.S.; Throckmorton, C.S.; Haverstock, G.; Baron, D.; Yohe, R.M.; Hark, R.R.; Knott, J.R. Connecting Obsidian Artifacts with Their Sources Using Multivariate Statistical Analysis of LIBS Spectral Signatures. Minerals 2023, 13, 1284. [Google Scholar] [CrossRef]
- Mattiello, S.; De Pascale, O.; Palleschi, V.; Fiorentino, G.; Senesi, G.S. Application of Handheld/Portable Spectroscopic Tools to the Identification, Inner Stratigraphy and Mapping of Archaeological Metal Artefacts. J. Phys. Photonics 2024, 6, 035005. [Google Scholar] [CrossRef]
- Avdeev, G.; Kukeva, R.; Yancheva, D.; Mihailov, V.; Tankova, V.; Dimitrov, M.; Nekhrizov, G.; Stoyanova, R.; Stamboliyska, B. Multi-Analytical Analysis of Decorative Color Plasters from the Thracian Tomb Near Alexandrovo, Bulgaria. Minerals 2024, 14, 374. [Google Scholar] [CrossRef]
- El-Saeid, R.H.; Abdelhamid, M.; Ali, M.F.; Abdel-Harith, M. LIBS Utilization for the Elemental Analysis of Black Resin and Gold Used by Ancient Egyptians in Embalming. J. Cult. Herit. 2024, 67, 101–110. [Google Scholar] [CrossRef]
- Cremers, D.A.; Radziemski, L.J. Handbook of Laser-Induced Breakdown Spectroscopy, 1st ed.; John Wiley & Sons Ltd: Chichester, UK, 2006. [Google Scholar]
- Analytical Methods Committee AMCTB No. 91. Laser-Induced Breakdown Spectroscopy (LIBS) in Cultural Heritage. Anal. Methods 2019, 11, 5833–5836. [Google Scholar] [CrossRef]
- Anglos, D. Chemical Analysis in Cultural Heritage; Sabbatini, L., van der Werf, I.D., Eds.; De Gruyter: Berlin, Germany, 2020; pp. 77–98. ISBN 978-3-11-045753-7. [Google Scholar]
- Detalle, V.; Bai, X. The Assets of Laser-Induced Breakdown Spectroscopy (LIBS) for the Future of Heritage Science. Spectrochim. Acta B 2022, 191, 106407. [Google Scholar] [CrossRef]
- Senesi, G.S.; Carrara, I.; Nicolodelli, G.; Milori, D.M.B.P.; De Pascale, O. Laser Cleaning and Laser-Induced Breakdown Spectroscopy Applied in Removing and Characterizing Black Crusts from Limestones of Castello Svevo, Bari, Italy: A Case Study. Microchem. J. 2016, 124, 296–305. [Google Scholar] [CrossRef]
- Kechaoglou, E.; Agrafioti, K.A.; Mastrotheodoros, G.P.; Anagnostopoulos, D.F.; Kosmidis, C. On the Study of Paintings’ Stratigraphy by Fs-LIBS and MA-XRF Techniques. J. Anal. At. Spectrom. 2024, 39, 854–867. [Google Scholar] [CrossRef]
- Donais, M.K.; Douglass, L.; Ramundt, W.H.; Bizzarri, C.; George, D.B. Handheld Laser-Induced Breakdown Spectroscopy for Field Archaeology: Characterization of Roman Wall Mortars and Etruscan Ceramics. Appl. Spectrosc. Pract. 2023, 1, 27551857231175847. [Google Scholar] [CrossRef]
- Le Guirriec, J.; Alcaina-Mateos, J.; Bousquet, B.; Le Bourdonnec, F.-X.; Sánchez De La Torre, M. Supervised Laser Induced Breakdown Spectroscopy Classification for Prehistoric Chert Provenance: A Methodological Framework. Chemom. Int. Lab. Syst. 2025, 263, 105411. [Google Scholar] [CrossRef]
- Fu, H.; Jia, J.J.; Wang, H.; Ni, Z.; Dong, F. Calibration Methods of Laser-Induced Breakdown Spectroscopy. In Calibration and Validation of Analytical Methods—A Sampling of Current Approaches; Stauffer, M.T., Ed.; IntechOpen: Rijeka, Croatia, 2018; pp. 87–98. [Google Scholar]
- Aramendia, J.; Gómez-Nubla, L.; Fdez-Ortiz De Vallejuelo, S.; Castro, K.; Arana, G.; Madariaga, J.M. The Combination of Raman Imaging and LIBS for Quantification of Original and Degradation Materials in Cultural Heritage. J. Raman Spectrosc. 2019, 50, 193–201. [Google Scholar] [CrossRef]
- Lepore, K.H.; Ytsma, C.R.; Dyar, M.D. Quantitative Prediction Accuracies Derived from Laser-Induced Breakdown Spectra Using Optimized Multivariate Submodels. Spectrochim. Acta B 2022, 191, 106408. [Google Scholar] [CrossRef]
- Anderson, R.B.; Forni, O.; Cousin, A.; Wiens, R.C.; Clegg, S.M.; Frydenvang, J.; Gabriel, T.S.J.; Ollila, A.; Schröder, S.; Beyssac, O.; et al. Post-Landing Major Element Quantification Using SuperCam Laser Induced Breakdown Spectroscopy. Spectrochim. Acta B 2022, 188, 106347. [Google Scholar] [CrossRef]
- Lepore, K.H.; Dyar, M.D.; Ytsma, C.R. Sharing Calibration Information among Laser-Induced Breakdown Spectroscopy Instruments Using Spectral Line Binning and Calibration Transfer. Spectrochim. Acta B 2024, 211, 106839. [Google Scholar] [CrossRef]
- Dyar, M.D.; Ytsma, C.R.; Lepore, K. Geochemistry by Laser-Induced Breakdown Spectroscopy on the Moon: Accuracy, Detection Limits, and Realistic Constraints on Interpretations. Earth Space Sci. 2024, 11, e2024EA003635. [Google Scholar] [CrossRef]
- Anderson, R.B.; Clegg, S.M.; Frydenvang, J.; Wiens, R.C.; McLennan, S.; Morris, R.V.; Ehlmann, B.; Dyar, M.D. Improved Accuracy in Quantitative Laser-Induced Breakdown Spectroscopy Using Sub-Models. Spectrochim. Acta B 2017, 129, 49–57. [Google Scholar] [CrossRef]
- Guirado, S.; Fortes, F.J.; Laserna, J.J. Elemental Analysis of Materials in an Underwater Archeological Shipwreck Using a Novel Remote Laser-Induced Breakdown Spectroscopy System. Talanta 2015, 137, 182–188. [Google Scholar] [CrossRef]
- Agresti, J.; Indelicato, C.; Perotti, M.; Moreschi, R.; Osticioli, I.; Cacciari, I.; Mencaglia, A.A.; Siano, S. Quantitative Compositional Analyses of Calcareous Rocks for Lime Industry Using LIBS. Molecules 2022, 27, 1813. [Google Scholar] [CrossRef]
- Li, M.; Ruan, F.; Li, R.; Zhou, J.; Zhang, T.; Tang, H.; Li, H. In Situ Simultaneous Quantitative Analysis Multi-Elements of Archaeological Ceramics via Laser-Induced Breakdown Spectroscopy Combined with Machine Learning Strategy. Microchem. J. 2022, 182, 107928. [Google Scholar] [CrossRef]
- Fabre, C.; Trebus, K.; Tarantola, A.; Cauzid, J.; Motto-Ros, V.; Voudouris, P. Advances on microLIBS and microXRF Mineralogical and Elemental Quantitative Imaging. Spectrochim. Acta B 2022, 194, 106470. [Google Scholar] [CrossRef]
- Leonidova, A.; Aseev, V.; Prokuratov, D.; Jolshin, D.; Khodasevich, M. Application of Laser-Induced Breakdown Spectroscopy for Quantitative Analysis of the Chemical Composition of Historical Lead Silicate Glasses. Quantum Beam Sci. 2023, 7, 24. [Google Scholar] [CrossRef]
- Maestro-Guijarro, L.; Sedano, M.; Schibille, N.; Pradell, T.; Castillejo, M.; Oujja, M.; Palomar, T. Determination of Boron Content in Surface Paintings from Historical Stained-Glass Windows. Chem. Methods 2025, 5, e202400057. [Google Scholar] [CrossRef]
- Lasheras, R.J.; Anzano, J.; Bello-Gálvez, C.; Escudero, M.; Cáceres, J. Quantitative Analysis of Roman Archeological Ceramics by Laser-Induced Breakdown Spectroscopy. Anal. Lett. 2017, 50, 1325–1334. [Google Scholar] [CrossRef]
- Tankova, V.; Blagoev, K.; Grozeva, M.; Malcheva, G.; Penkova, P. Qualitative and Quantitative Laser-Induced Breakdown Spectroscopy of Bronze Objects. J. Phys. Conf. Ser. 2016, 700, 012003. [Google Scholar] [CrossRef]
- Guan, C.; Wu, T.; Chen, J.; Li, M. Detection of Carbon Content from Pulverized Coal Using LIBS Coupled with DSC-PLS Method. Chemosensors 2022, 10, 490. [Google Scholar] [CrossRef]
- Nardecchia, A.; De Juan, A.; Motto-Ros, V.; Gaft, M.; Duponchel, L. Data Fusion of LIBS and PIL Hyperspectral Imaging: Understanding the Luminescence Phenomenon of a Complex Mineral Sample. Anal. Chim. Acta 2022, 1192, 339368. [Google Scholar] [CrossRef]
- Ciucci, A.; Corsi, M.; Palleschi, V.; Rastelli, S.; Salvetti, A.; Tognoni, E. New Procedure for Quantitative Elemental Analysis by Laser-Induced Plasma Spectroscopy. Appl. Spectrosc. 1999, 53, 960–964. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, D.; Wang, W.; Chen, F.; Xu, Y.; Nie, J.; Chu, Y.; Guo, L. A Review of Calibration-Free Laser-Induced Breakdown Spectroscopy. TrAC Trends Anal. Chem. 2022, 152, 116618. [Google Scholar] [CrossRef]
- John, L.M.; Issac, R.C.; Sankararaman, S.; Anoop, K.K. Multi-Element Saha Boltzmann Plot (MESBP) Coupled Calibration-Free Laser-Induced Breakdown Spectroscopy (CF-LIBS): An Efficient Approach for Quantitative Elemental Analysis. J. Anal. At. Spectrom. 2022, 37, 2451–2460. [Google Scholar] [CrossRef]
- Senesi, G.S.; Manzini, D.; De Pascale, O. Application of a Laser-Induced Breakdown Spectroscopy Handheld Instrument to the Diagnostic Analysis of Stone Monuments. Appl. Geochem. 2018, 96, 87–91. [Google Scholar] [CrossRef]
- Senesi, G.S.; Harmon, R.S.; Hark, R.R. Field-Portable and Handheld Laser-Induced Breakdown Spectroscopy: Historical Review, Current Status and Future Prospects. Spectrochim. Acta B 2021, 175, 106013. [Google Scholar] [CrossRef]
- Limbeck, A.; Brunnbauer, L.; Lohninger, H.; Pořízka, P.; Modlitbová, P.; Kaiser, J.; Janovszky, P.; Kéri, A.; Galbács, G. Methodology and Applications of Elemental Mapping by Laser Induced Breakdown Spectroscopy. Anal. Chim. Acta 2021, 1147, 72–98. [Google Scholar] [CrossRef]
- Ye, X.; Chen, Y.; Peng, L.; Yang, X.; Bai, Y. Application of Spectroscopy Technique in Cultural Heritage: Systematic Review and Bibliometric Analysis. npj Herit. Sci. 2025, 13, 169. [Google Scholar] [CrossRef]
- Bernabò Brea, L. Due Secoli Di Studi, Scavi e Restauri Del Teatro Greco Di Tindari. Riv. Dell’istituto Naz. D’archeologia E Stor. Dell’arte 1964/1965, 13–14, 99–144. [Google Scholar]
- Spigo, U. Tindari. L’area Archeologica e l’antiquarium; Regione Siciliana; Rebus edizioni: Messina, Italy, 2005. [Google Scholar]
- Leone, R.; Spigo, U. Tyndaris 1. Ricerche Nel Settore Occidentale: Campagne Di Scavo 1993–2004; Regione Siciliana: Palermo, Italy, 2008. [Google Scholar]
- Astolfi, A.; Bo, E.; Aletta, F.; Shtrepi, L. Measurements of Acoustical Parameters in the Ancient Open-Air Theatre of Tyndaris (Sicily, Italy). Appl. Sci. 2020, 10, 5680. [Google Scholar] [CrossRef]
- Panagiotonakou, M. Revisiting the Theater of Tyndaris: A New Chronology Proposal. J. Anc. Archit. 2023, 2, 9–30. [Google Scholar]
- SciAps 2019 LIBS Analyzer Models. Available online: https://www.sciaps.com/libs-handheld-laser-analyzers/z-series/ (accessed on 15 May 2025).
- Zhang, Z.-M.; Chen, S.; Liang, Y.-Z. Baseline Correction Using Adaptive Iteratively Reweighted Penalized Least Squares. Analyst 2010, 135, 1138. [Google Scholar] [CrossRef] [PubMed]
- Kennard, R.W.; Stone, L.A. Computer Aided Design of Experiments. Technometrics 1969, 11, 137–148. [Google Scholar] [CrossRef]
- Lopez, E.; Etxebarria-Elezgarai, J.; Amigo, J.M.; Seifert, A. The Importance of Choosing a Proper Validation Strategy in Predictive Models. A Tutorial with Real Examples. Anal. Chim. Acta 2023, 1275, 341532. [Google Scholar] [CrossRef]
- Chong, I.-G.; Jun, C.-H. Performance of some Variable Selection Methods When Multicollinearity is Present. Chemom. Int. Lab. Syst. 2005, 78, 103–112. [Google Scholar] [CrossRef]
- Jochum, K.P.; Nohl, U.; Herwig, K.; Lammel, E.; Stoll, B.; Hofmann, A.W. GeoReM: A New Geochemical Database for Reference Materials and Isotopic Standards. Geostand. Geoanal. Res. 2005, 29, 333–338. [Google Scholar] [CrossRef]
- Brown, R.H.; Baker, J.; Wilson, W.S. NOAA Technical Memorandum NOS ORCA 94; National Oceanic and Atmospheric Administration: Silver Springs, MD, USA, 1995; p. 480.
- Labmix24 GmbH Agricultural Soils. NCS ZC71024. Available online: https://labmix24.com/en/products/NCS%20ZC71024 (accessed on 15 March 2025).
- van der Voet, H. Comparing the Predictive Accuracy of Models Using a Simple Randomization Test. Chemom. Int. Lab. Syst. 1994, 25, 313–323. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-Regression: A Basic Tool of Chemometrics. Chemom. Int. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Silvestri, A.; Molin, G.; Salviulo, G. Archaeological Glass Alteration Products in Marine and Land-Based Environments: Morphological, Chemical and Microtextural Characterization. J. Non-Cryst. Solids 2005, 351, 1338–1349. [Google Scholar] [CrossRef]
- Palomar, T.; Oujja, M.; García-Heras, M.; Villegas, M.A.; Castillejo, M. Laser Induced Breakdown Spectroscopy for Analysis and Characterization of Degradation Pathologies of Roman Glasses. Spectrochim. Acta B 2013, 87, 114–120. [Google Scholar] [CrossRef]
- Gueli, A.M.; Pasquale, S.; Tanasi, D.; Hassam, S.; Lemasson, Q.; Moignard, B.; Pacheco, C.; Pichon, L.; Stella, G.; Politi, G. Weathering and Deterioration of Archeological Glasses from Late Roman Sicily. Int. J. Appl. Glass Sci. 2020, 11, 215–225. [Google Scholar] [CrossRef]
- Ricciardi, P.; Colomban, P.; Tournié, A.; Macchiarola, M.; Ayed, N. A Non-Invasive Study of Roman Age Mosaic Glass Tesserae by Means of Raman Spectroscopy. J. Archaeol. Sci. 2009, 36, 2551–2559. [Google Scholar] [CrossRef]
- Freestone, I.C.; Leslie, K.A.; Thirlwall, M.; Gorin-Rosen, Y. Strontium Isotopes in the Investigation of Early Glass Production: Byzantine and Early Islamic Glass from the Near East. Archaeometry 2003, 45, 19–32. [Google Scholar] [CrossRef]
- Degryse, P.; Scott, R.B.; Brems, D.T. The Archaeometry of Ancient Glassmaking: Reconstructing Ancient Technology and the Trade Ofraw Materials. Perspective 2014, 2, 224–238. [Google Scholar] [CrossRef]
- Silvestri, A. The Coloured Glass of Iulia Felix. J. Archaeol. Sci. 2008, 35, 1489–1501. [Google Scholar] [CrossRef]
- Peccerillo, A. Plio-Quaternary Volcanism in Italy Petrology, Geochemistry, Geodynamics; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]

| Sample Name | Material | Replicates |
|---|---|---|
| TY_MA_7 | Colorless glass | 1 |
| TY_MA_8 | Green glass | 1 |
| TY_MA_9 | Green glass | 3 |
| TY_MA_15 | Glass | 3 |
| TY_MA_20 | Glass | 3 |
| TY_MA_51 | Obsidian | 2 |
| TY_MA_52 | Volcanic rock | 7 |
| TY_OU_14 | Brick | 1 |
| TY_OU_15 | Brick | 1 |
| Standard Name | Type | Na | Mg | Al | Si | P | K | Ca | Ti | Mn | Fe | Be | Cu | Zn | Rb | Sr | Y | Mo | Ba | Pb | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BCR2 | CRM | 23,148 | 21,701 | 71,365 | 252,479 | 1569 | 14,720 | 50,814 | 13,567 | 1522 | 96,286 | 2 | 20 | 130 | 46 | 337 | 36 | 251 | 684 | 11 | a |
| BIR1A | CRM | 13,592 | 58,423 | 82,112 | 223,444 | 131 | 241 | 94,929 | 5743 | 1340 | 79,714 | 1 | 121 | 70 | 10 | 109 | 16 | 1 | 7 | 3 | a |
| GSP2 | CRM | 20,626 | 5789 | 78,882 | 311,391 | 1266 | 44,643 | 15,000 | 3953 | 320 | 34,263 | 2 | 43 | 120 | 245 | 240 | 28 | 2 | 2 | 42 | a |
| MK1 | CRM | 24,113 | 11,276 | 81,265 | 299,609 | 995 | 33,026 | 28,071 | 3097 | 1239 | 36,571 | 4 | 57 | 120 | 160 | 480 | 1 | 3 | 1400 | 160 | b |
| NIST612 | CRM | 97,639 | 1 | 12,282 | 337,434 | 44 | 83 | 86,357 | 39 | 77 | 140 | 35 | 34 | 34 | 32 | 10 | 37 | 37 | 36 | 1 | c |
| GBW07312 | CRM | 2839 | 2834 | 49,235 | 361,373 | 235 | 24,147 | 8286 | 1510 | 1400 | 34,123 | 8 | 1230 | 498 | 270 | 24 | 29 | 8 | 206 | 285 | d |
| GB07103 | CRM | 23,223 | 2533 | 70,941 | 340,520 | 405 | 41,572 | 11,071 | 1720 | 463 | 14,964 | 12 | 3 | 28 | 466 | 106 | 62 | 4 | 343 | 31 | e |
| NCSZC71024 | CRM | 14,765 | 7778 | 70,200 | 312,794 | 613 | 22,072 | 11,929 | 4310 | 820 | 30,907 | 2 | 63 | 100 | 99 | 196 | 23 | 14 | 783 | 182 | f |
| CAL1 | GEO | 4340 | 241 | 39,771 | 263,087 | 164 | 11,249 | 572 | 3386 | 39 | 420 | 1 | 87 | 37 | 10 | 373 | 4 | 2 | 619 | 10 | g |
| CAL9 | GEO | 2819 | 905 | 45,540 | 234,473 | 382 | 6641 | 1001 | 5196 | 39 | 17,767 | 1 | 36 | 9 | 10 | 841 | 13 | 23 | 1027 | 16 | g |
| CAL11-BIS | GEO | 3042 | 543 | 38,925 | 276,458 | 458 | 7513 | 1644 | 6299 | 39 | 2973 | 1 | 24 | 10 | 10 | 856 | 15 | 32 | 1023 | 23 | g |
| CAL11-ALTO | GEO | 964 | 9410 | 51,388 | 245,367 | 240 | 2739 | 4646 | 3704 | 287 | 21,369 | 1 | 259 | 188 | 10 | 385 | 18 | 3 | 514 | 13 | g |
| CAL13 | GEO | 3005 | 6575 | 42,629 | 248,172 | 164 | 6973 | 4145 | 3488 | 62 | 17,242 | 1 | 41 | 42 | 10 | 348 | 10 | 11 | 561 | 14 | g |
| CAL14-2 | GEO | 2003 | 7178 | 45,117 | 215,631 | 262 | 4151 | 500 | 3848 | 54 | 42,144 | 1 | 16 | 24 | 10 | 437 | 7 | 9 | 641 | 19 | g |
| CAL15 | GEO | 1150 | 11,039 | 45,910 | 246,816 | 175 | 3155 | 2859 | 4124 | 39 | 23,013 | 1 | 24 | 34 | 20 | 349 | 13 | 14 | 576 | 8 | g |
| CAL15-SUP | GEO | 5564 | 12,487 | 46,519 | 231,434 | 207 | 5479 | 2573 | 3716 | 54 | 28,714 | 1 | 27 | 24 | 10 | 364 | 9 | 15 | 562 | 16 | g |
| CAL16 | GEO | 2596 | 1086 | 44,799 | 272,905 | 229 | 9298 | 2501 | 5934 | 54 | 5421 | 1 | 65 | 28 | 30 | 608 | 11 | 11 | 1100 | 59 | g |
| m | 12,418 | 9139 | 52,421 | 272,380 | 416 | 12,284 | 16,649 | 4309 | 413 | 27,708 | 4 | 127 | 87 | 74 | 355 | 19 | 23 | 578 | 46 | ||
| s | 21,806 | 12,802 | 17,910 | 41,910 | 403 | 13,629 | 28,040 | 2639 | 532 | 24,440 | 8 | 271 | 113 | 122 | 227 | 14 | 54 | 369 | 75 | ||
| r | 97,008 | 58,423 | 69,829 | 145,742 | 1525 | 44,560 | 94,428 | 13,529 | 1483 | 96,147 | 35 | 1227 | 489 | 466 | 856 | 62 | 251 | 1399 | 285 | ||
| Min | 631 | 1 | 12,282 | 215,631 | 44 | 83 | 500 | 39 | 39 | 140 | 1 | 3 | 9 | 10 | 10 | 10 | 1 | 2 | 1 | ||
| Max | 97,639 | 58,423 | 82,112 | 361,373 | 1569 | 44,643 | 94,929 | 13,567 | 1522 | 96,286 | 35 | 1230 | 498 | 466 | 856 | 62 | 251 | 1400 | 285 |
| cal | CV | val | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
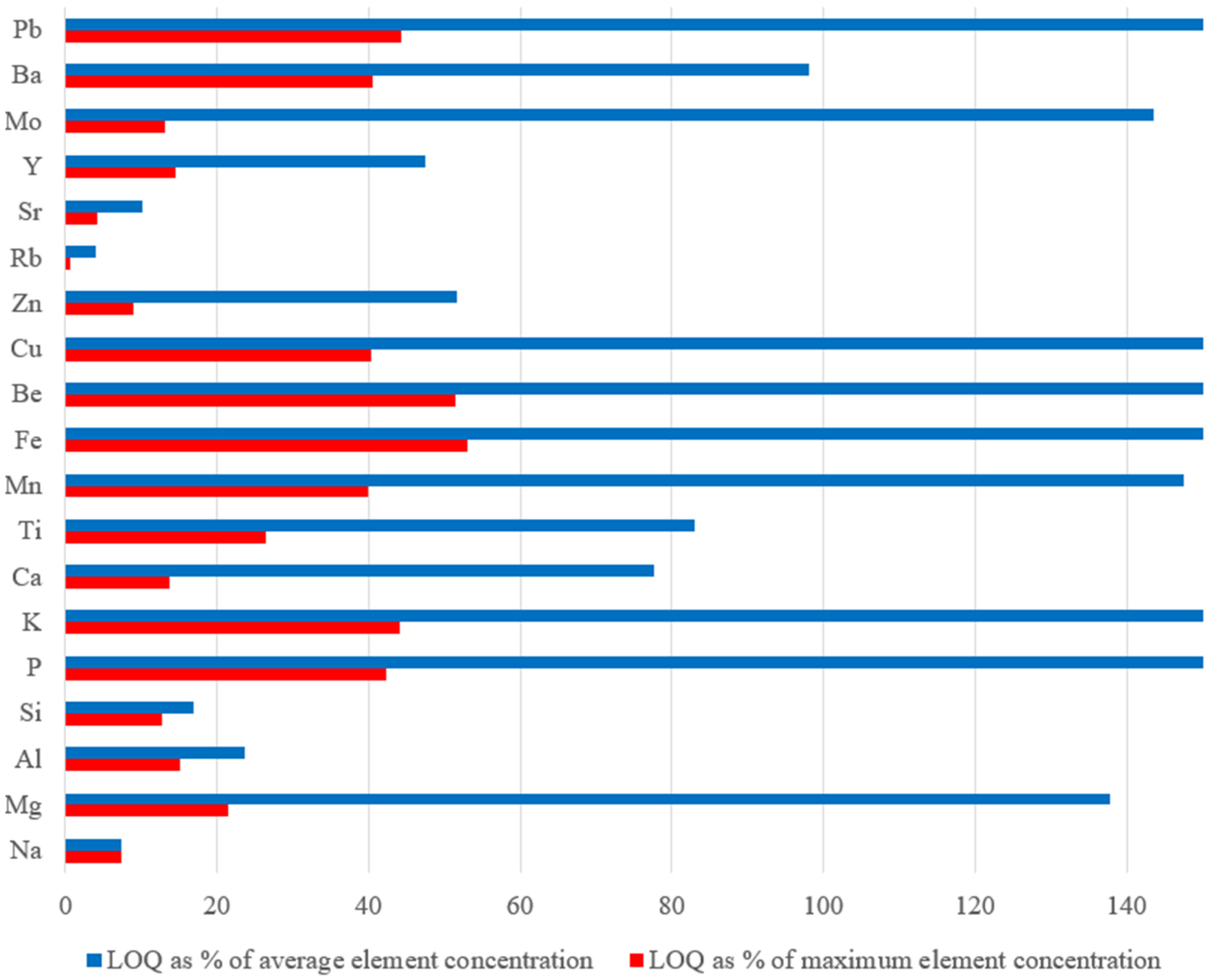
| Element | Number of Selected Variables | n. LV a | RMSEcal | Bias | R2cal | RMSECV | Bias | R2CV | RMSEval | Bias | R2val | LOD |
| Na | 196 | 2 | 2270 | 0 | 0.91 | 2630 | −24 | 0.88 | 2314 | 870 | 0.95 | 2427 |
| Mg | 87 | 5 | 3925 | −82 | 0.95 | 16,807 | −5000 | 0.25 | 6581 | −2583 | 0.90 | 4196 |
| Al | 180 | 3 | 3852 | 11 | 0.97 | 43,307 | 7771 | 0.04 | 16,112 | 2062 | 0.01 | 4118 |
| Si | 3893 | 3 | 14,261 | −110 | 0.89 | 22,349 | −2465 | 0.73 | 29,520 | −1545 | 0.69 | 15,246 |
| P | 1406 | 4 | 207 | −8 | 0.81 | 475 | −46 | 0.18 | 289 | 135 | 0.47 | 221 |
| K | 616 | 3 | 6145 | 15 | 0.83 | 13,842 | 3783 | 0.21 | 6072 | 2747 | 0.79 | 6569 |
| Ca | 106 | 3 | 4034 | −309 | 0.99 | 13,730 | −1875 | 0.84 | 3296 | −259 | 0.67 | 4313 |
| Ti b | 356 | 2 | 1115 | −10 | 0.67 | 1566 | −3 | 0.38 | 801 | 303 | 0.63 | 1192 |
| Mn | 30 | 6 | 190 | 0.1 | 0.89 | 871 | −206 | 0.01 | 307 | 199 | 0.02 | 203 |
| Fe | 622 | 3 | 15,902 | −182 | 0.72 | 46,406 | −10,000 | 0.20 | 14,742 | 8350 | 0.73 | 17,000 |
| Be | 21,584 | 2 | 6 | 0 | 0.67 | 13 | −2 | 0.07 | 7 | −7 | 0.63 | 6 |
| Cu | 266 | 3 | 154 | −4 | 0.53 | 423 | −87 | 0.05 | 465 | 300 | 0.63 | 165 |
| Zn | 3739 | 6 | 14 | 0 | 0.99 | 116 | −11 | 0.32 | 306 | 256 | 0.18 | 15 |
| Rb | 445 | 5 | 1.4 | 0 | 0.99 | 32 | 2 | 0.90 | 68 | −9 | 0.96 | 1 |
| Sr | 12,871 | 6 | 11 | 0 | 0.99 | 200 | −0.37 | 0.39 | 134 | 19 | 0.60 | 12 |
| Y c | 22 | 4 | 2.4 | 0 | 0.95 | 7 | −1 | 0.62 | 8.9 | 3.9 | 0.43 | 3 |
| Mo | 3893 | 6 | 10 | 0 | 0.98 | 90 | −27 | 0.01 | 110 | −51 | 0.05 | 11 |
| Ba | 21 | 4 | 177 | 8 | 0.86 | 246 | −21 | 0.75 | 503 | −287 | 0.01 | 189 |
| Pb | 328 | 5 | 39 | 0 | 0.84 | 125 | −7 | 0.05 | 106 | 51 | 0.02 | 42 |
| Whittaker + SNV | airPLS + SNV | |||||||
|---|---|---|---|---|---|---|---|---|
| Element | RMSEcal | R2cal | RMSEval | R2val | RMSEcal | R2cal | RMSEval | R2val |
| Na | 2270 | 0.91 | 2314 | 0.95 | 2301 | 0.90 | 2554 | 0.94 |
| Si | 14,261 | 0.89 | 29,520 | 0.69 | 17,087 | 0.84 | 26,189 | 0.85 |
| Al | 3852 | 0.97 | 16,112 | 0.01 | 3700 | 0.97 | 16,329 | 0.19 |
| K | 6145 | 0.83 | 6072 | 0.79 | 3942 | 0.93 | 8616 | 0.69 |
| Element | This Work | Dyar et al. [47] |
|---|---|---|
| Si | 1.5% | 1.7% |
| Ti | 0.2% | 0.2% |
| Al | 1.2% | 0.9% |
| Fe | 2.5% | 1.2% |
| Mg | 1.2% | 0.7% |
| Ca | 1.0% | 0.7% |
| Na | 0.5% | 0.4% |
| K | 0.5% | 0.6% |
| P | 300 ppm | 350 ppm |
| Ba | 450 ppm | 232 ppm |
| Be | 9 ppm | 0.7 ppm |
| Cu | 400 ppm | 26 ppm |
| Mn | 400 ppm | 282 ppm |
| Mo | 20 ppm | 0.8 ppm |
| Pb | 65 ppm | 7 ppm |
| Rb | 50 ppm | 52 ppm |
| Sr | 120 ppm | 85 ppm |
| Y | 25 ppm | 10 ppm |
| Zn | 150 ppm | 26 ppm |
| Element | TY_MA_7 | TY_MA_8 | TY_MA_9 | TY_MA_15 | TY_MA_20 | TY_MA_51 | TY_MA_52 | TY_OU_14 | TY_OU_15 |
|---|---|---|---|---|---|---|---|---|---|
| Na (%) | 2.0 | 2.3 | 2.3 | 2.2 | 2.7 | 1.0 | 1.5 | 1.1 | 0.9 |
| Mg (%) | <LOQ | <LOQ | <LOQ | <LOQ | 1.3 | <LOQ | 3.6 | 4.8 | 6.3 |
| Al (%) | 7.6 | 7.5 | 6.9 | 6.5 | 3.4 | 3.6 | 8.8 | 5.9 | 5.5 |
| Si (%) | 29.4 | 29.5 | 29.7 | 29.8 | 30.5 | 30.6 | 26.2 | 29.1 | 30.1 |
| K (%) | <LOQ | <LOQ | <LOQ | 0.5 | 0.8 | 1.7 | 1.1 | <LOQ | <LOQ |
| Ca (%) | 10.0 | 10.4 | 9.8 | 10.1 | 8.9 | 2.4 | 9.8 | 10.3 | 10.8 |
| Ti (%) | <LOQ | <LOQ | <LOQ | <LOQ | <LOQ | <LOQ | <LOQ | <LOQ | 0.3 |
| Mn (%) | 0.06 | 0.11 | <LOQ | <LOQ | 0.09 | <LOQ | 0.11 | 0.17 | 0.47 |
| Fe (%) | <LOQ | <LOQ | <LOQ | 5.8 | 9.8 | <LOQ | 6.6 | 8.3 | 11.5 |
| P (ppm) | <LOQ | <LOQ | <LOQ | <LOQ | <LOQ | <LOQ | <LOQ | <LOQ | <LOQ |
| Be (ppm) | <LOQ | <LOQ | <LOQ | 10 | 13 | 19 | 11 | 25 | 29 |
| Cu (ppm) | <LOQ | 464 | 545 | <LOQ | <LOQ | <LOQ | <LOQ | <LOQ | <LOQ |
| Zn (ppm) | <LOQ | <LOQ | <LOQ | <LOQ | <LOQ | 153 | <LOQ | <LOQ | <LOQ |
| Rb (ppm) | <LOQ | <LOQ | <LOQ | <LOQ | <LOQ | 77 | <LOQ | <LOQ | <LOQ |
| Sr (ppm) | 634 | 610 | 609 | 627 | 708 | 181 | 639 | 724 | 635 |
| Y (ppm) | <LOQ | <LOQ | 31 | <LOQ | <LOQ | <LOQ | <LOQ | <LOQ | <LOQ |
| Mo (ppm) | 46 | 34 | 63 | 54 | 60 | <LOQ | 43 | 22 | <LOQ |
| Ba (ppm) | 539 | <LOQ | <LOQ | 527 | 1622 | 589 | 547 | 513 | 646 |
| Pb (ppm) | <LOQ | <LOQ | <LOQ | 73 | 104 | 98 | <LOQ | <LOQ | <LOQ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lando, G.; Caridi, F.; Majolino, D.; Paladini, G.; Sabatino, G.; Venuti, V.; Cardiano, P. Chemometrics-Assisted Calibration of a Handheld LIBS Device for the Quantitative Determination of Major and Minor Elements in Artifacts from the Archaeological Park of Tindari (Italy). Appl. Sci. 2025, 15, 6929. https://doi.org/10.3390/app15126929
Lando G, Caridi F, Majolino D, Paladini G, Sabatino G, Venuti V, Cardiano P. Chemometrics-Assisted Calibration of a Handheld LIBS Device for the Quantitative Determination of Major and Minor Elements in Artifacts from the Archaeological Park of Tindari (Italy). Applied Sciences. 2025; 15(12):6929. https://doi.org/10.3390/app15126929
Chicago/Turabian StyleLando, Gabriele, Francesco Caridi, Domenico Majolino, Giuseppe Paladini, Giuseppe Sabatino, Valentina Venuti, and Paola Cardiano. 2025. "Chemometrics-Assisted Calibration of a Handheld LIBS Device for the Quantitative Determination of Major and Minor Elements in Artifacts from the Archaeological Park of Tindari (Italy)" Applied Sciences 15, no. 12: 6929. https://doi.org/10.3390/app15126929
APA StyleLando, G., Caridi, F., Majolino, D., Paladini, G., Sabatino, G., Venuti, V., & Cardiano, P. (2025). Chemometrics-Assisted Calibration of a Handheld LIBS Device for the Quantitative Determination of Major and Minor Elements in Artifacts from the Archaeological Park of Tindari (Italy). Applied Sciences, 15(12), 6929. https://doi.org/10.3390/app15126929











