Numerical Simulation and Experimental Validation of Masonry Walls Strengthened with Stiff-Type Polyurea Under Seismic Loads
Abstract
1. Introduction
2. Experimental Evaluation
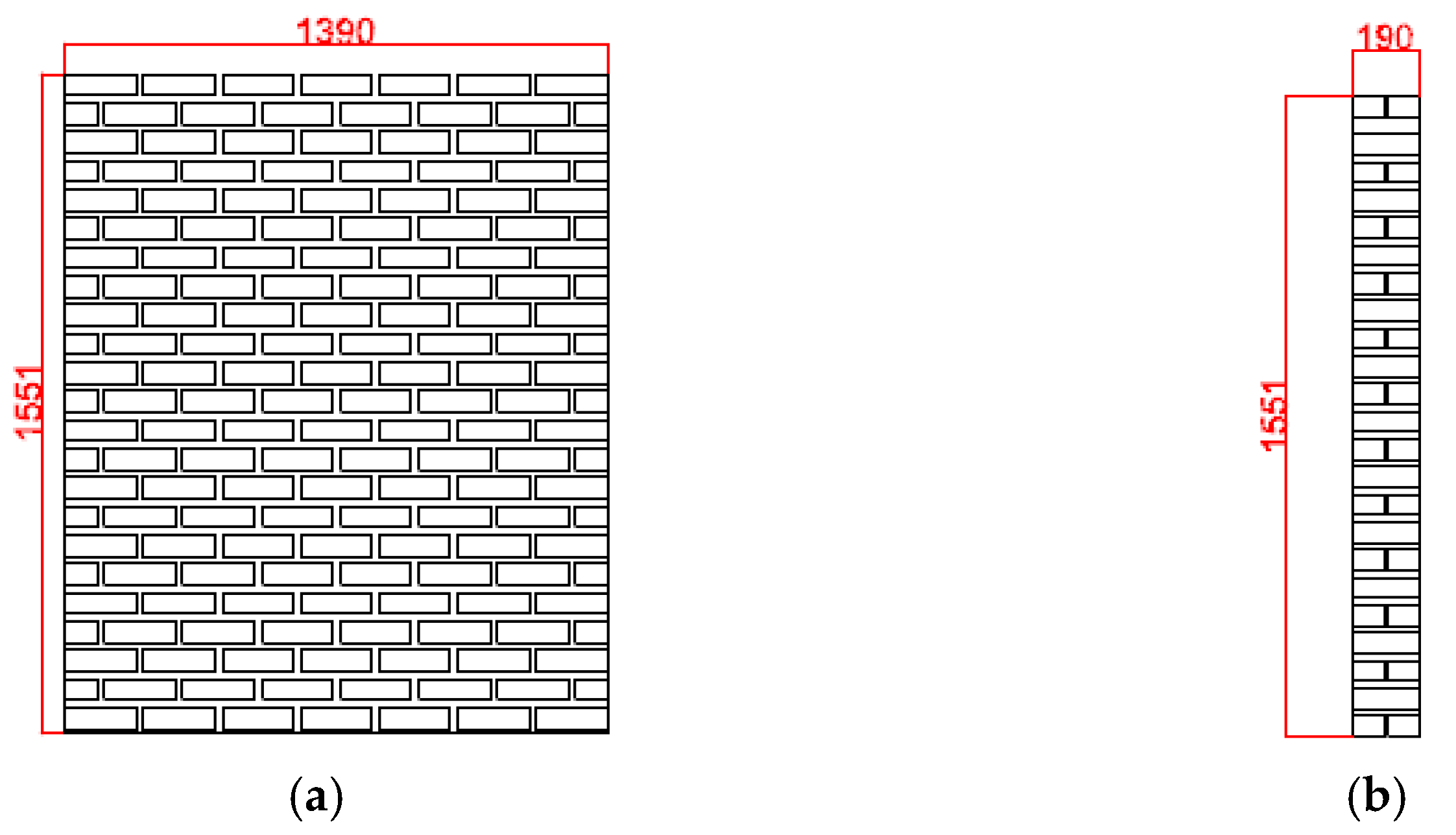
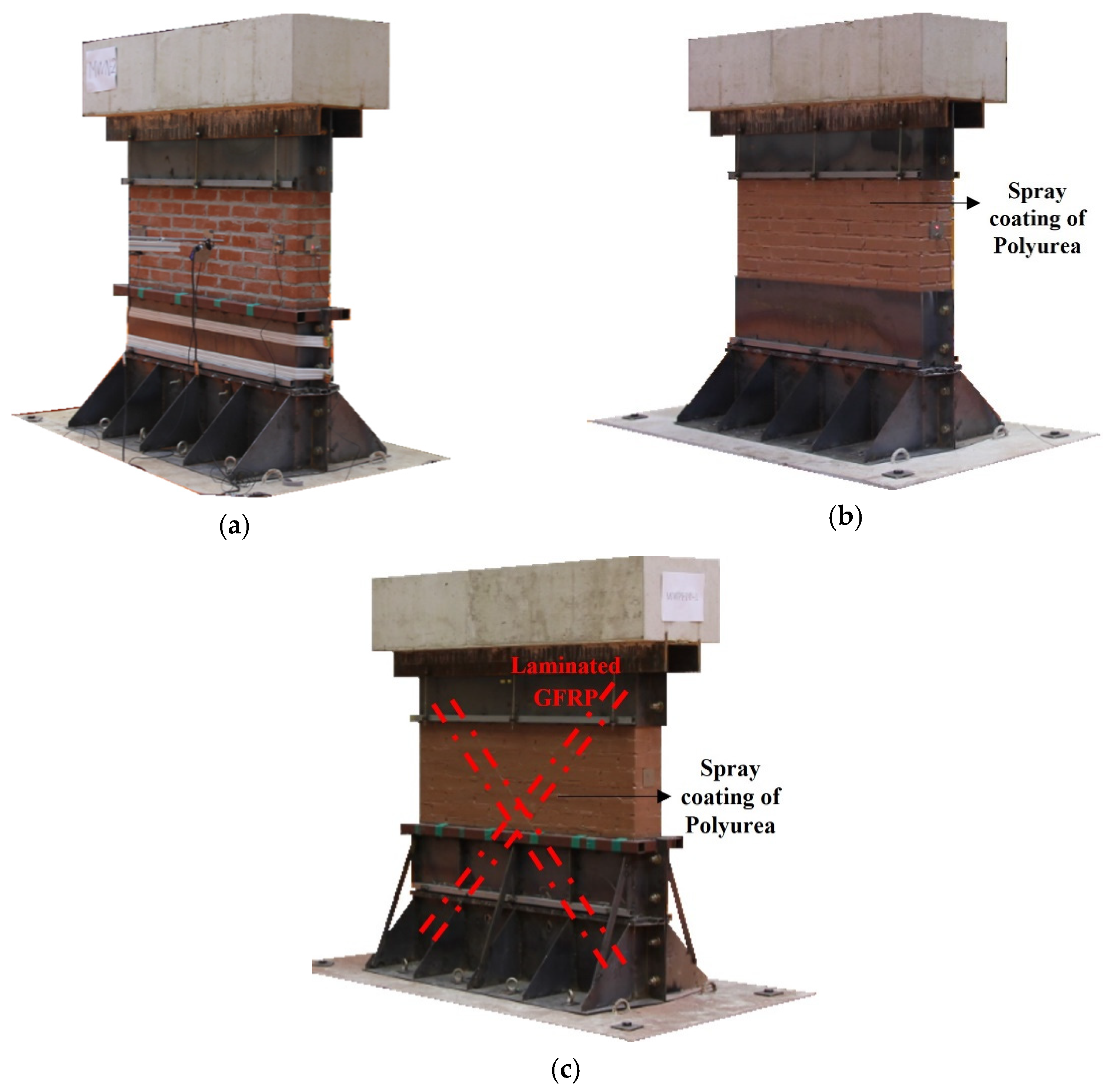
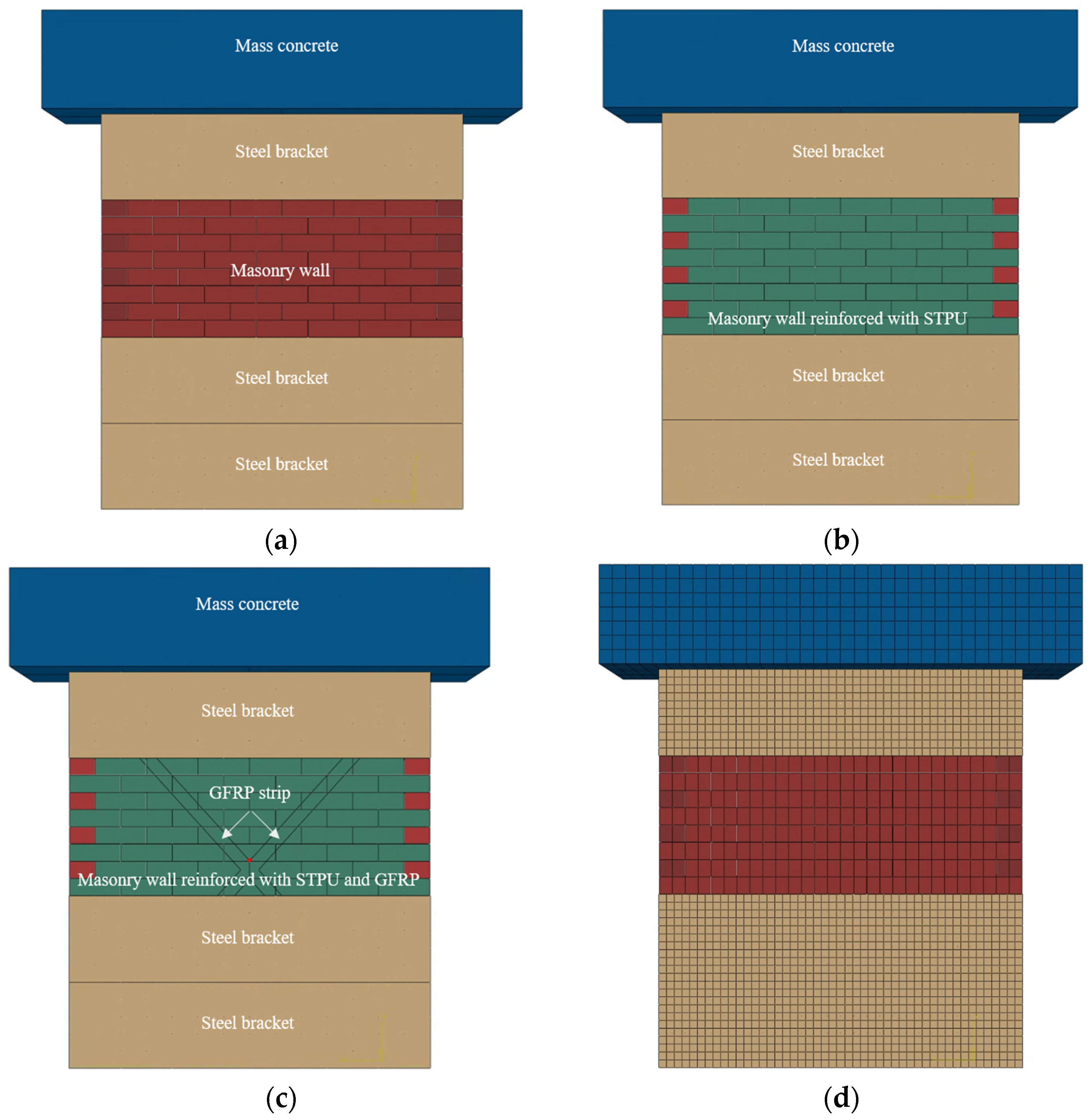
2.1. Shaking Table Test Specimens
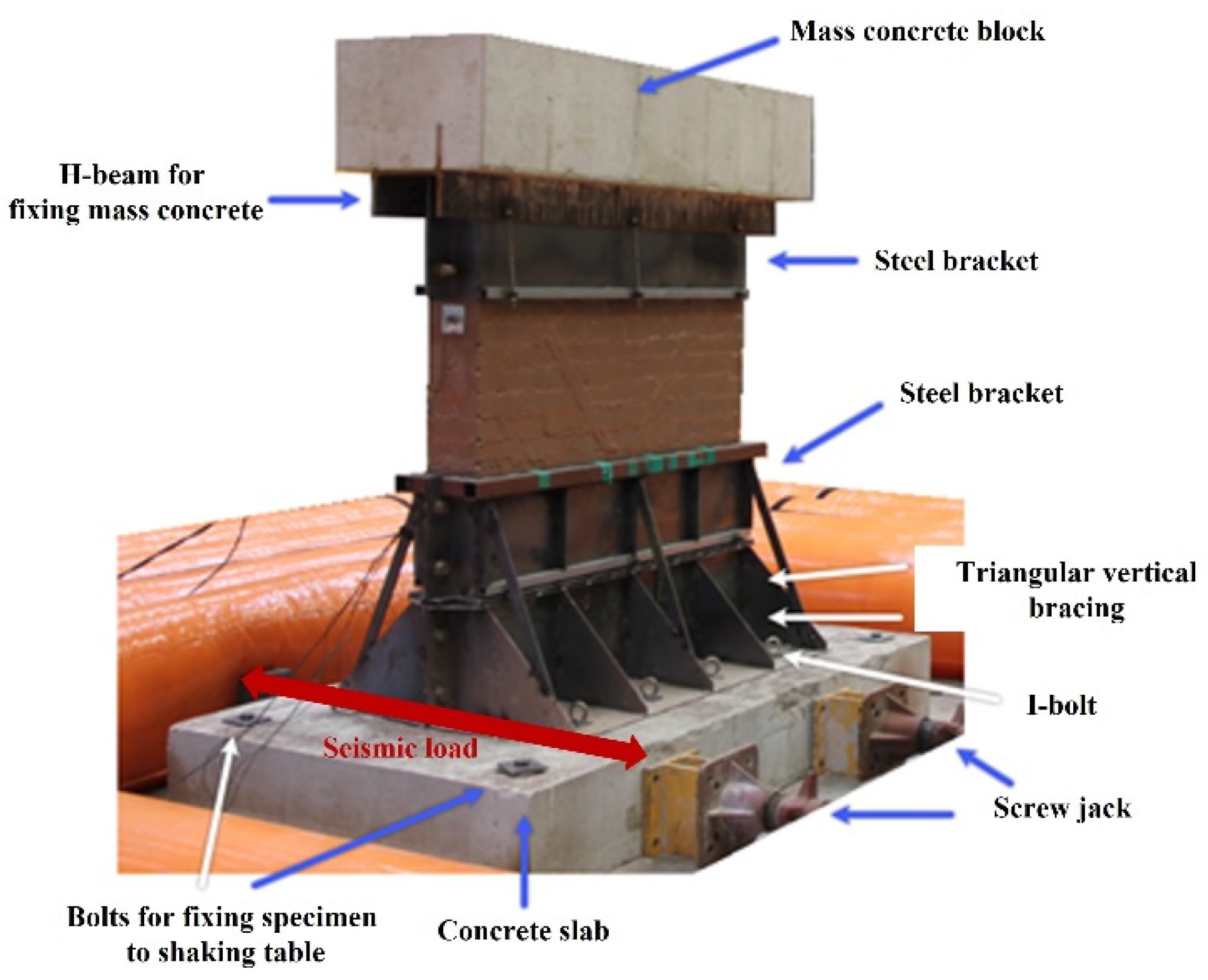
2.2. Shaking Table Test Setup
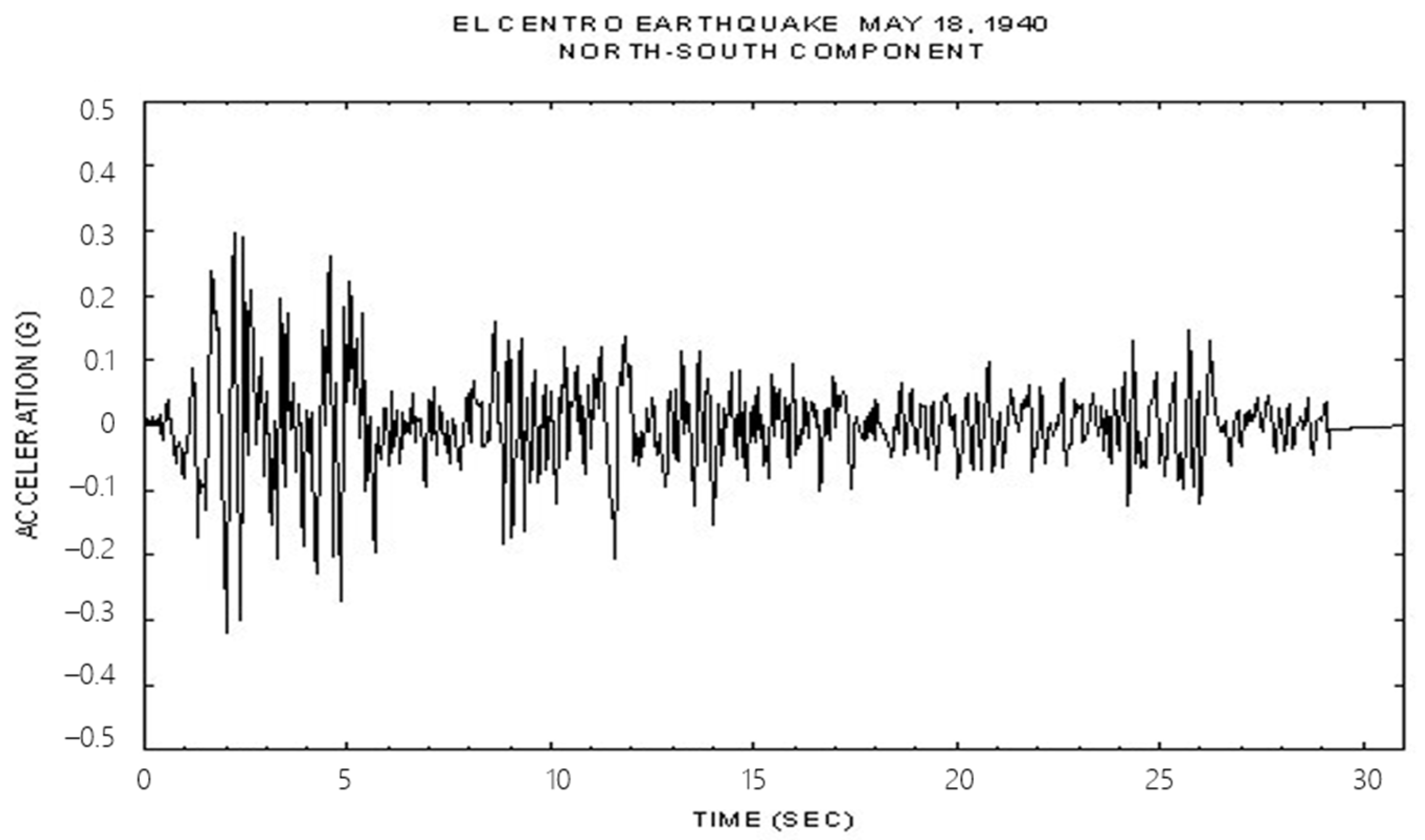
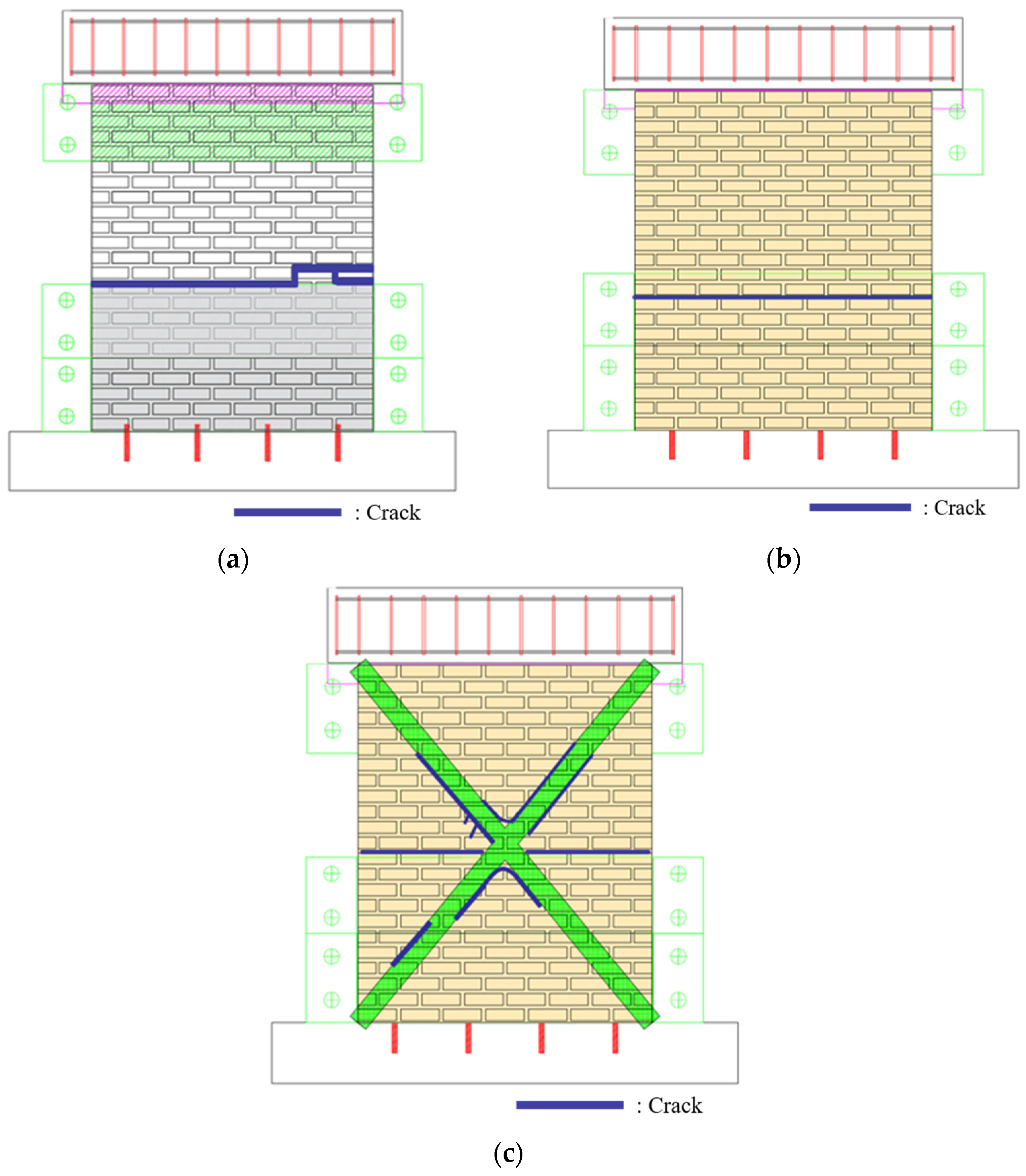
2.3. Shaking Table Test Results
3. Numerical Evaluation
3.1. Introduction to Numerical Modeling
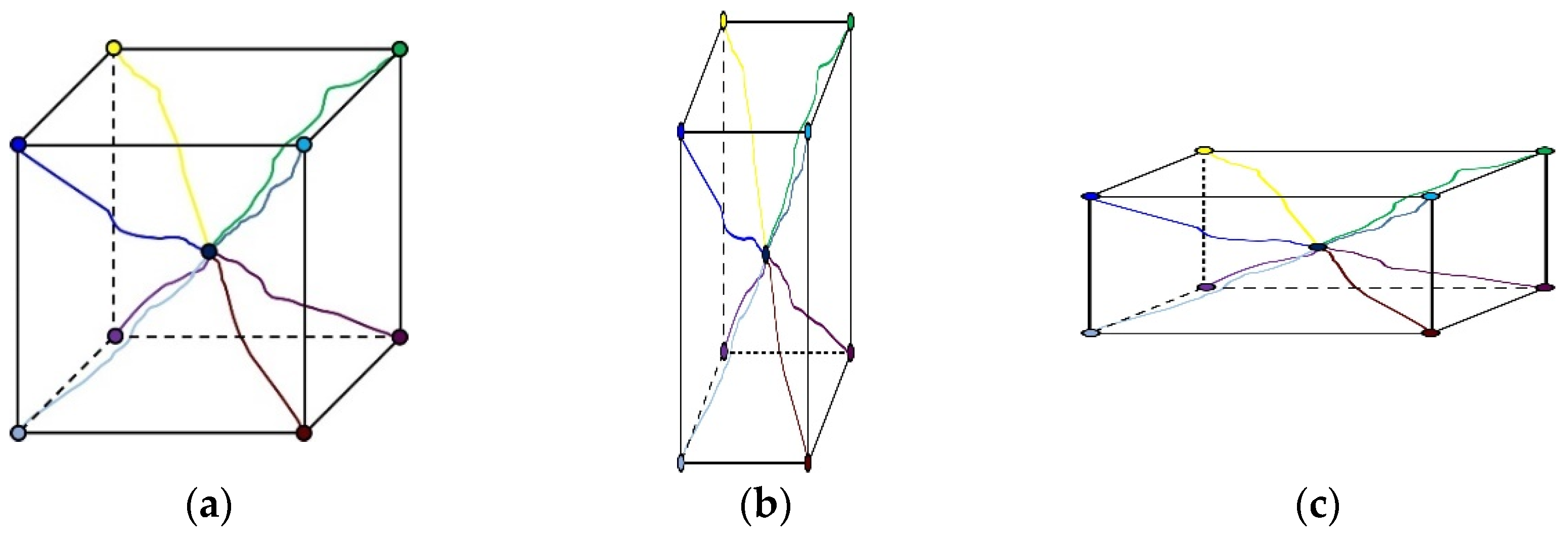
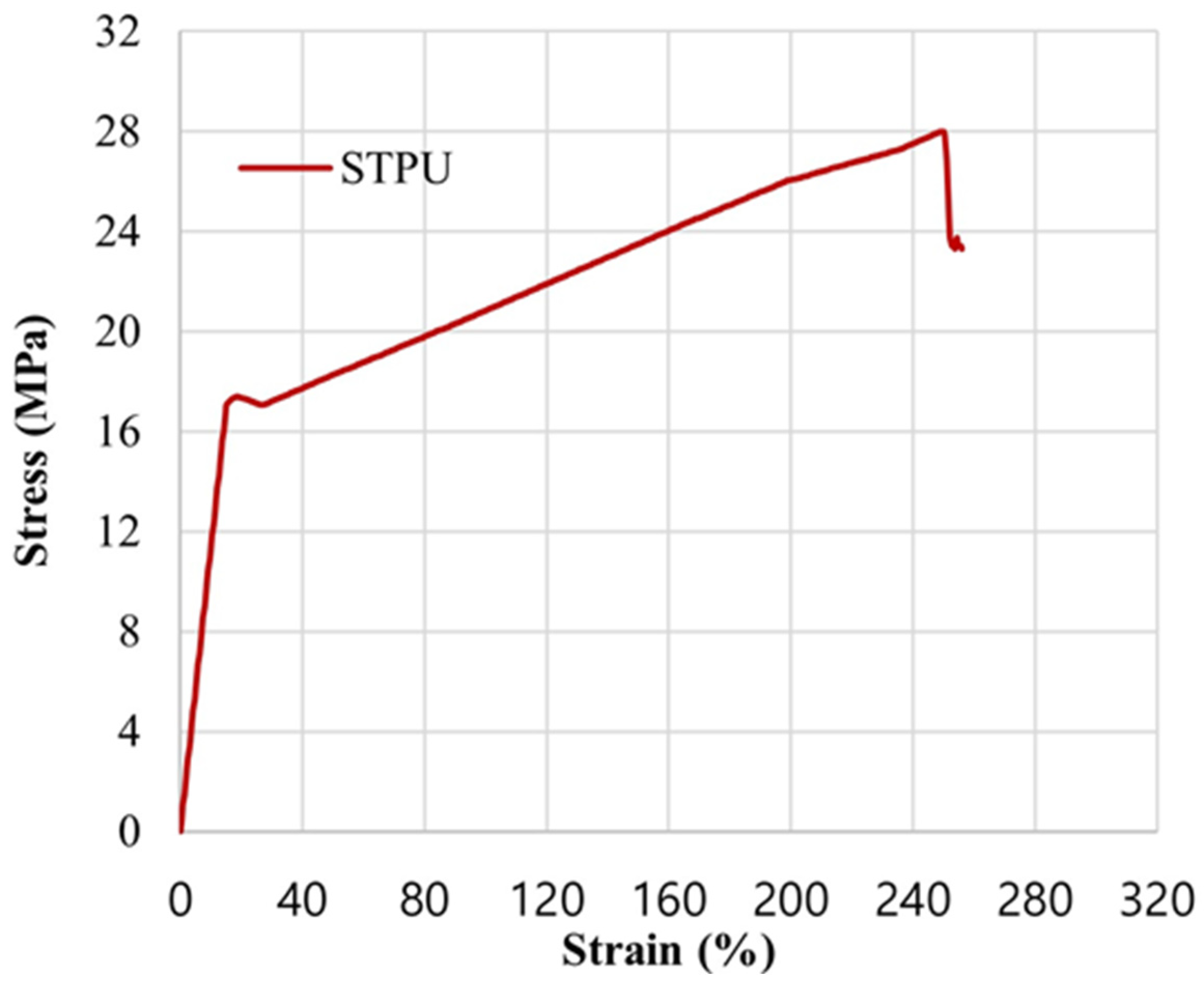
3.2. Material Model and Variables for Shaking Table Test
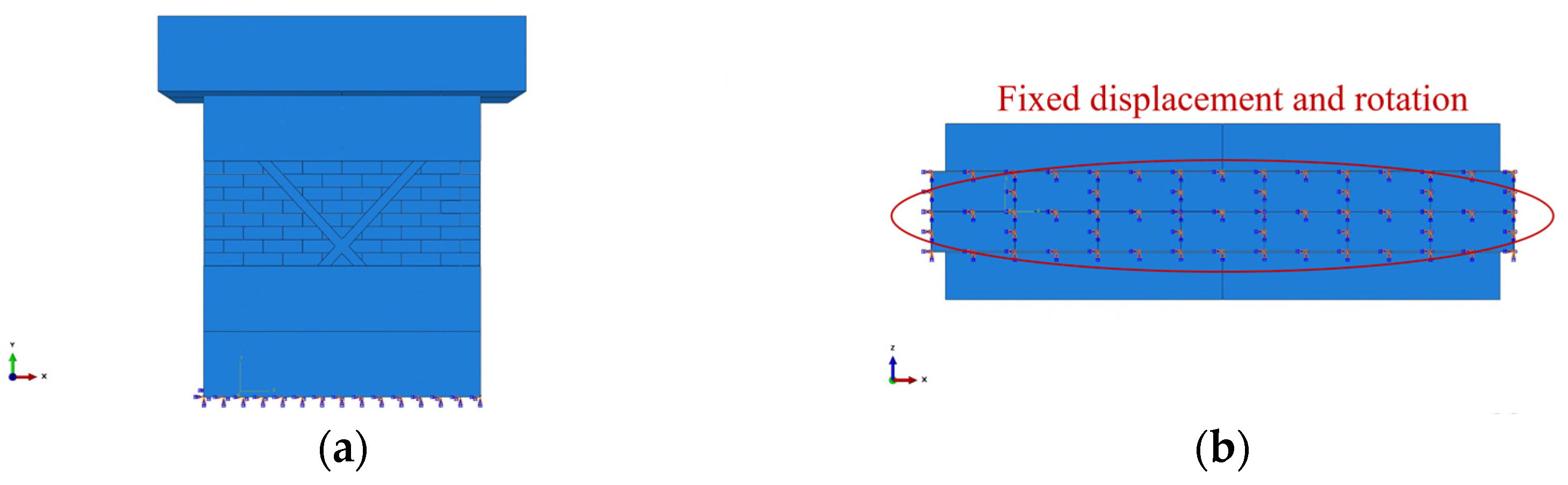
3.3. Numerical Modeling of Shaking Table Test
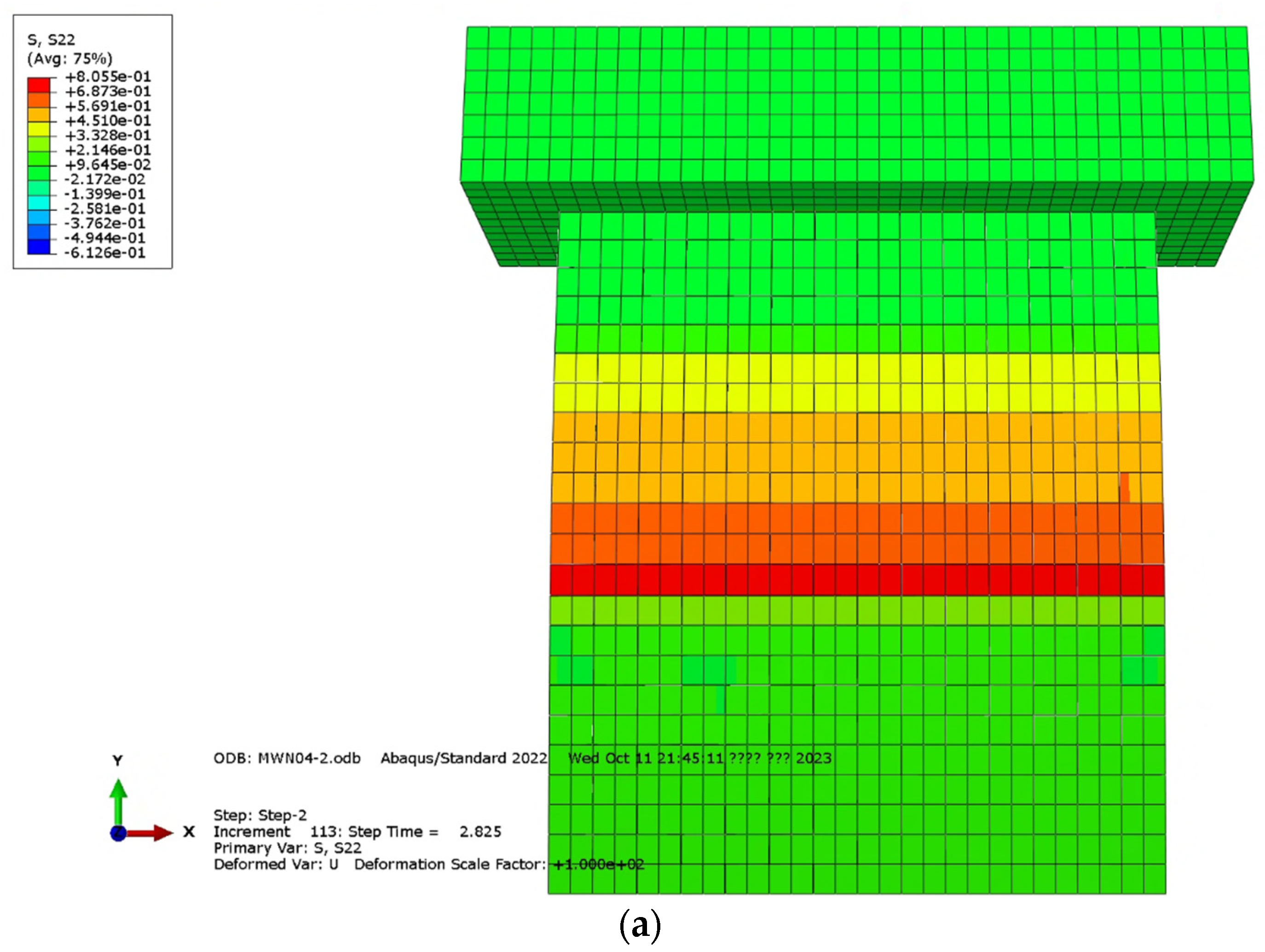
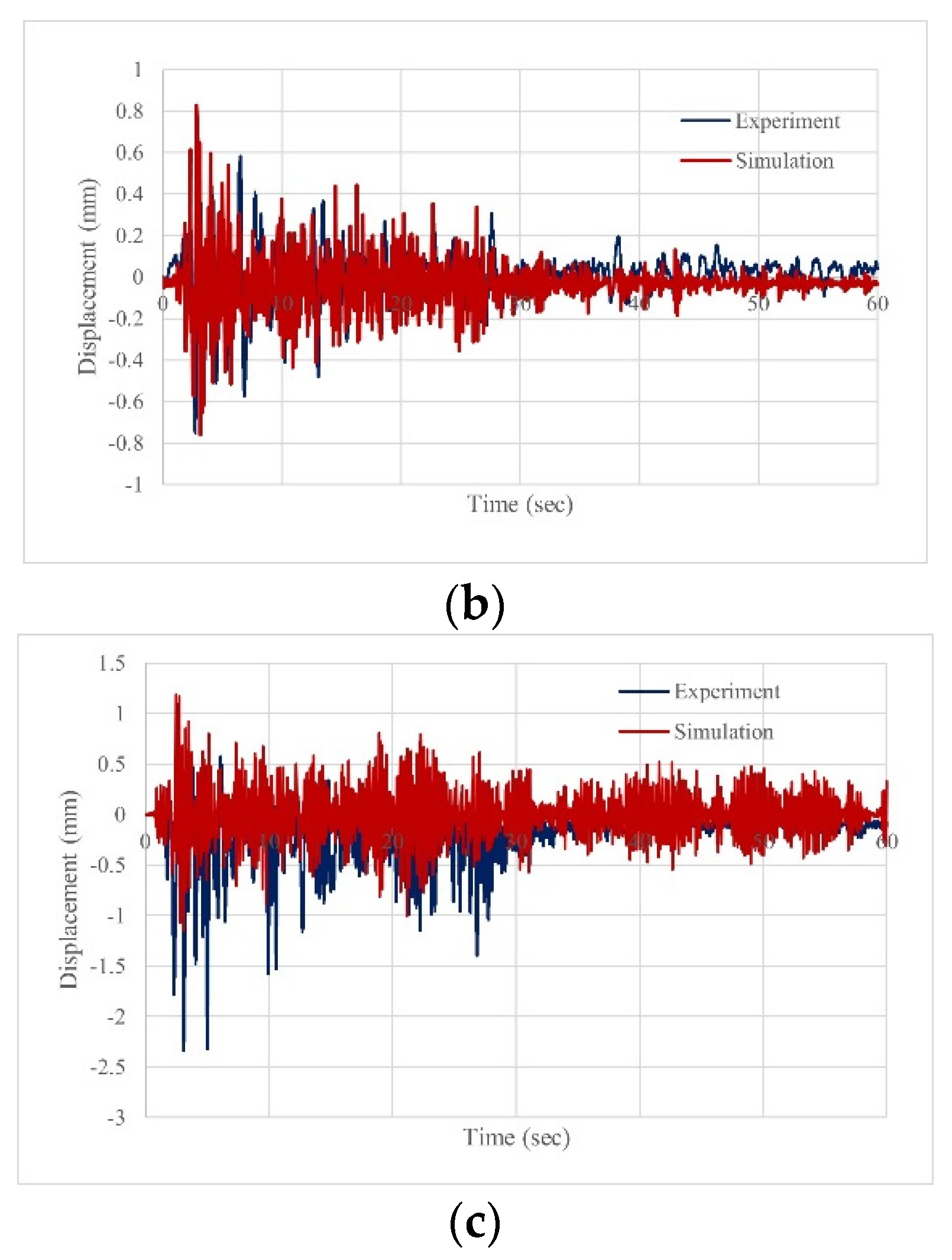
3.4. Validation of Numerical Model: Comparison with Experimental Results
4. Parametric Study
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RC | Reinforced concrete |
| FEA | Finite element analysis |
| GFRP | Glass-fiber-reinforced polymer |
| PU | Polyurea |
| STPU | Stiff-type polyurea |
| PGA | Peak ground acceleration |
| DOF | Degree of freedom |
References
- Capacci, L.; Biondini, F.; Frangopol, D.M. Resilience of aging structures and infrastructure systems with emphasis on seismic resilience of bridges and road networks. Resilient Cities Struct. Struct. 2022, 1, 23–41. [Google Scholar] [CrossRef]
- Briggs, K.M.; Dijkstra, T.A.; Glendinning, S. Assessing the deterioration of ageing infrastructure earthworks. GeoStrata Mag. Arch. 2022, 26, 26–33. [Google Scholar] [CrossRef]
- Biondini, F.; Frangopol, D.M. Life-Cycle of Structures and Infrastructure Systems. In Proceedings of the Eighth International Symposium on Life-Cycle Civil Engineering, Milan, Italy, 2–6 July 2023; CRC Press/Balkema: Milan, Italy, 2023. [Google Scholar]
- Little, R.G. Managing the Risk of Aging Infrastructure; IRGC, Public Sector Governance of Emerging Risks Council, Infrastructure Case: 2012. Available online: https://irgc.org/wp-content/uploads/2018/09/R.-Little_Risk-of-Aging-Infrastructure_revision-Nov2012.pdf (accessed on 28 October 2022).
- Ibrahim, A.; Abdelkhalek, S.; Zayed, T.; Qureshi, A.H.; Mohammed Abdelkader, E. A comprehensive review of the key deterioration factors of concrete bridge decks. Buildings 2024, 14, 3425. [Google Scholar] [CrossRef]
- Faris, N.; Zayed, T.; Fares, A. Review of Condition Rating and Deterioration Modeling Approaches for Concrete Bridges. Buildings 2025, 15, 219. [Google Scholar] [CrossRef]
- Ellingwood, B.R.; Mori, Y. Reliability-based service life assessment of concrete structures in nuclear power plants: Optimum inspection and repair. Nucl. Eng. Des. 1997, 175, 247–258. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Lin, K.Y.; Estes, A.C. Reliability of reinforced concrete girders under corrosion attack. J. Struct. Eng. 1997, 123, 286–297. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Liu, M. Maintenance and management of civil infrastructure based on condition, safety, optimization, and life-cycle cost. In Structures and Infrastructure Systems; Routledge: London, UK, 2019; pp. 96–108. [Google Scholar]
- Yang, S.I.; Frangopol, D.M.; Neves, L.C. Service life prediction of structural systems using lifetime functions with emphasis on bridges. Reliab. Eng. Syst. Saf. 2004, 86, 39–51. [Google Scholar] [CrossRef]
- Ministry of Land, Infrastructure and Transport (Korea). Report. Available online: https://www.molit.go.kr/USR/NEWS/m_71/dtl.jsp?id=95085286&lcmspage=1 (accessed on 1 August 2022).
- Lee, D.G.; Kim, T.H. Application of seismic isolation and vibration control in Korea. J. Earthq. Eng. Soc. Korea 2006, 10, 67–77. [Google Scholar]
- Seoul Institute of Technology (SIT). Spotlight. Available online: https://www.sit.re.kr/kr (accessed on 1 March 2021).
- Bruneau, M. State-of-the-art report on seismic performance of unreinforced masonry buildings. J. Struct. Eng. 1994, 120, 230–251. [Google Scholar] [CrossRef]
- Cholostiakow, S.; McKinley, B.; Mergos, P.; Hall, C.; Kappos, A.; Ayoub, A. Seismic retrofitting of URM masonry piers with helical steel reinforcement. Constr. Build. Mater. 2024, 431, 136499. [Google Scholar] [CrossRef]
- Meguro, K.; Sathiparan, N.; Sakurai, K.; Numada, M. Shaking table test of two-story masonry house model retrofitted by PP-band mesh. In Proceedings of the 15th World Conference on Earthquake Engineering (15WCEE), Sociedade Portuguesa de Engenharia Sismica (SPES), Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Karlos, K.; Tsantilis, A.; Triantafillou, T. Integrated seismic and energy retrofitting system for masonry walls using textile-reinforced mortars combined with thermal insulation: Experimental, analytical, and numerical study. J. Compos. Sci. 2020, 4, 189. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Karlos, K.; Kapsalis, P.; Georgiou, L. Innovative structural and energy retrofitting system for masonry walls using textile reinforced mortars combined with thermal insulation: In-plane mechanical behavior. J. Compos. Constr. 2018, 22, 04018029. [Google Scholar] [CrossRef]
- Boem, I. Masonry elements strengthened through Textile-Reinforced Mortar: Application of detailed level modelling with a free open-source Finite-Element code. Constr. Build. Mater. 2022, 357, 129333. [Google Scholar] [CrossRef]
- Alsayed, S.H.; Elsanadedy, H.M.; Al-Zaheri, Z.M.; Al-Salloum, Y.A.; Abbas, H. Blast response of GFRP-strengthened infill masonry walls. Constr. Build. Mater. 2016, 115, 438–451. [Google Scholar] [CrossRef]
- Gkournelos, P.D.; Triantafillou, T.C.; Bournas, D.A. Integrated structural and energy retrofitting of masonry walls: Effect of in-plane damage on the out-of-plane response. J. Compos. Constr. 2020, 24, 04020049. [Google Scholar] [CrossRef]
- Santos, A.P.; Chiquito, M.; Castedo, R.; López, L.M.; Gomes, G.; Mota, C.; Fangueiro, R.; Mingote, J.L. Experimental and numerical study of polyurea coating systems for blast mitigation of concrete masonry walls. Eng. Struct. 2023, 284, 116006. [Google Scholar] [CrossRef]
- Öztürk, Ş.; Aydın, F.; Arslan, Ş. Investigation of the effects of polyurea application on shear behavior in masonry wall elements. Constr. Build. Mater. 2025, 469, 140467. [Google Scholar] [CrossRef]
- He, J.; Sun, X.; Pi, D.; Wang, X.; Wu, M.; Qin, W.; Wu, A.; Qu, Y.; Wang, B. An experimental study on the resistance of a polyurea-sprayed structure to low-speed drop hammer impact. Constr. Build. Mater. 2024, 435, 136915. [Google Scholar] [CrossRef]
- Parniani, S.; Toutanji, H. Monotonic and fatigue performance of RC beams strengthened with a polyurea coating system. Constr. Build. Mater. 2015, 101, 22–29. [Google Scholar] [CrossRef]
- Davidson, J.S.; Porter, J.R.; Dinan, R.J.; Hammons, M.I.; Connell, J.D. Explosive testing of polymer retrofit masonry walls. J. Perform. Constr. Facil. 2004, 18, 100–106. [Google Scholar] [CrossRef]
- Guo, H.; Du, C.; Chen, Y.; Li, D.; Hu, W.; Lv, X. Study on protective performance of impact-resistant polyurea and its coated concrete under impact loading. Constr. Build. Mater. 2022, 340, 127749. [Google Scholar] [CrossRef]
- Huang, W.B.; Xiang, J.Y.; Lv, P.; Li, X.M. Study on mechanical properties aging of spray pure polyurea for hydraulic concrete protection. Adv. Mater. Res. 2012, 374, 1325–1329. [Google Scholar]
- Chen, D.; Wu, H.; Fang, Q.; Wei, J.S.; Xu, S.L. Out-of-plane behaviors of unreinforced and spray polyurea retrofitted one-way masonry infilled walls. J. Build. Eng. 2023, 67, 106006. [Google Scholar] [CrossRef]
- Lee, T.H.; Park, J.H.; Yang, D.H.; Kim, J.H.J.; Noor, N.B.M. Material enhancements of newly developed stiff type polyurea for retrofitting of concrete structures. Case Stud. Constr. Mater. 2022, 17, e01431. [Google Scholar] [CrossRef]
- Lamba, N.M.K.; Woodhouse, K.A.; Cooper, S.L. Polyurethanes in Biomedical Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 1998; pp. 14–23. [Google Scholar]
- Ahmad, B.; Najar, I.A. Comparative seismic analysis of EL Centro and Japan earthquakes using response spectra method. Int. J. Curr. Eng. Technol. 2016, 6, 1859–1864. [Google Scholar]
- Kim, J.S.; Kim, H.W.; Lee, J.H.; Park, B.C. Natural Frequency Analysis of Masonry Buildings Under Seismic Excitations. In Proceedings of the Korean Society for Noise and Vibration Engineering Conference; The Korean Society for Noise and Vibration Engineering: Jeju, Republic of Korea, 2012; pp. 495–496. [Google Scholar]
- Lourenço, P.B.; Rots, J.G. Multisurface interface model for analysis of masonry structures. J. Eng. Mech. 1997, 123, 660–668. [Google Scholar] [CrossRef]
- Lourenço, P.B. Computations on historic masonry structures. Prog. Struct. Eng. Mater. 2002, 4, 301–319. [Google Scholar] [CrossRef]
- Agüera, N.D.; Tornello, M.E.; Frau, C.D. Structural response of unreinforced masonry walls. J. Civ. Eng. Archit. 2016, 10, 219–231. [Google Scholar]
- Abdulla, K.F.; Cunningham, L.S.; Gillie, M. Simulating masonry wall behaviour using a simplified micro-model approach. Eng. Struct. 2017, 151, 349–365. [Google Scholar] [CrossRef]
- Rull, N.; Basnayake, A.; Heitzmann, M.; Frontini, P.M. Constitutive modelling of the mechanical response of a polycaprolactone based polyurethane elastomer: Finite element analysis and experimental validation through a bulge test. J. Strain Anal. Eng. Des. 2021, 56, 206–215. [Google Scholar] [CrossRef]
- Chen, D.; Wu, H.; Wei, J.S.; Xu, S.L.; Fang, Q. Nonlinear visco-hyperelastic tensile constitutive model of spray polyurea within wide strain-rate range. Int. J. Impact Eng. 2022, 163, 104184. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Gattesco, N.; Amadio, C.; Bedon, C. Experimental and numerical study on the shear behavior of stone masonry walls strengthened with GFRP reinforced mortar coating and steel-cord reinforced repointing. Eng. Struct. 2015, 90, 143–157. [Google Scholar] [CrossRef]
- Yang, K.H.; Lee, Y.; Hwang, Y.H. Evaluation of tensile stress-strain relationship of masonry elements. J. Archit. Inst. Korea Struct. Constr. 2019, 35, 27–33. [Google Scholar]
- Still, G.T. Strength of Cementitious Mortars: A Literature Review with Special Reference to Weak Mortars in Tension; University of Warwick: Coventry, UK, 2004. [Google Scholar]
- Park, J.C.; Lee, S.W.; Kim, S.B.; Kim, J.H.J. Performance evaluation of RC slabs strengthened by stiff type polyurea. KSCE J. Civ. Environ. Eng. Res. 2011, 31, 457–464. [Google Scholar]




| Density (kg/m3) | Elastic Modulus (MPa) | ψ | Flow Stress Ratio | Angle of Friction | Yield Compressive Stress (MPa) | ||
|---|---|---|---|---|---|---|---|
| Expanded unit | 1800 | 2888 | 0.15 | 11.3 | 1 | 36 | 16 |
| GFRP Elastic Property | Value |
|---|---|
| Density (kg/m3) | 1900 |
| Longitudinal modulus, E1 (GPa) | 73 |
| Transverse modulus, E2 (GPa) | 18 |
| In-plane Poisson’s ratio, | 0.25 |
| In-plane shear modulus, G12 (GPa) | 9 |
| Transverse shear modulus, G13 (GPa) | 9 |
| Through-thickness shear modulus, G23 (GPa) | 7 |
| Fail Stress Property | Fail Stress |
|---|---|
| Tensile stress in fiber direction (MPa) | 1500 |
| Compressive stress in fiber direction (MPa) | −700 |
| Tensile stress in transverse direction (MPa) | 90 |
| Compressive stress in transverse direction (MPa) | −140 |
| Shear strength (MPa) | 6 |
| Tangential Behavior | Cohesive Behavior | |||
|---|---|---|---|---|
| Friction Coefficient | Stiffness of Joint in the Normal Direction Knn (N/mm2) | Stiffness of Joint in the First Shear Direction Kss (N/mm2) | Stiffness of Joint in the Second Shear Direction Ktt (N/mm2) | |
| Brick-Brick | 0.75 | 63 | 25 | 25 |
| Brick-STPU, Brick-GFRP | 0.06 | 4160 | 1750 | 1750 |
| Specimen | MWN | MWP2 | MWPF5 | ||||
|---|---|---|---|---|---|---|---|
| PGA. | Strain | Y-Axis Stress (MPa) | Strain | Y-Axis Stress (MPa) | Strain | Y-Axis Stress (MPa) | |
| 0.1 g | Max. | 0.00008 | 0.22 | 0.00006 | 0.15 | 0.00008 | 0.20 |
| Min. | −0.00007 | −0.20 | −0.00007 | −0.20 | −0.00010 | −0.25 | |
| 0.2 g | Max. | 0.00012 | 0.32 | 0.00008 | 0.21 | 0.00011 | 0.28 |
| Min. | −0.00001 | −0.27 | −0.00014 | −0.36 | −0.00012 | −0.30 | |
| 0.3 g | Max. | 0.00019 (Crack occurred) | 0.52 | 0.00011 | 0.28 | 0.00017 (Crack occurred) | 0.45 |
| Min. | −0.00019 (Crack occurred) | −0.51 | −0.00011 | −0.29 | −0.00015 (Crack occurred) | −0.37 | |
| 0.4 g | Max. | 0.00024 (Crack occurred) | 0.66 | 0.00009 | 0.25 | 0.00012 | 0.31 |
| Min. | −0.0027 (Crack occurred) | −0.75 | −0.00017 (Crack occurred) | −0.49 | −0.00020 (Crack occurred) | −0.51 | |
| 0.5 g | Max. | 0.00014 | 0.40 | 0.00022 (Crack occurred) | 0.30 | ||
| Min. | −0.00020 (Crack occurred) | −0.55 | −0.00031 (Crack occurred) | −0.23 | |||
| 0.6 g | Max. | 0.00016 (Crack occurred) | 0.43 | 0.00021 (Crack occurred) | 0.56 | ||
| Min. | −0.00028 (Crack occurred) | −0.76 | −0.00026 (Crack occurred) | −0.64 | |||
| 0.7 g | Max. | 0.00015 (Crack occurred) | 0.41 | 0.00027 (Crack occurred) | 0.68 | ||
| Min. | −0.00032 (Crack occurred) | −0.88 (Failure occurred) | −0.00026 (Crack occurred) | −0.67 | |||
| 0.8 g | Max. | 0.00015 (Crack occurred) | 0.41 | 0.00030 (Crack occurred) | 0.76 | ||
| Min. | −0.00032 (Crack occurred) | −0.90 (Failure occurred) | −0.00034 (Crack occurred) | −0.88 (Failure occurred) | |||
| 0.9 g | Max. | 0.00039 (Crack occurred) | 0.99 (Failure occurred) | ||||
| Min. | −0.00041 (Crack occurred) | −1.05 (Failure occurred) | |||||
| Thickness | Numerical Analysis Result | |||
|---|---|---|---|---|
| Displacement | Strain | Y-Axis Stress (MPa) | ||
| 1 mm | Max. | 1.54 | 0.000095 | 0.26 |
| Min. | −0.80 | −0.000187 | −0.53 | |
| 2 mm | Max. | 1.48 | 0.000093 | 0.25 |
| Min. | −0.70 | −0.0000174 | −0.49 | |
| 3 mm | Max. | 1.50 | 0.000118 | 0.31 |
| Min. | −0.81 | −0.000189 | −0.51 | |
| 4 mm | Max. | 1.51 | 0.000119 | 0.32 |
| Min. | −0.82 | −0.000196 | −0.54 | |
| 5 mm | Max. | 1.51 | 0.000114 | 0.31 |
| Min. | −0.79 | −0.000175 | −0.50 | |
| 6 mm | Max. | 1.51 | 0.000103 | 0.28 |
| Min. | −0.79 | −0.00016 | −0.46 | |
| 7 mm | Max. | 1.51 | 0.000116 | 0.32 |
| Min. | −0.79 | −0.000187 | −0.51 | |
| 8 mm | Max. | 1.54 | 0.000111 | 0.32 |
| Min. | −0.80 | −0.000192 | −0.52 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, T.-H.; Kim, J.-W.; Lee, S.; Kim, J.-H.J. Numerical Simulation and Experimental Validation of Masonry Walls Strengthened with Stiff-Type Polyurea Under Seismic Loads. Appl. Sci. 2025, 15, 6912. https://doi.org/10.3390/app15126912
Lee T-H, Kim J-W, Lee S, Kim J-HJ. Numerical Simulation and Experimental Validation of Masonry Walls Strengthened with Stiff-Type Polyurea Under Seismic Loads. Applied Sciences. 2025; 15(12):6912. https://doi.org/10.3390/app15126912
Chicago/Turabian StyleLee, Tae-Hee, Jong-Wook Kim, Sangwon Lee, and Jang-Ho Jay Kim. 2025. "Numerical Simulation and Experimental Validation of Masonry Walls Strengthened with Stiff-Type Polyurea Under Seismic Loads" Applied Sciences 15, no. 12: 6912. https://doi.org/10.3390/app15126912
APA StyleLee, T.-H., Kim, J.-W., Lee, S., & Kim, J.-H. J. (2025). Numerical Simulation and Experimental Validation of Masonry Walls Strengthened with Stiff-Type Polyurea Under Seismic Loads. Applied Sciences, 15(12), 6912. https://doi.org/10.3390/app15126912







