Mechanical Response and Failure Mechanisms of Block Caving Bottom Structures Under Dynamic Conditions Induced by Slope Rockfalls
Abstract
1. Introduction
2. Test Method Aring Capacity of Bottom Structure
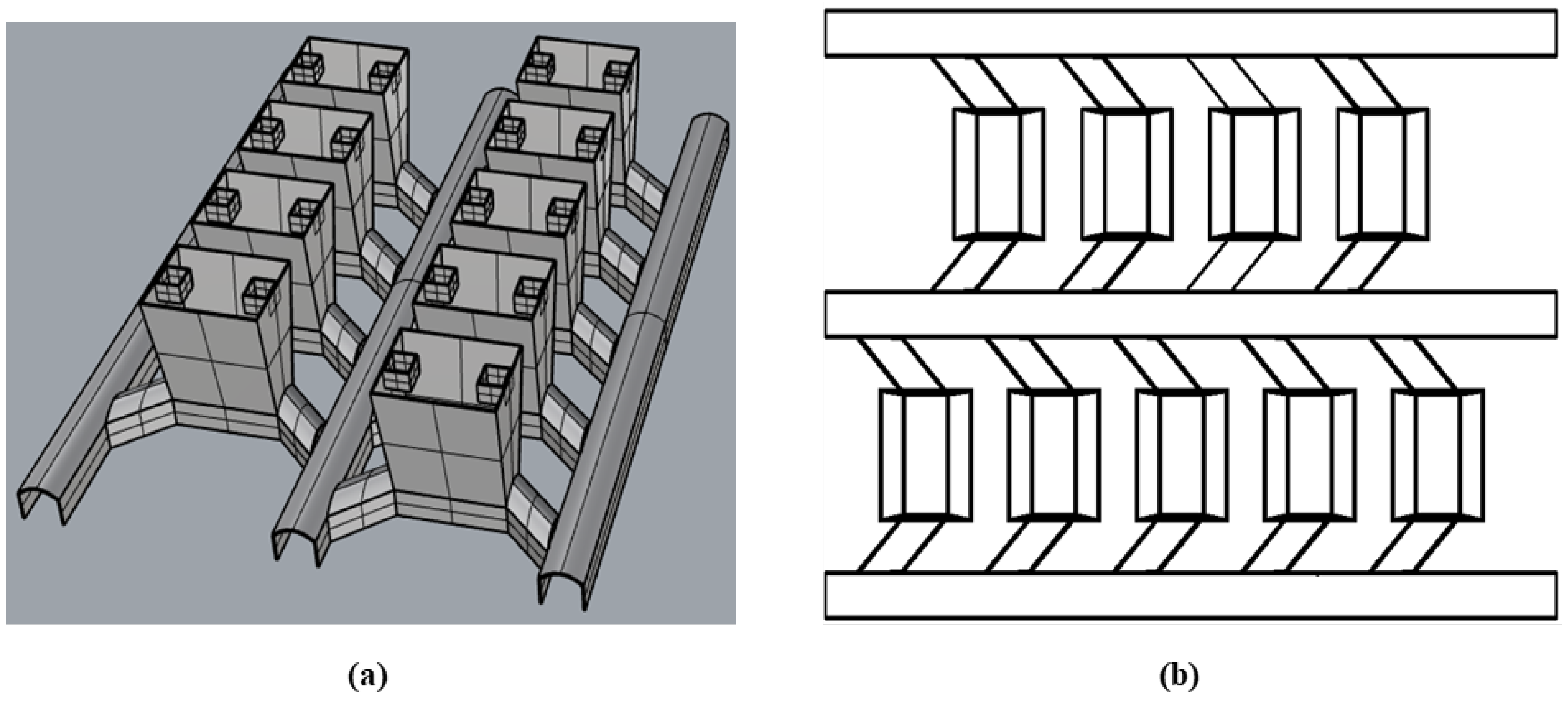
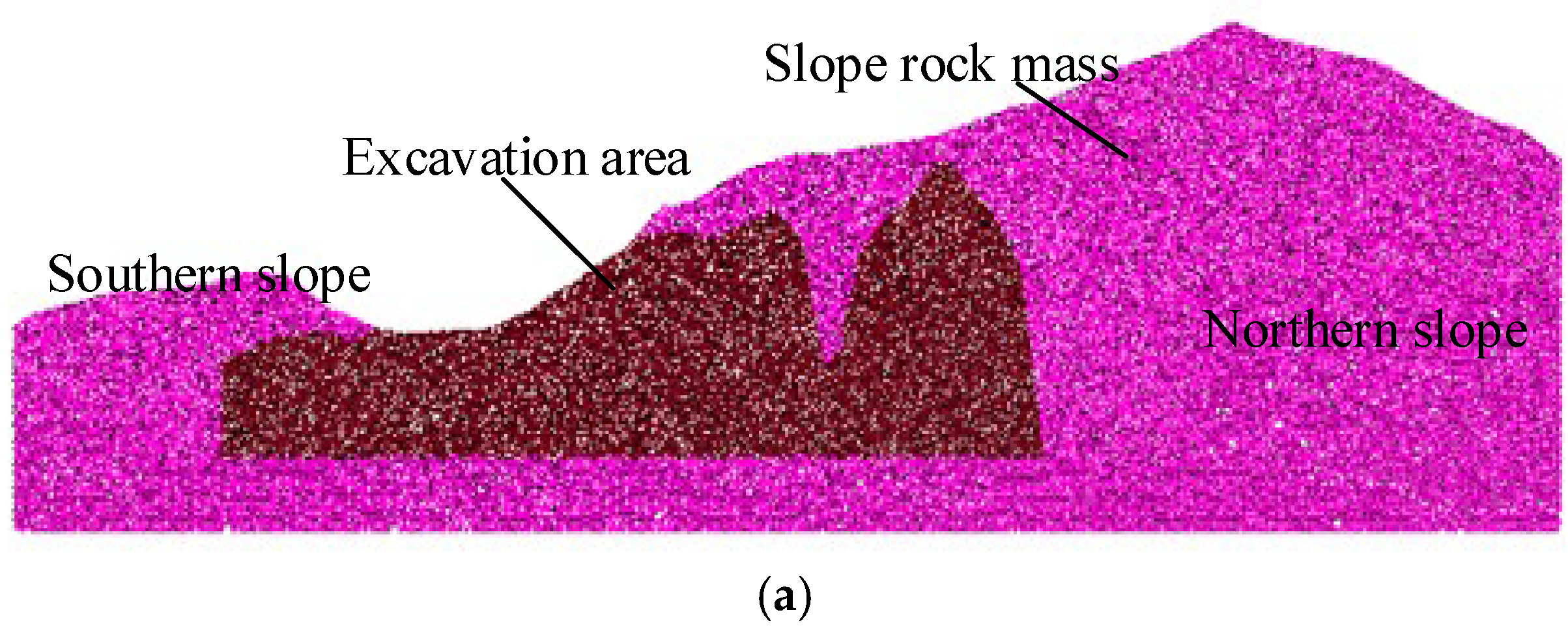
2.1. Bottom Structure Mold Design
2.2. Experimental Loading Plan
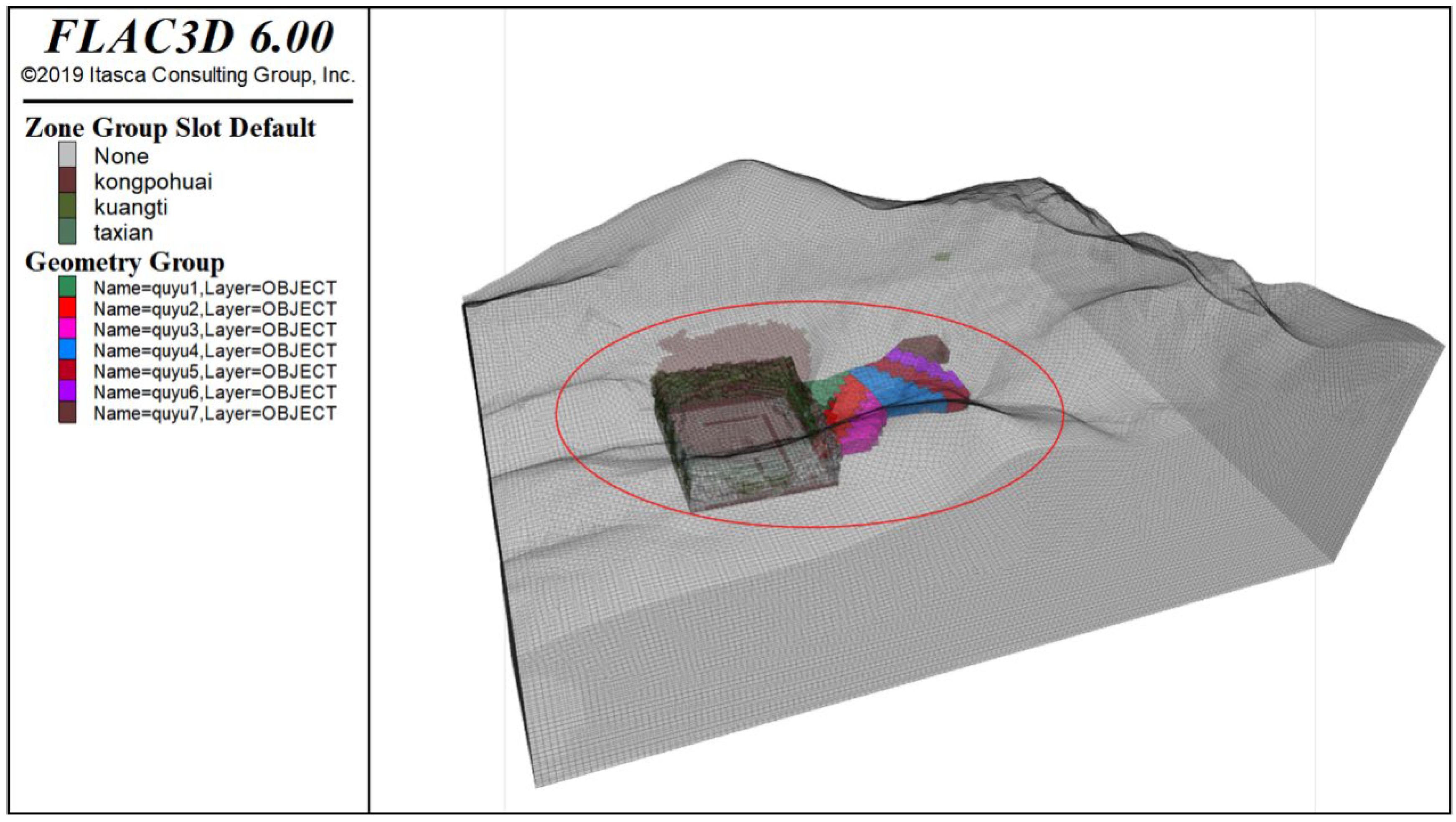
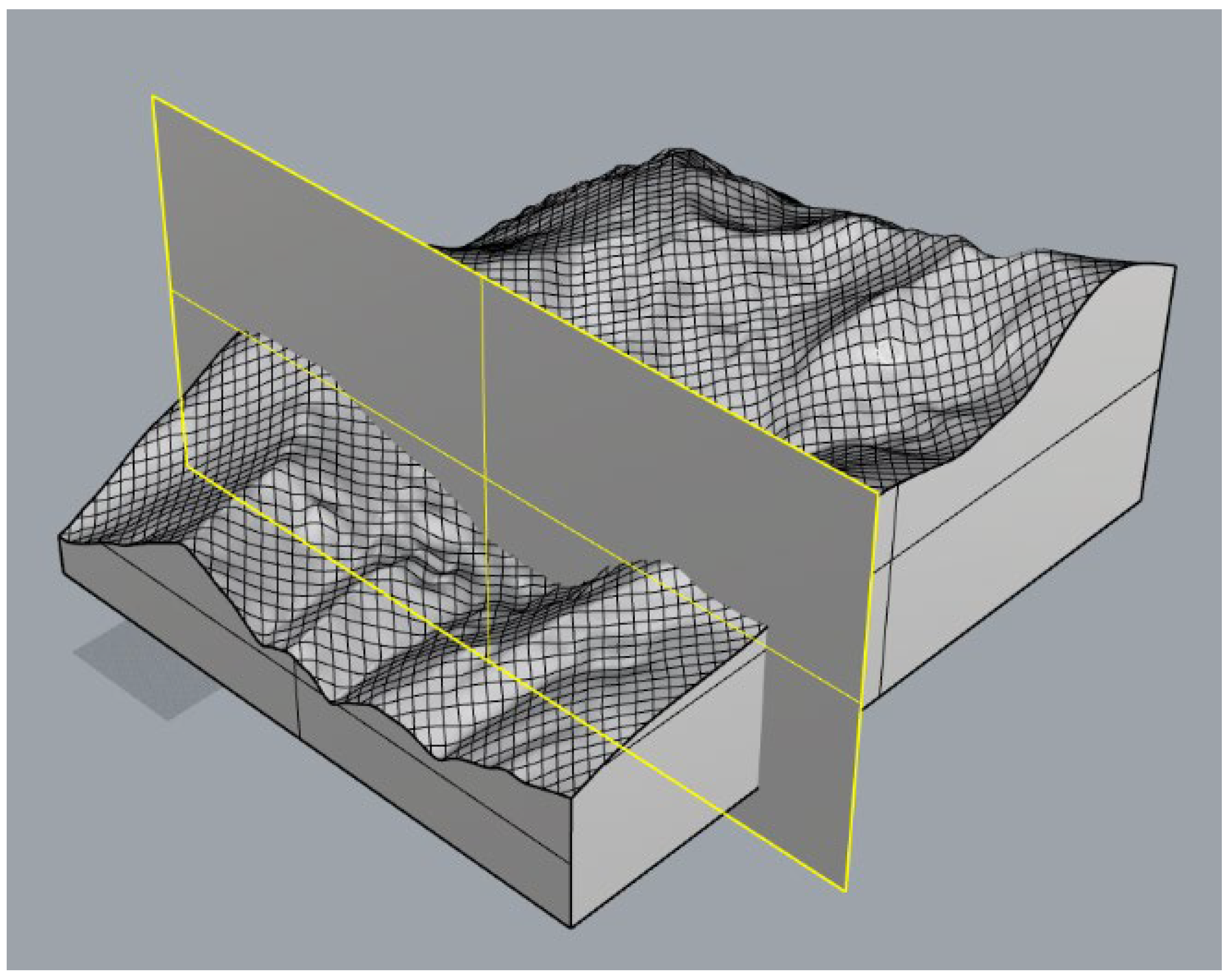
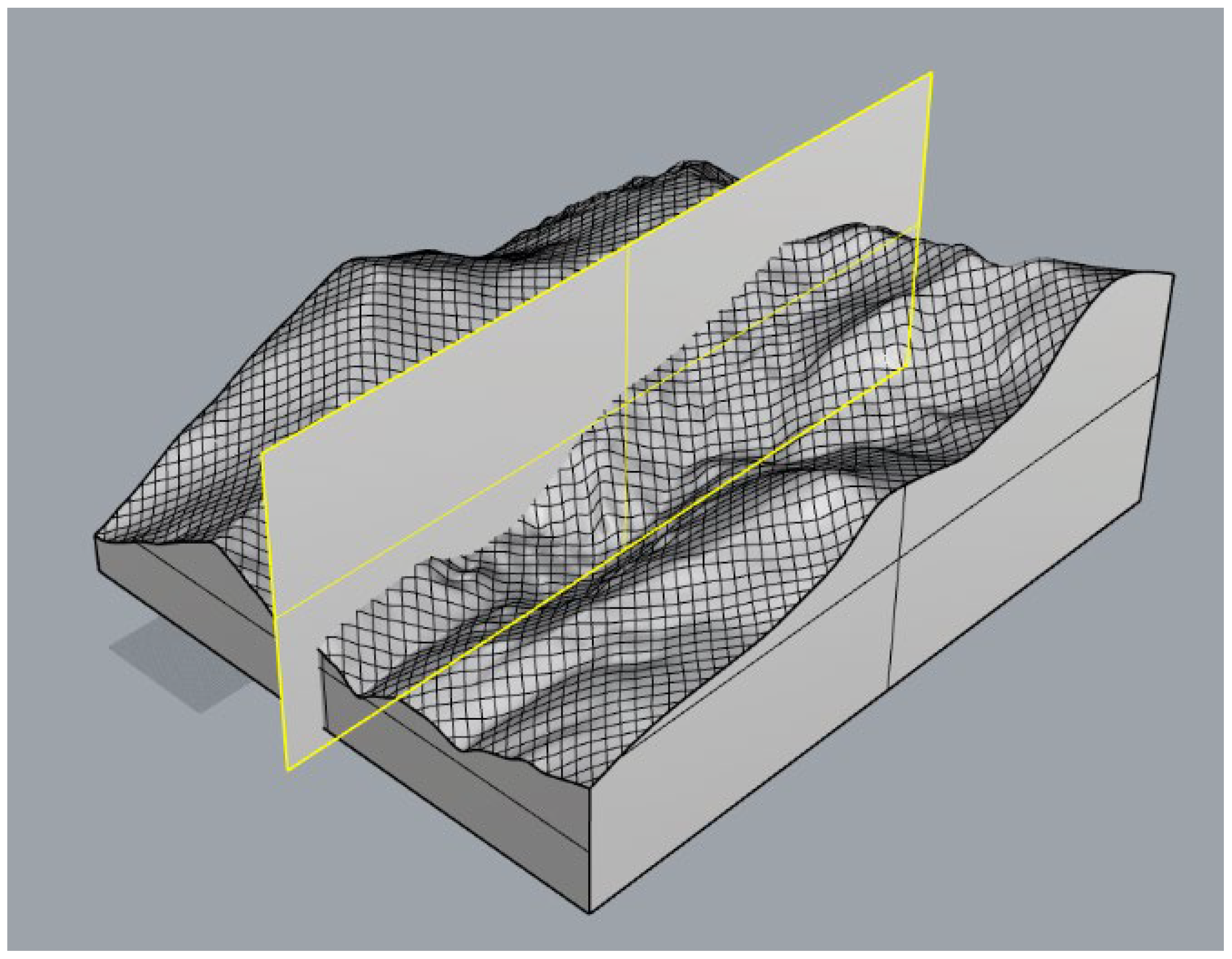
3. Simulation of Slope Collapse Impact Load
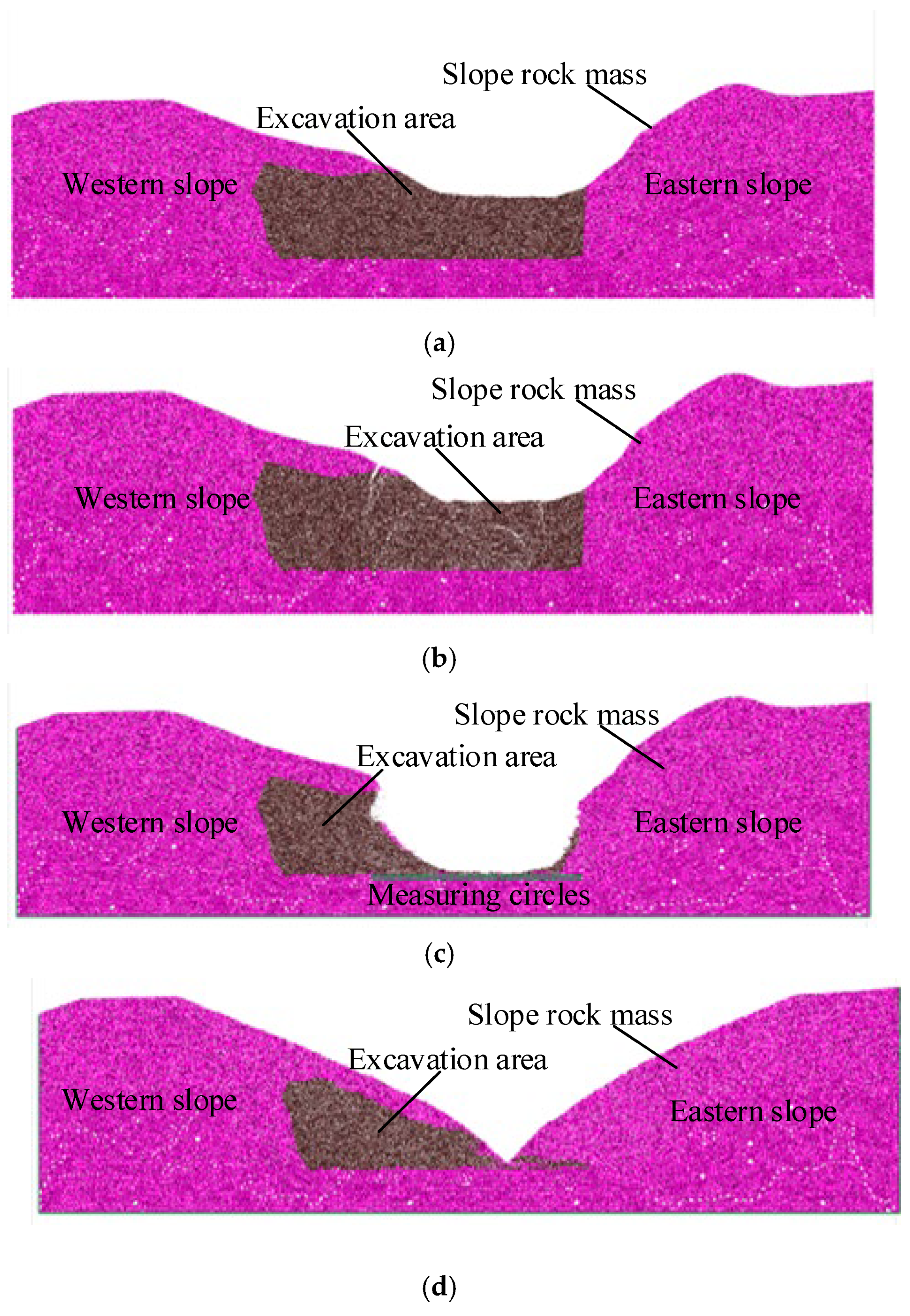
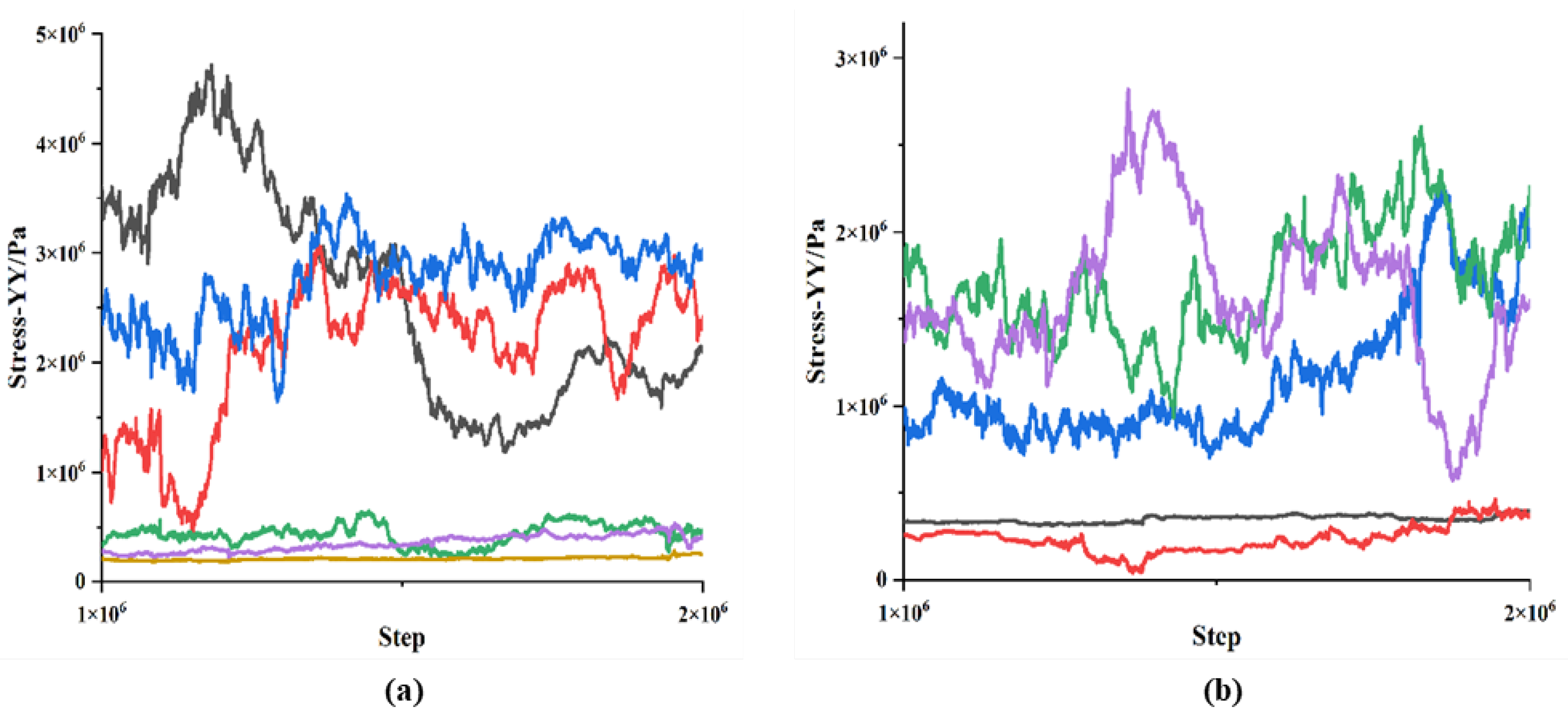
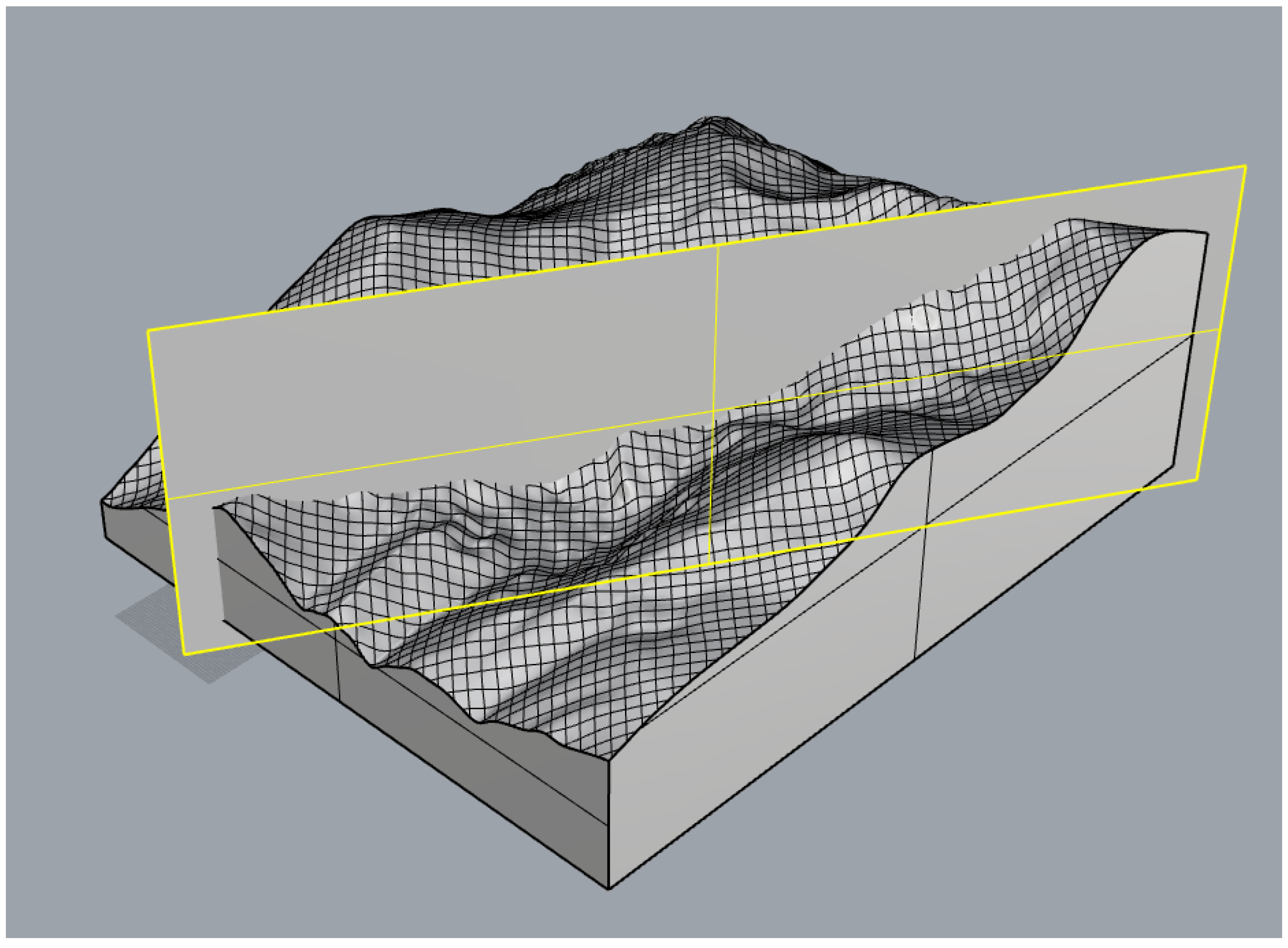
3.1. Transverse Section Impact Simulation
3.2. Longitudinal Profile Impact Simulation
3.3. Oblique Profile Impact Simulation
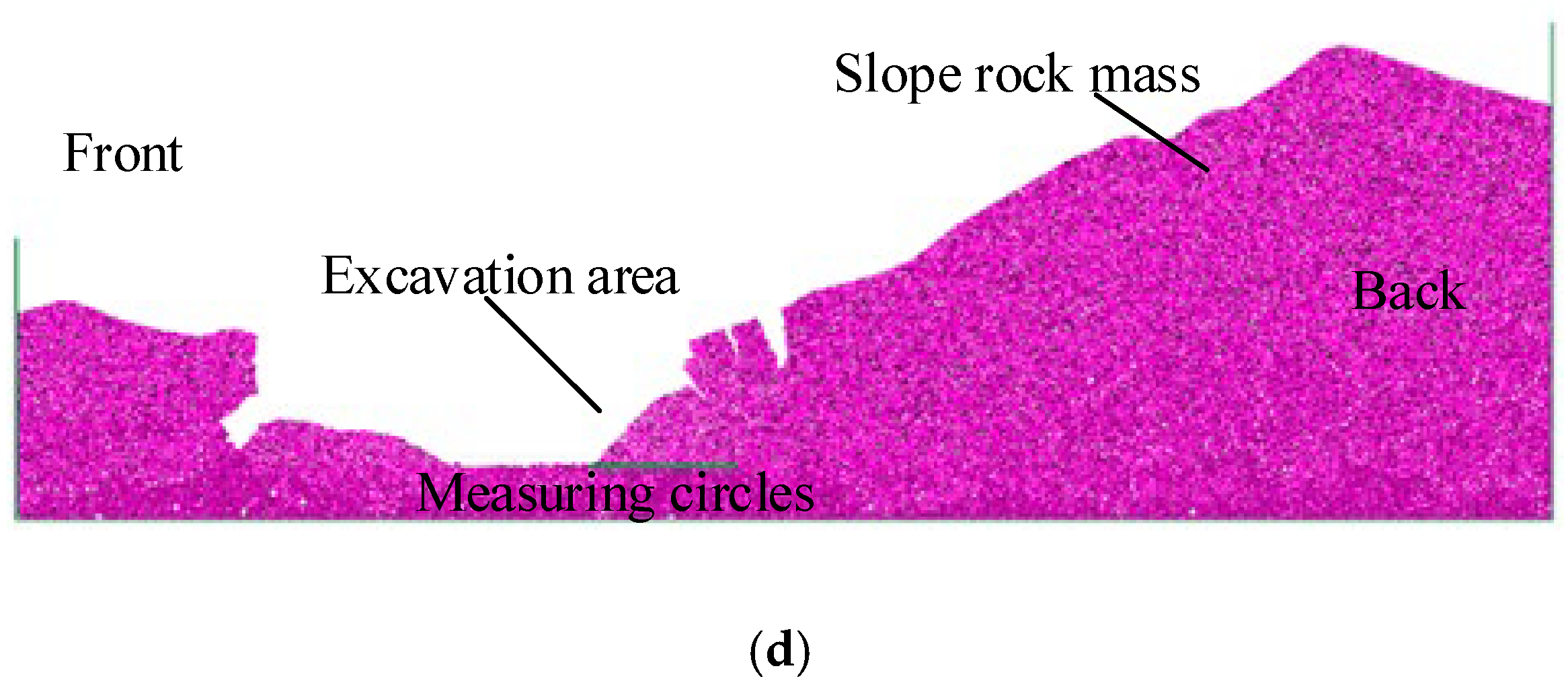
4. Experimental Procedures
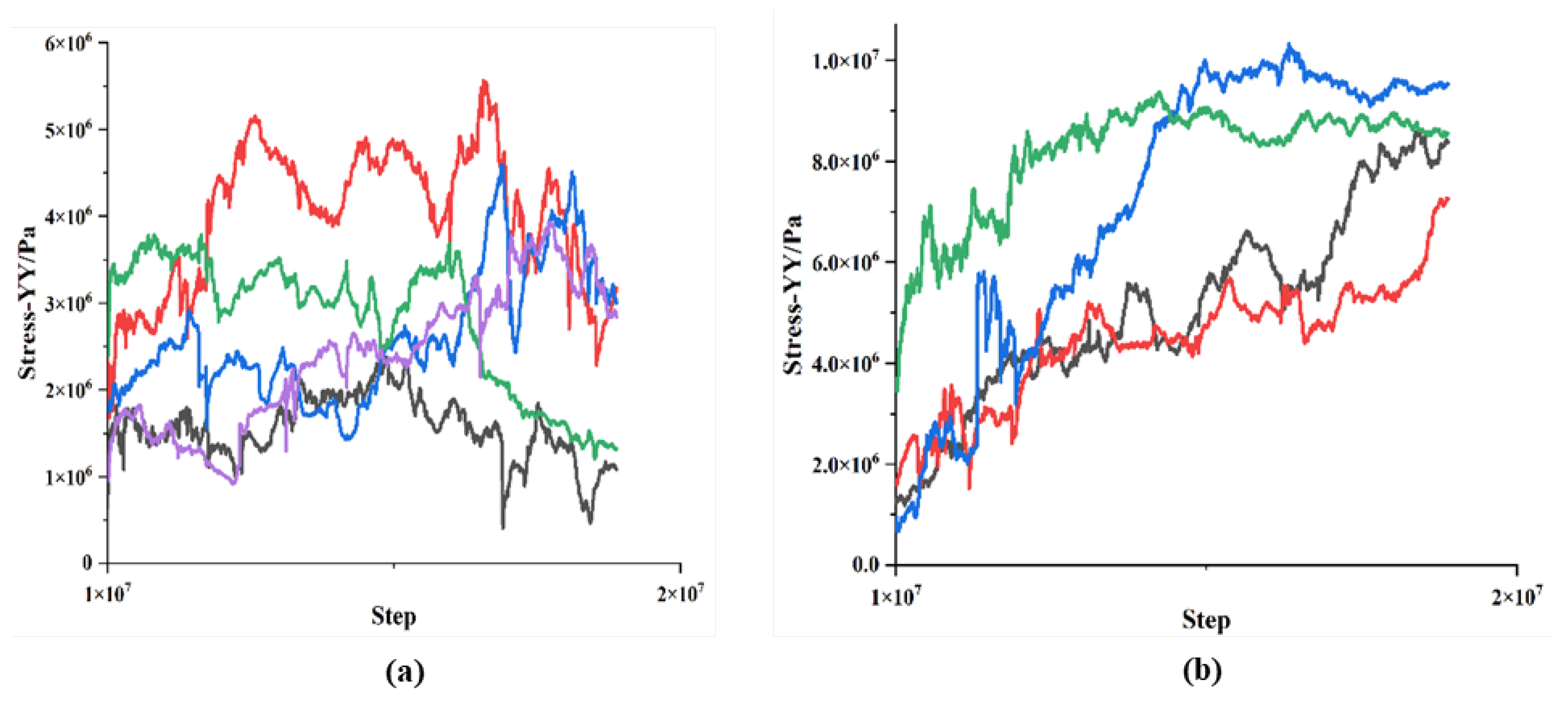
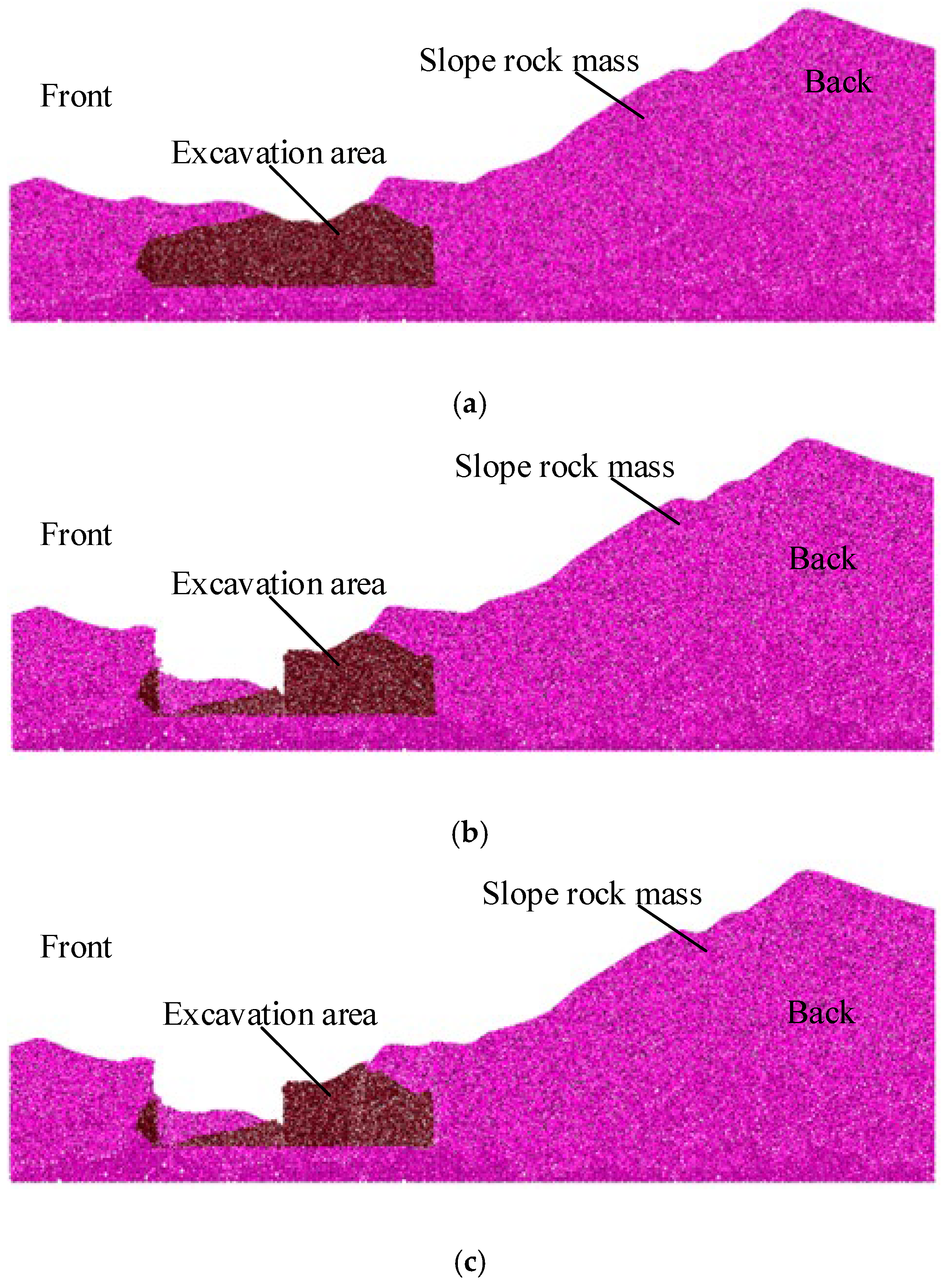
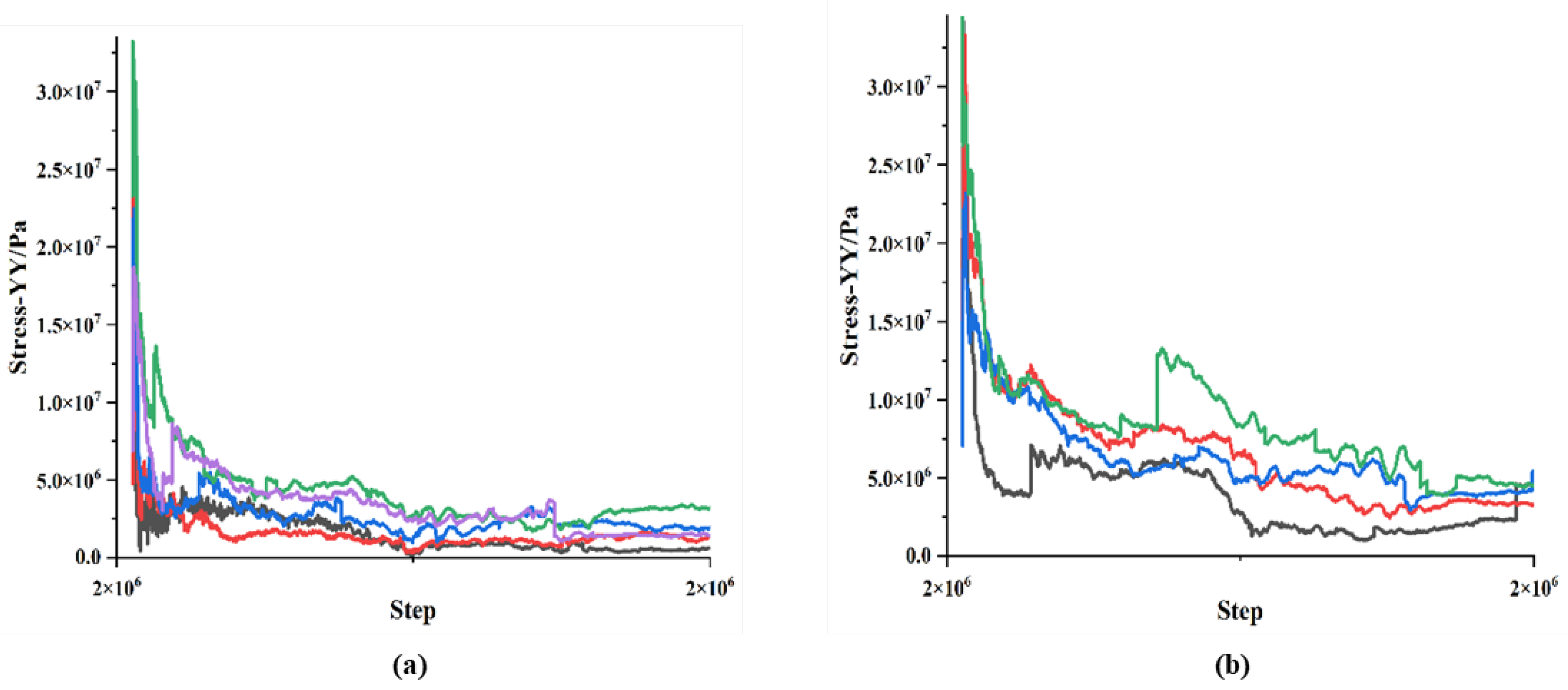
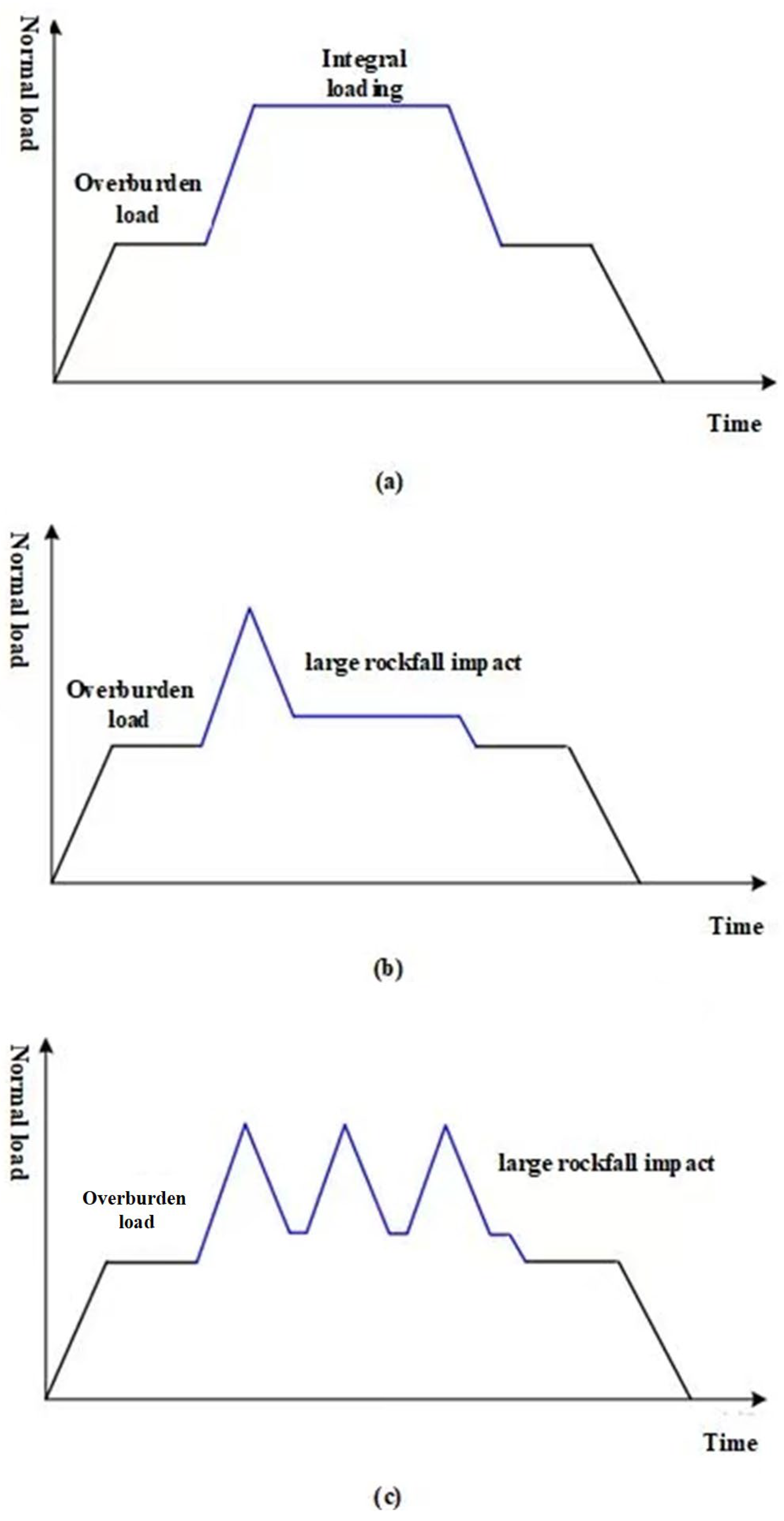
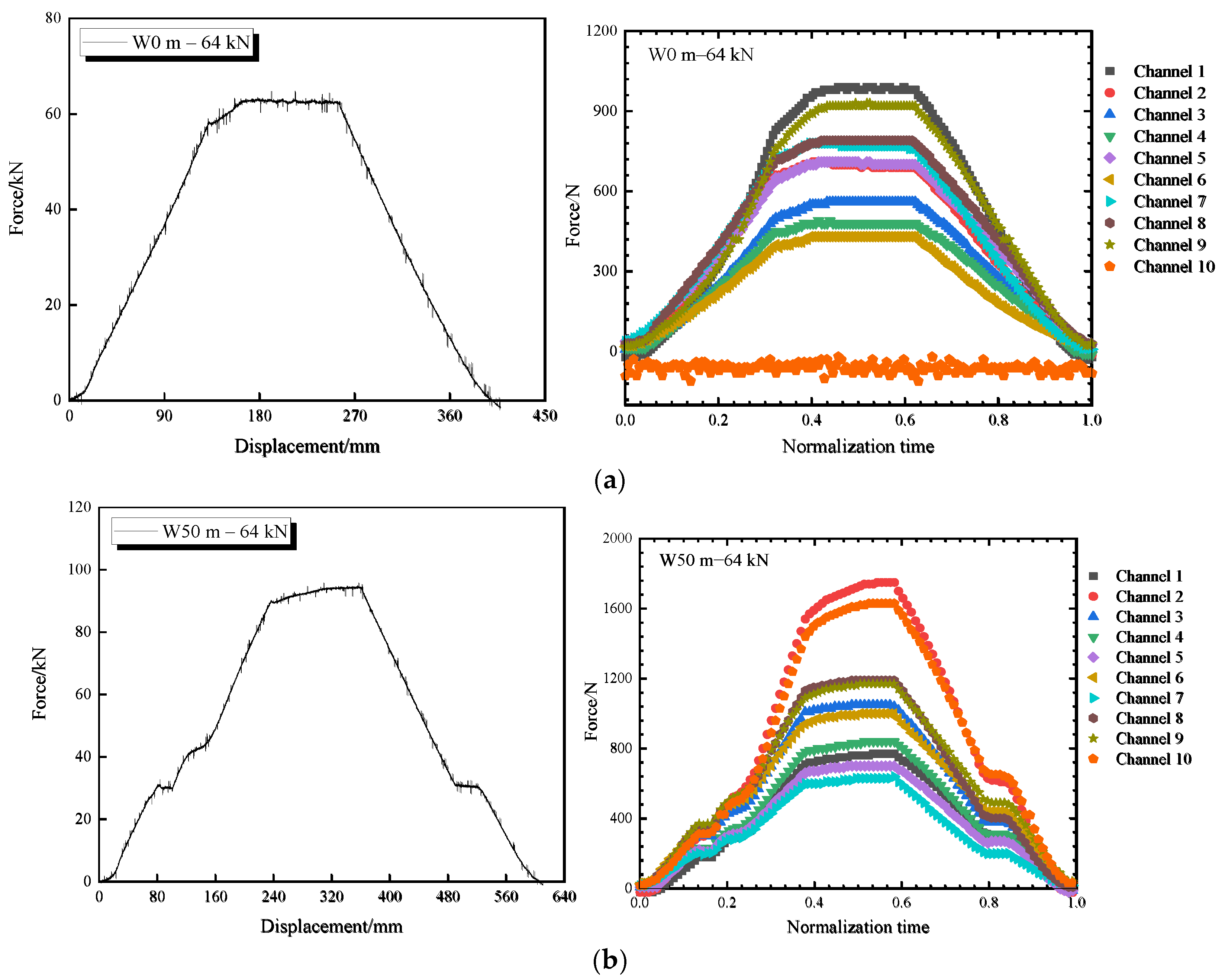
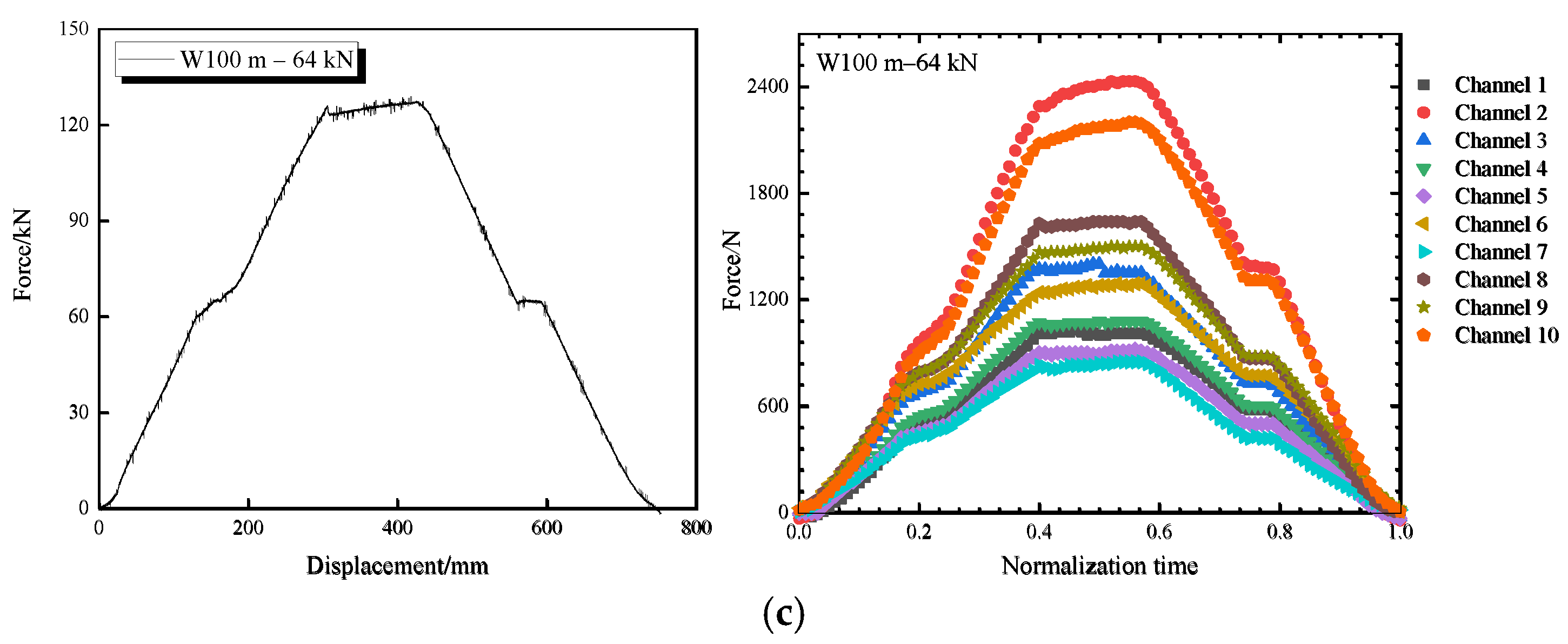
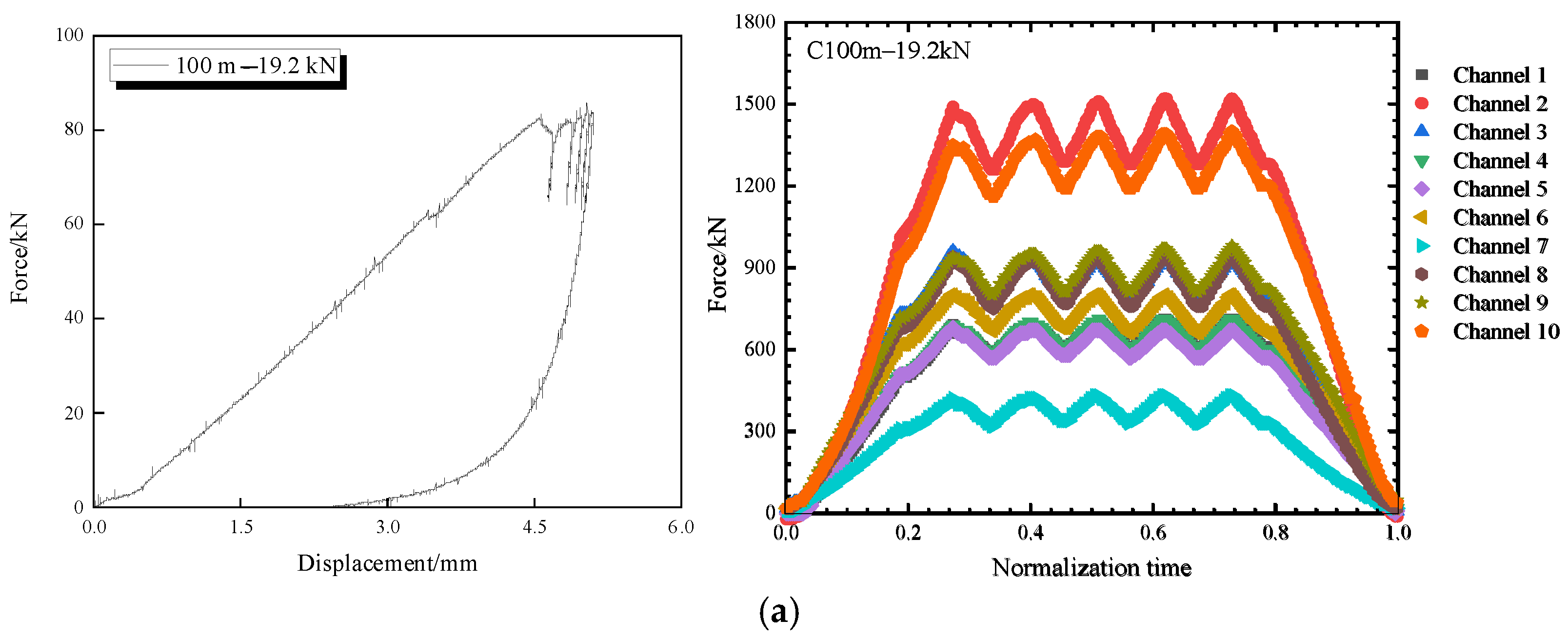
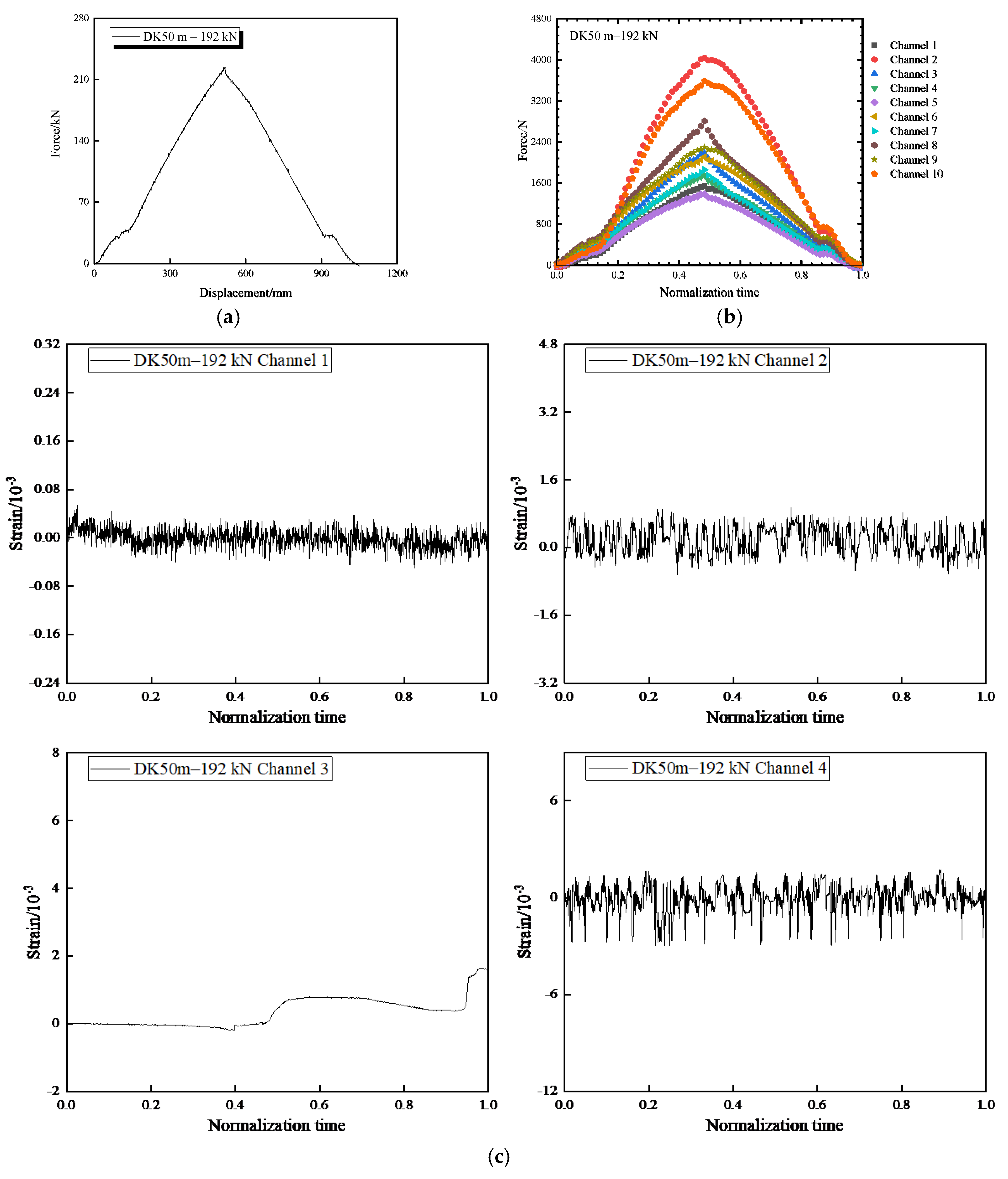
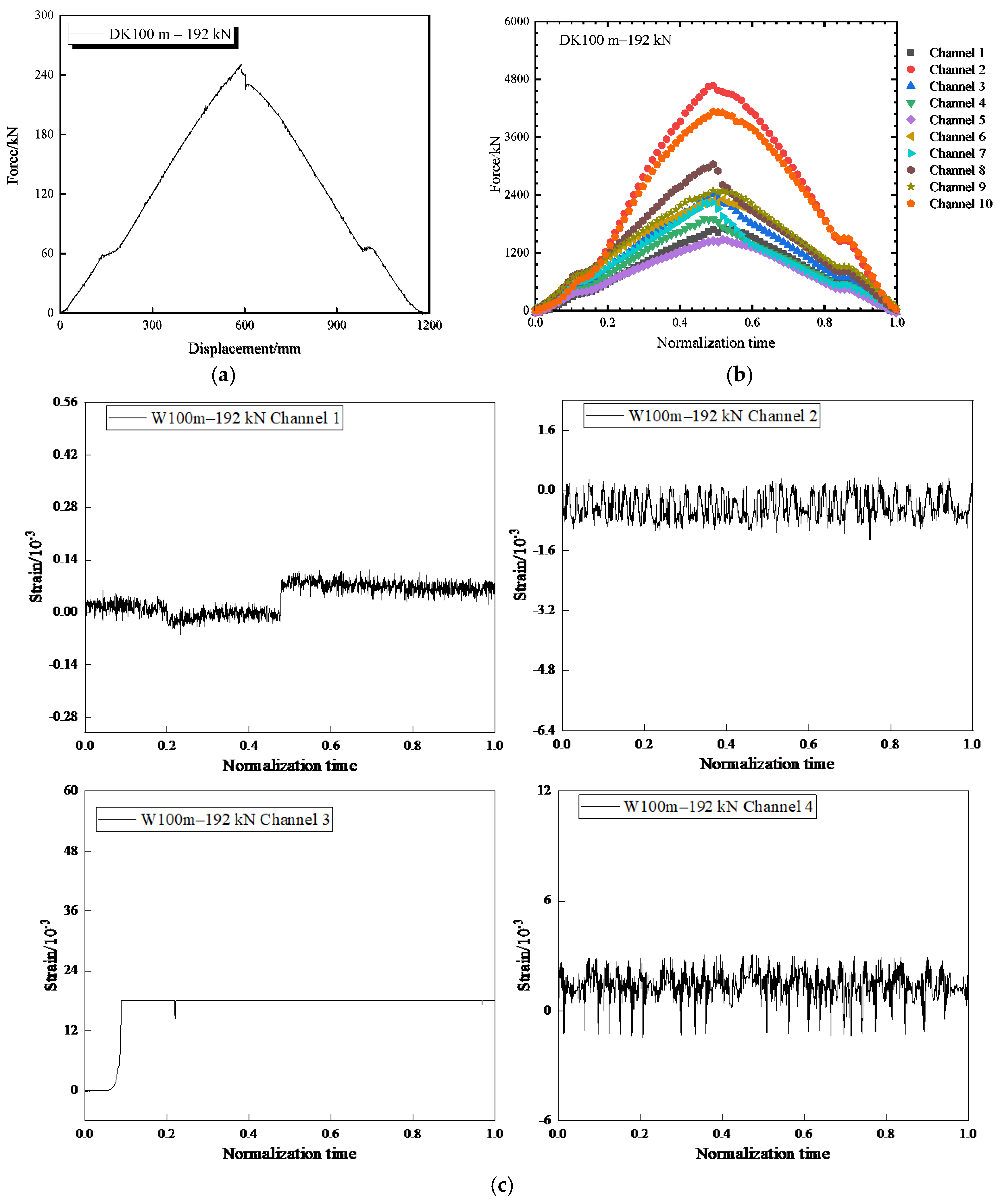
5. Overall Collapse Impact Effect
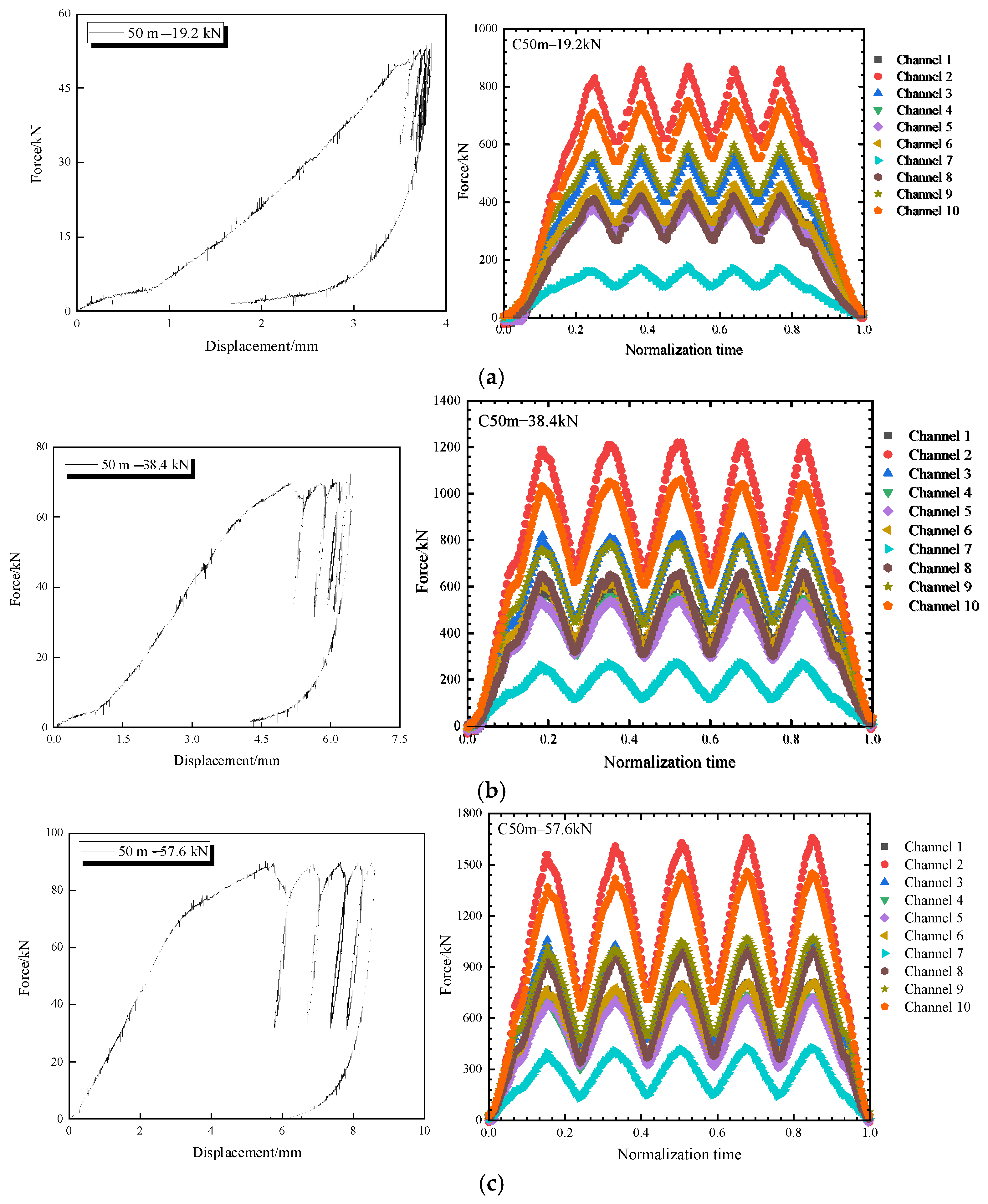
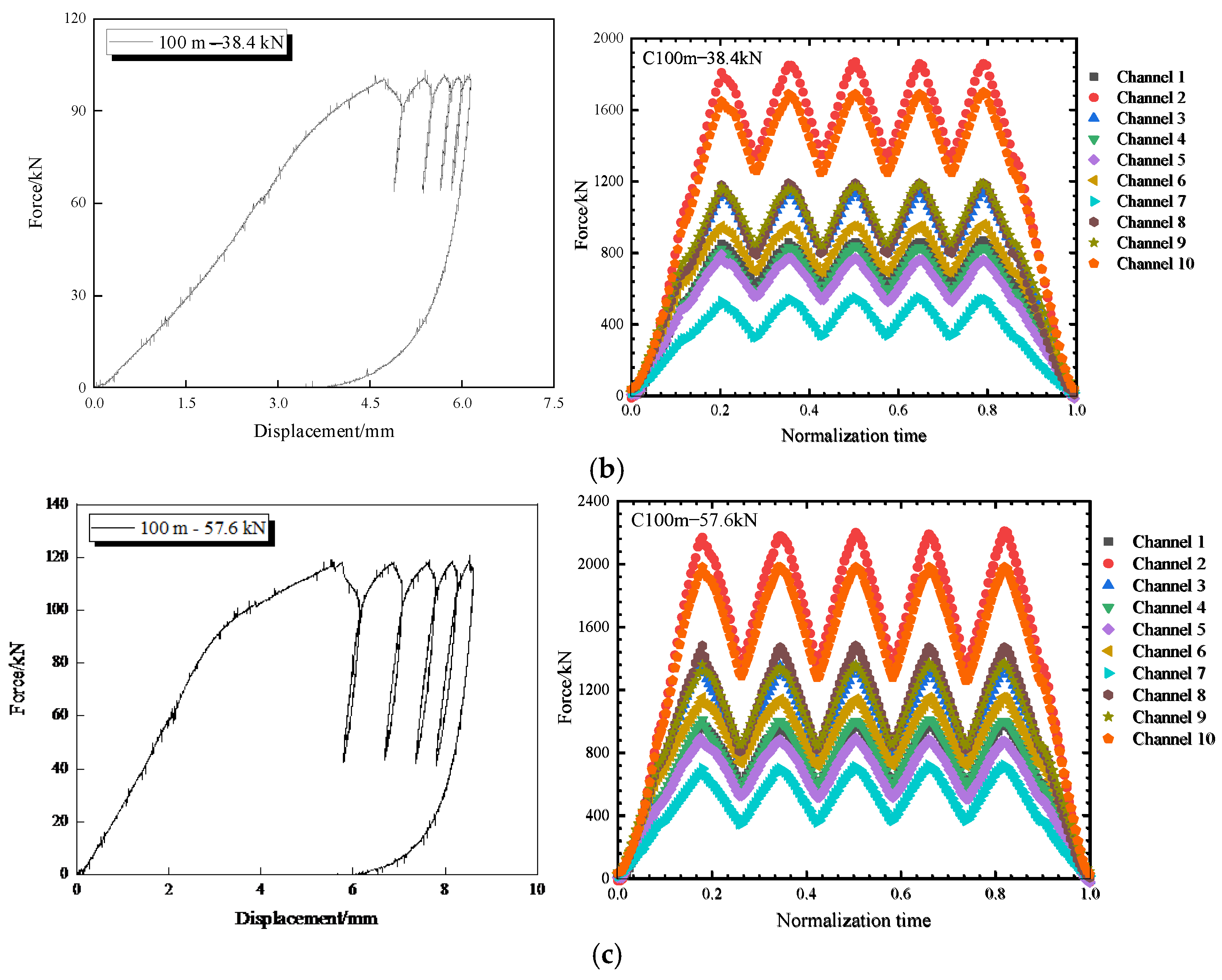
6. Multiple Impact Effects of Progressive Collapse
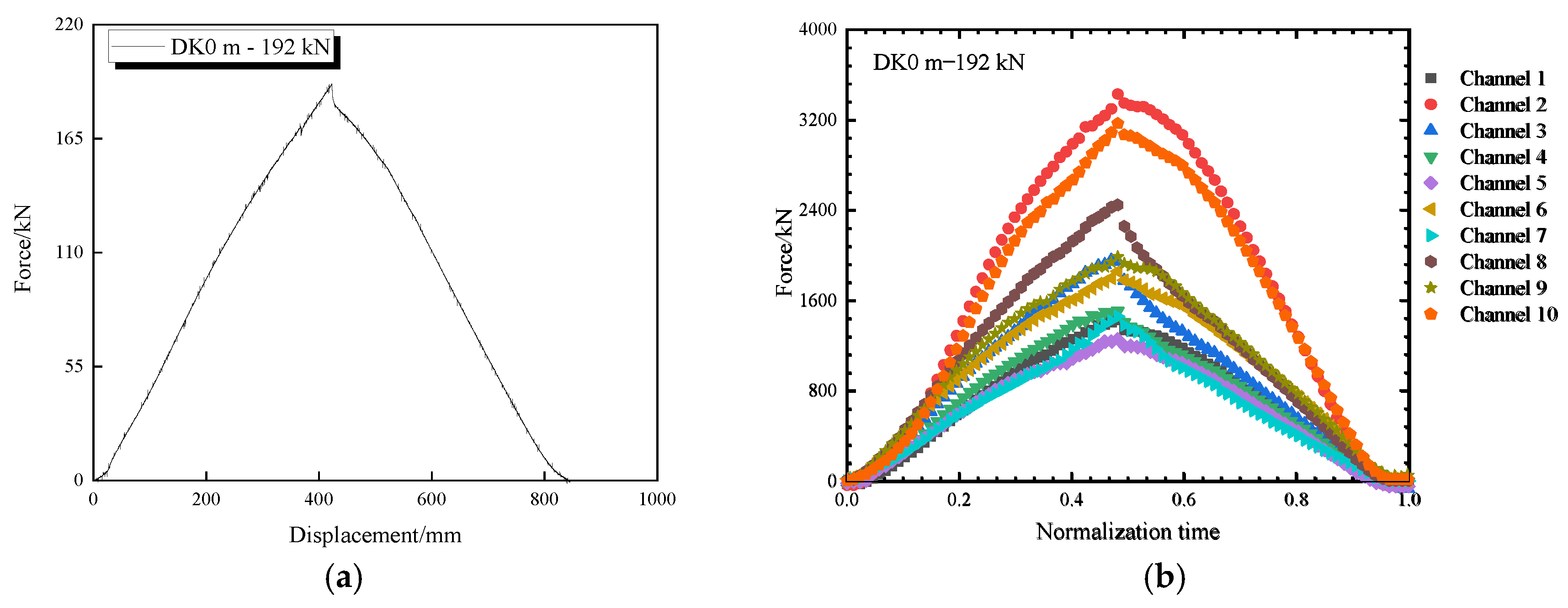
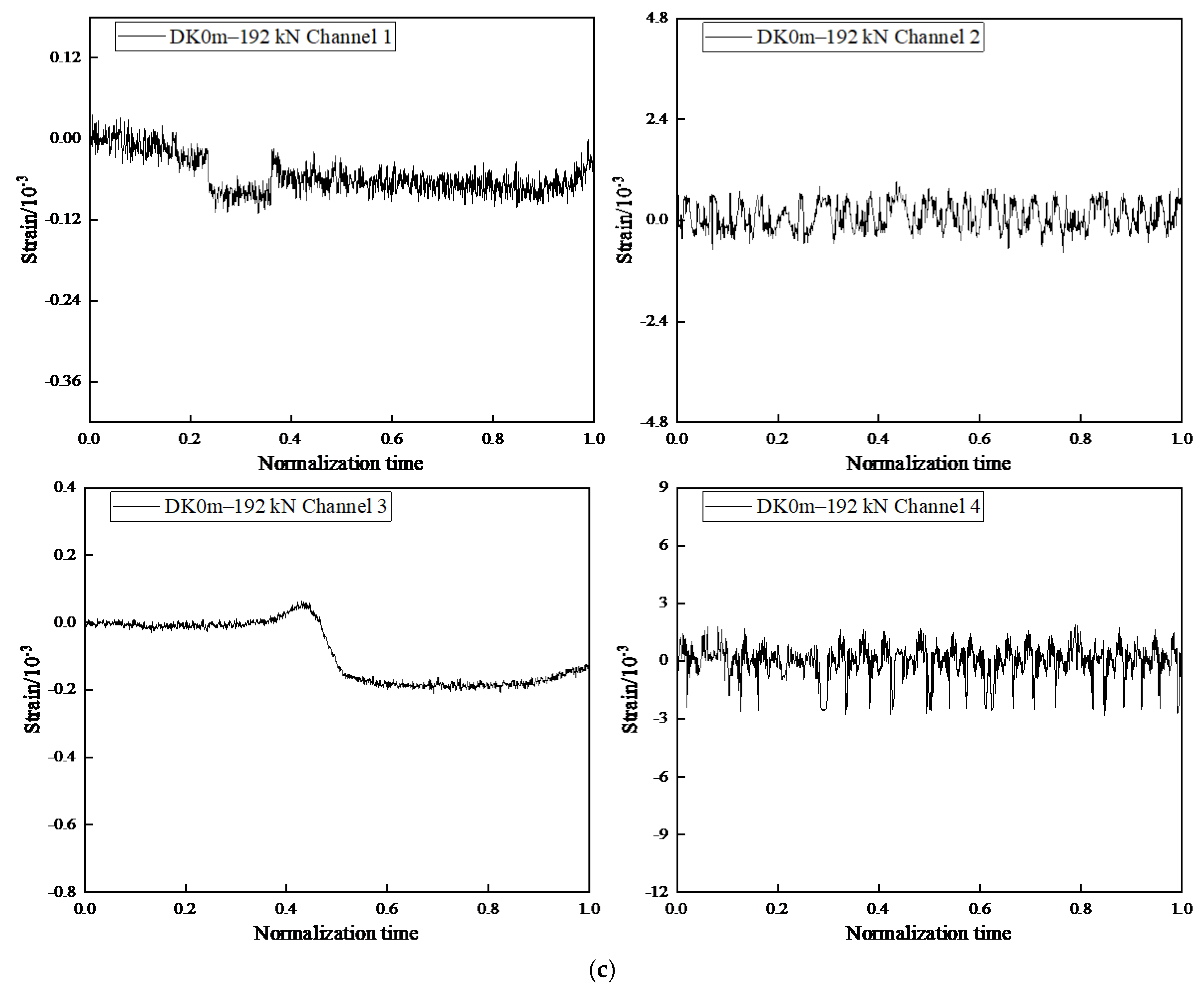
7. Overall Large Block Collapse Impact Effect
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brown, E.T. Block Caving Geomechanics; The University of Queensland: Brisbane, Australia, 2007. [Google Scholar]
- Brzovic, A.; Villaescusa, E. Rock mass characterization and assessment of block-forming geological discontinuities during caving of primary copper ore at the El Teniente mine, Chile. Int. J. Rock Mech. Min. Sci. 2007, 44, 565–583. [Google Scholar] [CrossRef]
- Wu, A.X.; Sun, Y.Z.; Gour, S.; Shen, H.M.; Yang, B.H. Characteristics of rockburst and its mining technology in mines. J. Cent. South Univ. 2002, 9, 255–259. [Google Scholar] [CrossRef]
- Dorador, L.; Eberhardt, E.; Elmo, D. Influence of Block Strength and Veining on Secondary Fragmentation Related to Block Caving; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2015. [Google Scholar]
- Vyazmensky, A.; Stead, D.; Elmo, D.; Moss, A. Numerical Analysis of Block Caving-Induced Instability in Large Open Pit Slopes: A Finite Element/Discrete Element Approach. Rock Mech. Rock Eng. 2010, 43, 21–39. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, H.; Yang, C. Fatigue-thermal damage characteristics of red sandstone with a hole under high-temperature cyclic loading coupling and microstructural degradation. J. Mater. Res. Technol. 2024, 33, 3250–3263. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, H.; Feng, X.; Yang, C.; Ou, K.; Chen, Y. Fracture characteristics and damage mechanisms of heat-treated sandstone with combined hole-joint flaws under uniaxial compression. Theor. Appl. Fract. Mech. 2025, 136, 104845. [Google Scholar] [CrossRef]
- Wang, Z.; Li, S.; Lin, H.; Chen, Y. Fatigue response and AE characteristics of soft and hard composite rock containing coplanar double joints. Int. J. Fatigue 2025, 198, 108994. [Google Scholar] [CrossRef]
- Haimson, B.; Chang, C. A new true triaxial cell for testing mechanical properties of rock, and its use to determine rock strength and deformability of Westerly granite. Int. J. Rock Mech. Min. Sci. 2000, 37, 285–296. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, R.; Li, S.; Lu, G.; Zhang, Q.; Qiu, S. A Novel Dynamic Fractional Mechanical Model for Rock Fracture Under True Triaxial Static-Dynamic Combined Loading and its Engineering Application. Rock Mech. Rock Eng. 2024, 57, 9343–9369. [Google Scholar] [CrossRef]
- Shen, F.; Qiu, W.; Zhu, H.; Wu, T.; Qi, L.; Xing, M. Numerical simulation of frost heaving deformation of fractured rocks considering heat-force coupling. Theor. Appl. Fract. Mech. 2025, 138, 104921. [Google Scholar] [CrossRef]
- Feng, X.-T.; Zhang, X.; Kong, R.; Wang, G. A Novel Mogi Type True Triaxial Testing Apparatus and Its Use to Obtain Complete Stress–Strain Curves of Hard Rocks. Rock Mech. Rock Eng. 2016, 49, 1649–1662. [Google Scholar] [CrossRef]
- He, M.C.; Miao, J.L.; Feng, J.L. Rock burst process of limestone and its acoustic emission characteristics under true-triaxial unloading conditions. Int. J. Rock Mech. Min. Sci. 2010, 47, 286–298. [Google Scholar] [CrossRef]
- Pierce, M.E. Forecasting vulnerability of deep extraction level excavations to draw-induced cave loads. J. Rock Mech. Geotech. Eng. 2019, 11, 527–534. [Google Scholar] [CrossRef]
- Castro, R.; Gómez, R.; Castillo, J.; Jerez, O. Fragmentation model integrated in a gravity flow simulator for block caving planning. Granul. Matter 2024, 26, 22. [Google Scholar] [CrossRef]
- Sun, H.; Zhou, S.; Chen, S.; Jin, A.; Yin, Z.; Wang, X.; Dai, Z. Flow characteristics of caved ore and rock under the influence of multiple coarse particles: Insight from interparticle interaction. Granul. Matter 2024, 26, 82. [Google Scholar] [CrossRef]
- Zhao, Y.; Wu, Y.; Wang, Y.; He, S.; Li, X.; Zhu, L.; Wang, Z. Study on the influence of 3D pre-existing joint on rockfall fragmentation during impact based on discrete element method. Comput. Geotech. 2025, 184, 107270. [Google Scholar] [CrossRef]
- Sánchez, V.; Castro, R.L.; Palma, S. Gravity flow characterization of fine granular material for Block Caving. Int. J. Rock Mech. Min. Sci. 2019, 114, 24–32. [Google Scholar] [CrossRef]
- Castro, R.; Gómez, R.; Pierce, M.; Canales, J. Experimental quantification of vertical stresses during gravity flow in block caving. Int. J. Rock Mech. Min. Sci. 2020, 127, 104237. [Google Scholar] [CrossRef]
- Xiao, J.-Q.; Ding, D.-X.; Jiang, F.-L.; Xu, G. Fatigue damage variable and evolution of rock subjected to cyclic loading. Int. J. Rock Mech. Min. Sci. 2010, 47, 461–468. [Google Scholar] [CrossRef]
- Saavedra, F.; Morales, N.; Nelis, G.; Gómez, R. A fast method to find smooth economic envelopes for block and panel caving mines. Resour. Policy 2023, 83, 103703. [Google Scholar] [CrossRef]
- Luo, S.; Gong, F.-q.; Li, L.-l.; Peng, K. Linear energy storage and dissipation laws and damage evolution characteristics of rock under triaxial cyclic compression with different confining pressures. Trans. Nonferrous Met. Soc. China 2023, 33, 2168–2182. [Google Scholar] [CrossRef]
- Guan, Z.; Li, Y.; Lai, Z.; Zhou, H.; Qin, J.; Wen, Y.; Chen, Y.; Huang, R. Size effect of concrete based on split Hopkinson pressure bar (SHPB) test. Constr. Build. Mater. 2024, 441, 137499. [Google Scholar] [CrossRef]
- Rafiee, R.; Ataei, M.; KhalooKakaie, R.; Jalali, S.E.; Sereshki, F.; Noroozi, M. Numerical modeling of influence parameters in cavabililty of rock mass in block caving mines. Int. J. Rock Mech. Min. Sci. 2018, 105, 22–27. [Google Scholar] [CrossRef]
- Zhou, K.-p.; Li, L.; Lin, Y.; Xiong, X.; Yang, N.-g.; Chen, S.-l. New method and application of disturbance range prediction for caving method of metal ore. Trans. Nonferrous Met. Soc. China 2023, 33, 889–901. [Google Scholar] [CrossRef]
- Jiang, M.; Sun, W.; Wang, S.; Feng, X.; Li, Z.; Chen, H.; Chen, C. Experimental and technological research on grouting and curing of surface moraine collapse pits in block caving mining. Eng. Fail. Anal. 2025, 175, 109574. [Google Scholar] [CrossRef]
- Woo, K.-S.; Eberhardt, E.; Rabus, B.; Stead, D.; Vyazmensky, A. Integration of field characterisation, mine production and InSAR monitoring data to constrain and calibrate 3-D numerical modelling of block caving-induced subsidence. Int. J. Rock Mech. Min. Sci. 2012, 53, 166–178. [Google Scholar] [CrossRef]
- Castro, R.; Perez, Á.; Gomez, R. Evaluating wet muck risk in block caving mines: A new model. Int. J. Rock Mech. Min. Sci. 2023, 170, 105485. [Google Scholar] [CrossRef]
- Wu, M.; Wang, J.; Zhao, B. DEM modeling of one-dimensional compression of sands incorporating statistical particle fragmentation scheme. Can. Geotech. J. 2021, 59, 144–157. [Google Scholar] [CrossRef]
- Le-Feaux, R.; Castro, R.; Cortez, D.; Gómez, R.; Silva, D. A hybrid extraction level layout design for block caving. Min. Technol. 2022, 131, 51–65. [Google Scholar] [CrossRef]
- Jiang, B.; Wang, L.; Lu, Y.; Wang, C. Combined early warning method for rockburst in a Deep Island, fully mechanized caving face. Arab. J. Geosci. 2016, 9, 1–13. [Google Scholar] [CrossRef]
- Puller, J.W.; Mills, K.W.; Jeffrey, R.G.; Walker, R.J. In-situ stress measurements and stress change monitoring to monitor overburden caving behaviour and hydraulic fracture pre-conditioning. Int. J. Min. Sci. Technol. 2016, 26, 103–110. [Google Scholar] [CrossRef]
- Lavoie, T.; Eberhardt, E.; Pierce, M.E. Numerical modelling of rock mass bulking and geometric dilation using a bonded block modelling approach to assist in support design for deep mining pillars. Int. J. Rock Mech. Min. Sci. 2022, 156, 105145. [Google Scholar] [CrossRef]










| Parameters Types | PFC Parameters | Magnitude |
|---|---|---|
| Basic parameters of particles | Density (kg/m3) | 2600 |
| Contact modulus (Ec/Gpa) | 6.3 | |
| Stiffness ratio (kn/ks) | 1.2 | |
| Coefficient of friction | 0.4 | |
| Small particle radius (m) | 1~1.66 | |
| Large particle radius (m) | 5~5.66 | |
| Porosity (P) | 0.16 | |
| Parallel bonding parameters | Parallel bonding stiffness ratio | 1.5 |
| Parallel bond modulus | 6.3 | |
| Parallel bonding internal friction angle (°) | 36.8 | |
| Parallel bonding tensile strength (MPa) | 41 | |
| Parallel bonding cohesion (MPa) | 38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, X.; Li, G.; Wang, Z.; Zhu, X.; Huang, Z.; Lin, H. Mechanical Response and Failure Mechanisms of Block Caving Bottom Structures Under Dynamic Conditions Induced by Slope Rockfalls. Appl. Sci. 2025, 15, 6867. https://doi.org/10.3390/app15126867
Feng X, Li G, Wang Z, Zhu X, Huang Z, Lin H. Mechanical Response and Failure Mechanisms of Block Caving Bottom Structures Under Dynamic Conditions Induced by Slope Rockfalls. Applied Sciences. 2025; 15(12):6867. https://doi.org/10.3390/app15126867
Chicago/Turabian StyleFeng, Xinglong, Guangquan Li, Zeyue Wang, Xiongpeng Zhu, Zhenggao Huang, and Hang Lin. 2025. "Mechanical Response and Failure Mechanisms of Block Caving Bottom Structures Under Dynamic Conditions Induced by Slope Rockfalls" Applied Sciences 15, no. 12: 6867. https://doi.org/10.3390/app15126867
APA StyleFeng, X., Li, G., Wang, Z., Zhu, X., Huang, Z., & Lin, H. (2025). Mechanical Response and Failure Mechanisms of Block Caving Bottom Structures Under Dynamic Conditions Induced by Slope Rockfalls. Applied Sciences, 15(12), 6867. https://doi.org/10.3390/app15126867







