Stress Characteristics and Mechanical Behavior of Rock Masses with an Opening under Complex Deep Underground Stress Conditions
Abstract
1. Introduction
2. Methods
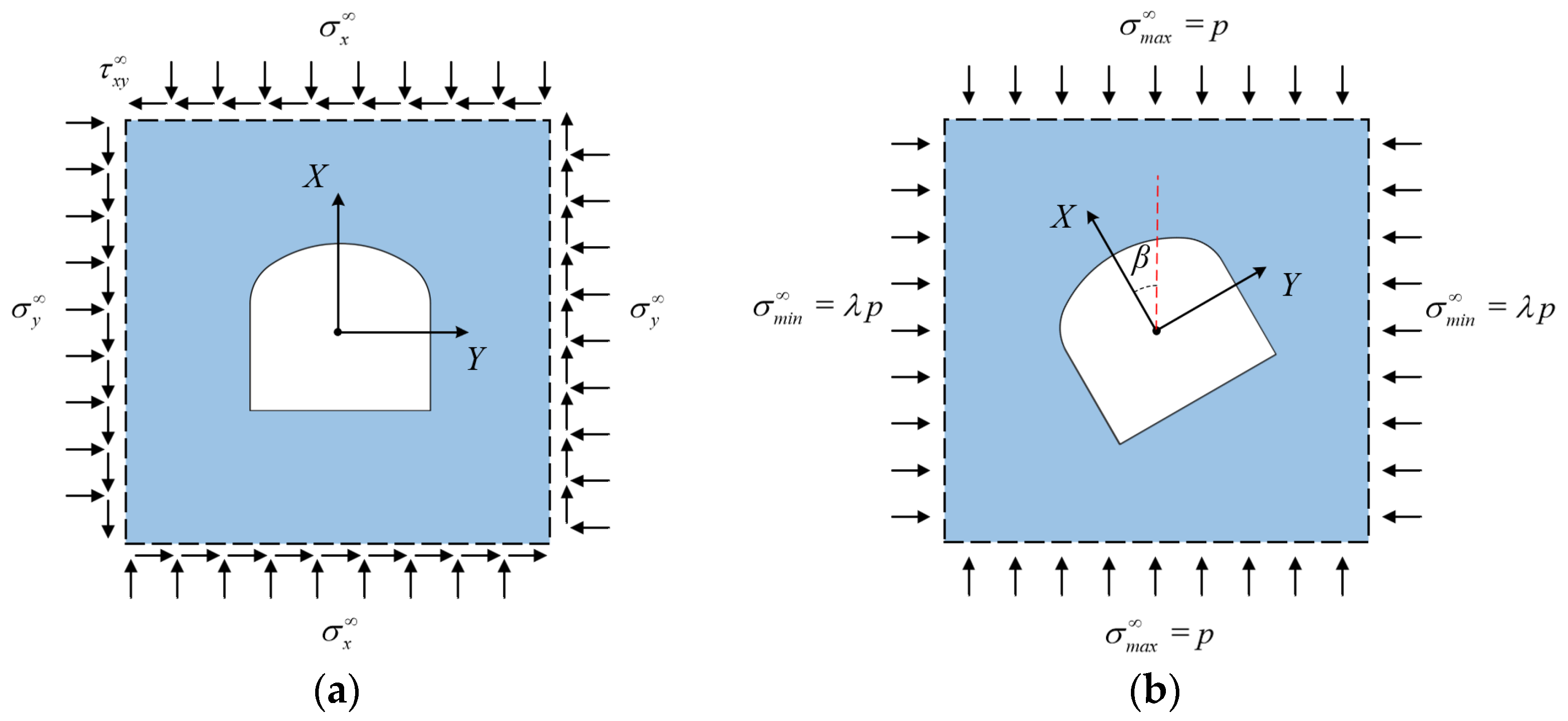
2.1. Complex Function Method for Analytical Stress Solutions
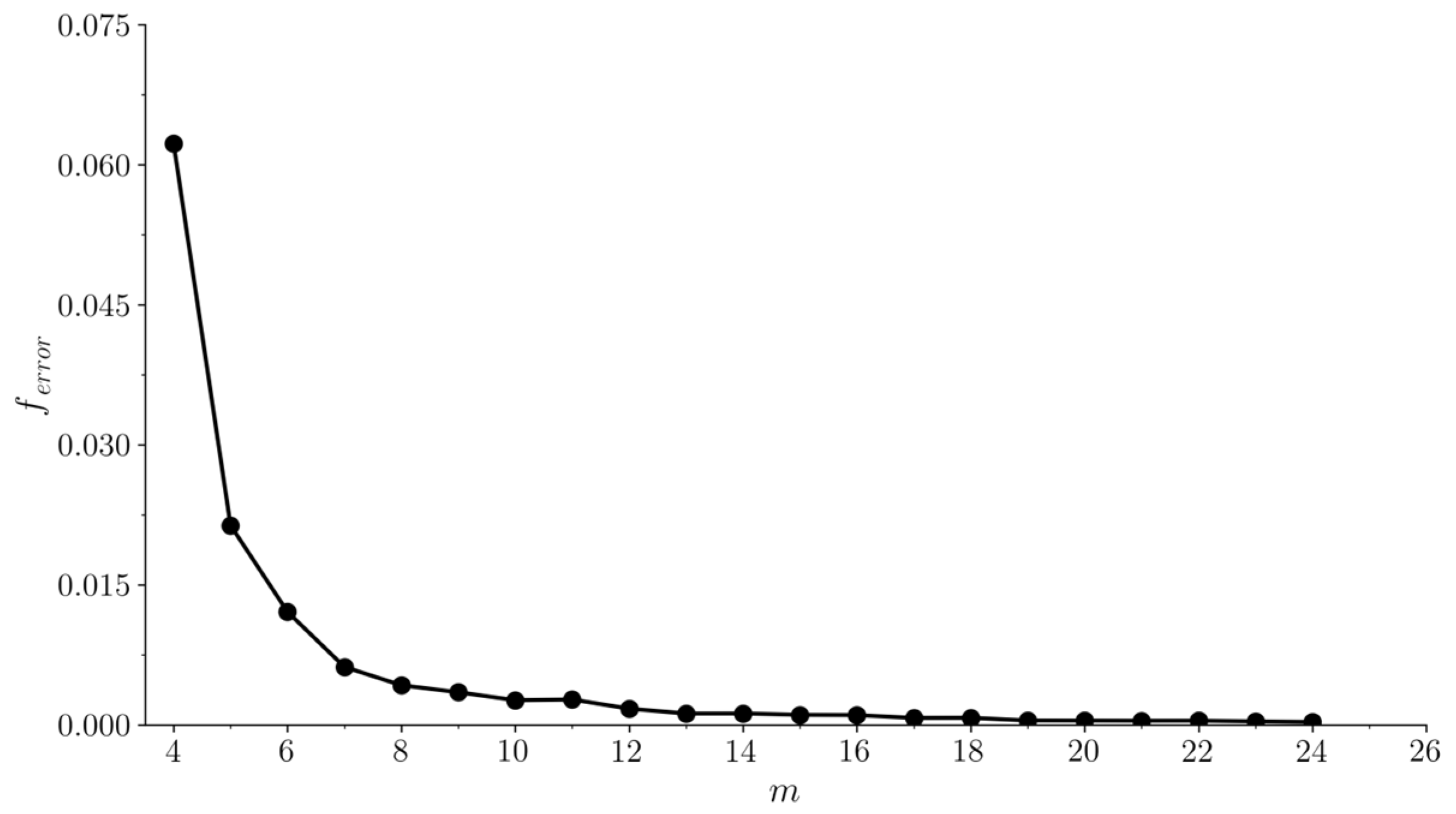
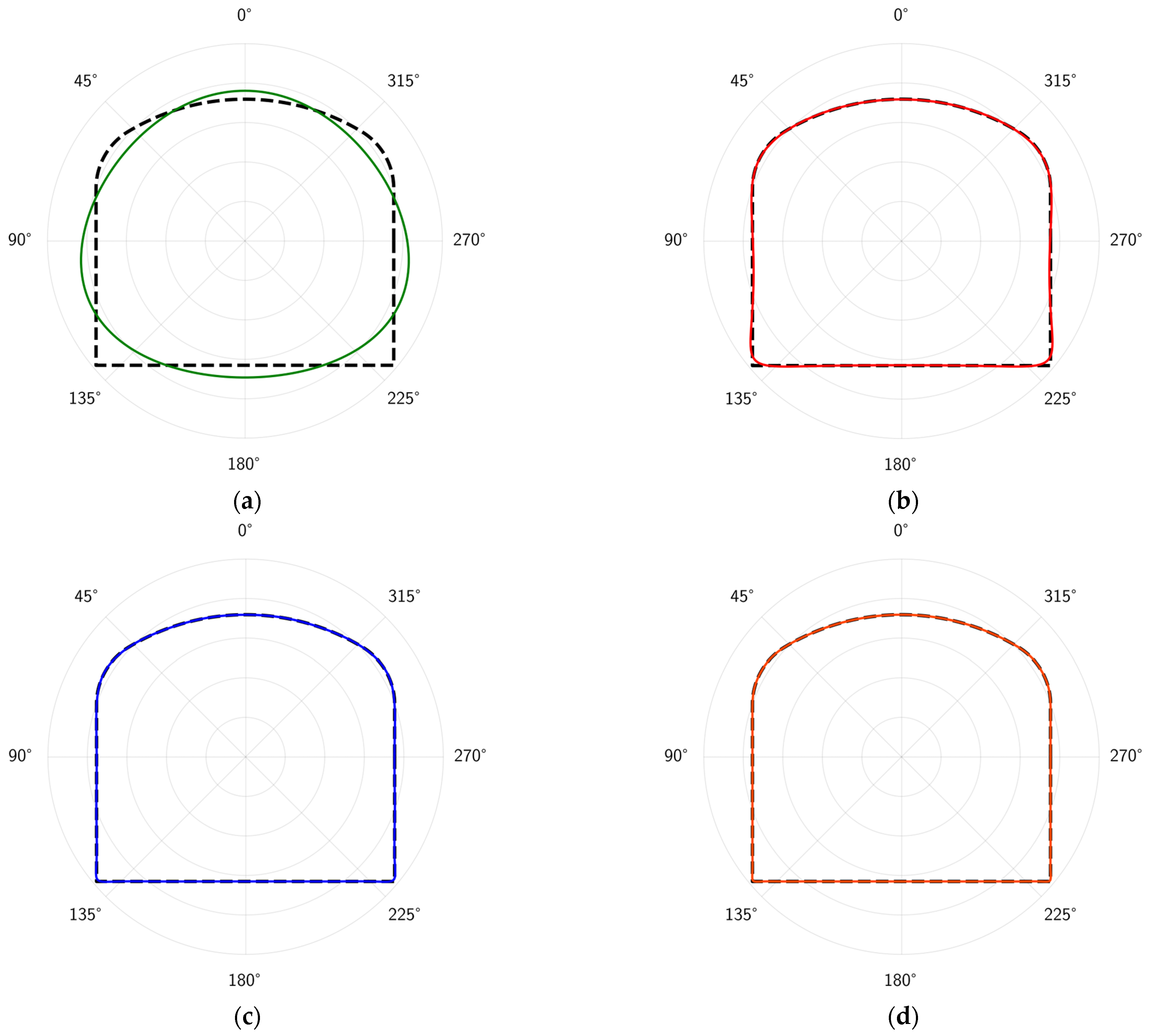
2.2. Determination of Mapping Function
3. Results
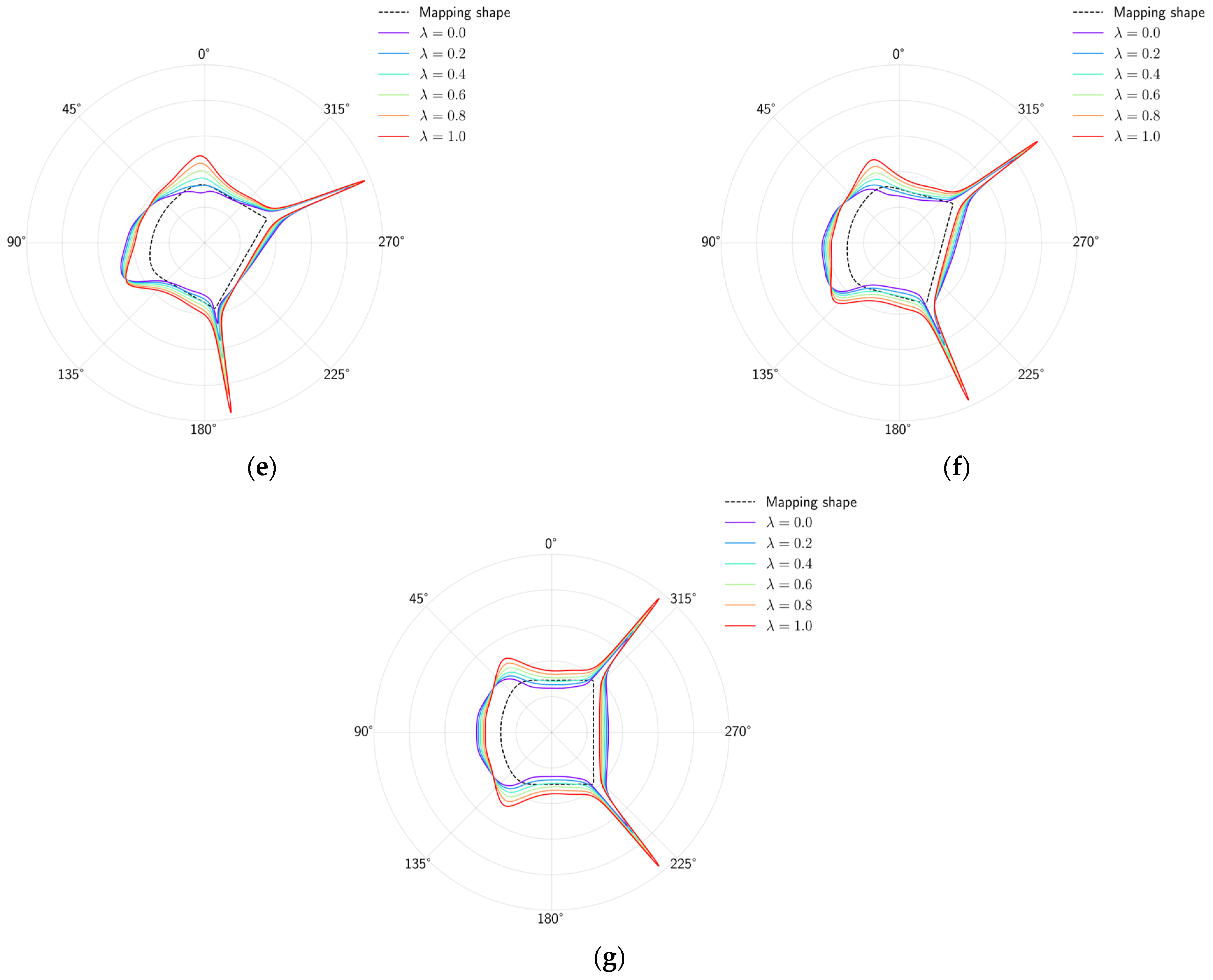
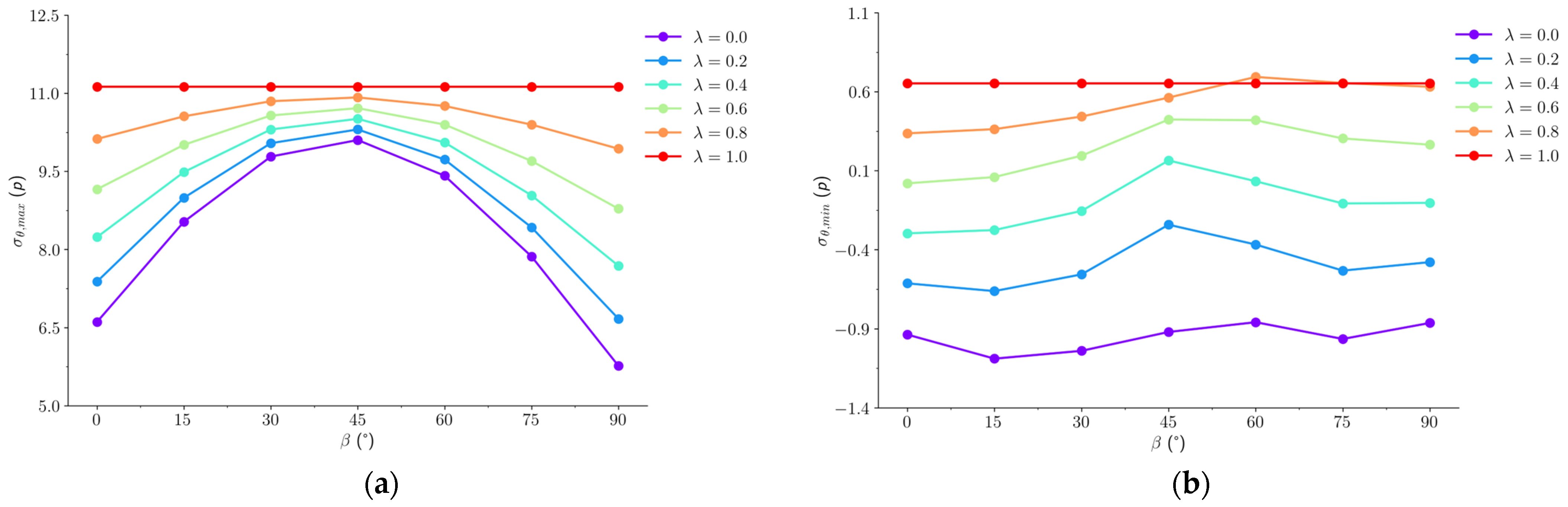
3.1. Stress Distribution Characteristics
3.2. Initial Failure Mode
4. Conclusions
- The lateral pressure coefficient mainly affects the stability of the opening by influencing the stress concentration around the surrounding rock. When the lateral pressure coefficient is at a low level, tensile stress concentration is likely to occur in the boundary area of the opening perpendicular to the maximum principal stress. Within the scope of this study, as the lateral pressure coefficient increases, the tensile stress disappears, and the compressive stress region expands, enhancing the stability of the opening.
- The direction of the principal stress has a minor effect on the degree of tensile stress concentration around the surrounding rock of the opening, but it significantly impacts the stress distribution at the boundary of the opening. When the angle between the maximum principal stress in the plane and the vertical direction is 45°, the compressive stress at the corners of the opening’s straight walls reaches its maximum. This region is prone to failure due to the high compressive stress. In cases where the lateral pressure coefficient is not equal to 1, the stress distribution asymmetry is most pronounced.
- DEM numerical simulations confirmed that initial failures occur in areas of compressive or tensile stress concentration, validating the analytical stress solutions. As the lateral pressure coefficient increases, the tensile stress decreases and eventually disappears, while the compressive stress-induced failure range significantly expands.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, Z.; Cai, X.; Li, X.; Cao, W.; Du, X. Dynamic Response and Energy Evolution of Sandstone under Coupled Static–Dynamic Compression: Insights from Experimental Study into Deep Rock Engineering Applications. Rock Mech. Rock Eng. 2020, 53, 1305–1331. [Google Scholar] [CrossRef]
- Li, Z.; Ren, T.; Li, X.; Cheng, Y.; He, X.; Lin, J.; Qiao, M.; Yang, X. Full-scale pore structure characterization of different rank coals and its impact on gas adsorption capacity: A theoretical model and experimental study. Energy 2023, 277, 127621. [Google Scholar] [CrossRef]
- Tan, L.; Ren, T.; Dou, L.; Sun, J.; Yang, X.; Qiao, M. Moisture penetration and distribution characterization of hard coal: A µ-CT study. Int. J. Coal Sci. Technol. 2024, 11, 55. [Google Scholar] [CrossRef]
- Tan, L.; Ren, T.; Yang, X.; He, X. A numerical simulation study on mechanical behaviour of coal with bedding planes under coupled static and dynamic load. Int. J. Min. Sci. Technol. 2018, 28, 791–797. [Google Scholar] [CrossRef]
- Cao, R.-h.; Yao, R.; Hu, T.; Wang, C.; Li, K.; Meng, J. Failure and mechanical behavior of transversely isotropic rock under compression-shear tests: Laboratory testing and numerical simulation. Eng. Fract. Mech. 2021, 241, 107389. [Google Scholar] [CrossRef]
- Xin, J.; Jiang, Q.; Li, S.; Chen, P.; Zhao, H. Fracturing and Energy Evolution of Rock around Prefabricated Rectangular and Circular Tunnels under Shearing Load: A Comparative Analysis. Rock Mech. Rock Eng. 2023, 56, 9057–9084. [Google Scholar] [CrossRef]
- Feng, F.; Li, X.; Rostami, J.; Li, D. Modeling hard rock failure induced by structural planes around deep circular tunnels. Eng. Fract. Mech. 2019, 205, 152–174. [Google Scholar] [CrossRef]
- Soni, S.; Saindane, U. Stress Analysis of Infinite Plate with Elliptical Hole; Springer: Singapore, 2019; pp. 535–545. [Google Scholar]
- Cao, X.; Gong, W.; Zhou, F.; Dai, G. Stress Analytical Solution for Shallow Buried Lined Circular Tunnel under the Deformation of Surrounding Rock Inner Edge. Geotech. Geol. Eng. 2019, 37, 3771–3780. [Google Scholar] [CrossRef]
- Xiao, W.; Zhang, D.; Li, S.; Lu, J. Fracture evolution and fracture mechanism of tunnel surrounding rock: A case study based on laboratory tests and theoretical analysis. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 2617–2638. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, G.-y.; Ma, S.-w. Failure behavior of horseshoe-shaped tunnel in hard rock under high stress: Phenomenon and mechanisms. Trans. Nonferrous Met. Soc. China 2022, 32, 639–656. [Google Scholar] [CrossRef]
- Zhao, G.; Yang, S. Analytical solutions for rock stress around square tunnels using complex variable theory. Int. J. Rock Mech. Min. Sci. 2015, 80, 302–307. [Google Scholar] [CrossRef]
- Wu, H.; Ma, D. Fracture response and mechanisms of brittle rock with different numbers of openings under uniaxial loading. Geomech. Eng. 2021, 25, 481–493. [Google Scholar]
- Tan, L.; Ren, T.; Dou, L.; Yang, X.; Qiao, M.; Peng, H. Analytical stress solution and mechanical properties for rock mass containing a hole with complex shape. Theor. Appl. Fract. Mech. 2021, 114, 103002. [Google Scholar] [CrossRef]
- Tan, L.; Ren, T.; Dou, L.; Yang, X.; Wang, G.; Peng, H. Analytical Stress Solution and Numerical Mechanical Behavior of Rock Mass Containing an Opening under Different Confining Stress Conditions. Mathematics 2021, 9, 2462. [Google Scholar] [CrossRef]
- Jiang, H.; Li, R.; Wang, L.; Li, C.; Su, G. Influence of Principal Stress Direction on the Fracture Characteristics of Granite with an Inverted U-Shaped Cavity. Int. J. Civ. Eng. 2023, 21, 1835–1851. [Google Scholar] [CrossRef]
- Lu, J.; Yin, G.; Zhang, D.; Li, X.; Huang, G.; Gao, H. Mechanical properties and failure mode of sandstone specimen with a prefabricated borehole under true triaxial stress condition. Geomech. Energy Environ. 2021, 25, 100207. [Google Scholar] [CrossRef]
- Zhao, Y.; Wu, J. The Influence of Underground Cavity on The Stability of Tunnel Excavation. Int. J. Nat. Resour. Environ. Stud. 2024, 2, 64–77. [Google Scholar] [CrossRef]
- Pu, S.; Wu, R.; Wu, S.; Cheng, H.; Cao, L.; Ren, Z. Analysis of Deformation Characteristics and Failure Mechanism of Interbedded Surrounding Rock Tunnels Based on Principal Stress Difference. Int. J. Geomech. 2024, 24, 04024197. [Google Scholar] [CrossRef]
- Abbaszadeh Shahri, A.; Larsson, S.; Renkel, C. Artificial intelligence models to generate visualized bedrock level: A case study in Sweden. Model. Earth Syst. Environ. 2020, 6, 1509–1528. [Google Scholar] [CrossRef]
- Muskhelishvili, N.I. Some Basic Problems of the Mathematical Theory of Elasticity; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Ukadgaonker, V.; Rao, D. Stress distribution around triangular holes in anisotropic plates. Compos. Struct. 1999, 45, 171–183. [Google Scholar] [CrossRef]
- Hromadka, T.V.; Lai, C. The Complex Variable Boundary Element Method in Engineering Analysis; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Itasca Consulting Group, Inc. Particle Flow Code 6.0; Itasca: Minneapolis, MN, USA, 2017; Volume 4. [Google Scholar]
- Zhang, X.-P.; Liu, Q.; Wu, S.; Tang, X. Crack coalescence between two non-parallel flaws in rock-like material under uniaxial compression. Eng. Geol. 2015, 199, 74–90. [Google Scholar] [CrossRef]

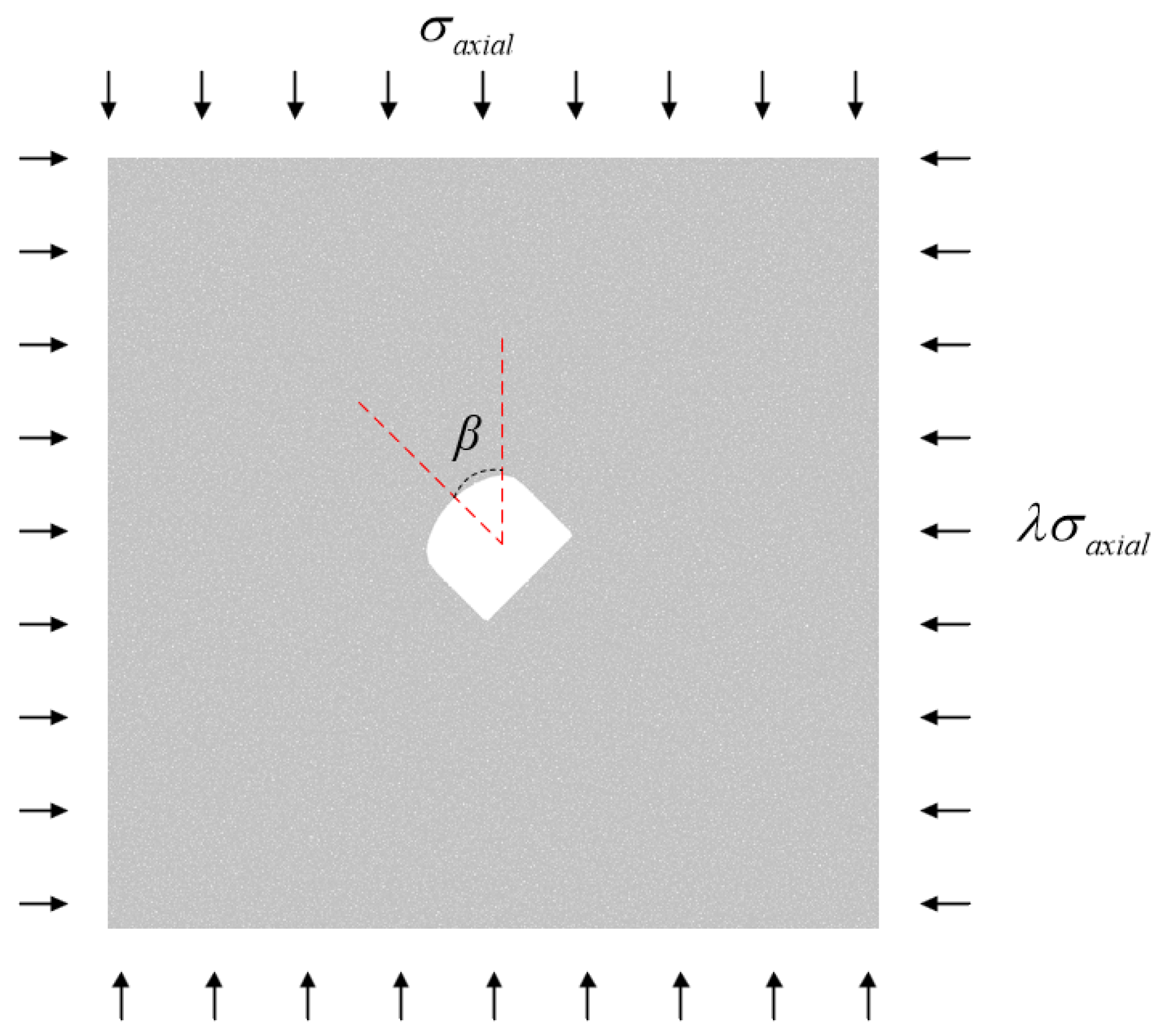


| Principal Stress State | Non-Principal Stress State | |||
|---|---|---|---|---|
| λ | β | σx | σy | τxy |
| 0 | 0 | 1.000 | 0.000 | 0.000 |
| 15 | 0.933 | 0.067 | 0.250 | |
| 30 | 0.750 | 0.250 | 0.433 | |
| 45 | 0.500 | 0.500 | 0.500 | |
| 60 | 0.250 | 0.750 | 0.433 | |
| 75 | 0.067 | 0.933 | 0.250 | |
| 90 | 0.000 | 1.000 | 0.000 | |
| 0.2 | 0 | 1.000 | 0.200 | 0.000 |
| 15 | 0.946 | 0.254 | 0.200 | |
| 30 | 0.800 | 0.400 | 0.346 | |
| 45 | 0.600 | 0.600 | 0.400 | |
| 60 | 0.400 | 0.800 | 0.346 | |
| 75 | 0.254 | 0.946 | 0.200 | |
| 90 | 0.200 | 1.000 | 0.000 | |
| 0.4 | 0 | 1.000 | 0.400 | 0.000 |
| 15 | 0.960 | 0.440 | 0.150 | |
| 30 | 0.850 | 0.550 | 0.260 | |
| 45 | 0.700 | 0.700 | 0.300 | |
| 60 | 0.550 | 0.850 | 0.260 | |
| 75 | 0.440 | 0.960 | 0.150 | |
| 90 | 0.400 | 1.000 | 0.000 | |
| 0.6 | 0 | 1.000 | 0.600 | 0.000 |
| 15 | 0.973 | 0.627 | 0.100 | |
| 30 | 0.900 | 0.700 | 0.173 | |
| 45 | 0.800 | 0.800 | 0.200 | |
| 60 | 0.700 | 0.900 | 0.173 | |
| 75 | 0.627 | 0.973 | 0.100 | |
| 90 | 0.600 | 1.000 | 0.000 | |
| 0.8 | 0 | 1.000 | 0.800 | 0.000 |
| 15 | 0.987 | 0.813 | 0.050 | |
| 30 | 0.950 | 0.850 | 0.087 | |
| 45 | 0.900 | 0.900 | 0.100 | |
| 60 | 0.850 | 0.950 | 0.087 | |
| 75 | 0.813 | 0.987 | 0.050 | |
| 90 | 0.800 | 1.000 | 0.000 | |
| 1.0 | 0 | 1.000 | 1.000 | 0.000 |
| 15 | 1.000 | 1.000 | 0.000 | |
| 30 | 1.000 | 1.000 | 0.000 | |
| 45 | 1.000 | 1.000 | 0.000 | |
| 60 | 1.000 | 1.000 | 0.000 | |
| 75 | 1.000 | 1.000 | 0.000 | |
| 90 | 1.000 | 1.000 | 0.000 | |
| ρ | μ | Ec | k* | ||||
|---|---|---|---|---|---|---|---|
| 2.70 g/cm3 | 0.577 | 3.2 GPa | 1.0 | 3.2 GPa | 1.0 | 21.1 MPa | 13.2 MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, M.; Qiu, X.; Cao, R.; Li, Z.; Shi, X.; Tan, L. Stress Characteristics and Mechanical Behavior of Rock Masses with an Opening under Complex Deep Underground Stress Conditions. Appl. Sci. 2024, 14, 7197. https://doi.org/10.3390/app14167197
Cao M, Qiu X, Cao R, Li Z, Shi X, Tan L. Stress Characteristics and Mechanical Behavior of Rock Masses with an Opening under Complex Deep Underground Stress Conditions. Applied Sciences. 2024; 14(16):7197. https://doi.org/10.3390/app14167197
Chicago/Turabian StyleCao, Mingyu, Xianyang Qiu, Rihong Cao, Zeyu Li, Xiuzhi Shi, and Lihai Tan. 2024. "Stress Characteristics and Mechanical Behavior of Rock Masses with an Opening under Complex Deep Underground Stress Conditions" Applied Sciences 14, no. 16: 7197. https://doi.org/10.3390/app14167197
APA StyleCao, M., Qiu, X., Cao, R., Li, Z., Shi, X., & Tan, L. (2024). Stress Characteristics and Mechanical Behavior of Rock Masses with an Opening under Complex Deep Underground Stress Conditions. Applied Sciences, 14(16), 7197. https://doi.org/10.3390/app14167197









