Reliability-Based Optimization of Impeller Structure Using Exponential Function Approximation
Abstract
1. Introduction
2. Reliability-Based Optimization
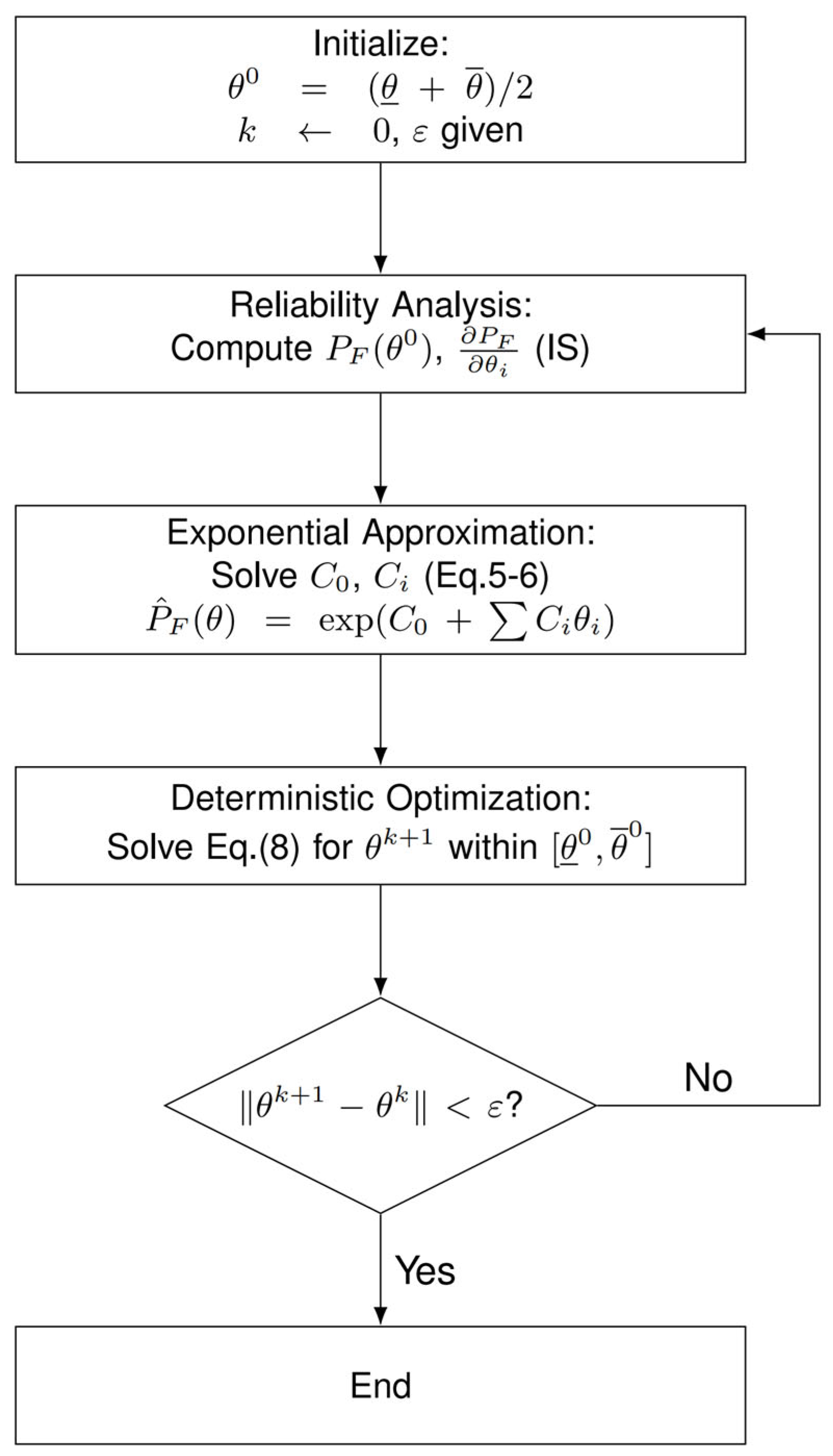
3. Proposed Reliability-Based Optimization Method
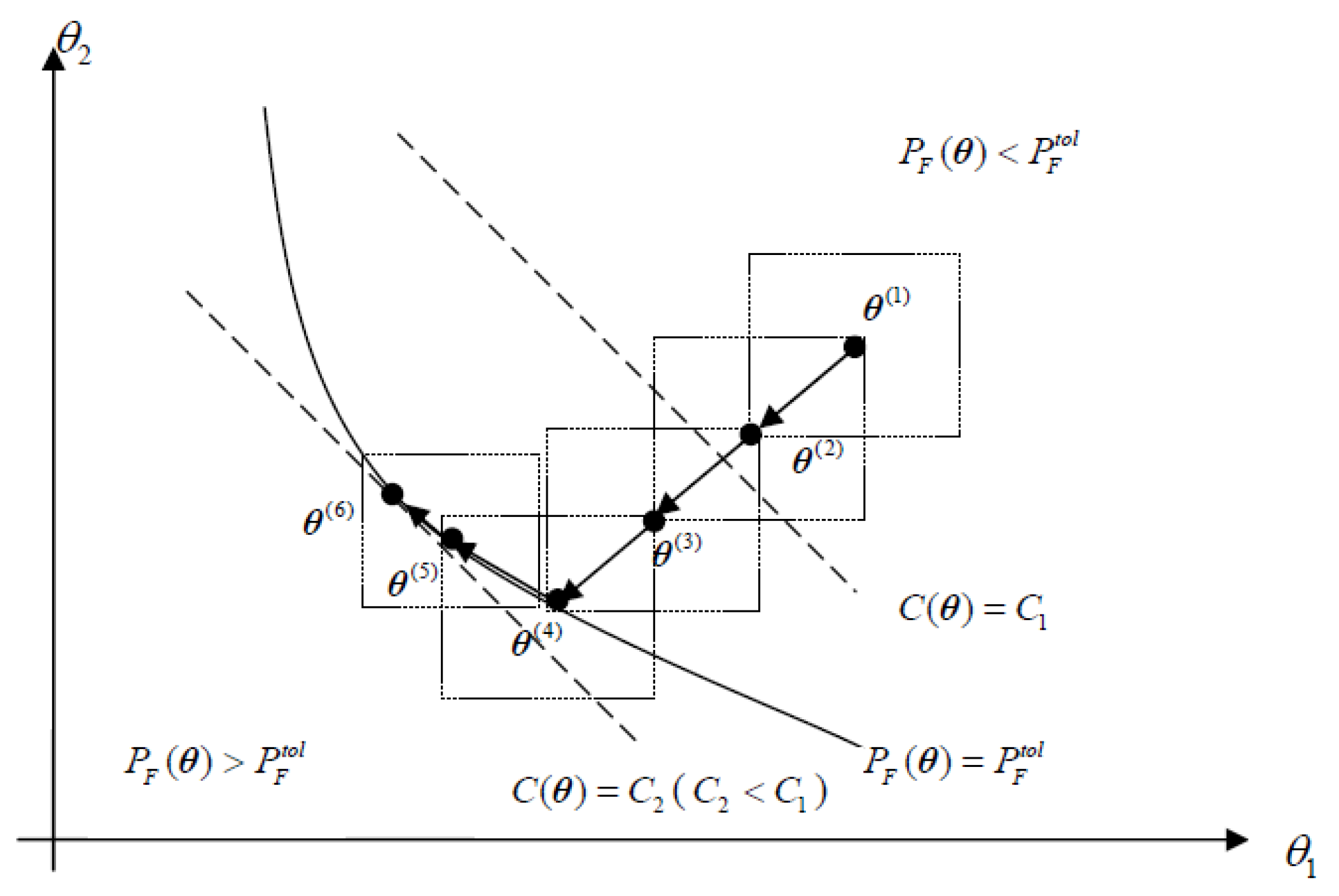
3.1. Failure Probability Function Approximation Using First-Order Exponential Function
3.2. Decoupling and Sequential Approximation Framework
4. Reliability-Based Optimization of an Impeller Structure
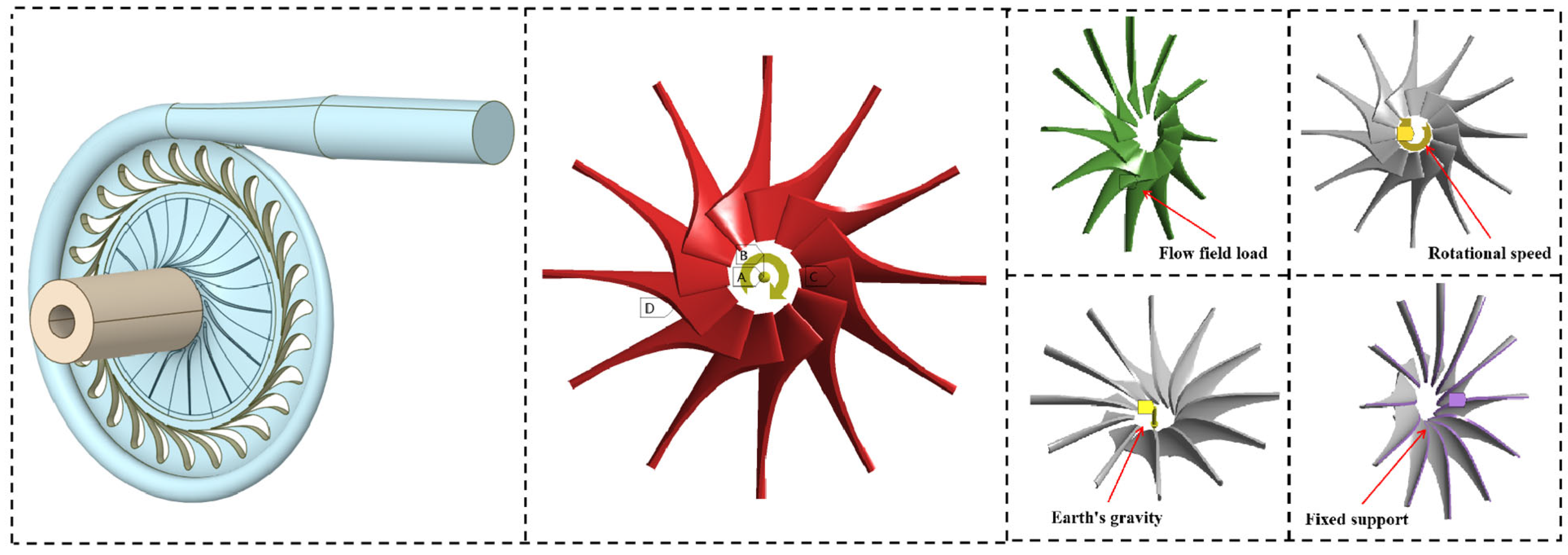
4.1. Centrifugal Compressor Impeller Structure
4.1.1. Modeling Assumptions and Limitations
4.1.2. Structural Analysis Methodology
4.2. Reliability-Based Optimization of the Impeller Structure
4.3. Sensitivity Analysis of Design Parameters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bono, F.M.; Radicioni, L.; Cinquemani, S.; Conese, C.; Tarabini, M. Development of soft sensors based on neural networks for detection of anomaly working condition in automated machinery. In NDE 4.0, Predictive Maintenance, and Communication and Energy Systems in a Globally Networked World; SPIE: Bellingham, WA, USA, 2022; Volume 12049, pp. 56–70. [Google Scholar]
- Valdebenito, M.A.; Schuëller, G.I. A survey on approaches for reliability-based optimization. Struct. Multidiscip. Optim. 2010, 42, 645–663. [Google Scholar] [CrossRef]
- Enevoldsen, I.; Sørensen, J. Reliability-based optimization in structural engineering. Struct. Saf. 1994, 15, 169–196. [Google Scholar] [CrossRef]
- Tu, J.; Park, Y. A new study on reliability-based design optimization. J. Mech. Des. 1999, 121, 557–564. [Google Scholar] [CrossRef]
- Rahman, S.; Xu, H. A univariate dimension-reduction method for multi-dimensional integration in stochastic mechanics. Probabilistic Eng. Mech. 2004, 19, 393–408. [Google Scholar] [CrossRef]
- Lehký, D.; Slowik, O.; Novák, D. Reliability-based design: Artificial neural networks and double-loop reliability-based optimization approaches. Adv. Eng. Softw. 2018, 117, 123–135. [Google Scholar] [CrossRef]
- Madsen, H.O.; Hansen, P.F. A Comparison of Some Algorithms for Reliability Based Structural Optimization and Sensitivity Analysis; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Chen, X.; Hasselman, T.; Neill, D. Reliability based structural design optimization for practical applications. In Proceedings of the Structures, Structural Dynamics & Materials Conference, Kissimmee, FL, USA, 7–10 April 1997; pp. 2724–2732. [Google Scholar]
- Lim, J.; Lee, B. A semi-single-loop method using approximation of most probable point for reliability-based design optimization. Struct. Multidiscip. Optim. 2015, 53, 745–757. [Google Scholar] [CrossRef]
- Zeng, M.; Yang, D.; Zhou, H.; Wang, B. Convergence control of single loop approach for reliability-based design optimization. Struct. Multidiscip. Optim. 2018, 57, 1079–1091. [Google Scholar]
- Jiang, C.; Qiu, H.; Gao, L.; Cai, X.; Li, P. An adaptive hybrid single-loop method for reliability-based design optimization using iterative control strategy. Struct. Multidiscip. Optim. 2017, 56, 1271–1286. [Google Scholar] [CrossRef]
- Lee, I.; Choi, K.K.; Liu, D.; David, G. Inverse analysis method using MPP-based dimension reduction for reliability-based design optimization of nonlinear and multi-dimensional systems. Comput. Methods Appl. Mech. Eng. 2008, 198, 14–27. [Google Scholar] [CrossRef]
- Lin, P.T.; Gea, H.C.; Jaluria, Y. A modified reliability index approach for reliability-based design optimization. J. Mech. Des. 2011, 133, 445–452. [Google Scholar]
- Keshtegar, B.; Hao, P. Enhanced single-loop method for efficient reliability-based design optimization with complex constraints. Struct. Multidiscip. Optim. 2018, 57, 1731–1741. [Google Scholar] [CrossRef]
- Wang, S.; Liu, S. Reliability based design optimization with approximate failure probability function in partitioned design space. Reliab. Eng. Syst. Saf. 2017, 167, 602–611. [Google Scholar]
- Jensen, H.A.; Catalan, M.A. On the effects of non-linear elements in the reliability-based optimal design of stochastic dynamical systems. Int. J. Non Linear Mech. 2007, 42, 802–816. [Google Scholar] [CrossRef]
- Jacobs, J.H.; Etman, L.F.P.; van Keulen, F.; Rooda, J.E. Framework for sequential approximate optimization. Struct. Multidiscip. Optim. 2004, 27, 384–400. [Google Scholar] [CrossRef]
- Gasser, M.; Schuëller, G.I. Reliability-Based Optimization of structural systems. Math. Methods Oper. Res. 1997, 46, 287–307. [Google Scholar] [CrossRef]
- Au, S.K. Reliability-based design sensitivity by efficient simulation. Comput. Struct. 2005, 83, 1048–1061. [Google Scholar] [CrossRef]
- Feng, K.; Lu, Z.; Ling, C.; Yun, W. An innovative estimation of failure probability function based on conditional probability of parameter interval and augmented failure probability. Mech. Syst. Signal Process. 2019, 123, 606–625. [Google Scholar] [CrossRef]
- Ching, J.H.Y. Approximate reliability-based optimization using a three-step approach based on subset simulation. J. Eng. Mech. 2007, 133, 481–493. [Google Scholar] [CrossRef]
- Zhou, Y.; Lu, Z.; Yun, W. Active sparse polynomial chaos expansion for system reliability analysis. Reliab. Eng. Syst. Saf. 2020, 202, 107025. [Google Scholar] [CrossRef]
- Yuan, X.; Liu, S.; Valdebenito, M.A.; Faes, M.G.; Jerez, D.J.; Jensen, H.A.; Beer, M. Decoupled reliability-based optimization using Markov chain Monte Carlo in augmented space. Adv. Eng. Softw. 2021, 157, 103020. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, C.; Zhao, H.; Zhang, Z. An ensemble model-based method for estimating failure probability function with application in reliability-based optimization. Appl. Math. Model. 2022, 108, 445–468. [Google Scholar] [CrossRef]
- Yang, S.; Lee, M.; Lee, I. A new sampling approach for system reliability-based design optimization under multiple simulation models. Reliab. Eng. Syst. Saf. 2023, 231, 109024. [Google Scholar] [CrossRef]
- Faes, M.G.; Valdebenito, M.A. Fully decoupled reliability-based optimization of linear structures subject to Gaussian dynamic loading considering discrete design variables. Mech. Syst. Signal Process. 2021, 156, 107616. [Google Scholar] [CrossRef]
- Jerez, D.J.; Jensen, H.A.; Valdebenito, M.A.; Misraji, M.A.; Mayorga, F.; Beer, M. On the use of directional importance sampling for reliability-based design and optimum design sensitivity of linear stochastic structures. Probabilistic Eng. Mech. 2022, 70, 103368. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, N.; Zeng, P.; Liu, J.; Beer, M. An efficient reliability analysis method for structures with hybrid time-dependent uncertainty. Reliab. Eng. Syst. Saf. 2022, 228, 108794. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Kramer, B.; Willcox, K.E. Information reuse for importance sampling in reliability-based design optimization. Reliab. Eng. Syst. Saf. 2020, 201, 106853. [Google Scholar] [CrossRef]
- Jerez, D.; Jensen, H.; Beer, M. Reliability-based design optimization of structural systems under stochastic excitation: An overview. Mech. Syst. Signal Process. 2022, 166, 108397. [Google Scholar] [CrossRef]
- Zhang, F.; Lu, Z.; Cui, L.; Song, S. Reliability Sensitivity Algorithm Based on Stratified Importance Sampling Method for Multiple Failure Modes Systems. Chin. J. Aeronaut. 2010, 23, 660–669. [Google Scholar]
- Au, S.K.; Beck, J.L. Estimation of small failure probabilities in high dimensions by subset simulation. Probabilistic Eng. Mech. 2001, 16, 263–277. [Google Scholar] [CrossRef]


| Variable | Mean Value | Standard Deviation |
|---|---|---|
| Rotational speed (rev/min) | 3000 | 200 |
| Inlet temperature (°C) | [−190.985, −130.985] | 10.7317 |
| Outlet pressure (MPa) | 0.18 | 0.01333 |
| Inlet pressure (MPa) | [1.62, 5.62] | 0.3 |
| Elastic modulus (GPa) | 200 | 13.3333 |
| Length (mm) | 112 | 3.6667 |
| Width (mm) | 30 | 1 |
| Method | Inlet Temperature (°C) | Inlet Pressure (MPa) | Objective Function | Failure Probability | Coefficient of Variation | Number of Function Evaluations |
|---|---|---|---|---|---|---|
| Double-loop IS | −158.68 | 5.6200 | −2.2291 | 1.00 × 10−4 | 0.0292 | 4.7 × 105 |
| Double-loop SS | −161.16 | 5.4153 | −2.1991 | 9.44 × 10−5 | 0.0965 | 2.0 × 106 |
| First-order exponential approximation (IS) | −153.65 | 5.6200 | −2.1978 | 3.20 × 10−5 | 0.0709 | 2.4 × 104 |
| Design Parameter | Current Value | Sensitivity Coefficient | Normalized Sensitivity | Ranking |
|---|---|---|---|---|
| Inlet Temperature Mean (°C) | −160.985 | −2.34 × 10−6 | 0.452 | 1 |
| Inlet Pressure Mean (MPa) | 3.62 | 1.87 × 10−5 | 0.318 | 2 |
| Temperature Std. Deviation (°C) | 10.73 | −8.92 × 10−7 | 0.165 | 3 |
| Pressure Std. Deviation (MPa) | 0.30 | 3.45 × 10−6 | 0.065 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, H.; Ren, Y.; Bao, H.; Zhang, F.; Zhao, F.; Bao, X. Reliability-Based Optimization of Impeller Structure Using Exponential Function Approximation. Appl. Sci. 2025, 15, 6856. https://doi.org/10.3390/app15126856
Lin H, Ren Y, Bao H, Zhang F, Zhao F, Bao X. Reliability-Based Optimization of Impeller Structure Using Exponential Function Approximation. Applied Sciences. 2025; 15(12):6856. https://doi.org/10.3390/app15126856
Chicago/Turabian StyleLin, Haiwei, Yiqun Ren, Hong Bao, Feng Zhang, Feifei Zhao, and Xiya Bao. 2025. "Reliability-Based Optimization of Impeller Structure Using Exponential Function Approximation" Applied Sciences 15, no. 12: 6856. https://doi.org/10.3390/app15126856
APA StyleLin, H., Ren, Y., Bao, H., Zhang, F., Zhao, F., & Bao, X. (2025). Reliability-Based Optimization of Impeller Structure Using Exponential Function Approximation. Applied Sciences, 15(12), 6856. https://doi.org/10.3390/app15126856







