Study on the Compressive Strength Predicting of Steel Fiber Reinforced Concrete Based on an Interpretable Deep Learning Method
Abstract
1. Introduction
2. Fundamental Principle and Main Formula
2.1. Deep Learning
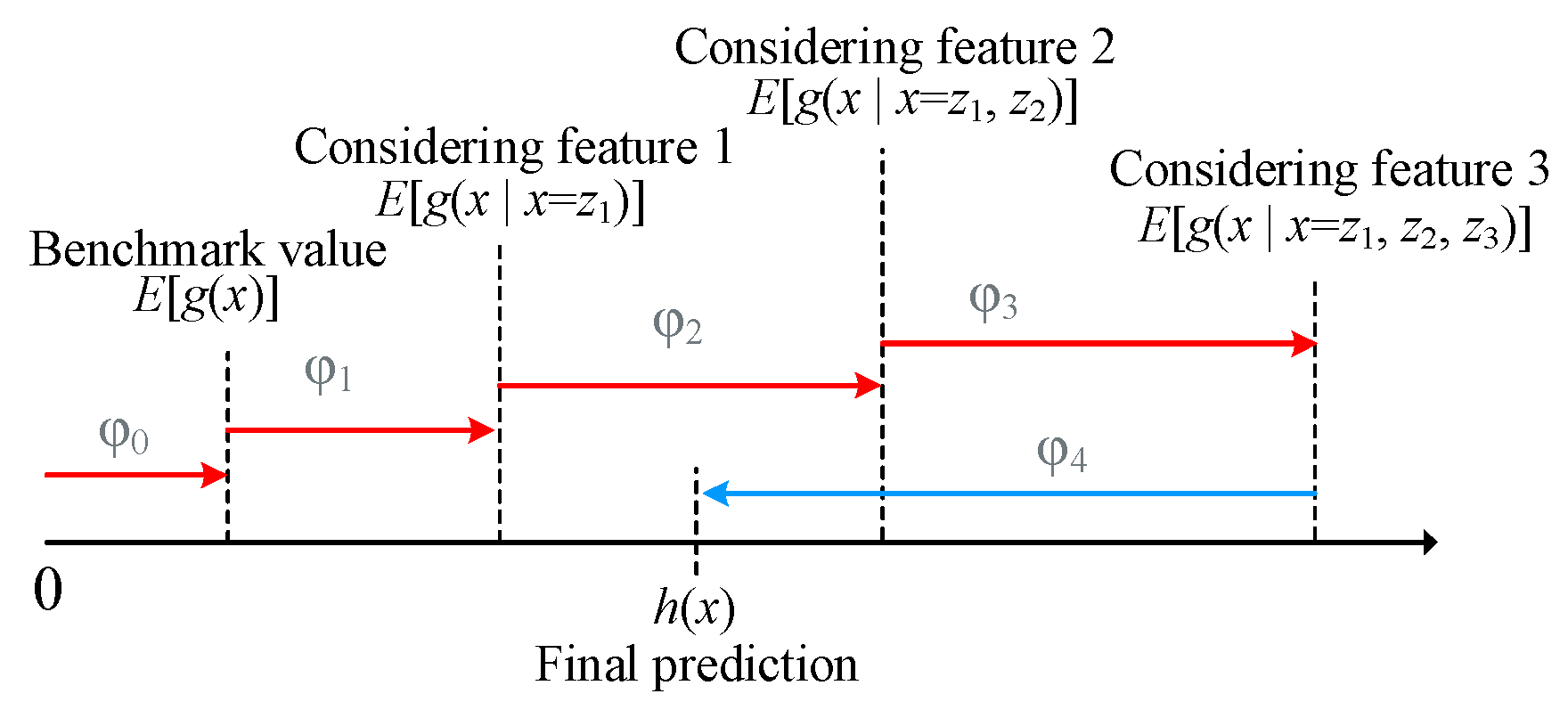
2.2. SHAP Interpretability Method
3. Model Construction and Prediction Results
3.1. Creation of the Experimental Results Database
3.2. Deep Learning Model Construction
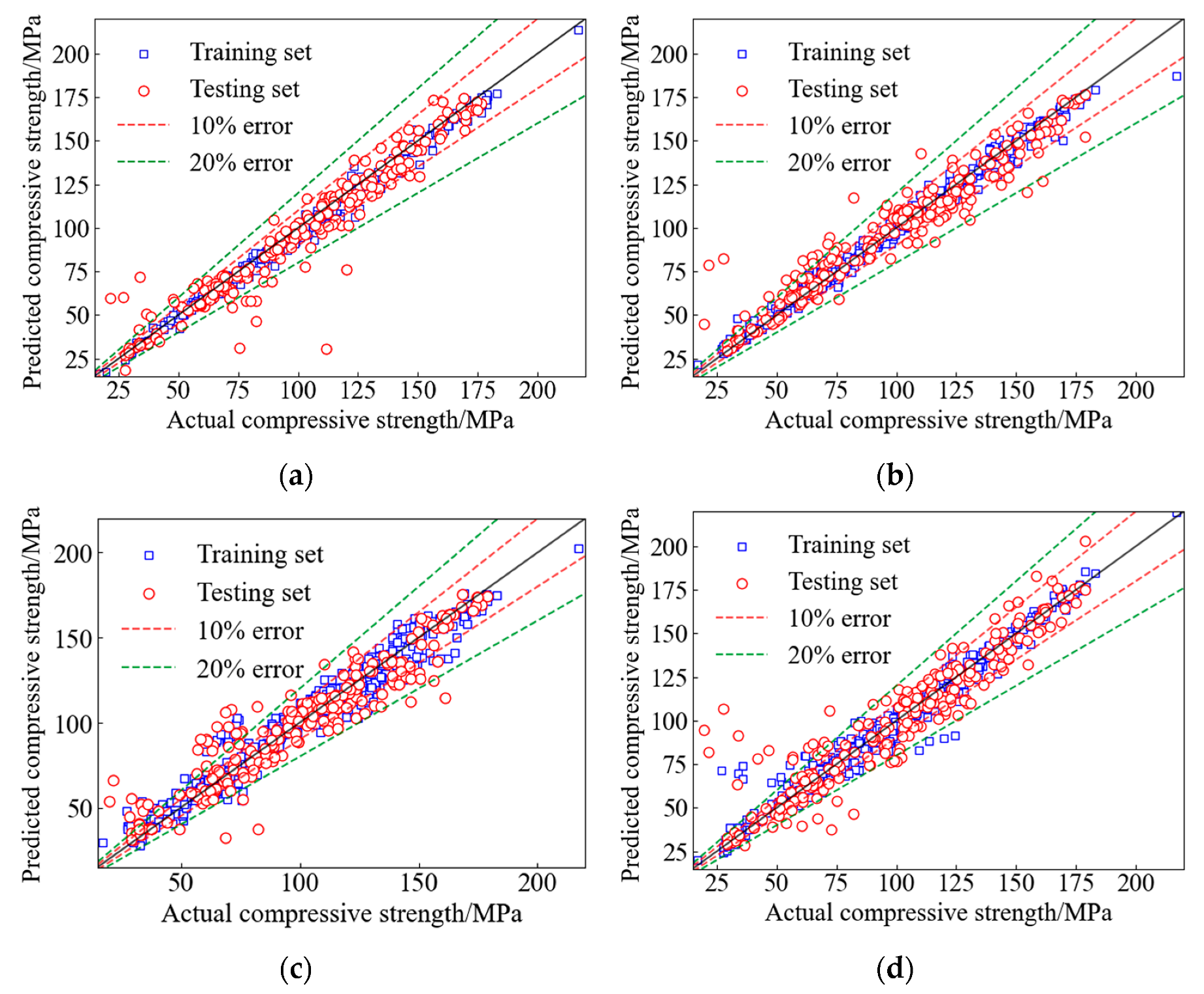
3.3. Comparison and Evaluation of Algorithm Model
3.4. Comparison and Evaluation of Empirical Formulas
4. Interpretable Analysis of Prediction Model Based on SHAP
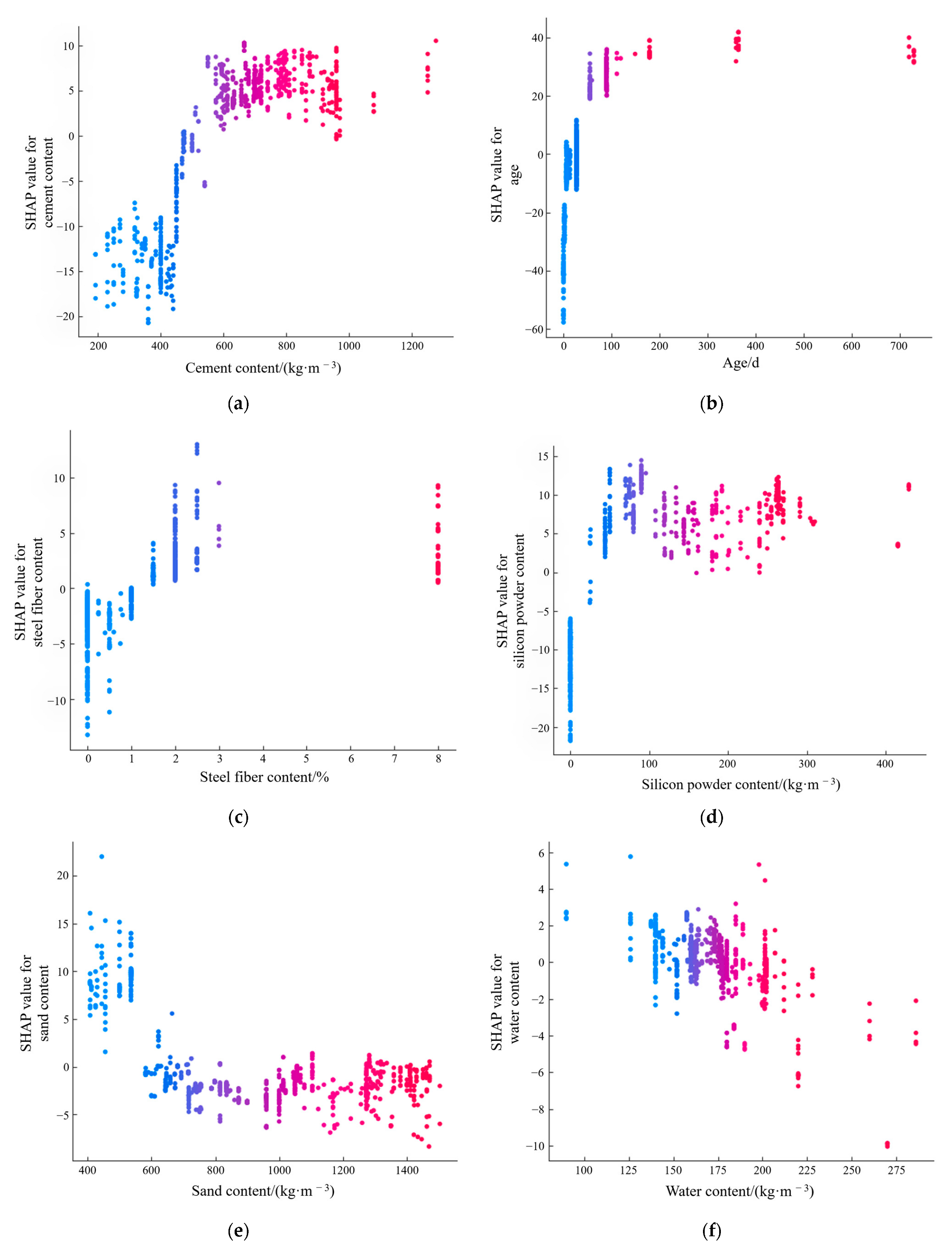
4.1. Partial Interpretation Based on SHAP
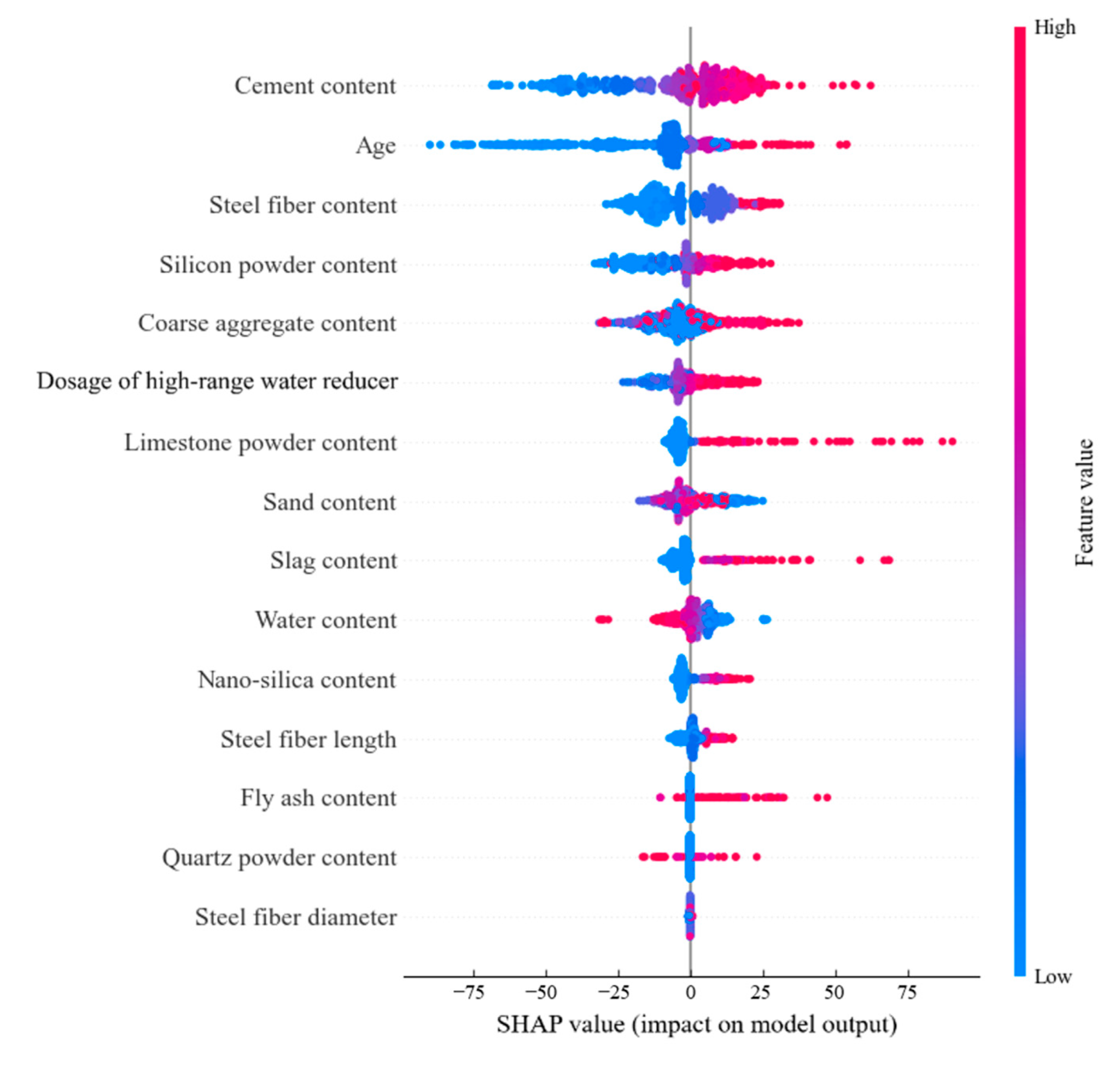
4.2. Global Interpretation Based on SHAP
5. Conclusions
- Model performance verification: The DNN model established in this study is compared and analyzed against three commonly used algorithmic models and three widely used empirical formulas. On the testing set, the model achieves an R² of 0.94 and a MAPE of 8.16%, indicating that the predicted compressive strength of SFRC is highly consistent with the experimental results. This demonstrates that the DL model proposed in this paper possesses high prediction accuracy and generalization ability, and effectively captures the complex nonlinear relationships among the characteristic parameters.
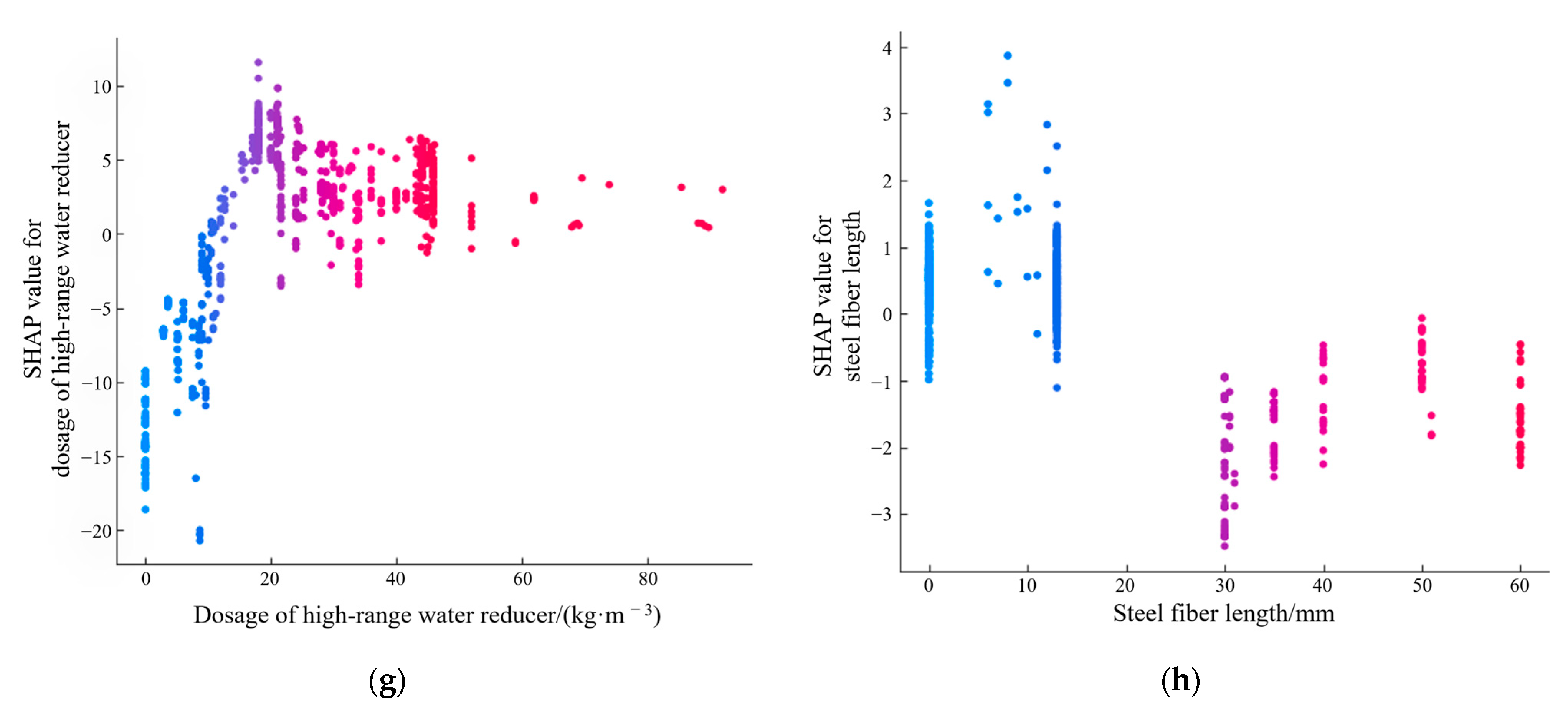
- Feature Importance Analysis: The SHAP value analysis results based on a wide range of experimental samples are consistent with the conclusions obtained from the experiments. Among the 14 input features, cement content, coarse aggregate content, and curing age are the most important factors affecting the compressive strength of concrete. For steel fiber reinforced concrete, in addition to the above three, an increase in steel fiber content, silicon powder content, dosage of high-range water reducer, and other parameter values has a positive impact on the compressive strength, providing useful guidance for the engineering design of concrete materials.
- The influence mechanism of steel fiber parameters: For steel fiber reinforced concrete, both local and global interpretation analysis based on SHAP shows that within an appropriate range, an increase in steel fiber content leads to an enhancement in the compressive strength of concrete, although the improvement is relatively small. The overall impact of steel fiber length on compressive strength is limited, but excessively long fiber has a negative effect. This is consistent with engineering practice, as overly long fibers can impair the workability of the mixture and the quality of construction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.R.; Su, S.; Xie, Y.P.; Shi, J.N. Influence of Steel Fiber on the Flexural Toughness and Fatigue Damage of Reinforced Concrete Beam. Bull. Chin. Ceram. Soc. 2018, 37, 260–266. [Google Scholar]
- Tanash, A.O.; Abu Bakar, B.; Muthusamy, K.; AL Biajawi, M.I. Effect of elevated temperature on mechanical properties of normal strength concrete: An overview. Mater. Today Proc. 2024, 107, 152–157. [Google Scholar]
- Zhang, P.; Wang, C.; Gao, Z.; Wang, F. A review on fracture properties of steel fiber reinforced concrete. J. Build. Eng. 2023, 67, 105975. [Google Scholar] [CrossRef]
- Ge, K.; Guo, Y.T.; Wang, C.; Hu, Z.Z. AI-based prediction of seismic time-history responses of RC frame structures considering varied structural parameters. J. Build. Eng. 2025, 106, 112643. [Google Scholar] [CrossRef]
- Han, J.; Zhao, M.; Chen, J.; Lan, X. Effects of steel fiber length and coarse aggregate maximum size on mechanical properties of steel fiber reinforced concrete. Constr. Build. Mater. 2019, 209, 577–591. [Google Scholar] [CrossRef]
- Fan, J.; Wang, C.; Song, L. Research and application of intelligent computation in civil engineering. J. Build. Struct. 2022, 43, 1–22. [Google Scholar]
- Shafighfard, T.; Bagherzadeh, F.; Rizi, R.A.; Yoo, D.-Y. Data-driven compressive strength prediction of steel fiber reinforced concrete (SFRC) subjected to elevated temperatures using stacked machine learning algorithms. J. Mater. Res. Technol. 2022, 21, 3777–3794. [Google Scholar] [CrossRef]
- Zhang, X.; Akber, M.Z.; Zheng, W. Prediction of seven-day compressive strength of field concrete. Constr. Build. Mater. 2021, 305, 124604. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Q.; Kamiński, P.; Deifalla, A.F.; Sufian, M.; Dyczko, A.; Ben Kahla, N.; Atig, M. Compressive Strength of Steel Fiber-Reinforced Concrete Employing Supervised Machine Learning Techniques. Materials 2022, 15, 4209. [Google Scholar] [CrossRef] [PubMed]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 4768–4777. [Google Scholar]
- Sarker, I.H. Deep Learning: A Comprehensive Overview on Techniques, Taxonomy, Applications and Research Directions. SN Comput. Sci. 2021, 2, 420. [Google Scholar] [CrossRef] [PubMed]
- An, P.; Cao, D.P.; Zhao, B.Y.; Yang, X.L.; Zhang, M. Reservoir physical parameters prediction based on LSTM recurrent neural network. Prog. Geophys. 2019, 34, 1849–1858. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 2951–2959. [Google Scholar]
- Hu, W.H.; Xu, Z.M.; Liu, Q.; Lu, W.; Teng, J. Study on internal force variation law of transfer truss and joint of a super high-rise building based on multi-scale finite element model modification by monitoring data. J. Build. Struct. 2023, 44, 236–246. [Google Scholar]
- Key Material Properties of Ultra-High Performance Concrete (UHPC)-Mendeley Data[EB/OL]. Available online: https://daks.uni-kassel.de/entities/dataset/ff37a8c0-aa9e-4b0c-ab4c-905c3ebbe797 (accessed on 6 September 2023).
- Mahjoubi, S.; Meng, W.; Bao, Y. Auto-tune learning framework for prediction of flowability, mechanical properties, and porosity of ultra-high-performance concrete (UHPC). Appl. Soft Comput. 2022, 115, 108182. [Google Scholar] [CrossRef]
- Atiş, C.D.; Karahan, O. Properties of steel fiber reinforced fly ash concrete. Constr. Build. Mater. 2009, 23, 392–399. [Google Scholar] [CrossRef]
- Dai, L.; Wu, X.; Zhou, M.; Ahmad, W.; Ali, M.; Sabri, M.M.S.; Salmi, A.; Ewais, D.Y.Z. Using Machine Learning Algorithms to Estimate the Compressive Property of High Strength Fiber Reinforced Concrete. Materials 2022, 15, 4450. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.F.; Huang, C.K. Performance and application of steel fiber reinforced concrete. Ind. Constr. 1989, 2–9. [Google Scholar]
- Soroush, M.; Yi, B. The Key Material Properties of Ultra-High-Performance Concrete (UHPC). Mendeley Data 2021. Available online: https://data.mendeley.com/datasets/dd62d5hyzr/1 (accessed on 6 September 2023).
- Feng, D.; Wu, G. Interpretable machine learning-based modeling approach for fundamental properties of concrete structures. J. Build. Struct. 2022, 43, 228–238. [Google Scholar]
- GB 50010-2010; Code for Design of Concrete Structures. China Standard Press: Beijing, China, 2010.
- ACI 544.4R-18; Guide to Design with Fiber-Reinforced Concrete. American Concrete Institute: Farmington Hills, MI, USA, 2018.
- CEB-FIP Model Code 1990; Comite Euro-lnternational Du Beton. Thomas Telford Publishing: London, UK, 1993.



| Feature Parameter | Unit | Maximum | Minimum | Average | Standard Deviation |
|---|---|---|---|---|---|
| Cement content | kg/m3 | 1277.40 | 192.00 | 639.79 | 151.05 |
| Fly ash content | kg/m3 | 989.57 | 0.00 | 34.60 | 356.14 |
| Slag content | kg/m3 | 768.00 | 0.00 | 40.45 | 0.00 |
| Silicon powder content | kg/m3 | 429.53 | 0.00 | 99.97 | 0.00 |
| Nano-silica content | kg/m3 | 43.70 | 0.00 | 5.39 | 12.15 |
| Limestone powder content | kg/m3 | 1058.20 | 0.00 | 50.66 | 0.00 |
| Sand content | kg/m3 | 1503.40 | 407.80 | 951.13 | 265.05 |
| Coarse aggregate content | kg/m3 | 1298.61 | 0.00 | 371.01 | 545.00 |
| Quartz powder content | kg/m3 | 259.00 | 0.00 | 14.26 | 0.00 |
| Water content | kg/m3 | 286.00 | 90.00 | 173.35 | 16.60 |
| Dosage of high-range water reducer | kg/m3 | 92.04 | 0.00 | 24.32 | 5.45 |
| Steel fiber content | % | 8.00 | 0.00 | 1.28 | 0.75 |
| Steel fiber diameter | mm | 1.00 | 0.00 | 0.22 | 0.28 |
| Steel fiber length | mm | 60.00 | 0.00 | 14.57 | 17.50 |
| Age | d | 500.00 | 1.00 | 46.51 | 117.00 |
| Parameter | Optimization Scope | Final Value |
|---|---|---|
| Number of hidden layers | 1~10 | 3 |
| Number of neurons | 8~200 | [32,136,168] |
| Activation function | relu, tanh, Lrelu | relu |
| Optimizer | SGD, Adam, RMSProp, AdaGrad | Adam |
| Rate of learning | [1,0.01,0.001,0.0001] | 0.001 |
| Regularization | - | Dropout |
| Epoch | - | 3500 |
| Batch_size | 1~50 | 32 |
| Model | Training Set | Test Set | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | MAPE | RMSE | MAE | R2 | MAPE | RMSE | MAE | |
| DNN | 0.9943 | 2.58% | 2.95 | 2.22 | 0.9398 | 8.16% | 9.41 | 6.62 |
| RF | 0.9892 | 3.04% | 3.93 | 2.63 | 0.9179 | 10.33% | 11.17 | 7.58 |
| XGBoost | 0.9417 | 8.27% | 9.11 | 6.81 | 0.8804 | 11.31% | 13.39 | 9.77 |
| BP | 0.9593 | 6.40% | 7.79 | 4.35 | 0.8900 | 9.63% | 12.32 | 8.86 |
| Model | Evaluation Indicators | ||
|---|---|---|---|
| MAPE/% | RMSE/MPa | MAE/MPa | |
| DNN | 8.16 | 9.41 | 6.62 |
| GB 50010 | 69.32 | 81.10 | 57.00 |
| ACI 544.4R | 58.10 | 58.10 | 56.00 |
| CEB-FIP | 453.12 | 820.90 | 391.28 |
| Feature Parameter/Unit | Sample1 (A3) | Sample2 (A5a) | Sample3 (A5b) |
|---|---|---|---|
| Cement content/kg·m−3 | 400 | 400 | 400 |
| Fly ash content/kg·m−3 | 0 | 0 | 0 |
| Slag content/kg·m−3 | 0 | 0 | 0 |
| Silicon powder content/kg·m−3 | 0 | 0 | 0 |
| Nano-silica content/kg·m−3 | 0 | 0 | 0 |
| Limestone powder content/kg·m−3 | 0 | 0 | 0 |
| Sand content/kg·m−3 | 751 | 740 | 740 |
| Coarse aggregate content/kg·m−3 | 1127 | 1111 | 1111 |
| Quartz powder content/kg·m−3 | 0 | 0 | 0 |
| Water content/kg·m−3 | 140 | 140 | 140 |
| Dosage of high-range water reducer/kg·m−3 | 24.42 | 24.15 | 24.15 |
| Steel fiber content/% | 0.5 | 1.5 | 1.5 |
| Steel fiber diameter/mm | 0.55 | 0.55 | 0.55 |
| Steel fiber length/mm | 35 | 35 | 35 |
| Age/d | 28 | 28 | 90 |
| Compressive strength/MPa | 78.2 | 81 | 89.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Lin, J.; Guo, S. Study on the Compressive Strength Predicting of Steel Fiber Reinforced Concrete Based on an Interpretable Deep Learning Method. Appl. Sci. 2025, 15, 6848. https://doi.org/10.3390/app15126848
Wang H, Lin J, Guo S. Study on the Compressive Strength Predicting of Steel Fiber Reinforced Concrete Based on an Interpretable Deep Learning Method. Applied Sciences. 2025; 15(12):6848. https://doi.org/10.3390/app15126848
Chicago/Turabian StyleWang, Huiming, Jie Lin, and Shengpin Guo. 2025. "Study on the Compressive Strength Predicting of Steel Fiber Reinforced Concrete Based on an Interpretable Deep Learning Method" Applied Sciences 15, no. 12: 6848. https://doi.org/10.3390/app15126848
APA StyleWang, H., Lin, J., & Guo, S. (2025). Study on the Compressive Strength Predicting of Steel Fiber Reinforced Concrete Based on an Interpretable Deep Learning Method. Applied Sciences, 15(12), 6848. https://doi.org/10.3390/app15126848





