Deformation Characteristics and Base Stability of a Circular Deep Foundation Pit with High-Pressure Jet Grouting Reinforcement
Abstract
1. Introduction
2. Project Overview
2.1. Bridge Overview
2.2. Anchorage Foundation Overview
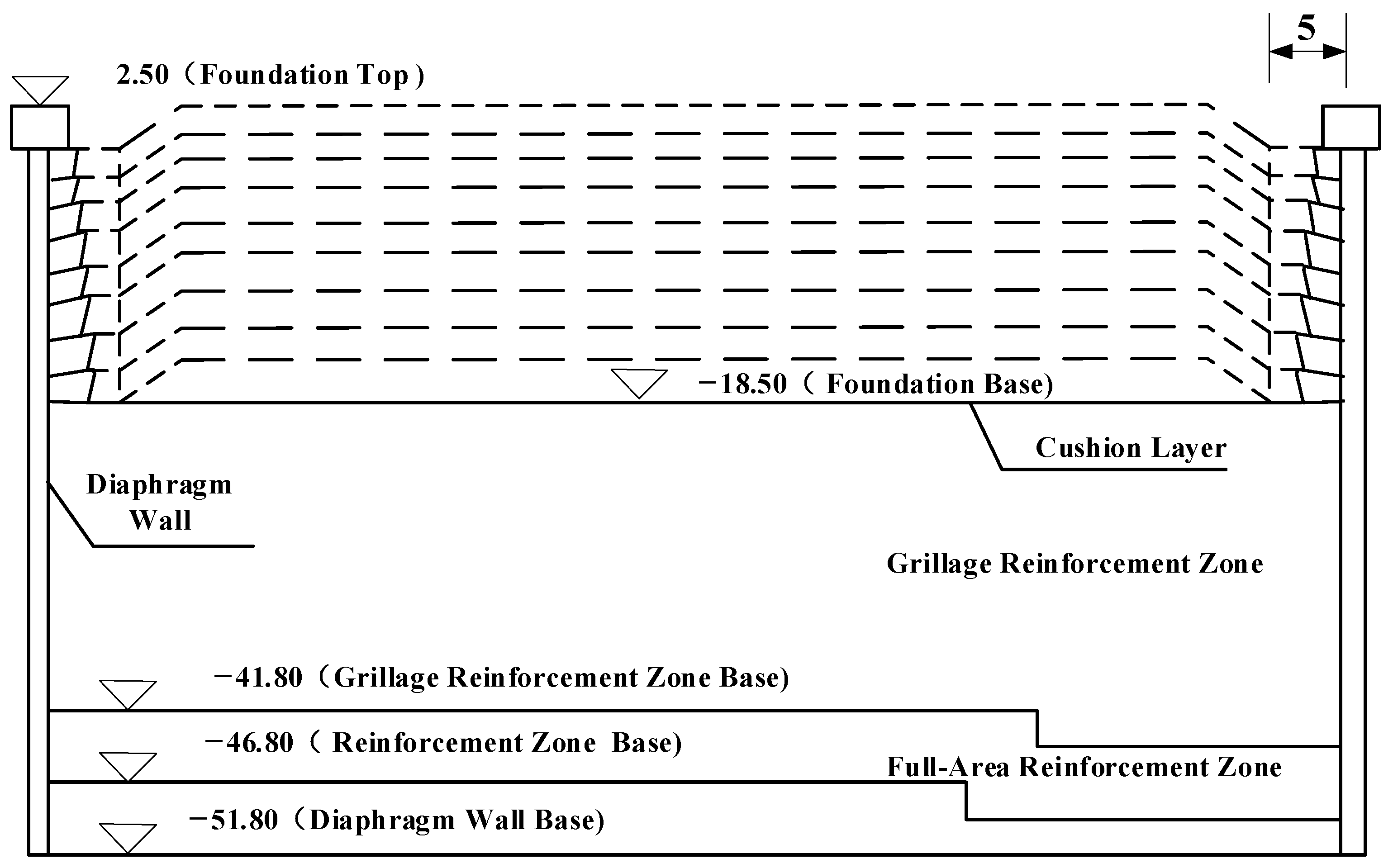
2.3. Ground Improvement Overview
2.4. Engineering Geological Conditions
2.4.1. Topography and Geomorphology
2.4.2. Geological Conditions
3. Excavation Scheme
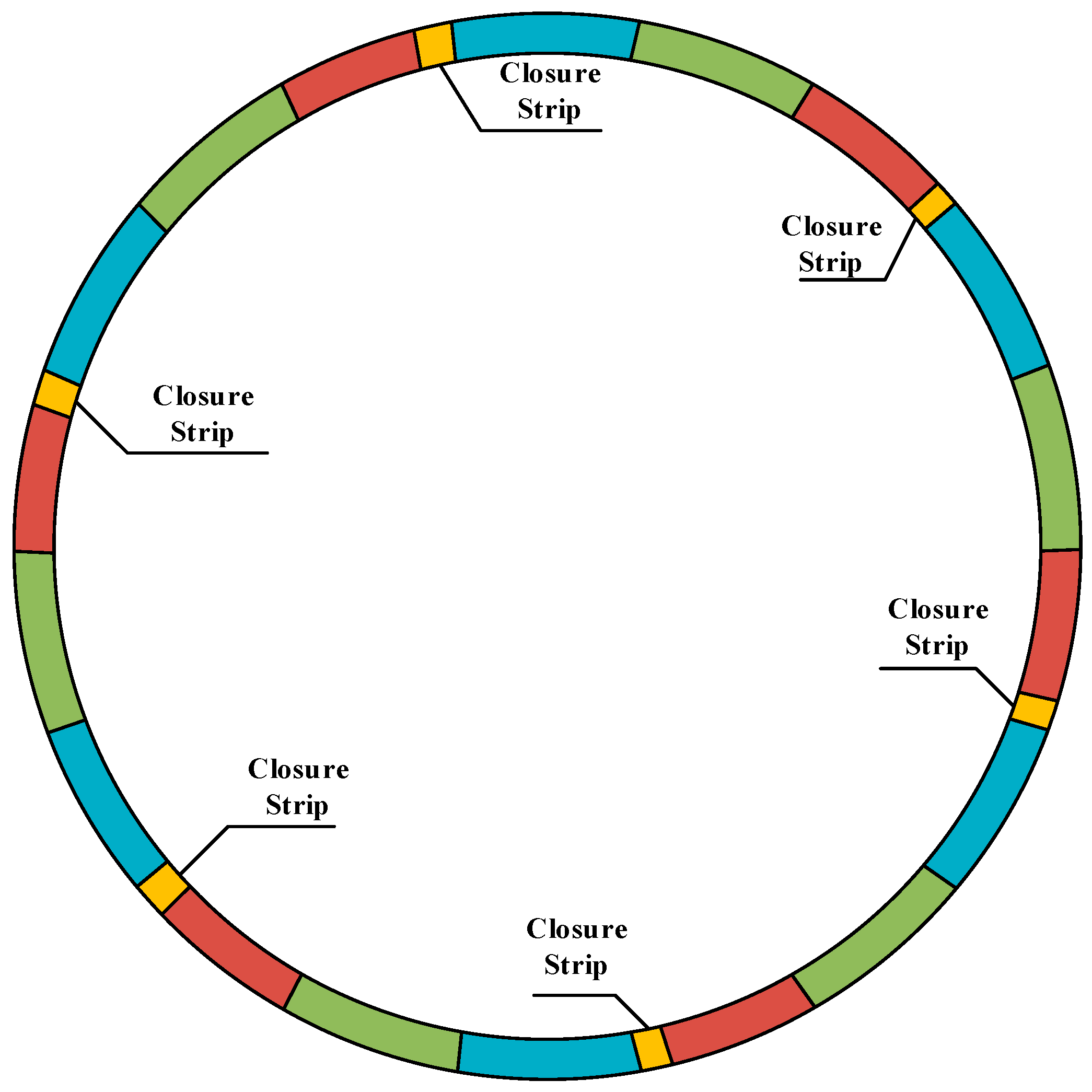
3.1. Excavation Sequence
3.2. Lining Construction
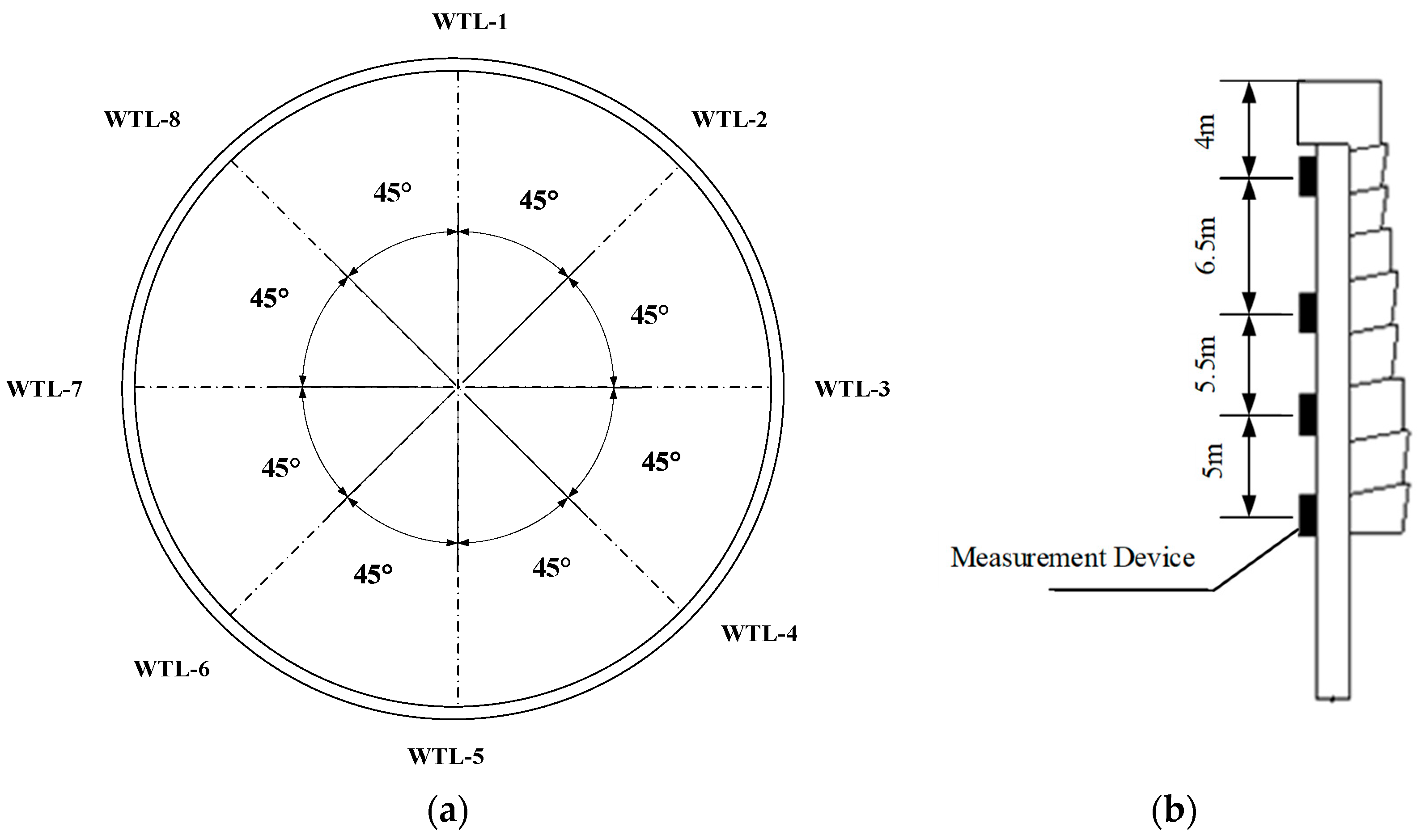
4. Monitoring Scheme
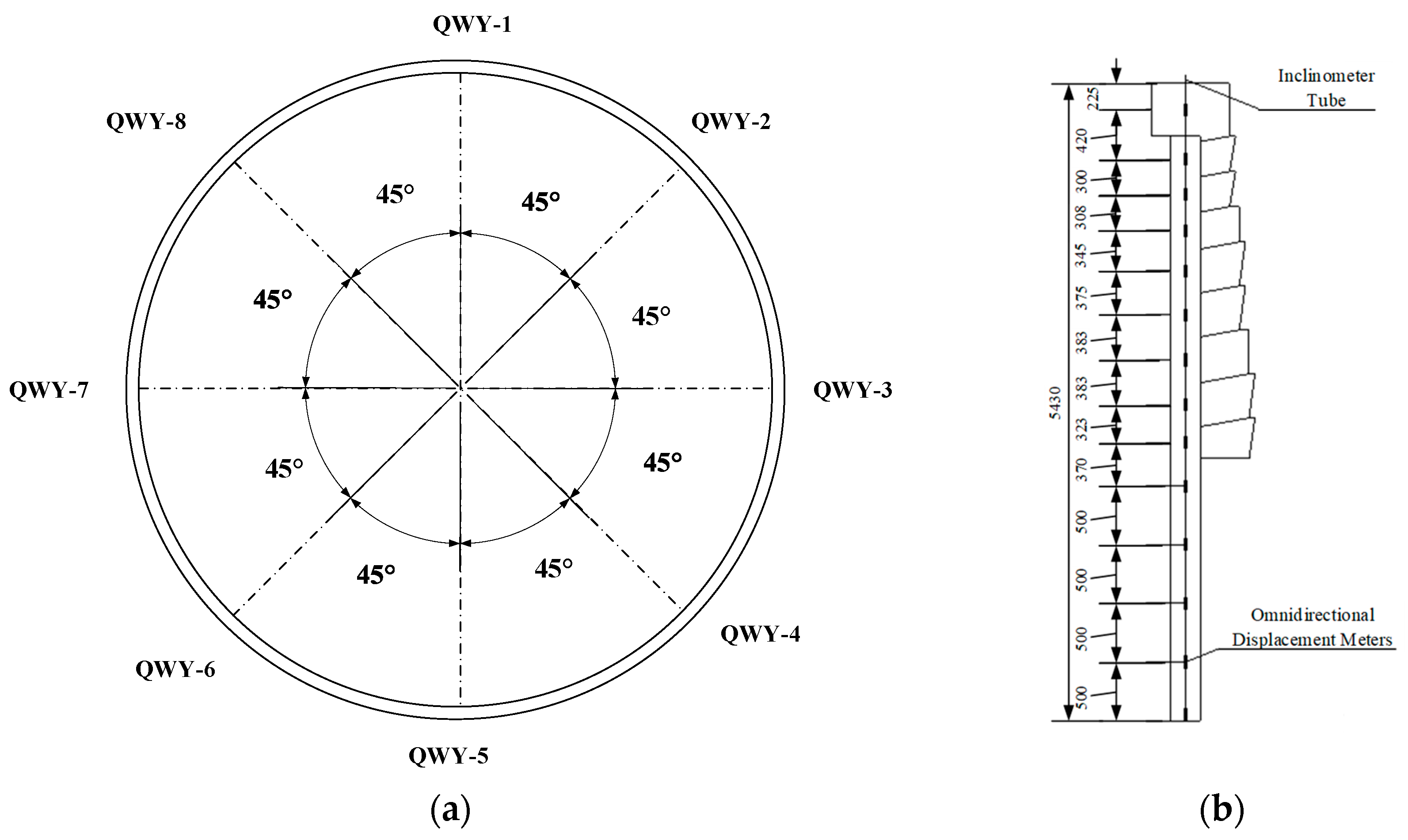
4.1. Deep Horizontal Displacement Monitoring of Diaphragm Wall
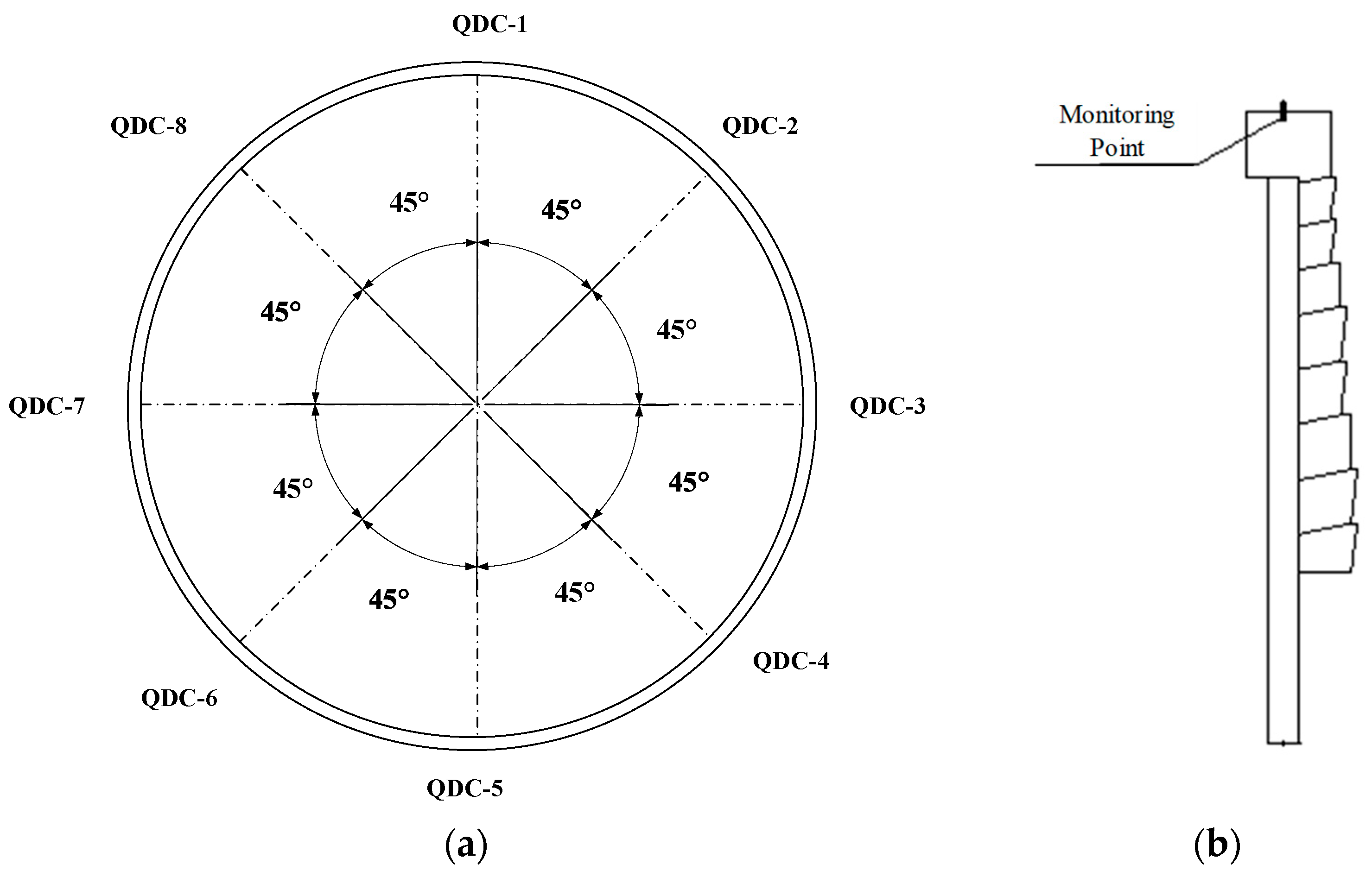
4.2. Vertical Displacement Monitoring at Wall Top
4.3. Earth Pressure Monitoring of Diaphragm Wall
5. Analysis of Monitoring Results
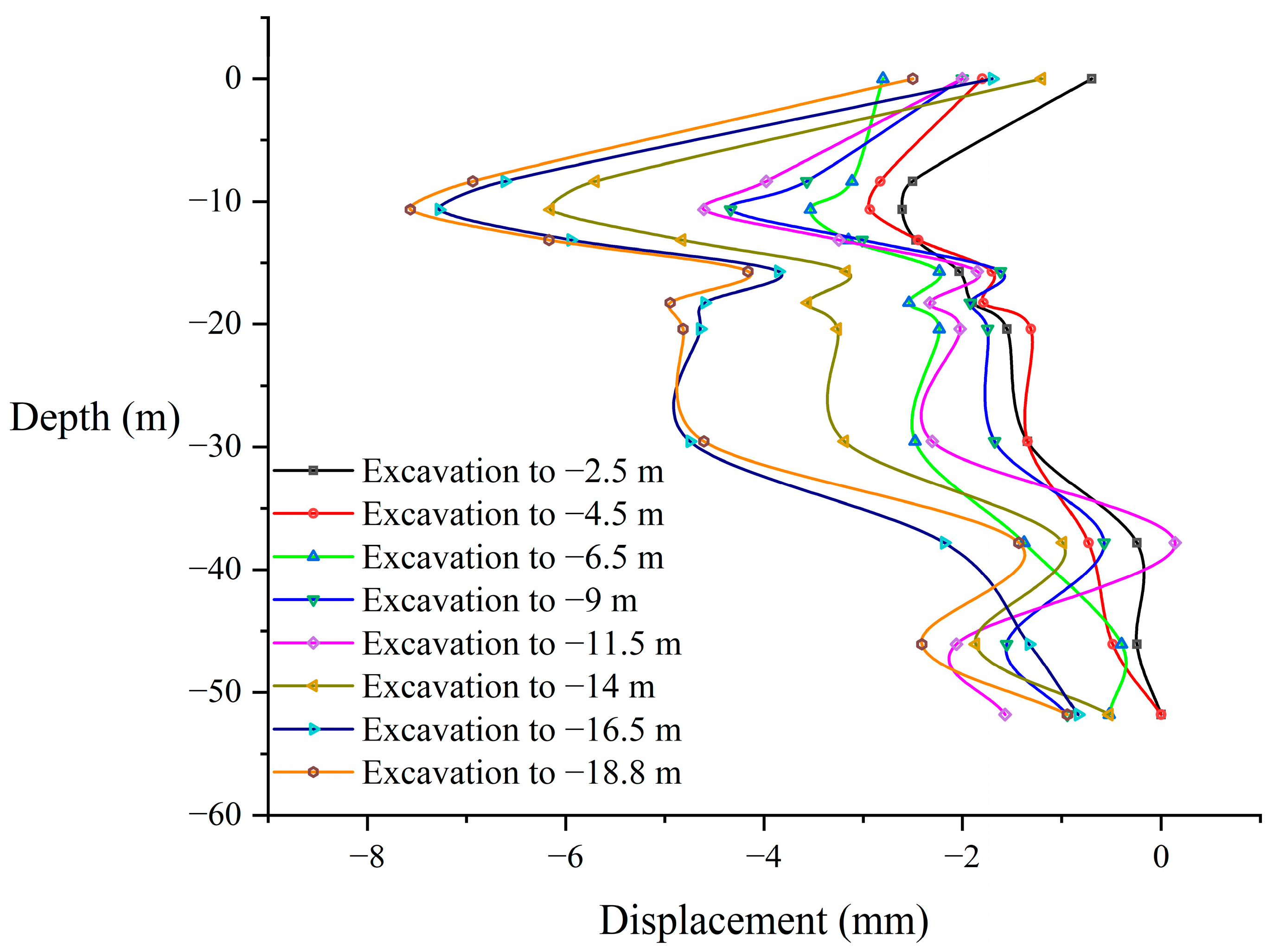
5.1. Deep Horizontal Displacement of Diaphragm Wall
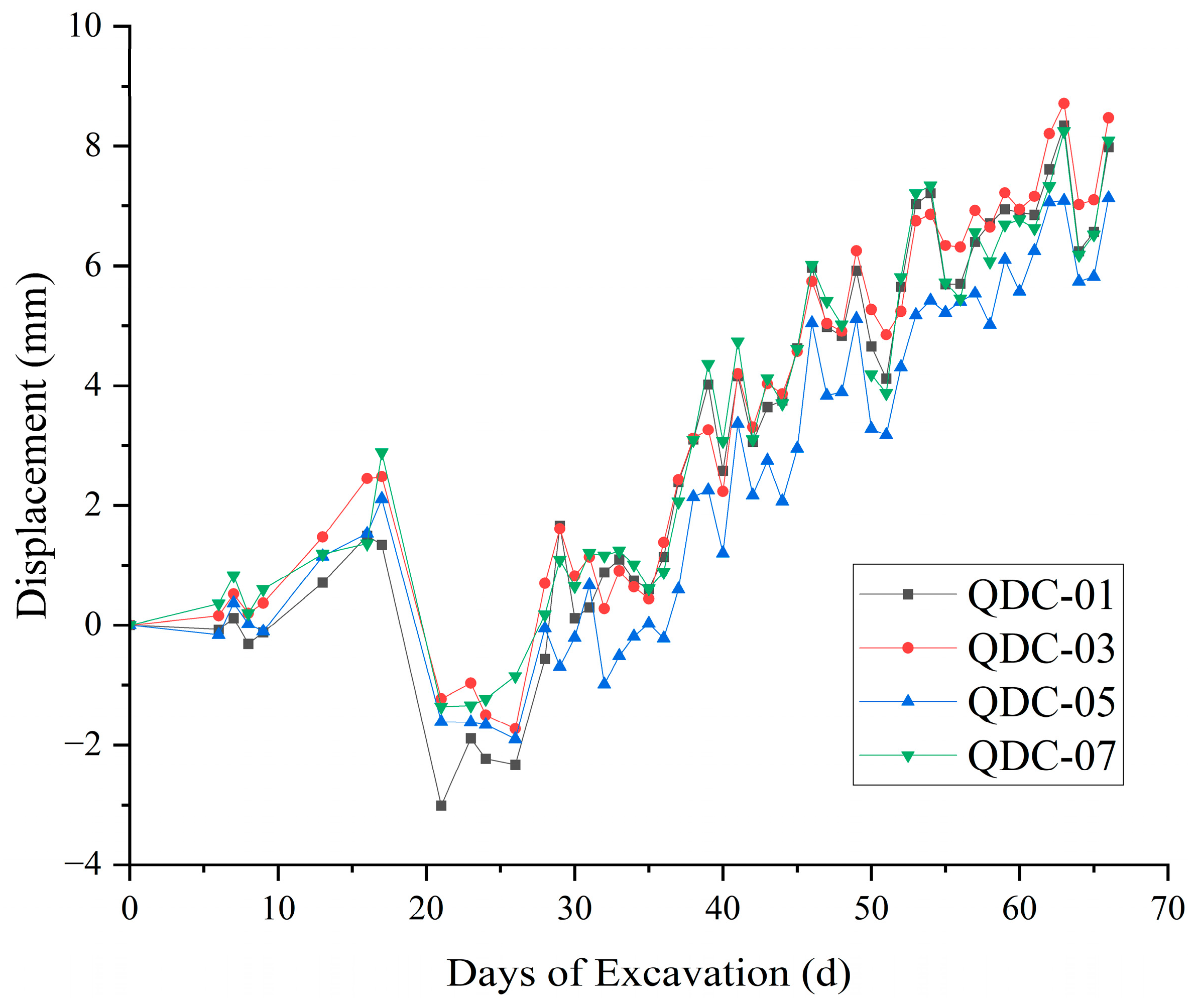
5.2. Vertical Displacement of Diaphragm Wall Top
5.3. Earth Pressure on Diaphragm Wall
6. Stability Analysis
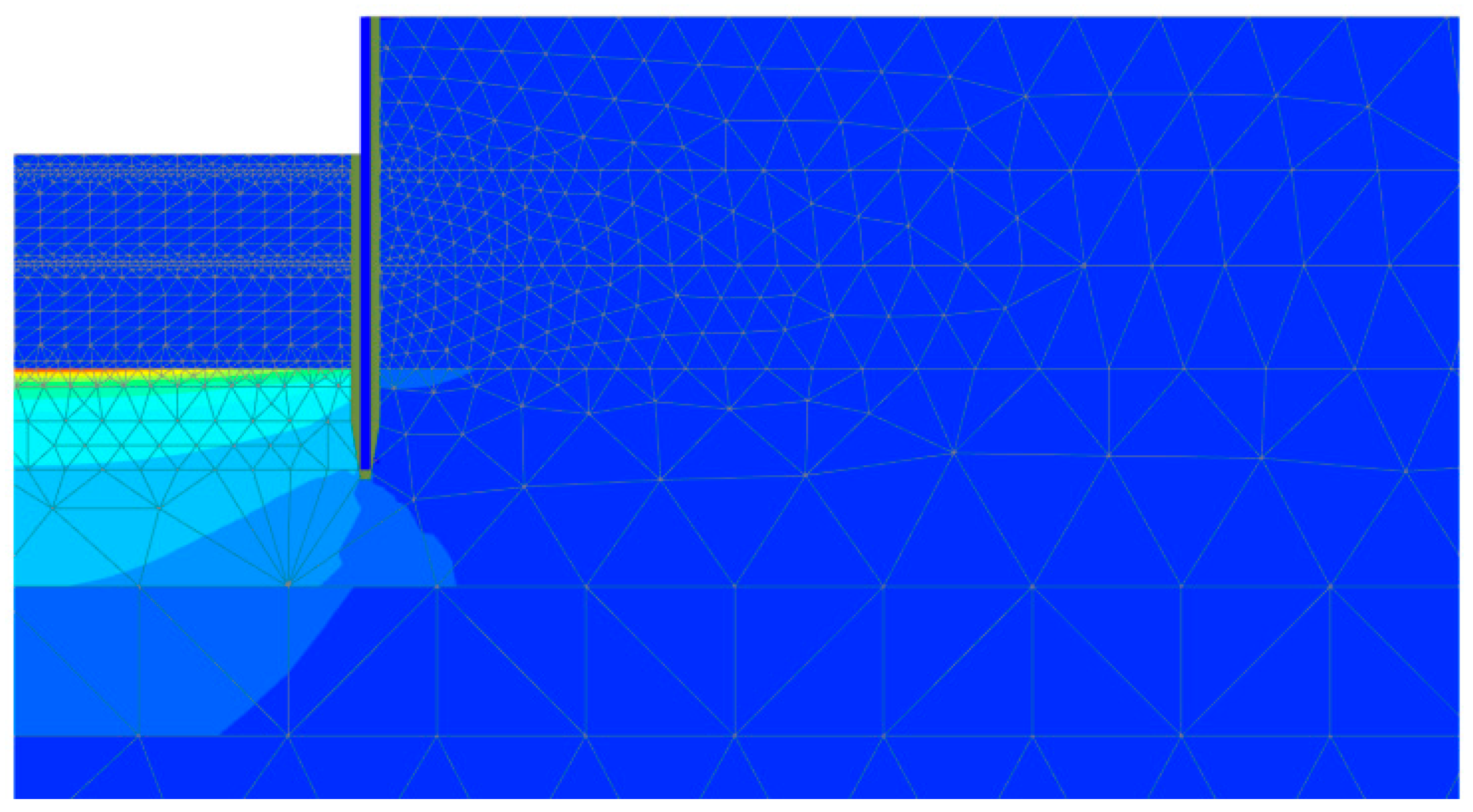
6.1. Finite Element Model Development
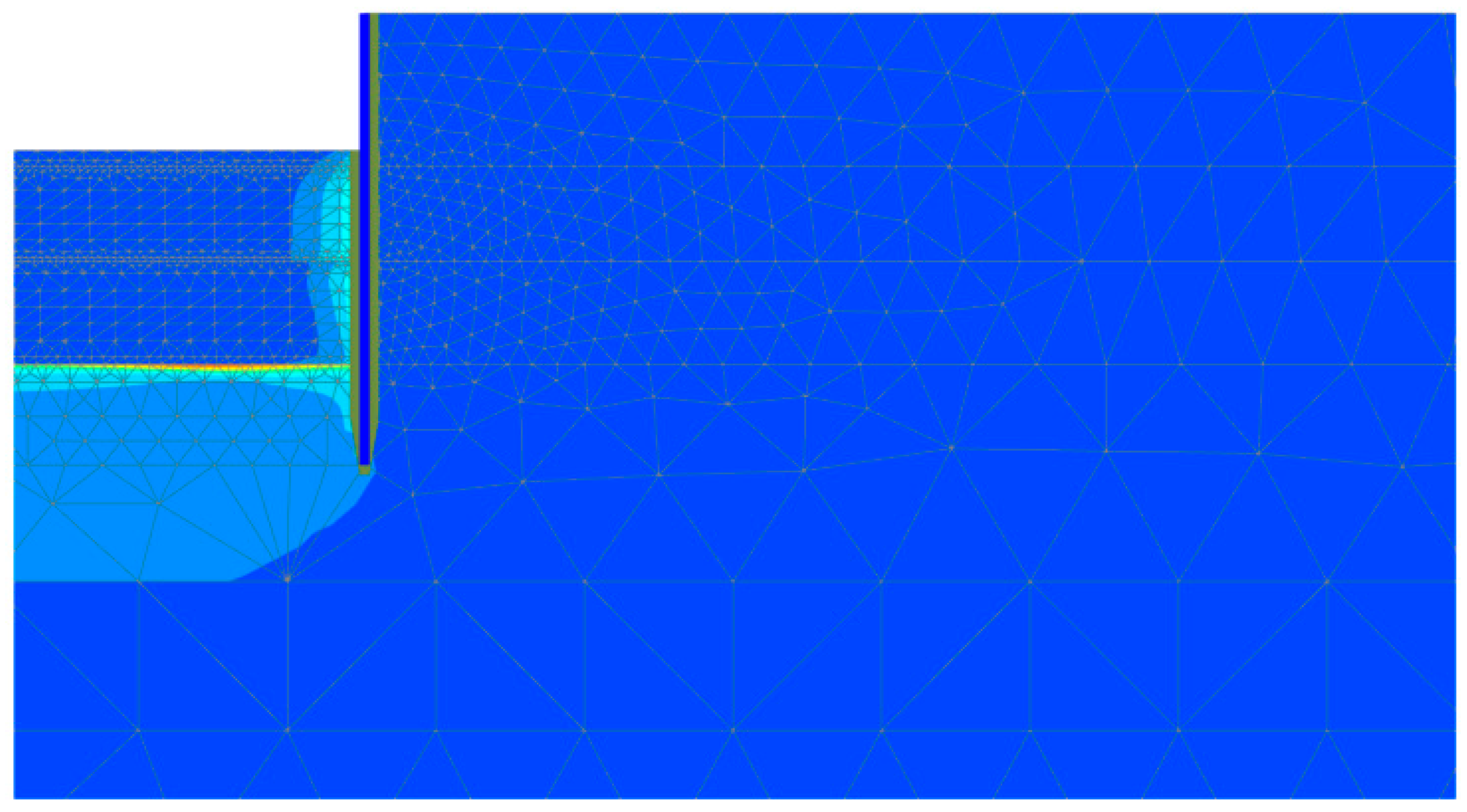
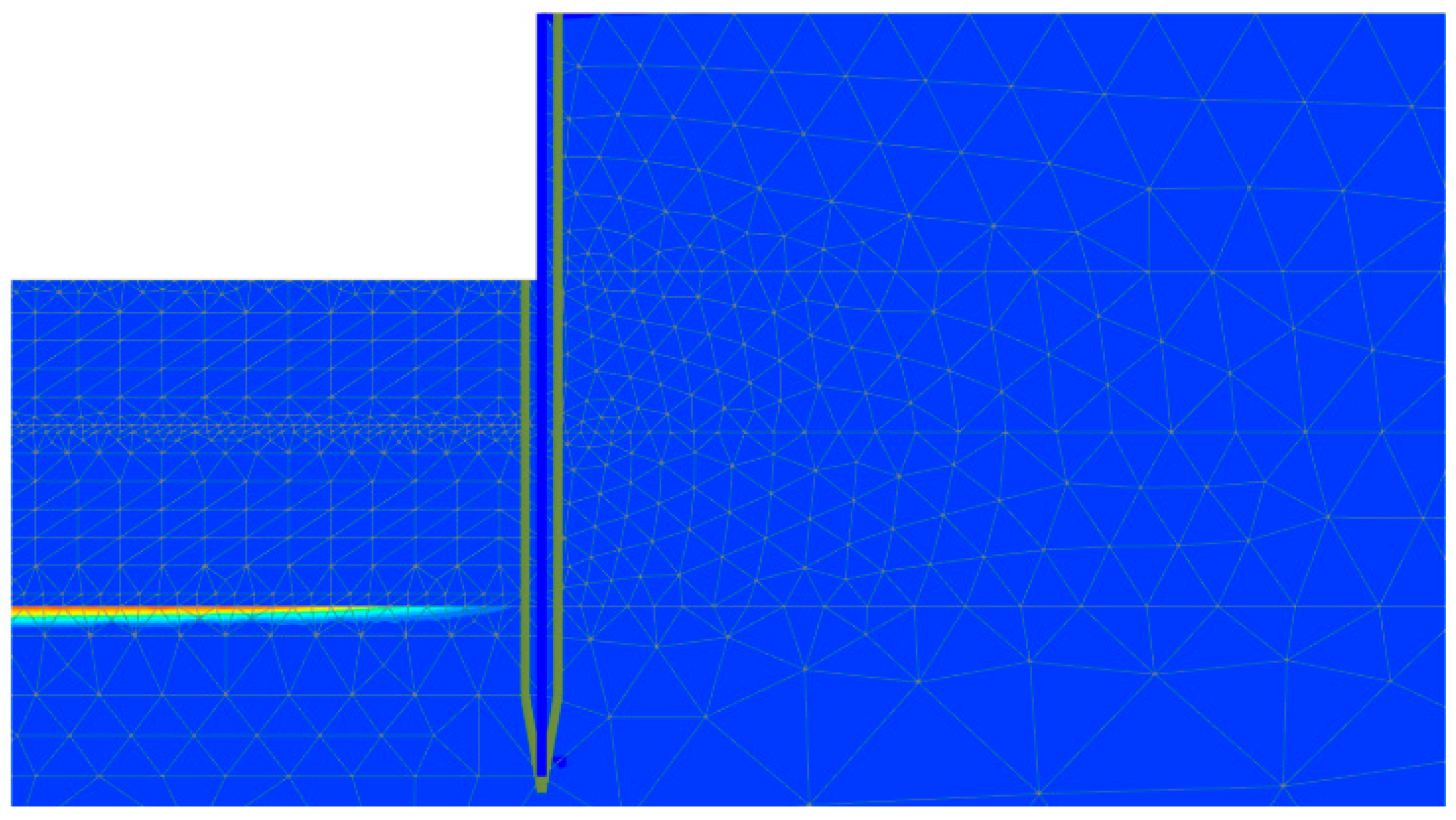
6.2. Mechanism of Foundation Pit Heave
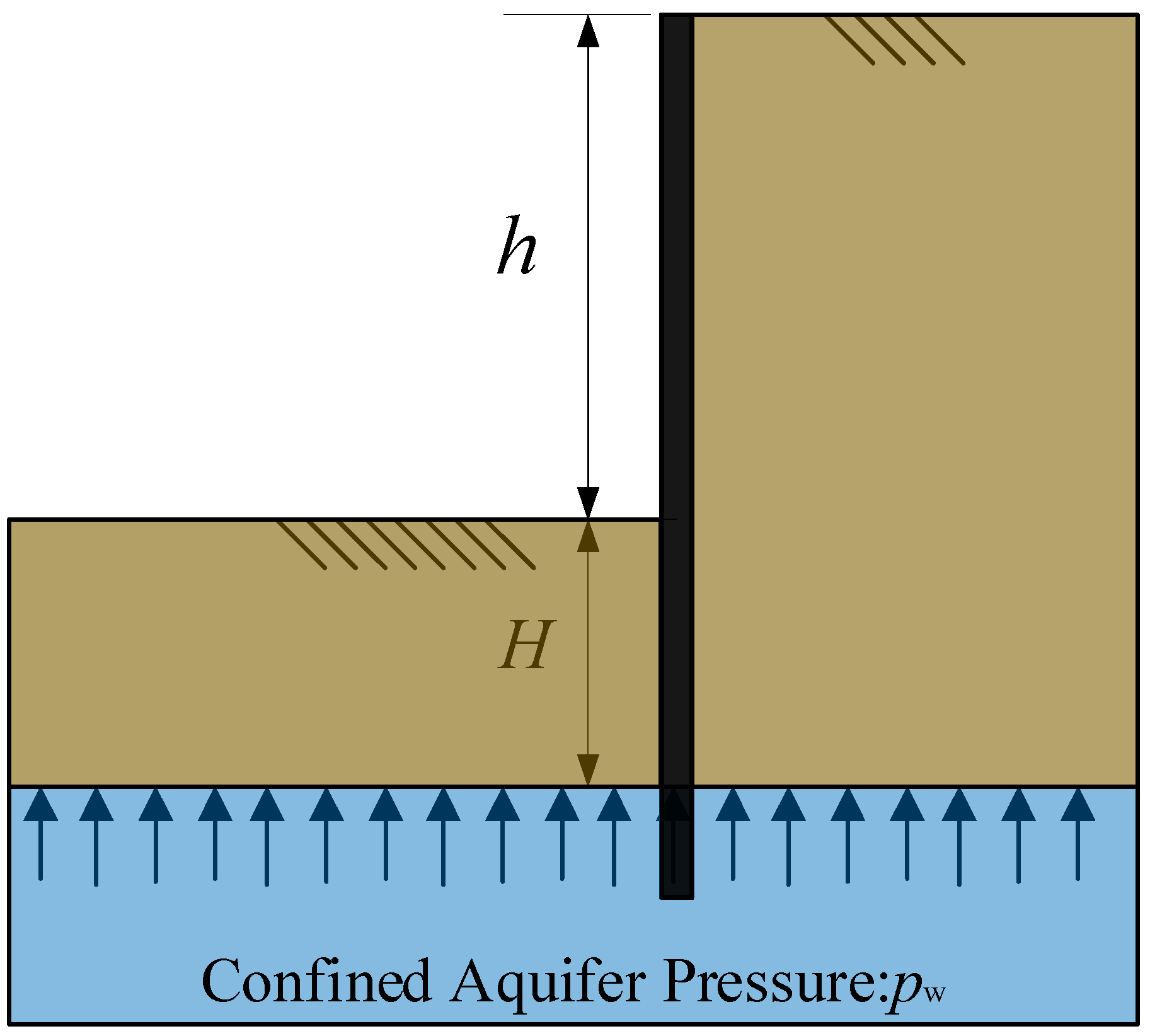
6.3. Stability Against Hydraulic Uplift Calculation
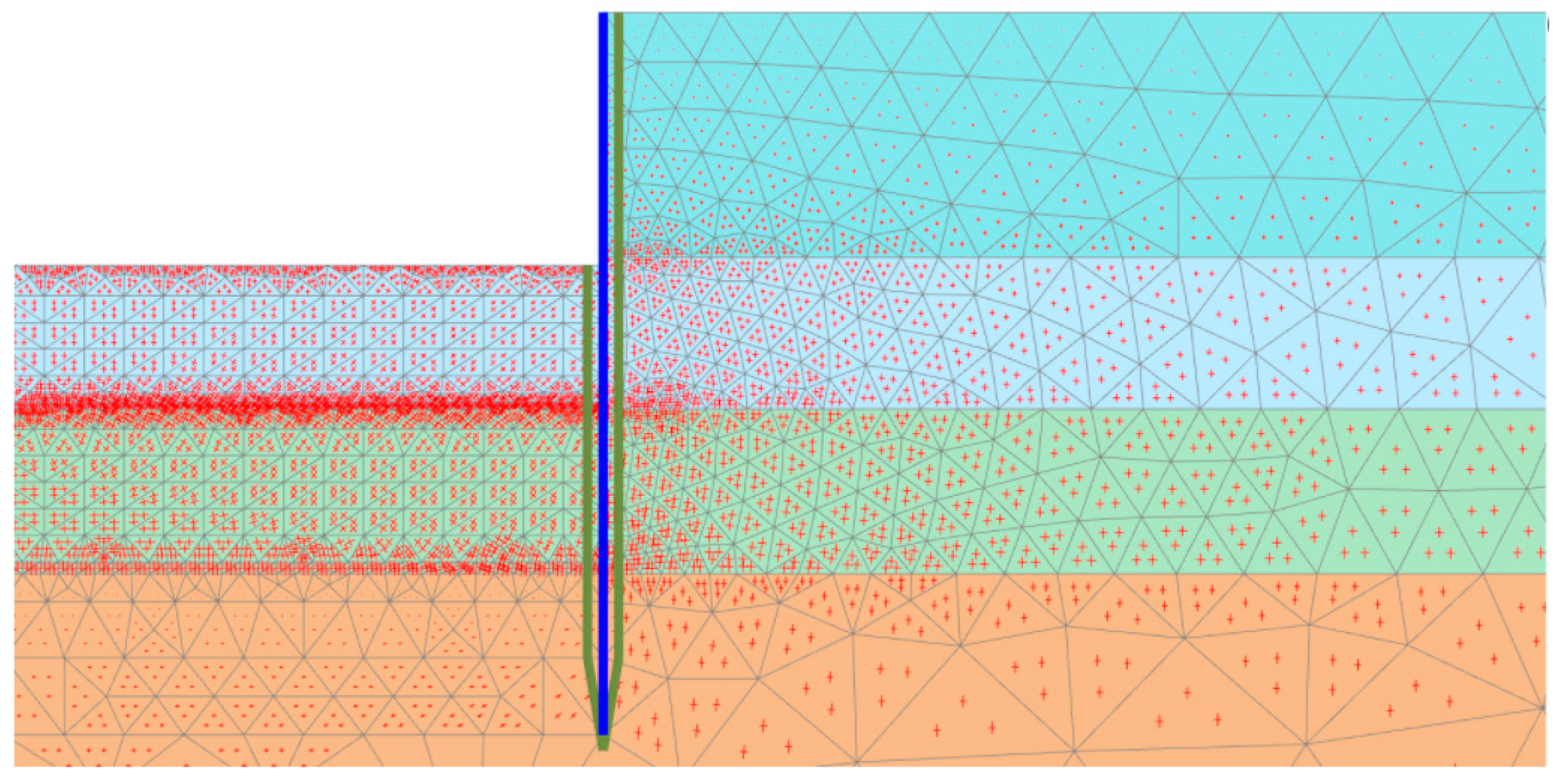
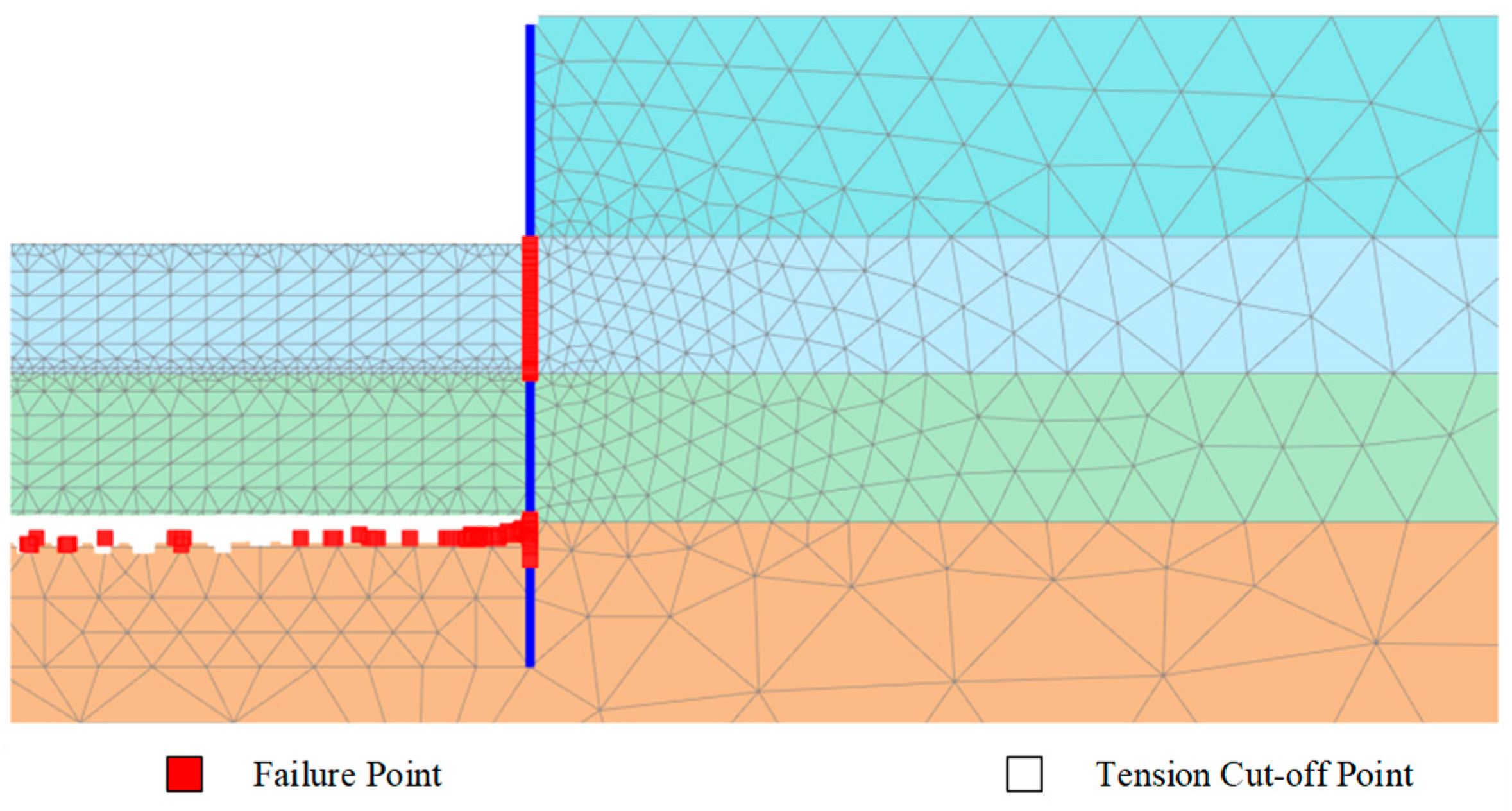
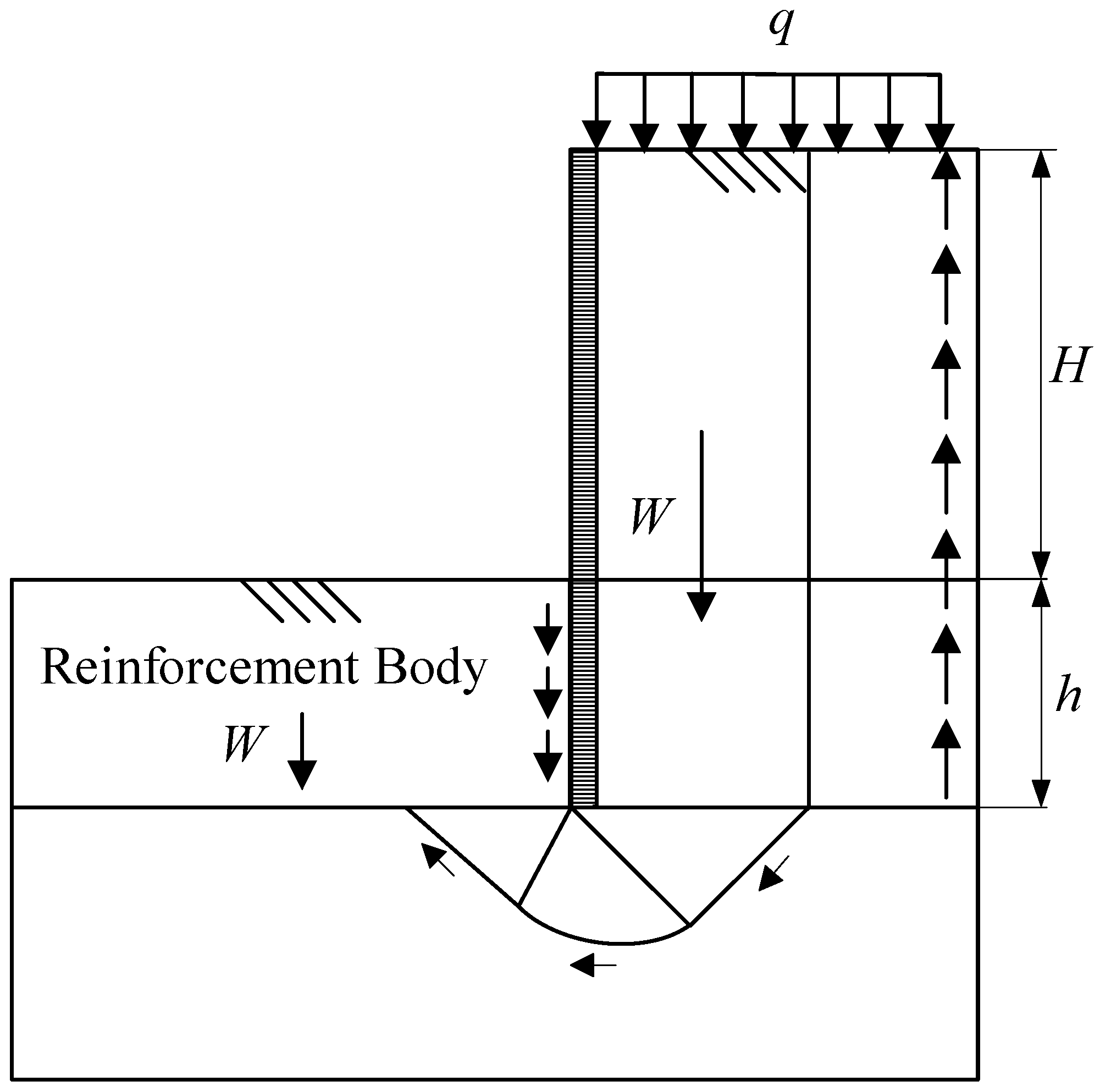
6.4. Base Heave Mechanism of Foundation Pit
7. Conclusions
- (1)
- During the final excavation stage, the maximum horizontal displacement developed within the circular diaphragm wall and concrete lining system. Simultaneously, the peak vertical displacement at the wall crown reached approximately 0.04% of the excavation depth. Both displacement metrics remained substantially below the code-specified control limits, demonstrating that the circular diaphragm wall and lining system effectively controlled pit deformation and ensured construction safety.
- (2)
- The earth pressure on the diaphragm wall exhibits a “decrease followed by increase” pattern during excavation. Initially, it transitions from at-rest earth pressure toward Rankine active earth pressure. However, the high-pressure jet grouting pile reinforcement at the pit bottom significantly enhances the embedment effect of the lower diaphragm wall, constraining deformation and redistributing earth pressures. This mechanism leads to temporary lower-than-active earth pressure values during intermediate excavation phases. As excavation progresses, progressive wall displacements enable gradual convergence with the theoretical Rankine active earth pressure limit.
- (3)
- The finite element simulation of the unreinforced excavation base revealed a distinct failure mechanism: confined aquifer water pressure induces sand particle suspension, triggering central heaving of overburden soil and interface shear failure along the soil–wall boundary. This failure mechanism confirms that the shear strength of ground improvement can effectively counter hydraulic uplift. The proposed calculation methodology, which incorporates the mobilization of side shear strength in the anti-uplift soil mass based on code-specified formulas, is particularly suitable for deep reinforcement techniques that enhance soil shear properties.
- (4)
- In the finite element model simulating the reinforced pit base, the soil failure mechanism of central uplift of the overburden soil layer and sliding shear failure in the external soil adjacent to the diaphragm wall demonstrate that ground improvement changes the soil failure mechanism of the pit base. The calculation method based on Terzaghi’s bearing capacity model for anti-heave stability verification, which accounts for the mobilization of side shear strength in the overburden soil, is better suited for deep reinforcement techniques that improve soil shear performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ge, C.H.; Yang, M.; Li, P.F.; Zhang, M.J. Influence of deep foundation pit excavation on surrounding environment: A case study in Nanjing, China. Acta Geophys. 2025, 73, 495–516. [Google Scholar] [CrossRef]
- Lin, G.; Lin, Z.R.; Zhao, Y.; Xu, C.J.; Sun, F.; Duan, Y.; Fang, T. Force and Deformation Characteristics of Large-Scale Zoning Excavation in Soft Soil: A Case Study in Hangzhou. Appl. Sci. 2024, 14, 6358. [Google Scholar] [CrossRef]
- Yin, S.Y.; Yang, Z.; Lu, C.T.; Dang, Y.K. Numerical Investigation of Underlying Curved Tunnel Heave during a New Foundation Pit Excavation. Int. J. Geomech. 2024, 24, 04024132. [Google Scholar] [CrossRef]
- Huang, J.Z.; Liu, J.Z.X.; Guo, K.; Wu, C.; Yang, S.; Luo, M.X.; Lu, Y.N. Numerical Simulation Study on the Impact of Deep Foundation Pit Excavation on Adjacent Rail Transit Structures-A Case Study. Buildings 2024, 14, 1853. [Google Scholar] [CrossRef]
- Wang, C.; Li, G.; Zou, S.; Yin, S.; Wang, S.; Xiao, Y.; Yu, Z. Intelligent Monitoring and Early Warning System for Deep Foundation Pit of Construction Site Based on Digital Twinning Process, Has Threshold Management Module Used as Early Warning Algorithm Corresponding to Deep Foundation Pit. CN113404029-A, 17 September 2021. [Google Scholar]
- Tan, Y.; Wang, D.L. Structural Behaviors of Large Underground Earth-Retaining Systems in Shanghai. I: Unpropped Circular Diaphragm Wall. J. Perform. Constr. Facil. 2015, 29, 04014058. [Google Scholar] [CrossRef]
- Schwamb, T. Performance Monitoring and Numerical Modelling of a Deep Circular Excavation. Doctoral Dissertation, University of Cambridge, Cambridge, UK, 2014. [Google Scholar]
- Cui, J.; Hu, J.; He, W.; He, Y. Hoop stiffness and its reduction factor of diaphragm wall panels for circular excavation. Chin. J. Geotech. Eng. 2017, 39, 2132–2138. [Google Scholar]
- Wang, Z.; Liang, Z.; Yan, Y.; Zhou, S. Design of Diaphragm Wall for South Anchorage of Qipanzhou Changjiang River Highway Bridge. Bridge Constr. 2018, 48, 89–93. [Google Scholar]
- Li, X.; Pan, D. Key Construction Techniques for Main Bridge of Yangsigang Changjiang River Bridge in Wuhan. Bridge Constr. 2020, 50, 9–16. [Google Scholar]
- Wang, Z.; Yan, Y.; Xu, G.; Zhou, S. Overall Design of Main Bridge of Qipanzhou Changjiang River Highway Bridge. Bridge Constr. 2022, 52, 106–112. [Google Scholar]
- Cui, J.; Hu, J.; He, Y. Force Analysis of Circular Underground Diaphragm Wall Based on Ritz Method. China J. Highw. Transp. 2017, 30, 48–55. [Google Scholar]
- Jia, J.; Zhai, J.Q.; Li, M.G.; Zhang, L.L.; Xie, X.L. Performance of Large-Diameter Circular Diaphragm Walls in a Deep Excavation: Case Study of Shanghai Tower. J. Aerosp. Eng. 2019, 32, 04019078. [Google Scholar] [CrossRef]
- Arai, Y.; Kusakabe, O.; Murata, O.; Konishi, S. A numerical study on ground displacement and stress during and after the installation of deep circular diaphragm walls and soil excavation. Comput. Geotech. 2008, 35, 791–807. [Google Scholar] [CrossRef]
- Wang, R.S.; Liu, S.J.; Xu, L.H.; Zhao, C.Y.; Ni, P.P.; Zheng, W.F. Performance of a 56 m deep circular excavation supported by diaphragm and cut-off double-wall system in Shanghai soft ground. Can. Geotech. J. 2023, 60, 521–540. [Google Scholar] [CrossRef]
- Wang, W.; Xu, Z.; Zong, L.; Zhu, Y.; Weng, Q. Optimal design and practice of a 56m ultra-deep circular excavation in soft soils. Build. Struct. 2022, 52, 1–10. [Google Scholar]
- He, W.; Fan, Z.; Cui, J.; Luo, C.; Zhang, J. Monitoring and Analysis on the Retaining System of Circular Diaphragm Wall for Nizhou Waterway Bridge. Chin. J. Undergr. Space Eng. 2019, 15, 549–555. [Google Scholar]
- Schwamb, T.; Soga, K.; Mair, R.J.; Elshafie, M.; Sutherden, R.; Boquet, C.; Greenwood, J. Fibre optic monitoring of a deep circular excavation. Proc. Inst. Civ. Eng.-Geotech. Eng. 2014, 167, 144–154. [Google Scholar] [CrossRef]
- Xu, Q.W.; Xie, J.L.; Zhu, H.H.; Lu, L.H. Supporting behavior evolution of ultra-deep circular diaphragm walls during excavation: Monitoring and assessment methods comparison. Tunn. Undergr. Space Technol. 2024, 143, 105495. [Google Scholar] [CrossRef]
- Arslan, E.; Akmaz, E.; Çakir, U.F.; Öztürk, Ö.; Pir, H.; Acartürk, S.; Akça, N.; Karakus, Y.; Sert, S. Finite Element Modeling with Sensitivity and Parameter Variation Analysis of a Deep Excavation: From a Case Study. Buildings 2025, 15, 658. [Google Scholar] [CrossRef]
- Song, Y.; Fan, X.; Liang, Y.; Peng, H.; Zhang, H. Deformation Monitoring and Analysis during the Excavation of Deep Circular Shafts in Intercity Railway Tunnels. Mod. Tunn. Technol. 2024, 61, 219–226. [Google Scholar]
- Wang, Y.; Zhang, Y.J.; Li, M.F.; Qi, Y.; Ma, T.H. A Numerical Investigation of the Deformation Mechanism of a Large Metro Station Foundation Pit under the Influence of Hydromechanical Processes. Geofluids 2021, 2021, 5536137. [Google Scholar] [CrossRef]
- Zhu, Y.H.; Wang, W.D.; Xu, Z.H.; Chen, J.J.; Zhang, J. Hydro-Mechanical Numerical Analysis of a Double-Wall Deep Excavation in a Multi-Aquifer Strata Considering Soil-Structure Interaction. Buildings 2025, 15, 989. [Google Scholar] [CrossRef]
- Liu, F.; Xing, H.; Wu, B.; Liu, G.; Ma, S.; Huang, H.; Meng, G. Study on the effect of dewatering-recharge-excavation of deep foundation pits on soil-structure-groundwater under a deep confined water environment. Arab. J. Geosci. 2022, 15, 710. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J.; Yang, B.; Tang, Y. Centrifugal model tests on hydraulic heave mechanism of excavation in cohesive soil with confined water. Chin. J. Rock Mech. Eng. 2013, 32, 598–604. [Google Scholar]
- Martak, L.; Publications Committee Of Xiv, I. Hydraulic uplift in silt and clay in deep and large excavations. In Proceedings of the 14th International Conference on Soil Mechanics and Foundation Engineering, Hamburg, Germany, 6–12 September 1997; pp. 1381–1386. [Google Scholar]
- Zhang, T.T.; Baroth, J.; Dias, D. Deterministic and probabilistic basal heave stability analysis of circular shafts against hydraulic uplift. Comput. Geotech. 2022, 150, 104922. [Google Scholar] [CrossRef]
- Chen, F.Q.; Miao, G.J.; Lai, F.W. Base Instability Triggered by Hydraulic Uplift of Pit-in-Pit Braced Excavations in Soft Clay Overlying a Confined Aquifer. Ksce J. Civ. Eng. 2020, 24, 1717–1730. [Google Scholar] [CrossRef]
- Zeng, S.; Tan, K.X.; Yang, S.J.; Sun, B. Fuzzy Reliability Analysis of Resistant Heave Stability for SMW Exterior-Protected Structure Deep Foundation Pit. In Proceedings of the International Symposium on Safety Science and Technology, Beijing, China, 24–27 September 2008; pp. 2144–2148. [Google Scholar]
- Qia, Y.F.; Yan, K.; Zhao, T.T.; Ding, W.Q. Characteristics and mechanism of soil heave at the bottom of ultra-deep circular shafts in soft soil areas. Rock Soil Mech. 2023, 44, 2707–2716. [Google Scholar] [CrossRef]
- Zhang, C.; Sui, J.; Fan, J.; Xu, H. Basal anti-heave stability of foundation pits in unsaturated soils. Chin. J. Geotech. Eng. 2024, 46, 1762. [Google Scholar]
- Li, Y.; Liu, A.J.; Liu, X.W. Basal heave stability of deep excavation considering virtual foundation width. Rock Soil Mech. 2023, 44, 2843–2850. [Google Scholar] [CrossRef]
- Wang, D.H.; Fu, Z.N.; Ye, C.H.; Jing, J.G.; Gao, J.J.; Liu, N.W.; Xu, H. Deformation Behavior of an Asymmetric Foundation Pit Under Varying Tides. Indian Geotech. J. 2025. [Google Scholar] [CrossRef]
- Luo, X.Y.; Yin, P.; Zheng, Y.S.; Li, X.D.; Zhang, Y.; Tang, Q. Engineering Geological Problems of Foundation Pit Construction in Quaternary Strata: Taking Suzhou Area as an Example. In Proceedings of the 2nd International Conference on Geospatial Technologies and Earth Resources (GTER), Hanoi Univ Min & Geol, Hanoi, Vietnam, 13–15 October 2022; pp. 447–461. [Google Scholar]
- Li, J.; Zhang, F.; Liang, F.; Song, Z. Centrifugal Model Tests and Numerical Simulation on Hydraulic Heave Mechanism in Excavation with Confined Water. J. Tongji Univ. Nat. Sci. 2012, 40, 837–842. [Google Scholar]
- Seitz, J.M. Diaphragm Walls for Deep Shafts for the Anchorage of a Suspension Bridge in Africa. In Proceedings of the 5th International Conference on Grouting, Deep Mixing, and Diaphragm Walls, Honolulu, HI, USA, 9–12 July 2017; pp. 491–501. [Google Scholar]
- Liu, L.; Wang, X.; Pi, J.; Cao, R.; Duan, Q.; Zhang, Q. Rock Mass Behavior During High Pressure Grouting: An In-Situ Experimental Investigation. Rock Mech. Rock Eng. 2025, 58, 2531–2547. [Google Scholar] [CrossRef]
- Wang, S.H.; Gan, F.; Zheng, G.; Zhou, H.Z.; Li, M.L.; Wang, H.; Bi, J.; Zhang, X.Y.; Liu, H.W.; Liu, B.; et al. Investigation of horizontal resistance behavior of vertical-inclined combined high-strength high-pressure jet grouting pile under lateral load. Mech. Adv. Mater. Struct. 2025. [Google Scholar] [CrossRef]
- Wang, D.; Zhao, W.; Shi, X.; Zhang, J.; Yang, Y.; Zhang, Y. Influence of high pressure jet grouting pile construction on deformation of existing railway subgrade. J. Railw. Sci. Eng. 2023, 20, 2500–2508. [Google Scholar]
- Yan, N.H.; Li, G.; Qin, F.; Qiao, X.L.; Lu, B.; Liang, N.; Zhao, S. Study on the deformation characteristics of diaphragm walls in deep excavations within the Ningbo soft soil region. Sci. Rep. 2025, 15, 15036. [Google Scholar] [CrossRef]
- Shi, L.; Yu, W.; Fu, L. Deformation analysis of deep foundation pit in soft soil area considering space–time effect. J. Eng. 2019, 2019, 8274–8281. [Google Scholar] [CrossRef]
- GB 50497-2019; Technical Standard for Monitoring of Building Excavation Engineering. Ministry of Housing and Urban-Rural Development: Beijing, China, 2019.
- Ju, S.W.; Liu, T.; Li, X.W.; Guo, Y.W. Study on the Influence of Different Excavation Sequences of Complex Group Foundation Pits on Subway Stations. Adv. Civ. Eng. 2025, 2025, 8120122. [Google Scholar] [CrossRef]
- Brinkgreve, R.; Kumarswamy, S.; Swolfs, W.; Waterman, D.; Chesaru, A.; Bonnier, P. PLAXIS 2016; PLAXIS bv: Delft, The Netherlands, 2016; pp. 1–16. [Google Scholar]
- Ren, Y.; Chen, Z.; Zhu, W. A Numerical Study of the Lateral Load-Sharing Mechanism of the Pile Cap in a 3 × 3 Pile Group. Buildings 2025, 15, 1431. [Google Scholar] [CrossRef]
- Huang, F.; Chen, Z.; Deng, H.; Zhu, W. Lateral Deformation Mechanisms of Piles in Coastal Regions Under Seawall Surcharge Loading and Mitigation Using Deep Cement Mixing (DCM) Piles. Buildings 2025, 15, 1936. [Google Scholar] [CrossRef]
- Sun, Y.Y. Experimental and theoretical investigation on the stability of deep excavations against confined aquifers in Shanghai, China. Ksce J. Civ. Eng. 2016, 20, 2746–2754. [Google Scholar] [CrossRef]
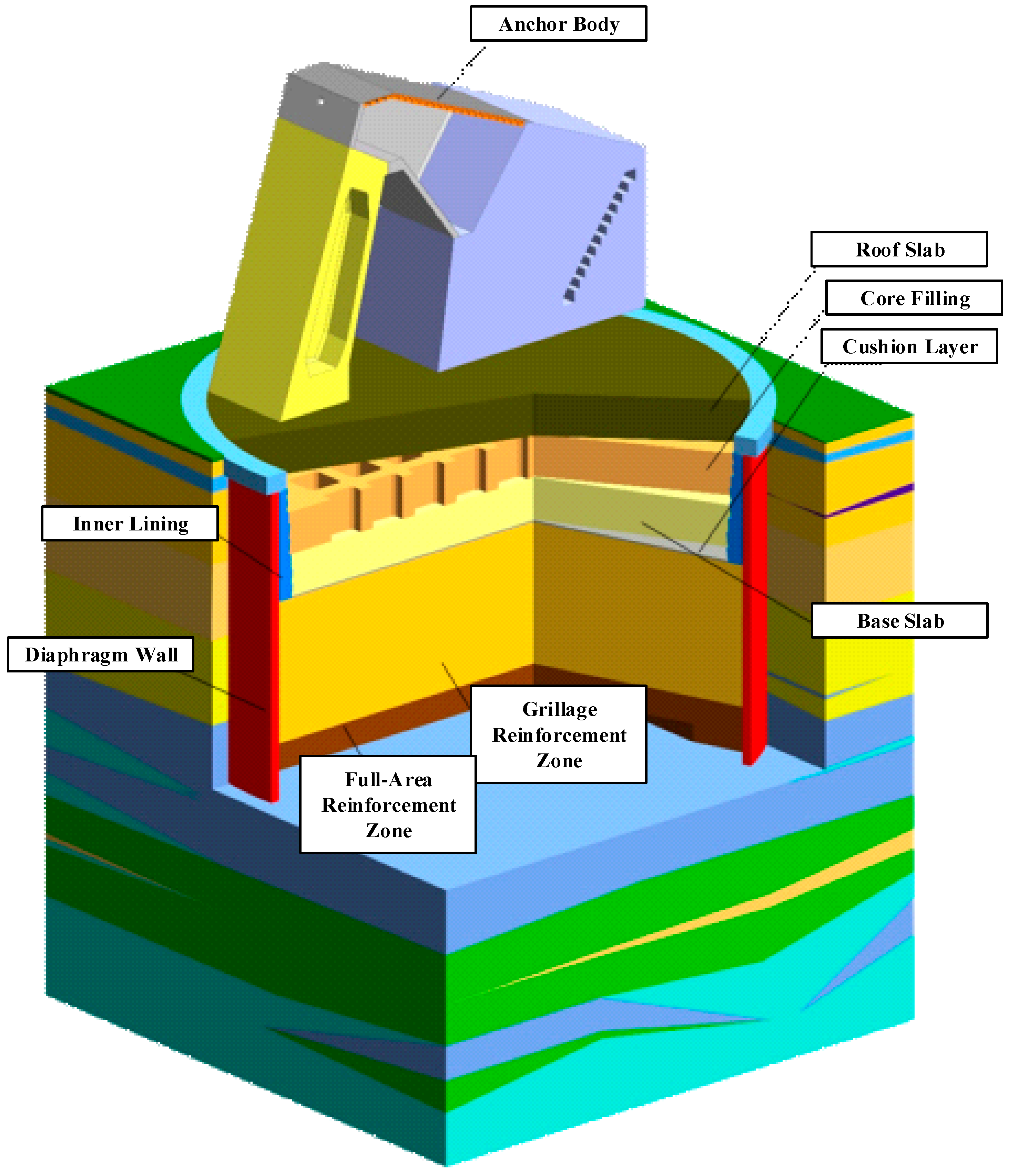
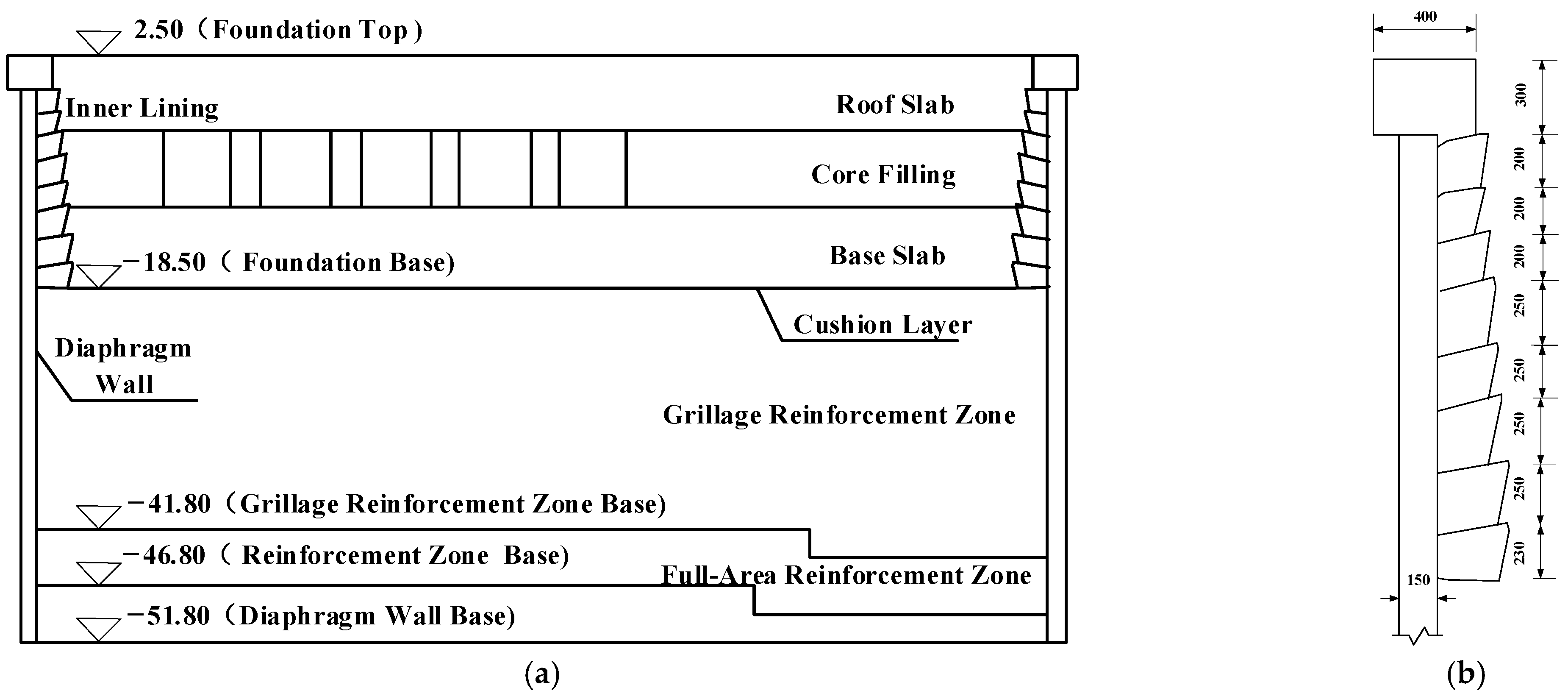
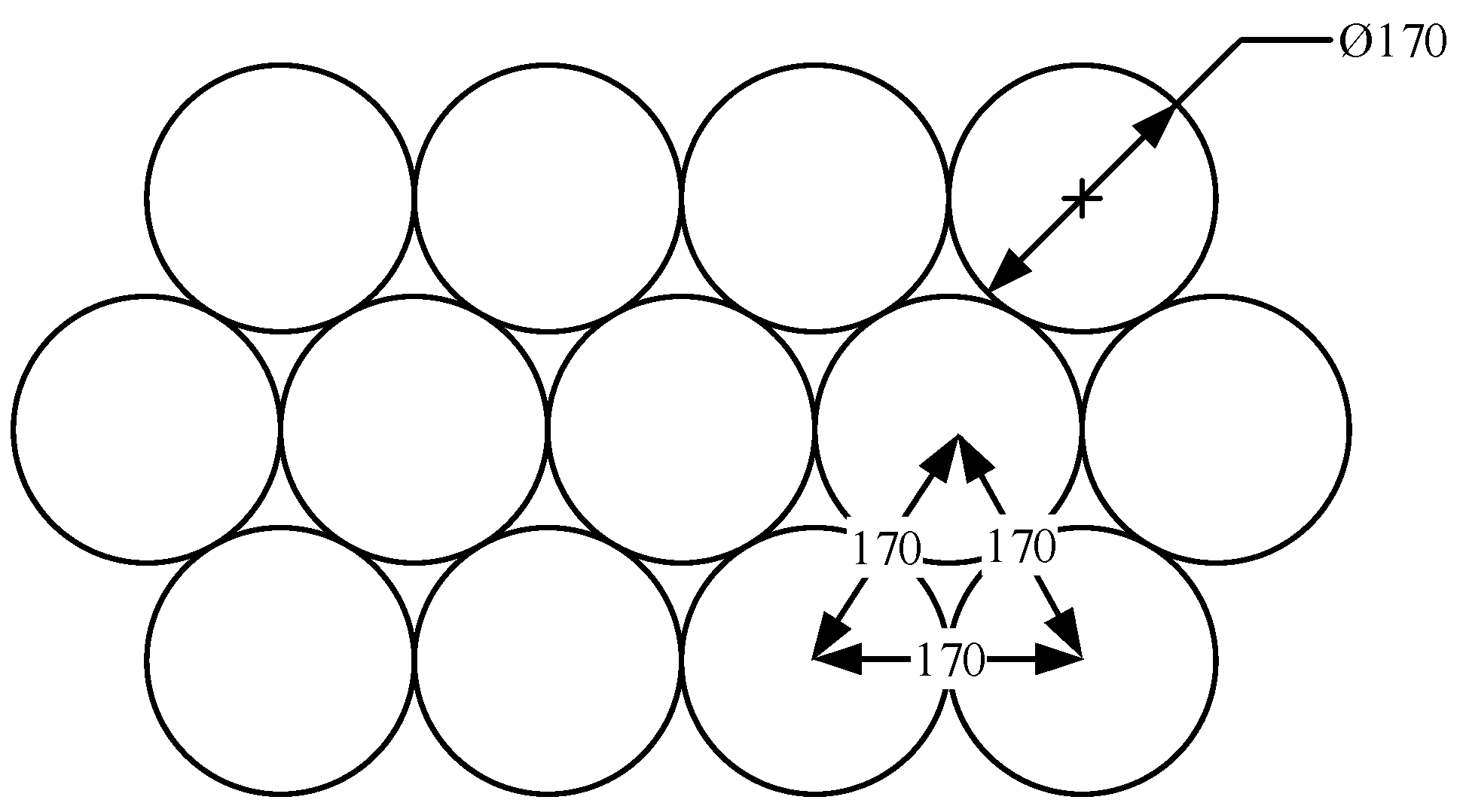
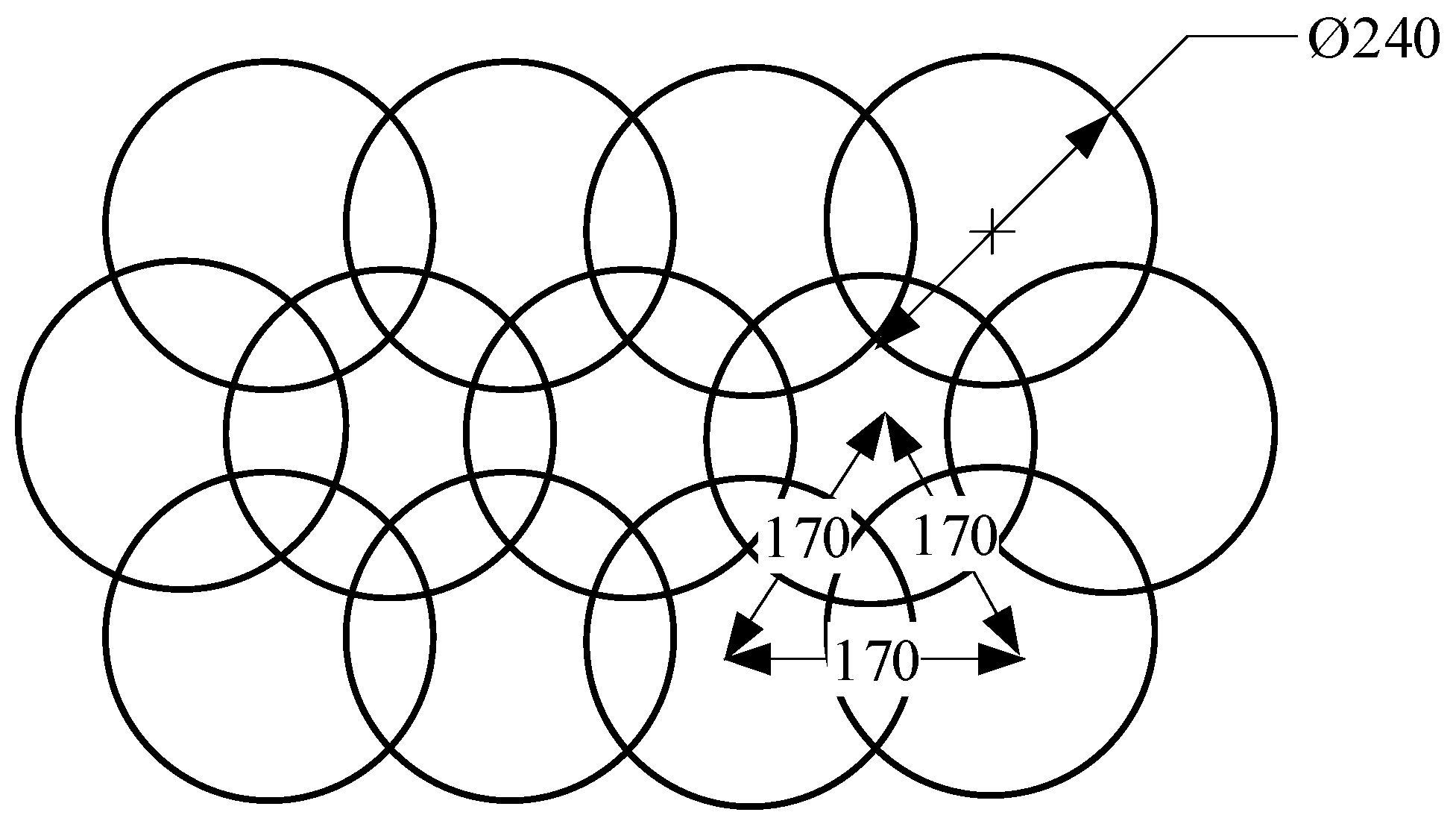





| No. | Soil Layer | Thickness (m) | Unit Weight (kN/m3) | Cohesion (kPa) | Friction Angle (°) | Elastic Modulus (MPa) |
|---|---|---|---|---|---|---|
| 1 | Silty Clay | 2.19 | 18.40 | 12.8 | 7.9 | 12.72 |
| 2 | Silt | 3.10 | 19.00 | 3.1 | 27.9 | 32.44 |
| 3 | Silty Clay | 5.70 | 18.40 | 12.8 | 7.9 | 12.72 |
| 4 | Silt | 2.50 | 19.00 | 3.1 | 27.9 | 32.44 |
| 5 | Silty Clay | 5.50 | 18.40 | 12.8 | 7.9 | 12.72 |
| 6 | Silty Clay | 8.60 | 18.10 | 11.5 | 7.6 | 11.91 |
| 7 | Silty Clay | 20.90 | 18.40 | 14.5 | 9.2 | 13.59 |
| 8 | Silt | 3.90 | 19.70 | 3.3 | 29 | 37.07 |
| 9 | Medium Sand | 2.10 | 19.80 | 4.0 | 28.3 | 42.05 |
| 10 | Silt | 5.90 | 19.70 | 3.3 | 29 | 37.07 |
| 11 | Medium Sand | 3.60 | 19.80 | 4.0 | 28.3 | 42.05 |
| 12 | Coarse Sand | 9.50 | 20.30 | 4.0 | 28.5 | 39.26 |
| 13 | Silt | 7.60 | 19.70 | 7.5 | 25.6 | 27.30 |
| 14 | Coarse Sand | 4.30 | 20.30 | 4.0 | 28.5 | 39.26 |
| 15 | Medium Sand | 12.61 | 20.30 | 3.4 | 28.8 | 36.17 |
| No. | Excavation Stage | Layer Thickness (m) | Duration (d) |
|---|---|---|---|
| 1 | Excavation to −2.5 m | 2.0 | 12 |
| 2 | Excavation to −4.5 m | 2.0 | 7 |
| 3 | Excavation to −6.5 m | 2.0 | 7 |
| 4 | Excavation to −9.0 m | 2.5 | 8 |
| 5 | Excavation to −11.5 m | 2.5 | 8 |
| 6 | Excavation to −14.0 m | 2.5 | 6 |
| 7 | Excavation to −16.5 m | 2.5 | 7 |
| 8 | Excavation to −18.8 m | 2.3 | 8 |
| Monitoring Item | Structure Type | Design Safety Grade of Foundation Pit | |
|---|---|---|---|
| Grade I | |||
| Cumulative Value | |||
| Absolute Value (mm) | Control Value Relative to Design Depth H | ||
| Vertical Displacement at Wall Top | Diaphragm Wall | 10~20 | 0.1%~0.2% |
| Deep Horizontal Displacement | Diaphragm Wall | 30~50 | 0.3%~0.4% |
| No. | Soil Layer | Thickness (m) | Unit Weight (kN/m3) | Cohesion (kPa) | Friction Angle (°) | Elastic Modulus (MPa) |
|---|---|---|---|---|---|---|
| 1 | Silty Clay | 2.19 | 18.40 | 12.8 | 7.9 | 12.72 |
| 2 | Silty Clay | 8.60 | 18.10 | 11.5 | 7.6 | 11.91 |
| 3 | Silty Clay | 20.90 | 18.40 | 14.5 | 9.2 | 13.59 |
| 4 | Silt | 3.90 | 19.70 | 3.3 | 29 | 37.07 |
| 5 | Medium Sand | 2.10 | 19.80 | 4.0 | 28.3 | 42.05 |
| 6 | Medium Sand | 12.61 | 20.30 | 3.4 | 28.8 | 36.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Zhao, W.; Zhao, J.; Dai, G.; Jin, R.; Chen, Z.; Zhu, W. Deformation Characteristics and Base Stability of a Circular Deep Foundation Pit with High-Pressure Jet Grouting Reinforcement. Appl. Sci. 2025, 15, 6825. https://doi.org/10.3390/app15126825
Zhu X, Zhao W, Zhao J, Dai G, Jin R, Chen Z, Zhu W. Deformation Characteristics and Base Stability of a Circular Deep Foundation Pit with High-Pressure Jet Grouting Reinforcement. Applied Sciences. 2025; 15(12):6825. https://doi.org/10.3390/app15126825
Chicago/Turabian StyleZhu, Xiaoliang, Wenqing Zhao, Junchen Zhao, Guoliang Dai, Ruizhe Jin, Zhiwei Chen, and Wenbo Zhu. 2025. "Deformation Characteristics and Base Stability of a Circular Deep Foundation Pit with High-Pressure Jet Grouting Reinforcement" Applied Sciences 15, no. 12: 6825. https://doi.org/10.3390/app15126825
APA StyleZhu, X., Zhao, W., Zhao, J., Dai, G., Jin, R., Chen, Z., & Zhu, W. (2025). Deformation Characteristics and Base Stability of a Circular Deep Foundation Pit with High-Pressure Jet Grouting Reinforcement. Applied Sciences, 15(12), 6825. https://doi.org/10.3390/app15126825






