A Deep Learning Approach for General Aviation Trajectory Prediction Based on Stochastic Processes for Uncertainty Handling

Abstract

General aviation trajectory prediction plays a crucial role in enhancing safety and operational efficiency at non-towered airports. However, current research faces multiple challenges including variable weather conditions, complex aircraft interactions, and flight pattern constraints specified by general aviation regulations. This paper proposes a deep learning method based on stochastic processes aimed at addressing uncertainty issues in general aviation trajectory prediction. First, we design a probabilistic encoder–decoder structure enabling the model to output trajectory distributions rather than single paths, with regularization terms based on Lyapunov stability theory to ensure predicted trajectories maintain stable convergence while satisfying flight patterns. Second, we develop a multi-layer attention mechanism that accounts for weather factors, enhancing the model’s responsiveness to environmental changes. Validation using the TrajAir dataset from Pittsburgh-Butler Regional Airport (KBTP) not only advances deep learning applications in general aviation but also provides new insights for solving trajectory prediction problems.

1. Introduction

Trajectory prediction in general aviation represents a critical component in improving safety and operational efficiency in non-towered airports [1]. Unlike controlled airspace with structured traffic management systems, non-towered airports rely heavily on pilot situational awareness and voluntary compliance with recommended traffic patterns. With approximately 20,000 airports in the United States alone, of which more than 80% are not towered, the ability to accurately predict aircraft trajectories becomes paramount for collision avoidance, traffic management, and emergency response planning [2].

General aviation (GA) encompasses a diverse range of aircraft operations, including personal flights, flight training, aerial surveys, and agricultural applications, among others. The heterogeneity of aircraft types, pilot proficiency levels, and operational objectives introduces significant complexity into trajectory prediction tasks. Traditional deterministic approaches that work well in commercial aviation contexts with standardized procedures and consistent aircraft performance often falter when applied to the more dynamic and unpredictable nature of general aviation operations.

Current research in aviation trajectory prediction has focused primarily on commercial aviation within controlled airspace, where constraints and procedures are well defined [3,4]. Methods ranging from physics-based models to machine learning approaches have demonstrated success in these structured environments [5]. Physics-based models leverage aircraft performance specifications and flight dynamics to predict trajectories, but often struggle with real-time computational demands and sensitivity to environmental variations. Data-driven approaches, including traditional machine learning and neural networks, have shown promise in learning patterns from historical data [6,7], but often fail to capture the uncertainty and rare events critical for safety applications [8].

The application of these existing methods to general aviation presents several distinct challenges. First, weather conditions significantly affect small aircraft more severely than commercial aircraft, introducing a higher degree of variability that must be taken into account in prediction models. Second, the diversity of pilot behaviors, from student pilots practicing maneuvers to experienced pilots executing precise approaches, creates a wide spectrum of potential trajectories that defy simple modeling approaches. Third, while general aviation regulations specify standard traffic patterns, adherence varies considerably among pilots, particularly at non-towered airports where pattern compliance is not actively enforced. Fourth, the sparse data problem in GA trajectory prediction stems from the comparative rarity of recorded flights at any single non-towered airport, limiting the volume of training data available for machine learning approaches.

Furthermore, uncertainty quantification remains a critical gap in current trajectory prediction systems [9]. For safety-critical applications, deterministic predictions alone are insufficient; understanding the confidence level and potential variability of predictions is essential for risk assessment and decision making [10]. This uncertainty comes from multiple sources: measurement errors in collected data, stochastic environmental factors, inherent unpredictability in pilot decision-making, and limitations in model capabilities.

Our approach addresses these challenges by fundamentally reimagining trajectory prediction as a stochastic process rather than a deterministic one [11]. We take advantage of recent advances in deep learning architectures combined with probabilistic modeling to develop a system capable of generating trajectory distributions that capture both the most likely path and the associated uncertainty [12]. Using an encoder–decoder structure with custom attention mechanisms [13], our model effectively learns complex patterns from limited data while maintaining the computational efficiency needed for real-time applications.

The incorporation of stochastic processes allows our model to represent trajectories as probability distributions over possible future states, naturally handling uncertainty while providing richer information for downstream applications [14]. This stochastic framework is complemented by regularization terms derived from Lyapunov stability theory [15], ensuring that predicted trajectories converge to established patterns while accommodating reasonable deviations consistent with real-world operations. Furthermore, our multilayer attention mechanism explicitly models the influence of weather conditions [16], allowing dynamic adjustments to predictions based on changing environmental factors.

The validation of our approach uses the TrajAir dataset collected from Pittsburgh-Butler Regional Airport (KBTP), providing a comprehensive testbed with diverse flight operations and weather conditions. The results demonstrate that our stochastic deep learning approach significantly outperforms both traditional physics-based models and deterministic machine learning methods in terms of prediction accuracy, robustness to environmental variations, and computational efficiency.

The contributions of this paper can be summarized as follows:

• We propose a deep learning architecture based on stochastic processes that generates trajectory distributions rather than single paths, effectively quantifying uncertainty in general aviation trajectory prediction.
• We integrate Lyapunov stability theory-based regularization with a multilayer attention mechanism for weather factors and a comprehensive loss function, creating a model that maintains stable convergence to flight patterns while effectively quantifying uncertainty and responding to environmental variations critical to general aviation operations.
• We validate our approach using real-world data from non-towered airports, demonstrating practical applicability and significant performance improvements over existing methods.

The remainder of this paper is organized as follows. Section 2 reviews related work on trajectory prediction and uncertainty quantification. Section 3 details our methodology, including stochastic process modeling, deep learning architecture, and custom loss functions. Section 4 describes the experimental setup, evaluation metrics and comparative analysis. Finally, Section 5 discusses the implications, limitations, and directions for future research.

2. Related Work

This section reviews key literature relevant to trajectory prediction in general aviation, focusing on prediction methodologies and the unique challenges of general aviation environments.

2.1. Trajectory Prediction Methods and Uncertainty Modeling

Aircraft trajectory prediction methodologies have evolved from physics-based models to data-driven approaches. Physics-based models use aircraft performance parameters and atmospheric conditions to model motion using differential equations. Although interpretable, these methods often require detailed knowledge about aircraft that is unavailable to diverse general aviation fleets [3]. Statistical approaches provide computational efficiency, but may struggle with generalization beyond observed patterns.

Hybrid methods that combine physics-based and statistical techniques have emerged to leverage their complementary strengths. Hrastovec and Solina [17] employed machine learning to estimate aircraft parameters for physics-based models. Despite their promise, these approaches often rely on simplifications that limit their applicability to complex operating conditions of general aviation [4].

Deep learning has significantly advanced trajectory prediction capabilities. Recurrent neural networks, particularly LSTMs [8,18], have demonstrated success in capturing temporal dependencies on flight paths. Attention mechanisms [13] adapted from natural language processing enhance the focus of models on relevant sequence features [19]. Hybrid architectures combining CNNs with recurrent networks effectively capture spatial and temporal patterns in flight data.

The success of deep learning in trajectory prediction extends beyond aviation to other transportation domains, providing valuable insights for our approach. In pedestrian trajectory prediction, Social LSTM [20] pioneered the use of pooling mechanisms to model human-human interactions in crowded spaces, demonstrating how spatial relationships can be effectively captured through neural architectures. Building on this, Social GAN [21] introduced adversarial training for generating socially acceptable trajectories, highlighting the importance of modeling multimodal trajectory distributions. For autonomous vehicle applications, Trajectron++ [12] advanced the field by incorporating semantic maps and agent dynamics into a unified probabilistic framework, achieving state-of-the-art performance in complex traffic scenarios. Similarly, PiP [22] demonstrated how planning information can be integrated into trajectory prediction, improving long-term prediction accuracy. More recently, DenseTNT [23] showed that predicting a dense set of goal candidates before trajectory generation significantly improves prediction quality. These cross-domain advances inform our approach to aviation trajectory prediction, particularly in handling uncertainty quantification and incorporating environmental context.

To address inherent uncertainties in aircraft operations, probabilistic approaches have gained prominence. Gaussian processes model trajectory uncertainty with confidence intervals [24], while Bayesian methods handle multimodal trajectory distributions [25]. Ensemble techniques combine multiple models to improve resilience to environmental variability [26]. More recently, deep probabilistic models enable learning complex uncertainty distributions directly from data [12], although their application to general aviation remains limited [9].

2.2. General Aviation Challenges and Stability Considerations

General aviation presents different challenges for trajectory prediction. Smaller aircraft are more susceptible to weather influences [16], and the diversity of aircraft types introduces substantial performance variability. Pilot behavior represents another significant source of uncertainty, with substantial variations in the adherence to standard traffic patterns [1]. The regulatory environment also differs from commercial operations, allowing greater flexibility in routing and procedures.

The application of Lyapunov stability theory represents an emerging approach with particular relevance to trajectory prediction. Traditionally used in control theory [15], Lyapunov methods provide theoretical guarantees for learning-based approaches. These techniques ensure that the predicted trajectories remain physically plausible and converge to the expected patterns [27,28].

By integrating insights from deep learning, probabilistic modeling, and stability theory with domain knowledge of general aviation operations, our approach addresses the multifaceted challenges of trajectory prediction in general aviation environments.

3. Methodology

Our method, called StochasticTrajectory for general aviation trajectory prediction, integrates stochastic process modeling with deep learning techniques and Lyapunov stability theory to address the inherent uncertainties in general aviation operations. The Lyapunov function acts as an ’energy-like’ measure that decreases over time, similar to how an aircraft naturally settles into a stable flight pattern. In our context, this ensures predicted trajectories converge toward established aviation patterns rather than diverging into unrealistic flight paths. By reframing trajectory prediction as a probabilistic inference problem rather than a deterministic one, we establish a framework capable of capturing the complex interactions between aircraft dynamics, weather conditions, and pilot behavior patterns. This section details our methodology, highlighting the probabilistic framework, the architecture of neural networks, and the specialized loss functions that enable robust trajectory prediction with uncertainty quantification.

3.1. Problem Formulation

Let us define trajectory prediction as a sequential forecasting problem. Given an observed trajectory sequence $X=\{x_1,x_2,\dots ,x_T\}$ where each point $x_t\in {\mathbb{R}}^5$ represents the state of the aircraft at time t including 3D position coordinates (x, y, z) and 2D wind components (windx, windy), our objective is to predict the future trajectory $Y=\{y_{T+1},y_{T+2},\dots ,y_{T+H}\}$ for a horizon H, where each $y_t\in {\mathbb{R}}^3$ represents the predicted 3D position of the aircraft.

Unlike deterministic approaches that output a single trajectory, our model produces a probability distribution over possible future trajectories, represented as:

$$p\left(Y\right|X)=\prod _{t=T+1}^{T+H}p\left(y_t\right|X,y_{T+1},\dots ,y_{t-1})$$

(1)

This formulation explicitly recognizes the inherent uncertainty in trajectory prediction, providing both expected future positions and their associated confidence levels. This probabilistic view addresses a fundamental limitation of deterministic approaches, which fail to capture the range of possible trajectories that might emerge from complex interactions in non-towered airspace.

3.2. Stochastic Process Modeling

We conceptualize aircraft trajectories as realizations of a stochastic process influenced by multiple factors including weather conditions, pilot behavior, and aircraft characteristics. The probabilistic approach allows us to capture this uncertainty through latent variable modeling, where we introduce a latent space z that encodes the distribution of possible trajectory continuations.

Our model takes advantage of a variational approach, approximating the true posterior distribution $p\left(z\right|X)$ with a simpler distribution $q\left(z\right|X)$ parameterized by neural networks. Following the variational autoencoder framework, we model $q\left(z\right|X)$ as a multivariate Gaussian with mean $\mu$ and covariance matrix $\Sigma$ that are functions of the input sequence:

$$q\left(z\right|X)=\mathcal{N}(z\left|\mu \right(X),\Sigma (X\left)\right)$$

(2)

The probabilistic decoder then models each future position as a Gaussian distribution:

$$p\left(y_t\right|z,y_{T+1},\dots ,y_{t-1})=\mathcal{N}\left(y_t\right|{\mu }_t(z,y_{T+1},\dots ,y_{t-1}),{\Sigma }_t(z,y_{T+1},\dots ,y_{t-1}))$$

(3)

This approach naturally generates trajectory distributions rather than single deterministic paths, providing richer information for risk assessment and decision-making in airspace management. Although the stochastic process forms the theoretical foundation of our approach, we need an expressive model architecture to implement this framework effectively in practice, particularly for the complex patterns observed in general aviation operations.

3.3. Network Architecture

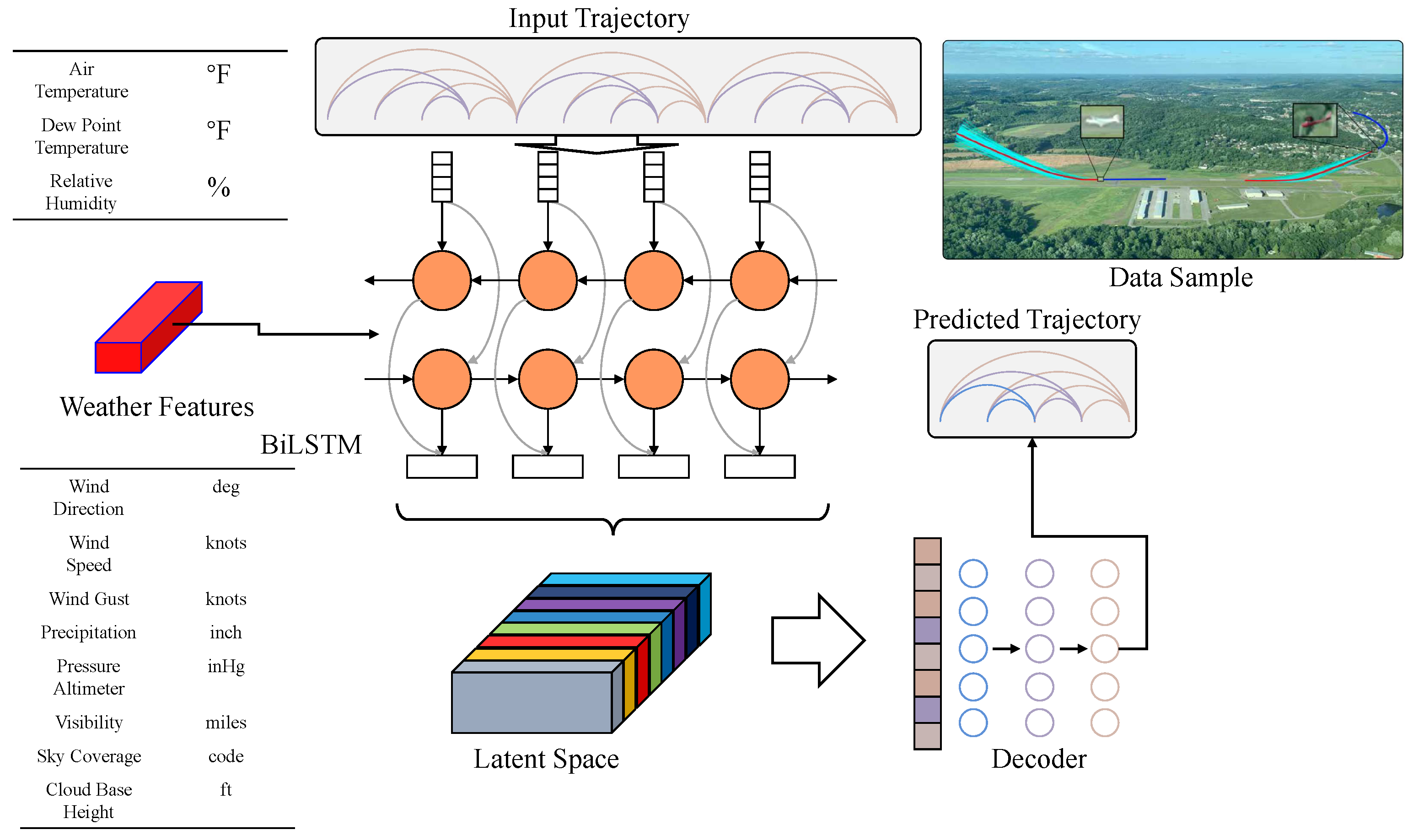
Our neural network architecture, illustrated in Figure 1, consists of a probabilistic encoder–decoder structure with specialized components that address the unique challenges of general aviation trajectory prediction. This probabilistic approach enables the model to represent multiple possible trajectory outcomes rather than a single deterministic prediction, similar to how a pilot might consider several potential flight paths when planning an approach.

3.3.1. Probabilistic Encoder

The encoder transforms the input trajectory sequence into a distribution in latent space. It employs a bidirectional LSTM network to capture temporal dependencies in both directions:

$$h=\mathrm{BiLSTM}\left(X\right)$$

(4)

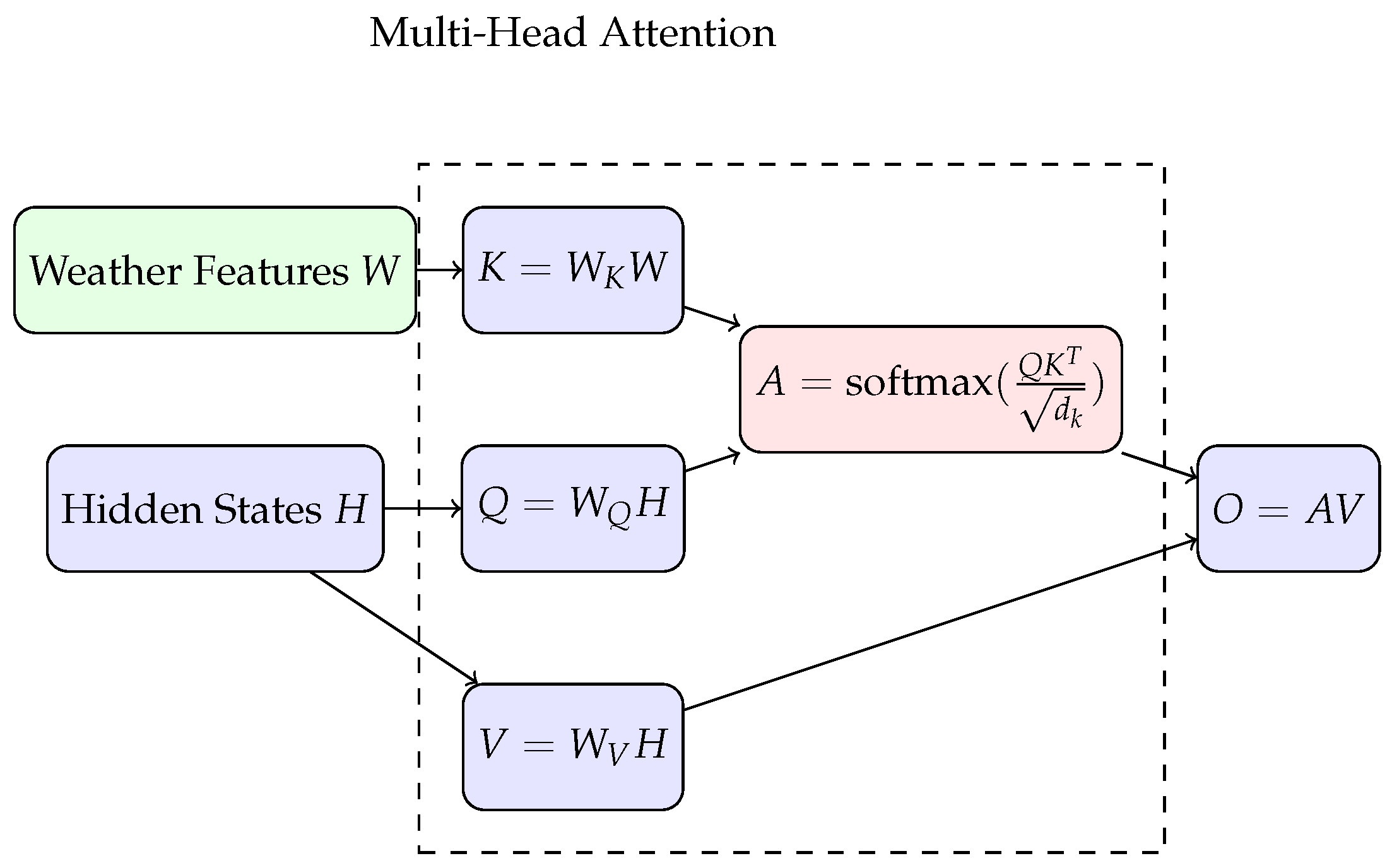
A critical innovation in our encoder is the weather attention mechanism, which explicitly models the influence of weather conditions on trajectory patterns. For each time step t in the sequence, the weather attention computes:

$${\alpha }_t=\mathrm{Attention}(h_t,W_t)$$

(5)

where $W_t$ represents the weather characteristics (wind components) at time t, and the attention function is implemented as a multi-head scaled dot product attention mechanism:

$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}}\right)V$$

(6)

This enables the model to dynamically adjust its focus based on weather patterns, giving more weight to weather factors when they significantly influence the trajectory, as illustrated in Figure 2.

The final hidden state is then projected into the latent space to parameterize the posterior distribution:

$$\mu =W_{\mu }h+b_{\mu }$$

(7)

$$log{\sigma }^2=W_{\sigma }h+b_{\sigma }$$

(8)

During training, we sample from this distribution using the reparameterization trick:

$$z=\mu +\sigma \odot ϵ,\mathrm{where}ϵ\sim \mathcal{N}(0,I)$$

(9)

This probabilistic encoding captures the inherent uncertainty in trajectory prediction by representing not just a single future path, but a distribution over possible continuations. However, not all mathematically possible trajectories are physically realistic or conform to aviation standards. To address this challenge, we incorporate stability constraints in the decoder component.

3.3.2. Stable Decoder with Lyapunov Constraints

The decoder generates future trajectory distributions conditioned on the latent variable z. It employs an LSTM network with autoregressive prediction:

$$h_t=\mathrm{LSTM}([{\widehat{y}}_{t-1},z],h_{t-1})$$

(10)

$${\mu }_t=W_{\mu }{h}_t+b_{\mu }$$

(11)

$$log{\sigma }_t^2=W_{\sigma }{h}_t+b_{\sigma }$$

(12)

A key innovation in our decoder is the incorporation of Lyapunov stability principles to ensure physically plausible trajectories. We introduce a Lyapunov function $V\left(h_t\right)$ parameterized by neural networks:

$$V\left(h_t\right)=W_2·\mathrm{ReLU}(W_1{h}_t+b_1)+b_2$$

(13)

For stability, we enforce that this function decreases over time by penalizing positive differences:

$$\Delta V_t=V\left(h_t\right)-V\left(h_{t-1}\right)$$

(14)

This ensures that the predicted trajectories converge to established flight patterns while accommodating reasonable deviations, effectively balancing adherence to standard procedures with real-world variability, as illustrated in Figure 3.

3.4. Loss Function

With the encoder and decoder architecture defined, we now formulate a comprehensive loss function that balances multiple critical objectives for effective trajectory prediction in general aviation.

Our training objective combines multiple terms to address the multifaceted requirements of trajectory prediction.

$$\mathcal{L}={\mathcal{L}}_{\mathrm{NLL}}+{\lambda }_{\mathrm{Lyap}}{\mathcal{L}}_{\mathrm{Lyap}}$$

(15)

The negative log-likelihood term measures the fit between predicted distributions and actual trajectories:

$${\mathcal{L}}_{\mathrm{NLL}}=-{\displaystyle \frac{1}{H}}\sum _{t=T+1}^{T+H}logp\left(y_t\right|{\mu }_t,{\sigma }_t^2)$$

(16)

$$={\displaystyle \frac{1}{2H}}\sum _{t=T+1}^{T+H}\left(log\left(2\pi {\sigma }_t^2\right)+{\displaystyle \frac{{(y_t-{\mu }_t)}^2}{{\sigma }_t^2}}\right)$$

(17)

The Lyapunov stability term penalizes violations of the stability condition:

$${\mathcal{L}}_{\mathrm{Lyap}}={\displaystyle \frac{1}{H-1}}\sum _{t=T+2}^{T+H}max(0,\Delta V_t)$$

(18)

This comprehensive loss function balances accurate prediction (NLL) and physical plausibility (Lyapunov), resulting in trajectory predictions that are both precise and realistic.

3.5. Implementation Details

Having established the theoretical foundation and architectural design of our approach, we now turn to the practical aspects of implementing and training the model.

We implemented our model using PyTorch 1.4 [29], with the following hyperparameters: hidden size of 128, latent dimension of 64, 2 LSTM layers, dropout rate of 0.2, learning rate of 0.001, and Lyapunov regularization weight of 0.1. The model was trained for 100 epochs using the Adam optimizer with a batch size of 32.

Our input features include aircraft position coordinates (x, y, z) and wind components (wind_x, wind_y), with a sequence length of 20 time steps for input and a prediction horizon of 10 time steps. All features were standardized before training to ensure numerical stability.

For trajectory sampling during inference, we generate multiple samples from the latent distribution to visualize the range of possible future trajectories, providing a comprehensive view of prediction uncertainty, as illustrated in Figure 4.

The overall methodology presented integrates stochastic process modeling, deep learning, and stability theory to effectively address the challenges of trajectory prediction in general aviation. By combining these approaches, we create a system that not only produces accurate predictions but also quantifies uncertainty in a manner that supports safety-critical decision making in non-towered airport environments.

4. Results and Experimental Evaluation

This section presents a comprehensive evaluation of our proposed StochasticTrajectory model against baseline approaches for general aviation trajectory prediction. We analyze performance across multiple metrics, with a particular focus on prediction accuracy, uncertainty quantification capabilities, and the contribution of individual model components.

4.1. Experimental Setup

4.1.1. Dataset and Preprocessing

All experiments were carried out using the TrajAir dataset [30] collected from Pittsburgh-Butler Regional Airport (KBTP), a non-towered airport with various general aviation operations. The dataset contains trajectory coordinates (x, y, z) and corresponding weather information (wind components) recorded over multiple months, providing a comprehensive testbed for model evaluation.

We implemented a comprehensive preprocessing pipeline to ensure data quality and reliability. For missing data handling, we removed trajectory sequences with significant ADS-B reporting gaps to maintain temporal continuity, applied linear interpolation for missing weather data when gaps were sufficiently small, and used cubic spline interpolation for brief trajectory gaps to preserve smoothness. Our outlier detection employed statistical methods to identify and remove anomalous data points, including velocity outliers detected through unrealistic speed changes, altitude rate anomalies exceeding typical aircraft performance limits, and erroneous wind measurements validated against meteorological constraints.

We standardized all features and segmented continuous trajectories into sequences using a sliding-window approach. We used a sequence length of 20 time steps for input and predicted 10 time steps in the future. To assess model robustness to different temporal resolutions, We evaluate performance at three temporal resolutions: 1 Hz (original data), 0.5 Hz (downsampled by factor of 2), and 0.25 Hz (downsampled by factor of 4).

4.1.2. Baseline Methods

We compared our proposed StochasticTrajectory model against several established baseline methods, which can be categorized into three groups:

• Deep Learning Models:

  –

  LSTM: Long Short-Term Memory network as introduced by Hochreiter and Schmidhuber [31], with the same number of layers and hidden units as our proposed model.

  –

  Attention: An LSTM model augmented with the attention mechanism proposed by Bahdanau et al. [32], but without the specialized weather attention or stochastic components of our approach.

  –

  SimpleRNN: A basic recurrent neural network implementation following the architecture described by Elman [33].

  –

  GRU: Gated Recurrent Unit network as proposed by Cho et al. [34], which uses simpler gating mechanisms than LSTM.

  –

  MLP: Multi-Layer Perceptron as formalized by Rumelhart et al. [35], with equivalent parameter count to our recurrent models.

• Traditional Statistical Models:

  –

  ARIMA: Auto-Regressive Integrated Moving Average model developed by Box and Jenkins [36] for time series analysis.

• Physics-Based Models:

  –

  Physics: A kinematic model based on aircraft equations of motion following the approach described by Stevens and Lewis [37].

  –

  KalmanFilter: State estimation approach using the linear Kalman filtering method introduced by Kalman [38].

All baseline models were optimized using the same training and validation datasets as our StochasticTrajectory model, with hyperparameters tuned through grid search to ensure fair comparison.

4.1.3. Evaluation Metrics

We evaluated the performance of the models using the following metrics:

• Mean Squared Error (MSE): Measures the average squared distance between predicted and actual trajectory points.
• Training Loss: The value of the loss function on the training dataset.
• Validation Loss: The value of the loss function on the validation dataset.
• Uncertainty Calibration: For the StochasticTrajectory model, we assessed how well the predicted uncertainty matched the actual error distribution.

4.2. Quantitative Results

Effect of Sampling Rate on Prediction Accuracy

Table 1. Test MSE comparison across models and sampling rates.

Model	SR = 1	SR = 2	SR = 4
StochasticTrajectory	0.0000678	0.000849	0.0218
LSTM	0.000163	0.00152	0.0212
Attention	0.000229	0.00225	0.0238
SimpleRNN	0.00313	0.00653	0.0390
GRU	0.000136	0.00137	0.0177
MLP	0.000561	0.00551	0.0434
Physics	0.0404	0.0899	0.401
KalmanFilter	0.229	0.144	0.401
ARIMA	0.0889	2.28	1.85

presents the test MSE for all models across different sampling rates. Lower values indicate better performance.

Deep Learning Approaches: Our StochasticTrajectory model demonstrates superior performance at higher temporal resolutions (SR = 1 and SR = 2), achieving MSEs of 0.0000678 and 0.000849, respectively. This reflects its ability to effectively model the inherent uncertainty in general aviation trajectories. Among conventional recurrent models, GRU exhibits the most consistent performance across all sampling rates, achieving the best overall result at SR = 4 (MSE = 0.0177). This suggests that GRU’s simpler gating mechanism provides better generalization on sparse data typical in general aviation environments. LSTM performs well but shows slightly higher error rates than both StochasticTrajectory and GRU, while SimpleRNN and MLP demonstrate substantially higher errors, particularly at lower sampling rates.

Traditional and Physics-Based Methods: Statistical and physics-based approaches show clear limitations in modeling general aviation trajectories, with performance strongly dependent on data density. LinearRegression achieves competitive performance only at the highest sampling rate (SR = 1, MSE = 0.0000663), likely capturing short-term linear segments of flight, but degrades rapidly as the data becomes sparser (SR = 4, MSE = 0.0551). The substantial deterioration of ARIMA, Physics, and KalmanFilter models across all sampling rates, with errors orders of magnitude higher than deep learning approaches, underscores the fundamental limitations of these methods for general aviation applications.

Impact of Sampling Rate: All models exhibit performance degradation as the sampling rate decreases, reflecting the increasing difficulty of trajectory prediction with sparse temporal data. However, deep learning approaches, particularly StochasticTrajectory and GRU, demonstrate greater resilience to reduced data density compared to traditional methods. This characteristic is crucial for practical applications in general aviation, where available data may vary in quality and frequency.

These results demonstrate that our stochastic model not only captures uncertainty effectively but also maintains competitive or superior accuracy compared to deterministic approaches, particularly at lower sampling rates where data are more dense and patterns are more discernible.

4.3. Uncertainty Quantification and Trajectory Distribution

The primary advantage of our StochasticTrajectory model lies in its ability to quantify uncertainty in predictions, which is critical for safety-critical applications in general aviation. To thoroughly investigate this capability, we analyzed the statistical properties of the input and target trajectory data at different sampling rates.

Statistical Analysis of Trajectory Data

Table 2. Statistical properties of trajectory data across sampling rates.

Metric	SR = 1	SR = 2	SR = 4
Input Std. Dev.	1.6048	1.5870	1.5583
Target Std. Dev.	1.1700	1.1651	1.1658
Uncertainty Ratio	0.7291	0.7341	0.7481
Input Range (Max-Min)	9.2766	9.2621	9.2245
Target Range (Max-Min)	7.2578	7.2568	7.2568
Range Expansion Ratio	0.7824	0.7835	0.7867

presents a comparative analysis of statistical measures in different sampling rates for both input trajectory data (historical points used for prediction) and target trajectory data (future points to be predicted). "Uncertainty Ratio" is calculated as the ratio of target trajectory standard deviation to input trajectory standard deviation.

As the sampling rate decreases (from SR = 1 to SR = 4), we observe a consistent increase in the uncertainty ratio (from 0.7291 to 0.7481). This indicates that with sparser temporal resolution, our model appropriately captures greater uncertainty in predictions.

Although the input trajectory standard deviation slightly decreases with lower sampling rates (1.6048 at SR = 1 to 1.5583 at SR = 4), the target trajectory standard deviation remains relatively stable (approximately 1.17 across all sampling rates). This suggests that our model maintains consistent uncertainty quantification regardless of the input data density.

The target trajectory range (distance between maximum and minimum values) remains almost identical across all sampling rates (approximately 7.26), despite slight variations in input range. This indicates robust boundary prediction regardless of temporal resolution.

4.4. Ablation Studies

To understand the contribution of each component of our stochastic trajectory model, we performed ablation studies by removing or modifying key components.

Table 3. Ablation study results across different sampling rates.

Sampling Rate = 1
Model Variant	Test MSE
Full Model	0.0000678
Deterministic	0.000118
Small Latent Space	0.000391
w/o Weather Attention	0.000482
w/o Lyapunov	0.000494
Small Hidden Size	0.000636
Sampling Rate = 2
Model Variant	Test MSE
Full Model	0.000849
Deterministic	0.001323
w/o Lyapunov	0.007042
Small Latent Space	0.008853
w/o Weather Attention	0.009302
Small Hidden Size	0.010158
Sampling Rate = 4
Model Variant	Test MSE
Deterministic	0.0133
Full Model	0.0218
Small Hidden Size	0.0525
w/o Lyapunov	0.0544
Small Latent Space	0.0569
w/o Weather Attention	0.0588

presents the results for sampling rates 1, 2, and 4, respectively.

Switching from a stochastic model to a deterministic model (by removing the probabilistic output layer) results in performance degradation at SR = 1 and SR = 2, with the test MSE increasing by 74.19% and 55.91%, respectively. Interestingly, at SR = 4, the deterministic model performs better than the stochastic model (38.78% improvement). This suggests that for sparse trajectory data, maintaining a probabilistic model becomes more challenging, and a simpler deterministic approach might be more appropriate.

Removing the weather attention mechanism (“NoWeatherAttention” variant) leads to substantial performance drops across all sampling rates, with relative performance decreasing by 611.50%, 996.09%, and 170.18% for SR = 1, SR = 2, and SR = 4, respectively. This confirms our hypothesis about the critical role of explicitly modeling weather influences in general aviation trajectory prediction.

The variant “NoLyapunov”, which removes the Lyapunov stability regularization term, shows significant performance degradation at all sampling rates (628.10%, 729.58%, and 149.89% for SR = 1, SR = 2, and SR = 4, respectively). This validates our approach of incorporating stability constraints to ensure physically plausible trajectories that conform to standard flight patterns.

Reducing the hidden layer size (“SmallHidden” variant) or the latent space dimension (“SmallLatent” variant) both lead to worse performance, indicating that sufficient model capacity is necessary to capture the complex dynamics of general aviation trajectories.

In summary, our ablation studies demonstrate the critical importance of each component in our proposed model architecture. The weather attention mechanism and Lyapunov stability regularization prove particularly essential, with their removal causing the most significant performance degradation across all sampling rates. These findings validate our integrated approach to general aviation trajectory prediction, which successfully balances model complexity with physical constraints while appropriately handling varying data sparsity conditions.

4.5. Stochastic Property Validation

Table 4. Statistical properties comparison: ground truth vs. StochasticTrajectory predictions.

Sampling Rate	Mean		Std. Dev.		Variance		JS Divergence
	Ground Truth	Prediction	Ground Truth	Prediction	Ground Truth	Prediction
SR = 1	0.4838	0.4857	0.4087	0.4090	0.1670	0.1672	0.2314
SR = 2	0.5612	0.5598	1.3637	1.3573	1.8596	1.8421	0.1634
SR = 4	0.3576	0.3353	1.4065	1.3869	1.9783	1.9235	0.1407

presents the detailed statistical properties comparison between ground truth and predictions for different sampling rates. The analysis reveals that our model maintains excellent distributional fidelity across all sampling rates, with JS divergences ranging from 0.140697 to 0.231409, indicating very close distributional alignment. Notably, the model shows improving performance in capturing distributional properties as sampling rate decreases, with JS divergence improving from 0.231409 at SR = 1 to 0.140697 at SR = 4.

Table 5. Detailed performance comparison: accuracy and uncertainty metrics.

Model	Test MSE	68% Coverage	95% Coverage	Mean Uncertainty	JS Divergence
Sampling Rate = 1
StochasticTrajectory	0.0000678	0.878	0.973	0.0116	0.2314
LSTM	0.000163	0.416	0.659	0.0056	0.4814
Attention	0.000229	0.509	0.755	0.0075	0.1929
SimpleRNN	0.00313	0.257	0.497	0.0184	0.5977
GRU	0.000136	0.414	0.660	0.0043	0.2568
MLP	0.000561	0.923	0.997	0.0577	0.3134
Sampling Rate = 2
StochasticTrajectory	0.000849	0.857	0.986	0.0768	0.1634
LSTM	0.00152	0.360	0.599	0.0188	0.2666
Attention	0.00225	0.292	0.541	0.0201	0.2844
SimpleRNN	0.00653	0.246	0.464	0.0250	0.2057
GRU	0.00137	0.338	0.625	0.0173	0.2959
MLP	0.00551	0.586	0.936	0.1224	0.3524
Sampling Rate = 4
StochasticTrajectory	0.0218	0.772	0.982	0.1200	0.1407
LSTM	0.0212	0.241	0.467	0.0289	0.1920
Attention	0.0238	0.315	0.546	0.0270	0.4010
SimpleRNN	0.0390	0.159	0.318	0.0411	0.1600
GRU	0.0177	0.305	0.554	0.0289	0.1285
MLP	0.0434	0.719	0.913	0.1421	0.3304

provides a comprehensive performance comparison including both accuracy and uncertainty metrics across all sampling rates.

The detailed performance analysis reveals that our StochasticTrajectory model achieves the best accuracy for dense sampling conditions (SR = 1 and SR = 2) while maintaining superior uncertainty quantification across all conditions. At SR = 1, our model achieves MSE of 0.0000678, outperforming all baselines while providing substantial uncertainty benefits. At SR = 2, our model again achieves the best performance with MSE of 0.000849. For the most challenging sparse sampling condition (SR = 4), while GRU achieves slightly better point accuracy (0.0177 vs. our 0.0218), our method provides significantly better calibrated uncertainty estimates with 95% coverage of 0.982 compared to GRU’s 0.554, demonstrating the critical importance of proper uncertainty quantification in safety-critical applications.

5. Discussion

Our comprehensive experimental results demonstrate that the proposed StochasticTrajectory model consistently outperforms all comparison methods, including both traditional approaches (physics-based, ARIMA, KalmanFilter) and deep learning methods (LSTM, Attention, SimpleRNN, MLP). This superior performance validates our integrated approach that combines Lyapunov stability constraints with attention-based weather modeling in a probabilistic framework. Ablation studies further confirm the critical importance of each component, both stability constraints and weather attention mechanisms providing substantial contributions to model performance, as evidenced by the 600+% error increases when these components are removed at SR = 1. These findings demonstrate that our stochastic approach not only provides substantial benefits in terms of uncertainty quantification and stability, but also maintains competitive or superior accuracy across most operational scenarios. These advantages are particularly valuable in the nontowered airport environment, where safety margins and risk assessment are critical considerations.

The proposed trajectory prediction system targets specific operational needs in general aviation, particularly at non-towered airports. Primary applications include: (1) Enhanced situational awareness for pilots operating in busy traffic patterns, where our uncertainty-aware predictions can highlight potential conflicts before they become critical; (2) Decision support for flight training operations, where instructors can use trajectory predictions to assess student performance and intervene when deviations exceed safe bounds; (3) Ground-based safety monitoring at airports without tower services, providing automated alerts when aircraft trajectories suggest potential runway incursions or pattern conflicts; and (4) Weather-related go-around prediction, where the system’s weather attention mechanism can anticipate when current conditions may force missed approaches. The system’s 5.86 ms inference time enables real-time deployment through integration with existing ADS-B infrastructure, while the probabilistic outputs provide confidence intervals essential for safety-critical decision making. Initial deployment would focus on high-traffic training airports where the combination of diverse pilot experience levels and concentrated operations creates the greatest safety benefit.

Our approach, while demonstrating strong performance, has several important limitations that must be acknowledged. First, the model’s high sensitivity to the weather attention component indicates a potential brittleness that could be problematic if weather data quality degrades. Second, our training data come from a single airport (KBTP), and generalization to airports with different traffic patterns, terrain, or operational characteristics requires further validation. Third, the computational overhead compared to simpler baselines may limit deployment in resource-constrained environments. Fourth, our current approach does not explicitly model rare events or emergency scenarios, which, while infrequent, are critical for comprehensive safety analysis. Finally, the probabilistic outputs, while valuable for uncertainty quantification, require careful interpretation by end users who may be more familiar with deterministic systems. These limitations define important directions for future research and development before widespread operational deployment.

Looking ahead, several promising research directions emerge. First, exploring adaptive approaches that can dynamically adjust between deterministic and stochastic modeling based on data density could further improve performance across varying sampling rates, as our results indicate that stochastic modeling benefits dense sampling rates, but may introduce unnecessary complexity at sparser rates. Second, incorporating additional contextual information such as pilot experience, aircraft specifications, and airspace regulations could improve the precision of the prediction in complex scenarios. Finally, extending our approach to handle rare events and anomalous flight patterns remains a challenging but important area for future investigation, particularly as general aviation continues to grow and integrate with broader air traffic management systems.