Sustainable Phosphate Capture from Urban Wastewater Treatment Plants Towards a Nutrient Recovery and Water Reuse Strategy
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials Collection
2.2. Fixed-Bed Experiments
2.2.1. Experimental Design Planning
2.2.2. Influence of Feed Concentration and Co-Existing Ions
2.3. Scale-Up Design
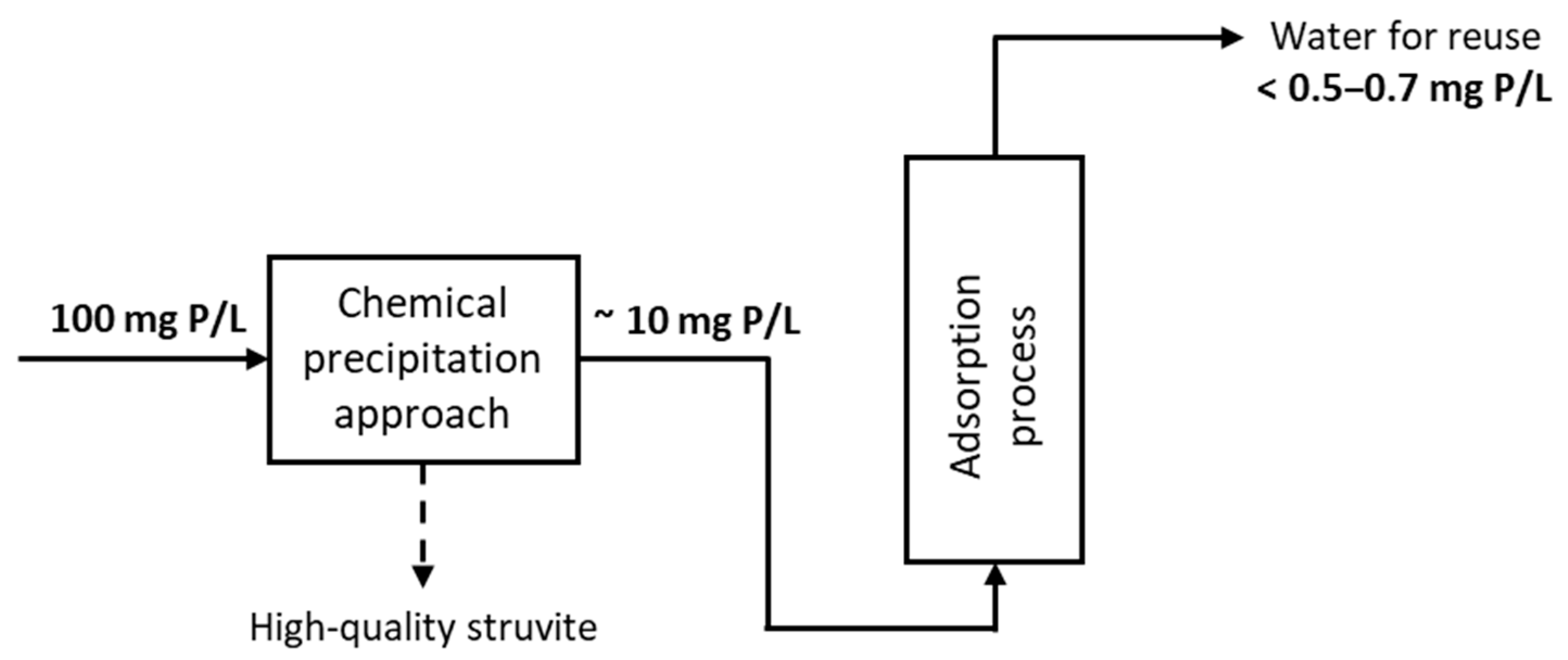
3. Results and Discussion
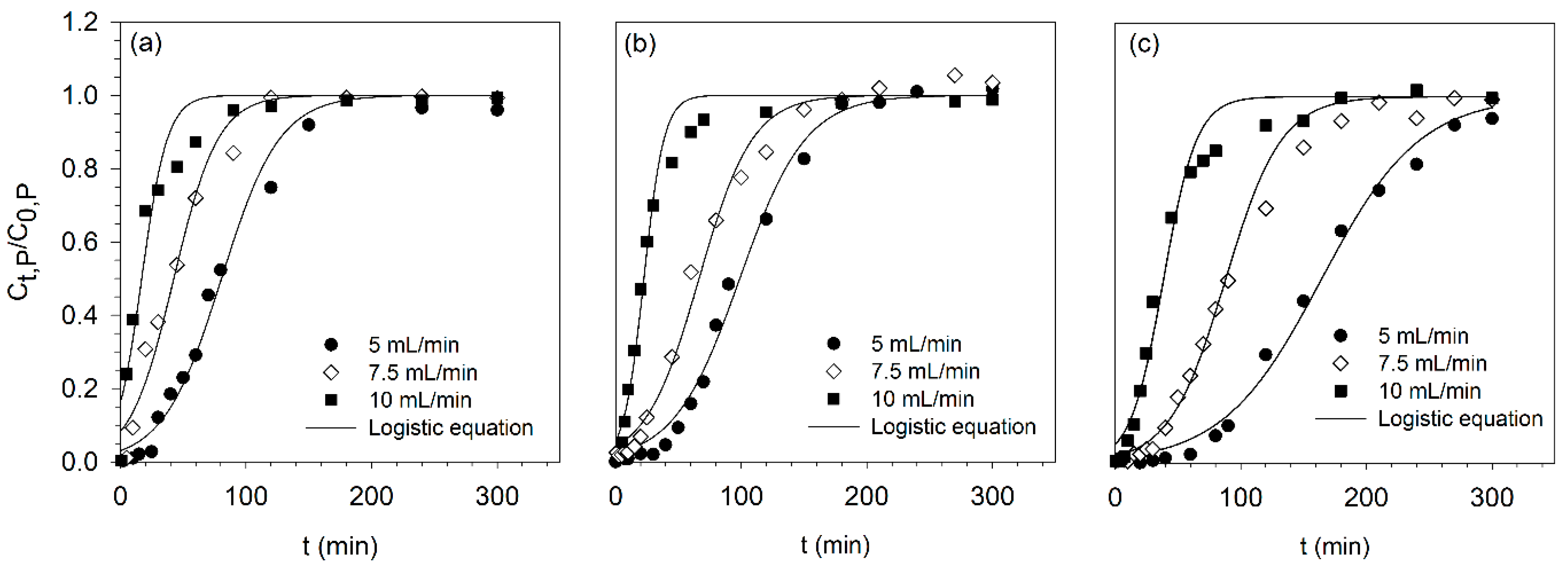
3.1. Optimization of Phosphorus Adsorption in Fixed-Bed Column
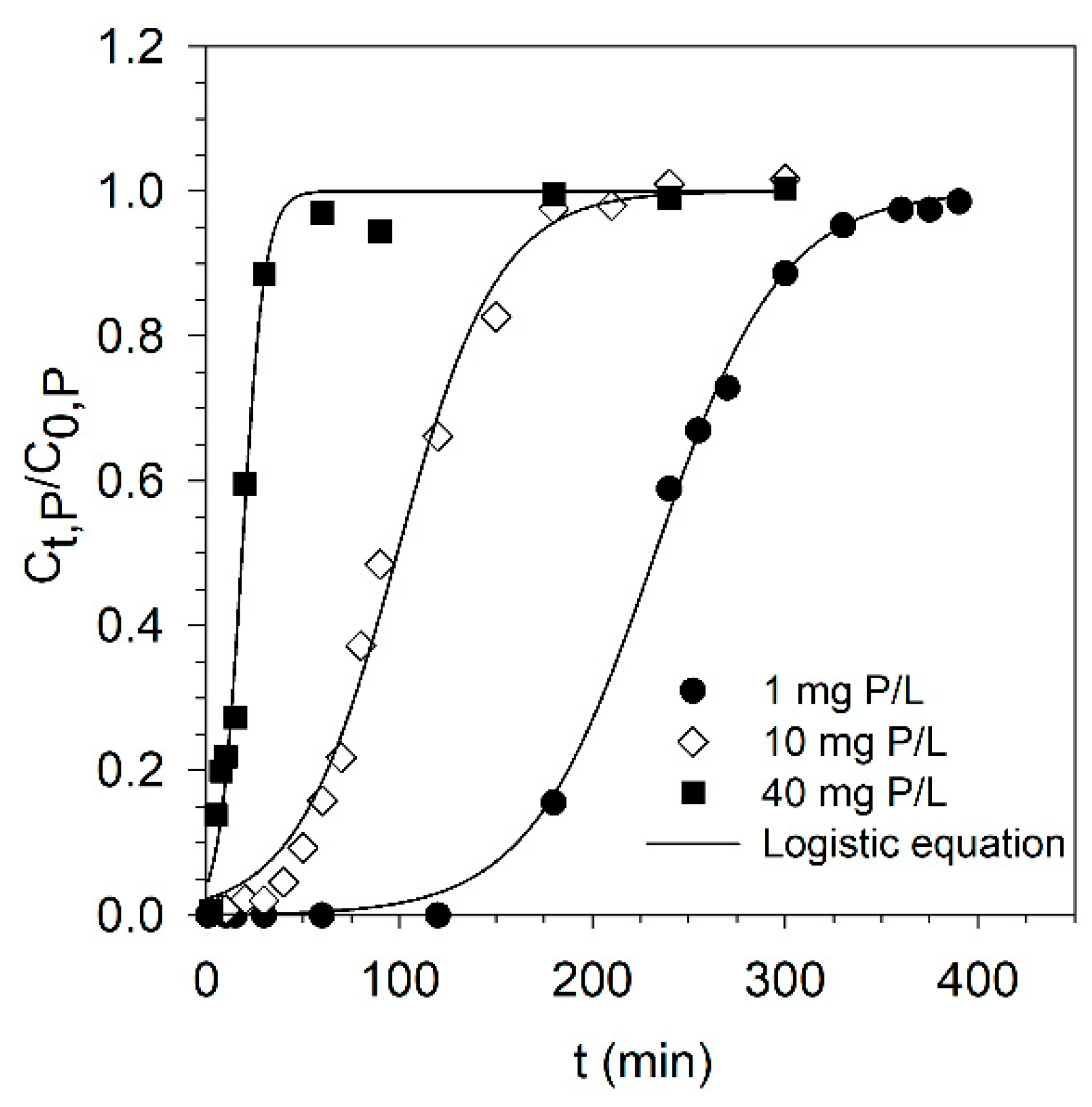
3.2. Effect of Feed Concentration on Breakthrough Curve
3.3. Simulation of Sorption Data
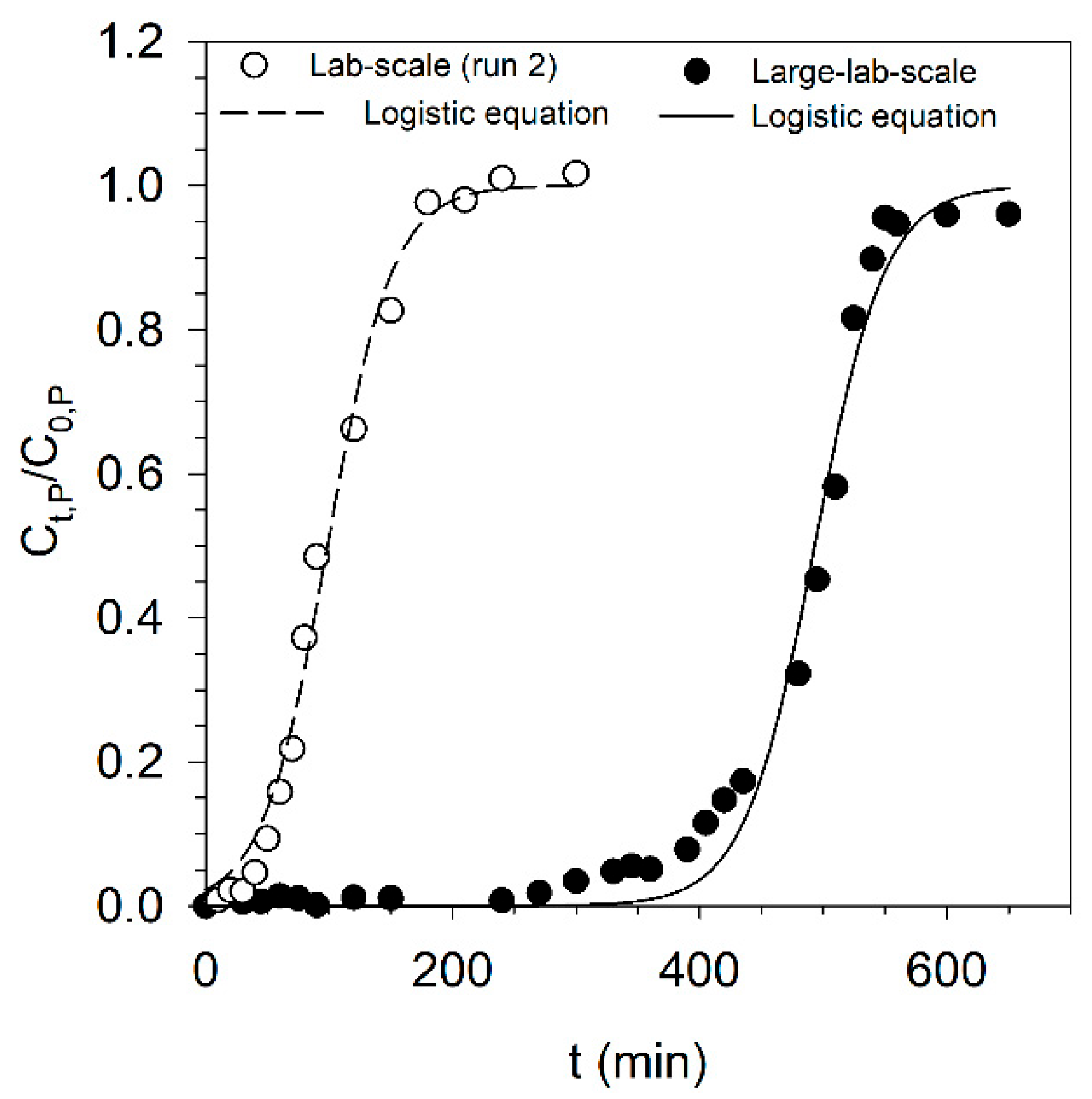
3.4. Scale-Up
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- De Boer, M.A.; Wolzak, L.; Slootweg, J.C. Phosphorus Recovery and Recycling, 1st ed.; Ohtake, H., Tsuneda, S., Eds.; Springer: Singapore, 2019; ISBN 978-981-10-8030-2. [Google Scholar]
- Cieślik, B.; Konieczka, P. A review of phosphorus recovery methods at various steps of wastewater treatment and sewage sludge management. The concept of “no solid waste generation” and analytical methods. J. Clean. Prod. 2017, 142, 1728–1740. [Google Scholar] [CrossRef]
- Huygens, D.; Saveyn, H. Agronomic efficiency of selected phosphorus fertilisers derived from secondary raw materials for European agriculture. A meta-analysis. Agron. Sustain. Dev. 2018, 38, 38–52. [Google Scholar] [CrossRef]
- Carrillo, V.; Fuentes, B.; Gómez, G.; Vidal, G. Characterization and recovery of phosphorus from wastewater by combined technologies. Rev. Environ. Sci. Biotechnol. 2020, 19, 389–418. [Google Scholar] [CrossRef]
- Mayer, N.; Kaltschmitt, M. Closing the phosphorus cycle: Current P balance and future prospects in Germany. J. Clean. Prod. 2022, 347, 131272. [Google Scholar] [CrossRef]
- European Commission. Study on the Critical Raw Materials for the EU 2023: Final Report; European Commission: Brussels, Belgium, 2023. [Google Scholar]
- European Commission. Critical Raw Materials Act. Available online: https://single-market-economy.ec.europa.eu/sectors/raw-materials/areas-specific-interest/critical-raw-materials/critical-raw-materials-act_en (accessed on 11 June 2024).
- Santos, A.F.; Alvarenga, P.; Gando-Ferreira, L.M.; Quina, M.J. Urban Wastewater as a Source of Reclaimed Water for Irrigation: Barriers and Future Possibilities. Environments 2023, 10, 17. [Google Scholar] [CrossRef]
- Santos, A.F.; Abreu, R.L.; Alvarenga, P.; Gando-Ferreira, L.M.; Quina, M.J. An innovative two-step methodology for struvite recovery from wastewater with high purity and agronomic potential. J. Water Process Eng. 2024, 67, 106206. [Google Scholar] [CrossRef]
- Mekonnen, D.T.; Alemayehu, E.; Lennartz, B. Fixed-Bed Column Technique for the Removal of Phosphate from Water Using Leftover Coal. Materials 2021, 14, 5466. [Google Scholar] [CrossRef]
- Negrea, A.; Mihailescu, M.; Mosoarca, G.; Ciopec, M.; Duteanu, N.; Negrea, P.; Minzatu, V. Estimation on Fixed-Bed Column Parameters of Breakthrough Behaviors for Gold Recovery by Adsorption onto Modified/Functionalized Amberlite XAD7. Int. J. Environ. Res. Public Health 2020, 17, 6868. [Google Scholar] [CrossRef]
- Sun, C.; Cao, H.; Huang, C.; Wang, P.; Yin, J.; Liu, H.; Tian, H.; Xu, H.; Zhu, J.; Liu, Z. Eggshell based biochar for highly efficient adsorption and recovery of phosphorus from aqueous solution: Kinetics, mechanism and potential as phosphorus fertilizer. Bioresour. Technol. 2022, 362, 127851. [Google Scholar] [CrossRef]
- Sun, C.; Huang, C.; Wang, P.; Yin, J.; Tian, H.; Liu, Z.; Xu, H.; Zhu, J.; Hu, X.; Liu, Z. Low-cost eggshell-fly ash adsorbent for phosphate recovery: A potential slow-release phosphate fertilizer. Water Res. 2024, 255, 121483. [Google Scholar] [CrossRef]
- Photiou, P.; Poulizou, M.; Vyrides, I. Recovery of phosphates from anaerobic MBR effluent using columns of eggshell and seagrass residues and their final use as a fertilizer. Sustain. Chem. Pharm. 2023, 33, 101039. [Google Scholar] [CrossRef]
- Worch, E. Adsorption Technology in Water Treatment, 1st ed.; De Gruyter: Berlin, Germany, 2012. [Google Scholar]
- Muscarella, S.M.; Trapani, D.D.; Laudicina, V.A.; Mannina, G. Phosphorus recovery from ultrafiltered membrane wastewater by biochar adsorption columns: The effect of loading rates. Heliyon 2024, 10, e34659. [Google Scholar] [CrossRef]
- Pap, S.; Karmann, C.; Thompson, T.; McConnell, R.; Kennedy, T.; Taggart, M.A. Insights into phosphate removal and recovery from wastewater using biosolids biochar: Pyrolysis optimisation, mechanistic and column studies. J. Water. Proc. Eng. 2025, 75, 107954. [Google Scholar] [CrossRef]
- Santos, A.F.; Lopes, D.V.; Alvarenga, P.; Gando-Ferreira, L.M.; Quina, M.J. Phosphorus removal from urban wastewater through adsorption using biogenic calcium carbonate. J. Environ. Manag. 2024, 351, 119875. [Google Scholar] [CrossRef]
- Santos, A.F.; Alvarenga, P.; Gando-Ferreira, L.M.; Quina, M.J. Phosphorus concentration and speciation in urban wastewater for potential recovery. In WASTES: Solutions, Treatments and Opportunities IV; CRC Press: Boca Raton, FL, USA, 2023; ISBN 9781003345084. [Google Scholar]
- European Commission. Electricity Price Statistics. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Electricity_price_statistics (accessed on 6 May 2025).
- Pap, S.; Kirk, C.; Bremner, B.; Sekulic, M.T.; Gibb, S.W.; Maletic, S.; Taggart, M.A. Synthesis optimisation and characterisation of chitosan-calcite adsorbent from fishery-food waste for phosphorus removal. Environ. Sci. Pollut. Res. 2020, 27, 9790–9802. [Google Scholar] [CrossRef]
- Zhang, M.; He, M.; Chen, Q.; Huang, Y.; Zhang, C.; Yue, C.; Yang, L.; Mu, J. Feasible synthesis of a novel and low-cost seawater-modified biochar and its potential application in phosphate removal/recovery from wastewater. Sci. Total. Environ. 2020, 824, 153833. [Google Scholar] [CrossRef]
- Silva, B.; Martins, M.; Rosca, M.; Rocha, V.; Lago, A.; Neves, I.C.; Tavares, T. Waste-based biosorbents as cost-effective alternatives to commercial adsorbents for the retention of fluoxetine from water. Sep. Purif. Technol. 2020, 235, 116139. [Google Scholar] [CrossRef]
- Santos, A.F.; Arim, A.L.; Lopes, D.V.; Gando-Ferreira, L.M.; Quina, M.J. Recovery of phosphate from aqueous solutions using calcined eggshell as an eco-friendly adsorbent. J. Environ. Manag. 2019, 238, 451–459. [Google Scholar] [CrossRef]
- Arim, A.L.; Neves, K.; Quina, M.J.; Gando-Ferreira, L.M. Experimental and mathematical modelling of Cr(III) sorption in fixed-bed column using modified pine bark. J. Clean. Prod. 2018, 183, 272–281. [Google Scholar] [CrossRef]
- Vilardi, G.; Rodriguez-Rodriguez, J.; Ochando-Pulido, J.; di Palma, L.; Verdone, N. Fixed-bed reactor scale-up and modelling for Cr(VI) removal using nano iron-based coated biomass as packing material. Chem. Eng. J. 2019, 361, 990–998. [Google Scholar] [CrossRef]
- Juela, D.; Vera, M.; Cruzat, C.; Astudillo, A.; Vanegas, E. A new approach for scaling up fixed-bed adsorption columns for aqueous systems: A case of antibiotic removal on natural adsorbent. Process Saf. Environ. Prot. 2022, 159, 953–963. [Google Scholar] [CrossRef]
- Bohart, G.S.; Adams, E.Q. Some aspects of the beahvior of charcoal with repect to chlorine. J. Am. Chem. Soc. 1920, 42, 523–544. [Google Scholar] [CrossRef]
- Thomas, H.C. Heterogeneous ion exchange in a flowing system. J. Am. Chem. Soc. 1944, 66, 1664–1666. [Google Scholar] [CrossRef]
- Yoon, Y.H.; Nelson, J.H. Application of Gas Adsorption Kinetics I. A Theoretical Model for Respirator Cartridge Service Life. Am. Ind. Hyg. Assoc. J. 1984, 45, 509–516. [Google Scholar] [CrossRef]
- Chu, K.H. Breakthrough curve analysis by simplistic models of fixed bed adsorption: In defense of the century-old Bohart-Adams model. Chem. Eng. J. 2020, 380, 122513. [Google Scholar] [CrossRef]
- Lv, N.; Li, X. Phosphorus removal from wastewater using Ca-modified attapulgite: Fixed-bed column performance and breakthrough curves analysis. J. Environ. Manag. 2023, 328, 116905. [Google Scholar] [CrossRef]
- Jang, J.; Lee, D.S. Effective phosphorus removal using chitosan/Ca-organically modified montmorillonite beads in batch and fixed-bed column studies. J. Hazard. Mater. 2019, 375, 9–18. [Google Scholar] [CrossRef]
- Nguyen, T.A.H.; Ngo, H.H.; Guo, W.S.; Pham, T.Q.; Li, F.M.; Nguyen, T.V.; Bui, X.T. Adsorption of phosphate from aqueous solutions and sewage using zirconium loaded okara (ZLO): Fixed-bed column study. Sci. Total Environ. 2015, 523, 40–49. [Google Scholar] [CrossRef]
- Santos, A.F.; Mendes, L.S.; Alvarenga, P.; Gando-Ferreira, L.M.; Quina, M.J. Nutrient Recovery via Struvite Precipitation from Wastewater Treatment Plants: Influence of Operating Parameters, Coexisting Ions, and Seeding. Water 2024, 16, 1675. [Google Scholar] [CrossRef]
- Jurado-Davila, V.; De Oliveira, J.T.; Estumano, D.; Féris, L.A. Fixed-bed column for phosphate adsorption combining experimental observation, mathematical simulation, and statistics: Classical and Bayesian. Sep. Purif. Technol. 2023, 317, 123914. [Google Scholar] [CrossRef]

| dp (mm) | εb | ρb (g/cm3) | pH | pHzpc | SBET (m2/g) | Vpore (cm3/g) |
|---|---|---|---|---|---|---|
| 0.5–1.19 | 0.52 | 0.70–0.75 | 9.84 | 8.43 | 1.83 | 0.003 |
| Run | Q (mL/min) | h (cm) | Run | Q (mL/min) | h (cm) | Run | Q (mL/min) | h (cm) |
|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 20 | 4 | 7.5 | 20 | 7 | 10 | 20 |
| 2 | 5 | 30 | 5 | 7.5 | 30 | 8 | 10 | 30 |
| 3 | 5 | 40 | 6 | 7.5 | 40 | 9 | 10 | 40 |
| Run | Q (mL/min) | h (cm) | tbp (min) | tex (min) | tst (min) | Δtads (min) | FSB | qe (mg P/kg Adsorbent) | MTZ (cm) | tr (min) | LUB (cm) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5.0 | 20 | 26.1 | 148 | 84.3 | 122 | 0.309 | 107 | 16.5 | 6.66 | 13.8 |
| 2 | 5.0 | 30 | 40.4 | 166 | 95.1 | 126 | 0.425 | 70.9 | 22.7 | 9.99 | 17.3 |
| 3 | 5.0 | 40 | 69.4 | 266 | 159 | 196 | 0.436 | 85.8 | 29.6 | 13.3 | 22.5 |
| 4 | 7.5 | 20 | 7.41 | 111 | 46.9 | 104 | 0.149 | 91.2 | 18.7 | 4.44 | 17.0 |
| 5 | 7.5 | 30 | 16.5 | 147 | 69.0 | 131 | 0.239 | 72.3 | 26.6 | 6.66 | 22.8 |
| 6 | 7.5 | 40 | 31.9 | 190 | 98.5 | 158 | 0.325 | 94.7 | 33.3 | 8.88 | 27.0 |
| 7 | 10 | 20 | 1.78 | 86.7 | 26.6 | 84.9 | 0.067 | 58.7 | 19.6 | 3.33 | 18.7 |
| 8 | 10 | 30 | 4.88 | 110 | 32.8 | 105 | 0.149 | 37.4 | 28.7 | 5.00 | 25.5 |
| 9 | 10 | 40 | 9.37 | 158 | 46.5 | 148 | 0.201 | 66.6 | 37.6 | 6.66 | 31.9 |
| Run | FSB Experimental | FSB Predicted | REFSB (%) | Δtads (min) Experimental | Δtads (min) Predicted | REΔtads (%) |
|---|---|---|---|---|---|---|
| 1 | 0.309 | 0.309 | 0 | 122 | 121 | 0.82 |
| 2 | 0.425 | 0.405 | 4.70 | 126 | 138 | 9.52 |
| 3 | 0.436 | 0.455 | 4.36 | 196 | 185 | 5.62 |
| 4 | 0.149 | 0.157 | 5.37 | 104 | 104 | 0.00 |
| 5 | 0.239 | 0.253 | 5.88 | 131 | 121 | 7.63 |
| 6 | 0.325 | 0.303 | 6.77 | 158 | 168 | 6.33 |
| 7 | 0.067 | 0.058 | 13.4 | 84.9 | 85.9 | 1.18 |
| 8 | 0.149 | 0.154 | 3.36 | 105 | 103 | 1.90 |
| 9 | 0.201 | 0.204 | 1.49 | 148 | 150 | 1.35 |
| 10 | 0.204 | 0.167 | 18.2 | 119 | 98.3 | 17.4 |
| 11 | 0.352 | 0.334 | 5.11 | 155 | 144 | 7.09 |
| C0 (mg P/L) | |||
|---|---|---|---|
| 1 (Run 12) | 10 (Run 2) | 40 (Run 13) | |
| tbp (min) | 139 | 40.4 | 3.34 |
| tex (min) | 329 | 166 | 52.9 |
| tst (min) | 228 | 101 | 23.7 |
| Δtads (min) | 189 | 126 | 49.5 |
| FSB | 0.612 | 0.425 | 0.141 |
| qe (mg P/kg) | 17.5 | 70.9 | 60.1 |
| MTZ (cm) | 17.3 | 22.7 | 28.1 |
| LUB (cm) | 11.6 | 17.3 | 25.6 |
| Logistic Equation | Bohart-Adams Model | Thomas Model | Yoon-Nelson Model | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Run | a (-) | b (1/min) | kba (L/mg min) | qba (mg/kg) | kth (L/mg min) | qth (mg/kg) | kyn (1/min) | τyn (min) | t50% (min) |
| 1 | 3.479 | 0.043 | 0.004 | 27.1 | 0.004 | 94.2 | 0.043 | 80.5 | 76.7 |
| 2 | 3.771 | 0.038 | 0.004 | 22.3 | 0.004 | 77.3 | 0.038 | 98.9 | 92.6 |
| 3 | 4.189 | 0.026 | 0.003 | 27.6 | 0.003 | 89.9 | 0.026 | 164 | 159 |
| 4 | 2.421 | 0.057 | 0.006 | 18.3 | 0.006 | 64.5 | 0.057 | 42.6 | 41.4 |
| 5 | 3.127 | 0.047 | 0.005 | 21.1 | 0.005 | 71.2 | 0.047 | 66.5 | 58.9 |
| 6 | 3.952 | 0.045 | 0.005 | 18.0 | 0.005 | 62.3 | 0.045 | 87.8 | 90.3 |
| 7 | 1.666 | 0.098 | 0.010 | 12.2 | 0.010 | 44.5 | 0.098 | 17.1 | 13.8 |
| 8 | 2.820 | 0.125 | 0.013 | 9.58 | 0.013 | 30.6 | 0.125 | 22.6 | 21.1 |
| 9 | 2.944 | 0.077 | 0.008 | 11.2 | 0.008 | 36.8 | 0.077 | 38.5 | 33.9 |
| 12 | 7.126 | 0.031 | 0.003 | 5.78 | 0.003 | 18.5 | 0.031 | 232 | 228 |
| 13 | 3.163 | 0.171 | 0.017 | 17.9 | 0.017 | 59.1 | 0.171 | 18.4 | 18.5 |
| Experimental Results | Predicted Results | ||
|---|---|---|---|
| tbp (min) | 334 | Logistic Equation | |
| tex (min) | 570 | a (-) | 17.33 |
| tst (min) | 438 | b (1/min) | 0.035 |
| Δtads (min) | 236 | Bohart-Adams model | |
| FSB | 0.764 | kba (L/mg.min) | 0.003 |
| qe (mg P/kg) | 84.1 | qba (mg/kg) | 61.29 |
| MTZ (cm) | 24.8 | Thomas model | |
| LUB (cm) | 14.2 | kth (L/mg.min) | 0.003 |
| qths (mg/kg) | 121 | ||
| Yoon-Nelson model | |||
| kyn (1/min) | 0.035 | ||
| τ (min) | 495 | ||
| t50% (min) | 506 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, A.F.; Alvarenga, P.; Gando-Ferreira, L.M.; Quina, M.J. Sustainable Phosphate Capture from Urban Wastewater Treatment Plants Towards a Nutrient Recovery and Water Reuse Strategy. Appl. Sci. 2025, 15, 6761. https://doi.org/10.3390/app15126761
Santos AF, Alvarenga P, Gando-Ferreira LM, Quina MJ. Sustainable Phosphate Capture from Urban Wastewater Treatment Plants Towards a Nutrient Recovery and Water Reuse Strategy. Applied Sciences. 2025; 15(12):6761. https://doi.org/10.3390/app15126761
Chicago/Turabian StyleSantos, Andreia F., Paula Alvarenga, Licínio M. Gando-Ferreira, and Margarida J. Quina. 2025. "Sustainable Phosphate Capture from Urban Wastewater Treatment Plants Towards a Nutrient Recovery and Water Reuse Strategy" Applied Sciences 15, no. 12: 6761. https://doi.org/10.3390/app15126761
APA StyleSantos, A. F., Alvarenga, P., Gando-Ferreira, L. M., & Quina, M. J. (2025). Sustainable Phosphate Capture from Urban Wastewater Treatment Plants Towards a Nutrient Recovery and Water Reuse Strategy. Applied Sciences, 15(12), 6761. https://doi.org/10.3390/app15126761









