DRKG: Faithful and Interpretable Multi-Hop Knowledge Graph Question Answering via LLM-Guided Reasoning Plans

Abstract

Multi-Hop Knowledge Graph Question Answering (multi-hop KGQA) aims to obtain answers by analyzing the semantics of natural language questions and performing multi-step reasoning across multiple entities and relations in knowledge graphs. Traditional embedding-based methods map natural language questions and knowledge graphs into vector spaces for answer matching through vector operations. While these approaches have improved model performance, they face two critical challenges: the lack of clear interpretability caused by implicit reasoning mechanisms, and the semantic gap between natural language queries and structured knowledge representations. This study proposes the DRKG (Decomposed Reasoning over Knowledge Graph), a constrained multi-hop reasoning framework based on large language models (LLMs) that introduces explicit reasoning plans as logical boundary controllers. The innovation of the DRKG lies in two key aspects: First, the DRKG generates hop-constrained reasoning plans through semantic parsing based on LLMs, explicitly defining the traversal path length and entity-retrieval logic in knowledge graphs. Second, the DRKG conducts selective retrieval during knowledge graph traversal based on these reasoning plans, ensuring faithfulness to structured knowledge. We evaluate the DRKG on four datasets, and the experimental results demonstrate that the DRKG achieves 1%–5% accuracy improvements over the best baseline models. Additional ablation studies verify the effectiveness of explicit reasoning plans in enhancing interpretability while constraining path divergence. A reliability analysis further examines the impact of different parameters combinations on the DRKG’s performance.

1. Introduction

Knowledge graphs are structured data representations designed to store and convey knowledge, where nodes denote entities and edges represent diverse relationships between them [1]. Large-scale knowledge graphs, such as Freebase [2] and Wikidata [3], typically span multiple domains and incorporate rich multilingual textual representations of entities and relations. Recent advancements in knowledge graph research have demonstrated significant progress across various downstream application tasks, with knowledge graph question answering remaining a cornerstone research direction in this field.

Multi-Hop Knowledge Graph Question Answering is a complex task that leverages natural language processing to interpret intricate query logic and retrieve answers through multi-hop reasoning over structured knowledge graphs. As illustrated in Figure 1, unlike single-hop methods, which resolve queries by retrieving answers from a single entity or relation, multi-hop KGQA requires aligning the natural language query logic with entities and relations in the knowledge graph. This process demands multi-step reasoning, traversing multiple edges in the knowledge graph to derive answers. There are two critical challenges in KGQA: the semantic gap between natural language queries and structured knowledge representations, and the interpretability in reasoning processes [4].

Building upon these challenges, this study specifically addresses the following research questions. RQ1: How can the semantic gap between unstructured natural language queries and structured knowledge graph representations be effectively bridged? RQ2: What mechanisms can enhance the interpretability of multi-hop reasoning processes without compromising KGQA system performance? The semantic gap (RQ1) primarily stems from the fundamental disparity between the structured nature of knowledge graphs and the unstructured characteristics of natural language. Bridging this structural mismatch constitutes a critical prerequisite for effective multi-hop KGQA systems [4]. Traditional approaches address this challenge using embedding-based methods, which map entities and relations into continuous vector spaces. These embeddings are then combined with word vectors to compute answers through vector-space operations. Although such methods partially mitigate the semantic gap, they suffer from inherent limitations: their internal decision-making mechanisms remain opaque to users (RQ2), acting as a “black box” that outputs answers without transparently revealing the reasoning process [5]. Ideally, multi-hop KGQA systems should not only provide correct answers but also elucidate their reasoning paths [6].

To address these challenges, the DRKG innovatively integrates the explicit reasoning capabilities of LLMs with the structured retrievability of a knowledge graph. During reasoning, the DRKG first inputs linearized knowledge graph information into LLMs, which dynamically filter and select relevant information. Subsequently, leveraging the structured organization of the knowledge graph, the system efficiently retrieves answers based on the filtered information. Our framework is the explicit reasoning plan, which acts as a logical boundary controller to ensure both interpretability and controllability. Unlike previous methods, the DRKG employs LLMs to generate structured reasoning plans through semantic parsing. These plans explicitly define two critical constraints: hop thresholds to limit traversal depth in the knowledge graph and logical relation constraints. This mechanism enforces strict adherence to predefined reasoning paths during the traversal of the knowledge graph, effectively mitigating the risks of knowledge hallucination and path divergence. Furthermore, the entire reasoning process becomes transparent and aligns with human-interpretable logic, addressing long-standing interpretability concerns in multi-hop KGQA.

We evaluated the DRKG’s accuracy on four widely used benchmark datasets and tested its faithfulness on two of these datasets. The experimental results demonstrate that the DRKG’s design significantly enhances multi-hop KGQA performance while delivering interpretable reasoning processes that align more closely with human reasoning patterns. The key contributions of this work are summarized as follows:

(1)

Synergistic reasoning plan–knowledge retrieval mechanism: We propose a novel framework that synchronously addresses interpretability deficits and path divergence in multi-hop KGQA through reasoning instructions. This mechanism equips the model with dual capabilities: generating human-understandable reasoning plans via LLMs and ensuring faithful knowledge retrieval through hop constraints and logical boundary control.

(2)

Hybrid supervised fine-tuning and reinforcement learning: Our methodology integrates supervised fine-tuning for foundational semantic understanding with reinforcement learning enhanced by path constraints and keyword-aware reward functions. The reinforcement learning phase improves reasoning robustness in complex scenarios by penalizing overstepping or understepping hop behaviors in generated plans.

(3)

State-of-the-art performance: DRKG achieves 100% accuracy in the MetaQA dataset and outperforms the best baseline models by 1–5% in the PathQuestion, WebQuestionsSP, and ComplexWebQuestions benchmarks.

(4)

Comprehensive reliability analysis: We conduct systematic ablation studies to examine critical factors affecting multi-hop KGQA performance, analyze parameter sensitivity, and provide empirically validated configuration recommendations.

The rest of this manuscript is organized as follows. Section 2 provides a critical review of related work on knowledge graph reasoning and explainable question–answering systems. Section 3 details the DRKG architecture, addresses Research Question 1 (RQ1) through a two-stage training approach, and solves Research Question 2 (RQ2) via a structured reasoning plan, and it also elaborates in detail on interpretability. Section 4 experimentally verifies the research questions through comparative studies, ablation experiments, and a reliability experiment analysis. Section 5 discusses the broader implications and acknowledges the limitations. Finally, Section 6 summarizes this study and outlines the future research directions.

2. Literature Review

2.1. Embedded Methods

Embedding methods map entities and relationships in the knowledge graph to a low-dimensional vector space and use vector operations to achieve semantic matching and reasoning. The core idea of these methods is to transform structured knowledge into continuous numerical representations, thus enabling end-to-end training compatible with deep learning models. Sardana et al. proposed a knowledge graph embedding approach that learns high-dimensional embeddings for entities and relations in knowledge graphs [7]. By combining these embeddings with question representations, their method scores candidate answers to select the final result [7]. Wang et al. introduced hypergraphs and reasoning chains for multi-hop inference [8]. Their framework generates entity embeddings with high-order semantic features via hypergraphs and employs a reasoning chain modeling module to evaluate the importance of inference paths. A scoring network also assesses candidate responses based on both factual triples and reasoning processes [8]. Shi et al. proposed TransferNet, a model that iteratively propagates entity scores across multiple steps to infer answers [9]. Starting from the topic entity in a question, the model calculates the activation probabilities for the entities; computes the activation scores of the relation, focusing on the key semantic tokens of the query; and traverses the high-scoring relations to reach the target entity [9]. Jiang et al. developed the UNIKGQA model, which comprises two core modules: a semantic matching module that leverages pretrained language models to align questions with relations and a matching information propagation module that computes entity matching scores based on semantic features [10]. Sukhbaatar et al. proposed the MemNN, which stores knowledge graph triples through memory units and uses an end-to-end multi-layer attention mechanism for multi-hop reasoning [11]. Essentially, it implicitly encodes structured knowledge as vector representations in memory and calculates answers relying on attention weights [11]. Miller et al. proposed a key–value separation structure, introduced based on the MemNN [12]. The key encodes the vector of the “subject–relation” pair, and the value corresponds to the target entity. More accurate semantic alignment is achieved through key–value matching [12]. Embedded methods make full use of the efficiency of spatial operations of vectors and have obvious advantages in retrieval efficiency. However, this reliance on implicit vector operations also has certain limitations: on the one hand, this black-box reasoning mode makes it difficult to trace the specific reasoning path, and it is impossible to explain why a certain entity is selected. On the other hand, there is insufficient semantic alignment between natural language questions and structured embeddings.

2.2. Symbolic Methods

Symbolic methods directly perform reasoning based on the explicit structure (entities, relationships, and paths) of the knowledge graph, emphasizing logical rules and transparent operations. Typical methods include path traversal, template matching, and logical query generation. Sun et al. designed a method to extract task-specific subgraphs from a knowledge graph and supplement them with textual documents [13,14]. They then applied graph convolutional networks to extract answers from the enriched subgraphs [13,14]. Schltchtkrull et al. proposed the IRN model, which generates explicit reasoning paths by iteratively predicting intermediate entities and relationships [15]. The paths are traceable and conform to the explicit logical characteristics of symbolic reasoning [15]. Abujabal et al. proposed a method for automatically generating templates to convert natural language questions into structured queries for knowledge graphs [16]. The core idea is to automatically construct utterance–query templates by learning the alignment relationship between questions and queries [16]. AlAgha et al. proposed a method for converting natural language queries to SPARQL based on a language analysis [17]. A language parser is used to extract noun phrases and relations from Arabic sentences, and combined with ontology information, they are mapped to the entities and predicates of the knowledge graph. The knowledge in the ontology is utilized to group noun phrases into triple representations, and SPARQL queries are generated according to the query objectives and modifiers [17]. Luz F F et al. proposed a semantic parsing method based on the neural attention mechanism for converting natural language questions into SPARQL queries [18]. The core technology adopts a sequence-to-sequence (seq2seq) architecture, which is combined with the attention mechanism to align the structures of natural language and SPARQL [18]. Sun Y et al. proposed a skeleton grammar to decompose the semantics of complex questions into an abstract structure containing entities, relationships, and constraints (such as multi-hop relationships and aggregation operations) [19]. The skeleton represents the core logic of the question through a coarse-grained formalization, thereby constructing a high-level abstract structure of the question to achieve the generation of structured queries for complex questions [19]. Symbolic methods are completely transparent and highly interpretable, and the skeleton strictly follows the topology of the knowledge graph, avoiding the path divergence problem of the embedding method. However, it has two limitations: First, it is difficult for predefined rules to cover complex language expressions. Second, it highly depends on the generated equivalent query statements. The cost of manually designing templates or rules is high, and it is difficult to adapt to dynamic knowledge updates.

2.3. LLM-Driven Methods

In recent years, large language models, exemplified by ChatGPT [20,21,22], Llama [23,24], and ChatGLM [25], have garnered significant attention in natural language processing (NLP). Studies have revealed that when model parameters exceed a critical scale, transformer-based [26] pretrained models not only achieve remarkable performance improvements but also exhibit emergent capabilities absent in smaller models, such as in-context learning [27]. Leveraging their exceptional contextual understanding and semantic parsing abilities, these models excel across diverse NLP tasks [22,28,29,30]. However, LLMs remain constrained in domain-specific knowledge acquisition, primarily due to their reliance on the breadth and quality of training data. In specialized or niche domains, having insufficient relevant training data often leads to knowledge scarcity [27,28], thus impairing their reasoning accuracy and reliability. In complex knowledge-intensive reasoning tasks specifically, LLMs are prone to knowledge hallucination—generating plausible but unfounded responses even when relevant knowledge exists in their parameters [5,31,32]. To address these limitations, recent works propose integrating structured knowledge from knowledge graphs with LLMs. For example, Sun et al. introduced a plug-and-play framework that incrementally retrieves local knowledge graph information during inference, allowing LLMs to autonomously select traversal paths based on retrieved knowledge [33]. Luo et al. designed a plan–retrieve–reason paradigm, where LLMs first generate relational paths as reasoning plans, retrieve relevant knowledge graph subgraphs guided by these plans, and finally execute inference over the retrieved evidence [34]. This approach improves the interpretability and trustworthiness of LLM-based reasoning. Luo et al. proposed ChatKBQA, which leverages LLMs to generate SPARQL query templates and populates them with knowledge graph entities/relations to produce executable logical queries [35]. Although these methods capitalize on the linguistic understanding capabilities of LLMs, they rely on loosely coupled integrations with knowledge graph, failing to robustly mitigate knowledge hallucination or ensure faithful reasoning grounded in structured knowledge.

3. Limitations of Existing Work

Although existing methods have made progress in the multi-hop KGQA task, there are still problems in interpretability, semantic gap, knowledge hallucination, and dynamic knowledge adaptability (

Table 1. Summary of existing work.

Method Categories	Advantages	Limitations	Interpretability
Embedded Methods	Efficient retrieval	Black-box reasoning	Low
Symbolic Methods	Path transparency	Highly dependent template	High
LLM-Driven Methods	Strong semantic understanding	Knowledge illusion	Middle

). The details are as follows:

(1)

Insufficient Interpretability: Embedding methods rely on black-box vector operations, making it impossible for users to trace the specific paths on which the answers are based. Although some LLM methods generate intermediate plans, the plans are disconnected from the retrieval process, potentially resulting in “seemingly reasonable but actually wrong” reasoning chains.

(2)

Semantic Gap: There is a semantic mismatch between natural language questions and structured knowledge representation. For example, the word “leader” in a question may correspond to CEO, founder, or director in the knowledge graph, and traditional methods struggle to achieve precise alignment. Although LLM can understand language diversity, the relationship descriptions it generates may not be consistent with the relationship labels in the knowledge graph (e.g., expressing “direct” as “direct works”).

(3)

Knowledge Hallucination and Path Divergence: LLM-driven models may generate relationships that do not exist in the knowledge graph, leading to incorrect answers. In multi-hop scenarios, embedding methods may deviate from the correct path due to vector combination errors (e.g., wrongly jumping from “director” to “screenwriter”).

(4)

Poor Dynamic Knowledge Adaptability: Symbolic methods rely on static knowledge graphs and have difficulty handling real-time updated knowledge (such as information about newly released movies). Most methods do not consider the noise in the knowledge graph (such as incorrect edges or missing entities), resulting in interruption of the reasoning chain.

4. Approach

The DRKG comprises two core components: problem decomposition and a reasoning analysis. The primary objective is to enable efficient and accurate answer retrieval from knowledge graphs by guiding LLMs through multi-step logical reasoning for complex questions. Initially, the DRKG employs carefully designed prompts to instruct LLMs to decompose complex natural language questions into executable reasoning plans based on semantic logic. This decomposition not only significantly reduces the problem’s complexity but also establishes a transparent logical pathway for subsequent reasoning. More importantly, it limits the number of steps in multi-hop retrieval. Subsequently, a prompting strategy is applied to linearize structured data into a natural language format. This transformation enables LLMs to dynamically process structured knowledge graph information through natural language reasoning, facilitating iterative multi-hop reasoning. The model then selects the correct traversal path based on the reasoning plan and linearized knowledge graph information, thereby efficiently retrieving answers by leveraging the structured nature of the knowledge graph. Finally, through multiple iterations of reasoning and retrieval, the DRKG dynamically integrates intermediate information from generated reasoning chains to localize the final answer within the knowledge graph. The complete DRKG framework, illustrated in Figure 2, details the end-to-end process from question decomposition to answer retrieval.

4.1. Problem Definition

Definition 1. 

Knowledge Graph.

A knowledge graph is defined as $\mathcal{G}=(\mathcal{E},\mathcal{R},\mathcal{T})$, where $\mathcal{E}=\{e_1,e_2,\dots ,e_n\}$ is the set of entities, $\mathcal{R}=\{r_1,r_2,\dots ,r_n\}$ is the set of relations, and $\mathcal{T}\subseteq \mathcal{E}\times \mathcal{R}\times \mathcal{E}$ is the set of labeled edges. Each triple $(e_h,r,e_t)\in T$ represents a directed relationship r from head entity $e_h$ to tail entity $e_t$, inducing a heterogeneous graph structure where entities are interconnected through relational paths and the graph topology emerges through the closure of triples under path composition. The graph structure enables two fundamental operations: forward and backward traversal. In the former, given $e_h\in \mathcal{E}$ and $r\in \mathcal{R}$, $\left\{e_t\right|(e_h,r,e_t)\in \mathcal{T}\}$ is returned; in the latter, given $e_t\in \mathcal{E}$ and $r\in \mathcal{R}$, $\left\{e_h\right|(e_h,r,e_t)\in \mathcal{T}\}$ is returned.

Definition 2. 

Natural Language Question.

A natural language question $\mathcal{Q}$ is a semantic query expressed through a sequence of tokens $\{q_1,q_2\dots q_n\}$, which implicitly or explicitly contain the following: a topic entity and a set of reasoning objectives. The topic entity is defined as $e_{topic}\in \mathcal{E}$, which explicitly refers to an entity in the knowledge graph. A set of reasoning objectives can be represented as a multi-step reasoning intention, where each step of the intention implicitly corresponds to a relation in the knowledge graph. The goal of the multi-hop knowledge question answering is as follows: First, identify the topic entity in the natural language question. Subsequently, starting from the topic entity, traverse and retrieve from the graph by filtering relationships that match the query intention according to the natural language. Finally, find the answer entities.

Definition 3. 

Reasoning Plan.

Natural language questions often do not explicitly show the relationships required during traversal and retrieval. Instead, these relationships need to be parsed by understanding the semantic meaning of the context. Additionally, multiple retrieval relationships also have a strict sequential order. Before retrieving the answer, generating a concise and clear reasoning plan can therefore guide the model to perform retrieval accurately and in sequence. The reasoning plan is defined as $\mathcal{P}=\{p_1,p_2,\dots ,p_n\}$. Each $\mathcal{P}$ corresponds to a unique retrieval relation r in the knowledge graph.

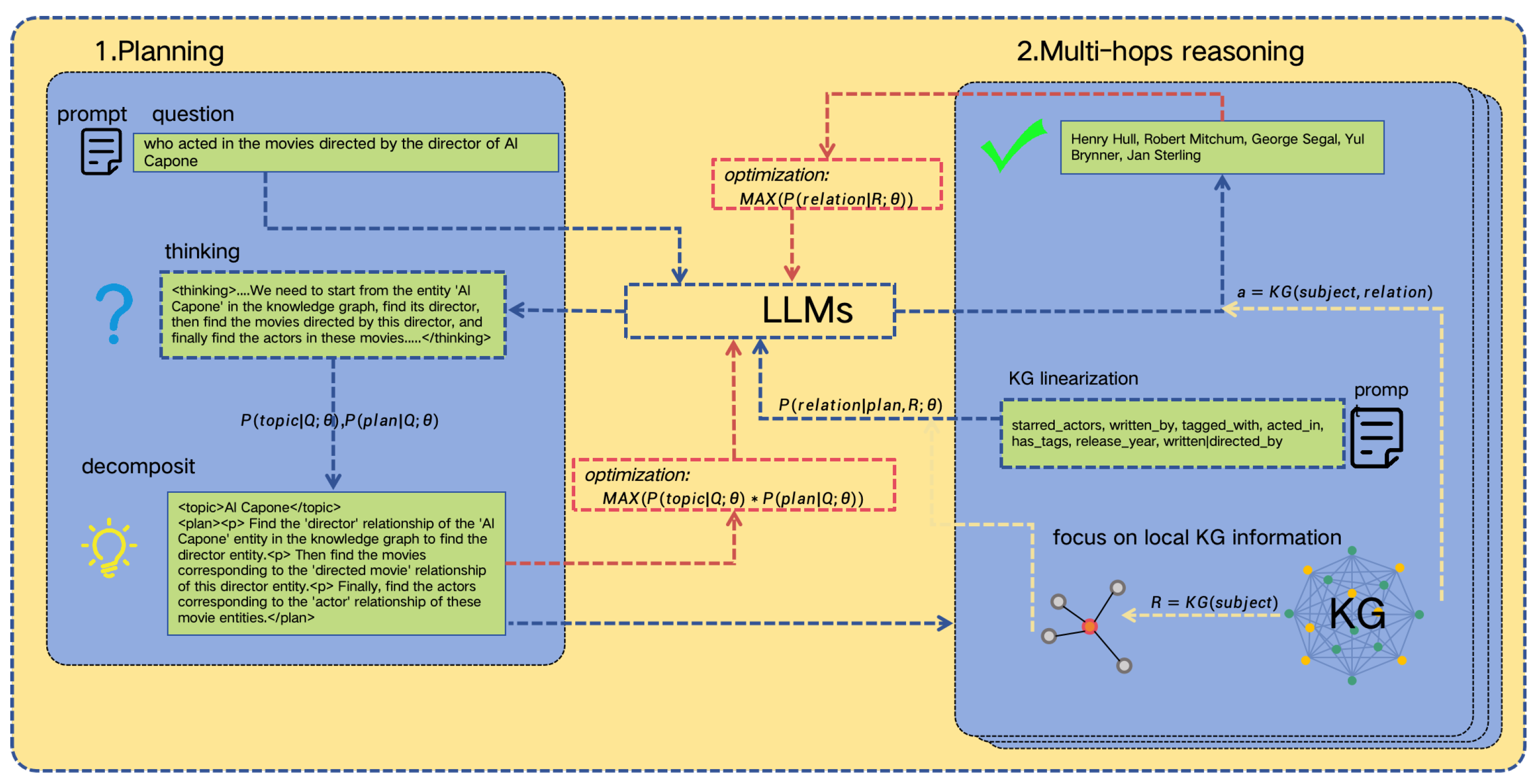
4.2. Decomposition and Reasoning

A core challenge in multi-hop KGQA lies in semantically parsing complex natural language queries. Similarly to human reasoning processes, this requires decomposing intricate questions into simpler sub-questions and resolving them sequentially [36]. Fundamentally, multi-hop QA can be conceptualized as a structured composition of single-hop QA units, where each unit addresses a specific aspect of the query. Crucially, the identification and formulation of sub-questions depend on two critical components: topic words and relation words. Topic words act as starting entities for knowledge graph traversal, while relation words define traversal paths from these entities, guiding the search and reasoning along specific relational chains in the knowledge graph.

The model first identifies topic entities from the natural language query and subsequently generates structured reasoning plans. This process can be formally represented as follows:

$$P\left(\mathcal{T}\right|Q;\theta )=\prod _{i=1}^{m}P\left(y_i\right|q_1,q_2,\cdots ,q_{i-1};\theta )$$

(1)

$$\mathcal{P}\sim LLM\left(Q\right)=\prod _{t=1}^{n}P(p_t\mid Q,p_{<t};\theta )$$

(2)

$\mathcal{Q}\in {\mathbb{R}}^{d\times n}$ is the question embedding matrix, and each $q_i\in {\mathbb{R}}^d$ is the embedding vector for the $i-th$ token. $\theta \in {\mathbb{R}}^D$ is the parameter vector. $P\left(\mathcal{T}\right|\mathcal{Q};\theta )$ denotes the probability of identifying $\mathcal{T}$ from the given $\mathcal{Q}$. $\mathcal{P}\in {\mathbb{R}}^{d\times n}$ is the reasoning plan generated by the model, and $p\in {\mathbb{R}}^{d\times n}$ is an independent reasoning sub-plan. $P(p_t\mid Q,p_{<t};\theta )$ represents the probability of generating a reasoning plan $p_t$ conditioned on $\mathcal{Q}$ and previous plans $p_{<t}$. For each token $y_i$, the probability of a specific label (topic or non-topic) is computed using the softmax function:

$$P\left(y_i\mid q_1,q_2,\cdots ,q_{i-1};\theta \right)={\displaystyle \frac{\exp \left({\mathbf{e}}_{y_i}^T{\mathbf{W}}_{tag}{\mathbf{h}}_i\right)}{{\sum }_{y\in \{0,1\}}\exp \left({\mathbf{e}}_y^T{\mathbf{W}}_{tag}{\mathbf{h}}_i\right)}}$$

(3)

where $h_i\in {\mathbb{R}}^k$ is the hidden state of the model decoder at the $i-th$ token and ${\mathbf{W}}_{tag}\in {\mathbb{R}}^{R\times k}$ is the weight matrix mapping hidden states to labels. The label space projection matrix maps the k-dimensional hidden state to the m-dimensional label space, and $e_y\in {\mathbb{R}}^m$ denotes the embedding vector of label y. The decoder hidden state $h_i$ is projected into the label space, and the matching degree between the label and the current context is measured through the vector inner product.

Given the input question $\mathcal{Q}$ and the previously generated plans $p_{<t}$, the probability distribution of reasoning steps $p_t$ generated at each time step t is calculated through the softmax function:

$$P(p_t\mid Q,p_{<t};\theta )={\displaystyle \frac{\exp \left({\mathbf{W}}_{pt}{\mathbf{h}}_t\right)}{{\sum }_{j=1}^V\exp \left({\mathbf{W}}_j{\mathbf{h}}_t\right)}}$$

(4)

where ${\mathbf{W}}_{pt}\in {\mathbb{R}}^k$ and ${\mathbf{W}}_j\in {\mathbb{R}}^k$ are the weight matrices mapping the vocab, and ${\mathbf{h}}_t\in {\mathbb{R}}^k$ represents the model’s hidden layer state. The context state is then linearly mapped to the vocabulary space to generate normalized vocabulary scores.

Retrieval is subsequently performed using the identified topic entities and reasoning plans, formalized as follows:

$$P\left(r_i\mathrm{matches}p\right|p,R;\theta )={\displaystyle \frac{\exp \left(s(r_i,p;\theta )\right)}{{\sum }_{j=1}^n\exp \left(s(r_j,p;\theta )\right)}}$$

(5)

where $\mathcal{R}=(r_1,r_2,\dots ,r_n|r_n\in {\mathbb{R}}^d)$ represents the set of all relations associated with the topic entity. Here, $P\left(r_i\mathrm{matches}p\right|p,R;\theta )$ quantifies the probability of selecting the correct relation r given the current reasoning plan p and candidate relations $\mathcal{R}$.

4.3. Interpretability

Unlike traditional embedding methods, the DRKG achieves interpretability through a symbolic explicit multi-hop reasoning mechanism. Specifically, given a natural language question $\mathcal{Q}$, its reasoning process can be formalized as a path search algorithm: $\mathcal{P}={\bigcup }_{k=1}^K\left\{(e_{k-1},r_k,e_k)\right|e_k\}$. This process strictly simulates the two-stage characteristics of human reasoning: First, the DRKG identifies the topic entity of the natural language question, then locates the entity in the knowledge graph, and obtains the information directly related to the entity. Subsequently, the information directly related to the entity and the query logic of the natural language question are subjected to path pruning based on attention weights to obtain the retrieval answer for this hop. After that, this action is repeated until all the query logic in the natural language question is fully covered, and then, the final answer can be obtained.

This approach has an obvious advantage as well as a weak feature. On the one hand, the advantage of the DRKG lies in the fact that its traversal process leaves a complete and clear chain of reasoning evidence, which is in line with the process of human thinking and reasoning. At the same time, this clear chain of reasoning can be applied to more downstream tasks, such as judicial judgments and disease diagnoses; as for these tasks, the reasoning answer and reasoning process are equally important. On the other hand, compared with the embedding method, the disadvantage of the DRKG is that its inference time is longer. Assume that the single-hop retrieval delay is t; then, $T_{DRKG}=K\times t$ and $T_{Emb}=\left|\mathcal{E}\right|\times d$, where K is the total number of reasoning steps, $\left|\mathcal{E}\right|$ is the total number of entities, and d is the dimension of model. Moreover, the reasoning result of each step will affect the reasoning process of the next step. If there is an error in one of the intermediate steps of reasoning, it is very likely that the subsequent reasoning will be invalid. Of course, this problem is not completely unsolvable. We can conduct repeated training on the error-prone jump numbers in places where reasoning errors are likely to occur.

To show the explainability of the DRKG model, we selected a three-hop question answering task for analysis, as shown in Figure 3. The left side of the figure shows the interaction process with the LLMS, while the right side shows the traversal process in the knowledge graph. The yellow nodes represent the topic entity of the question, the red paths represent interactions with the knowledge graph during reasoning, and the green nodes represent the final answer.

The specific reasoning steps are as follows:

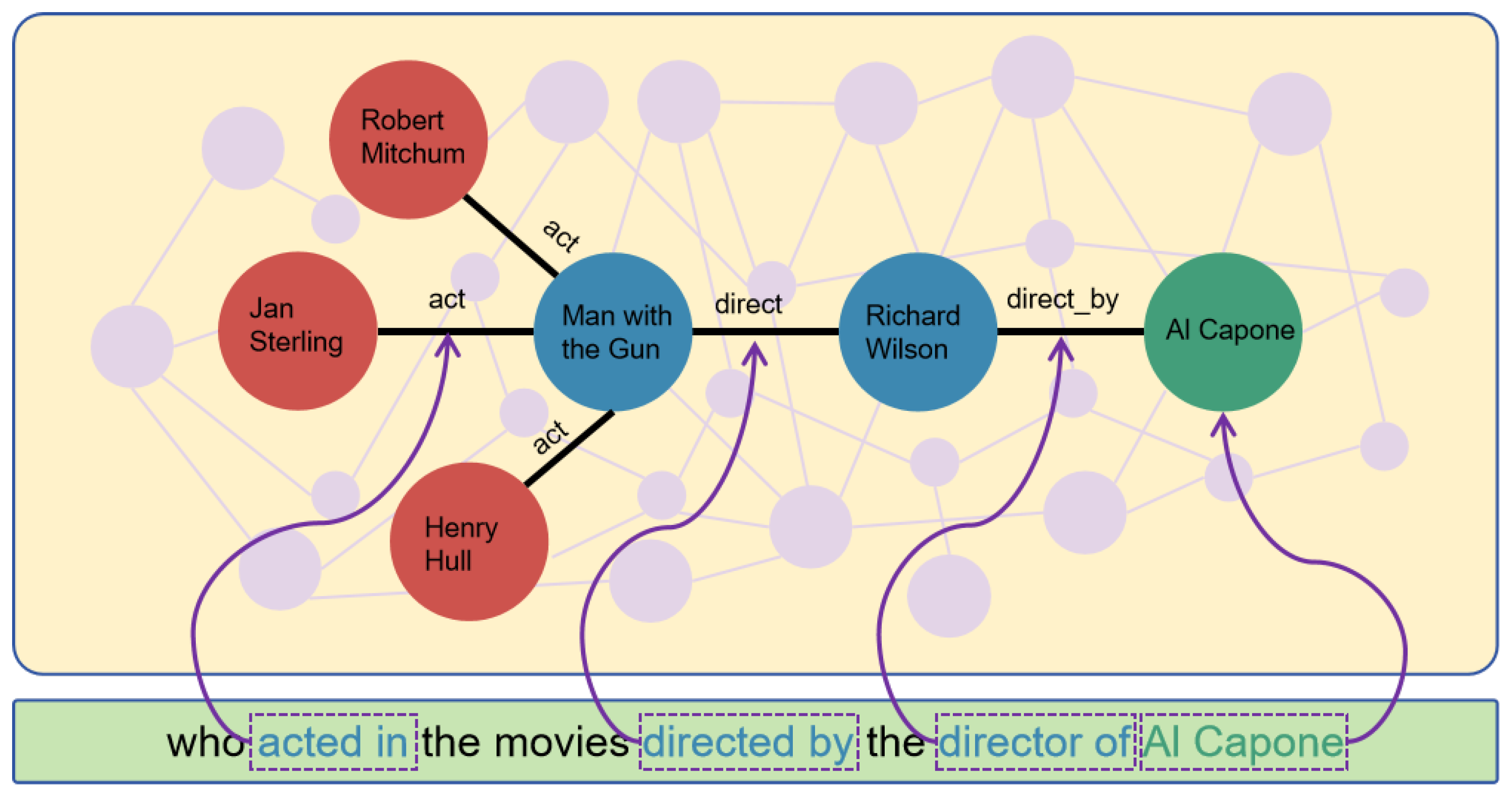
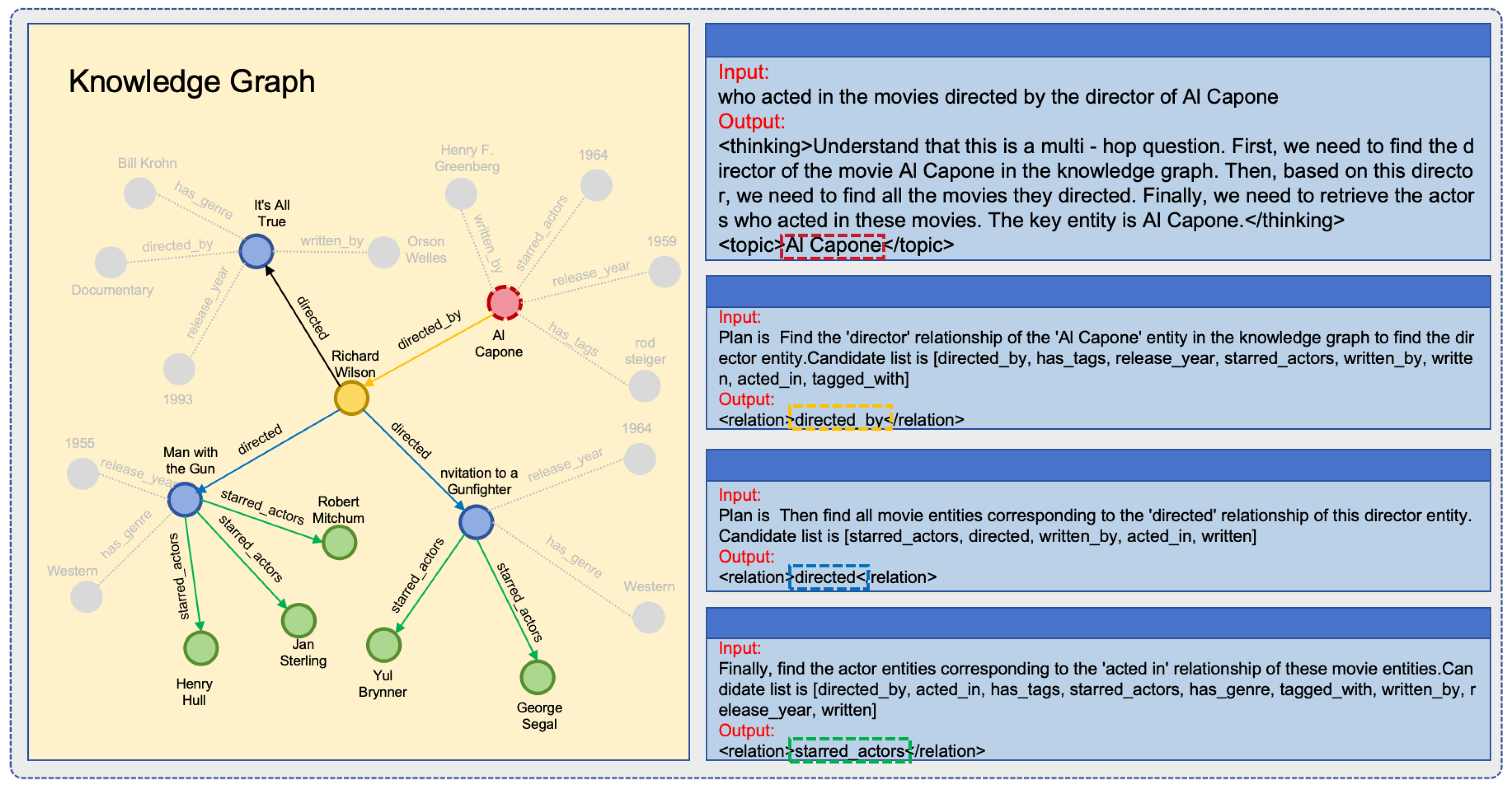
Step 0:

Identify the topic entity Al Capone, and generate reasoning plans from the question semantics.

Step 1:

From the topic entity, retrieve all the relations directed_by, has_tags, release_year, starred_actors, written_by, written, acted_in, tagged_with, and match the reasoning plan Plan is Find the ’director’ relationship of the ’Al Capone’ entity in the knowledge graph to find the director entity, selecting the directed_by relation. Richard Wilson can then be retrieved from the knowledge graph.

Step 2:

Based on Step 1, retrieve all the relations of the entity Richard Wilson as a candidate list (starred_actors, directed, written_by, acted_in, written), and match the reasoning plan Plan is Then find all movie entities corresponding to the ’directed’ relationship of this director entity, selecting the directed relation. Man with the Gun, It’s All True, Invitation to a Gunfighter can then be retrieved from the knowledge graph.

Step 3:

Based on Step 2, retrieve the relations of Richard Wilson as a candidate list (directed_by, acted_in, has_tags, starred_actors, has_genre, tagged_with, written_by, release_year, written), and match the reasoning path Finally, find the actor entities corresponding to the ’acted in’ relationship of these movie entities, ultimately obtaining the answer Robert Mitchum, Jan Sterling, Yul Brynner, George Segal.

4.4. Training

The DRKG proposes a two-stage hybrid training paradigm to synergize large language model semantic understanding capabilities with structured knowledge reasoning. The training framework integrates the supervised fine-tuning and reinforcement learning phases, addressing format alignment and controllable reasoning optimization, respectively. This process is shown in Figure 4, and each step will be discussed in detail in the following sections.

4.4.1. Data Preprocessing

The original training dataset usually only marks the final answer entity without providing the intermediate process. Its format is <question, answer> rather than the ideal form <question, reasoning path (or reasoning plan), answer>. To address the problem of the lack of inference path annotation in the original data, we use a relatively large pretrained model to generate multi-hop inference paths through structured prompts for automated annotation. Specifically, we use the zero-shot method with Chain-of-Thought to expand the original <question, answer> pair into <question, reasoning path (or reasoning plan), answer>. To control the quality of the generation, we filter samples with incorrect formats using predefined regular expression templates, manually correct the incorrect samples, and then conduct a manual review using a stratified sampling strategy.

4.4.2. Supervised Fine-Tuning

Supervised fine-tuning, a core paradigm in deep learning, adapts pretrained language models to downstream tasks using domain-specific data. For DRKG, the supervised fine-tuning phase focuses on two objectives: enforcing structured output generation to ensure compatibility with knowledge graph traversal logic and bootstrapping the model’s problem parsing and reasoning planning abilities using limited annotated samples, thus establishing a stable policy baseline for subsequent reinforcement learning optimization. Example input and output of the trained model are illustrated in

Table 2. This is an example of formatted input and output.

Input: {PROMPT} Who acted in the movies directed by director [Al Capone]?

Output: <thinking>Understand that this is a multi-hop question. First, we need to find the director of the movie [Al Capone] from the knowledge graph. Then, for the obtained director entity, we need to find all the movies they directed. Finally, we need to find the actors who acted in these movies. The key entity is [Al Capone].</thinking>

<topic>Al Capone</topic>

<plan><p> Find the ‘director’ relationship of the ‘Al Capone’ entity in the knowledge graph to find the director entity. <p> Next, find the content corresponding to the ‘directed movie’ relationship of this director entity. <p> Finally, find the ‘actor’ relationship of these movie entities to obtain the actor entities.</p></plan>

.

To establish foundational reasoning capabilities during the supervised fine-tuning phase, we optimize the model using the cross-entropy loss function. This choice is motivated by its effectiveness in aligning the predicted probability distribution of the model with the structured outputs based on the ground truth. The loss is computed as follows:

$$L\left(\theta \right)=-{\displaystyle \frac{1}{N}}\sum _{j=1}^N[\log P\left({\mathcal{T}}_j\right|Q_j;\theta )+\log P(p_t\mid Q,p_{<t};\theta )]$$

(6)

4.4.3. Reinforcement Learning

Building on the foundational reasoning capabilities acquired through supervised fine-tuning, we further refine the robustness and generalization of the model’s reasoning via reinforcement learning. To guide the reinforcement learning phase, we design three reward functions that incentivize the model to prioritize high-reward actions while suppressing low-reward behaviors, thereby progressively optimizing the reinforcement learning objective of maximizing the expected long-term return. This process is formalized as follows:

$${\nabla }_{\theta }J\left(\theta \right)={\mathbb{E}}_{\tau \sim p_{\theta }\left(\tau \right)}\left[\sum _{t=0}^T{\nabla }_{\theta }\log {\pi }_{\theta }\left(a_t\right|s_t)·R\left(\tau \right)\right]$$

(7)

In the equation, ${\nabla }_{\theta }J\left(\theta \right)$ denotes the gradient with respect to policy parameters $\theta$. The objective is to maximize the expected return $J\left(\theta \right)$ by optimizing $\theta$. The probability of trajectory $\pi$ occurring under policy $\theta$ is denoted as the term $p_{\theta }\left(\tau \right)$. $R\left(\tau \right)$ denotes the reward function, which quantitatively evaluates the quality of a trajectory.

$R\left(\tau \right)$ represents the reward function, which consists of three components: text formatting reward, key entity recognition reward, and reasoning plan reward. The text-formatting reward and entity recognition reward are computed by matching the model’s output against the samples. The reasoning plan reward calculation is more nuanced, we intentionally avoid supervised fine-tuning style training for this component to preserve model generalization. To address this, we employ a self-comparison approach where the model evaluates semantic equivalence between generated and target reasoning plans. This process can be formally expressed as follows:

$$R_{format}=\left\{\begin{array}{cc}score,\hfill & \mathrm{if}{f}_{gen}=samples\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(8)

$$R_{topic}=\left\{\begin{array}{cc}score,\hfill & \mathrm{if}{f}_{gen}=samples\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(9)

$$R_{plan}=\sum _{i=1}^{n}cosine(p_i,a_i)$$

(10)

where $R_{format}$ represents the text formatting reward function which uses regular expression matching to determine whether the output text complies with predefined standards; $R_{topic}$ represents the key entity recognition reward function, which grants a score for correctly identifying key entities and 0 otherwise; and $R_{plan}$ represents the reasoning plan generation reward function, which calculates the score based on the cosine similarity between the semantic embeddings of the generated plan and the truth plan.

4.4.4. Implementation Details

This section details the hardware and software configurations and hyperparameter settings in this experiment. The hardware configurations we used are as follows: GPU, NVIDIA A100-80G; CPU, Intel(R) Xeon(R) Gold 6348 CPU @2.60 GHz; and system memory, 128 GB. The software environment we used is as follows: operating system, CentOS Linux 8, PyTorch 2.3.0 with CUDA 12.1. The hyperparameters we used are as follows: In the fine-tuning step, the learning rate is 5 × 10 ⁻⁶, weight decay is 0.01, and batch size is 2. In the reinforcement learning step, the learning rate is 5 × 10⁻⁶, weight decay is 0.1, the number of generations is 4, and batch size is 4.

5. Experiment

5.1. Datasets

This study evaluated four benchmark datasets that are extensively discussed in the relevant literature [37]. The selection of the dataset is based on the following two points: the completeness of the knowledge graph and the diversity of question sources. Specifically, a complete and closed-loop knowledge graph environment can avoid unexpected errors caused by incomplete graph information. Additionally, a complete knowledge graph can better demonstrate the reasoning process to verify the reliability of the model. The questions in these four datasets are collected from actual queries of network users or generated through templates. The query logic in the questions is more in line with the real usage scenario, and it is also convenient to verify the interpretability of the model.

Table 3. Entity and relation count statistics.

Knowledge Graph	Number of Entities	Number of Relations
MetaQA	41,159	12
PathQuestion	2258	14
WebQSP	16,069	594
CWQ	38,671	1577

and

Table 4. Dataset count statistics.

Dataset	Number of Training Data	Number of Development Data	Number of Test Data
MetaQA (1-hop)	96,106	9992	9947
MetaQA (2-hop)	118,980	14,872	14,872
MetaQA (3-hop)	114,196	14,274	14,274
PathQuestion (2-hop)	1526	-	382
PathQuestion (3-hop)	4158	-	1040
WebQSP	2848	250	1639
CWQ	27,639	3519	3531

present the statistical details of these datasets.

MetaQA [38] is a large-scale KGQA dataset derived from the WikiMovies dataset [12] and encompasses a substantial quantity of natural language questions along with their corresponding multi-hop reasoning paths. Specifically, it includes one-hop, two-hop, and three-hop questions, each of which is associated with one or more correct answer entities.

PathQuestion [39] (PQ) is constructed using a subset of Freebase as the knowledge source. The dataset generation process involves extracting two-hop or three-hop relational paths between entities and formulating natural language questions through template-based generation. Each question is associated with only one answer entity.

WebQSP [40] is built on the foundation of the WebQuestions dataset [41] and represents a KGQA dataset. It incorporates natural language questions as well as their corresponding SPARQL queries. In particular, the questions within the WebQSP dataset exhibit enhanced diversity in content and possess more intricate semantics. Each question is associated with one or more correct answer entities.

CWQ [42] constitutes an extension of the WebQSP dataset [41], wherein additional constraints and intermediate entities are incorporated during the reasoning process. As a result, the CWQ dataset exhibits a higher level of complexity, with reasoning paths extending up to six hops. Following the research findings reported in [12], we opted for the training set to conduct the training and used the development set to evaluate model performance. Each question is associated with one or more correct answer entities.

5.2. Evaluation Metrics

Following established practices in KGQA research, we adopt hit@1 and macro-averaged F1 score as evaluation metrics: (1) hit@1 measures the percentage of questions where the top-ranked prediction matches any ground-truth answer. This metric prioritizes precise answer retrieval in single-answer scenarios. (2) F1 computes the harmonic mean of precision and recall, averaged across all questions. Given the multi-answer nature of some queries, this metric evaluates the model’s ability to comprehensively identify all valid answers, calculated as follows:

$$F1={\displaystyle \frac{2\times Precision\times Recall}{Precision+Recall}}$$

(11)

$$Precision={\displaystyle \frac{TP}{TP+FP}}$$

(12)

$$Recall={\displaystyle \frac{TP}{TP+FN}}$$

(13)

where TP (True Positive) indicates the number of correctly predicted positive samples where the model’s prediction matches the actual positive class. FP (False Positive) denotes the number of incorrectly predicted positive samples where the model predicts a positive class but the actual label is negative. FN (False Negative) refers to the count of samples that were incorrectly predicted as negative by the model when they actually belong to the positive class.

5.3. Baseline Models

To comprehensively evaluate the model performance, we compare against several state-of-the-art baselines:

MemNN [11] is an end-to-end framework for reading comprehension and QA. All triples are stored in memory cells, and multi-hop reasoning is achieved through stacked memory layers.

KVMemNN [12] extends MemNN with key–value memory structures. For each triple, the key slot encodes the subject–relation pair, while the value slot corresponds to the object entity.

IRN [15] generates traceable reasoning paths by predicting intermediate entities and relations at each hop.

PullNet [13] and GraftNet [14] both employ graph neural networks (GNNs) for subgraph construction and inference. PullNet extracts critical information to build precise subgraphs, whereas GraftNet constructs question-specific subgraphs. While effective in localized reasoning, scalability challenges arise with large-scale knowledge graph.

Hic-KGQA [8] resolves complex queries via hypergraph construction and inference chain generation. This method excels in intricate reasoning tasks but faces computational bottlenecks with large-scale data.

EmbedKGQA [7] performs multi-hop reasoning using pretrained entity and question embeddings. It mainly relies on static entity and question representations, which are suitable for basic reasoning tasks, but its performance is limited for more complex multi-hop reasoning tasks.

TransferNet [9] and UNIKGQA [10] both leverage pretrained language models (LMs) for semantic alignment. TransferNet focuses on relation–question relevance, while UNIKGQA computes entity matching scores. Both benefit from LM semantic understanding but struggle with hallucination control.

ROG [34] is a plan–retrieve–reason framework that mitigates hallucination and knowledge gaps by generating LLM-guided structured plans, ensuring faithful and interpretable reasoning.

These baselines adopt diverse reasoning strategies, predominantly built on transformer-based [26] architectures and reliant on graph structures for multi-hop inference. Our comparisons aim to elucidate performance gaps between traditional methods and LLM-enhanced approaches, particularly when transitioning from conventional base models to more capable LLMs for handling complex reasoning tasks.

5.4. Results

5.4.1. Overall Evaluation

The experimental results of applying the DRKG model across four benchmark datasets demonstrate its substantial performance advantages over existing methods. As shown in

Table 5. Overall performance of DRKG.

	Hit@1	F1
MetaQA (1-hop)	100	100
MetaQA (2-hop)	100	100
MetaQA (3-hop)	100	100
PathQuestion (2-hop)	96.6	96.6
PathQuestion (3-hop)	89.3	89.3
WebQSP	88.16	84.05
CWQ	66.99	58.04

, the DRKG achieves perfect scores of 100% on both the hit@1 and F1 metrics for the MetaQA dataset, while achieving 96. 6% on hit@1 and 89. 3% on the PathQuestion dataset. Since each question in PathQuestion has only one standard answer, the hit@1 and F1 scores of the evaluation results of this dataset are the same. For more complex scenarios, scores of 88.16% on hit@1 and 84.05 F1 on WebQSP are obtained, along with 66.99% on hit@1 and 58.04 F1 on CWQ. This performance disparity primarily stems from the characteristics of the dataset: MetaQA and PathQuestion benefit from the comprehensive coverage of the knowledge graph, enabling the DRKG to effectively comprehend the logic of the questions and precisely retrieve the answers through the knowledge graph interfaces. Performance degradation on WebQSP and CWQ correlates with increasing linguistic complexity and knowledge graph incompleteness, and although the DRKG maintains reasoning capabilities, missing nodes or relations in these datasets frequently disrupt reasoning chains.

5.4.2. MetaQA Dataset Analysis

The MetaQA dataset explicitly distinguishes reasoning tasks into one-hop, two-hop, and three-hop questions, where the reasoning complexity progressively increases with the number of hops. Remarkably, the DRKG achieves perfect performance across all tasks, attaining 100% on hit@1 and the same for coverage. This near-flawless performance can be attributed to MetaQA’s comprehensive knowledge graph structure and standardized question syntax, allowing the DRKG to more readily achieve optimal convergence during training. As shown in

Table 6. Comparative results on MetaQA dataset.

	MetaQA (1-hop)	MetaQA (2-hop)	MetaQA (3-hop)
MemN2N	78.50	30.50	19.00
KVMemN2N	93.50	84.30	53.80
IRN	85.90	71.30	35.60
GraftNet	97.0	94.8	77.7
PullNet	97.0	99.9	91.4
EmbedKGQA	97.5	98.8	94.8
TransferNet	97.5	100	100
UNIKGQA	98.0	99.9	99.9
Hic-KGQA	98.6	99.9	99.3
DRKG (Ours)	100	100	100

, comparative experiments reveal that the accuracy of MemN2N, KVMemN2N, and IRN significantly declines as the number of hops increases. This degradation stems from two factors. For MemN2N and KVMemN2N, the memory units of these two models incorporate excessive triples, leading to an expanded search space. While performing QA tasks, IRN simultaneously learns knowledge graph embeddings through a multi-task training schema, which introduces optimization target divergence.

5.4.3. PathQuestion Dataset Analysis

Similarly to MetaQA, the PathQuestion dataset also has a complete knowledge graph. However, PathQuestion presents greater parsing complexity due to the prevalence of domain-specific logical phrases in its questions, which often lack intuitive semantic coherence. This characteristic leads to deviations between parsed logical phrases and the actual query intent. As demonstrated in

Table 7. Comparative results on PathQuestion dataset.

	PathQuestion (2-hop)	PathQuestion (3-hop)
MemN2N	89.9	77.0
KVMemN2N	93.7	87.9
IRN	96.0	87.7
DRKG (Ours)	96.6	89.3

, experimental comparisons reveal that the DRKG achieves only marginal performance improvements over the three baseline models on PathQuestion.

5.4.4. WebQSP and CWQ Dataset Analysis

WebQSP and CWQ are analyzed together, given that CWQ extends WebQSP with enhanced complexity. These two datasets present substantial challenges due to three primary factors: the linguistic intricacy of natural language questions, the expansive scale of the underlying knowledge graph, and the increased reasoning hops required for accurate answers. As shown in

Table 8. Comparative results on WebQSP and CWQ dataset.

	WebQSP		CWQ
	Hit@1	F1	Hit@1	F1
GraftNet	66.4	60.4	36.8	32.7
PullNet	68.1	-	45.9	-
EmbedKGQA	66.6	-	-	-
TransferNet	71.4	-	48.6	-
UNIKGQA	77.2	72.2	51.2	49
Hic-KGQA	70.8	-	50.9	-
ROG	85.7	70.8	62.6	56.2
DRKG (Ours)	88.16	84.05	66.99	58.04

, comparative experiments reveal that all models exhibit a markedly lower performance for WebQSP and CWQ compared to MetaQA and PathQuestion. Notably, the DRKG and ROG frameworks, both leveraging LLMs as their foundation, significantly outperform traditional embedding-based methods. However, their methodologies critically diverge: ROG relies on KG-driven query plan generation, while the DRKG emphasizes semantic query plan generation directly from natural language input. This distinction enables the DRKG to achieve superior scalability and effectiveness in large-scale knowledge graph scenarios, where semantic alignment with complex questions becomes paramount.

5.5. Ablation Studies

To ascertain the efficacy of disparate components within the DRKG model, we devised ablation experiments with the aim of probing the influence exerted by the question decomposition module and the reasoning analysis module on model performance. We examined two experimental setups in particular. Experimental Setup 1 (ES1): Eliminate the fine-tuning process of the question decomposition module, and conduct direct multi-hop retrieval solely by leveraging the LLMs. Experimental Setup 2 (ES2): Omit the fine-tuning of the reasoning analysis module, and rely exclusively on question recognition for multi-hop reasoning.

The experimental outcomes are presented in

Table 9. Ablation experiment results.

	MetaQA(3-hop)		PQ(3-hop)		WebQSP		CWQ
	hit@1	F1	hit@1	F1	hit@1	F1	hit@1	F1
ES1	70.9	76.22	33.4	33.4	53.27	73.59	13.5	15.92
ES2	28.63	73.91	41.6	41.6	44.49	52.03	28.51	23.21
DRKG	100	100	89.3	89.3	78.16	74.05	66.99	58.04

. In comparison with the fully fledged DRKG model, the removal of any module precipitates a significant deterioration in performance. Under Experimental Setup 1, notwithstanding the fact that the LLMs can accurately identify the topic words and formulate a reasoning plan, a marginal decline in performance is witnessed due to the absence of the fine-tuned question decomposition module. In Experimental Setup 2, the excision of the reasoning analysis module induces a substantial decrease in both hit@1 and F1 scores. This indicates that the precise identification of topic words within a question is of paramount importance for multi-hop question answering tasks. Without appropriate semantic understanding, subsequent reasoning efforts prove fruitless. The ablation experiments corroborate the significance of both the question decomposition and reasoning analysis modules within the DRKG model.

5.6. Reliability

The reliability of KGQA systems directly impacts their trustworthiness in real-world applications (e.g., medical diagnosis and financial decision making). Reliability here encompasses output stability—the model’s ability to consistently return correct answers across multiple executions [43,44]. For LLMs, three critical parameters govern output reliability: temperature, top-k, and top-p.

Temperature: The temperature parameter fundamentally reshapes the token probability distribution through entropy scaling. Given the original logits $z_w$ for token w, the temperature-scaled probability is computed as follows:

$$P\left(w\right)={\displaystyle \frac{\exp (z_w/T)}{{\sum }_{w^{\prime }}\exp (z_{w^{\prime }}/T)}}$$

(14)

where T controls the steepness of the distribution: Low temperatures ($T\to 0$) maximize the probability gap between the top token and others, effectively implementing greedy decoding. High temperatures ($T>1$) flatten the distribution, increasing the generation diversity at the cost of reliability.

Top-k Sampling constrains decoding to the top k tokens by probability at each step:

$$V_{top-k}=\left\{w_i\right|P\left(w_i\right)\ge P\left(w\left(k\right)\right)\}$$

(15)

A smaller k suppresses low-probability noise but risks ignoring domain-specific rare tokens.

Top-p dynamically constructs a minimal candidate set covering cumulative probability p:

$$\sum _{w\in V_{top-p}}P\left(w\right)\ge p$$

(16)

Compared to fixed-k sampling, top-p adapts to the distribution shape, balancing reliability and flexibility.

To quantify the parameter impacts, we evaluated six parameter combinations on the MetaQA and PathQuestion datasets, chosen for their comprehensive KG coverage to minimize noise from incomplete knowledge. During testing, 100 inference runs were conducted for each parameter combination using the same validation dataset. The average correct rate (ACR) and average variance (AV) of the inferred results were calculated, with the formula defined as follows:

$$\mathrm{Average}\mathrm{Correct}\mathrm{Rate}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\displaystyle \frac{\mathrm{Correct}{\mathrm{Predictions}}_i}{\mathrm{Total}{\mathrm{Predictions}}_i}}$$

(17)

$$\mathrm{Average}\mathrm{Variance}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{({\mathrm{Accuracy}}_i-\mathrm{Mean}\mathrm{Accuracy})}^2$$

(18)

As shown in

Table 10. Reliability experiment results.

Temperature	Top-k	Top-p	MetaQA		PathQuestion
			ACR	AV	ACR	AV
0.1	10	0.1	100.0	0.0	87.65	$\pm 3.20$
0.1	10	0.5	100.0	0.0	83.29	$\pm 4.92$
0.5	50	0.1	98.72	≈$\pm 0.00$	76.82	$\pm 8.69$
0.5	50	0.5	98.13	≈$\pm 0.00$	76.42	$\pm 8.09$
0.8	10	0.95	87.63	$\pm 3.92$	53.15	$\pm 13.09$
1.0	100	1.0	84.63	$\pm 5.32$	50.30	$\pm 15.09$

, the experimental results demonstrate that temperature significantly impacts model accuracy. Low-temperature settings ($T\le 0.1$) achieve perfect accuracy, while high-temperature settings ($T\ge 0.8$) cause substantial performance degradation. This occurs because low temperatures enforce greedy decoding, which suppresses stochasticity by consistently selecting the highest-probability entities. Notably, this pattern holds across both the MetaQA and PathQuestion datasets, yielding optimal performance under low-temperature conditions. In contrast, top-k and top-p exhibit minimal regulatory effects except in extreme parameter ranges (e.g., $k\le 5$ or $p\le 0.3$). These characteristics necessitate a stability-first optimization principle. Low-temperature configurations maximize reliability by eliminating randomness, while top-k/top-p parameters show negligible influence due to DRKG’s inherent structural constraints. For applications demanding precision without generative diversity (e.g., mission-critical systems), we recommend prioritizing low-temperature settings ($T\le 0.1$) and minimal top-p values ($p\le 0.1$) to ensure deterministic, high-fidelity outputs.

5.7. Interpretability of Scenarios in the Medical Field

To verify the applicability and interpretability advantages of the DRKG framework in real-world scenarios, this study constructs a vertical domain knowledge graph based on the de-identified electronic medical record data of a certain hospital and designs a multi-hop diagnosis reasoning task for a special assessment. Specifically, the knowledge graph covers 48,612 medical entities and 18 types of core relationships. The question-answering data generation automatically generates 8,806 multi-hop questions based on the large model API, covering typical scenarios such as diagnostic path reasoning (e.g., “What are the symptoms and preventive measures of cholecystitis?”) and treatment plan tracing (e.g., “What are the examination items and treatment methods for pulmonary alveolar proteinosis?”).

In terms of experimental settings, the stratified sampling method was used to divide the training set (70%), validation set (20%), and test set (10%). Additionally, 30% of the samples (a total of 260) were randomly selected from the test set for manual interpretability verification. In the manually evaluated samples, the complete coincidence rate between the reasoning plans generated by DRKG and the paths marked by physicians reached 100%, and its step-by-step logic strictly followed the clinical decision tree. For example, for the question “After treatment, what are the cure rate and treatment course for patients with symptoms such as cyanosis and chest pain?”, the model completed the reasoning process in three steps. Step 1: Through the feature entities “cyanosis” and “chest pain” and the relationship “disease symptoms”, the disease name of the entity “pulmonary alveolar proteinosis” was queried. Step 2: Through the relationship between the entity “pulmonary alveolar proteinosis” and “cure rate”, the cure rate of this disease was found to be “about 40%”. Step 3: Through the relationship between the entity “pulmonary alveolar proteinosis” and “treatment course”, the treatment course of this disease was found to be “about 3 months”.

6. Discussion

The experimental results demonstrate that the DRKG achieves a state-of-the-art level of performance across multiple benchmark datasets while providing human-interpretable reasoning processes. This section contextualizes these findings within the broader landscape of KGQA research, examines their implications, and explores how they advance our understanding of integrating LLMs with structured knowledge reasoning.

6.1. Interpretable Reasoning and Performance Gains

The DRKG address a critical limitation of traditional embedding-based methods: the lack of transparency in multi-hop inference. By decomposing questions into reasoning plans with hop constraints, the DRKG aligns its reasoning steps with human logic, as evidenced by the interpretability case study. This design validates the hypothesis that explicit path control mitigates knowledge hallucination—a persistent issue in LLMs. Compared to ROG [34], which relies on fixed KG-driven plans, the DRKG’s dynamic semantic parsing adapts to diverse query structures, explaining its superior performance on bench datasets (Table 5). These results underscore the importance of balancing structural fidelity with linguistic flexibility in complex mutil-hop KGQA tasks.

6.2. Bridging the Semantic Gap

The DRKG’s hybrid training paradigm—combining supervised fine-tuning and reinforcement learning—effectively bridges the semantic gap between natural language and structured knowledge. Unlike UNIKGQA [10] and TransferNet [9], which focus on entity–relation matching, the DRKG leverages LLMs to generate intermediate reasoning steps that mirror human problem decomposition. This approach resolves ambiguities in domain-specific phrasing, where traditional models struggle with non-intuitive logical phrases (Table 6, Table 7 and Table 8). The ablation studies (Table 9) further confirm that semantic understanding and structured retrieval are mutually reinforced, aligning with recent findings on LLM-KG synergy.

6.3. Broader Implications

The success of the DRKG has significant implications for applications requiring reliable and explainable reasoning. In healthcare, for instance, clinicians could trace diagnostic reasoning paths to validate conclusions. In finance, transparent multi-hop inference could enhance auditability for regulatory compliance. Furthermore, the DRKG’s robustness under low-temperature configurations (Section 5.7) suggests its suitability for mission-critical systems where deterministic outputs are paramount.

7. Conclusions

This study proposes the DRKG, an innovative framework for knowledge graph question answering that reliably and interpretably integrates the natural language processing capabilities of LLMs with structured knowledge reasoning. Compared to conventional approaches, the DRKG addresses the black-box limitations of embedding-based methods and mitigates the hallucination risks inherent in direct answer generation via pure LLMs. The framework operates through a dual-phase reasoning mechanism: it first generates multi-step structured reasoning plans based on question semantics and then executes controlled knowledge graph reasoning guided by these plans. We further design a two-stage training paradigm combining supervised learning for foundational reasoning capability with reinforcement learning to optimize path selection strategies, effectively balancing knowledge accuracy and model generalizability. Extensive experiments demonstrate the framework’s effectiveness, showing significant improvements in reasoning accuracy while maintaining transparent decision processes. Ablation studies validate the critical roles of both reasoning plan generation and guided traversal components. A reliability analysis reveals the temperature parameter’s pivotal impact on inference stability. This work establishes a principled approach for trustworthy knowledge reasoning, with future directions including LLM-augmented knowledge graph completion and failure backtracking mechanisms for robust multi-hop reasoning.