Dynamic Weight Model Predictive Control for Longitudinal Adaptive Cruise Systems in Electric Vehicles

Abstract

This paper proposes a dynamic weight model predictive control (DWMPC) strategy for adaptive cruise control (ACC) in pure electric vehicles, aiming to enhance robustness, energy efficiency, and ride comfort under complex traffic conditions. Unlike conventional MPC with static weights, the proposed method integrates a fuzzy inference system that evaluates driving urgency based on real-time spacing and velocity errors. The resulting emergency coefficient is mapped through a nonlinear function to dynamically adjust the velocity tracking weight in the MPC cost function. Additionally, a four-mode coordination mechanism adaptively modifies acceleration and jerk penalties according to risk levels, enabling balanced responses between safety and comfort. A composite performance evaluation index (PEI) is formulated to quantitatively assess energy consumption, ride comfort, spacing accuracy, and emergency responsiveness. Simulation results under WLTC and typical urban driving scenarios demonstrate that DWMPC outperforms fixed-weight MPC and PI controllers, reducing energy consumption by 6.5%, jerk by 42.9%, and response time by 41.8% while improving coordination in speed tracking, inter-vehicle distance regulation, and energy-efficient control.

1. Introduction

Driven by the ongoing electrification of transportation [1], advances in intelligent sensing, control algorithms, and vehicle-to-everything (V2X) communication have positioned automated vehicles (AVs) as a cornerstone of intelligent transportation systems. Unlike human drivers, AVs respond swiftly and operate with consistent logic, thereby reducing behavioral uncertainty and improving both safety and traffic efficiency [2,3,4,5]. These capabilities make AVs well-suited for mitigating traffic congestion [6,7], enhancing road safety [8,9], and supporting sustainable mobility [10,11]. However, large-scale deployment remains limited by the absence of robust, interpretable, and real-time control strategies capable of handling complex scenarios such as sudden cut-ins, unpredictable pedestrians, sensor noise, and abrupt traffic fluctuations.

As a core function in longitudinal automation, adaptive cruise control (ACC) is responsible for maintaining appropriate speed and inter-vehicle distance to ensure safety, comfort, and energy efficiency. Early ACC systems based on PID and rule-based control offered low computational costs [12,13], but their static nature limited adaptability to diverse traffic conditions. Model predictive control (MPC) has emerged as a mainstream solution, enabling multi-objective optimization over finite horizons while respecting system constraints [14,15,16]. Several extensions to MPC have been proposed, such as lead vehicle acceleration modeling [17], Bayesian prediction [18], and Gaussian process-based uncertainty modeling [19]. In addition, hybrid frameworks incorporating fuzzy logic [20,21], adaptive weight adjustment [22], and multi-objective optimization [23,24,25] have shown improved performance under dynamic traffic conditions. Other strategies include variable headway models [26,27], driving style-aware control [28], and optimization-based mode switching [29], often deployed within hierarchical structures [30].

Despite recent advances, many MPC-based methods still rely on fixed or manually tuned parameters, limiting their adaptability to changing traffic contexts. Moreover, few offer a unified mechanism to dynamically balance safety, comfort, and energy efficiency, an issue particularly critical for electric vehicles (EVs), where real-time energy management is essential. The increasing electrification of transportation has further intensified the demand for energy-aware control strategies. Although several approaches attempt to improve efficiency by incorporating motor energy models into the MPC cost function [31], applying genetic algorithms for speed planning [32], or adopting embedded-oriented multi-mode optimization [33], many of these strategies overlook real-time responsiveness and hardware constraints.

Learning-based strategies have recently gained traction for their ability to handle complex and uncertain environments. Some integrate driving style recognition with LQR control [34], while others adopt deep reinforcement learning (DRL) to optimize energy usage and responsiveness under dense traffic [35]. Neural networks have also been employed for deceleration prediction [36], and distributionally robust MPC frameworks have been developed to improve robustness in lane-changing scenarios [37]. However, these methods typically function as black boxes and impose high computational burdens, limiting their applicability in embedded, safety-critical systems.

In summary, although the ACC field has seen significant advances, three major challenges remain unresolved: (1) fixed control weights limit responsiveness in dynamic environments; (2) black-box AI models lack interpretability and demand high computational resources; (3) there is a lack of a unified framework for quantitatively evaluating safety, comfort, and energy efficiency. To address these challenges, we propose a dynamic weight model predictive control (DWMPC) strategy tailored for the longitudinal control of battery electric vehicles. This method enhances conventional MPC by introducing dynamic weight adjustment based on real-time traffic urgency, enabling adaptive prioritization among competing control objectives.

The proposed DWMPC framework integrates a fuzzy inference system to evaluate an emergency coefficient from relative distance and velocity errors. This coefficient is mapped through a nonlinear exponential function to dynamically tune the velocity tracking weight. Additionally, a four-mode switching mechanism adjusts the acceleration and jerk penalties according to the driving context, facilitating flexible trade-offs between safety, comfort, and energy efficiency. Simulation results under WLTC and stochastic urban driving conditions demonstrate that the proposed approach significantly outperforms fixed-weight MPC and traditional PID control in terms of tracking accuracy, energy efficiency, and emergency responsiveness.

Specifically, the core contributions of this study are as follows:

• A fuzzy inference mechanism to evaluate an emergency coefficient from distance and velocity errors;
• An exponential mapping function to dynamically adjust the velocity tracking weight;
• A four-mode control scheme for adaptive tuning of acceleration and jerk penalties;
• Simulation validation under WLTC and stochastic urban conditions;
• A unified performance evaluation index (PEI) for multi-objective performance assessment.

2. Car-Following Dynamics Model

2.1. Hierarchical Control Architecture

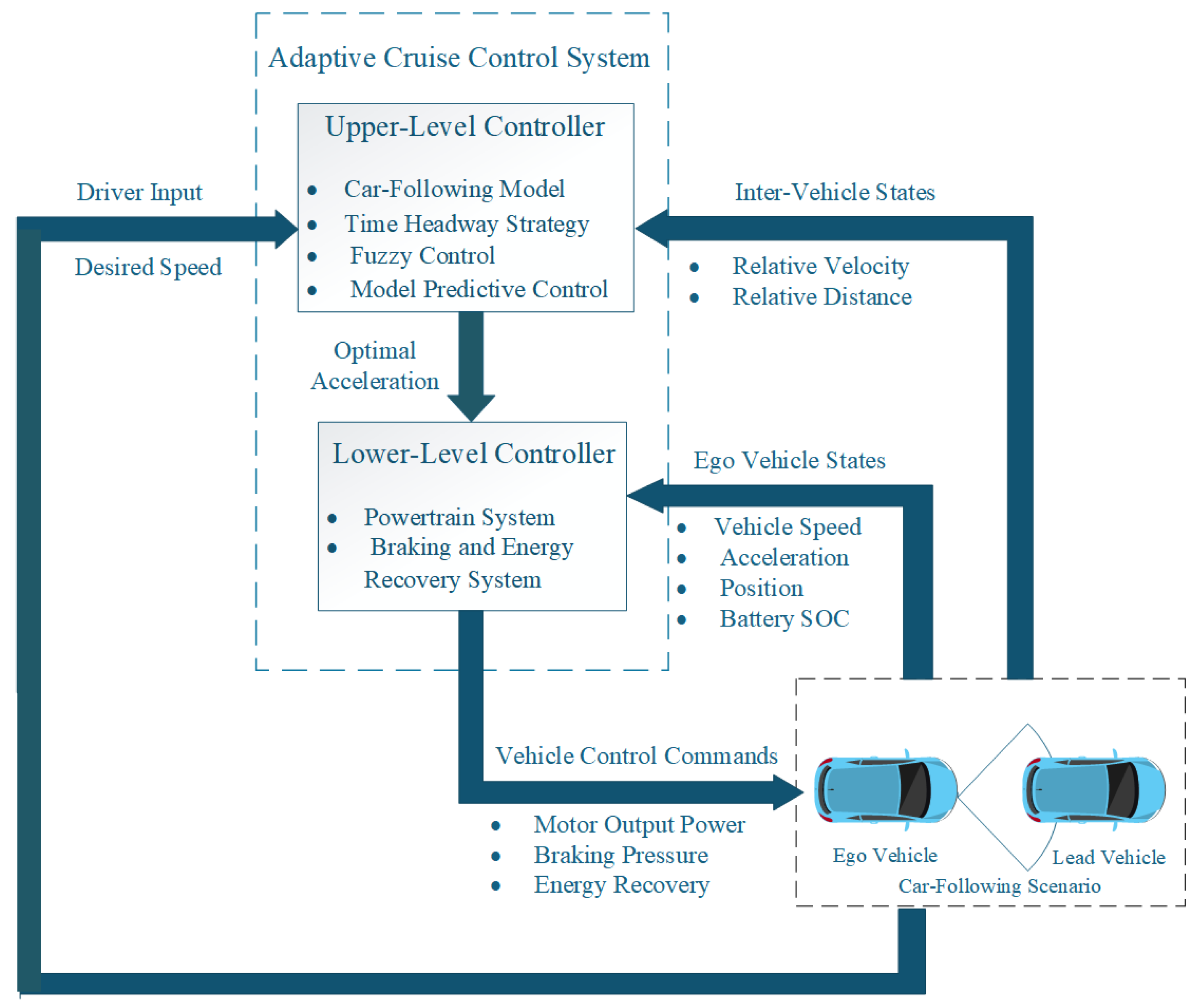
Figure 1 presents the hierarchical control structure employed in this study. The upper-level controller computes the optimal acceleration using a fuzzy-enhanced MPC algorithm, while the lower-level controller executes the command via the powertrain and braking subsystems.

This architecture separates high-level decision-making from low-level actuation, and the figure illustrates key signal flows between modules such as vehicle state estimation, fuzzy inference, and MPC optimization. The overall control structure is adapted from the two-layer predictive cruise control framework proposed in [30].

2.2. Relative Dynamics in Continuous Time

The car-following behavior is modeled in a relative coordinate frame, where the ego vehicle’s motion is expressed with respect to the preceding vehicle. Let $d_k$ denote the inter-vehicle distance, $v_{f,k}$ the ego vehicle speed, and $v_{p,k}$ the speed of the preceding vehicle. The relative states are defined as follows:

$$\Delta d_k=d_k-d_{\mathrm{safe}},\Delta v_k=v_{f,k}-v_{p,k}.$$

(1)

Here, $d_{\mathrm{safe}}$ is the desired safety distance, modeled as follows:

$$d_{\mathrm{safe}}=d_0+T_h{v}_{f,k},$$

(2)

where $d_0$ is the standstill spacing, and $T_h$ the time headway.

The state variables and control input are defined as follows. The acceleration of the ego vehicle is denoted as $a_f\left(t\right)$, and the acceleration of the lead vehicle is denoted as $a_p\left(t\right)$, which is treated as a measured external disturbance. The control input $u\left(t\right)$ represents the jerk applied to the ego vehicle, i.e., the derivative of its acceleration.

The complete continuous-time car-following model can be written as a third-order system with the following state vector:

$$\mathbf{x}\left(t\right)=\left[\begin{array}{c}\Delta d\left(t\right)\\ \Delta v\left(t\right)\\ a_f\left(t\right)\end{array}\right].$$

(3)

Taking time derivatives of each state yields the system dynamics:

$${\dot{x}}_1\left(t\right)=\Delta v\left(t\right)=x_2\left(t\right),$$

(4)

$${\dot{x}}_2\left(t\right)=a_f\left(t\right)-a_p\left(t\right)=x_3\left(t\right)-a_p\left(t\right),$$

(5)

$${\dot{x}}_3\left(t\right)=u\left(t\right).$$

(6)

Thus, the continuous-time state–space model becomes the following:

$$\dot{\mathbf{x}}\left(t\right)=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right]\mathbf{x}\left(t\right)+\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]u\left(t\right)+\left[\begin{array}{c}0\\ -1\\ 0\end{array}\right]a_p\left(t\right).$$

(7)

This third-order model explicitly incorporates jerk as the control input, enabling smooth transitions in acceleration profiles, which enhances ride comfort and reduces actuator wear. It also allows the MPC to generate anticipatory control strategies that avoid aggressive or abrupt changes.

2.3. Linearized Discrete-Time Prediction Model

Using zero-order hold discretization with sampling time T, the model is transformed into a discrete-time state–space form:

$$x_{k+1}=A{x}_k+B{u}_k+\Gamma a_{p,k},$$

(8)

with the following state and input variables:

$$x_k=\left[\begin{array}{c}\Delta d_k\\ \Delta v_k\\ a_{f,k}\end{array}\right],u_k=\Delta a_k=a_{f,k}-a_{f,k-1}.$$

(9)

The system matrices are as follows:

$$A=\left[\begin{array}{ccc}1& T& -{\displaystyle \frac{5T^2}{2}}\\ 0& 1& -T\\ 0& 0& 1-{\displaystyle \frac{20T}{9}}\end{array}\right],B=\left[\begin{array}{c}0\\ 0\\ {\displaystyle \frac{20T}{9}}\end{array}\right],\Gamma =\left[\begin{array}{c}0\\ T\\ 0\end{array}\right].$$

(10)

This discrete model serves as the predictive foundation for the MPC formulation, capturing the coupling effects between vehicle spacing, velocity gap, and acceleration in a tractable linear structure.

2.4. Model Predictive Control Framework

To incorporate control increments and enable reference tracking, the system is augmented by defining the extended state vector:

$${\kappa }_k=\left[\begin{array}{c}{x}_k\\ u_{k-1}\end{array}\right].$$

(11)

The tracking error at each time step is then provided by the following:

$$e_k=y_{\mathrm{ref},k}-y_k=y_{\mathrm{ref},k}-C{\kappa }_k.$$

(12)

To track both relative distance and velocity, the output matrix C is defined as follows:

$$C=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\end{array}\right].$$

(13)

The objective of the MPC is to minimize the cumulative tracking error and control effort over a prediction horizon $N_p$. The cost function is expressed as follows:

$$J=\sum _{k=0}^{N_p-1}\left(e_k^{\top }Q{e}_k+\Delta u_k^{\top }R\Delta u_k\right)+\rho {\epsilon }^2.$$

(14)

Here, $Q⪰0$ and $R\succ 0$ are the weighting matrices for state errors and control increments, respectively. The slack variable $\epsilon$ allows constraint relaxation, with $\rho >0$ being its associated penalty.

The optimization is subject to the following constraints:

$$\begin{array}{cc}\hfill u_{min}& \le u_k\le u_{max},\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill \Delta u_{min}& \le \Delta u_k\le \Delta u_{max},\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill y_{min}& \le y_k\le y_{max}.\hfill \end{array}$$

(17)

These constraints ensure safety, comfort, and actuator feasibility during control execution.

The constrained optimization problem is cast into the standard quadratic programming (QP) form:

$$\underset{\Delta U}{min}{\displaystyle \frac{1}{2}}\Delta U^{\top }H\Delta U+f^{\top }\Delta U,$$

(18)

where $\Delta U$ is the stacked vector of control increments over the prediction horizon. The matrices H and f are derived from the system dynamics and the cost function. The QP is solved using MATLAB’s quadprog solver, and only the first element of $\Delta U$ is applied in each sampling period, following the receding horizon principle.

The weighting matrices Q and R define the relative importance of each control objective. $Q\in {\mathbb{R}}^{3\times 3}$ is diagonal and positive semi-definite:

$$Q=\left[\begin{array}{ccc}{\alpha }_1& 0& 0\\ 0& {\alpha }_2& 0\\ 0& 0& {\alpha }_3\end{array}\right],R=\beta .$$

(19)

Here, ${\alpha }_1$, ${\alpha }_2$, and ${\alpha }_3$ correspond to the weights for relative distance $\Delta d$, relative velocity $\Delta v$, and acceleration $a_f$, respectively. Larger values indicate higher priority in minimizing the associated state error.

The weight configuration of the fixed-MPC controller in this study is devised with reference to the multi-objective control structure presented in [22], which outlines a representative MPC framework for adaptive cruise control in electric vehicles. Drawing inspiration from its design philosophy, we assign weighting coefficients of 100, 1.0, and 1.0 to the spacing error, velocity error, and acceleration terms, respectively, thereby prioritizing safety while ensuring smooth and responsive control behavior. Additionally, a control increment penalty of 1000 is applied to discourage excessive actuation. This configuration is adopted as a baseline for comparative analysis, offering a balanced representation of conventional fixed-weight control strategies.

$${\alpha }_1=100,{\alpha }_2=1.0,{\alpha }_3=1.0,\beta =1000.$$

(20)

This parameter set provides a balanced trade-off among tracking accuracy, smoothness, and constraint satisfaction and has demonstrated stable performance under standard conditions such as the WLTC cycle.

3. Emergency-Aware Fuzzy Logic-Based Dynamic Weighting for MPC

3.1. Fuzzy-Based Adaptive Weight Adjustment

To enhance the adaptability of MPC across varying traffic conditions, we introduce a fuzzy logic-based module that dynamically adjusts the cost function weights. Following practices in adaptive cruise control design, the fuzzy controller takes two input variables: spacing error $\Delta d$ and relative velocity error $\Delta v$, both of which are widely used in fuzzy-MPC frameworks due to their direct relevance to car-following safety and stability.

The universe of discourse for $\Delta d$ is set to $[-40\mathrm{m},80\mathrm{m}]$, encompassing scenarios from dangerously short gaps to extended highway headways. For $\Delta v$, the range $[-20\mathrm{m}/\mathrm{s},20\mathrm{m}/\mathrm{s}]$ covers conditions from emergency braking to high-speed acceleration. These intervals align with real-world car-following behavior and ensure consistent fuzzy inference across traffic environments. The fuzzy rule structure follows a typical five-by-five grid based on these inputs, as demonstrated in [38].

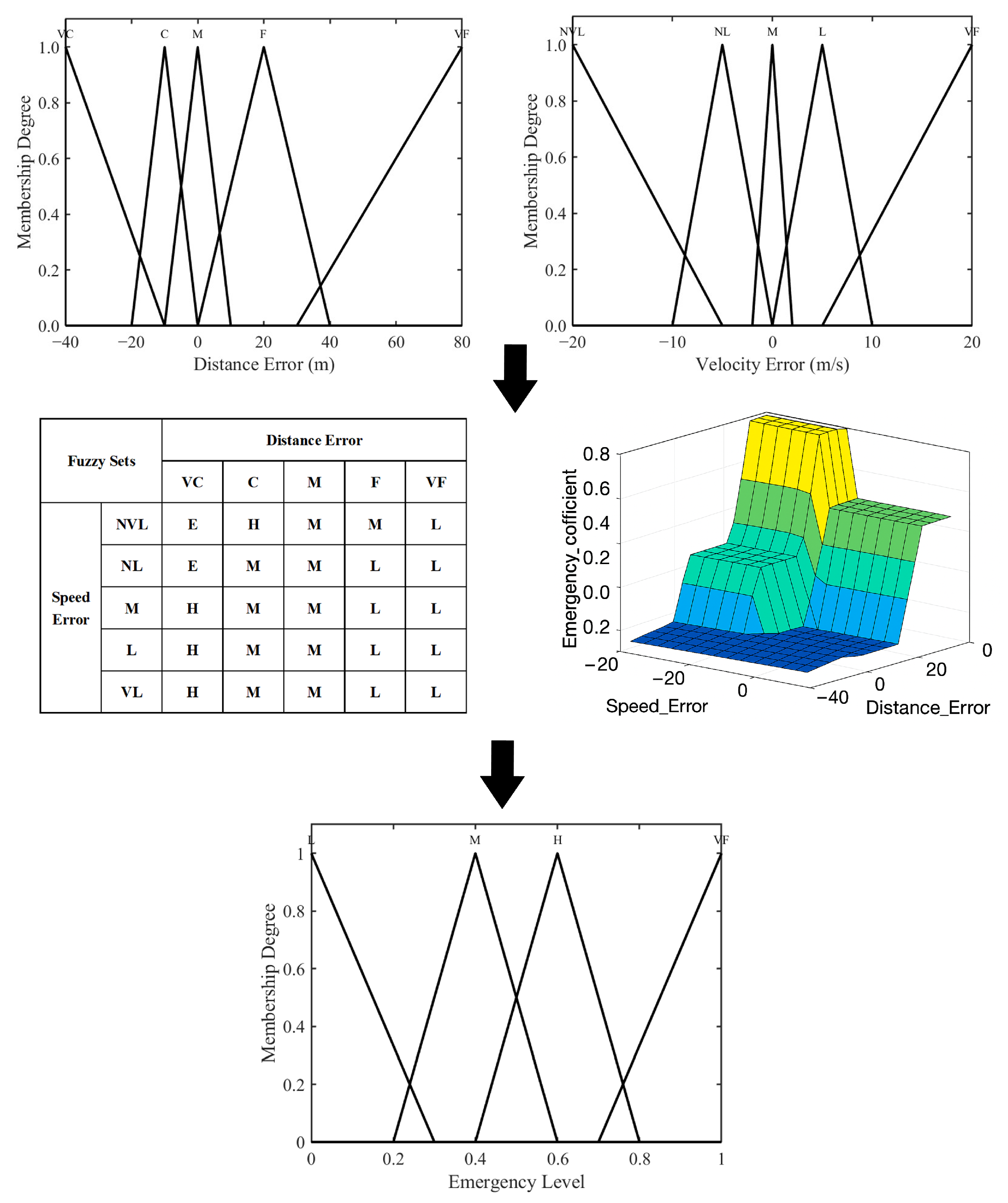
Figure 2 illustrates the complete fuzzy inference structure and its components:

• Top-left and top-right: Membership functions for $\Delta d$ and $\Delta v$. Triangular functions are used for intermediate terms, while trapezoidal functions define extreme values. For instance,

  −

  ${\mu }_{VC}(\Delta d)$ = trimf($\Delta d$, $[-40,-30,-10]$);

  −

  ${\mu }_{NVL}(\Delta v)$ = trapmf($\Delta v$, $[-20,-20,-15,-10]$).

• Bottom-left: The fuzzy rule table is composed of 25 inference rules by combining all possible input term pairs. Each rule outputs a qualitative urgency level: emergency (E), high (H), medium (M), or low (L).
• Center-right: A 3D surface plot shows the defuzzified emergency coefficient E as a function of $\Delta d$ and $\Delta v$. This visualization reflects how the system evaluates urgency in different traffic scenarios.
• Bottom: The output membership functions for the emergency level $E\in [0,1]$, divided into three fuzzy sets (L, M, and H) to support smooth weight transitions.

The fuzzy rule outputs are defuzzified using the centroid method to obtain a quantitative emergency coefficient $E\in [0,1]$. This value serves as the real-time indicator of traffic urgency.

This coefficient is then mapped to the velocity-tracking weight ${\alpha }_1$ in the MPC cost function through an exponential mapping:

$${\alpha }_1\left(E\right)={\alpha }_{1,\min }+({\alpha }_{1,\max }-{\alpha }_{1,\min })·\left({\displaystyle \frac{{10}^E-1}{9}}\right).$$

(21)

This mapping function ensures that in critical situations (higher E), the weight ${\alpha }_1$ increases sharply, thereby enhancing tracking aggressiveness. Under normal or safe conditions, ${\alpha }_1$ remains relatively stable, reducing unnecessary actuation and ensuring smooth control.

Overall, this structure enables interpretable, real-time, and context-sensitive adjustment of control priorities within the MPC framework. It combines the robustness of rule-based reasoning with the flexibility of continuous tuning.

Each input is fuzzified into five linguistic terms:

• Very close, close, medium, far, and very far (for $\Delta d$);
• Negative very large, negative large, medium, positive large, and positive very large (for $\Delta v$).

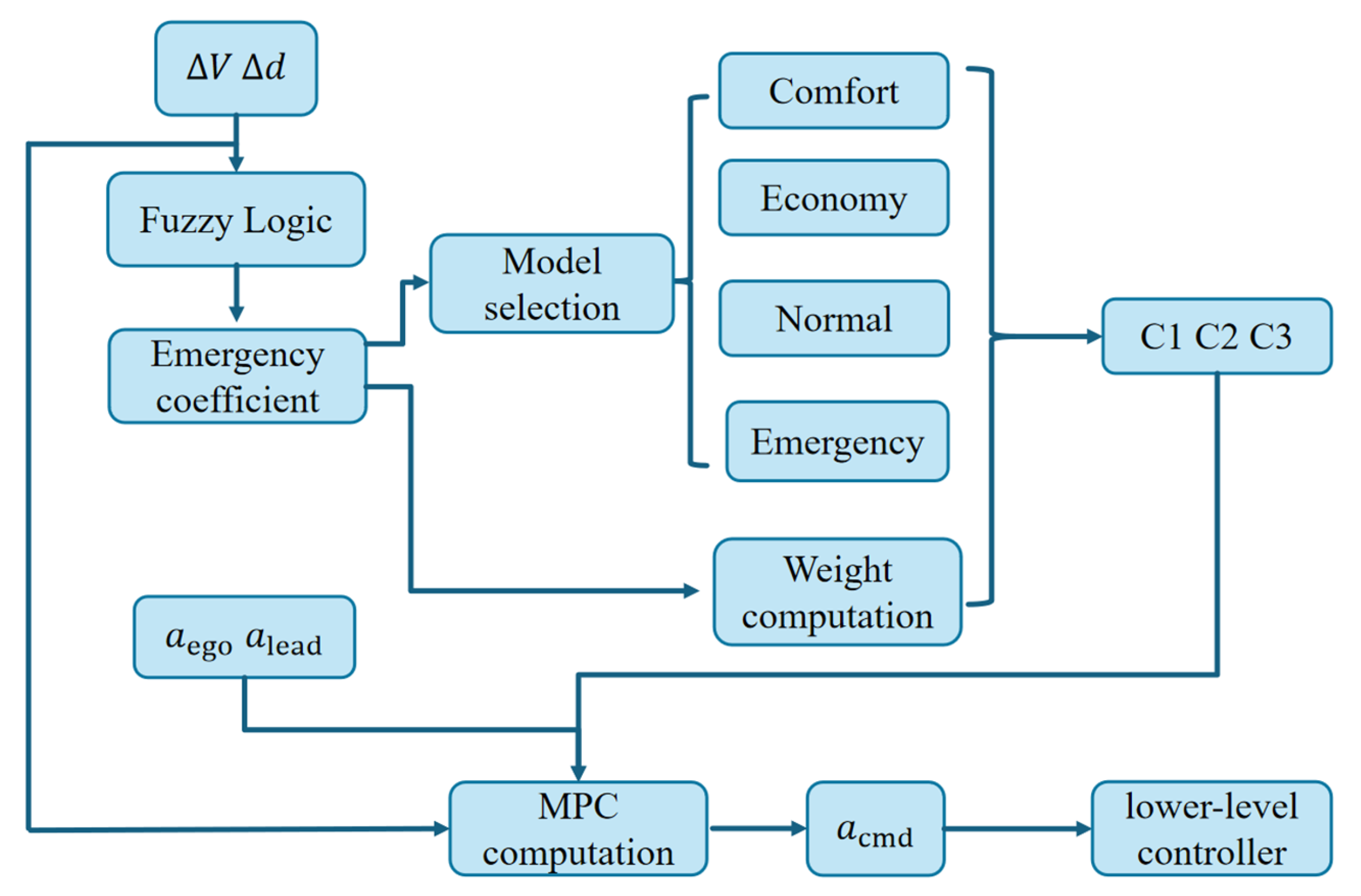
3.2. Emergency-Driven Nonlinear Weight Adaptation and Mode-Specific Control Strategy

To enhance responsiveness under critical conditions, refined nonlinear mapping $C_1\left(E\right)$ is introduced to amplify the velocity tracking weight adaptively. While ${\alpha }_1\left(E\right)$ already reflects emergency-aware adjustment, $C_1\left(E\right)$ enables sharper and faster prioritization for high-risk scenarios.

The mapping is defined as follows:

$$C_1\left(E\right)=100·{10}^{\left({\displaystyle \frac{E-0.1}{0.9}}·{\displaystyle \frac{1}{1+exp(-10(E-0.25\left)\right)}}\right)},$$

(22)

which ensures smooth scaling in nominal conditions and rapid escalation when emergency levels rise.

For real-time implementation, the control space is divided into four discrete driving modes according to the emergency coefficient E. Each mode is associated with fixed values of acceleration ($C_2$) and control effort ($C_3$) weights, as summarized in

Table 1. Weight parameters corresponding to four driving modes based on an emergency coefficient.

Mode	E Range	${\mathit{C}}_2$	${\mathit{C}}_3$	Control Priority
1	$E<0.25$	1	2000	Comfort (smoothness dominant)
2	$0.25\le E<0.5$	10	1000	Economy (efficiency dominant)
3	$0.5\le E<0.75$	50	800	Normal (balanced control)
4	$E\ge 0.75$	100	500	Emergency (fast response)

. The specific threshold values (0.25, 0.5, and 0.75) were selected through empirical tuning to reflect gradual shifts in urgency level observed under typical car-following scenarios and to ensure stable transitions between adjacent driving modes.

The weight parameters in Table 1 are designed according to the control priorities of each driving mode. In low-risk conditions ($E<0.25$), the controller emphasizes comfort, assigning a high jerk penalty ($C_3=2000$) and low acceleration responsiveness ($C_2=1$). As the emergency coefficient increases, $C_2$ is elevated to enable faster acceleration, while $C_3$ is reduced to allow more aggressive but less smooth actions. This mode-specific philosophy enables smooth transitions between energy-saving and safety-critical behavior and has been validated through simulation results presented in Section 5.

The overall structure of the proposed emergency-aware dynamic weighting mechanism is illustrated in Figure 3.

4. Simulation Environment and Scenario Setup

4.1. Simulink-Based ACC Platform Architecture

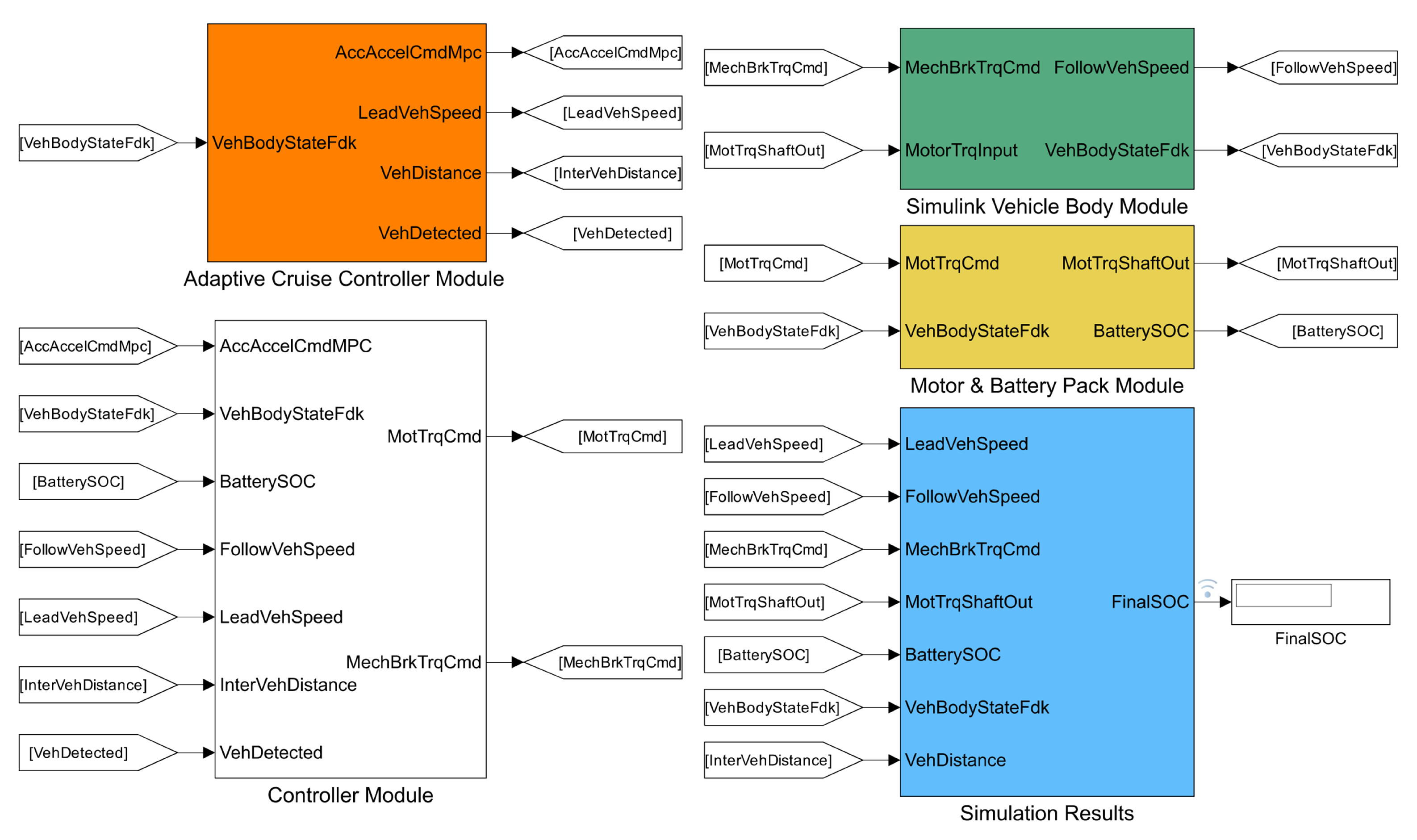
To evaluate the proposed DWMPC strategy, a complete adaptive cruise control (ACC) simulation platform was constructed in MATLAB/Simulink R2024a. The system integrates multiple modules, including the DWMPC-based controller, vehicle body dynamics, electric motor, and battery pack.

As shown in Figure 4, the simulation framework is modularly organized into five components.

• Adaptive cruise controller module: Computes optimal acceleration via the DWMPC algorithm.
• Controller module: Converts acceleration to motor torque and braking commands, accounting for battery SOC.
• Simulink vehicle body module: Simulates vehicle longitudinal dynamics under input torque and braking.
• Motor and battery pack module: Models energy conversion, SOC evolution, and drivetrain efficiency.
• Simulation results module: Collects outputs such as velocity, distance, SOC, and control commands.

A comprehensive set of physical and drivetrain parameters was configured to represent a mid-size pure electric vehicle. These parameters govern the longitudinal dynamics, energy consumption, and regenerative behavior throughout the test scenarios.

To ensure realism, the selected values reflect the typical specifications of commercially available EVs in the C-segment. The mass, rolling resistance, aerodynamic drag, and road grade directly influence longitudinal forces in the dynamic model. Meanwhile, drivetrain-related parameters, such as gear ratio, motor inertia, and wheel inertia, affect acceleration response and torque transmission. Battery specifications determine the available energy, while the initial state of charge (SOC) defines the baseline for evaluating energy consumption and regenerative braking effectiveness.

These parameters are integrated into the vehicle’s longitudinal force balance and drivetrain efficiency models, forming the basis for simulating acceleration, deceleration, and power consumption under different traffic scenarios. The main vehicle parameters used in the simulation model are summarized in

Table 2. Main vehicle parameters used in the simulation environment.

Parameter	Value
Vehicle mass m (kg)	1650
Gravitational acceleration g (m/s2)	9.81
Tire rolling radius r (m)	0.353
Rolling resistance coefficient f	0.009
Frontal area $A_f$ (m2)	2.2
Air drag coefficient $C_d$	0.35
Air density $\rho$ (kg/m3)	1.206
Road grade $\theta$ (rad)	0
Final drive ratio $i_0$	8.47
Motor inertia $J_m$ (kg·m2)	0.08
Final drive inertia $J_{fd}$ (kg·m2)	0.001
Single wheel inertia $J_w$ (kg·m2)	1.4
Equivalent body rotational inertia $J_{eq}$ (kg·m2)	2.7
Initial battery SOC	0.8
Battery capacity (Ah)	60
Battery voltage (V)	380
Rated motor power (kW)	150
Maximum motor torque (N·m)	500

.

For baseline comparison, a classical PI controller is implemented with the control law:

$$a_{\mathrm{PI}}\left(t\right)=K_p·e_v\left(t\right)+K_i·{\int }_0^t{e}_v\left(\tau \right)d\tau ,$$

(23)

where $e_v\left(t\right)=v_{\mathrm{ref}}\left(t\right)-v_f\left(t\right)$ is the velocity tracking error. The gains were tuned using the Ziegler–Nichols method and fine-adjusted for stable tracking under the WLTC cycle. The final settings are $K_p=0.6$ and $K_i=0.4$.

4.2. Driving Scenario Setup

Table 3. Test scenarios for ACC performance evaluation.

Scenario	Duration ($\mathbf{s}$)	Initial Speed ($\mathbf{km}/\mathbf{h}$)	Initial Distance ($\mathbf{m}$)
WLTC Standard Cycle	500	0	5
Stop-and-Go	100	50	20
Lead Vehicle Departing	100	80	30
Steady Cruise Following	100	40	50
Cut-in Scenario	100	60	50
Emergency Braking	50	100	50

outlines six representative driving scenarios designed to rigorously examine the robustness and adaptability of the proposed controller. These scenarios span a spectrum of real-world conditions, including regulatory cycles, urban congestion, and critical emergency responses, each varying in urgency and dynamic complexity.

To comprehensively evaluate control performance across diverse traffic contexts, six representative driving scenarios are designed. The WLTC cycle represents standardized regulatory driving conditions involving frequent acceleration and deceleration and is used to assess overall tracking accuracy and energy efficiency across different dynamic phases. The stop-and-go scenario emulates congested urban traffic, testing the controller’s ability to maintain safety and comfort under frequent low-speed oscillations. The cut-in scenario introduces a sudden intrusion from a neighboring vehicle, examining the system’s emergency responsiveness and stability during abrupt spacing disruptions.

The lead vehicle departing test evaluates how promptly and smoothly the controller transitions from car-following to free-driving mode when the preceding vehicle accelerates away. The steady cruise following case assesses control precision and energy usage under relatively calm, steady-state conditions. Finally, the emergency braking scenario imposes a safety-critical deceleration event to test the controller’s capability to mitigate collision risk while ensuring comfort and compliance with physical constraints.

This comprehensive test set enables a balanced evaluation of the controller’s generalization ability, safety response, and energy-efficient performance across diverse longitudinal driving tasks.

5. Simulation-Based Performance Evaluation

5.1. Tracking and Robustness Analysis Under WLTC Conditions

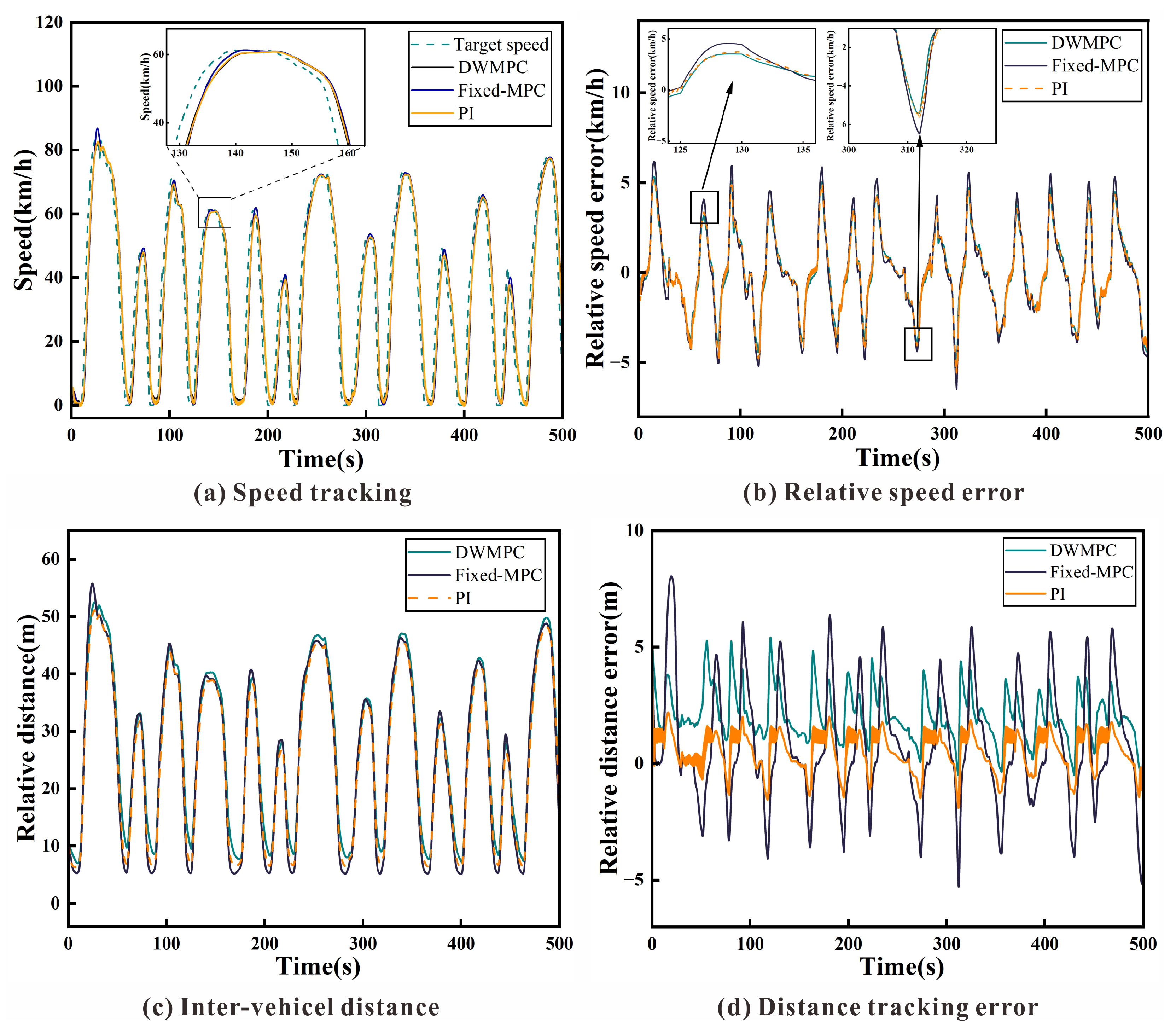
To assess the tracking performance and robustness of the proposed DWMPC strategy, simulations were conducted under the WLTC driving cycle, which features frequent acceleration, deceleration, and abrupt speed changes, challenging scenarios for longitudinal control.

As shown in Figure 5a,b, DWMPC achieves superior velocity tracking with rapid convergence and minimal steady-state error. The zoomed-in view in Figure 5a highlights its responsiveness to sharp speed changes without overshoot or delay. This is further supported by the relative velocity error in Figure 5b, where DWMPC maintains the narrowest error band and low-frequency oscillations, outperforming both fixed-MPC and PI controllers. These improvements are driven by the dynamic tuning of the velocity weight $C_1$, which increases during high-urgency situations to enhance response and decreases during steady states to ensure smooth control.

Compared to the fuzzy-MPC approach in [20], which relies on rule-based weight assignment, DWMPC achieves faster response and lower tracking errors by continuously adapting weights based on driving context.

In terms of spacing control, Figure 5c,d shows that DWMPC maintains a stable inter-vehicle distance with low fluctuation. Other controllers tend to over- or under-compensate, especially under high-frequency variations. The corresponding distance error plot (Figure 5d) shows that DWMPC consistently keeps the error close to zero with reduced amplitude. This robustness benefits from the coordinated adjustment of weights $C_2$ and $C_3$: $C_2$ increases in critical moments to enhance braking response, while a lower $C_3$ reduces the control penalty, enabling more decisive actions. These mechanisms allow DWMPC to balance safety and stability under dynamic driving conditions.

5.2. Comfort and Energy Analysis Under WLTC Conditions

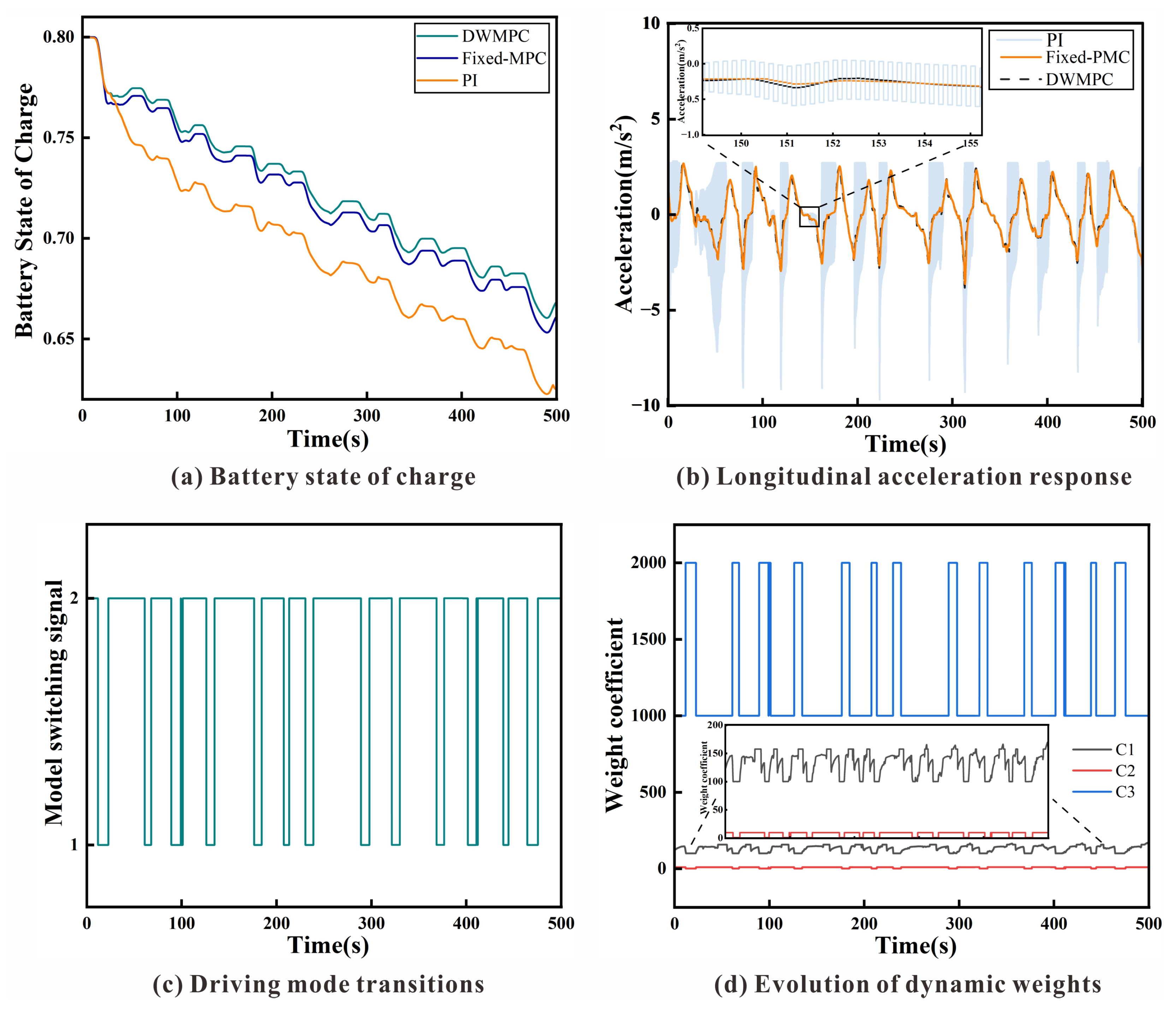
To evaluate the internal performance of different controllers, Figure 6 and

Table 4. Acceleration and jerk statistics of the three controllers.

Controller	Mean ($\mathbf{m}/{\mathbf{s}}^2$)	Std. Dev ($\mathbf{m}/{\mathbf{s}}^2$)	Min ($\mathbf{m}/{\mathbf{s}}^2$)	Max ($\mathbf{m}/{\mathbf{s}}^2$)	Jerk ($\mathbf{m}/{\mathbf{s}}^3$)
DWMPC	0.40	1.12	−3.84	2.68	2.81
Fixed-MPC	0.42	1.16	−3.64	2.68	3.12
PID	0.77	2.10	−9.68	2.78	4.92

present a detailed comparison in terms of energy consumption, acceleration behavior, and adaptive control activity under WLTC conditions.

A key advantage of DWMPC lies in energy efficiency. As shown in Figure 6a, it consistently maintains a higher battery state-of-charge (SOC) than both Fixed-MPC and PI throughout the cycle. By the end of the drive, its SOC level is approximately 6.5% higher than fixed-MPC and 12.1% higher than PI. This improvement stems not from passivity but from the controller’s ability to anticipate dynamic demands and avoid unnecessary high-power events under stable conditions.

Equally important is its contribution to ride comfort. Figure 6b shows that DWMPC produces a smoother acceleration trajectory with fewer spikes and oscillations. In contrast, the PI controller frequently exhibits abrupt transitions, while fixed-MPC displays delayed responses during transients. DWMPC not only suppresses these behaviors but also keeps acceleration values tightly clustered around zero. Its acceleration distribution confirms this: most values lie within $\pm 2.5$ m/s², indicating enhanced stability and control balance.

These observations are supported by the numerical results in Table 4. DWMPC achieves the lowest standard deviation in acceleration (1.12 m/s²) and the smallest average jerk (2.81 m/s³), significantly outperforming the alternatives. Lower jerk indicates fewer abrupt control changes, contributing to improved comfort, reduced mechanical wear, and greater drivetrain durability.

Furthermore, the mean acceleration under DWMPC stabilizes around 0.40 m/s², reflecting a well-balanced response without persistent bias toward acceleration or braking. Its acceleration extremes range from $-3.84$ m/s² to $2.68$ m/s², markedly narrower than those of the PI controller, which range from $-9.68$ m/s² to $2.78$ m/s². This reduced range suggests that DWMPC effectively avoids excessive braking or acceleration, resulting in smoother and more predictable behavior.

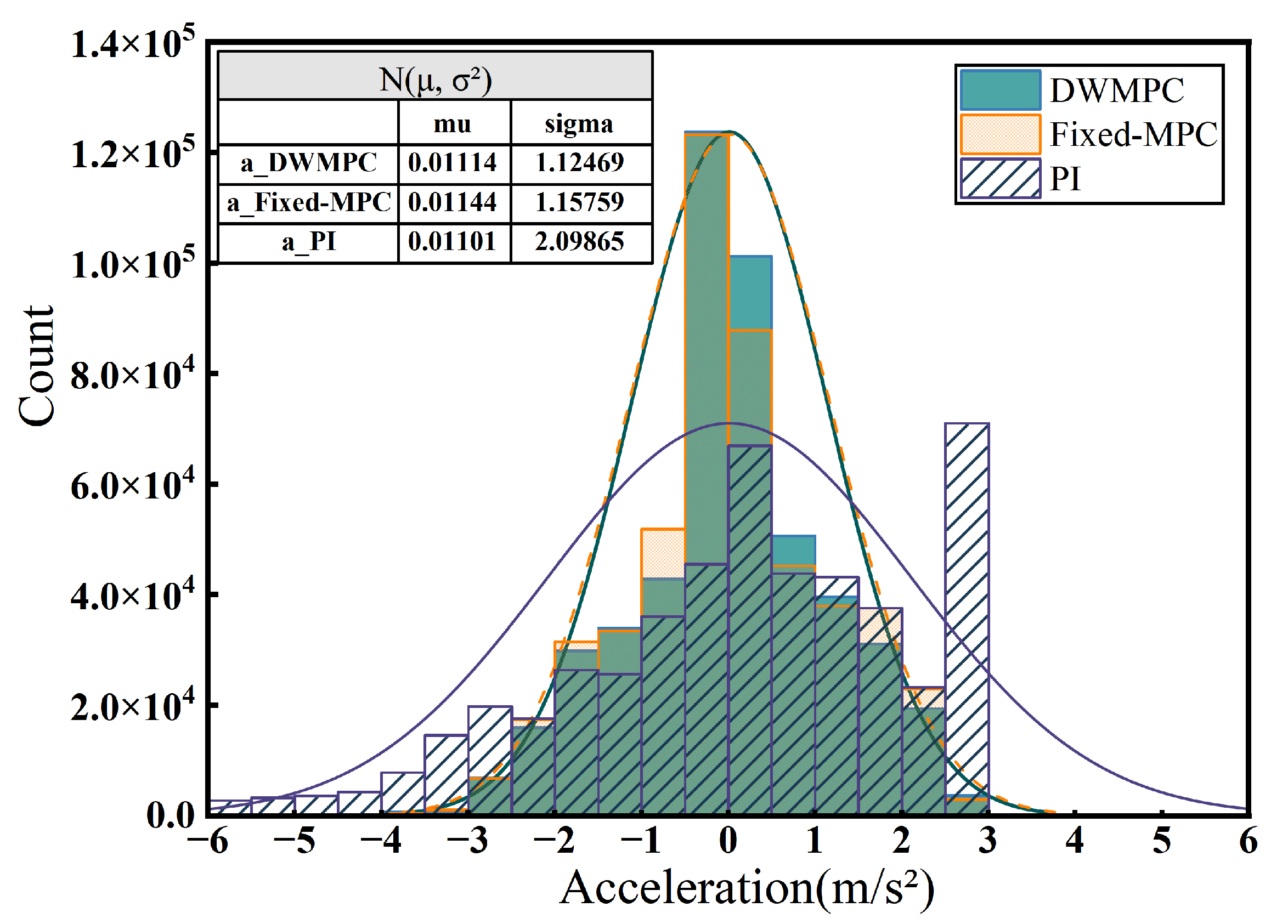
The statistical distribution shown in Figure 7 further supports these findings. Compared with the broader, asymmetric distributions of PI and fixed-MPC, the acceleration histogram of DWMPC is compact and symmetric around zero. Most values fall within $\pm 2.5$ m/s², indicating tighter control modulation. The overlaid Gaussian curves visually confirm this trend, and the embedded table summarizes the key statistics: DWMPC exhibits the lowest standard deviation and highest probability density near zero, reflecting smoother actuator dynamics.

Underlying these improvements is DWMPC’s internal adaptive coordination. As shown in Figure 6c, the controller actively switches modes based on real-time traffic risk, quantified by the fuzzy-derived emergency coefficient. These transitions occur precisely during high-demand periods, such as sharp acceleration or emergency braking.

This behavior is governed by the control logic in Section 3.2, where Equation (21) defines the nonlinear exponential mapping of the emergency coefficient to the velocity tracking weight $C_1$, enhancing responsiveness under critical conditions. Table 1 specifies the mode-switching mechanism based on threshold segmentation of the emergency coefficient, enabling smooth and situation-adaptive coordination of acceleration and jerk penalties.

Correspondingly, Figure 6d illustrates the dynamic adjustment of internal weights. The velocity tracking weight $C_1$ increases sharply during critical phases to enhance responsiveness, while acceleration ($C_2$) and jerk ($C_3$) penalties are relaxed to permit decisive control actions. As the situation stabilizes, the weights gradually return to promote comfort and efficiency.

In summary, DWMPC excels not only in static performance but also through a self-regulating, risk-aware control architecture. By continuously sensing traffic context and adjusting control priorities in real time, it maintains a robust balance among energy economy, ride comfort, and safety responsiveness, surpassing the limitations of fixed-weight strategies.

Compared with the recent fuzzy-MPC-based strategy [20], which demonstrated energy-saving capabilities, the proposed DWMPC achieves similar efficiency while further enhancing control coordination through dynamic mode switching and jerk-adaptive weight adjustment under complex transient scenarios.

5.3. Multi-Objective Quantitative Indicator Comparison

To systematically evaluate the control performance across key objectives, four standardized evaluation metrics are defined, using fixed-MPC as the baseline. These cost-type indicators are designed such that lower values indicate better performance.

The energy consumption ratio reflects the efficiency of energy usage:

$${\displaystyle \frac{E}{E_{\mathrm{ref}}}}={\displaystyle \frac{E_{\mathrm{ctrl}}}{E_{\mathrm{ref}}}}.$$

(24)

The jerk-based comfort index evaluates ride comfort based on the average longitudinal jerk:

$${\displaystyle \frac{J}{J_{\mathrm{ref}}}}={\displaystyle \frac{J_{\mathrm{ctrl}}}{J_{\mathrm{ref}}}}.$$

(25)

The following distance error ratio quantifies the accuracy in spacing control:

$${\displaystyle \frac{FDE}{FD{E}_{\mathrm{ref}}}}={\displaystyle \frac{FD{E}_{\mathrm{ctrl}}}{FD{E}_{\mathrm{ref}}}}.$$

(26)

The response time ratio measures the speed at which the controller responds to sudden events:

$${\displaystyle \frac{RT}{R{T}_{\mathrm{ref}}}}={\displaystyle \frac{R{T}_{\mathrm{ctrl}}}{R{T}_{\mathrm{ref}}}}$$

(27)

An overall composite score, referred to as the performance evaluation index (PEI), is computed as the arithmetic mean of the four normalized metrics:

$$\mathit{PEI}={\displaystyle \frac{1}{4}}\left({\displaystyle \frac{E}{E_{\mathrm{ref}}}}+{\displaystyle \frac{J}{J_{\mathrm{ref}}}}+{\displaystyle \frac{FDE}{FD{E}_{\mathrm{ref}}}}+{\displaystyle \frac{RT}{R{T}_{\mathrm{ref}}}}\right).$$

(28)

Table 5. Normalized performance metrics and overall performance evaluation index (PEI).

Controller	$\frac{\mathit{E}}{{\mathit{E}}_{\mathbf{ref}}}$	$\frac{\mathit{J}}{{\mathit{J}}_{\mathbf{ref}}}$	$\frac{\mathbf{FDE}}{{\mathbf{FDE}}_{\mathbf{ref}}}$	$\frac{\mathbf{RT}}{{\mathbf{RT}}_{\mathbf{ref}}}$	PEI
DWMPC	0.985	0.571	0.660	0.582	0.700
Fixed-MPC	1.000	0.634	1.000	1.000	0.909
PID	1.030	1.000	1.260	0.873	1.041

summarizes the indicator values for each controller. Among them, DWMPC achieves the lowest values in energy consumption (0.985) and jerk (0.571), indicating high efficiency and comfort. It also excels in tracking precision ($FDE=0.660$) and emergency response time ($RT=0.582$), outperforming both fixed-MPC and PI across all dimensions.

As a result, DWMPC attains the lowest composite performance evaluation index (PEI = 0.700), showing a 22.9% improvement over fixed-MPC (PEI = 0.909) and a 32.8% gain over PI (PEI = 1.041). These improvements stem from its dynamic weighting strategy, which enables the controller to continuously prioritize the most critical objective depending on real-time driving conditions.

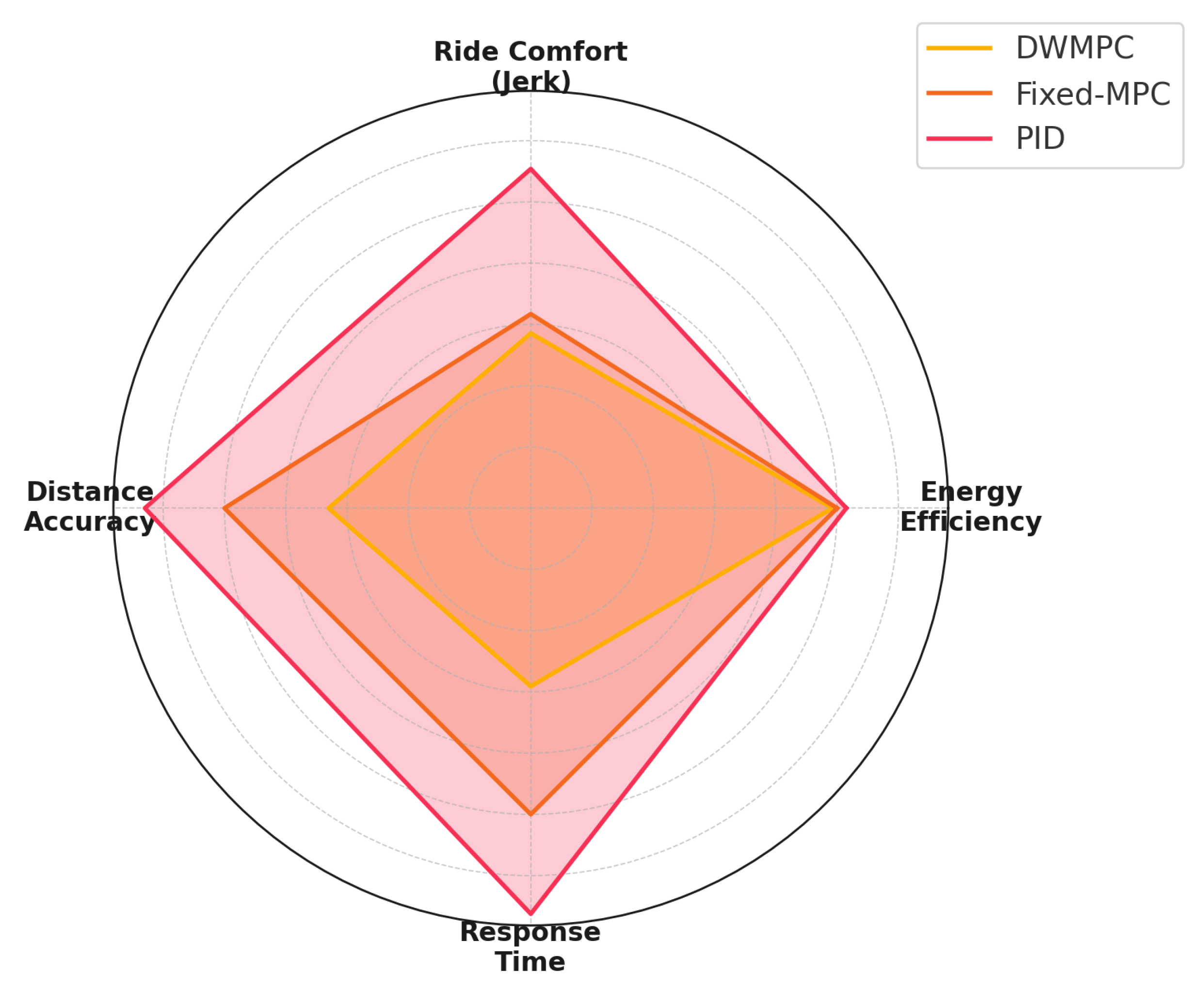
This comparative performance is further visualized in Figure 8, where each axis represents one evaluation dimension. The radar plot reveals that DWMPC encloses the smallest performance region, implying the most balanced and efficient trade-off among energy efficiency, comfort, tracking accuracy, and responsiveness. In contrast, PI forms the widest area, suggesting significant compromise in multiple objectives.

5.4. Performance Under Representative Driving Scenarios

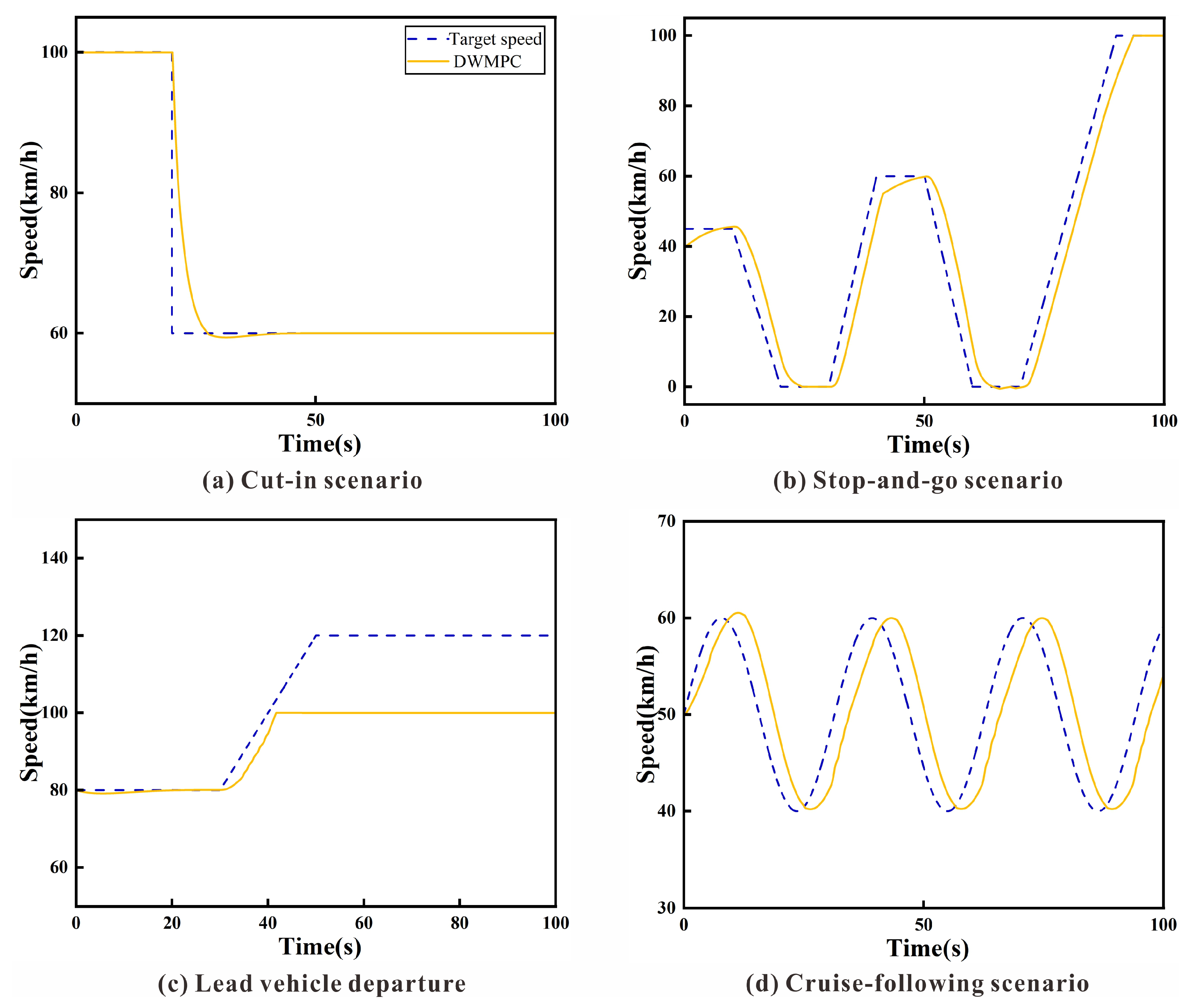
To complement the WLTC-based evaluation, four typical driving scenarios are designed to further validate the control effectiveness of DWMPC in diverse and challenging conditions. These scenarios include a sudden cut-in event, stop-and-go traffic, lead vehicle departure, and steady-state following. Each case isolates a key dynamic pattern to test specific aspects of controller behavior.

As shown in Figure 9, the DWMPC controller responds effectively in all scenarios. In the cut-in case (Figure 9a), the controller initiates timely deceleration to maintain a safe distance without abrupt braking, achieving a smooth transition. During stop-and-go conditions (Figure 9b), it handles frequent acceleration and deceleration smoothly, minimizing overshoot and undershoot.

In the lead vehicle departure case (Figure 9c), DWMPC smoothly increases speed and stabilizes at the predefined cruise speed of 100 km/h, indicating effective recognition of reduced urgency and efficient mode switching. In the cruise-following scenario (Figure 9d), the controller maintains consistent spacing with low tracking error, demonstrating precise velocity and distance control under low dynamic variation.

These scenario-based results further highlight the adaptive intelligence of DWMPC. By dynamically adjusting control weights in response to varying traffic contexts, the controller demonstrates an inherent ability to balance responsiveness, comfort, and safety, without requiring manual mode switching. This context-aware adaptability not only ensures robust performance in transient and steady-state conditions but also paves the way for scalable integration into more complex, real-world autonomous driving systems.

5.5. Emergency Braking Scenario Analysis

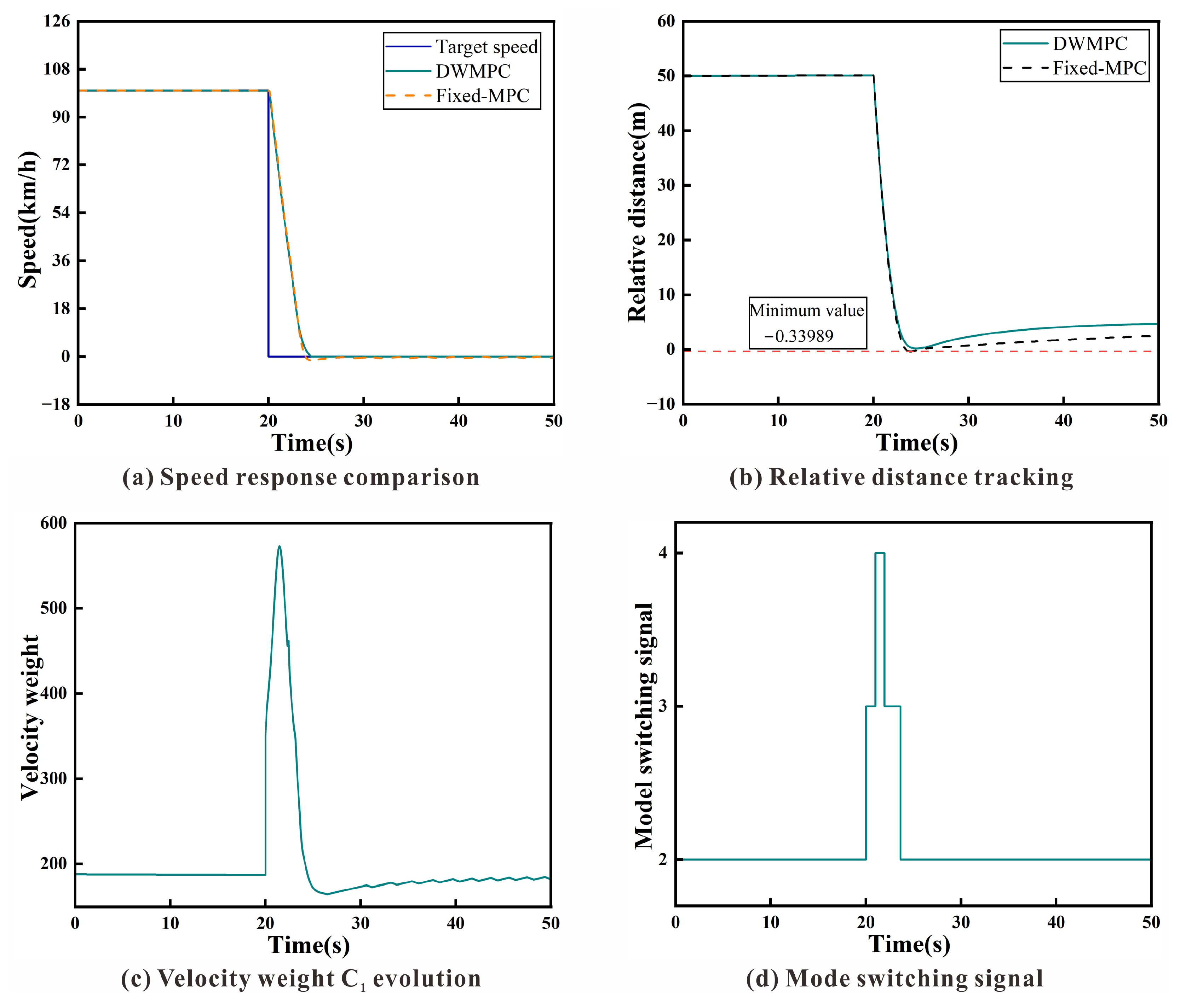
In order to further assess the controller’s robustness in safety-critical situations, a sudden emergency braking scenario was introduced, simulating a lead vehicle deceleration to a complete stop at 20 s. This test isolates a high-risk event to examine not only tracking accuracy but also responsiveness and safety margins under time-sensitive conditions.

As depicted in Figure 10a, both controllers manage to follow the deceleration profile; however, DWMPC exhibits a noticeably faster reaction time, initiating braking earlier and reducing velocity lag. This enhanced responsiveness is reflected in the spacing trajectory shown in Figure 10b, where fixed-MPC briefly violates the safe following distance with a minimum headway of $-0.34\mathrm{m}$, whereas DWMPC consistently maintains a positive gap, effectively avoiding collision risk.

The underlying mechanism is revealed in Figure 10c, where the dynamic weight coefficient $C_1$ spikes sharply upon detecting the threat, reaching values above 600. This surge temporarily increases the weight on velocity tracking, thereby intensifying deceleration behavior. As the critical phase passes, $C_1$ gradually returns to nominal levels, preventing aggressive control oscillations.

Figure 10d further illustrates the control mode transition, where DWMPC swiftly shifts from economic mode (Mode 2) to more urgent states (Modes 3 and 4), thereby relaxing acceleration constraints and allowing decisive braking. After the threat is mitigated, the controller seamlessly reverts to less aggressive operation, preserving comfort and energy efficiency.

Overall, this scenario highlights a key advantage of the proposed strategy: DWMPC not only ensures rapid and stable emergency response through its adaptive weighting and mode-switching mechanisms but also preserves post-event drivability, demonstrating an intelligent and risk-aware control architecture suitable for real-world safety challenges.

6. Discussion and Conclusions

This study presents a dynamic weight model predictive control (DWMPC) strategy for adaptive cruise control (ACC) in electric vehicles, aimed at real-time optimization of tracking accuracy, safety, energy efficiency, and comfort. The core innovation lies in the integration of fuzzy logic with a four-mode switching mechanism, enabling context-aware adjustment of MPC weights. Simulations under WLTC and urban scenarios confirm that DWMPC consistently outperforms fixed-weight MPC and PI controllers in both control precision and comfort.

Simulations confirm that DWMPC significantly reduces velocity tracking errors and mitigates abrupt acceleration changes during critical events such as emergency braking and stop-and-go traffic. Its dynamic weighting mechanism enables real-time prioritization among competing objectives, striking a flexible balance between safety and energy efficiency, which is an essential requirement for intelligent electric vehicle deployment.

A key strength of the proposed approach is its interpretability. The fuzzy-evaluated emergency coefficient offers an interpretable mechanism for adjusting control sensitivity, enhancing reliability compared to black-box models in safety-critical contexts. The four-mode structure also promotes modularity and scalability, facilitating integration with high-level planning or cooperative driving frameworks.

Nevertheless, some limitations remain. The fuzzy rule base and emergency thresholds depend on expert knowledge and may require re-tuning for different vehicle platforms. While simulation results confirm real-time feasibility, practical implementation on embedded systems must account for computational load, sensor noise, and actuator delays. Radar and camera-based relative measurements are susceptible to environmental interference, occlusion, and sensor drift, potentially compromising control performance.

To mitigate these issues, signal processing techniques such as Kalman or complementary filtering can be adopted to improve perception robustness. Lightweight QP solvers (e.g., OSQP and qpOASES) with warm-start techniques can further reduce computation time and facilitate real-time deployment on embedded hardware. These improvements will be explored in future research to enhance robustness and practical applicability.

From a control system design standpoint, this work highlights the effectiveness of scenario-adaptive weight adjustment for multi-objective optimization. The proposed metrics and architecture provide a reusable template for interpretable and flexible ACC design. For policymakers and practitioners, the interpretable structure and real-time feasibility of the proposed control strategy provide a practical foundation for deploying safety-compliant ACC systems under future regulatory frameworks.

Future work will extend the framework using reinforcement learning and neural networks to replace static fuzzy mappings with data-driven, self-adaptive mechanisms. To preserve interpretability, hybrid structures that combine rule-based reasoning with learning will be prioritized. Hardware-in-the-loop and real-vehicle testing will also be conducted to assess system robustness under real-world uncertainties such as sensor noise, modeling errors, and actuation constraints, ultimately bridging the gap between simulation and real-world deployment in safety-critical intelligent driving applications.