Geant4 Simulations of a Scintillator Cosmic-Ray Detector
Abstract
1. Introduction
2. Geant4 Software
2.1. Detector Geometry and Composition
3. Estimation of Sensitivity
3.1. Calculation of Signal’s Amplitude
- In the end, the amplitude of the produced signal is calculated using the following formula [19]:
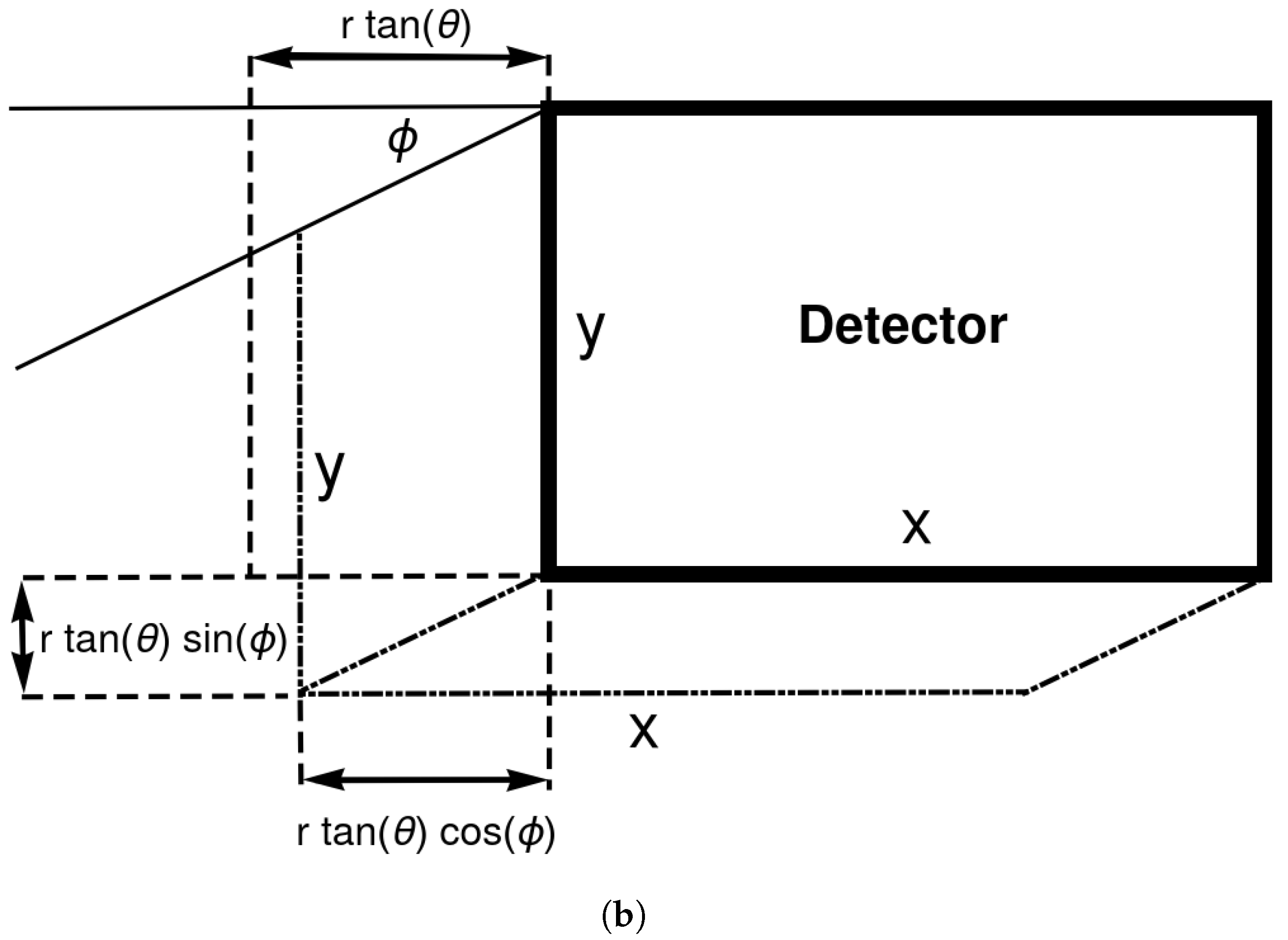
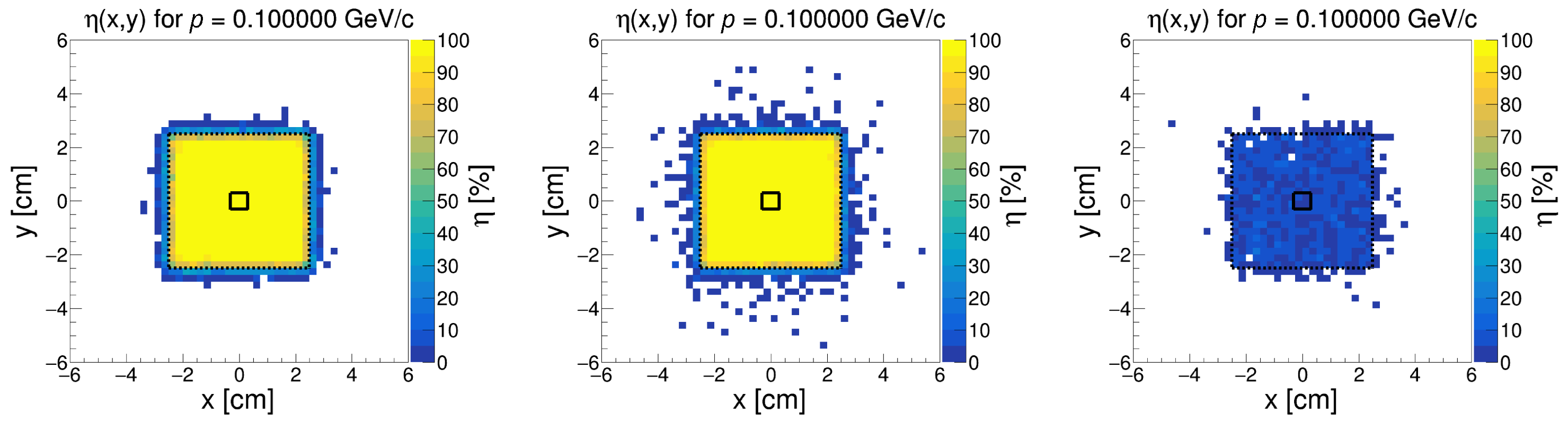
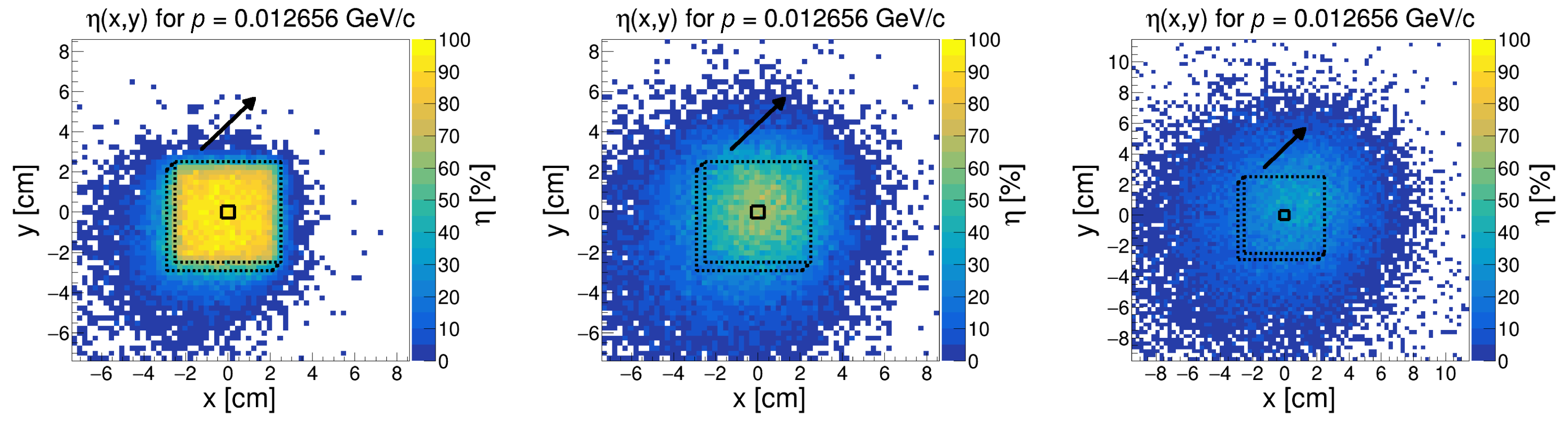
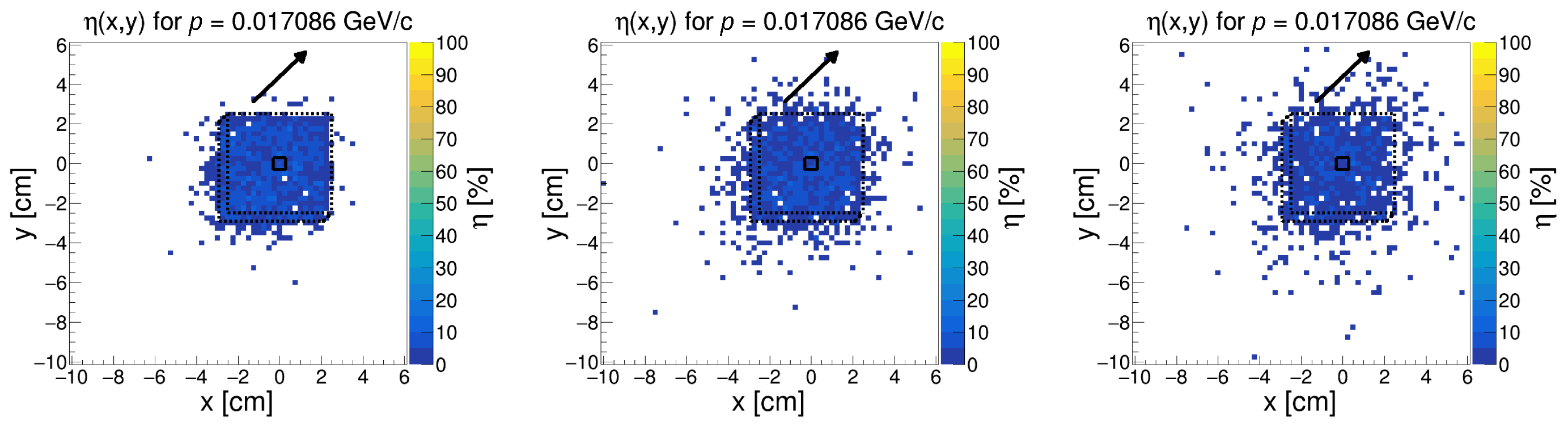
3.2. Mapping Detector
4. Results
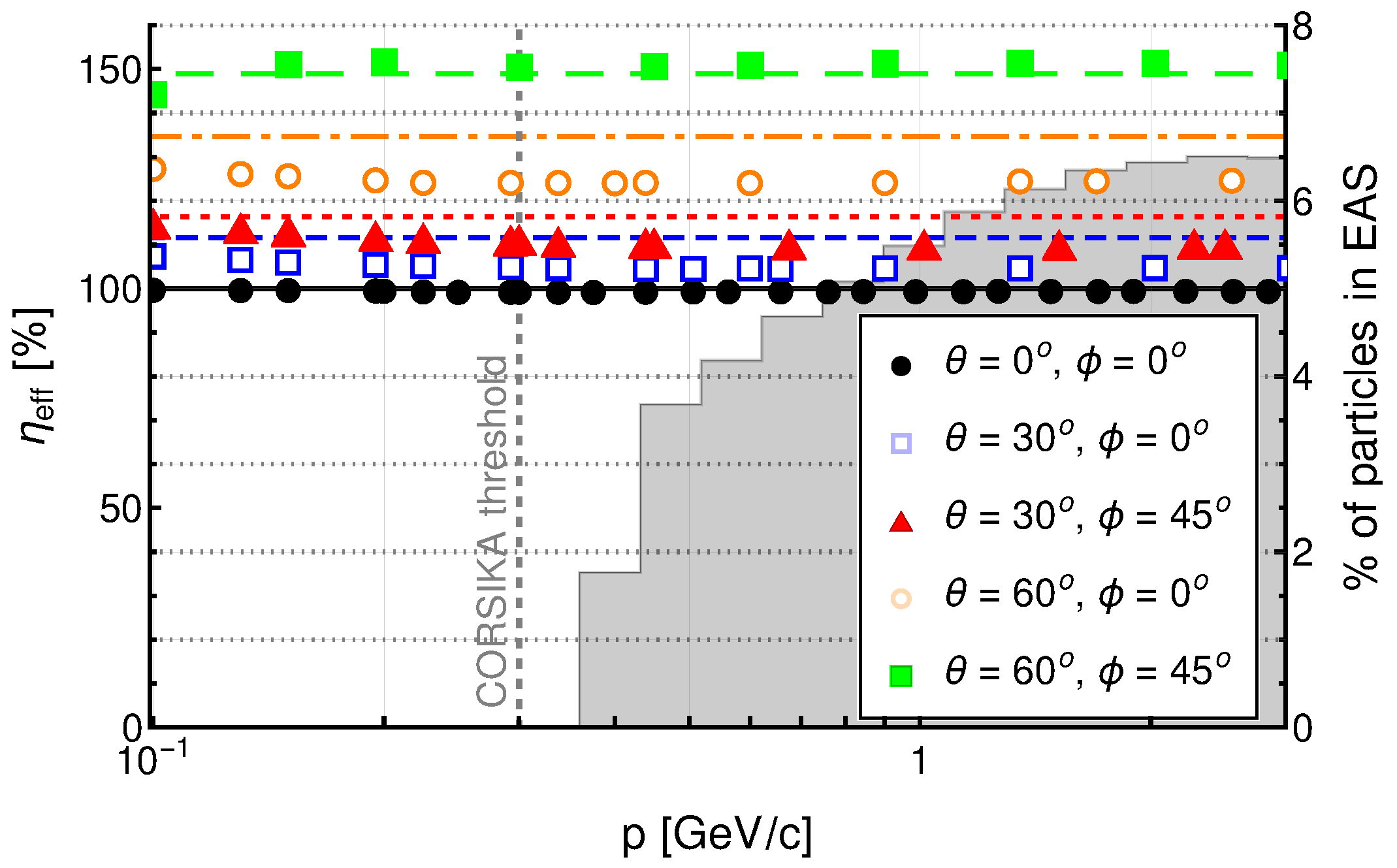
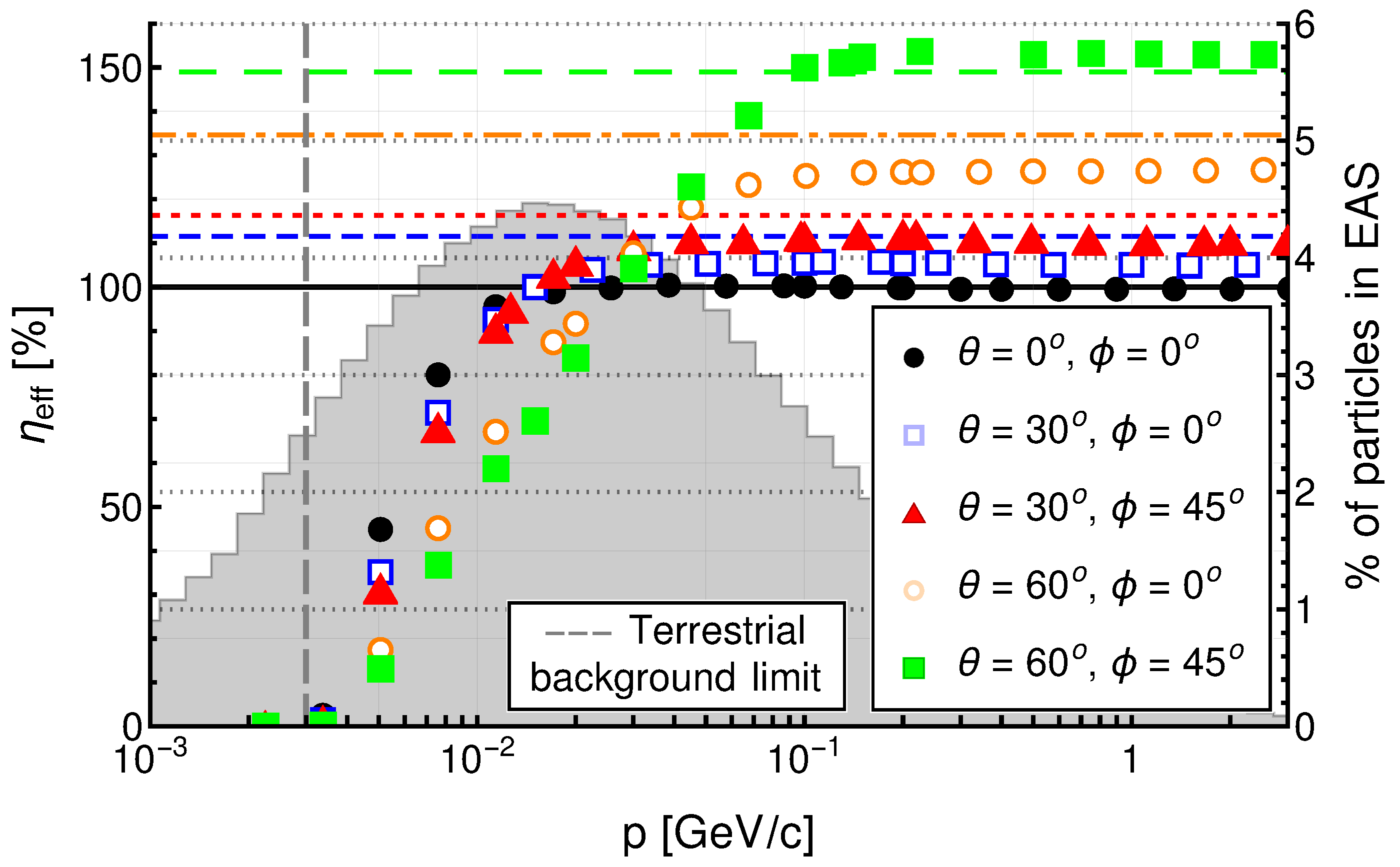
4.1. Muons
4.2. Electrons
4.3. Photons
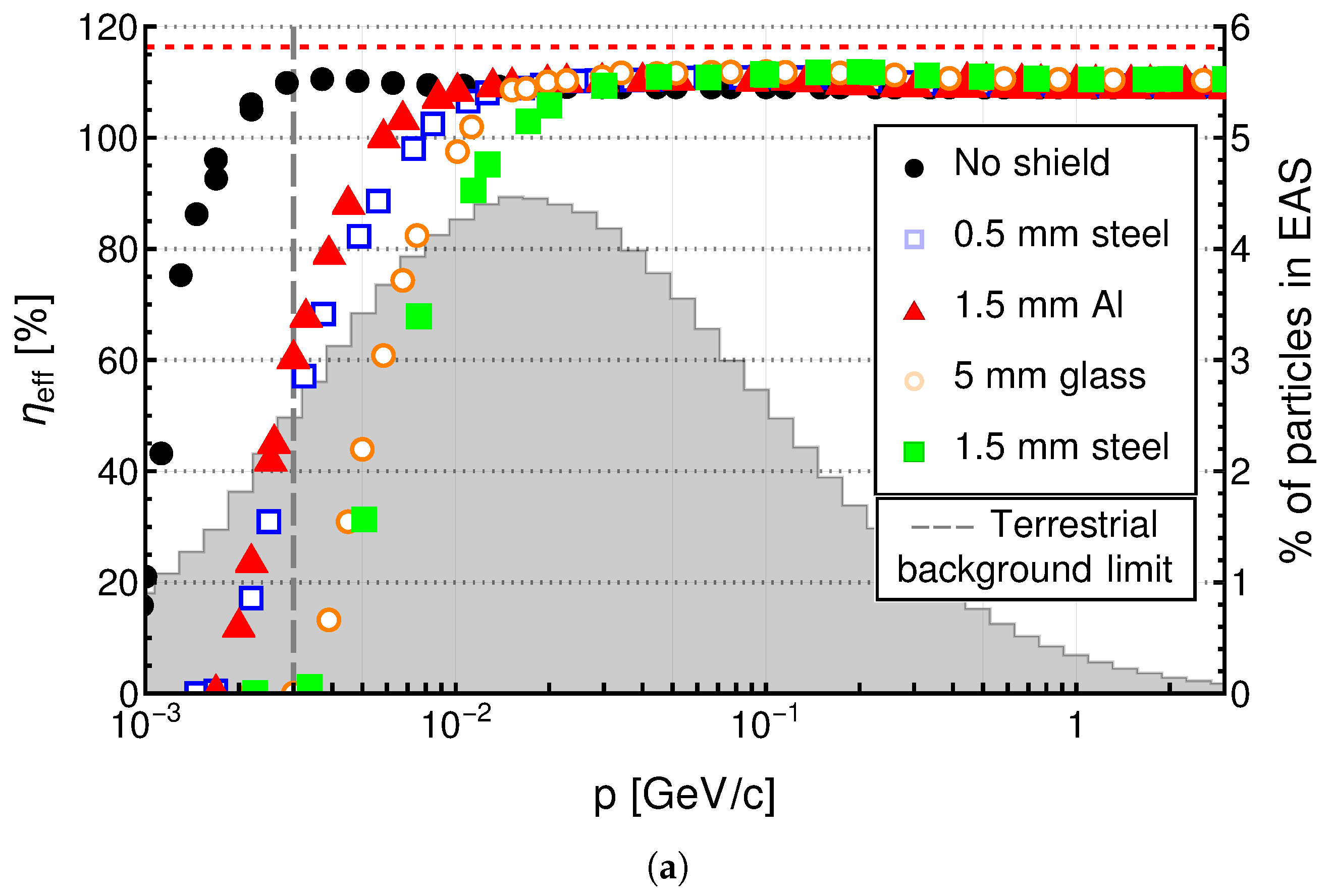
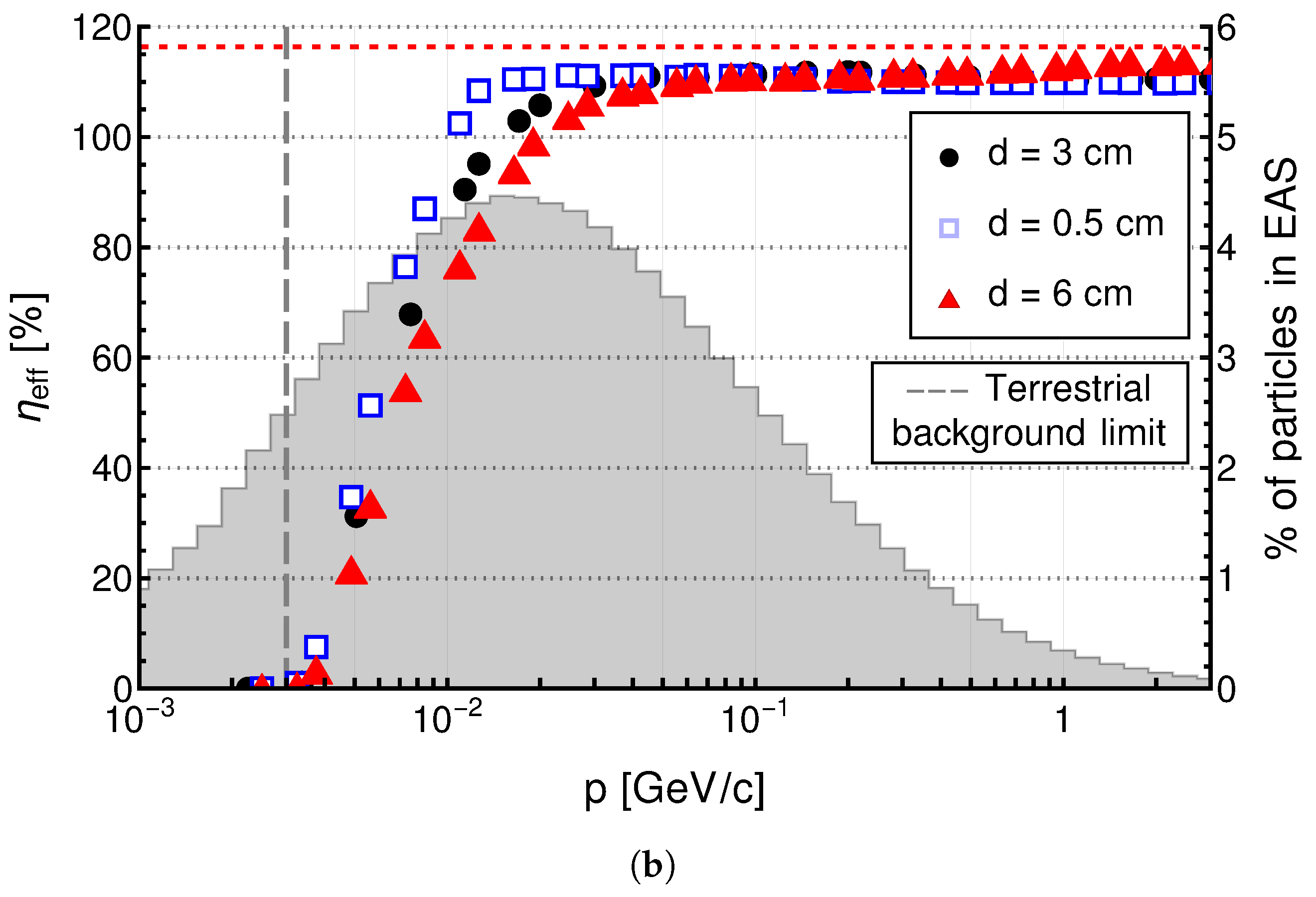
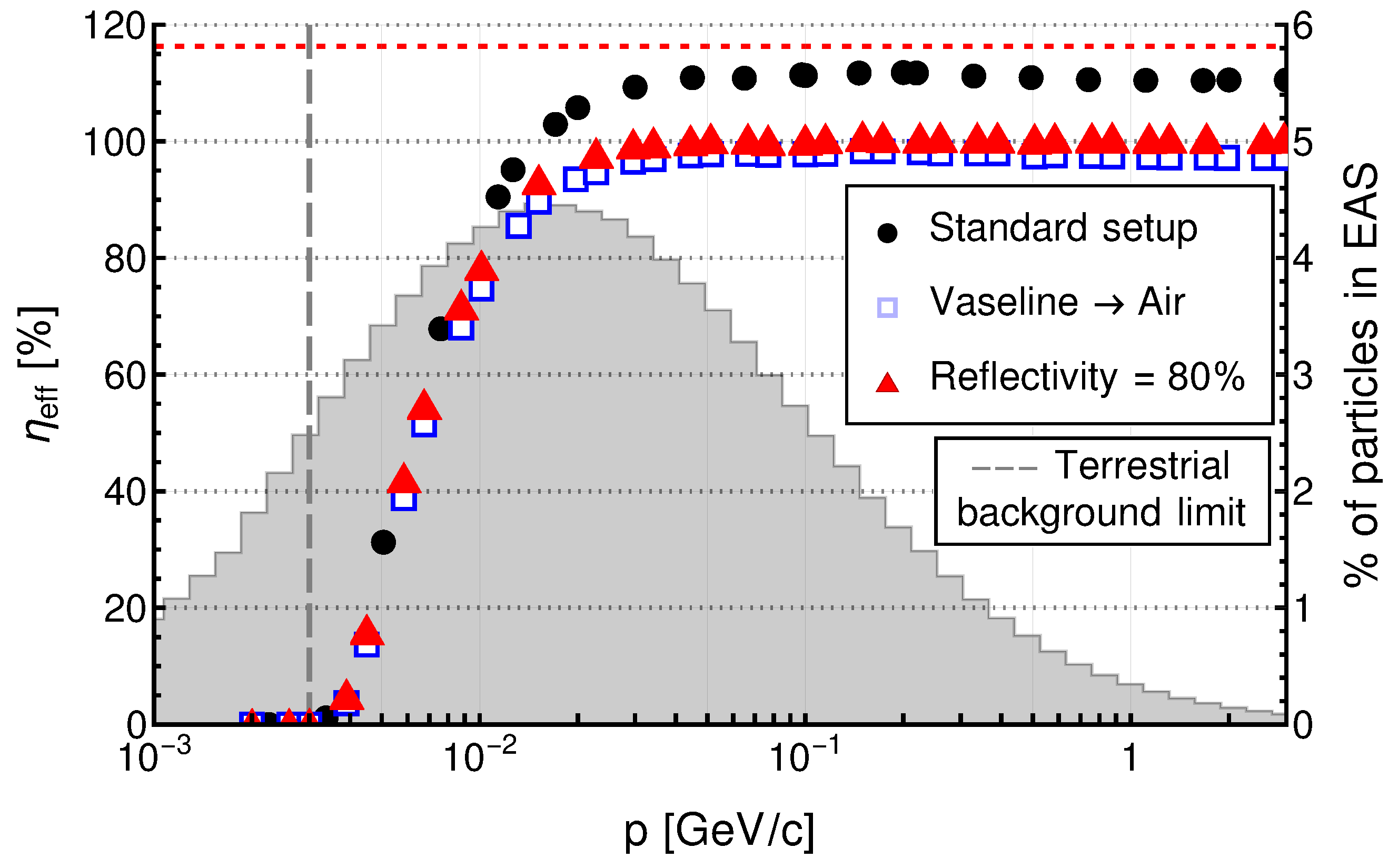
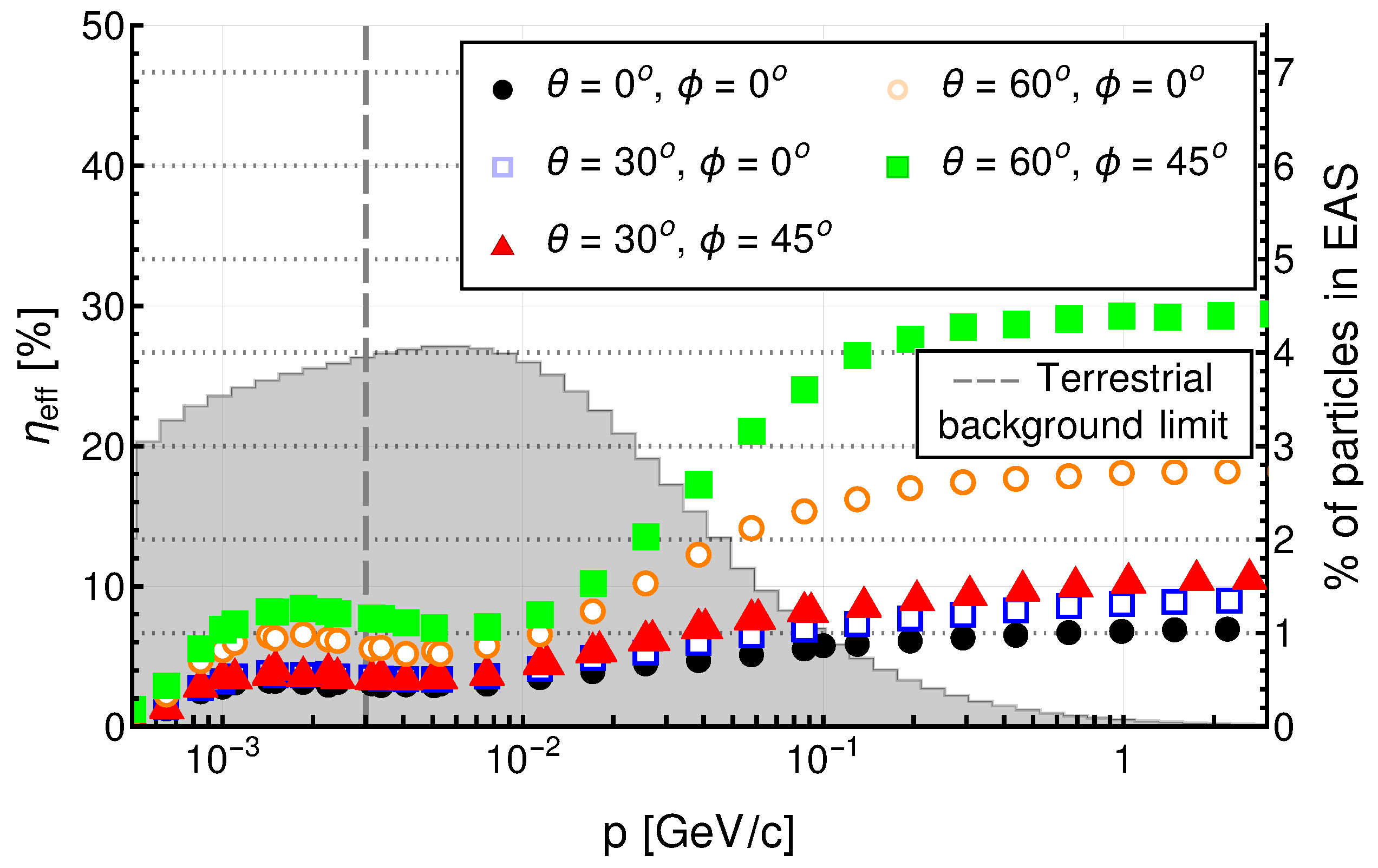
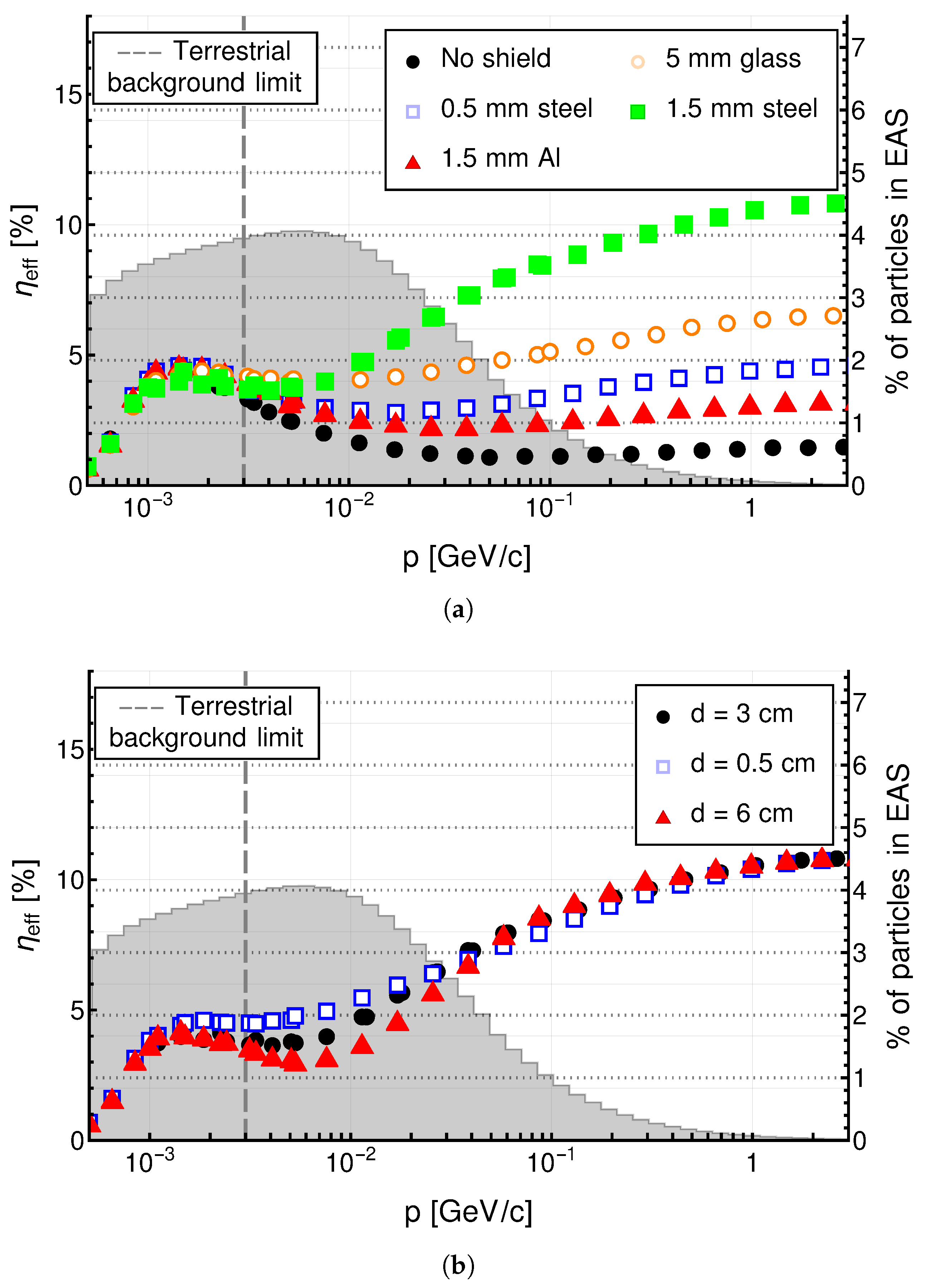
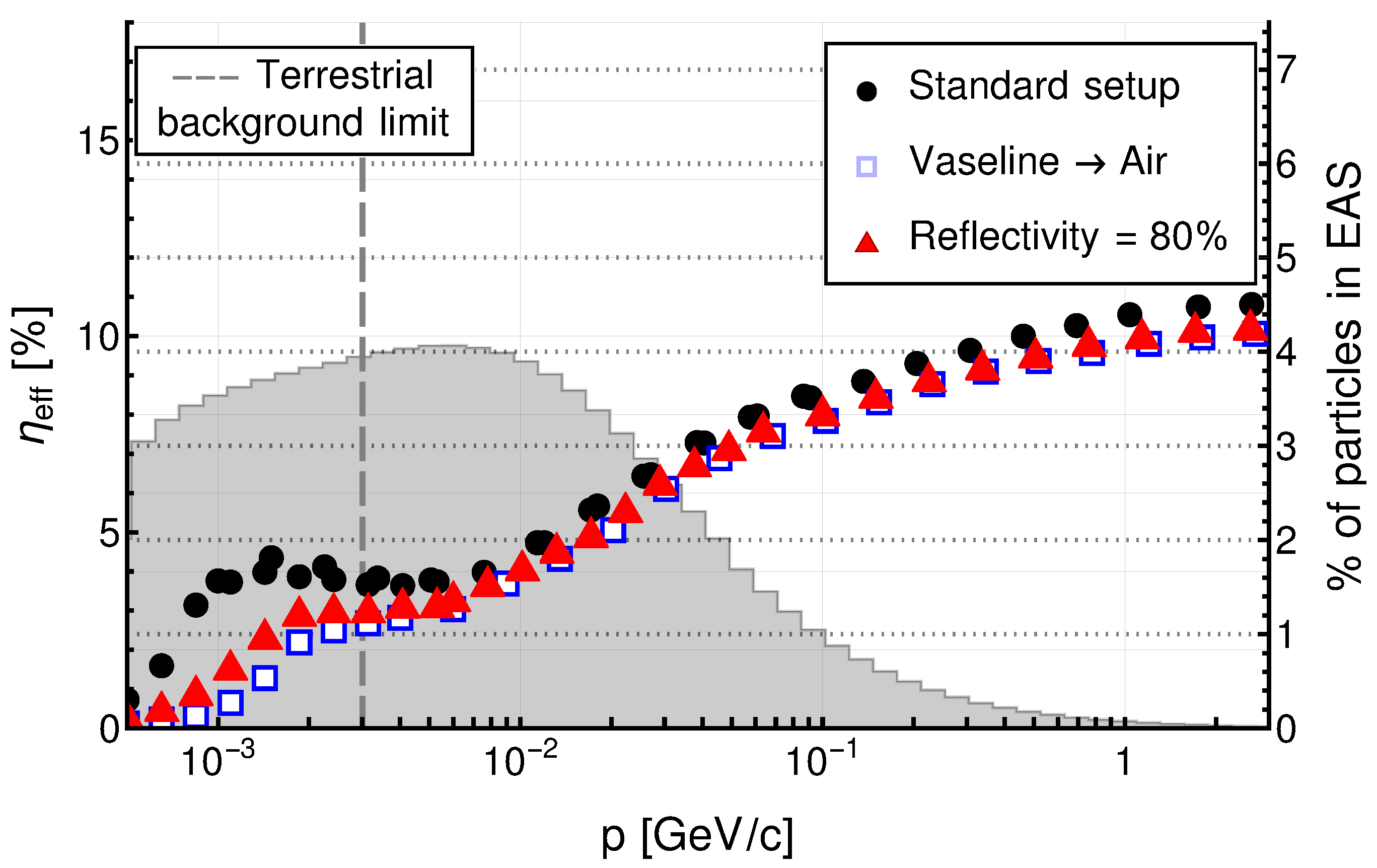
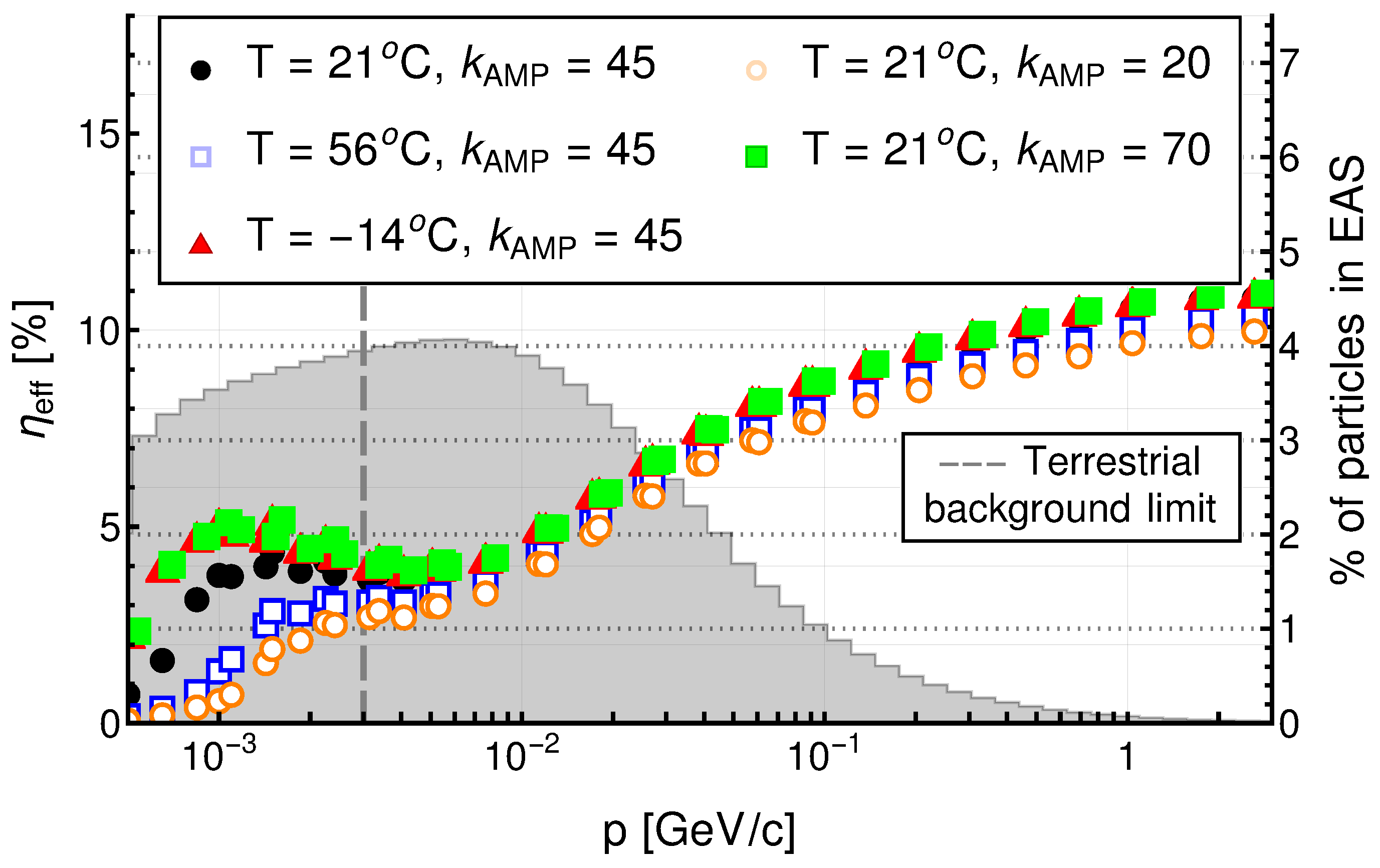
4.4. External Factors
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CREDO | Cosmic Ray Extremely Distributed Observatory |
| CR | Cosmic ray |
| EAS | Extensive Air Shower |
| SiPM | Silicon Photomultiplier |
References
- Allekotte, I.; Barbosa, A.; Bauleo, P.; Bonifazi, C.; Civit, B.; Escobar, C.; García, B.; Guedes, G.; Berisso, M.; Harton, J.; et al. The surface detector system of the Pierre Auger Observatory. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2008, 2008586, 409–420. [Google Scholar] [CrossRef]
- Abu-Zayyad, T.; Aida, R.; Allen, M.; Anderson, R.; Azuma, R.; Barcikowski, E.; Belz, J.; Bergman, D.; Blake, S.; Cady, R.; et al. The cosmic-ray energy spectrum observed with the surface detector of the telescope array experiment. Astrophys. J. Lett. 2013, 768, L1. [Google Scholar] [CrossRef]
- Zhen, C.; Ming-Jun, C.; Song-Zhan, C.; Hong-Bo, H.; Cheng, L.; Ye, L.; Ling-Ling, M.; Xin-Hua, M.; Xiang-Dong, S.; Han-Rong, W.; et al. Introduction to large high altitude air shower observatory (LHAASO). Chin. Astron. Astrophys. 2019, 43, 457–478. [Google Scholar] [CrossRef]
- Dhital, N.; Homola, P.; Alvarez-Castillo, D.; Góra, D.; Wilczyński, H.; Cheminant, K.; Poncyljusz, B.; Mędrala, J.; Opiła, G.; Bhatt, A.; et al. Cosmic ray ensembles as signatures of ultra-high energy photons interacting with the solar magnetic field. J. Cosmol. Astropart. Phys. 2022, 2022, 038. [Google Scholar] [CrossRef]
- Fegan, D.; McBreen, B.; O’Sullivan, C. Observation of a burst of cosmic rays at energies above 7 × 1013 eV. Phys. Rev. Lett. 1983, 51, 2341. [Google Scholar] [CrossRef]
- Homola, P.; Beznosko, D.; Bhatta, G.; Bibrzycki, Ł.; Borczyńska, M.; Bratek, Ł.; Budnev, N.; Burakowski, D.; Alvarez-Castillo, D.E.; Cheminant, K.A.; et al. Cosmic-ray extremely distributed observatory. Symmetry 2020, 12, 1835. [Google Scholar] [CrossRef]
- Karbowiak, M.; Wibig, T.; Alvarez-Castillo, D.; Beznosko, D.; Duffy, A.R.; Góra, D.; Homola, P.; Kasztelan, M.; Niedźwiecki, M. The first credo registration of extensive air shower. Phys. Educ. 2020, 55, 055021. [Google Scholar] [CrossRef]
- Clay, R.; Singh, J.; Homola, P.; Bar, O.; Beznosko, D.; Bhatt, A.; Bhatta, G.; Bibrzycki, Ł.; Budnev, N.; Alvarez-Castillo, D.E.; et al. A search for cosmic ray bursts at 0.1 pev with a small air shower array. Symmetry 2022, 14, 501. [Google Scholar] [CrossRef]
- Axani, S.; Frankiewicz, K.; Conrad, J. Cosmicwatch: The desktop muon detector. J. Instrum. 2018, 13, 03. [Google Scholar] [CrossRef]
- Ros, G.; Sáez-Cano, G.; Medina-Tanco, G.; Supanitsky, A. On the design of experiments based on plastic scintillators using GEANT4 simulations. Radiat. Phys. Chem. 2018, 153, 140–151. [Google Scholar] [CrossRef]
- Min, S.; Kim, Y.; Ko, K.; Seo, B.; Cheong, J.; Roh, C.; Hong, S. Optimization of plastic scintillator for detection of gamma-rays: Simulation and experimental study. Chemosensors 2021, 9, 239. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Dubois, P.A.; Asai, M.; Barrand, G.; Capra, R.; Chauvie, S.; Chytracek, R.; et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 2006, 53, 270–278. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.a.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—a simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; et al. Recent developments in geant4. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Brun, R.; Rademakers, F. Root—an object oriented data analysis framework. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 1997, 389, 81–86. [Google Scholar] [CrossRef]
- Caravaca, J.; Descamps, F.; Land, B.J.; Wallig, J.; Yeh, M.; Orebi Gann, G. Experiment to demonstrate separation of Cherenkov and scintillation signals. Phys. Rev. C 2017, 95, 055801. [Google Scholar] [CrossRef]
- Polyanskiy, M.N. Refractiveindex.info database of optical constants. Sci. Data 2024, 11, 94. [Google Scholar] [CrossRef] [PubMed]
- Riggi, S.; Rocca, P.L.; Leonora, E.; Presti, D.L.; Pappalardo, G.; Riggi, F.; Russo, G. Geant4 simulation of plastic scintillator strips with embedded optical fibers for a prototype of tomographic system. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2010, 624, 583–590. [Google Scholar] [CrossRef]
- Introduction to the Silicon Photomultiplier (SiPM), AND9770/D Rev. 9, ON Semiconductor Corporation (Onsemi), July 2023. Available online: https://www.onsemi.com/download/application-notes/pdf/and9770-d.pdf (accessed on 10 May 2025).
- Rogalski, A.; Bielecki, Z.; Mikolajczyk, J. Detection of optical radiation. Bull. Pol. Acad. Sci. Tech. Sci. 2004, 52, 65–124. Available online: https://journals.pan.pl/Content/111805/PDF/%2852-1%2943.pdf (accessed on 10 May 2025).
- Simhony, Y.; Segal, A.; Orlov, Y.; Amrani, O.; Etzion, E. Scintillator-sipm detector for tracking and energy deposition measurements. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2024, 1069, 169955. [Google Scholar] [CrossRef]
- Heck, D.; Knapp, J.; Capdevielle, J.N.; Schatz, G.; Thouw, T. CORSIKA: A Monte Carlo code to simulate extensive air showers. FZKA 6019 1998, 6019, 11. [Google Scholar]
- Radomir, B.; Dimitrije, M.; Dejan, J.; Nikola, V.; Aleksandar, D.; Vladimir, U.; Ivan, A. On the omnipresent background gamma radiation of the continuous spectrum. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2014, 749, 7–11. [Google Scholar] [CrossRef][Green Version]
- Fallu-Labruyere, A.; Geryes, T.; Ravera, C.; Jeanjacquot, N. Sparta: A comprehensive alpha, beta and gamma particulate radiation measurement system for environment monitoring. In Proceedings of the 2011 IEEE Nuclear Science Symposium Conference Record, Valencia, Spain, 23–29 October 2011; pp. 350–351. [Google Scholar] [CrossRef]
- Baszczyk, M.; Dorosz, P.; Głąb, S.; Kucewicz, W.; Mik, L.U.; Sapor, M. Silicon photomultiplier gain compensation algorithm in multidetector measurements. Metrol. Meas. Syst. 2013, 4, 655–666. [Google Scholar] [CrossRef]
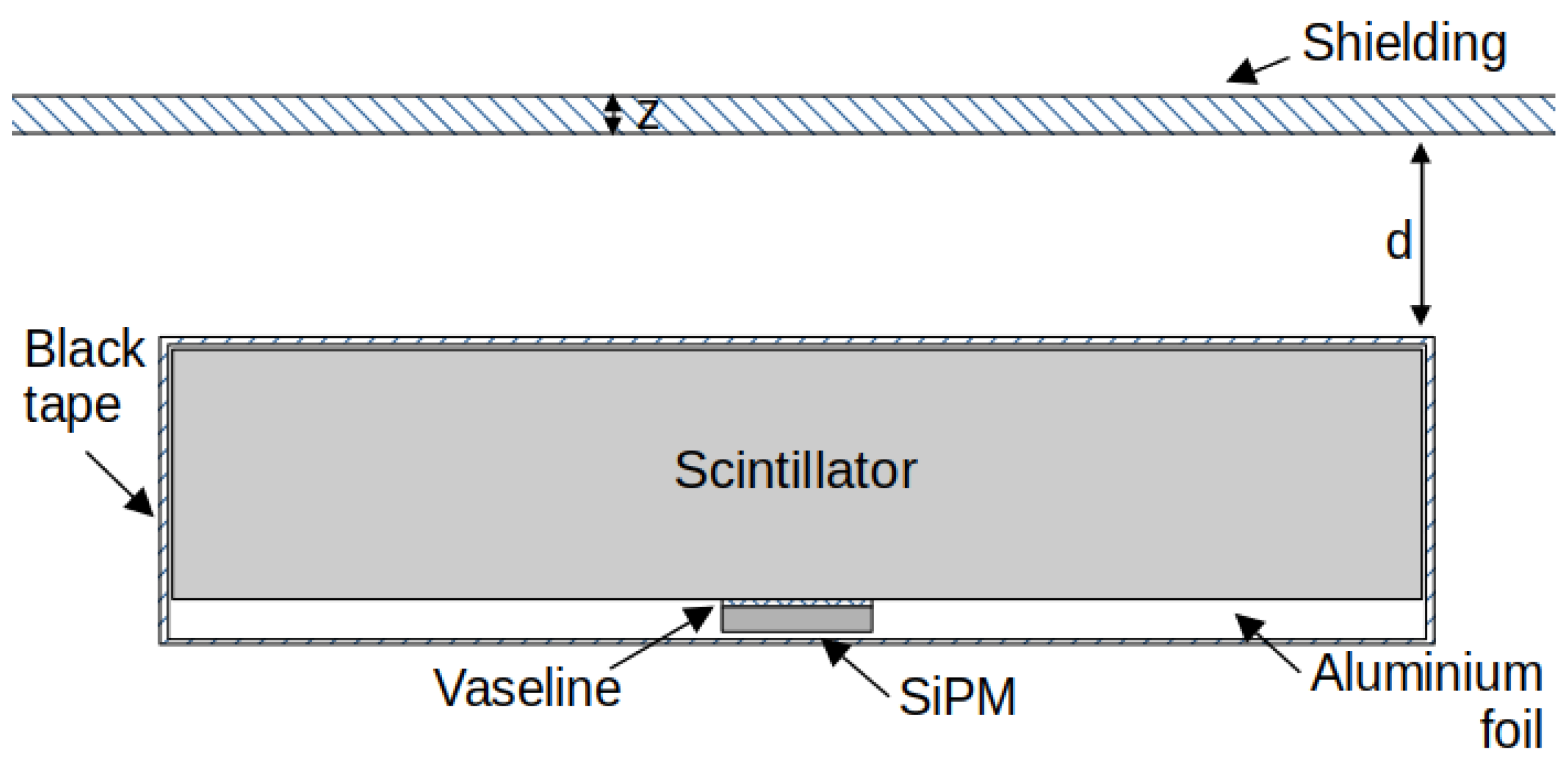




| Parameter | Scintillator | Al Foil | Black Tape | SiPM | Vaseline |
|---|---|---|---|---|---|
| Density [g cm−3] | 1.032 | 2.7 | 1.28 | 2.329 | 0.82 |
| Thickness [mm] | 10 | 0.14 | 0.36 | 1 | 0.6 |
| Composition | H, C | Al | H, C, Cl | Si | H, C, N |
| Ratio of elements | 11:10 | 1 | 3:2:1 | 1 | 15:15:1 |
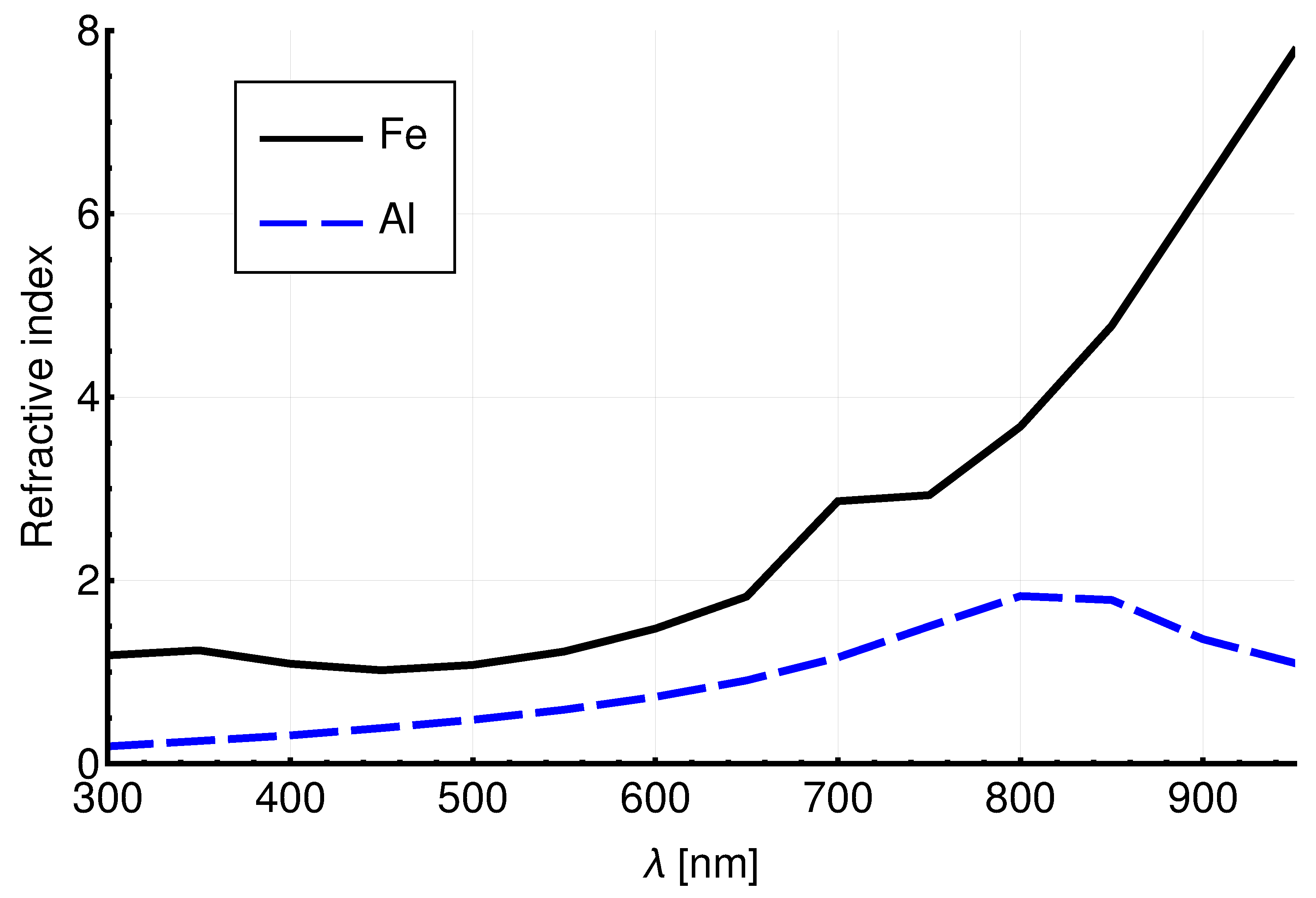
| Refractive index | 1.58 | Figure 2 | 1.54 | 1.59 | 1.467 |
| Absorption coefficient [cm−1] | 0.001 | 966,850 | 0.069339 | - | 0.0173 |
| Attenuation length [cm] | 210 | - | - | - | - |
| Scintillation yield [MeV−1] | 11,136 | - | - | - | - |
| Scintillation yield 1 | 0.27 | - | - | - | - |
| Scintillation constant 1 [ns] | 2.1 | - | - | - | - |
| Scintillation constant 2 [ns] | 14.2 | - | - | - | - |
| Resolution scale | 1.0 | - | - | - | - |
| Parameter | Stainless Steel | Aluminium | Iron | Glass |
|---|---|---|---|---|
| Density [g cm−3] | 1.032 | 2.7 | 1.28 | 2.329 |
| Thickness [mm] | 0.5, 1.5 | 1.5 | 1.5 | 5 |
| Composition | Fe, Cr, Ni, C | Al | Fe | O, Na, Si, Ca |
| Percent of elements [%] | 70.67, 20, 9.25, 0.08 | 100 | 100 | 45.98, 9.64411, 33.6553, 10.7205 |
| Refractive index | Figure 2 | Figure 2 | Figure 2 | 1.51 |
| Absorption coefficient [cm−1] | 1,643,500 | 966,850 | 1,643,500 | 0.0021033 |
| Distance from scintillator, [cm] | 0.5, 3, 6 | 3 | 3 | 3 |
| [V] | G | C [pF] | V [V] | M | [%] |
|---|---|---|---|---|---|
| 24.5 | 3400 | 0.00014 | 18,980 | 64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pryga, J.; Woźniak, K.W.; Bibrzycki, Ł.; Homola, P.; Stuglik, S.; Almeida Cheminant, K.; Ruimi, O.; Bar, O. Geant4 Simulations of a Scintillator Cosmic-Ray Detector. Appl. Sci. 2025, 15, 6652. https://doi.org/10.3390/app15126652
Pryga J, Woźniak KW, Bibrzycki Ł, Homola P, Stuglik S, Almeida Cheminant K, Ruimi O, Bar O. Geant4 Simulations of a Scintillator Cosmic-Ray Detector. Applied Sciences. 2025; 15(12):6652. https://doi.org/10.3390/app15126652
Chicago/Turabian StylePryga, Jerzy, Krzysztof Wiesław Woźniak, Łukasz Bibrzycki, Piotr Homola, Sławomir Stuglik, Kévin Almeida Cheminant, Ophir Ruimi, and Olaf Bar. 2025. "Geant4 Simulations of a Scintillator Cosmic-Ray Detector" Applied Sciences 15, no. 12: 6652. https://doi.org/10.3390/app15126652
APA StylePryga, J., Woźniak, K. W., Bibrzycki, Ł., Homola, P., Stuglik, S., Almeida Cheminant, K., Ruimi, O., & Bar, O. (2025). Geant4 Simulations of a Scintillator Cosmic-Ray Detector. Applied Sciences, 15(12), 6652. https://doi.org/10.3390/app15126652







