Optimizing Parcel Locker Selection in Campus Last-Mile Logistics: A Path Planning Model Integrating Spatial–Temporal Behavior Analysis and Kernel Density Estimation
Abstract
1. Introduction
2. Literature Review
2.1. Last-Mile Distribution Solution
2.2. Optimization of Parcel Locker Location Selection
2.3. User Preferences and Logistics Path Planning
2.4. Application of Kernel Density Estimation Method
3. Methodology
3.1. Problem Description
3.2. Research Approach
3.3. Path Planning Model
3.3.1. Model Assumptions
3.3.2. Variable Definitions
3.3.3. Hotspot Identification
3.3.4. Activity Hotspot Screening
3.3.5. Regular Activity Hotspot Selection
3.3.6. PLC Selection
3.4. Data Acquisition and Model Parameter Settings
3.5. Benchmark Model Comparative Analysis
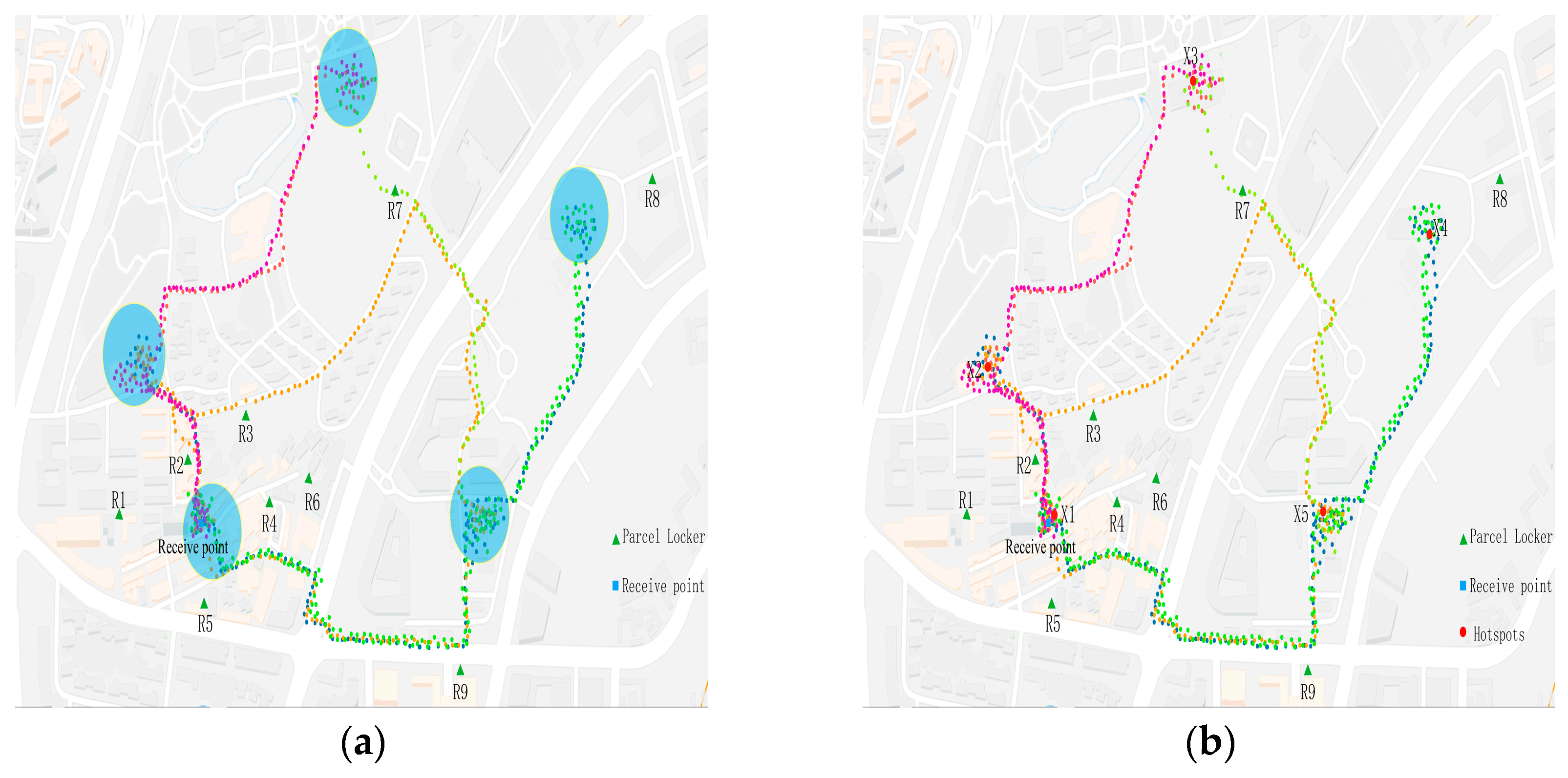
4. Results
4.1. Efficiency Analysis
4.2. Weight–Volume–Urgency Parameter Sensitivity Analysis
4.3. Benchmark Model Simulation Results
5. Discussion
5.1. Key Findings and Their Implications
5.2. Comparison with Existing Studies
5.3. Limitations and Urban Applicability
5.4. Future Research Directions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leung, A.; Lachapelle, U.; Burke, M. Spatio-Temporal Analysis of Australia Post Parcel Locker Use during the Initial System Growth Phase in Queensland (2013–2017). J. Transp. Geogr. 2023, 110, 103634. [Google Scholar] [CrossRef]
- Wang, D.; Xie, C.D.; Wang, C.; Yin, Z.X. Research on the regularity and predictability of individual spatiotemporal behavior: Taking the activities of Shanghai residents on weekdays as an example. Prog. Geogr. 2021, 40, 433–440. [Google Scholar] [CrossRef]
- Ranjbari, A.; Diehl, C.; Dalla Chiara, G.; Goodchild, A. Do Parcel Lockers Reduce Delivery Times? Evidence from the Field. Transp. Res. Part E Logist. Transp. Rev. 2023, 172, 103070. [Google Scholar] [CrossRef]
- Anand, N.; Mahmud, S.; van Duin, R. Parcel Lockers Feasibility Analysis Considering Multi-Stakeholder Perspectives. In Proceedings of the 6th International Conference Green Cities 2024: Green Logistics for Greener Cities, Szczecin, Poland, 22–24 May 2024; pp. 1–10. [Google Scholar]
- Russo, A.; Basbas, S.; Bouhouras, E.; Tesoriere, G.; Campisi, T. The Study of the 5-Min Walking Accessibility for Pickup Points in Thessaloniki: Enhancing Logistics’ Last Mile Sustainability. In Computational Science and Its Applications—ICCSA 2024 Workshops; Gervasi, O., Murgante, B., Garau, C., Taniar, D., C. Rocha, A.M.A., Faginas Lago, M.N., Eds.; Lecture Notes in Computer Science; Springer Nature Switzerland: Cham, Switzerland, 2024; Volume 14821, pp. 41–53. ISBN 978-3-031-65307-0. [Google Scholar]
- Ding, M.; Ullah, N.; Grigoryan, S.; Hu, Y.; Song, Y. Variations in the Spatial Distribution of Smart Parcel Lockers in the Central Metropolitan Region of Tianjin, China: A Comparative Analysis before and after COVID-19. ISPRS Int. J. Geo-Inf. 2023, 12, 203. [Google Scholar] [CrossRef]
- Deutsch, Y.; Golany, B. A Parcel Locker Network as a Solution to the Logistics Last Mile Problem. Int. J. Prod. Res. 2018, 56, 251–261. [Google Scholar] [CrossRef]
- Olsson, J.; Hellström, D.; Pålsson, H. Framework of Last Mile Logistics Research: A Systematic Review of the Literature. Sustainability 2019, 11, 7131. [Google Scholar] [CrossRef]
- Mohammad, W.A.; Nazih Diab, Y.; Elomri, A.; Triki, C. Innovative Solutions in Last Mile Delivery: Concepts, Practices, Challenges, and Future Directions. Supply Chain Forum Int. J. 2023, 24, 151–169. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.; Liu, Q.; Shen, F.; Lee, L.H. Towards Enhancing the Last-Mile Delivery: An Effective Crowd-Tasking Model with Scalable Solutions. Transp. Res. Part E Logist. Transp. Rev. 2016, 93, 279–293. [Google Scholar] [CrossRef]
- Garg, V.; Niranjan, S.; Prybutok, V.; Pohlen, T.; Gligor, D. Drones in Last-Mile Delivery: A Systematic Review on Efficiency, Accessibility, and Sustainability. Transp. Res. Part D Transp. Environ. 2023, 123, 103831. [Google Scholar] [CrossRef]
- Bouhouras, E.; Ftergioti, S.; Russo, A.; Basbas, S.; Campisi, T.; Symeon, P. Unlocking the Potential of Pick-Up Points in Last-Mile Delivery in Relation to Gen Z: Case Studies from Greece and Italy. Appl. Sci. 2024, 14, 10629. [Google Scholar] [CrossRef]
- Dong, B.; Hovi, I.B.; Pinchasik, D.R. Analysis of Service Efficiency of Parcel Locker in Last-Mile Delivery: A Case Study in Norway. Transp. Res. Procedia 2023, 69, 918–925. [Google Scholar] [CrossRef]
- Seghezzi, A.; Siragusa, C.; Mangiaracina, R. Parcel Lockers vs. Home Delivery: A Model to Compare Last-Mile Delivery Cost in Urban and Rural Areas. Int. J. Phys. Distrib. Logist. Manag. 2022, 52, 213–237. [Google Scholar] [CrossRef]
- Schwerdfeger, S.; Boysen, N. Who Moves the Locker? A Benchmark Study of Alternative Mobile Parcel Locker Concepts. Transp. Res. Part C Emerg. Technol. 2022, 142, 103780. [Google Scholar] [CrossRef]
- Kahr, M. Determining Locations and Layouts for Parcel Lockers to Support Supply Chain Viability at the Last Mile. Omega 2022, 113, 102721. [Google Scholar] [CrossRef]
- Cui, Q.; Zhang, Y.; Yang, G.; Huang, Y.; Chen, Y. Analysing Gender Differences in the Perceived Safety from Street View Imagery. Int. J. Appl. Earth Obs. Geoinf. 2023, 124, 103537. [Google Scholar] [CrossRef]
- Lagorio, A.; Pinto, R. The Parcel Locker Location Issues: An Overview of Factors Affecting Their Location. In Proceedings of the 8th International Conference on Information Systems, Logistics and Supply Chain: Interconnected Supply Chains in an Era of Innovation, ILS, Austin, TX, USA, 22–24 April 2020. [Google Scholar]
- Peppel, M.; Spinler, S. The Impact of Optimal Parcel Locker Locations on Costs and the Environment. Int. J. Phys. Distrib. Logist. Manag. 2022, 52, 324–350. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, J.; Chen, Y.; Luo, J. Research on the Selection of Self-Pickup Points Based on Customers’ Bounded Rationality. Ind. Eng. Manag. 2015, 20, 92–100. [Google Scholar] [CrossRef]
- Qiu, H.; Li, H.; Song, H. Location-Routing Problem for Urban Parcel Lockers Considering Demand-Dependent Last-Mile Delivery and Time Windows. Comput. Integr. Manuf. Syst. 2018, 24, 2612–2621. [Google Scholar] [CrossRef]
- Wu, H.; Shao, D.; Ng, W.S. Locating Self-Collection Points for Last-Mile Logistics Using Public Transport Data. In Advances in Knowledge Discovery and Data Mining; Cao, T., Lim, E.-P., Zhou, Z.-H., Ho, T.-B., Cheung, D., Motoda, H., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2015; Volume 9077, pp. 498–510. ISBN 978-3-319-18037-3. [Google Scholar]
- Fang, J.; Giuliano, G.; Wu, A.-M. The Spatial Dynamics of Amazon Lockers in Los Angeles County; METRANS Transportation Center: Los Angeles, CA, USA, 2019. [Google Scholar]
- Patowary, M.M.I.; Peulers, D.; Richter, T.; Melovic, A.; Nilsson, D.; Söilen, K.S. Improving Last-Mile Delivery for e-Commerce: The Case of Sweden. Int. J. Logist. Res. Appl. 2023, 26, 872–893. [Google Scholar] [CrossRef]
- Wang, X.; Wong, Y.D.; Shi, W.; Yuen, K.F. An Investigation on Consumers’ Preferences for Parcel Deliveries: Applying Consumer Logistics in Omni-Channel Shopping. Int. J. Logist. Manag. 2023, 35, 557–576. [Google Scholar] [CrossRef]
- Pan, X.; Wu, L.; Long, F.; Ma, A. Exploiting User Behavior Learning for Personalized Trajectory Recommendations. Front. Comput. Sci. 2021, 16, 163610. [Google Scholar] [CrossRef]
- Chen, J.; Chen, P. Tourism Route Recommendation Algorithm Utilizing Interest Hotspot Maps. Comput. Eng. Des. 2018, 39, 2941–2946. [Google Scholar] [CrossRef]
- Xu, C.; Meng, F.; Yuan, G.; Li, Y.; Liu, X. Point-of-Interest Recommendation Algorithm Incorporating Location Influence. J. Comput. Appl. 2019, 39, 3178–3183. [Google Scholar]
- Wenhao, Y.U.; Tinghua, A.I.; Min, Y.; Jiping, L.I.U. Detecting “Hot Spots” of Facility POIs Based on Kernel Density Estimation and Spatial Autocorrelation Technique. Geomat. Inf. Sci. Wuhan Univ. 2016, 41, 221–227. [Google Scholar] [CrossRef]
- Węglarczyk, S. Kernel Density Estimation and Its Application. ITM Web Conf. 2018, 23, 00037. [Google Scholar] [CrossRef]
- Cao, W.; Li, Z.; Wei, Q.; Chu, Y. Trajectory Classification Approach Based on Probability Density Estimation of Regional Distribution. Comput. Eng. 2018, 44, 262–267, 286. [Google Scholar]
- King, T.L.; Thornton, L.E.; Bentley, R.J.; Kavanagh, A.M. The Use of Kernel Density Estimation to Examine Associations between Neighborhood Destination Intensity and Walking and Physical Activity. PLoS ONE 2015, 10, e0137402. [Google Scholar] [CrossRef]
- Lv, A.; Sun, B.; Sun, Y.; Yang, C. Spatial Point Pattern Analysis of Inbound Logistics Activities Based on GPS Trajectory Data. In Proceedings of the 2022 10th International Conference on Traffic and Logistic Engineering (ICTLE), Macau, China, 12–14 August 2022; pp. 107–111. [Google Scholar]
- Güngör, E.; Özmen, A. Distance and Density Based Clustering Algorithm Using Gaussian Kernel. Expert Syst. Appl. 2017, 69, 10–20. [Google Scholar] [CrossRef]
- Soh, Y.; Hae, Y.; Mehmood, A.; Hadi Ashraf, R.; Kim, I. Performance Evaluation of Various Functions for Kernel Density Estimation. Open J. Appl. Sci. 2013, 3, 58–64. [Google Scholar] [CrossRef]
- Xie, Z.; Yan, J. Kernel Density Estimation of Traffic Accidents in a Network Space. Comput. Environ. Urban Syst. 2008, 32, 396–406. [Google Scholar] [CrossRef]
- Giannoulaki, M.; Christoforou, Z. Pedestrian Walking Speed Analysis: A Systematic Review. Sustainability 2024, 16, 4813. [Google Scholar] [CrossRef]
- Shi, H.; Huang, H.; Ma, D.; Chen, L.; Zhao, M. Capturing Urban Recreational Hotspots from GPS Data: A New Framework in the Lens of Spatial Heterogeneity. Comput. Environ. Urban Syst. 2023, 103, 101972. [Google Scholar] [CrossRef]
- Su, N.; Zhang, Z.; Chen, J.; Li, W.; Long, Y. Assessing Personal Screen Exposure with Ever-Changing Contexts Using Wearable Cameras and Computer Vision. Build. Environ. 2024, 261, 111720. [Google Scholar] [CrossRef]
- Li, W.; Long, Y.; Kwan, M.-P.; Liu, N.; Li, Y.; Zhang, Y. Measuring Individuals’ Mobility-Based Exposure to Neighborhood Physical Disorder with Wearable Cameras. Appl. Geogr. 2022, 145, 102728. [Google Scholar] [CrossRef]
- Yu, W.; Ai, T.; Liu, P.; He, Y. Network Kernel Density Estimation Method for Analyzing Hotspots in POI Facility Distribution. Acta Geod. Et Cartogr. Sin. 2015, 44, 1378–1383, 1400. [Google Scholar]
- Cui, Q.; Tan, L.; Ma, H.; Wei, X.; Yi, S.; Zhao, D.; Lu, H.; Lin, P. Effective or Useless? Assessing the Impact of Park Entrance Addition Policy on Green Space Services from the 15-Min City Perspective. J. Clean. Prod. 2024, 467, 142951. [Google Scholar] [CrossRef]
- Jebbor, I.; Benmamoun, Z.; Hachimi, H. Forecasting Supply Chain Disruptions in the Textile Industry Using Machine Learning: A Case Study. Ain Shams Eng. J. 2024, 15, 103116. [Google Scholar] [CrossRef]
- Khlie, K.; Benmamoun, Z.; Fethallah, W.; Jebbor, I. Leveraging Variational Autoencoders and Recurrent Neural Networks for Demand Forecasting in Supply Chain Management: A Case Study. J. Infras. Policy. Dev. 2024, 8, 6639. [Google Scholar] [CrossRef]






| Test Object | User A | User B | User C | User D |
|---|---|---|---|---|
| Number of hotspots | 24 | 29 | 17 | 36 |
| Selected regular hotspot number | 2 | 5 | 2 | 4 |
| Selected PLC number (α = 2) | 7 | 6 | 1 | 4 |
| Distance reduction rate | 68% | 62% | 65% | 57% |
| Hotspot Number | Longitude | Latitude | Arrival Time | Leave Time |
|---|---|---|---|---|
| 2 | 113.9334564 | 22.5290144 | 10:49:30 | 22:19:03 |
| PLC Number | Distance to the Receipt Point (Meter) | Distance from the Regular Hotspot (Meter) | |
|---|---|---|---|
| 2 | 7 | 110 | 512 |
| Indicator | Model in This Paper | Greedy Algorithm | Static KDE | ST-DBSCAN |
|---|---|---|---|---|
| Bypass distance reduction rate (%) | 68.2 | 38.4 | 52.1 | 47.6 |
| Path matching degree | 85.3 | 62.7 | 74.2 | 69.8 |
| Time efficiency (minutes) | 7.5 | 12.3 | 9.1 | 10.4 |
| Load balancing degree (standard deviation) | 0.18 | 0.42 | 0.29 | 0.35 |
| PLC utilization rate (%) | 41.5 | 26.7 | 34.2 | 29.8 |
| p-value | - | 0.0001 | 0.0023 | 0.0004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Lin, P.; Zou, L. Optimizing Parcel Locker Selection in Campus Last-Mile Logistics: A Path Planning Model Integrating Spatial–Temporal Behavior Analysis and Kernel Density Estimation. Appl. Sci. 2025, 15, 6607. https://doi.org/10.3390/app15126607
Zhang H, Lin P, Zou L. Optimizing Parcel Locker Selection in Campus Last-Mile Logistics: A Path Planning Model Integrating Spatial–Temporal Behavior Analysis and Kernel Density Estimation. Applied Sciences. 2025; 15(12):6607. https://doi.org/10.3390/app15126607
Chicago/Turabian StyleZhang, Hongbin, Peiqun Lin, and Liang Zou. 2025. "Optimizing Parcel Locker Selection in Campus Last-Mile Logistics: A Path Planning Model Integrating Spatial–Temporal Behavior Analysis and Kernel Density Estimation" Applied Sciences 15, no. 12: 6607. https://doi.org/10.3390/app15126607
APA StyleZhang, H., Lin, P., & Zou, L. (2025). Optimizing Parcel Locker Selection in Campus Last-Mile Logistics: A Path Planning Model Integrating Spatial–Temporal Behavior Analysis and Kernel Density Estimation. Applied Sciences, 15(12), 6607. https://doi.org/10.3390/app15126607








