Abstract
(1) Background: Due to its imaging principle, OCT generates images laden with significant speckle noise. The quality of OCT images is a crucial factor influencing diagnostic effectiveness, highlighting the importance of OCT image denoising. (2) Methods: The OCT image undergoes a Discrete Wavelet Transform (DWT) to decompose it into multiple scales, isolating high-frequency wavelet coefficients that encapsulate fine texture details. These high-frequency coefficients are further processed using a Shift-Invariant Wavelet Transform (SWT) to generate an additional set of coefficients, ensuring an enhanced feature preservation and reduced artifacts. Both the original DWT high-frequency coefficients and their SWT-transformed counterparts are independently denoised using a Deep Neural Convolutional Network (DnCNN). This dual-pathway approach leverages the complementary strengths of both transform domains to suppress noise effectively. The denoised outputs from the two pathways are fused using a correlation-based strategy. This step ensures the optimal integration of texture features by weighting the contributions of each pathway according to their correlation with the original image, preserving critical diagnostic information. Finally, the Inverse Wavelet Transform is applied to the fused coefficients to reconstruct the denoised OCT image in the spatial domain. This reconstruction step maintains structural integrity and enhances diagnostic clarity by preserving essential spatial features. (3) Results: The MSE, PSNR, and SSIM indices of the proposed algorithm in this paper were 4.9052, 44.8603, and 0.9514, respectively, achieving commendable results compared to other algorithms. The Sobel, Prewitt, and Canny operators were utilized for edge detection on images, which validated the enhancement effect of the proposed algorithm on image edges. (4) Conclusions: The proposed algorithm in this paper exhibits an exceptional performance in noise suppression and detail preservation, demonstrating its potential application in OCT image denoising. Future research can further explore the adaptability and optimization directions of this algorithm in complex noise environments, aiming to provide more theoretical support and practical evidence for enhancing OCT image quality.
1. Introduction
Optical coherence tomography (OCT) [] represents a cutting-edge, non-invasive imaging technology that harnesses the interference of reflected light to produce high-resolution two-dimensional or three-dimensional images. This technique enables an in-depth examination of tissue microstructures and facilitates the detection of subtle structural and laminar alterations, thereby establishing its prominence across multiple medical domains, particularly in ophthalmology.
With the widespread application of OCT, the quality of OCT images has emerged as a significant factor influencing diagnostic effectiveness. Although OCT systems are capable of providing high-resolution structural information during imaging, the image quality is often compromised by the presence of speckle noise [,]. To enhance the visualization of OCT images and extract more precise diagnostic information, image denoising has become a crucial task in post-imaging processing [,,,,].
Traditional image denoising methods [], such as the least squares method [] and median filtering, have been extensively applied to denoise OCT images. While these methods can effectively reduce speckle noise to some extent, they often result in the loss of image details. Another common denoising approach is Anisotropic Diffusion [], which, while preserving certain edge information while removing noise, often falls short when dealing with high-noise OCT data, failing to meet the requirements for high-quality image restorations. In comparison, wavelet transform methods [] have demonstrated superior performances in image denoising, effectively distinguishing between noise and signal components through a multiscale processing approach.
Recent advancements in wavelet-based denoising have focused on incorporating adaptive mechanisms to address heterogeneous noise characteristics in medical imagery [,]. Zaki et al. introduced a noise-adaptive wavelet thresholding (NAWT) framework that leverages a spectral discrepancy analysis across wavelet sub-bands, demonstrating performance gains in the ultrasonic tissue characterization []. Building upon multi-resolution analysis foundations, Cao et al. proposed a hybrid threshold function combining hard and soft thresholding paradigms, achieving an improved edge preservation through spatially variant coefficient manipulation []. For optical coherence tomography (OCT) applications, Subhedar et al. developed a particle swarm optimization (PSO)-driven threshold selection strategy, incorporating local texture descriptors (variance/gradient metrics) to enable context-aware noise suppression in retinal layer segmentation tasks [].
These methodologies collectively advance wavelet denoising through two principal innovations: the implementation of spatially adaptive threshold modulation mechanisms that retain critical diagnostic features while attenuating stochastic artifacts and the integration of local statistical descriptors, such as inter-scale correlation and directional variance, into multiscale processing pipelines. Notably, the PSO-OCT framework achieved a 12.7% improvement in the SNR over conventional thresholding methods through a dynamic parameter optimization across 256 × 256 pixel regions.
Concurrently, hybrid architectures combining wavelet transforms with deep learning have emerged as promising alternatives [,,,]. Zhang et al. demonstrated a convolutional neural network (CNN)-augmented wavelet denoiser that outperformed traditional methods by 8.2 dB in PSNR metrics through the joint optimization of thresholding matrices and feature extraction kernels []. More recently, residual learning paradigms integrated with Stationary Wavelet Transforms (SWTs) have shown particular efficacy in preserving microstructural details critical for an OCT diagnosis [].
In conclusion, the field of OCT image denoising continues to evolve, with adaptive denoising methods based on wavelet transforms emerging as the focal point of contemporary research due to their superior noise suppression capabilities and detail preservation efficacy. This chapter investigates novel algorithmic approaches for OCT image denoising, refining existing methodologies while introducing a synergistic integration of wavelet transforms with DnCNN architectures. The proposed framework decomposes images into low-frequency and high-frequency components via the DWT, processes both the original high-frequency coefficients and those derived from the SWT through DnCNN-based denoising, and finally fuses the outputs using image correlation maximization. The complete denoising pipeline is visualized in Figure 1, demonstrating innovative signal processing strategies that hold significant promise for advancing the OCT imaging quality in clinical applications.
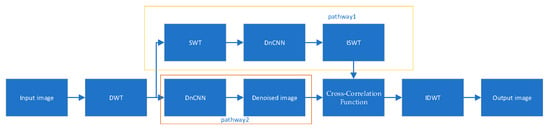
Figure 1.
Process of wavelet transform denoising.
2. Materials and Methods
2.1. Wavelet Transform
The Mallat wavelet transform provides a powerful framework for signal analysis by decomposing signals into components characterized by diverse frequency spectra and resolution levels. This transformation enables the capture of essential signal features across multiple scales, forming the basis of multi-resolution analysis. Within this paradigm, signal details are represented hierarchically, permitting dynamic adaptation of the analysis scale to accommodate varying local signal characteristics. A critical advantage of this approach lies in its ability to effectively separate signal components from noise across different scales, thereby facilitating robust image denoising strategies.
Building upon this theoretical foundation, the present study employs two distinct wavelet transform methodologies for image processing: the Discrete Wavelet Transform (DWT) and the Stationary Wavelet Transform (SWT). These transforms are selected for their complementary strengths in decomposing image data into frequency sub-bands, which is crucial for subsequent denoising procedures.
2.1.1. Discrete Wavelet Transform
Employing DWT, the image undergoes hierarchical decomposition to isolate and extract specific sub-bands for targeted processing. Subsequently, denoising operations are applied to these sub-bands to enhance signal quality. The processed sub-bands are then reconstructed through the inverse DWT, with final image synthesis achieved via merging in the spatial domain according to Equation (2).
k represents the number of wavelet decomposition levels, n and m are the translation factors, h() denotes the low-pass filter, and g() denotes the high-pass filter.
DWT decomposes images into four orthogonal frequency sub-bands, enabling multi-resolution analysis.
Low–Low (LL) captures the low-frequency approximation of the original image, preserving coarse-grained spatial information and overall structural features. It essentially contains the averaged version of the image with reduced resolution. Low–High (LH) encodes high-frequency information along the horizontal axis. It captures vertical edge features and texture variations occurring in the horizontal direction, corresponding to abrupt intensity changes between adjacent columns of pixels. High–Low (HL) contains high-frequency information along the vertical axis. It represents horizontal edge features and texture variations in the vertical direction, reflecting intensity discontinuities between adjacent rows of pixels. High–High (HH) captures high-frequency information along both spatial dimensions. It primarily represents diagonal edge features and texture details that manifest as intensity variations along oblique directions, corresponding to fine-grained structural components in the image.
These sub-bands facilitate targeted image feature processing by separating signal components into distinct frequency channels. Visualization of wavelet transform applications tailored to specific image characteristics is presented in Figure 2.
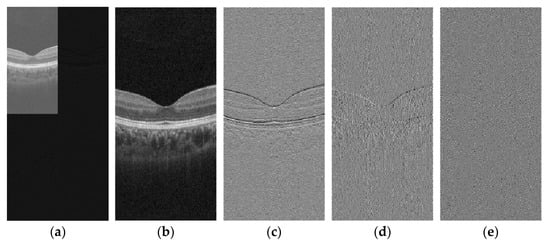
Figure 2.
Schematic of DWT: (a) First-order wavelet transform; (b) LL; (c) LH; (d) HL; and (e) HH.
Through analysis of wavelet transform coefficients derived from OCT images, we observe significant horizontal texture features in the imagery, with noise primarily concentrated in the high-frequency components. This distribution underscores the structural characteristics of OCT data and highlights the necessity for targeted denoising strategies in high-frequency sub-bands to preserve diagnostic image quality.
2.1.2. Stationary Wavelet Transform
SWT and DWT both employ separable filter banks to perform two-dimensional wavelet decomposition along the row and column directions of an image []. However, SWT distinguishes itself by eliminating downsampling operations, which yields distinct signal representation properties as formulated in Equation (3). Unlike DWT, which reduces spatial resolution via dyadic downsampling at each decomposition level, SWT maintains constant image dimensions across all scales, preserving full spatial resolution.
SWT adopts a non-decimated framework that retains complete sampling density throughout each decomposition stage. This redundancy-based approach, with a redundancy factor of 3J + 1 for J decomposition levels, ensures translation invariance—guaranteeing consistent feature representation irrespective of spatial positioning. The preserved resolution characteristics render SWT particularly advantageous for applications demanding simultaneous detail preservation and multiscale analysis, such as image fusion and denoising.
Figure 3 illustrates the result of applying SWT to Figure 2b. This transformed image was generated through multi-level SWT decomposition, which preserves spatial information while capturing frequency domain characteristics essential for denoising.

Figure 3.
Schematic of SWT: (a) LL; (b) LH; (c) HL; and (d) HH.
The Inverse Stationary Wavelet Transform (ISWT) reconstructs the original image by combining sub-band coefficients through inverse filtering and weighted synthesis operations, as formulated in Equation (4).
2.2. Denoising Convolutional Neural Network
Denoising convolutional neural network (DnCNN) represents a deep convolutional neural network architecture specifically designed for image denoising tasks. This model leverages a deep supervised learning paradigm to adaptively characterize image noise distribution patterns, optimizing network parameters through backpropagation algorithms to achieve nonlinear end-to-end mapping from noisy to clean images. Under Gaussian noise conditions, DnCNN demonstrates superior denoising performance. The optical coherence tomography (OCT) images addressed in this study exhibit Poisson-distributed noise characteristics. To accommodate DnCNN’s input requirements, we apply variance stabilizing transformation (VST) to preprocess raw images via square root operations, converting signal-dependent noise into additive Gaussian noise []. The adopted DnCNN network topology, as illustrated in Figure 4, comprises alternately stacked convolutional layers and batch normalization units, incorporating residual learning mechanisms with skip connections to enhance feature reuse capabilities and further improve denoising efficacy. The network depth is represented by B, with B = 25 employed in the experimental setup. The convolution kernel adopted in the architecture is of size 3 × 3 × 64.
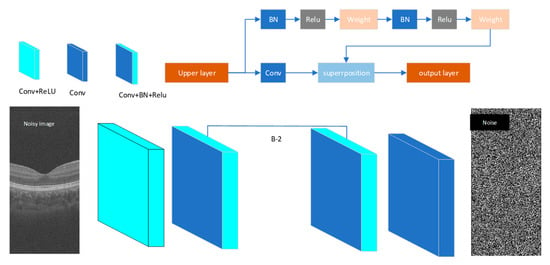
Figure 4.
The architecture of the proposed DnCNN network.
The network architecture was optimized using a residual learning paradigm, where the Mean Squared Error (MSE) loss function quantified the reconstruction fidelity between paired noisy–clean OCT image domains. This objective function facilitated gradient-efficient backpropagation through identity mapping connections, enabling effective minimization of structural discrepancies.
All experimental datasets comprised B-scan optical coherence tomography (OCT) images with dimensions of 3 mm × 3 mm, yielding a resolution of 640 × 304 pixels. The training cohort was sourced from the Nanjing University repository, containing 115,520 OCT images acquired from 380 subjects. This cohort included 49 age-related macular degeneration (AMD) cases, 16 choroidal neovascularization (CNV) cases, 64 diabetic retinopathy (DR) cases, and 251 healthy controls. For model validation, an independent dataset was utilized, consisting of 10,640 OCT images obtained from 35 subjects at Shanxi Eye Hospital, comprising 5 AMD cases, 7 CNV cases, 16 DR cases, and 7 healthy controls.
The training pipeline of the proposed DnCNN architecture is illustrated in Figure 5, incorporating a multi-resolution feature extraction strategy. Each OCT image from the dataset underwent DWT decomposition, yielding four sub-band components: LL, LH, HL, and HH. The LL sub-band, representing coarse-scale structural information, subsequently underwent SWT decomposition to generate four additional frequency-specific representations.
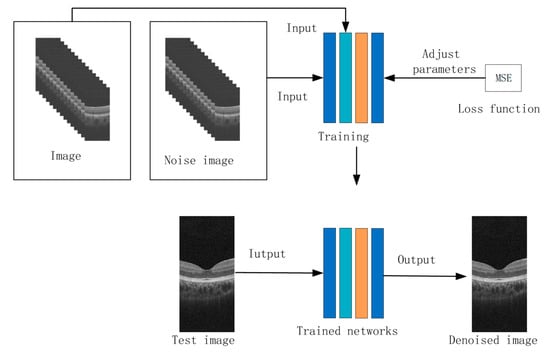
Figure 5.
The process of the DnCNN network training.
This multiscale decomposition enabled parallel channel processing, where each wavelet-derived component (4 DWT sub-bands + 4 SWT sub-bands) was independently fed into the denoising network. All channels adopted identical network configurations, ensuring consistent feature extraction across spatial frequency domains. The training objective minimized the MSE loss between network outputs and corresponding noise-free ground truths, with gradient updates propagated through residual connections to preserve low-frequency contextual information.
To enhance convergence stability, the Adam optimizer (β1 = 0.9, β2 = 0.999) was employed with an initial learning rate of 1 × 10−4, while batch normalization layers regulated internal covariate shift during the 50-epoch training regimen.
2.3. Correlation Function
Image correlation serves as a quantitative method for assessing the inherent relationships between two images by measuring their similarity or statistical interdependence. As a foundational analytical tool in this domain, the cross-correlation function provides a canonical framework for similarity measurement, with its mathematical formulation essentially equivalent to convolution operations within normalized spatial domains.
This formulation involves systematically sliding a template image across the target image while computing localized similarity metrics through pixel-wise multiplication and summation. The resulting correlation coefficients form a response surface where peak values indicate optimal template–target alignment positions, with magnitude reflecting the strength of structural correspondence.
denotes the target image, represents the template image, and (h,k) signifies the spatial displacement vector.
The dual processing pathways independently generate images f and g, reflecting inherent methodological discrepancies in their denoising paradigms. While complete noise elimination through dual-path processing remains unattainable due to the inherent stochasticity of noise contamination, we propose a correlation-guided refinement framework to mitigate residual artifacts while preserving critical texture information in OCT imagery.
Correlation analysis confirms significant texture-related coherence between the processed images, particularly in structural regions of diagnostic relevance. Notably, the SWT applied to pathway g incorporates an additional decomposition level compared to pathway f, enabling superior preservation of microstructural details at lower spatial frequency bands. This architectural difference forms the basis for adaptive feature fusion.
To achieve optimal noise–texture balance, a hybrid fusion strategy is implemented through spatially variant weight allocation. In low-correlation regions (), where noise dominance persists, the enhanced detail representation from pathway g is prioritized to maintain anatomical integrity. In high-correlation regions (), where signal reliability is confirmed, an arithmetic mean of both pathways is adopted to balance noise suppression and feature preservation. In intermediate-correlation regions (), a weighted preference toward pathway f is maintained to ensure perceptual continuity, as excessive detail inclusion from g may introduce interpretative ambiguity. This hierarchical fusion mechanism, formally described by Equation (6), ensures progressive integration of complementary features across spatial scales.
The correlation coefficients and are set to 0.2 and 0.7 times the maximum correlation coefficient value, respectively. Here, f denotes the image generated through Pathway 1, while g represents the image produced via Pathway 2. This parameter configuration ensures balanced integration of texture features from both processing streams during image fusion.
The resultant synthesis achieves effective suppression of stochastic noise components while maintaining diagnostic-grade structural fidelity. By prioritizing texture coherence in heterogeneous tissue boundaries, this approach demonstrates measurable improvements in image interpretability without compromising quantitative measurement accuracy.
3. Results
3.1. Evaluation
This paper employs three quantitative metrics—the Mean Squared Error (MSE), Peak Signal-to-Noise Ratio (PSNR), and Structural Similarity Index (SSIM)—to comprehensively evaluate the denoising effect of OCT images.
The MSE (Mean Squared Error) is the average of the squares of the errors between the original image and the denoised image. It is one of the commonly used scales for comparing variable differences. A smaller MSE value indicates a higher degree of the restoration fidelity of the recovered image.
M and N represent the number of pixels along the length and width of an image, respectively. denotes the pixel value of the original image, while represents the pixel value of the denoised image.
The PSNR (Peak Signal-to-Noise Ratio) measures the similarity between two images and evaluates the noise intensity of an image relative to its original. A higher PSNR value indicates a better denoising effect for the image.
The SSIM (Structural Similarity Index Measure) measures the similarity between two images based on their luminance, contrast, and structural information. An SSIM value closer to one indicates a better denoising effect for the image.
In this context, x and y represent the original image and the processed image, respectively. and are the mean pixel values of x and y. denotes the covariance between x and y, while and are the pixel variances of x and y. and are constants that ensure the denominators do not become zero.
3.2. OCT Image Denoising
The denoising algorithms selected for OCT images [] include mean flitering (with a 3 × 3 filter window), median filtering (with a 3 × 3 filter window), isotropic filtering, anisotropic filtering, non-local mean filtering (NLM), the DnCNN, and the algorithm proposed in this paper.
Table 1 presents the denoising evaluation metrics for these algorithms. These quantitative results were derived from 304 optical coherence tomography (OCT) images acquired through a single 3 mm × 3 mm scanning session, with each image processed independently using distinct denoising algorithms, and the reported values represent the arithmetic mean of performance metrics across the dataset. The experimental results reveal that the MSE, PSNR, and SSIM achieved by the proposed algorithm in this paper are 4.9052, 44.8603, and 0.9514, respectively, yielding excellent results compared to other algorithms.

Table 1.
Evaluation metrics for image denoising performance.
This study systematically validates the proposed denoising algorithm’s balanced performance between structural fidelity preservation and noise suppression through the quantitative analysis of objective evaluation metrics. Experimental results demonstrate that the proposed method achieves an average SSIM improvement of 4.5% compared to the DnCNN, indicating a superior capability in preserving structural information such as image edges and textures. Concurrently, a 69.1% reduction in the MSE directly reflects the effective mitigation of pixel-wise reconstruction errors, while a 2.73 dB enhancement in the PSNR corroborates the algorithm’s improvement in visual quality from a signal fidelity perspective.
Notably, in high-detail preservation scenarios such as OCT image datasets, the proposed method maintains SSIM values above 0.95 while achieving a PSNR breakthrough of 44 dB. This performance validates the effectiveness of its multiscale feature fusion mechanism. Unlike conventional methods that struggle with the trade-off between denoising intensity and detail preservation, our approach achieves synergistic improvements across three critical dimensions, establishing a novel paradigm for the collaborative optimization of structural perception and noise suppression in image restoration tasks.
A comprehensive analysis of the denoised image presented in Figure 6 yields the subsequent findings.

Figure 6.
Comparison of denoising effects on OCT images. (a) Original OCT image; (b) mean; (c) median; (d) isotropic; (e) anisotropic; (f) non-local means; (g) DnCNN; and (h) our proposed algorithm.
Traditional filtering techniques, such as mean and median filtering, demonstrate a suboptimal efficacy in denoising applications, often leaving significant noise residuals within the processed images. Specifically, mean filtering exhibits pronounced deficiencies in this regard. Both isotropic and anisotropic filtering methods struggle to adequately eliminate noise, with the latter additionally introducing blurred edge textures. While the NLM and DnCNN algorithms perform commendably in noise reduction, they exhibit less clarity in preserving edge details compared to the proposed algorithm. In contrast, the novel approach presented herein excels in real-world image denoising, not only achieving superior noise elimination but also providing a more precise restoration of structural details and textures. The processed images exhibit an enhanced contrast and finer texture preservation, with previously blurred regions showing marked improvements in definition, as illustrated in Figure 6h. Post-denoising, the image quality is significantly enhanced, establishing a cleaner and more reliable data foundation for subsequent analytical and processing tasks.
4. Discussion
One of the critical parameters in ocular fundus OCT images is the integrity of the structural layers of the ocular fundus cells, which manifests as clear edges in the images. Therefore, edge detection [] in OCT images before and after denoising is also an important indicator for assessing the effectiveness of denoising. Sobel, Prewitt, and Canny are commonly used edge detection algorithms []. The Sobel operator detects image edges by calculating gradients in both horizontal and vertical directions. The Prewitt operator is very similar to the Sobel operator, as both perform edge detection by computing image gradients. However, the Sobel operator applies a weighting to the smoothness of the image, whereas the convolution kernel weights of the Prewitt operator are relatively uniform, without assigning a greater weight to the central part. The Canny operator is a multi-stage edge detection algorithm often regarded as one of the optimal edge detection methods. It can accurately detect image edges and extract complex and detailed edges, albeit with challenges in parameter selection.
To verify the impact of the proposed algorithm on image edges, Sobel, Prewitt, and Canny operators were utilized for edge detection on images, and comparisons were made between edge detections before and after denoising to validate the effectiveness of the proposed algorithm, as shown in Figure 7. Specifically, Figure 7a–c displays the results of the edge detection using Sobel, Prewitt, and Canny operators on the original images, respectively, while Figure 7d–f presents the results of the edge detection using the same operators on the denoised images.

Figure 7.
Edge detection on OCT images before and after denoising using Sobel, Prewitt, and Canny: (a) edge detection map of original OCT image using Sobel; (b) edge detection map of original OCT image using Prewitt; (c) edge detection map of original OCT image using Canny; (d) edge detection map of denoised OCT image using Sobel; (e) edge detection map of denoised OCT image using Prewitt; and (f) edge detection map of denoised OCT image using Canny.
As illustrated in Figure 7, the speckle noise present in OCT images adversely affects the identification of image edges, particularly the boundaries between retinal layers, which are significantly impacted by this noise. Following denoising, the image boundaries become distinct, and the edges appear smooth, thereby providing a solid foundation for subsequent image processing tasks.
The texture of the OCT images can be disrupted by pathological conditions. The edge detection was performed on lesion sites affected by common diseases such as AMD, CNV, and DR, which exhibit distinct morphological distortions due to their different pathogeneses. The Canny edge detection algorithm was employed for this purpose, with results presented in Figure 8.

Figure 8.
Denoised OCT images and Canny edge detection results for common retinal diseases: (a) AMD image denoising; (b) CNV image denoising; (c) DR image denoising; (d) AMD image edge detection; (e) CNV image edge detection; and (f) DR image edge detection.
As demonstrated in Figure 8, the proposed algorithm exhibits exceptional edge enhancement capabilities post-denoising, effectively extracting retinal layer boundaries across all tested conditions. For disease-specific retinal deformations and pathological regions, the algorithm demonstrates a robust edge detection performance, providing favorable conditions for subsequent segmentation tasks.
5. Conclusions
In the domain of OCT image processing, the presence of speckle noise significantly compromises the diagnostic image quality, necessitating advanced denoising strategies to enhance the clinical interpretation accuracy. This study introduces an enhanced wavelet-based framework integrating the DWT and SWT for multiscale decomposition, coupled with a DnCNN architecture for adaptive noise suppression. The proposed methodology achieves a structure-preserving reconstruction through hierarchical feature extraction, demonstrating a superior capability in mitigating speckle artifacts while retaining critical anatomical details in OCT imagery.
Quantitative evaluations utilizing the MSE, PSNR, and SSIM confirm that the algorithm achieves an optimal trade-off between noise reduction and detail preservation, outperforming conventional approaches. Notably, the edge detection analysis corroborates the framework’s efficacy in maintaining subtle structural boundaries. These results collectively validate the clinical applicability of the proposed method for improving the OCT diagnostic precision in ophthalmic and cardiovascular imaging contexts.
However, the computational complexity remains a challenge due to the iterative multiscale wavelet transformations required for model training. Future work should focus on optimizing the implementation efficiency through parallel computing architectures and exploring hybrid deep learning paradigms that balance performance with computational feasibility. This study not only underscores the potential of wavelet–CNN synergies in biomedical imaging but also advocates for an adaptive algorithm development tailored to complex noise environments, providing both theoretical foundations and the empirical validation for advancing OCT image quality in clinical practice.
Author Contributions
Writing original draft preparation, F.L.; Software, Z.Y.; formal analysis, B.J.; data curation, B.J.; supervision, Q.W. All authors have read and agreed to the published version of the manuscript.
Funding
Fund Program for the Scientific Activities of Selected Returned Overseas Professionals in Shanxi Province, grant number 20210038.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
Thanks to the Shanxi Eye Hospital for providing data support for this work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Huang, D.; Swanson, E.A.; Lin, C.P.; Schuman, J.S.; Stinson, W.G.; Chang, W.; Hee, M.R.; Flotte, T.; Gregory, K.; Puliafito, C.A. Optical coherence tomography. Science 1991, 254, 1178–1181. [Google Scholar] [CrossRef] [PubMed]
- Cameron, A.; Lui, D.; Boroomand, A.; Glaister, J.; Wong, A.; Bizheva, K. Stochastic speckle noise compensation in optical coherence tomography using non-stationary spline-based speckle noise modelling. Biomed. Opt. Express 2013, 4, 1769–1785. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Tebini, S.; Seddik, H.; Ben Braiek, E. An advanced and adaptive mathematical function for an efficient anisotropic image filtering. Comput. Math. Appl. 2016, 72, 1369–1385. [Google Scholar] [CrossRef]
- Chen, Y.; Yamanaka, M.; Nishizawa, N. Speckle-Reduced Optical Coherence Tomography Using a Tunable Quasi-Supercontinuum Source. Photonics 2023, 10, 1338. [Google Scholar] [CrossRef]
- Fang, Y.; Shao, X.; Liu, B.; Lv, H. Optical coherence tomography image despeckling based on tensor singular value decomposition and fractional edge detection. Heliyon 2023, 9, e17735. [Google Scholar] [CrossRef]
- Proskurin, S.G. Raster scanning and averaging for reducing the influence of speckles in optical coherence tomography. Quantum Electron. 2012, 42, 495–499. [Google Scholar] [CrossRef]
- Duan, L.; Lee, H.Y.; Lee, G.; Agrawal, M.; Smith, G.T.; Ellerbee, A.K. Single-shot speckle noise reduction by interleaved optical coherence tomography. J. Biomed. Opt. 2014, 19, 120501. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Azam, M.A.; Gunalan, A.; Mattos, L.S. One-Step Enhancer: Deblurring and Denoising of OCT Images. Appl. Sci. 2022, 12, 10092. [Google Scholar] [CrossRef]
- Ozcan, A.; Bilenca, A.; Desjardins, A.E.; Bouma, B.E.; Tearney, G.J. Speckle reduction in optical coherence tomography images using digital filtering. J. Opt. Soc. Am. A-Opt. Image Sci. Vis. 2007, 24, 1901–1910. [Google Scholar] [CrossRef]
- Yang, L.; Lu, J.; Dai, M.; Ren, L.J.; Liu, W.Z.; Li, Z.Z.; Gong, X.H. Speckle noise removal applied to ultrasound image of carotid artery based on total least squares model. J. X-Ray Sci. Technol. 2016, 24, 749–760. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, Y.; Wang, J.; Zhang, S. Image improvement in the wavelet domain for optical coherence tomograms. J. Innov. Opt. Health Sci. 2011, 4, 73–78. [Google Scholar] [CrossRef]
- Chitchian, S.; Fiddy, M.A.; Fried, N.M. Denoising during optical coherence tomography of the prostate nerves via wavelet shrinkage using dual-tree complex wavelet transform. J. Biomed. Opt. 2009, 14, 014031. [Google Scholar] [CrossRef] [PubMed]
- Ismael, A.A.; Baykara, M. Image Denoising Based on Implementing Threshold Techniques in Multi-Resolution Wavelet Domain and Spatial Domain Filters. Trait. Du Signal 2022, 39, 1119–1131. [Google Scholar] [CrossRef]
- Zaki, F.; Wang, Y.; Su, H.; Yuan, X.; Liu, X. Noise adaptive wavelet thresholding for speckle noise removal in optical coherence tomography. Biomed. Opt. Express 2017, 8, 2720–2731. [Google Scholar] [CrossRef]
- Cao, J.; Wang, P.; Wu, B.; Shi, G.; Zhang, Y.; Li, X.; Zhang, Y.; Liu, Y. Improved wavelet hierarchical threshold filter method for optical coherence tomography image de-noising. J. Innov. Opt. Health Sci. 2018, 11, 1850012. [Google Scholar] [CrossRef]
- Subhedar, J.; Urooj, S.; Mahajan, A. Retinal Optical Coherence Tomography Image Denoising Using Modified Soft Thresholding Wavelet Transform. Trait. Du Signal 2023, 40, 1179–1185. [Google Scholar] [CrossRef]
- Duan, L.; Cai, J.; Wang, L.; Shi, Y. Research on Seismic Signal Denoising Model Based on DnCNN Network. Appl. Sci. 2025, 15, 2083. [Google Scholar] [CrossRef]
- Ran, A.R.; Tham, C.C.; Chan, P.P.; Cheng, C.Y.; Tham, Y.C.; Rim, T.H.; Cheung, C.Y. Deep learning in glaucoma with optical coherence tomography: A review. Eye 2021, 35, 188–201. [Google Scholar] [CrossRef]
- Bogacki, P.; Dziech, A. Effective Deep Learning Approach to Denoise Optical Coherence Tomography Images Using BM3D-Based Preprocessing of the Training Data Including Both Healthy and Pathological Cases. IEEE Access 2023, 11, 65395–65406. [Google Scholar] [CrossRef]
- Lee, W.; Nam, H.S.; Seok, J.Y.; Oh, W.Y.; Kim, J.W.; Yoo, H. Deep learning-based image enhancement in optical coherence tomography by exploiting interference fringe. Commun. Biol. 2023, 6, 464. [Google Scholar] [CrossRef]
- Devalla, S.K.; Subramanian, G.; Pham, T.H.; Wang, X.; Perera, S.; Tun, T.A.; Aung, T.; Schmetterer, L.; Thiéry, A.H.; Girard, M.J. A Deep Learning Approach to Denoise Optical Coherence Tomography Images of the Optic Nerve Head. Sci. Rep. 2019, 9, 14454. [Google Scholar] [CrossRef]
- Chen, Z.; Zeng, Z.; Shen, H.; Zheng, X.; Dai, P.; Ouyang, P. DN-GAN: Denoising generative adversarial networks for speckle noise reduction in optical coherence tomography images. Biomed. Signal Process. Control 2020, 55, 101632. [Google Scholar] [CrossRef]
- Idress, W.M.; Zhao, Y.; Abouda, K.A.; Yang, S. DRDA-Net: Deep Residual Dual-Attention Network with Multi-Scale Approach for Enhancing Liver and Tumor Segmentation from CT Images. Appl. Sci. 2025, 15, 2311. [Google Scholar] [CrossRef]
- Hu, Y.; Ren, J.; Yang, J.; Bai, R.; Liu, J. Noise reduction by adaptive-SIN filtering for retinal OCT images. Sci. Rep. 2021, 11, 19498. [Google Scholar] [CrossRef]
- Song, D.; Liu, Y.; Lin, X.; Liu, J.; Tan, J. Research and Comparison of OCT Image Speckle Denoising Algorithm. In Proceedings of the 2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 24–26 May 2019; pp. 1554–1558. [Google Scholar]
- Agrawal, H.; Desai, K. Canny edge detection: A comprehensive review. Int. J. Tech. Res. Sci. 2024, 9, 27–35. [Google Scholar] [CrossRef]
- Wang, L.; Sun, Y. Improved Canny edge detection algorithm. In Proceedings of the 2021 2nd International Conference on Computer Science and Management Technology (ICCSMT), Shanghai, China, 12–14 November 2021; pp. 414–417. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).