PGA Estimates for Vertical Ground Motion and Varying Deep Geology Site Surroundings—A Case Study of Banja Luka
Abstract
1. Introduction
2. Regional Seismicity, Geological Site Surroundings, and Official Vertical PGA Estimates for Banja Luka
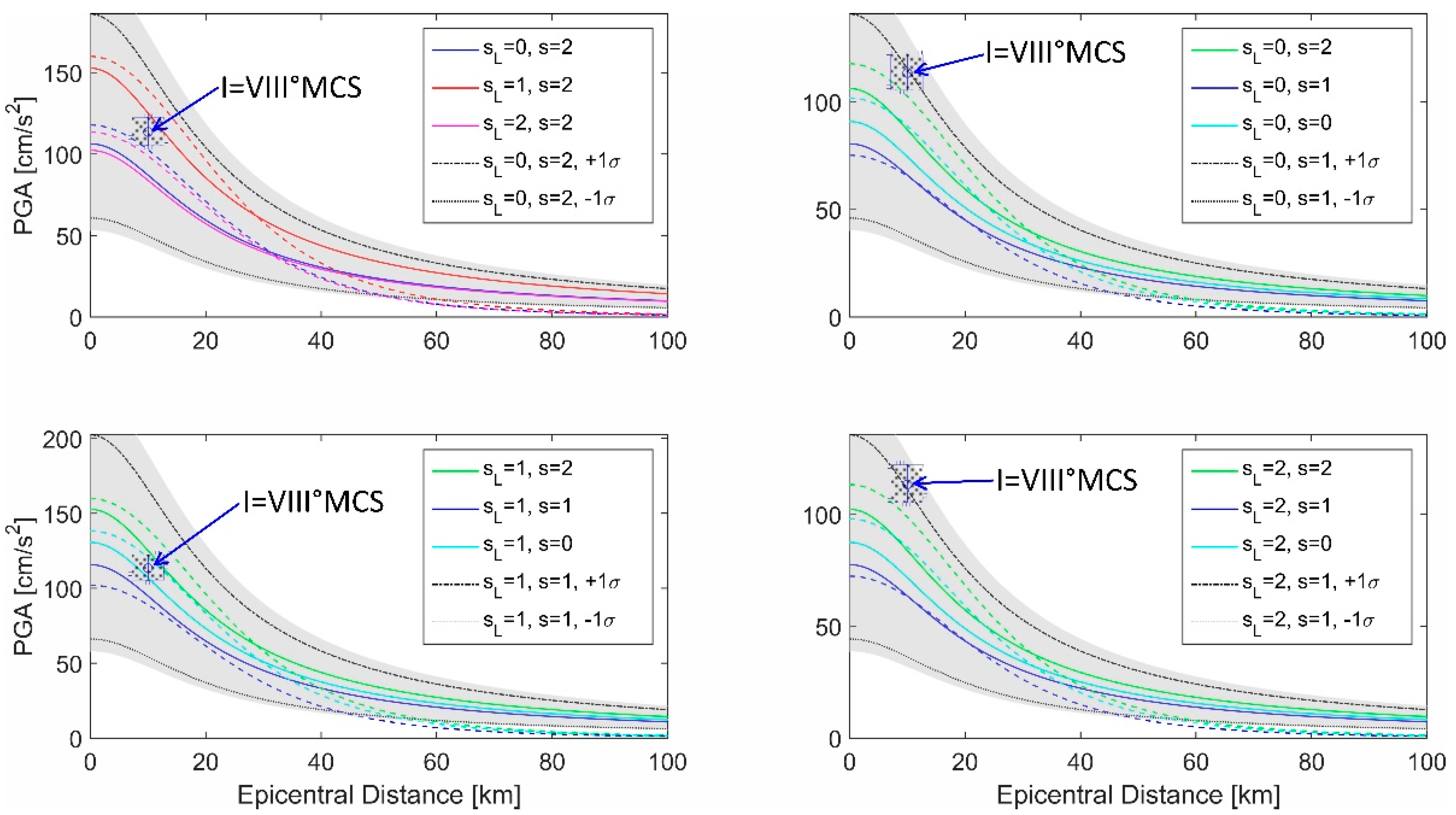
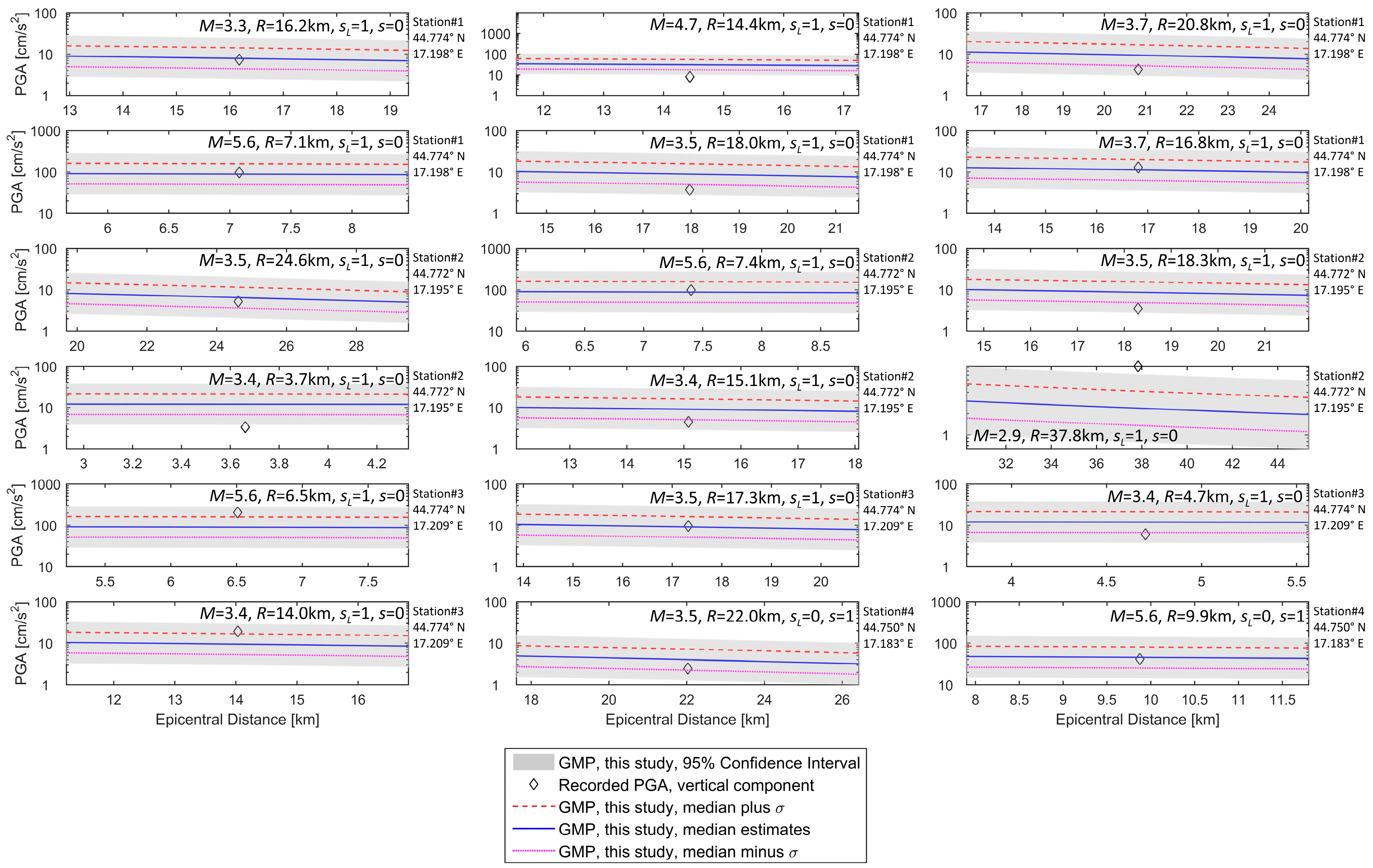
3. GMPEs for Vertical PGA Values for Varying Deep Geology
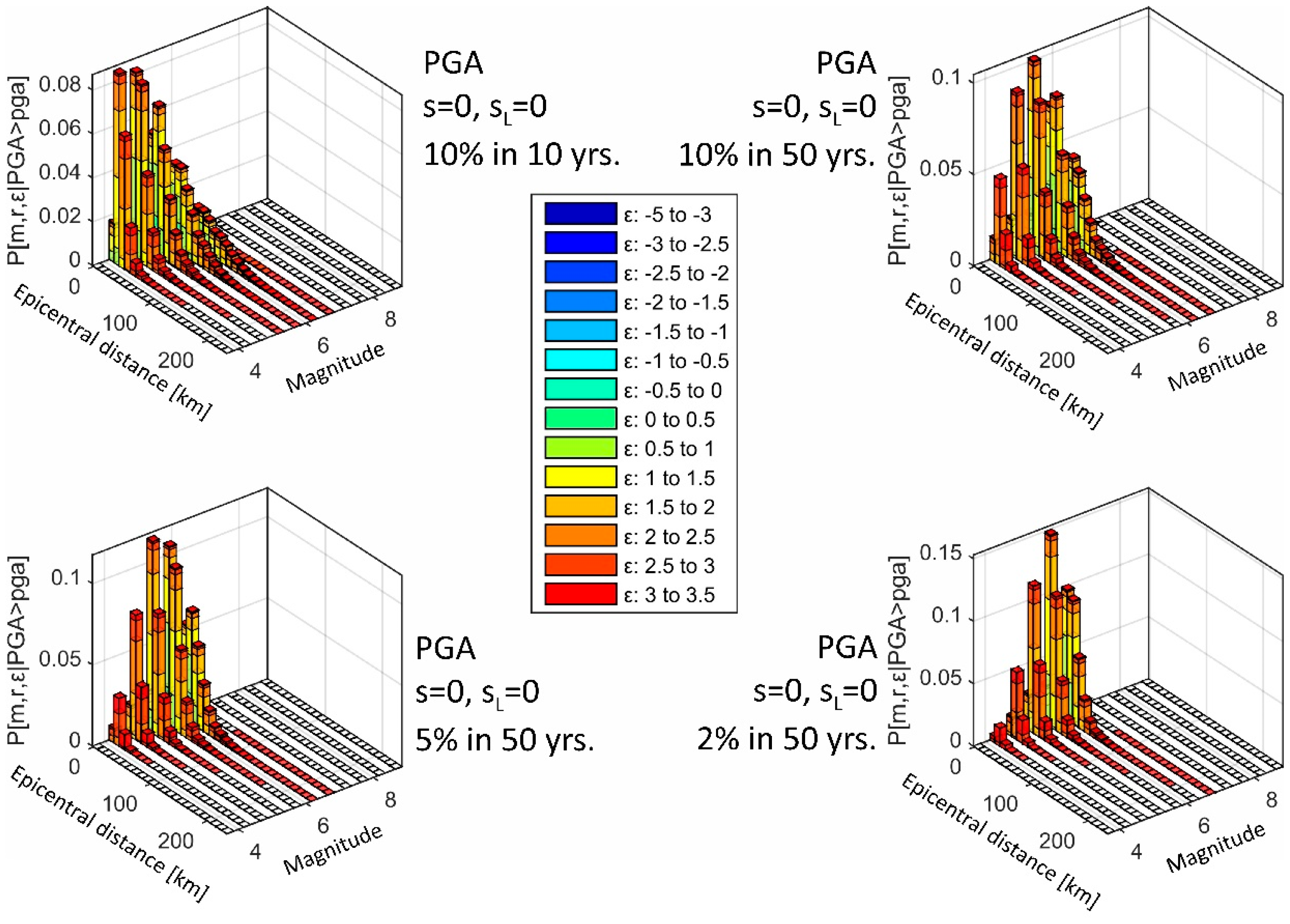
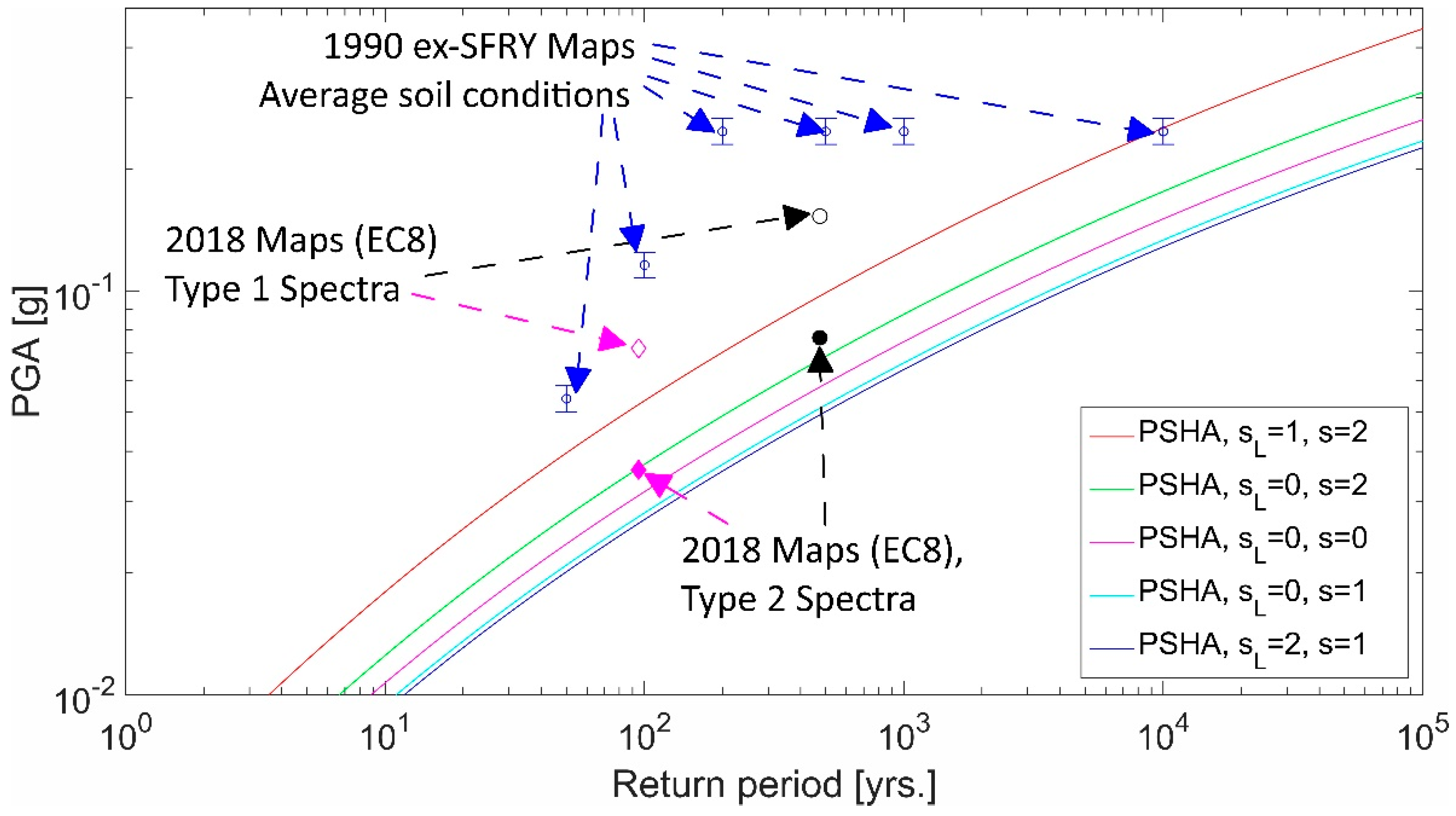
4. PSHA for the Case Study Site in Banja Luka
5. Conclusions
- Site conditions have a significant impact on the vertical PGA,
- The deep geology effects are even greater than the local soil effects,
- VHpga values are influenced by deep geology, local soil, source-to-site distance, and the probability level of empirical estimates,
- Only the combination of stiff soil and deep geology rocks may produce a median empirical vertical PGA equivalent to that associated with VIII °MCS, which was the predominant intensity of the 1969 Earthquake in Banja Luka,
- Vertical PGA probabilistic hazard estimates are dominated by local seismicity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ag | Horizontal PGA value from the official seismic hazard map |
| EC8 | Eurocode 8 |
| GMPE | Ground Motion Prediction Equations |
| PGA | Peak Ground Acceleration |
| PGAvert | Peak Ground Acceleration for vertical ground motion direction |
| PSHA | Probabilistic Seismic Hazard Assessment |
| s | Deep geology parameter |
| S | Soil factor according to Eurocode 8 |
| sL | Local soil parameter |
| Tr | Return period |
| VHpga | Vertical to horizontal PGA ratio |
| VS | Average shear wave velocity |
References
- EN 1998-1:2004; Eurocode 8: Design of Structures for Earthquake Resistance. Part 1: General Rules, Seismic Actions and Rules for Buildings. CEN: Brussels, Belgium, 2004.
- Bulajić, B.Đ.; Pavić, G.; Hadzima-Nyarko, M. PGA vertical estimates for deep soils and deep geological sediments—A case study of Osijek (Croatia). Comput. Geosci. 2022, 158, 104985. [Google Scholar] [CrossRef]
- Nemutlu, Ö.F.; Sarı, A. Seismic Performance of the Kahramanmaraş Earthquakes: Ground Motion Prediction Models and the Role of Vertical Components. Bitlis Eren Üniversitesi Fen Bilim. Derg. 2025, 14, 610–632. [Google Scholar] [CrossRef]
- Nogoshi, M.; Igarashi, T. On the Amplitude Characteristics of Microtremor (Part 1). Zisin (J. Seismol. Soc. Japan. 2nd Ser.) 1970, 23, 281–303. [Google Scholar] [CrossRef][Green Version]
- Nogoshi, M.; Igarashi, T. On the Amplitude Characteristics of Microtremor (Part 2). Zisin (J. Seismol. Soc. Japan. 2nd Ser.) 1971, 24, 26–40. [Google Scholar] [CrossRef]
- Nakamura, Y. Clear identification of fundamental idea of Nakamura’s technique and its applications. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000; pp. 1–8. [Google Scholar]
- Nakamura, Y. A method for Dynamic Characteristics Estimation of Subsurface Using Microtremor on The Ground Surface; Railway Technical Research Institute: Tokyo, Japan, 1989; pp. 25–30. [Google Scholar]
- Nakamura, Y. Real-time information systems for hazards mitigation. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. [Google Scholar]
- Bonnefoy-Claudet, S.; Köhler, A.; Cornou, C.; Wathelet, M.; Bard, P.-Y. Effects of Love Waves on Microtremor H/V Ratio. Bull. Seismol. Soc. Am. 2008, 98, 288–300. [Google Scholar] [CrossRef]
- Trifunac, M.D.; Brady, A.G. On the correlation of seismic intensity scales with the peaks of recorded strong ground motion. Bull. Seismol. Soc. Am. 1975, 65, 139–162. [Google Scholar]
- Seed, H.B.; Murarka, R.; Lysmer, J.; Idriss, I.M. Relationships of maximum acceleration, maximum velocity, distance from source, and local site conditions for moderately strong earthquakes. Bull. Seismol. Soc. Am. 1976, 66, 1323–1342. [Google Scholar]
- Seed, H.B.; Ugas, C.; Lysmer, J. Site-dependent spectra for earthquake-resistant design. Bull. Seismol. Soc. Am. 1976, 66, 221–243. [Google Scholar] [CrossRef]
- Bulajić, B.Đ.; Bajić, S.; Stojnić, N. The effects of geological surroundings on earthquake-induced snow avalanche prone areas in the Kopaonik region. Cold Reg. Sci. Technol. 2018, 149, 29–45. [Google Scholar] [CrossRef]
- Bulajić, B.Đ.; Hadzima-Nyarko, M.; Pavić, G. Vertical to Horizontal UHS Ratios for Low to Medium Seismicity Regions with Deep Soil atop Deep Geological Sediments—An Example of the City of Osijek, Croatia. Appl. Sci. 2021, 11, 6782. [Google Scholar] [CrossRef]
- Bulajić, B.Đ.; Hadzima-Nyarko, M.; Pavić, G. Horizontal UHS Amplitudes for Regions with Deep Soil Atop Deep Geological Sediments—An Example of Osijek, Croatia. Appl. Sci. 2021, 11, 6296. [Google Scholar] [CrossRef]
- Bulajic, B.Đ.; Hadzima-Nyarko, M.; Pavic, G. PGA estimates for deep soils atop deep geological sediments—An example of Osijek, Croatia. Geomech. Eng. 2022, 30, 233–246. [Google Scholar] [CrossRef]
- Bulajić, B.Ð.; Manić, M.I.; Lađinović, Đ. Effects of shallow and deep geology on seismic hazard estimates: A case study of pseudo-acceleration response spectra for the northwestern Balkans. Nat. Hazards 2013, 69, 573–588. [Google Scholar] [CrossRef]
- Jordanovski, L.R.; Lee, V.W.; Manić, M.I.; Olumčeva, T.; Sinadnovski, C.; Todorovska, M.I.; Trifunac, M.D. Strong Earthquake Ground Motion Data in EQINFOS: Yugoslavia. Part I.; Department of Civil Engineering, University of Southern California: Los Angeles, CA, USA, 1987. [Google Scholar]
- Lee, V.W. Influence of Local Soil and Geologic Site Conditions on Pseudo Relative Velocity Spectrum Amplitudes of Recorded Strong Motion Accelerations; Department of Civil Engineering, University of Southern California: Los Angeles, CA, USA, 1987. [Google Scholar]
- Trifunac, M.; Lee, V.; Živčić, M.; Manić, M. On the correlation of Mercalli-Cancani-Sieberg intensity scale in Yugoslavia with the peaks of recorded strong earthquake ground motion. Eur. Earthq. Eng. 1991, 5, 27–33. [Google Scholar]
- Lee, V.; Trifunac, M. Empirical scaling of Fourier amplitude spectra in former Yugoslavia. Eur. Earthq. Eng. 1993, 7, 47–61. [Google Scholar]
- Lee, V.W.; Manić, M.I. Empirical scaling of response spectra in former Yugoslavia. In Proceedings of the 10th European Conference on Earthquake Engineering, Vienna, Austria, 28 August–2 September 1994; pp. 2567–2572. [Google Scholar]
- Lee, V.W.; Trifunac, M.D.; Bulajić, B.Đ. Seismic microzoning in Novi Sad, Serbia—A case study in a low-seismicity region that is exposed to large and distant earthquakes. J. Seismol. 2023, 27, 979–997. [Google Scholar] [CrossRef]
- Lee, V.W.; Trifunac, M.D.; Bulajić, B.Đ. Seismic hazard mapping for peak ground velocity: Microzonation of Novi Sad, Serbia—A case study in a low-seismicity region exposed to large and distant earthquakes. J. Seismol. 2025, 29, 85–105. [Google Scholar] [CrossRef]
- Lee, V.W.; Trifunac, M.D.; Bulajić, B.Đ.; Manić, M.I.; Herak, D.; Herak, M. Seismic microzoning of Belgrade. Soil Dyn. Earthq. Eng. 2017, 97, 395–412. [Google Scholar] [CrossRef]
- Lee, V.W.; Trifunac, M.D.; Bulajić, B.D.; Manić, M.I.; Herak, D.; Herak, M.; Dimov, G. Seismic microzoning in Skopje, Macedonia. Soil Dyn. Earthq. Eng. 2017, 98, 166–182. [Google Scholar] [CrossRef]
- Lee, V.W.; Trifunac, M.D.; Bulajić, B.Đ.; Manić, M.I.; Herak, D.; Herak, M.; Dimov, G.; Gičev, V. Seismic microzoning of Štip in Macedonia. Soil Dyn. Earthq. Eng. 2017, 98, 54–66. [Google Scholar] [CrossRef]
- Ustaszewski, K.; Herak, M.; Tomljenović, B.; Herak, D.; Matej, S. Neotectonics of the Dinarides–Pannonian Basin transition and possible earthquake sources in the Banja Luka epicentral area. J. Geodyn. 2014, 82, 52–68. [Google Scholar] [CrossRef]
- USGS. Earthquake Catalogue for all Earthquakes with Mw ≥ 3.0 in the Period Between 1900 and April 2025 for the Geographic Region Between 41° N and 47° N, and 13° E and 23° E; USGS: Reston, VA, USA, 2025.
- EMSC-CSEM. M 5.4–CROATIA–2020-03-22 05:24:02 UTC. Available online: https://www.emsc-csem.org/Earthquake/earthquake.php?id=840695#scientific (accessed on 17 April 2025).
- Ganas, A.; Elias, P.; Valkaniotis, S.; Tsironi, V.; Karasante, I.; Briole, P. Petrinja Earthquake Moved Crust 10 Feet. Available online: https://temblor.net/earthquake-insights/petrinja-earthquake-moved-crust-10-feet-12410/ (accessed on 17 April 2025).
- Lee, V.W.; Manić, M.I.; Bulajić, B.Ð.; Herak, D.; Herak, M.; Trifunac, M.D. Microzonation of Banja Luka for performance-based earthquake-resistant design. Soil Dyn. Earthq. Eng. 2015, 78, 71–88. [Google Scholar] [CrossRef]
- Mojičević, M.; Vilovski, S.; Tomić, B. Basic Geological Map–Banja Luka, L33-119; Federal Geologal Survey: Belgrade, Serbia, 1976. [Google Scholar]
- BAS EN 1998-1/NA:2018; Seismic Zone Maps and Reference Ground Accelerations Therein of B&H. Maps Accompanying National Annexes (NA): Bosnia and Herzegovina, 2018. Available online: http://eurokodovi.ba/seizmika/ (accessed on 1 May 2025).
- Ademović, N.; Demir, V.; Cvijić-Amulić, S.; Málek, J.; Prachař, I.; Vackář, J. Compilation of the seismic hazard maps in Bosnia and Herzegovina. Soil Dyn. Earthq. Eng. 2021, 141, 106500, Erratum in Soil Dyn. Earthq. Eng. 2023, 164, 107633. [Google Scholar] [CrossRef]
- SFRY. Temporary Technical Regulations for Construction in Seismic Areas; 39/64; Official Gazette of SFRY: Belgrade, Serbia, 1964. [Google Scholar]
- SFRY. Book of Rules on Technical Norms for Construction of High-Rise Buildings in Seismic Regions; 31/81, 49/82; Official Gazette of SFRY: Belgrade, Serbia, 1982. [Google Scholar]
- SFRY. Book of Rules on Technical Norms for Construction of High-Rise Buildings in Seismic Regions; 31/81, 49/82, 29/83, 21/88, 52/90; Official Gazette of SFRY: Belgrade, Serbia, 1990. [Google Scholar]
- SFRY. Book of Rules on Technical Norms for Construction of High-Rise Buildings in Seismic Regions; 31/81; Official Gazette of SFRY: Belgrade, Serbia, 1981. [Google Scholar]
- Lee, V.; Trifunac, M.; Herak, M.; Živčič, M.; Herak, D. MLSM computed from strong motion accelerograms recorded in Yugoslavia. Earthq. Eng. Struct. Dyn. 1990, 19, 1167–1179. [Google Scholar] [CrossRef]
- Datta, T.K. Seismic Analysis of Structures; John Wiley & Sons (Asia) Pte Ltd.: Singapore, 2010; p. 464. [Google Scholar]
- Herak, M. Conversion between the local magnitude (ML) and the moment magnitude (Mw) for earthquakes in the Croatian Earthquake Catalogue. Geofizika 2020, 37, 197–211. [Google Scholar] [CrossRef]
- Scordilis, E.M. Empirical Global Relations Converting MS and mb to Moment Magnitude. J. Seismol. 2006, 10, 225–236. [Google Scholar] [CrossRef]
- Das, R.; Sharma, M.L.; Wason, H.R.; Choudhury, D.; Gonzalez, G. A Seismic Moment Magnitude Scale. Bull. Seismol. Soc. Am. 2019, 109, 1542–1555. [Google Scholar] [CrossRef]
- Das, R.; Das, A. Limitations of Mw and M Scales: Compelling Evidence Advocating for the Das Magnitude Scale (Mwg)—A Critical Review and Analysis. Indian Geotech. J. 2025, in press. [Google Scholar] [CrossRef]
- Ambraseys, N.; Douglas, J.; Margaris, B.; Sigbjörnsson, R.; Berge-Thierry, C.; Suhadolc, P.; Costa, G.; Smit, P. Dissemination of European strong-motion data. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Ambraseys, N.; Douglas, J.; Margaris, B.; Sigbjörnsson, R.; Smit, P.; Suhadolc, P. Internet site for European strong motion data. In Proceedings of the 12th European Conference on Earthquake Engineering, London, UK, 9–13 September 2002. [Google Scholar]
- Bilgin, H.; Hysenlliu, M. Comparison of near and far-fault ground motion effects on low and mid-rise masonry buildings. J. Build. Eng. 2020, 30, 101248. [Google Scholar] [CrossRef]
- Bulajić, B.Đ.; Lozančić, S.; Bajić, S.; Radu, D.; Işık, E.; Negovanović, M.; Hadzima-Nyarko, M. UHS estimates for vertical strong ground motion and varying deep geological site surroundings—A case study of the city of Banja Luka. Appl. Sci. 2025. submitted for publication. [Google Scholar]
- Bulajić, B.Đ.; Lozančić, S.; Bajić, S.; Radu, D.; Işık, E.; Negovanović, M.; Hadzima-Nyarko, M. Horizontal UHS predictions for varying deep geology conditions—A case study of the city of Banja Luka. Sustainability 2025. submitted for publication. [Google Scholar]
- Bulajić, B.Đ.; Lozančić, S.; Bajić, S.; Starčev-Ćurčin, A.; Šešlija, M.; Kovačević, M.; Hadzima-Nyarko, M. Horizontal PGA estimates for varying deep geological conditions—A case study of Banja Luka. Appl. Sci. 2025. submitted for publication. [Google Scholar]
- Chioccarelli, E.; Cito, P.; Iervolino, I.; Giorgio, M. REASSESS V2.0: Software for single- and multi-site probabilistic seismic hazard analysis. Bull. Earthq. Eng. 2019, 17, 1769–1793. [Google Scholar] [CrossRef]
- McGuire, R.K. FORTRAN Computer Program for Seismic Risk Analysis; US Geological Survey: Reston, VA, USA, 1976; pp. 67–76. [Google Scholar]
- Cornell, C.A. Engineering seismic risk analysis. Bull. Seismol. Soc. Am. 1968, 58, 1583–1606. [Google Scholar] [CrossRef]
- Giardini, D.; Woessner, J.; Danciu, L.; Crowley, H.; Cotton, F.; Grünthal, G.; Pinho, R.; Valensise, L.; Consortium, S. European Seismic Hazard Map for Peak Ground Acceleration, 10% Exceedance Probabilities in 50 years; Swiss Seismological Servise: Zurich, Switzerland, 2013. [Google Scholar]
- Woessner, J.; Laurentiu, D.; Giardini, D.; Crowley, H.; Cotton, F.; Grünthal, G.; Valensise, G.; Arvidsson, R.; Basili, R.; Demircioglu, M.B.; et al. The 2013 European Seismic Hazard Model: Key components and results. Bull. Earthq. Eng. 2015, 13, 3553–3596. [Google Scholar] [CrossRef]
- Pagani, M.; Garcia-Pelaez, J.; Gee, R.; Johnson, K.; Poggi, V.; Styron, R.; Weatherill, G.; Simionato, M.; Viganò, D.; Danciu, L.; et al. Global Earthquake Model (GEM) Seismic Hazard Map (Version 2018.1–December 2018); GEM Foundation: Pavia, Italy, 2018. [Google Scholar]
- Stucchi, M.; Rovida, A.; Gomez Capera, A.A.; Alexandre, P.; Camelbeeck, T.; Demircioglu, M.B.; Gasperini, P.; Kouskouna, V.; Musson, R.M.W.; Radulian, M.; et al. The SHARE European Earthquake Catalogue (SHEEC) 1000–1899. J. Seismol. 2013, 17, 523–544. [Google Scholar] [CrossRef]
- Grünthal, G.; Wahlström, R.; Stromeyer, D. The SHARE European Earthquake Catalogue (SHEEC) for the time period 1900–2006 and its comparison to the European-Mediterranean Earthquake Catalogue (EMEC). J. Seismol. 2013, 17, 1339–1344. [Google Scholar] [CrossRef]
- Grünthal, G.; Wahlström, R. The European-Mediterranean Earthquake Catalogue (EMEC) for the last millennium. J. Seismol. 2012, 16, 535–570. [Google Scholar] [CrossRef]
- Lee, V.W.; Trifunac, M.D.; Bulajić, B.; Manić, M. A preliminary empirical model for frequency-dependent attenuation of Fourier amplitude spectra In Serbia from the Vrancea earthquakes. Soil Dyn. Earthq. Eng. 2016, 83, 167–179. [Google Scholar] [CrossRef]
- Lee, V.W.; Trifunac, M.D.; Bulajić, B.Đ.; Manić, M.I. Preliminary empirical scaling of pseudo relative velocity spectra in Serbia from the Vrancea earthquakes. Soil Dyn. Earthq. Eng. 2016, 86, 41–54. [Google Scholar] [CrossRef]
- Bazzurro, P.; Allin Cornell, C. Disaggregation of seismic hazard. Bull. Seismol. Soc. Am. 1999, 89, 501–520. [Google Scholar] [CrossRef]
- Trkulja, D. Earthquakes in Banja Luka. In Proceedings of the International Conference on Earthquake Engineering, Banja Luka, Bosnia and Herzegovina, 26–28 October 2009; pp. 43–57. [Google Scholar]
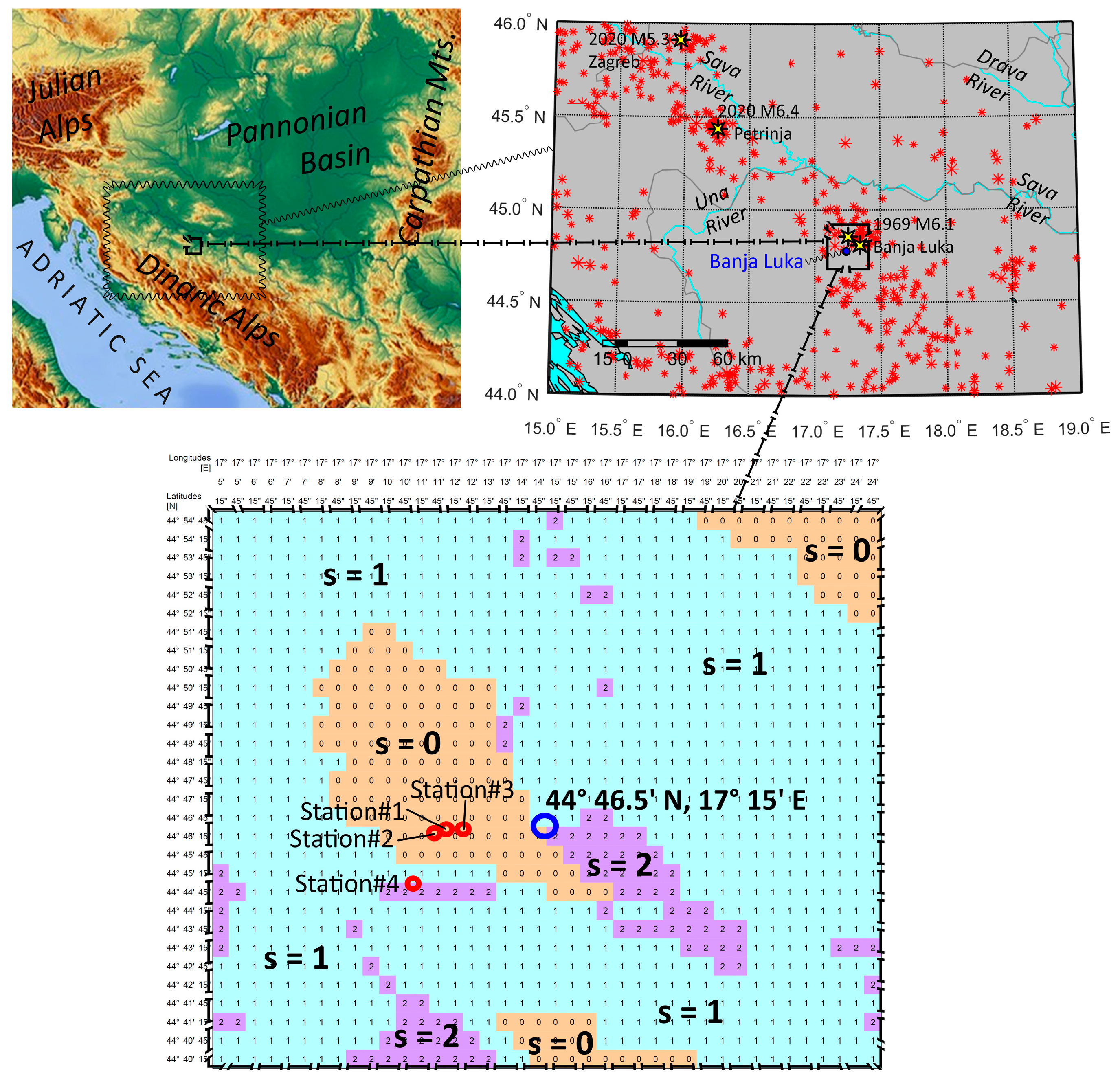


| Official Zoning Map | I [°MCS] | PGA [g] |
|---|---|---|
| 1950 | VII | 0.052–0.056 |
| 1982 | VIII | 0.112–0.120 |
| 1990—50 yrs. | VII | 0.052–0.056 |
| 1990—100 yrs. | VIII | 0.112–0.120 |
| 1990—200 yrs. | IX | 0.239–0.257 |
| 1990—500 yrs. | IX | 0.239–0.257 |
| 1990—1000 yrs. | IX | 0.239–0.257 |
| 1990—10,000 yrs. | IX | 0.239–0.257 |
| 2018—95 yrs. | VI–VIII | 0.036–0.072 |
| 2018—475 yrs. | VII–IX | 0.077–0.153 |
| I | PGA [g] | VHpga | ||||
|---|---|---|---|---|---|---|
| −1σ | Median | +1σ | −1σ | Median | +1σ | |
| V °MCS | 0.0113 | 0.0118 | 0.0122 | 0.530 | 0.491 | 0.455 |
| VI °MCS | 0.0243 | 0.0252 | 0.0261 | 0.582 | 0.540 | 0.500 |
| VII °MCS | 0.0521 | 0.0540 | 0.0560 | 0.640 | 0.593 | 0.550 |
| VIII °MCS | 0.1115 | 0.1157 | 0.1201 | 0.703 | 0.652 | 0.604 |
| IX °MCS | 0.2390 | 0.2480 | 0.2573 | 0.773 | 0.716 | 0.664 |
| X °MCS | 0.5122 | 0.5315 | 0.5514 | 0.849 | 0.787 | 0.729 |
| Eurocode 8 [1] Ground Types | Vertical PGA |
|---|---|
| Eurocode 8, Type 1 Spectrum (MS > 5.5), all ground types [1] | ag × 0.900 |
| Eurocode 8, Type 2 Spectrum (MS ≤ 5.5), all ground types [1] | ag × 0.450 |
| 1964 code of former Yugoslavia [36] | ag × 0.330 |
| 1981 code of former Yugoslavia [39] | ag × 0.700 |
| GMPEs for California, USA [19], geological rocks | ag × 0.760 |
| GMPEs for California, USA [19], intermediate geological sites | ag × 0.718 |
| GMPEs for California, USA [19], geological sediments | ag × 0.681 |
| GMPEs for former Yugoslavia [22], all deep geology types | ag × 0.720 |
| Local Soil Parameters | Local Soil Categorical Variables | Deep Geology Parameters | Deep Geology Categorical Variables |
|---|---|---|---|
| “Rock” soil sites: sL = 0 | SL1 = SL2 = 0 | Basement (geological) rock: s = 2 | SG1 = SG2 = 0 |
| Stiff soil sites: sL = 1 | SL1 = 1 and SL2 = 0 | Intermediate (or complex) sites: s = 1 | SG1 = 1 and SG2 = 0 |
| Deep soil sites: sL = 2 | SL1 = 0 and SL2 = 1 | (Deep geological) Sediments: s = 0 | SG1 = 0 and SG2 = 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulajić, B.; Lozančić, S.; Bajić, S.; Starčev-Ćurčin, A.; Šešlija, M.; Kovačević, M.; Hadzima-Nyarko, M. PGA Estimates for Vertical Ground Motion and Varying Deep Geology Site Surroundings—A Case Study of Banja Luka. Appl. Sci. 2025, 15, 6542. https://doi.org/10.3390/app15126542
Bulajić B, Lozančić S, Bajić S, Starčev-Ćurčin A, Šešlija M, Kovačević M, Hadzima-Nyarko M. PGA Estimates for Vertical Ground Motion and Varying Deep Geology Site Surroundings—A Case Study of Banja Luka. Applied Sciences. 2025; 15(12):6542. https://doi.org/10.3390/app15126542
Chicago/Turabian StyleBulajić, Borko, Silva Lozančić, Senka Bajić, Anka Starčev-Ćurčin, Miloš Šešlija, Miljan Kovačević, and Marijana Hadzima-Nyarko. 2025. "PGA Estimates for Vertical Ground Motion and Varying Deep Geology Site Surroundings—A Case Study of Banja Luka" Applied Sciences 15, no. 12: 6542. https://doi.org/10.3390/app15126542
APA StyleBulajić, B., Lozančić, S., Bajić, S., Starčev-Ćurčin, A., Šešlija, M., Kovačević, M., & Hadzima-Nyarko, M. (2025). PGA Estimates for Vertical Ground Motion and Varying Deep Geology Site Surroundings—A Case Study of Banja Luka. Applied Sciences, 15(12), 6542. https://doi.org/10.3390/app15126542










