Rugby Sevens sRPE Workload Imputation Using Objective Models of Measurement
Abstract
1. Introduction
2. Materials and Methods
2.1. General Methods
2.2. Imputation of sRPE
3. Results
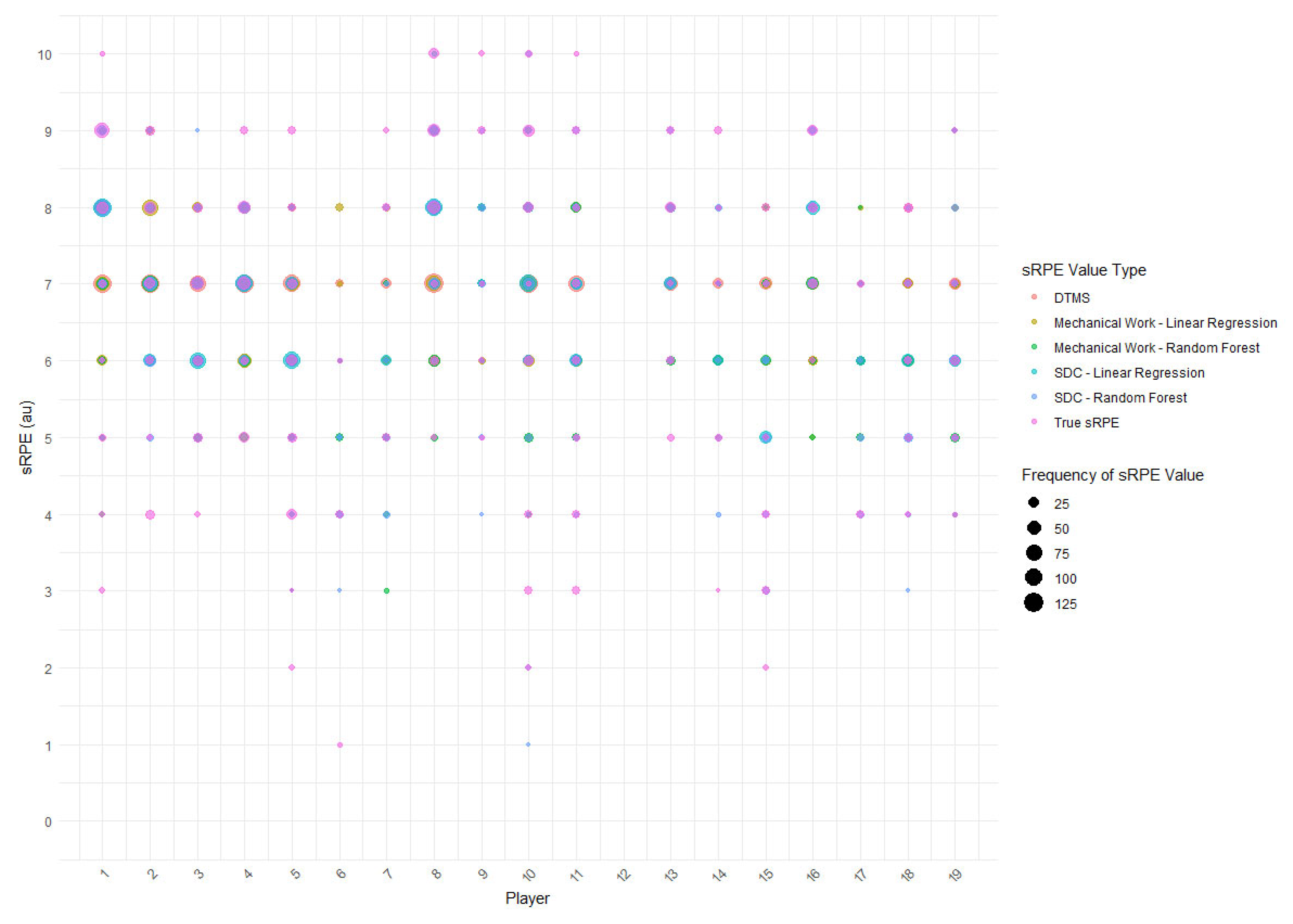
3.1. Description of Data
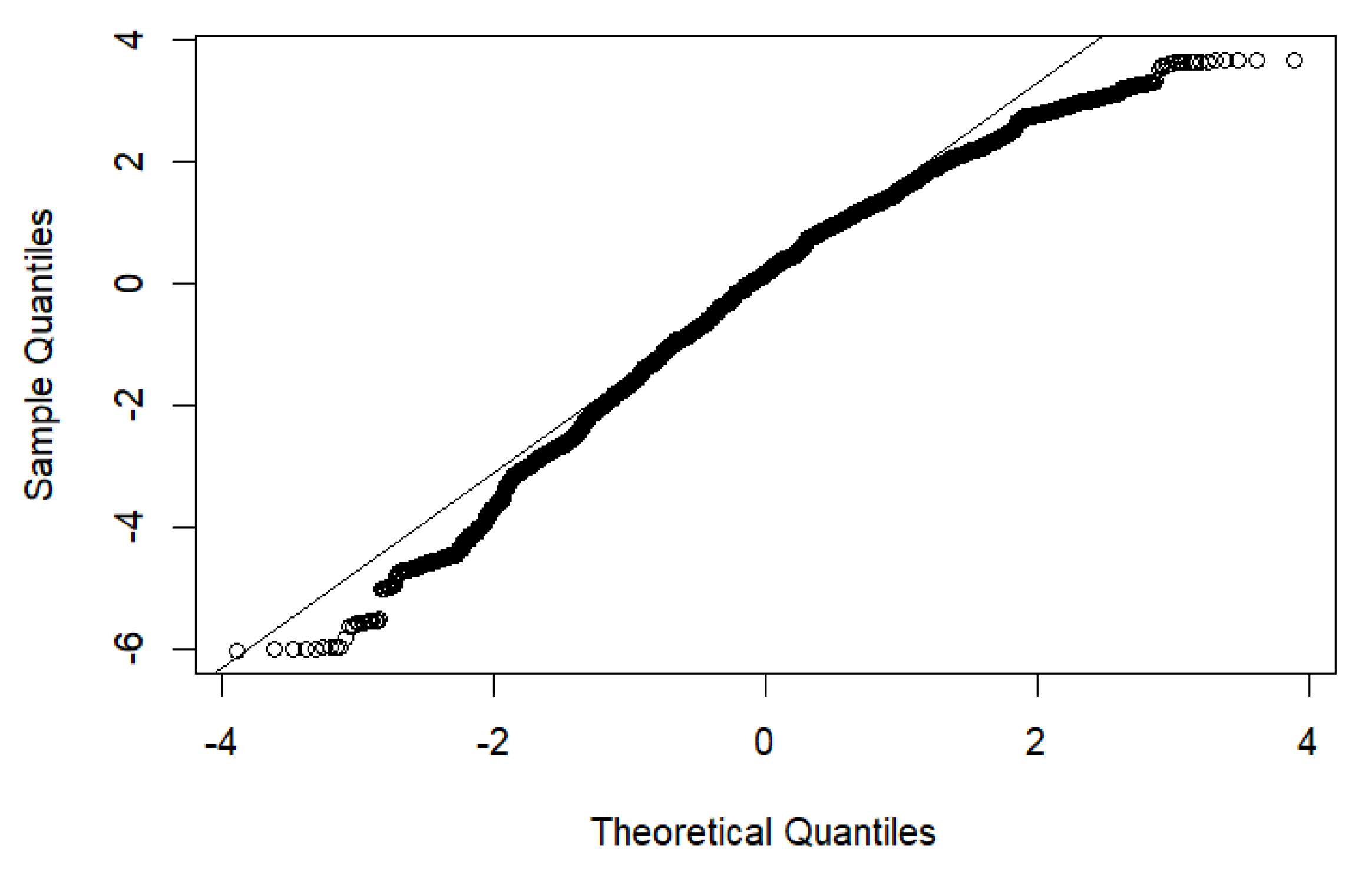
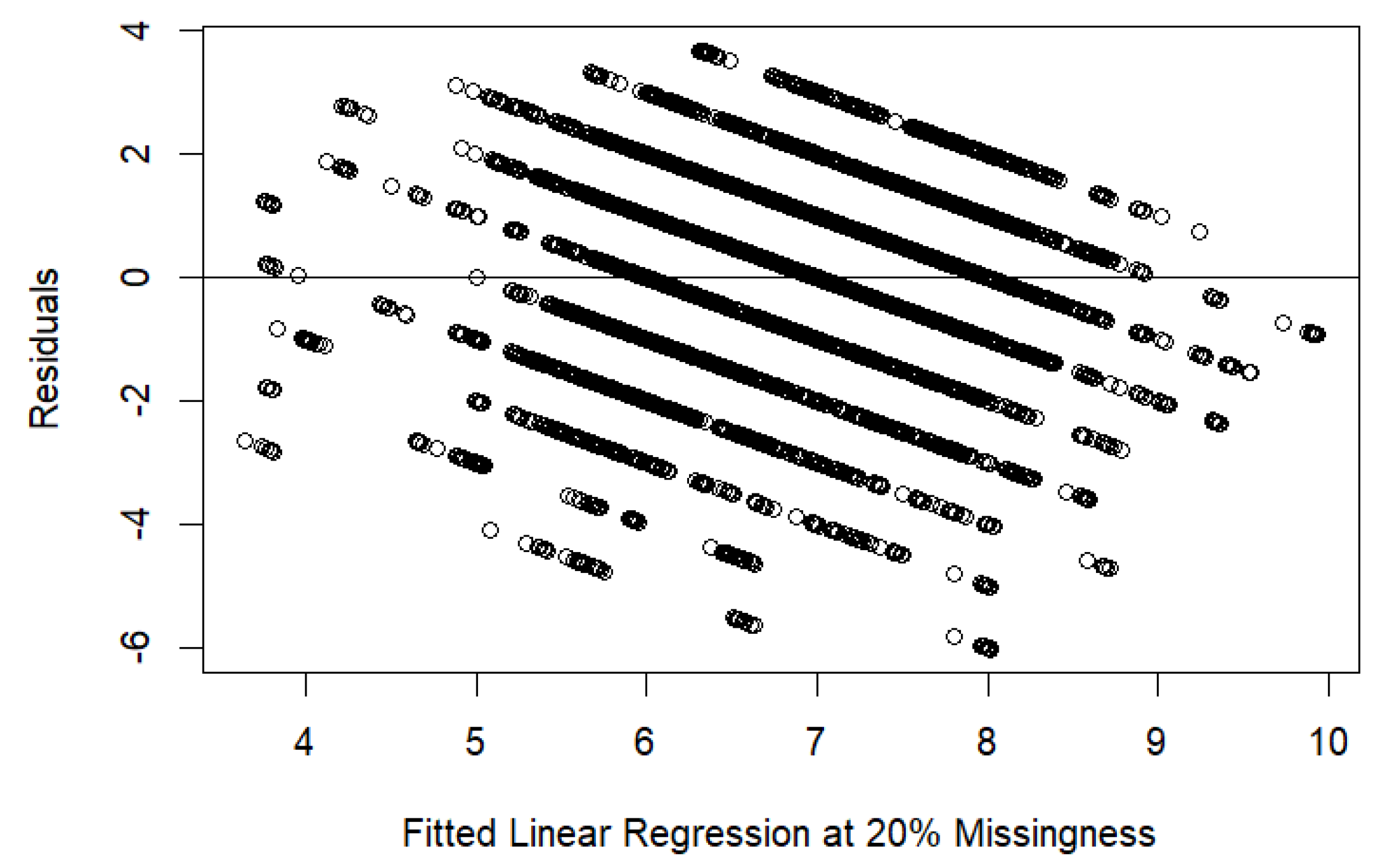
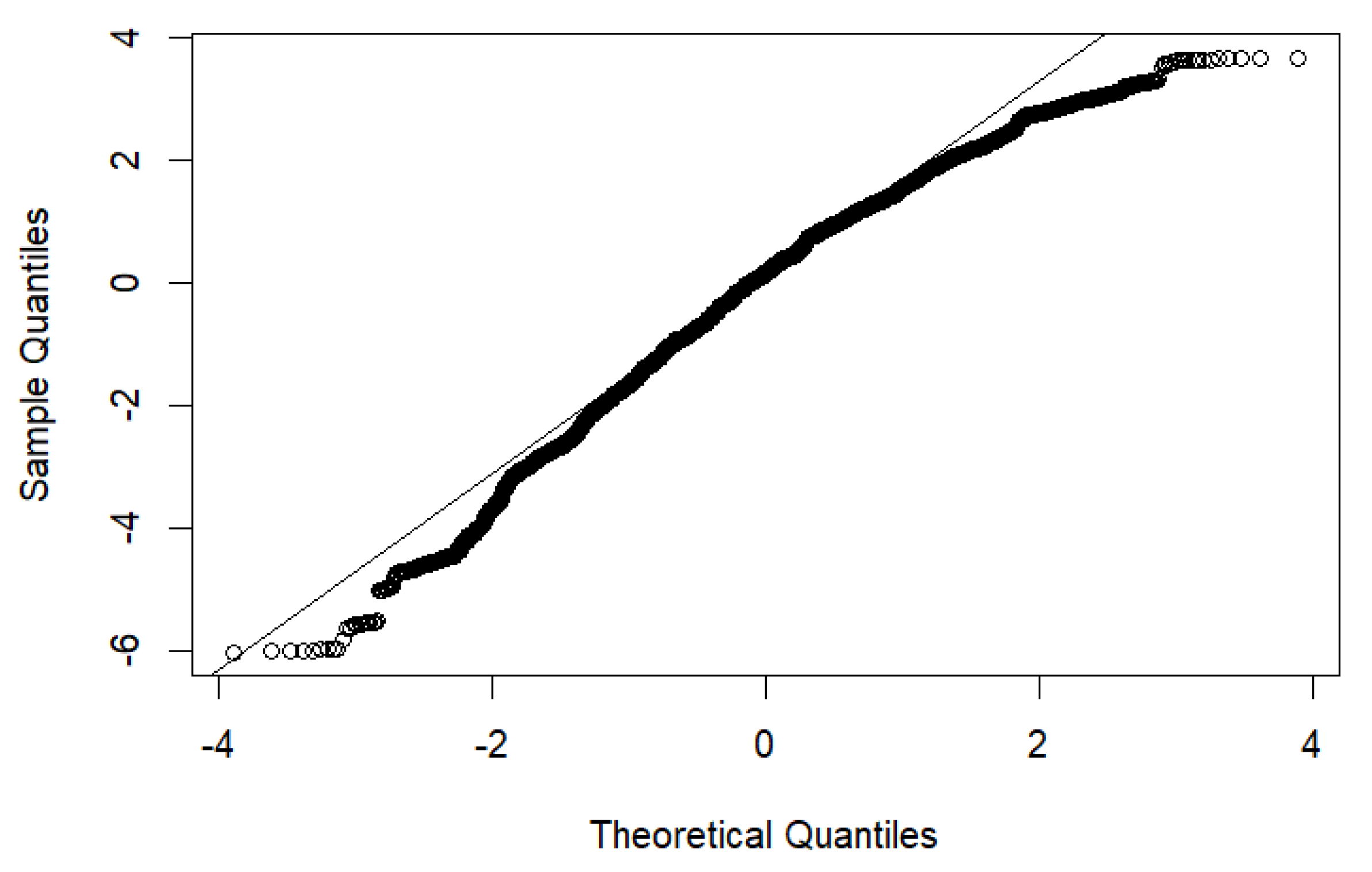
3.2. Model Performance for Imputation of sRPE
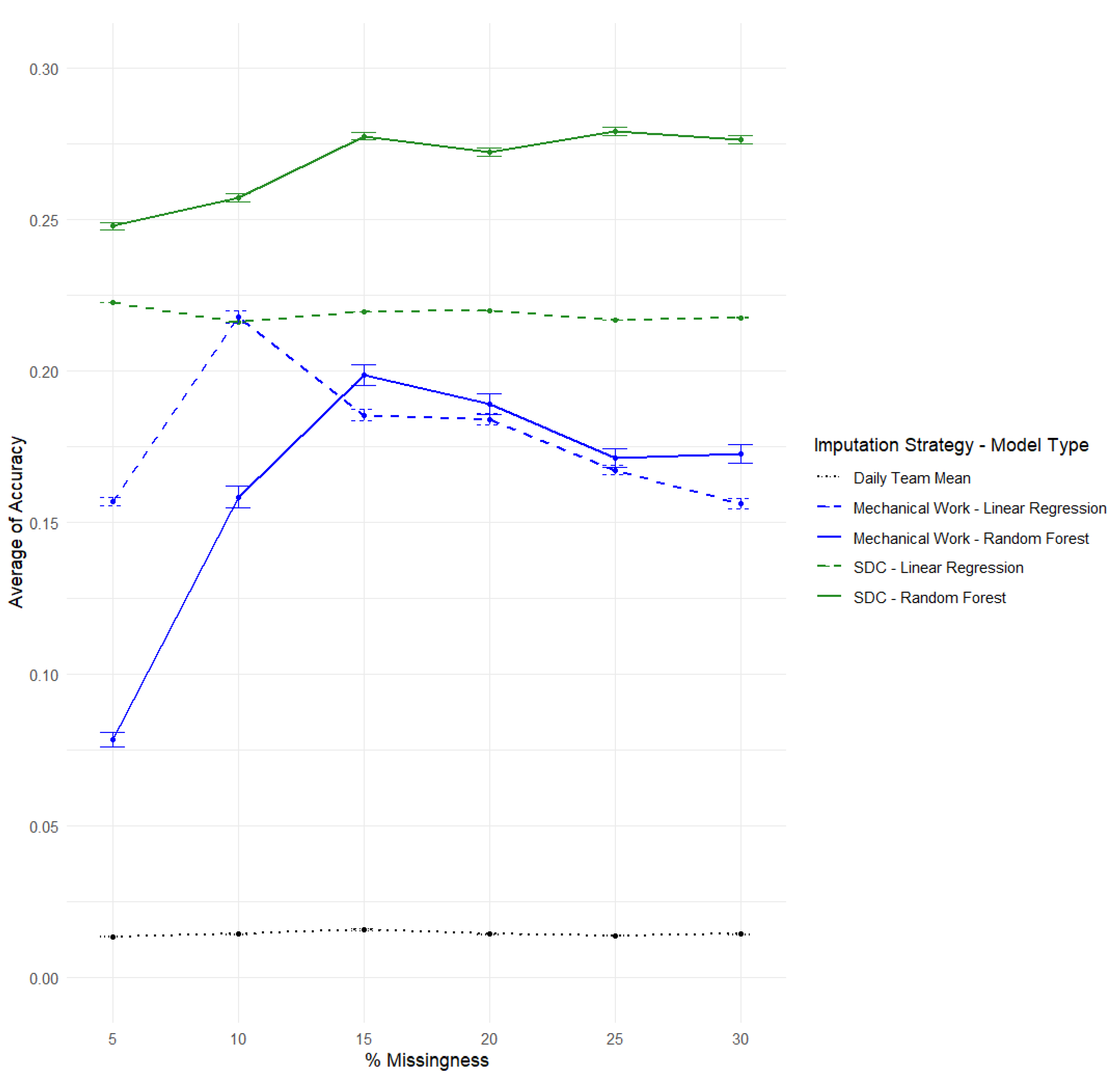
3.3. Comparison of All Models Regarding sRPE Imputation Explanatory Power by Missingness
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gabbett, T.J. The training-injury prevention paradox: Should athletes be training smarter and harder? Br. J. Sports Med. 2016, 50, 273–280. [Google Scholar] [CrossRef] [PubMed]
- Foster, C.; Rodriguez-Marroyo, J.A.; De Koning, J.J. Monitoring training loads: The past, the present, and the future. Int. J. Sports Physiol. Perform. 2017, 12, s2-2–s2-8. [Google Scholar] [CrossRef] [PubMed]
- World Rugby. Approved Devices. World Rugby, 2025. Available online: https://www.world.rugby/the-game/facilities-equipment/equipment/devices/ (accessed on 13 February 2025).
- Cummins, C.; Orr, R.; O’Connor, H.; West, C. Global positioning systems (GPS) and microtechnology sensors in team sports: A systematic review. Sports Med. 2013, 43, 1025–1042. [Google Scholar] [CrossRef]
- Clarke, A.C.; Anson, J.M.; Pyne, D.B. Physiologically based GPS speed zones for evaluating running demands in women’s rugby sevens. J. Sport Sci. 2015, 33, 1101–1108. [Google Scholar] [CrossRef]
- Clarke, A.C.; Anson, J.M.; Pyne, D.B. Proof of concept of automated collision detection technology in rugby sevens. J. Strength Cond. Res. 2017, 31, 1116–1120. [Google Scholar] [CrossRef]
- Haddad, M.; Stylianides, G.; Djaoui, L.; Dellal, A.; Chamari, K. Session-RPE method for training load monitoring: Validity, ecological usefulness, and influencing factors. Front. Neurosci. 2017, 11, 612. [Google Scholar] [CrossRef] [PubMed]
- Benson, L.C.; Stilling, C.; Owoeye, O.B.A.; Emery, C.A. Evaluating methods for imputing missing data from longitudinal monitoring of athlete workload. J. Sports Sci. Med. 2021, 20, 188–196. [Google Scholar] [CrossRef]
- Griffin, A.; Kenny, I.C.; Comyns, T.M.; Purtill, H.; Tiernan, C.; O’Shaughnessy, E.; Lyons, M. Training load monitoring in team sports: A practical approach to addressing missing data. J. Sports Sci. 2021, 39, 2161–2171. [Google Scholar] [CrossRef]
- Eston, R. Use of ratings of perceived exertion in sports. Int. J. Sports Physiol. Perform. 2012, 7, 175–182. [Google Scholar] [CrossRef]
- Saw, A.E.; Main, L.C.; Gastin, P.B. Monitoring the athlete training response: Subjective self-reported measures trump commonly used objective measures: A systematic review. Br. J. Sports Med. 2016, 50, 281–291. [Google Scholar] [CrossRef]
- Windt, J.; Ardern, C.L.; Gabbett, T.J.; Khan, K.M.; Cook, C.E.; Sporer, B.C.; Zumbo, B.D. Getting the most out of intensive longitudinal data: A methodological review of workload–injury studies. BMJ Open 2018, 8, e022626. [Google Scholar] [CrossRef]
- Carey, D.; Ong, K.; Morris, M.; Crow, J.; Crossley, K. Predicting ratings of perceived exertion in Australian football players: Methods for live estimation. Int. J. Comput. Sci. Sport 2016, 15, 64–77. [Google Scholar] [CrossRef]
- Epp-Stobbe, A.; Tsai, M.-C.; Klimstra, M. Comparison of imputation methods for missing rate of perceived exertion data in rugby. Mach. Learn. Knowl. Extr. 2022, 4, 827–838. [Google Scholar] [CrossRef]
- Delaney, J.A.; Cummins, C.J.; Thornton, H.R.; Duthie, G.M. Importance, reliability, and usefulness of acceleration measures in team sports. J. Strength Cond. Res. 2018, 32, 3485–3493. [Google Scholar] [CrossRef]
- Buchheit, M. Programming high-speed running and mechanical work in relation to technical contents and match schedule in professional soccer. Sport Perform. Sci. Rep. 2019, 69, 1–3. [Google Scholar]
- Tuft, K.; Kavaliauskas, M. Relationship between internal and external training load in field hockey. Int. J. Strength Cond. 2020, 1, 24. [Google Scholar] [CrossRef]
- Epp-Stobbe, A.; Tsai, M.C.; Klimstra, M. Work smarter not harder: Mechanical work as a measure of athlete workload. ISBS Proc. Arch. 2024, 42, 51. Available online: https://commons.nmu.edu/isbs/vol42/iss1/51 (accessed on 13 May 2025).
- Bartlett, J.D.; O’Connor, F.; Pitchford, N.; Torres-Ronda, L.; Robertson, S.J. Relationships between internal and external training load in team-sport athletes: Evidence for an individualized approach. Int. J. Sports Physiol. Perform. 2017, 12, 230–234. [Google Scholar] [CrossRef]
- Epp-Stobbe, A.; Tsai, M.-C.; Klimstra, M.D. Predicting athlete workload in women’s rugby sevens using GNSS sensor data, contact count and mass. Sensors 2024, 24, 6699. [Google Scholar] [CrossRef]
- King, D.; Hume, P.; Clark, T. Video analysis of tackles in professional rugby league matches by player position, tackle height and tackle location. Int. J. Perform. Anal. Sport 2010, 10, 241–254. [Google Scholar] [CrossRef]
- Wheeler, W.K.; Wiseman, R.; Lyons, K. Tactical and technical factors associated with effective ball offloading strategies during the tackle in rugby league. Int. J. Perform. Anal. 2011, 11, 392–409. [Google Scholar] [CrossRef]
- R Core Team. The R Stats Package. (n.d.). Available online: https://stat.ethz.ch/R-manual/R-devel/library/stats/html/stats-package.html (accessed on 25 August 2022).
- Ripley, B.; Venables, B.; Bates, D.M.; Hornik, K.; Gebhardt, A.; Firth, D. Package “MASS”. 2022. Available online: https://cran.r-project.org/web/packages/MASS/MASS.pdf (accessed on 25 August 2022).
- Friedman, J.; Hastie, T.; Tibshirani, R.; Narasimhan, B.; Tay, K.; Simon, N.; Qian, J.; Yang, J. Package “glmnet”. 2022. Available online: https://cran.r-project.org/web/packages/glmnet/glmnet.pdf (accessed on 25 August 2022).
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Beygelzimer, A.; Kakadet, S.; Langford, J.; Arya, S.; Mount, D.; Li, S. Package “FNN”. 2022. Available online: https://cran.r-project.org/web/packages/FNN/FNN.pdf (accessed on 25 August 2022).
- Liaw, A.; Wiener, M. Package “randomForest”. 2022. Available online: https://cran.rproject.org/web/packages/randomForest/randomForest.pdf (accessed on 25 August 2022).
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F.; Chang, C.C.; Lin, C.C. Package “e1071”. 2022. Available online: https://cran.r-project.org/web/packages/e1071/e1071.pdf (accessed on 25 August 2022).
- Hsu, C.; Chang, C.C.; Lin, C.J. A Practical Guide to Support Vector Classification. 2003, pp. 1396–1400. Available online: https://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf (accessed on 25 August 2022).
- Fritsch, S.; Guenther, F.; Wright, M.N.; Suling, M.; Mueller, S.M. Package “neuralnet”. 2019. Available online: https://cran.r-project.org/web/packages/neuralnet/neuralnet.pdf (accessed on 25 August 2022).
- Celton, M.; Malpertuy, A.; Lelandais, G.; de Brevern, A.G. Comparative analysis of missing value imputation methods to improve clustering and interpretation of microarray experiments. BMC Genom. 2010, 11, 15. [Google Scholar] [CrossRef]
- Lakens, D.; Scheel, A.M.; Isager, P.M. Equivalence testing for psychological research: A tutorial. Adv. Methods Pract. Psychol. Sci. 2018, 1, 259–269. [Google Scholar] [CrossRef]
- Lakens, D. Equivalence tests: A practical primer for t tests, correlations, and meta-analyses. Soc. Psychol. Pers. Sci. 2017, 8, 355–362. [Google Scholar] [CrossRef]
- Kang, H. The prevention and handling of the missing data. Korean J. Anesthesiol. 2013, 64, 402–406. [Google Scholar] [CrossRef]
- Schmitt, P.; Mandel, J.; Guedj, M. A comparison of six methods for missing data imputation. J. Biomet. Biostat. 2015, 6, 1. Available online: https://lgreski.github.io/datasciencedepot/references/a-comparison-of-six-methods-for-missing-data-imputation-2155-6180-1000224.pdf (accessed on 13 May 2025).
- Waljee, A.K.; Mukherjee, A.; Singal, A.G.; Zhang, Y.; Warren, J.; Balis, U.; Marrero, J.; Zhu, J.; Higgins, P.D. Comparison of imputation methods for missing laboratory data in medicine. BMJ Open 2013, 3, e002847. [Google Scholar] [CrossRef]
- Fuller, C.W.; Taylor, A. Injury Surveillance Studies: 2023/24 Men’s and Women’s Tournaments Final Report. World Rugby, 2024. Available online: https://www.world.rugby/the-game/player-welfare/research/injury-surveillance (accessed on 13 May 2025).
- Hong, S.; Lynn, H.S. Accuracy of random-forest-based imputation of missing data in the presence of non-normality, non-linearity, and interaction. BMC Med. Res. Methodol. 2020, 20, 199. [Google Scholar] [CrossRef]
- Stavseth, M.R.; Clausen, T.; Røislien, J. How handling missing data may impact conclusions: A comparison of six different imputation methods for categorical questionnaire data. SAGE Open Med. 2019, 7, 2050312118822912. [Google Scholar] [CrossRef]
- Kokla, M.; Virtanen, J.; Kolehmainen, M.; Paananen, J.; Hanhineva, K. Random forest-based imputation outperforms other methods for imputing LC-MS metabolomics data: A comparative study. BMC Bioinform. 2019, 20, 492. [Google Scholar] [CrossRef] [PubMed]
- Shah, A.D.; Bartlett, J.W.; Carpenter, J.; Nicholas, O.; Hemingway, H. Comparison of random forest and parametric imputation models for imputing missing data using MICE: A CALIBER study. Am. J. Epidemiol. 2014, 179, 764–774. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.G.; Islam, M.Z. Missing value imputation using a fuzzy clustering-based EM approach. Knowl. Inf. Syst. 2016, 46, 389–422. [Google Scholar] [CrossRef]
- Waldmann, P.; Mészáros, G.; Gredler, B.; Fürst, C.; Sölkner, J. Evaluation of the lasso and the elastic net in genome-wide association studies. Front. Genet. 2013, 4, 270. [Google Scholar] [CrossRef]
- Epp-Stobbe, A.; Tsai, M.; Morris, C.; Klimstra, M. The influence of physical contact on athlete load in international female rugby sevens. J. Strength Cond. Res. 2022, 37, 383–387. [Google Scholar] [CrossRef]
- Griffin, A.; Kenny, I.C.; Comyns, T.M.; Lyons, M. The Development and Evaluation of a Training Monitoring System for Amateur Rugby Union. Appl. Sci. 2020, 10, 7816. [Google Scholar] [CrossRef]
- Bourdon, P.C.; Cardinale, M.; Murray, A.; Gastin, P.; Kellmann, M.; Varley, M.C.; Gabbett, T.J.; Coutts, A.J.; Burgess, D.J.; Gregson, W.; et al. Monitoring athlete training loads: Consensus statement. Int. J. Sport Physiol. 2017, 12, 161–170. [Google Scholar] [CrossRef]
- Yin, M.; Wortman Vaughan, J.; Wallach, H. Understanding the Effect of Accuracy on Trust in Machine Learning Models. In Proceedings of the 2019 CHI Conference on Human Factors in Computing Systems, Glasgow, UK, 4–9 May 2019. [Google Scholar] [CrossRef]
- Bartlett, J.D.; Drust, B. A framework for effective knowledge translation and performance delivery of Sport Scientists in professional sport. Eur. J. Sport Sci. 2021, 21, 1579–1587. [Google Scholar] [CrossRef]
- Brocherie, F.; Beard, A. All alone we go faster, together we go further: The necessary evolution of professional and elite sporting environment to bridge the gap between research and practice. Front. Sports Act Living 2021, 2, 631147. [Google Scholar] [CrossRef]
- Coutts, A.J. Working fast and working slow: The benefits of embedding research in high performance sport. Int. J. Sports Physiol. Perform. 2016, 11, 1–2. [Google Scholar] [CrossRef]



| Strategy | Model | Accuracy | R2 | RMSE |
|---|---|---|---|---|
| DTMS | 0.0000 | 0.0377 | 1.80 | |
| Mechanical Work | Linear Regression | 0.1841 | 0.0854 | 1.78 |
| Random Forest | 0.1891 | 0.1590 | 1.71 | |
| SDC Model | Linear Regression | 0.2200 | 0.2287 | 1.61 |
| Random Forest | 0.2724 | 0.3383 | 1.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Epp-Stobbe, A.; Tsai, M.-C.; Klimstra, M. Rugby Sevens sRPE Workload Imputation Using Objective Models of Measurement. Appl. Sci. 2025, 15, 6520. https://doi.org/10.3390/app15126520
Epp-Stobbe A, Tsai M-C, Klimstra M. Rugby Sevens sRPE Workload Imputation Using Objective Models of Measurement. Applied Sciences. 2025; 15(12):6520. https://doi.org/10.3390/app15126520
Chicago/Turabian StyleEpp-Stobbe, Amarah, Ming-Chang Tsai, and Marc Klimstra. 2025. "Rugby Sevens sRPE Workload Imputation Using Objective Models of Measurement" Applied Sciences 15, no. 12: 6520. https://doi.org/10.3390/app15126520
APA StyleEpp-Stobbe, A., Tsai, M.-C., & Klimstra, M. (2025). Rugby Sevens sRPE Workload Imputation Using Objective Models of Measurement. Applied Sciences, 15(12), 6520. https://doi.org/10.3390/app15126520







