Point Deflection in Topological Interlocking Plates
Abstract
Featured Application
Abstract
1. Introduction
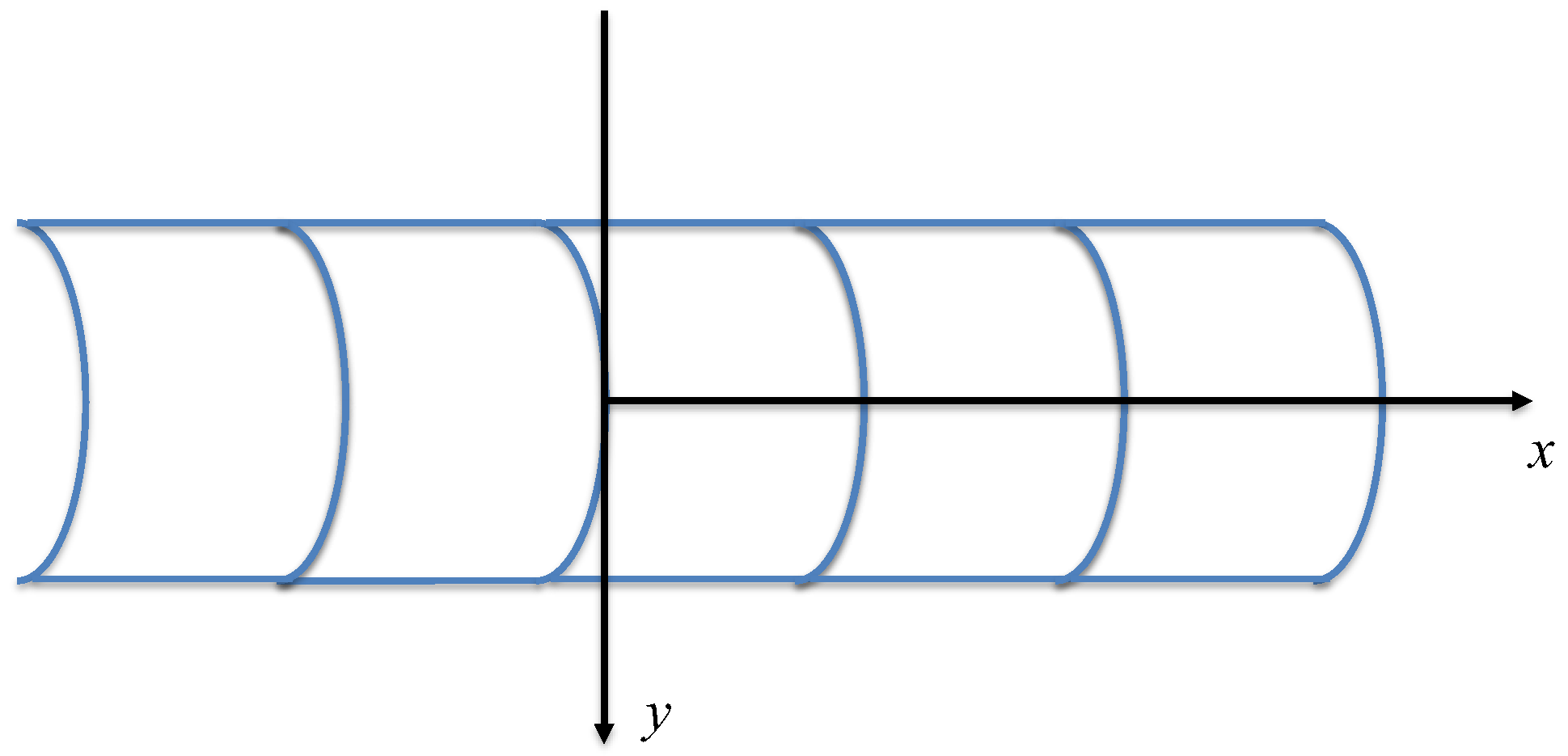
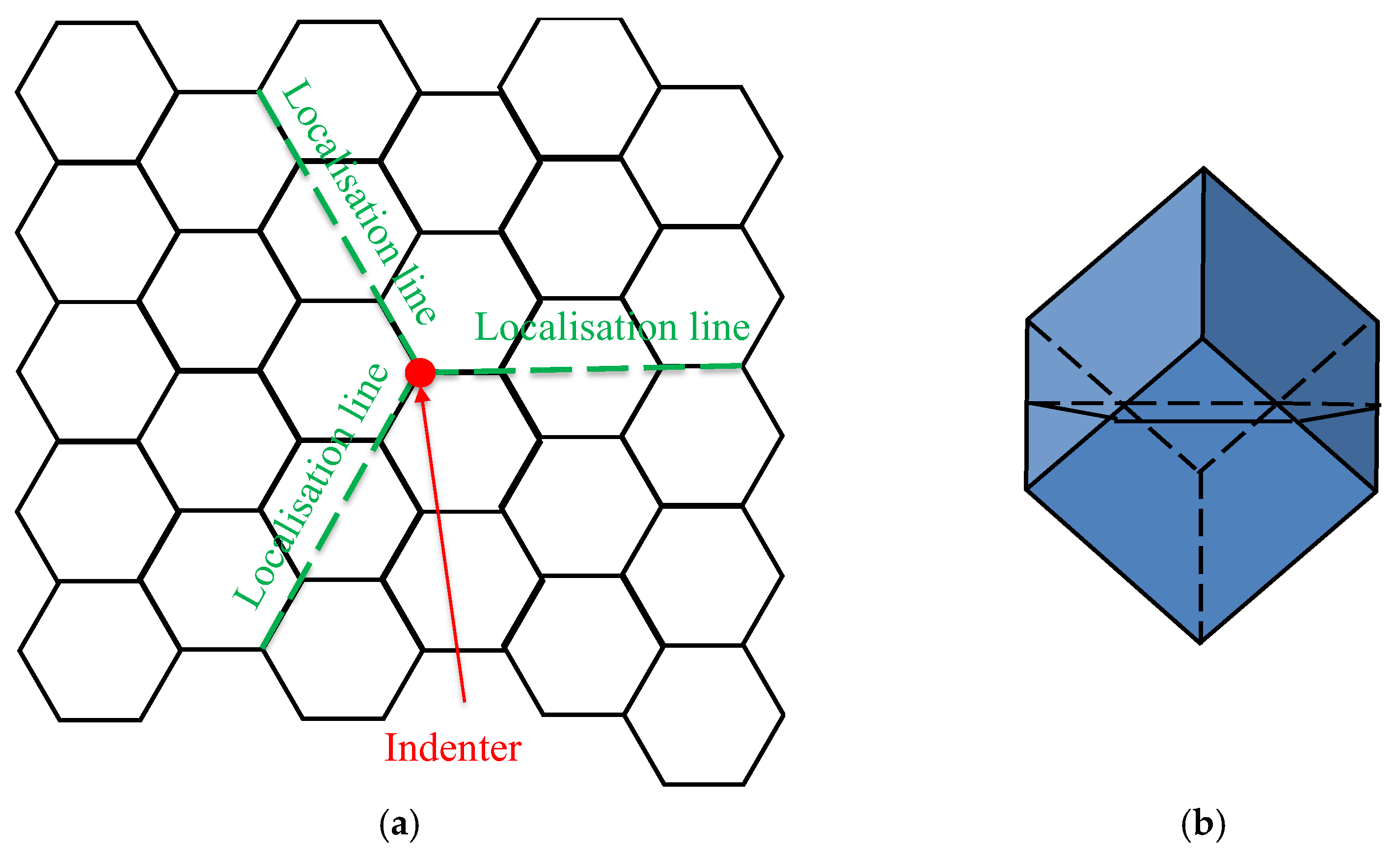
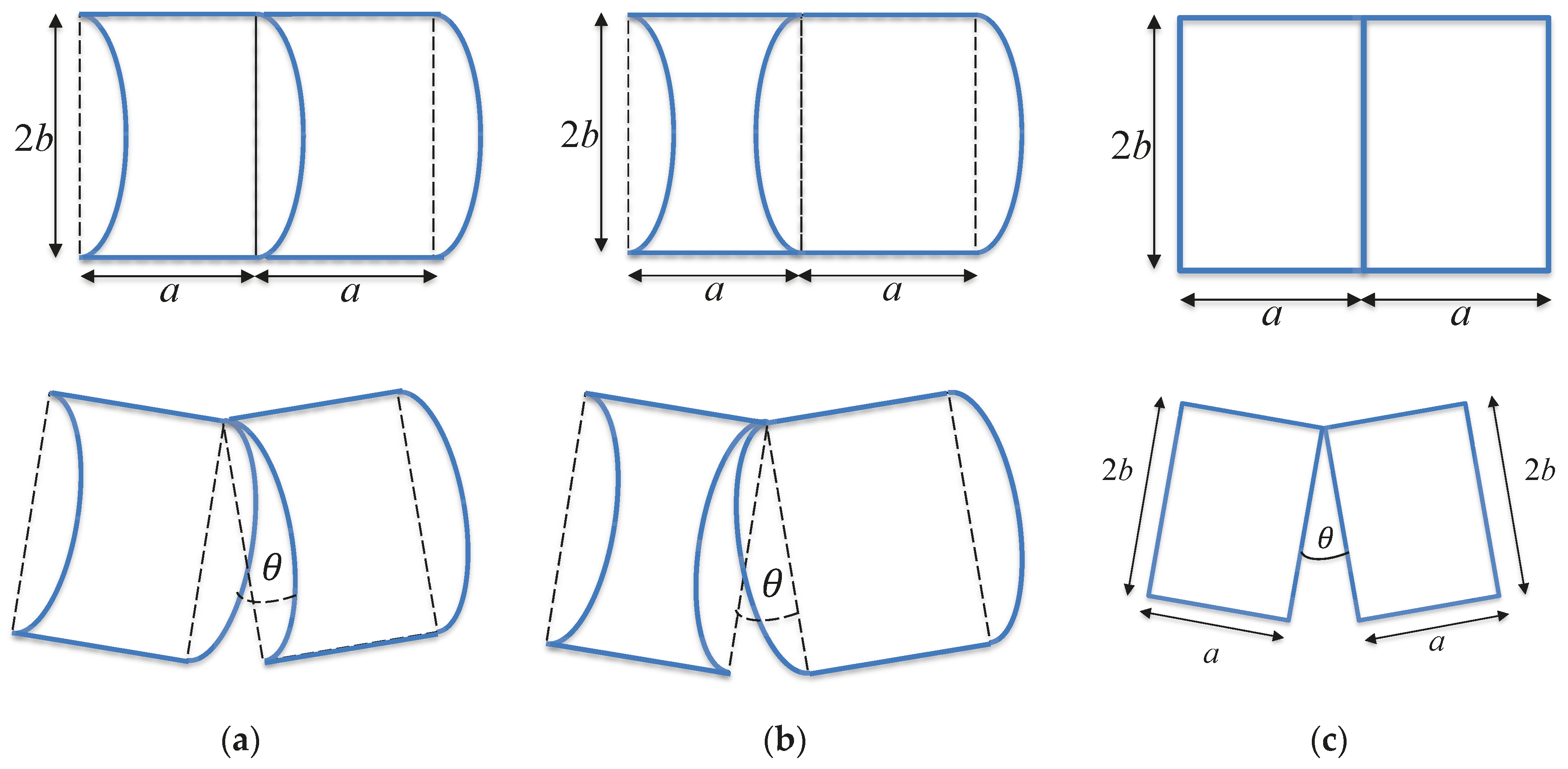
2. Motion of Blocks in Topological Interlocking Beams/Plates and Simplified Modeling
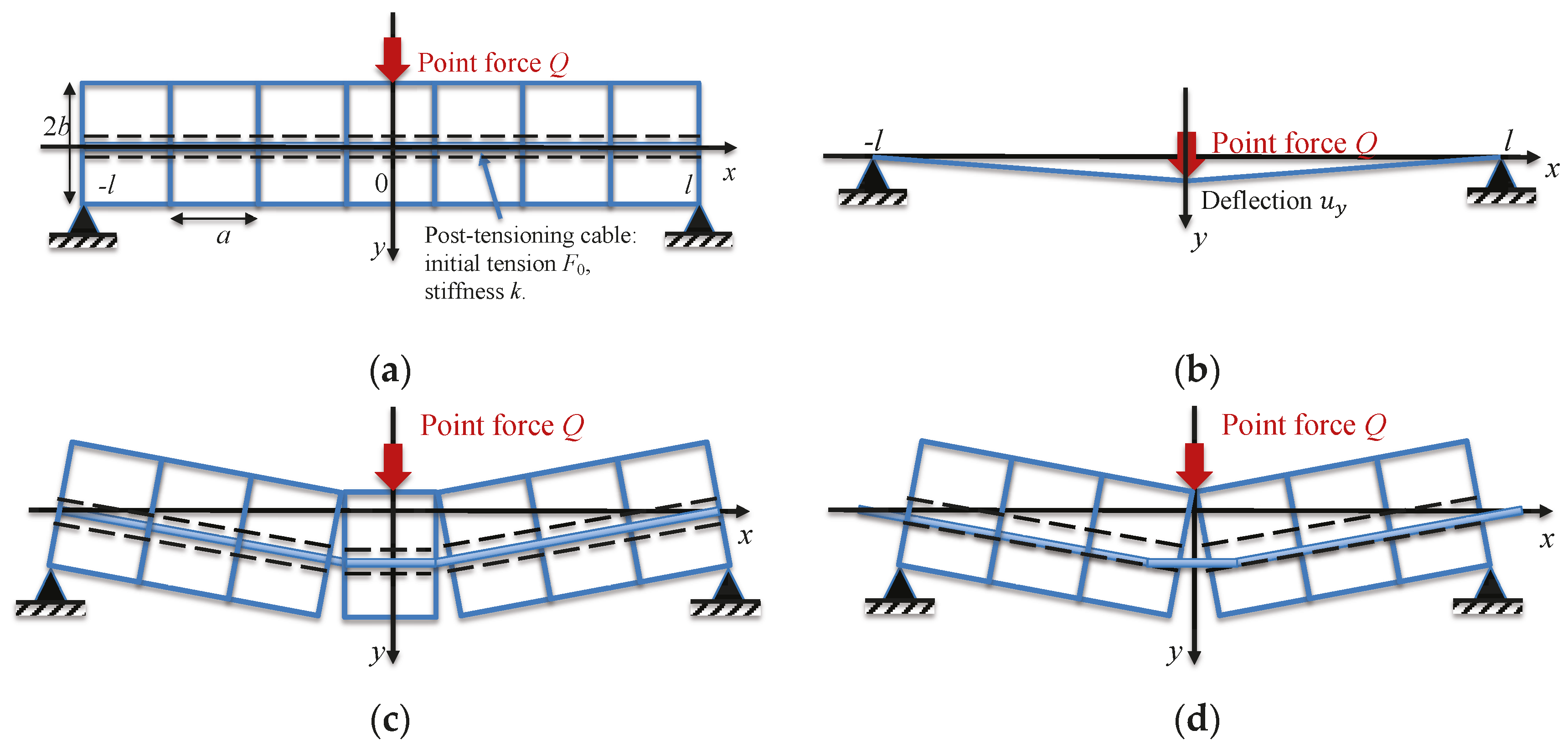
3. Rectangular Block Model of Topological Interlocking Beams
4. Apparent Negative Stiffness and Post-Peak Softening
5. Oscillations of TI Beams with Discontinuous Linear Damping
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Equivalence of Constraining by the Post-Tensioning Cable and by the Peripheral Constraint
References
- Dyskin, A.V.; Estrin, Y.; Kanel-Belov, A.J.; Pasternak, E. A new concept in design of materials and structures: Assemblies of interlocked tetrahedron-shaped elements. Scr. Mater. 2001, 44, 2689–2694. [Google Scholar] [CrossRef]
- Dyskin, A.V.; Estrin, Y.; Kanel-Belov, A.J.; Pasternak, E. Topological interlocking of platonic solids: A way to new materials and structures. Phil. Mag. Lett. 2003, 83, 197–203. [Google Scholar] [CrossRef]
- Dyskin, A.V.; Estrin, Y.; Kanel-Belov, A.J.; Pasternak, E. Interlocking properties of buckyballs. Phys. Lett. A 2003, 319, 373–378. [Google Scholar] [CrossRef]
- Kanel-Belov, A.J.; Dyskin, A.V.; Estrin, Y.; Pasternak, E.; Ivanov-Pogodaev, I.A. Interlocking of convex polyhedra: Towards a geometric theory of fragmented solids. Mosc. Math. J. 2010, 10, 337–342. [Google Scholar] [CrossRef]
- Dyskin, A.V.; Estrin, Y.; Kanel-Belov, A.Y.; Pasternak, E. Toughening by fragmentation—How topology helps. Adv. Eng. Mater. 2001, 3, 885–888. [Google Scholar] [CrossRef]
- Dyskin, A.V.; Estrin, Y.; Pasternak, E.; Khor, H.C.; Kanel-Belov, A.J. Fracture resistant structures based on topological interlocking with non-planar contacts. Adv. Eng. Mater. 2003, 5, 116–119. [Google Scholar] [CrossRef]
- Rezaee Javan, A.; Seifi, H.; Xu, S.; Xie, Y.M. Design of a new type of interlocking brick and evaluation of its dynamic performance. In Proceedings of the IASS Annual Symposium 2016: Spatial Structures in the 21 Century, Tokyo, Japan, 26–30 September 2016; Kawaguchi, K., Ohsaki, M., Takeuchi, T., Eds.; International Association for Shell and Spatial Structures (IASS): Tokyo, Japan, 2016; pp. 1–8. [Google Scholar]
- Oikonomopoulou, F.; Bristogianni, T.; Barou, L.; Jacobs, E.; Frigo, G.; Veer, F.A.; Nijsse, R. A novel, demountable structural glass system out of dry-assembly, interlocking cast glass components. In Challenging Glass 6, Proceedings of the Conference on Architectural and Structural Applications of Glass, Delft, The Netherlands, 17–18 May 2018; Louter, C., Bos, F., Belis, J., Eds.; Delft University of Technology: Delft, The Netherlands, 2018; Paper 6. [Google Scholar]
- Bejarano, A.; Hoffmann, C. A generalized framework for designing topological interlocking configurations. Int. J. Archit. Comput. 2019, 17, 53–73. [Google Scholar] [CrossRef]
- Wang, Z.; Song, P.; Pauly, M. Design and structural optimization of topological interlocking assemblies. ACM Trans. Graph. 2019, 38, 193. [Google Scholar] [CrossRef]
- Loing, V.; Baverel, O.; Caron, J.-F.; Mesnil, R. Free-form structures from topologically interlocking masonries. Autom. Constr. 2020, 113, 103117. [Google Scholar] [CrossRef]
- Piekarski, N. Floor slabs made from topologically interlocking prefabs of small size. Buildings 2020, 10, 76. [Google Scholar] [CrossRef]
- Kim, D.Y.; Siegmund, T. Mechanics and design of topologically interlocked irregular quadrilateral tessellations. Mater. Des. 2021, 212, 110155. [Google Scholar] [CrossRef]
- Lecci, F.; Mazzoli, C.; Bartolomei, C.; Gulli, R. Design of flat vaults with topological interlocking solids. Nexus Netw. J. 2021, 23, 607–627. [Google Scholar] [CrossRef]
- Koureas, I.; Pundir, M.; Feldfogel, S.; Kammer, D.S. On the failure of beam-like topologically interlocked structures. Intern. J. Solids Struct. 2022, 259, 112029. [Google Scholar] [CrossRef]
- Akpanya, R.; Goertzen, T.; Niemeyer, A.C. A group-theoretic approach for constructing spherical-interlocking assemblies. In Proceedings of the of the IASS Annual Symposium 2023: Integration of Design and Fabrication, Melbourne, Australia, 10–14 July 2023. [Google Scholar]
- Stüttgen, S.; Akpanya, R.; Beckmann, B.; Chudoba, R.; Robertz, D.; Niemeyer, A.C. Modular construction of topological interlocking blocks—An algebraic approach for resource-efficient carbon-reinforced concrete structures. Buildings 2023, 13, 2565. [Google Scholar] [CrossRef]
- Kim, D.Y.; Siegmund, T. Chirality in topologically interlocked material systems. Mech. Mater. 2024, 191, 104956. [Google Scholar] [CrossRef]
- Akleman, E.; Krishnamurthy, V.R.; Fu, C.-A.; Subramanian, S.G.; Ebert, M.; Eng, M.; Starrett, C.; Panchal, H. Generalized Abeille tiles: Topologically interlocked space-filling shapes generated based on fabric symmetries. Comput. Graph. 2020, 89, 156–166. [Google Scholar] [CrossRef]
- Hua, H. Porous interlocking assembly: Performance-based dry masonry construction with digital stereotomy. Archit. Intell. 2024, 3, 20. [Google Scholar] [CrossRef]
- Shilova, E.; Bencini, N. A framework for parametric structural design of topological interlocking flat vaults. In Proceedings of the IASS 2024 Symposium: Redefining the Art of Structural Design, Zurich, Switzerland, 26–30 August 2024; Block, P., Boller, G., DeWolf, C., Pauli, J., Kaufmann, W., Eds.; 2024. [Google Scholar]
- Laudage, S.; Guenther, E.; Siegmund, T. Design and analysis of a lightweight beam-type topologically interlocked material system. Structures 2023, 51, 1402–1413. [Google Scholar] [CrossRef]
- Koureas, I.; Pundir, M.; Feldfogel, S.; Kammer, D.S. Beam-like topologically interlocked structures with hierarchical interlocking. ASME J. Appl. Mech. 2023, 90, 081008. [Google Scholar] [CrossRef]
- Patton, F.D. Multiple modes of shear failure in rock. In Proceedings of the 1st Congress of the International Society for Rock Mechanics (ISRM), Lisbon, Portugal, 25 September–1 October 1966; pp. 509–513. [Google Scholar]
- Dyskin, A.V.; Estrin, Y.; Kanel-Belov, A.J.; Pasternak, E. A new principle in design of composite materials: Reinforcement by interlocked elements. Compos. Sci. Technol. 2003, 63, 483–491. [Google Scholar] [CrossRef]
- Autruffe, A.; Pelloux, F.; Brugger, C.; Duval, P.; Bréchet, Y.; Fivel, M. Indentation behaviour of interlocked structures made of ice: Influence of the friction coefficient. Adv. Eng. Mater. 2007, 9, 663–666. [Google Scholar] [CrossRef]
- Dyskin, A.V.; Caballero, A. Orthogonal crack approaching an interface. Eng. Fract. Mech. 2009, 76, 2476–2485. [Google Scholar] [CrossRef]
- Tessmann, O.; Becker, M. Extremely heavy and incredibly light: Performative assemblies in dynamic environments. In Proceedings of the 18th International Conference on Computer-Aided Architectural Design Research in Asia (CAADRIA 2013), Singapore, 15–18 May 2013; pp. 469–478. [Google Scholar]
- Weizmann, M.; Amir, O.; Grobman, Y.J. Topological interlocking in buildings: A case for the design and construction of floors. Autom. Constr. 2016, 72 Pt 1, 18–25. [Google Scholar] [CrossRef]
- Alothman, S.; Chavan, C. Topological interlocking systems for the construction of seismic-proof shell structures. In Proceedings of the IASS Symposium 2018: Creativity in Structural Design, Boston, MA, USA, 16–20 July 2018. [Google Scholar]
- Totoev, Y.; Al Harthy, A. Semi interlocking masonry as infill wall system for earthquake resistant buildings: A review. J. Eng. Res. (TJER) 2016, 13, 33–41. [Google Scholar] [CrossRef]
- Piirainen, V.Y.; Estrin, Y. Topological interlocking as a principle of engineering design in construction of marine and coastal structures. J. Min. Inst. 2017, 226, 480–486. [Google Scholar]
- Molotnikov, A.; Gerbrand, R.; Qi, Y.; Simon, G.P.; Estrin, Y. Design of responsive materials using topologically interlocked elements. Smart Mater. Struct. 2015, 24, 25034. [Google Scholar] [CrossRef]
- Estrin, Y.; Molotnikov, A.; Simon, G.P.; Kaloshkin, S.; Senatov, F.; Maksimkin, A. Flexible ceramics with self-stiffening capability. In Proceedings of the European Symposium on Intelligent Materials 2015, Kiel, Germany, 10–12 June 2015. [Google Scholar]
- Djumas, L.; Molotnikov, A.; Simon, G.P.; Estrin, Y. Enhanced mechanical performance of bio-inspired hybrid structures utilising topological interlocking geometry. Sci. Rep. 2016, 6, 26706. [Google Scholar] [CrossRef] [PubMed]
- Djumas, L.; Simon, G.P.; Estrin, Y.; Molotnikov, A. Deformation mechanics of non-planar topologically interlocked assemblies with structural hierarchy and varying geometry. Sci. Rep. 2017, 7, 11844. [Google Scholar] [CrossRef]
- Molotnikov, A.; Estrin, Y.; Dyskin, A.V.; Pasternak, E.; Kanel-Belov, A.J. Percolation mechanism of failure of a planar assembly of interlocked osteomorphic elements. Eng. Fract. Mech. 2007, 74, 1222–1232. [Google Scholar] [CrossRef]
- Thompson, J.M.T.; Bokaian, A.R.; Ghaffari, R. Subharmonic resonances and chaotic motions of a bilinear oscillator. IMA J. Appl. Math. 1983, 31, 207–234. [Google Scholar] [CrossRef]
- Dyskin, A.V.; Pasternak, E.; Pelinovsky, E. Periodic motions and resonances of impact oscillators. J. Sound Vib. 2012, 331, 2856–2873. [Google Scholar] [CrossRef]
- Khudyakov, M.; Dyskin, A.V.; Pasternak, E. Continuum model of wave propagation in fragmented media: Linear damping approximation. Nonlinear Process. Geophys. 2017, 24, 461–466. [Google Scholar] [CrossRef]
- Carlesso, M.; Molotnikov, A.; Krause, T.; Tushtev, K.; Kroll, S.; Rezwan, K.; Estrin, Y. Enhancement of sound absorption properties using topologically interlocked elements. Scripta Mater. 2012, 66, 483–486. [Google Scholar] [CrossRef]
- Ali, M.; Briet, R.; Chouw, N. Dynamic response of mortar-free interlocking structures. Constr. Build. Mater. 2013, 42, 168–189. [Google Scholar] [CrossRef]
- Schapira, Y.; Chernin, L.; Shufrin, I. Blast energy absorption in topological interlocking elastic columns. Mech. Adv. Mater. Struct. 2024, 31, 935–947. [Google Scholar] [CrossRef]
- Feng, Y.; Siegmund, T.; Habtour, E.; Riddick, J. Impact mechanics of topologically interlocked material assemblies. Intl. J. Impact Eng. 2015, 75, 140–149. [Google Scholar] [CrossRef]
- Pantaleone, J. How the air slows a closing book. Am. J. Phys. 2024, 92, 7–13. [Google Scholar] [CrossRef]
- Estrin, Y.; Dyskin, A.V.; Pasternak, E.; Schaare, S.; Stanchits, S.; Kanel-Belov, A.J. Negative stiffness of a layer with topologically interlocked elements. Scr. Mater. 2004, 50, 291–294. [Google Scholar] [CrossRef]
- Schaare, S.; Dyskin, A.V.; Estrin, Y.; Arndt, S.; Pasternak, E.; Kanel-Belov, A.J. Point loading of assemblies of interlocked cube-shaped elements. Int. J. Eng. Sci. 2008, 46, 1228–1238. [Google Scholar] [CrossRef]
- Mather, A.; Cipra, R.; Siegmund, T. Structural integrity during remanufacture of a topologically interlocked material. Intern. J. Struct. Integr. 2012, 3, 61–78. [Google Scholar] [CrossRef]
- Safiee, N.A.; Jaafar, M.S.; Alwathaf, A.H.; Noorzaei, J.; Abdulkadir, M.R. Structural behavior of mortarless interlocking load bearing hollow block wall panel under out-of-plane loading. Adv. Struct. Eng. 2011, 14, 1184–1196. [Google Scholar] [CrossRef]
- Krause, T.; Molotnikov, A.; Carlesso, M.; Rente, J.; Rezwan, K.; Estrin, Y.; Koch, D. Mechanical properties of topologically interlocked structures with elements produced by freeze gelation of ceramic slurries. Adv. Eng. Mater. 2012, 14, 335–341. [Google Scholar] [CrossRef]
- Khandelwal, S.; Siegmund, T.; Cipra, R.J.; Bolton, J.S. Scaling of the elastic behavior of two-dimensional topologically interlocked materials under transverse loading. J. Appl. Mech. 2014, 81, 031011. [Google Scholar] [CrossRef]
- Pasternak, E.; Dyskin, A.V.; Estrin, Y. Deformations in transform faults with rotating crustal blocks. Pure Appl. Geophys. 2006, 163, 2011–2030. [Google Scholar] [CrossRef]
- Odessa, I.; Shufrin, I. Nonlinear mechanics of fragmented beams. Eur. J. Mech. A/Solids 2022, 93, 104488. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity; Pergamon: Oxford, UK, 1959. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dyskin, A.V.; Pasternak, E. Point Deflection in Topological Interlocking Plates. Appl. Sci. 2025, 15, 6496. https://doi.org/10.3390/app15126496
Dyskin AV, Pasternak E. Point Deflection in Topological Interlocking Plates. Applied Sciences. 2025; 15(12):6496. https://doi.org/10.3390/app15126496
Chicago/Turabian StyleDyskin, Arcady V., and Elena Pasternak. 2025. "Point Deflection in Topological Interlocking Plates" Applied Sciences 15, no. 12: 6496. https://doi.org/10.3390/app15126496
APA StyleDyskin, A. V., & Pasternak, E. (2025). Point Deflection in Topological Interlocking Plates. Applied Sciences, 15(12), 6496. https://doi.org/10.3390/app15126496







