Abstract
A topological interlocking assembly (TIA) is an assembly of blocks together with a non-empty subset of blocks called the frame such that every non-empty set of blocks is kinematically constrained and can therefore not be removed from the assembly without causing intersections between blocks of the assembly. TIA provides a wide range of real-world applications, from modular construction in architectural design to potential solutions for sound insulation. Various methods to construct TIA have been proposed in the literature. In this paper, the approach of constructing TIA by applying the Escher trick to tilings of orientable surfaces is discussed. First, the strengths of this approach are highlighted for planar tilings, and the Escher trick is then exploited to construct a planar TIA that is based on the truncated square tiling, which is a semi-regular tiling of the Euclidean plane. Next, the Escher-Like approach is modified to construct TIAs that are based on arbitrary orientable surfaces. Finally, the capabilities of this modified construction method are demonstrated by constructing TIAs that are based on the unit sphere, the truncated icosahedron, and the deltoidal hexecontahedron.
1. Introduction
Since the influential work of Dyskin et al. [1], topological interlocking assemblies have been studied extensively. TIA can be applied as block systems in various architectural settings; see [2,3,4,5,6]. Moreover, there are other wide-ranging applications, from extraterrestrial construction [7] to solutions for sound insulation systems; see [8]. The common ground is that TIA, in contrast to monolithic systems, provides solutions for modular systems, where the geometry of the blocks and contact with neighbouring blocks play a key role.
In this work, the main focus lies on the design and construction of TIA. The construction of topological interlocking assemblies (TIA) can often be formulated using the mathematical framework of tilings. The fundamental idea involves starting with a given tiling and continuously transforming it into other tilings, akin to a growth process observed in biological systems.
In the convex case, the tiles of the initial tilings are contracted, enabling the construction of TIA with all Platonic solids, as detailed in [9,10]. Among these, the tetrahedron is one of the most extensively studied interlocking blocks [1,11]. Its truncated form, known as the “Abeille Block”, named after M. Abeille, was patented in 1699 for a flat-vault structure [12].
Continuous deformation of tilings can also be achieved using Voronoi cells, as described in [13,14]. A block in this construction has the property that its intersection with any intermediate plane is a Voronoi cell with a centre point determined by a given curve. By varying the choice of curves that are used to connect two corresponding points in the given parallel planes, one obtains assemblies of three-dimensional blocks with different interlocking properties. This approach yields TIA with space-filling properties that can be tailored to specific requirements [15,16]. This paper focuses on constructing TIA based on tilings derived from the Escher trick, where regular tiles are deformed to create more complex configurations. This approach is initially discussed in [17] and further developed in [18] for tilings with wallpaper symmetry. The assemblies generated with this method are mathematically proven to possess interlocking properties, as shown in [19].
In the literature, the construction methods for non-planar TIA are mainly focused on TIA with convex blocks, see [20,21,22]. The main goal of this work is the development of a general method that can be applied in order to obtain both planar and non-planar TIA with non-convex blocks. For this endeavour, the Escher-like method is generalised to create TIA based on arbitrary orientable surfaces. We demonstrate the versatility of this modified approach by constructing TIA based on the unit sphere, the truncated icosahedron, and the deltoidal hexecontahedron. Furthermore, we explore a TIA arising from a semi-regular tiling, which consists of regular polygons arranged in a repeating pattern. Semi-regular tilings provide a rich ground for constructing TIA due to their high symmetry and structural diversity. This exploration underscores the robustness of the Escher-like method in generating both planar and non-planar TIA, offering significant potential for innovative applications in various fields. The blocks of the constructed assemblies (both planar and non-planar) possess triangulated boundaries, and together with a fixed frame consisting of the most-outer blocks (in the planar case) or two distinct blocks in the spherical case, they can be shown to be TIA. For this, the infinitesimal criterion introduced in [20] can be used, which implies the regular TIA definition; see [19].
2. Symmetries and the Escher Trick
Throughout history, humans have employed patterns for decorations, and those regarded as beautiful often display a high level of symmetry. In more recent times, symmetric patterns have become particularly interesting due to their efficiency in manufacturing decorated objects such as textiles. A straightforward method to generate a pattern that covers the plane is to start with a tessellation of the plane that is invariant under certain symmetry operations, draw a pattern into a given tile, and then transfer this pattern via symmetry operations to the entire plane.
For example, consider tiling the plane with congruent squares. A pattern drawn in a given square can then be translated to every other square in the plane. More intricate patterns can be created by also allowing rotations around certain points in the plane, combined with specific translations. Such patterns are known as wallpaper patterns, and their symmetries are described by 2D-crystallographic groups, often referred to as wallpaper groups.A wallpaper group is a discrete subgroup of the group of Euclidean motions E(2) for which there exists a bounded fundamental region which yields a tiling of under the symmetries of the group.
The Dutch artist M.C. Escher exploited the concept of generating patterns by filling a fundamental region with an image and then tiling the entire plane using a wallpaper group. What distinguishes his patterns from those commonly seen in art, architecture, or textiles is his use of unusually shaped fundamental domains.
Starting with a fundamental domain for a given wallpaper group, such as a Dirichlet cell with a polygonal boundary, Escher created more intriguing fundamental domains. Since a fundamental domain tiles the entire plane, an edge of its boundary is naturally identified with the adjacent edge of a neighbouring domain. Escher modified the boundary of one domain in such a way that it remained a fundamental domain for the same group. If one edge of a fundamental domain is replaced by a different path, the adjacent fundamental domain has to be modified accordingly. This in turn implies a modification of a second edge of the initial fundamental domain, which is identified with the first edge under the action of the symmetry group. The result is a modified fundamental domain and, thereby, a different tiling of the plane with the same symmetry group, a technique known as the Escher trick, see Figure 1. A complementary approach to approximate a given shape by a fundamental domain of a wallpaper group is referred to as Escherization in the literature (see [23]). Escherization of a given image could be achieved by applying the Escher trick iteratively to an initial fundamental domain.
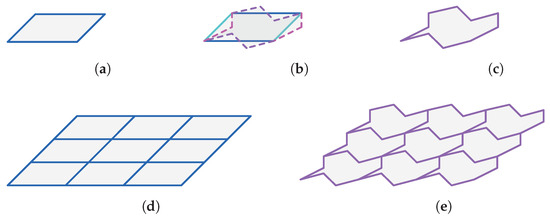
Figure 1.
Escher-Trick visualised. (a) Starting tile. (b) Escher trick: colours show identified edges. (c) Modified tile. (d) Starting tessellation. (e) Modified tessellation.
It should be noted that the Escher trick can also be applied to tilings of the plane in the absence of a symmetry group. Consider, for example, the aperiodic tiling of with the Einstein tiles, see [24,25]. It is still possible to modify an individual tile in such a way that copies of the modified tile tessellate the entire plane. The family of spectres described in [25] yields such an aperiodic tiling and can be obtained in this way from a 14 sided polygon.
3. Constructing Planar Topological Interlocking Assemblies
The Escher-Trick allows one to obtain one tile from another by deforming the edges of the initial tile. This method can be exploited in order to obtain planar TIA by placing these two tiles in two parallel planes and continuously interpolating between them such that in each intermediate step we obtain a tile satisfying the same tiling rule; see Figure 2. This method is first discussed in [17] and detailed in [18] for constructions of TIA with planar crystallographic symmetries. The method can be generalised further to any tiling of , where the initial tiling is placed in one plane and a deformed tiling in a parallel plane. The position of the obtained block depends on the position of the two tiles that yield the block.
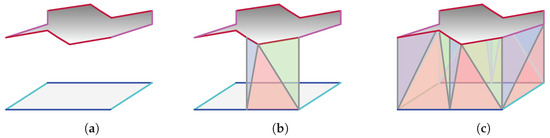
Figure 2.
We can place the two fundamental domains (which can be triangulated) obtained by applying the Escher Trick, as shown in Figure 1 in two parallel planes (a) and interpolate between them using an interpolation with triangles (b). The resulting triangulated block (c) gives rise to a topological interlocking assembly; see [19].
For many purposes, monolithic tilings, or TIA, which consist only of tiles or blocks that are congruent to each other, are of special interest. Monolithic assemblies with congruent blocks yield a significant simplification of the assembly process and also allow for cheaper and more efficient production compared to assemblies with individual components. Planar crystallographic groups and their corresponding tilings naturally give rise to TIA with a single type of block by deformations of the initial tiling by means of the Escher-Trick. Another property of the resulting blocks is that we obtain a triangulation of the block as a side-effect of its construction, as the interpolation between the initial and final tile can be described by a triangulation; see Figure 2. Similar to the Escher-Trick, the method of constructing TIA can be iterated in order to approximate interlocking blocks with smooth surfaces; see [18].
In Figure 3 and Figure 4, two constructions of planar TIAs based on the Escher-Trick are shown. The block shown in Figure 3 is obtained by using tile deformation of the Einstein tile inside the spectre family; see [26].
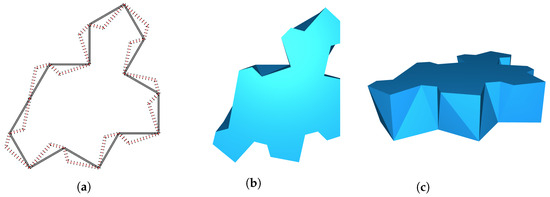
Figure 3.
We can apply the Escher trick (a) to obtain and interpolate between two tiles to obtain an interlocking block (b,c); see [26]. In this specific case, the Escher trick describes the families of the spectre family.
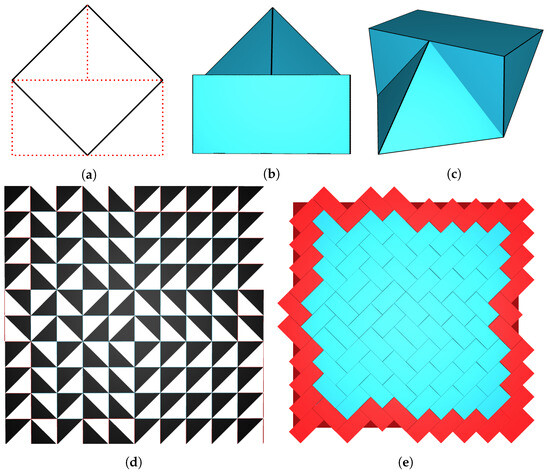
Figure 4.
Both a square and a rectangle yield the fundamental domains of several wallpaper groups. We can deform a square into a rectangle (a) by means of the Escher trick as described in Section 2 to obtain a particular interesting block (b,c), called Versatile Block first constructed in [17]. All possible planar assemblies are classified by the tiling rules of so-called Truchet tiles, which are square tiles that consist of a black and white triangle, and the tiling rule is given by the condition that two neighbouring Truchet tiles only meet at distinct colours; see [27]. An example of a interlocking assembly with versatile blocks and fixed boundary blocks (in red) is given in (d,e). Other blocks with these properties are classified in [18] and their interlocking properties are investigated in [19]. Moreover, different assemblies of these blocks possess different mechanical properties; see [28].
In Figure 4, the versatile block, first introduced in [17], gives rise to many planar assemblies, which are classified combinatorially by assembling rules of so-called Truchet tiles; see [27].
In the following, the semi-regular tiling known as the truncated square tiling (see [29]) is exploited in order to construct a TIA consisting of two different block types. The truncated square tiling is a tiling of the Euclidean plane that consists of infinitely many squares and (regular) octagons satisfying that the edge lengths of all these polygons are the same. Typically, these polygons are scaled such that all edge lengths are equal to 1. In order to realise the truncated square tiling, these polygons are placed in the Euclidean plane, as illustrated in Figure 5.
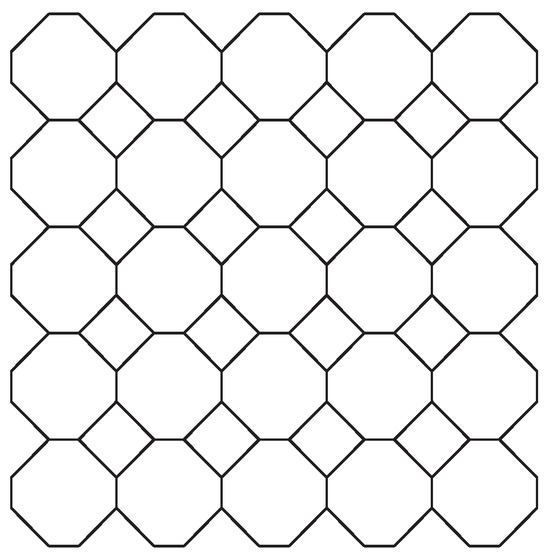
Figure 5.
The truncated square tiling of the Euclidean plane that consists of squares and octagons; at every vertex, two octagons and one square meet without causing intersections of the three polygons.
The reader is referred to [29,30] for more details on this tiling and its properties. In this work, the desired TIA is constructed by applying the Escher-like approach to the truncated square tiling. The aim is to construct two blocks such that copies of these blocks can be assembled in a fashion that corresponds to the truncated square tiling. The details of this constructions are addressed in the following. For simplicity, we depend heavily on the information that is illustrated in Figure 5, Figure 6 and Figure 7 in order to describe the construction of the different tiles and blocks.
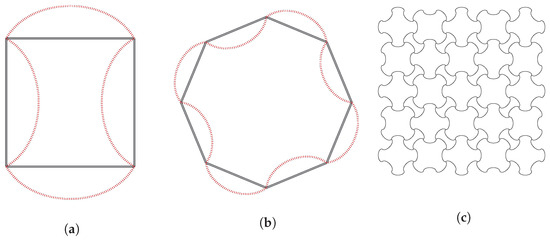
Figure 6.
(a) Deforming the edges of a square to obtain the modified square tile; (b) Deforming the edges of an octagon to obtain the modified octagon tile; (c) The tiling of the Euclidean plane consisting of modified square and octagon tiles that are arranged in the fashion of the truncated square tiling.
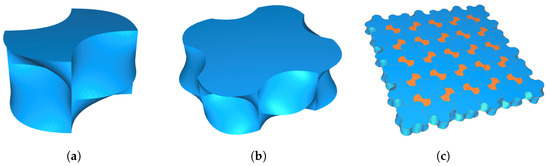
Figure 7.
(a) The square block that results from interpolating between three copies of modified square tiles; (b) The octagon block that results from interpolating between three modified octagon tiles; (c) TIA of the square and the octagon block in the fashion of the truncated square tiling where the frame consists of the 20 most outer octagon blocks.
For the construction of the desired block types, it is necessary to construct two tiles that admit a tiling in a fashion that corresponds to the truncated square tiling. Here, these two tiles are referred to as the modified square tile and the modified octagon tile. The modified square-tile is obtained by deforming the black edges of the square (Figure 6a), as indicated by the red dotted curves. Similarly, the modified octagon tile is derived by deforming the black edges of the octagon illustrated in Figure 6b, as indicated by the red dotted curves. Note that the illustrated deformations of the square and the octagon can be carried out in such a way that the arising modified square and octagon tile admit a tiling of the Euclidean plane in the fashion of the truncated square tiling. The tiling that results from these modified tiles is illustrated in Figure 6c.
Hence, these tiles can be used to construct the desired interlocking blocks. First, the construction of the square-block is described. For simplicity, the square s in Figure 6a is assumed to be given by the convex hull . This results in the modified square tile in Figure 6a being placed in the Euclidean plane such that the points lie on the boundary of the tile. Thus, let be the set that corresponds to the modified square tile in Figure 6a. Next, let be the set that is obtained by applying a 90 degree rotation around the point to the points in The two sets M and are used to place copies of the modified square tile on three parallel planes in In particular, this is achieved by defining the sets and by
The square block (illustrated in Figure 7a) is then obtained by interpolating between the tiles and Similarly, three copies of the modified octagon tile can be rotated and then embedded into by placing them on parallel planes. The octagon block (Figure 7b) results from interpolating between these three copies of the modified octagon tiles. The interpolations to construct these two blocks can be carried out in such a way that copies of these blocks can be assembled in the fashion of the truncated square tiling; see Figure 7c.
We note that the construction of the block corresponding to the square is inspired by the osteomorphic block that has been introduced in [31]. By using the methods presented in [19,20,32], it could be verified that the assembly shown in Figure 7c is a TIA. In order to establish the interlocking property of the given assembly, we have to choose the corresponding frame as the 20 outer octagon blocks.
4. Constructing Spherical Topological Interlocking Assemblies
As described in Section 2, applying the Escher trick to deform tiles of a given tiling opens up a wide range of possibilities to create tilings of the Euclidean plane. Section 3 describes how TIA can be obtained by means of this method via interpolating between constructed tilings. Therefore, the Escher-Like approach turns out to be a versatile method to construct and design planar TIA. In this work, the strengths of the Escher trick are further demonstrated by modifying the Escher-Like approach for a construction method that yields non-planar TIA that are based on arbitrary orientable surfaces.
4.1. The Modified Escher-like Approach
The main aim of this work is to modify the Escher-like approach in such a way that it is possible to construct TIA based on tessellations of arbitrary orientable surfaces. So by introducing this modification, we establish the construction of TIA that result from structures such as curved surfaces, convex, and non-convex polyhedra, the unit sphere and the torus. First examples of TIA arising from a slight modification of the Escher-like approach have been illustrated in [33], where Akpanya et al. formulate a construction method that produces TIA realising the surface of given convex polyhedra whose vertices all lie on the unit sphere. Based on this formulation, Akpanya et al. provide different examples of TIA constructed by exploiting the structure of the Platonic solids and (angular) tubes. The approach proposed here can be viewed as a generalisation of the method introduced in [33], expanding the design space of TIA and additionally enabling the customisation and optimisation of interlocking structures for specific applications.
The modified Escher-Like approach to construct TIA realising arbitrary orientable surfaces can be described as follows: For simplicity, the orientable surfaces in this paper are considered to be surfaces without boundaries. First, let be a set of orientable surfaces such that
- for two real numbers the surfaces and are disjoint, i.e., the intersection is empty,
- the set defined as is a connected set in .
As is a surface without boundary, the set consists of exactly two connected components, and In order to formulate the desired construction, assume that for all the surface is contained either in or in . Further, let be a natural number and let be a tiling of . Lastly, let be a continuous function such that for all the set is a tiling of the surface With this information, the construction of the desired interlocking blocks can be achieved. In particular, for all , the block is constructed by defining Since two blocks and with satisfy the equality the resulting set is an assembly of blocks that satisfies
Another interpretation of this modified Escher-Like approach is that for , the block is obtained by interpolating between the tiles and . Moreover, this interpolation is specified by the function f and is carried out in such a way that for every , the set forms a tiling of the surface For simplicity, the interpretation just described, omitting the function f, is used to present the following examples of TIA. Note that an assembly of blocks resulting from this construction is not necessarily a TIA. In order to show that a constructed assembly is indeed a TIA, a suitable frame has to be chosen, and the interlocking property has to be verified with established procedures; see [19,20,32].
Moreover, we highlight that the surfaces that are exploited to construct TIA via the modified Escher-like approach are only required to be orientable and to allow a tessellation by different tiles. Hence, the modified Escher-Like approach forms a generalisation of the Escher-like approach that has been established in [17] to construct planar TIA.
4.2. Examples of TIA That Arise from the Modified Escher-like Approach
In the following, the modified Escher-Like approach is illustrated by presenting examples of TIA that are based on the unit sphere and convex polyhedra. In general, we are interested in constructing TIAs that consist of a small number of different block types. Therefore, the platonic solids have been exploited in [33] to construct first examples of non-planar TIA that consist of copies of a single non-convex block. In the described context, the number of blocks of a given TIA is exactly the number of faces of the corresponding platonic solid. Hence, these non-planar TIA consist of a small number of blocks. In this work, we make use of Archimedean and Catalan solids to construct TIA via the modified Escher-like approach that consists of an increased number of blocks. These solids form examples of highly symmetrical polyhedra. Hence, the face-transitivity of the Catalan solids and the vertex-transitivity of the Archimedean solids guarantee that the TIA resulting from these polyhedra consists of a small number of different block types. In the literature, these polyhedra have been exploited to construct TIA. In [34] Viana illustrates planar TIA that consists of copies of a given Archimedean or Catalan solid. Furthermore, Viana establishes a connection between these TIA and tessellations of the Euclidean plane by taking cross-sections of the given assembly. In this work, the Archimedean and Catalan solids are exploited to construct non-planar TIA consisting of non-convex blocks.
4.2.1. TIA Based on an Archimedean Solid
In literature, the Archimedean solids form a class of convex uniform polyhedra. That means that these polyhedra are vertex-transitive and that the faces of these polyhedra form regular polygons. There are exactly 13 Archimedean solids. The solid that forms the focus of this work is the truncated icosahedron . This polyhedron consists of 20 hexagonal and 12 pentagonal faces; see Figure 8.
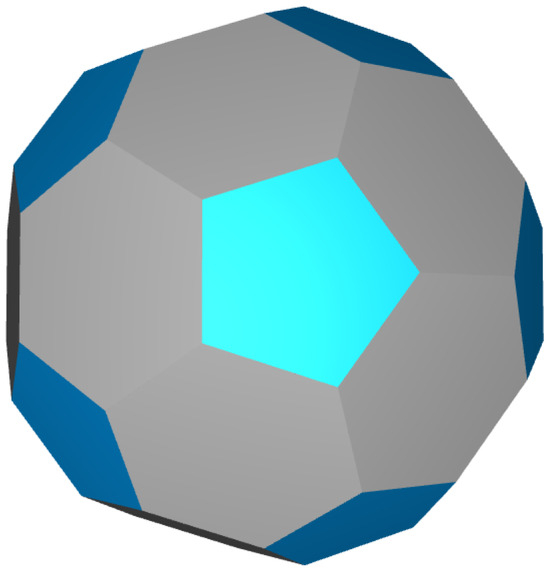
Figure 8.
The truncated icosahedron, i.e., the Archimedean solid consisting of 20 hexagonal and 12 pentagonal faces.
Hence, these polygons form a tiling of the surface of the truncated icosahedron. The truncated icosahedron is therefore a suitable candidate for constructing a non-planar TIA that consists of two different block types. It is assumed that the polyhedron is centred at the origin and that all vertices lie on the sphere with radius 1. In order to construct the desired TIA, let be the 20 hexagonal faces and be the 12 pentagonal faces of the polyhedron . Hence, the faces of the scaled polyhedron are given by and The surface of the polyhedron can be tiled by tiles and that are obtained as described in the following:
- For , the tile is constructed by deforming the edges of the hexagonal face such that the projection of the tile onto a plane containing the face is the polygon that is indicated by the blue dotted lines in Figure 9a.
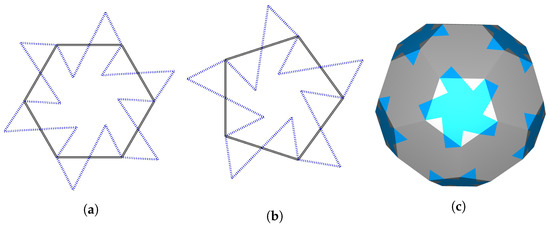 Figure 9. Applying the Escher-Like approach to hexagons (a) and pentagons (b) of the truncated icosahedron (c).
Figure 9. Applying the Escher-Like approach to hexagons (a) and pentagons (b) of the truncated icosahedron (c). - Furthermore, for , the tile is obtained by deforming the edges of the pentagonal face such that the projection of the modified tile onto a plane containing the face is the polygon that is indicated by the blue dotted lines in Figure 9b.
Figure 9c illustrates that the set forms a tiling of the surface
By interpolating between the hexagonal face and the modified tile for , and between the pentagonal face and the modified tile for , copies of the blocks shown in Figure 10a,b are constructed.

Figure 10.
(a) Different views of the block that result from interpolating between a pentagonal face of the truncated icosahedron and a modified tile that is contained on the surface of a scaled truncated icosahedron (b) Different views of the block that result from interpolating between a hexagonal face of the truncated icosahedron and a modified tile that is contained on the surface of a scaled truncated icosahedron.
The process of interpolating between the above tiles can be carried out in such a way that the resulting blocks admit an assembly that realises the surface of the truncated icosahedron; see Figure 11.

Figure 11.
Two exploded views of the TIA that realises the surface of the truncated icosahedron.
It is not clear how a minimal frame of the TIA illustrated above has to be chosen in order to establish the interlocking property of the given assembly. By employing experiments with 3D-printed assemblies, we observed that the modified Escher-like approach can be iterated in order to construct a TIA with a reduced number of frame blocks. For instance, for and for , it is possible to interpolate between the tiles and between the tiles in such a way that a TIA realising the surface of the truncated icosahedron is constructed. A 3D-printed version of the described assembly is illustrated in Figure 15 on the left. The interlocking property of this assembly can be computationally verified by choosing any two blocks as the frame.
4.2.2. TIA Based on the Unit Sphere
As a next example, the unit sphere is examined. In particular, the unit sphere is used to construct a spherical example of a TIA that consists of two different block types. For this goal, the truncated icosahedron is very useful. The existence of the truncated icosahedron establishes that the unit sphere can be tiled with 20 spherical hexagons and 12 spherical pentagons ; see Figure 12.

Figure 12.
Tiling of (approximated) unit sphere consisting of 20 spherical hexagons and 12 spherical pentagons.
Hence, this tiling can be exploited to construct the desired TIA. We recall that the hexagonal faces of the truncated icosahedron are given by and that the pentagonal faces of this polyhedron are given by Moreover, recall that the modified tiles that are obtained from these hexagonal and pentagonal faces are denoted by and . In order to achieve the goal of constructing a TIA that is based on the unit sphere, the following two assumptions are made:
- For , the intersection between the hexagonal face and the spherical hexagon satisfies That means that this intersection contains the vertices of the hexagonal face
- For , the intersection between the pentagonal face and the spherical pentagon satisfy the equality , which means that this intersection contains the vertices of the pentagonal face
Thus, the desired interlocking blocks are constructed by interpolating between the tiles for and between the tiles for . Figure 13 shows different views of the block that result from interpolating between the tiles

Figure 13.
Three different views of the interlocking block that results from interpolating between a hexagonal face of the truncated icosahedron, a modified tile of a scaled truncated icosahedron and a spherical hexagon that forms a tile of the unit sphere.
The TIA that arises from the above construction is illustrated in Figure 14. The TIA arising from the truncated icosahedron and the above construction have been 3D-printed, see Figure 15.

Figure 14.
Two exploded views of the TIA that is based on the unit sphere.

Figure 15.
3D-printed models of truncated icosahedron and corresponding TIA of unit sphere where any two blocks can be chosen as the frame.
In order to establish the interlocking property of the given assembly, it is sufficient to choose a frame that consists of any two blocks of the assembly.
4.2.3. TIA Based on a Catalan Solid
Lastly, the modified Escher-like approach is used to construct a TIA that is derived from manipulating the surface of a Catalan solid. The Catalan solids are the polyhedra that form the duals of the Archimedean solids. Hence, these 13 polyhedra are face-transitive. Here, the deltoidal hexecontahedron is introduced in order to exemplify another construction of a TIA that is based on a convex polyhedron. Since the deltoidal hexecontahedron is the Catalan solid consisting of 60 kites as faces (see Figure 16), the TIA that results from applying the modified Escher-like approach to this polyhedron consists of copies of one block type.

Figure 16.
The deltoidal hexecontahedron, i.e., the solid whose surface consists of 60 kites as faces.
For this purpose, we assume that the polyhedron is centered at the origin and that all vertices of lie on the sphere with radius 1. Furthermore, let be the kites that form the faces of the polyhedron Thus, the faces of the polyhedron are given by The surface of the polyhedron can be tiled by tiles that are constructed by deforming the edges of the kites for These modified tiles are obtained as described in the following: For , the tile is obtained by deforming the edges of the kite such that projecting the tile onto the plane that contains the face gives rise to the polygon that is indicated by the blue dotted lines in Figure 17a. The block that results from interpolating between the tiles and is shown in Figure 17b.
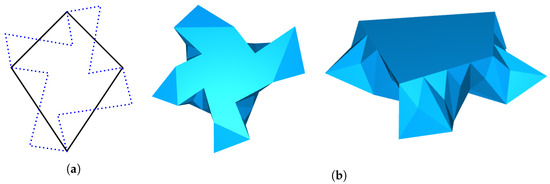
Figure 17.
(a) Projection of a modified tile resulting from deforming the edges of a kite that forms a face of the deltoidal hexecontahedron (b) Different views of the block that results from interpolating between a kite that forms a face of the deltoidal hexecontahedron and a modified tile that is contained on the surface of a scaled deltoidal hexecontahedron.
Copies of the above block can be assembled in order to achieve an assembly of blocks that realises the surface of the deltoidal hexecontahedron; see Figure 18.

Figure 18.
Two exploited views of the TIA that realises the surface of the deltoidal hexecontahedron.
Note that it is not clear how a minimal frame establishing the interlocking property can be chosen for the above assembly of blocks. As described Section 4.2.1, it can be observed that iterating the modified Escher-like approach applied to the deltoidal hexecontahedron constructs a TIA with a reduced number of blocks being contained in the frame.
5. Conclusions and Outlook
In this work, the versatility of the Escher-like approach for constructing topological interlocking assemblies (TIA) has been demonstrated. By considering both regular and semi-regular tilings, as well as extending the method to arbitrary orientable surfaces, a wide range of potential TIA configurations are constructed. The key findings of this work include:
- The successful construction of planar and non-planar TIA using the Escher-like method;
- The exploration of a semi-regular tiling yielding an interlocking structure;
- The extension of the method to non-planar surfaces, such as the unit sphere and various convex polyhedra, demonstrates the feasibility of constructing spherical and polyhedral TIA.
- Practical insights gained from 3D-printed models provides a profound understanding of the assembly and interlocking processes.
The Escher-like approach, including its modified versions, has proven to be a powerful tool for the construction of TIA, with practical implications for fields such as architecture and 3D printing; see [27,33].
Future research will focus on refining the described construction technique for given applications and for optimising mechanical properties tailored to practical scenarios such as the construction of domes with non-planar TIA, the investigation of columned-shaped TIAs for tunnel systems, or spherical-shaped TIAs for interlocking puzzles. For this, generalisations of reliable tools for fast evaluation of interlocking assemblies, like the “Interlocking Flow Method” presented in [28], should be generalised in order to gain a profound understanding of the assemblies constructed in this work.
Moreover, future research will explore different materials for constructing TIA. One specific scenario could involve using additive manufacturing techniques, such as 3D concrete printing, to produce large-scale spherical TIA blocks.
Author Contributions
Conceptualization, methodology, writing (draft, review and editing) R.A., T.G. and A.C.N.; visualization and software R.A. and T.G.; funding acquisition A.C.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)–SFB/TRR280, Project-ID 417002380 (A04).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dyskin, A.V.; Estrin, Y.; Kanel-Belov, A.J.; Pasternak, E. A new concept in design of materials and structures: Assemblies of interlocked tetrahedron-shaped elements. Scr. Mater. 2001, 44, 2689–2694. [Google Scholar] [CrossRef]
- Weizmann, M.; Amir, O.; Grobman, Y.J. Topological interlocking in buildings: A case for the design and construction of floors. Autom. Constr. 2016, 72, 18–25. [Google Scholar] [CrossRef]
- Miodragovic Vella, I.; Kotnik, T. Stereotomy, an Early Example of a Material System. In Proceedings of the 35th eCAADe Conference, Rome, Italy, 20–22 September 2017; pp. 251–258. [Google Scholar] [CrossRef]
- Tessmann, O.; Rossi, A. Geometry as Interface: Parametric and Combinatorial Topological Interlocking Assemblies. J. Appl. Mech. 2019, 86, 111002. [Google Scholar] [CrossRef]
- Harsono, K.; Shih, S.G.; Wagiri, F.; Alfred, W. Integration of Design and Performance Evaluation for Reusable Osteomorphic-Block Masonry. Nexus Netw. J. 2023, 26, 71–94. [Google Scholar] [CrossRef]
- Hua, H. Porous interlocking assembly: Performance-based dry masonry construction with digital stereotomy. Archit. Intell. 2024, 3, 20. [Google Scholar] [CrossRef]
- Dyskin, A.V.; Estrin, Y.; Pasternak, E.; Khor, H.C.; Kanel-Belov, A.J. The principle of topological interlocking in extraterrestrial construction. Acta Astronaut. 2005, 57, 10–21. [Google Scholar] [CrossRef]
- Carlesso, M.; Giacomelli, R.; Krause, T.; Molotnikov, A.; Koch, D.; Kroll, S.; Tushtev, K.; Estrin, Y.; Rezwan, K. Improvement of sound absorption and flexural compliance of porous alumina-mullite ceramics by engineering the microstructure and segmentation into topologically interlocked blocks. J. Eur. Ceram. Soc. 2013, 33, 2549–2558. [Google Scholar] [CrossRef]
- Dyskin, A.; Estrin, Y.; Kanel-Belov, A.; Pasternak, E. Topological interlocking of platonic solids: A way to new materials and structures. Philos. Mag. Lett. 2003, 83, 197–203. [Google Scholar] [CrossRef]
- Kanel-Belov, A.J.; Dyskin, A.V.; Estrin, Y.; Pasternak, E.; Ivanov-Pogodaev, I.A. Interlocking of Convex Polyhedra: Towards a Geometrical Theory of Fragmented Solids. Mosc. Math. J. 2010, 10, 337–342. [Google Scholar] [CrossRef]
- Glickman, M. The G-block system of vertically interlocking paving. In Proceedings of the Second International Conference on Concrete Block Paving, Delft, The Netherlands, 10–12 April 1984; pp. 10–12. [Google Scholar]
- Gallon, J.G. Machines et Inventions Approuvées par l’Académie Royale des Sciences Depuis son Établissement Jusqu’à Present; Avec Leur Description; l’Académie Royale des Sciences: Paris, France, 1735. [Google Scholar]
- Subramanian, S.G.; Eng, M.; Krishnamurthy, V.R.; Akleman, E. Delaunay Lofts: A biologically inspired approach for modeling space filling modular structures. Comput. Graph. 2019, 82, 73–83. [Google Scholar] [CrossRef]
- Akleman, E.; Krishnamurthy, V.R.; Fu, C.A.; Subramanian, S.G.; Ebert, M.; Eng, M.; Starrett, C.; Panchal, H. Generalized abeille tiles: Topologically interlocked space-filling shapes generated based on fabric symmetries. Comput. Graph. 2020, 89, 156–166. [Google Scholar] [CrossRef]
- Mullins, C.; Ebert, M.; Akleman, E.; Krishnamurthy, V. Voronoi Spaghetti & VoroNoodles: Topologically Interlocked, Space-Filling, Corrugated & Congruent Tiles. In Proceedings of the SIGGRAPH Asia 2022 Technical Communications, SA ’22, Daegu, Republic of Korea, 6–9 December 2022. [Google Scholar] [CrossRef]
- Ebert, M.; Akleman, E.; Krishnamurthy, V.; Kulagin, R.; Estrin, Y. VoroNoodles: Topological Interlocking with Helical Layered 2-Honeycombs. Adv. Eng. Mater. 2023, 26, 2300831. [Google Scholar] [CrossRef]
- Goertzen, T.; Niemeyer, A.; Plesken, W. Topological Interlocking via Symmetry. In Proceedings of the 6th FIB International Congress 2022, Oslo, Norway, 12–16 June 2022; Novus Press: Oslo, Norway, 2022. [Google Scholar]
- Goertzen, T. Constructing Interlocking Assemblies with Crystallographic Symmetries. arXiv 2024, arXiv:2405.15080. [Google Scholar]
- Goertzen, T. Mathematical Foundations of Interlocking Assemblies. arXiv 2024, arXiv:2405.17644. [Google Scholar] [CrossRef]
- Wang, Z.; Song, P.; Isvoranu, F.; Pauly, M. Design and Structural Optimization of Topological Interlocking Assemblies. ACM Trans. Graph. 2019, 38, 1–13. [Google Scholar] [CrossRef]
- Bejarano, A.; Hoffmann, C. A generalized framework for designing topological interlocking configurations. Int. J. Archit. Comput. 2019, 17, 53–73. [Google Scholar] [CrossRef]
- Loing, V.; Baverel, O.; Caron, J.F.; Mesnil, R. Free-form structures from topologically interlocking masonries. Autom. Constr. 2020, 113, 103117. [Google Scholar] [CrossRef]
- Kaplan, C.S.; Salesin, D.H. Escherization. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 23–28 July 2000; SIGGRAPH ’00. pp. 499–510. [Google Scholar] [CrossRef]
- Smith, D.; Myers, J.S.; Kaplan, C.S.; Goodman-Strauss, C. An aperiodic monotile. arXiv 2023, arXiv:2303.10798. [Google Scholar] [CrossRef]
- Smith, D.; Myers, J.S.; Kaplan, C.S.; Goodman-Strauss, C. A chiral aperiodic monotile. arXiv 2023, arXiv:2305.17743. [Google Scholar] [CrossRef]
- Akpanya, R.; Goertzen, T.; Liu, Y.; Stüttgen, S.; Robertz, D.; Xie, Y.M.; Niemeyer, A.C. Constructing Topological Interlocking Assemblies Based on an Aperiodic Monotile. In Proceedings of the IASS 2024 Symposium: Redefining the Art of Structural Design, Zurich, Switzerland, 26–30 August 2024; Block, P., Boller, G., DeWolf, C., Pauli, J., Kaufmann, W., Eds.; International Association for Shell and Spatial Structures (IASS): Madrid, Spain, 2024. accepted, not yet published. [Google Scholar]
- Akpanya, R.; Goertzen, T.; Wiesenhuetter, S.; Niemeyer, A.C.; Noennig, J. Topological Interlocking, Truchet Tiles and Self-Assemblies: A Construction-Kit for Civil Engineering Design. In Proceedings of the Bridges 2023: Mathematics, Art, Music, Architecture, Culture, Halifax, NS, Canada, 27–31 July 2023; Holdener, J., Torrence, E., Fong, C., Seaton, K., Eds.; Tessellations Publishing: Phoenix, AZ, USA, 2023; pp. 61–68. [Google Scholar]
- Goertzen, T.; Macek, D.; Schnelle, L.; Weiß, M.; Reese, S.; Holthusen, H.; Niemeyer, A.C. Mechanical Comparison of Arrangement Strategies for Topological Interlocking Assemblies. arXiv 2023, arXiv:2312.01958. [Google Scholar] [CrossRef]
- Conway, J.H.; Burgiel, H.; Goodman-Strauss, C. The Symmetries of Things; A K Peters, Ltd.: Wellesley, MA, USA; New York, NY, USA, 2008; pp. xviii+426. [Google Scholar]
- Grünbaum, B.; Shephard, G.C. Tilings and Patterns; A Series of Books in the Mathematical Sciences; An introduction; W. H. Freeman and Company: New York, NY, USA, 1989; pp. xii+446. [Google Scholar]
- Dyskin, A.; Estrin, Y.; Pasternak, E.; Khor, H.; Kanel-Belov, A. Fracture Resistant Structures Based on Topological Interlocking with Non-planar Contacts. Adv. Eng. Mater. 2003, 5, 116–119. [Google Scholar] [CrossRef]
- Stüttgen, S.; Akpanya, R.; Beckmann, B.; Chudoba, R.; Robertz, D.; Niemeyer, A.C. Modular Construction of Topological Interlocking Blocks—An Algebraic Approach for Resource-Efficient Carbon-Reinforced Concrete Structures. Buildings 2023, 13, 2565. [Google Scholar] [CrossRef]
- Akpanya, R.; Goertzen, T.; Niemeyer, A.C. A Group-Theoretic Approach for Constructing Spherical-Interlocking Assemblies. In Proceedings of the IASS Annual Symposium 2023: Integration of Design and Fabrication, Melbourne, Australia, 10–14 July 2023; Xie, Y., Burry, J., Lee, T., Ma, J., Eds.; International Association for Shell and Spatial Structures (IASS): Madrid, Spain, 2023; pp. 470–480. [Google Scholar]
- Viana, V. From Solid to Plane Tessellations, and Back. Nexus Netw. J. 2018, 20, 741–768. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).