Tube-Based Robust Model Predictive Control for Autonomous Vehicle with Complex Road Scenarios

Abstract

This study proposes a Tube-based Robust Model Predictive Control (Tube-RMPC) strategy for autonomous vehicle control to address model parameter uncertainties and variations in road–tire adhesion coefficients in complex road scenarios. More specifically, the proposed approach improves the representation of vehicle dynamic behavior by introducing a unified vehicle–tire modeling framework. To facilitate computational tractability and algorithmic implementation, the model is systematically linearized and discretized. Furthermore, the Tube-based Robust Model Predictive Control strategy is developed to improve adaptability to uncertainty in the road surface adhesion coefficient. The Tube-based Robust Model Predictive controller ensures robustness by establishing a robust invariant tube around the nominal trajectory, effectively mitigating road surface variations and enhancing stability. Finally, a co-simulation platform integrating CarSim and Simulink is employed to validate the proposed method’s effectiveness. The experimental results demonstrate that Tube-RMPC improves the path-tracking performance, reducing the maximum tracking error by up to 9.17% on an S-curve and 2.25% in a double lane change, while significantly lowering RMSE and enhancing yaw stability compared to MPC and PID.

1. Introduction

Autonomous driving technology drives innovation in the fields of artificial intelligence, sensor technology, and vehicle dynamics [1]. However, challenges such as system reliability, ethical decision-making, and integration into mixed traffic must be addressed to fully realize its transformative societal impact, making autonomous driving a critical and multidisciplinary research area [2]. While autonomous driving promises transformative societal benefits, achieving stable and reliable control under complex road conditions remains a pressing challenge. Diverse surfaces introduce dynamic uncertainties that can compromise vehicle stability, especially during sudden or unexpected events [3]. Addressing these challenges necessitates a focused exploration of advanced control strategies that are capable of ensuring stability under varying conditions, making this a crucial direction in autonomous driving technology research [4]. In this context, the design of robust and adaptive vehicle control strategies plays a pivotal role in ensuring safe navigation and trajectory tracking. Effective control systems must be capable of handling not only modeling uncertainties but also real-world disturbances such as variations in road tire adhesion. These variations, which are difficult to measure directly in real-time, significantly affect lateral dynamics and must be addressed within the control framework to enhance safety and performance.

In recent years, research on trajectory-tracking controller design has prioritized minimizing the deviation between a vehicle’s real-time trajectory and its desired path. To address this critical challenge, a variety of advanced control methodologies have been developed, including fuzzy control [5], linear quadratic regulators [6], sliding-mode control [7], and model predictive control (MPC) [8,9,10,11]. Among these, MPC has gained significant prominence due to its predictive capability for complex dynamic systems, effective constraint handling, and optimization-driven performance enhancement. Despite its inherent strengths, numerous studies have proposed refinements to the conventional MPC framework to tackle specific challenges encountered in practical applications. For instance, a study introduced an enhanced approach [12] to improve stability in complex operational scenarios. Failure to address these challenges can escalate into adverse phenomena, such as oversteering, drifting, or complete loss of vehicle stability, underscoring the need for further research and innovation in this domain. To address these phenomena, an MPC-based trajectory-tracking controller [13] was applied. A sophisticated model parameter adjustment strategy was utilized to improve control precision and enhance the trajectory-tracking performance of autonomous vehicles. Nevertheless, this approach remains highly sensitive to variations in road surface adhesion, potentially limiting its robustness and adaptability in complex driving conditions. To mitigate these limitations, an MPC algorithm incorporating dynamic parameter adaptation [14] was proposed to counteract parameter sensitivity issues. Through the introduction of a nonlinear predictive model and dynamic adjustment mechanisms, system behavior is effectively optimized, and trajectory constraints are managed in complex dynamic environments. In addition to these efforts, recent research has extended MPC applications to novel traffic paradigms, such as lane-free environments [15,16] proposed an optimal path planning framework for connected and automated vehicles (CAVs) operating in lane-free traffic conditions, demonstrating the versatility of MPC in unstructured scenarios where traditional lane-based assumptions are not applicable. However, despite its demonstrated advantages in sensitivity control, the algorithm remains limited in its ability to handle uncertainties in model parameters.

Data-driven methodologies have emerged as a powerful and efficient paradigm for modeling complex and partially unknown dynamic systems [17]. Among these, Koopman operator theory [18,19,20] has become a pivotal framework, enabling the representation of nonlinear system dynamics through linear evolution within an augmented observable space. In the domain of automated driving, this approach has been applied by leveraging deep Koopman-based modeling of vehicle dynamics, often integrated with MPC strategies for trajectory-tracking tasks [21]. Despite its advantages in facilitating global linear representations, the integration of Koopman operator theory with MPC introduces substantial computational complexity and demands extensive, high-precision data for effective implementation. This reliance on large-scale data can lead to potential safety risks and unintended behaviors in automated driving scenarios [18]. To enhance robustness and reduce reliance on precise, high-volume data, robust model predictive control (RMPC) frameworks [19,20] such as min–max MPC [21] and Tube-based MPC [22,23] have garnered significant attention. These approaches confine parameter variations within a predefined region, ensuring improved robustness and computational efficiency. Min–max MPC [24]—a widely studied RMPC approach—explicitly incorporates system uncertainties by formulating constraints on state variables and control inputs. However, its worst-case optimization strategy results in a computational complexity that scales with the input dimensionality and prediction horizon, posing challenges in multi-input multi-output systems. As a result, its real-time feasibility remains a key limitation in practical implementations.

Considering the integration of predictive information and constraints, RMPC methods have been extensively studied and applied in automated vehicle (AV) systems. As previously discussed, to address uncertainties such as model inaccuracies under extreme conditions, two primary approaches have emerged: stochastic MPC, which employs probabilistic descriptions, and robust MPC (RMPC), which relies on bounded-set representations [25]. Due to the inherent challenges in accurately describing model uncertainties probabilistically, RMPC is generally regarded as a more promising solution for motion control. A more computationally efficient alternative is Tube-based RMPC (TRMPC) [26], which confines system uncertainties to a robust tube, reducing the online optimization problem to a nominal MPC problem with tightened constraints. TRMPC has found extensive applications in AV control, including lateral control [27], trajectory tracking in autonomous racing [28], fault-tolerant control [29], and vehicle platooning [30]. Despite its effectiveness in handling structured model uncertainties, TRMPC primarily focuses on system disturbances rather than external environmental variations. Consequently, the impact of road–tire adhesion variations on control performance remains insufficiently explored, posing challenges in adapting to diverse road conditions, such as wet, snowy, or dry asphalt surfaces. Ensuring robust control across varying road surface conditions remains a critical challenge that warrants further investigation.

To address the limitations identified in existing methods, this study proposes a Tube-RMPC-based vehicle control approach to explicitly address model parameter uncertainties and variations in road–tire adhesion coefficients. The primary contributions of this research are as follows:

(1)

A unified vehicle–tire modeling framework is proposed to enhance the representation of vehicle dynamic behavior.

(2)

A robust model predictive control framework is developed to enhance adaptability to road surface model parameter uncertainties.

(3)

A co-simulation model integrating CarSim and Simulink is established to validate the effectiveness of the experimental methodology.

2. Problem Statement and Preliminaries

To formulate this control problem in a mathematically tractable way, a unified dynamic vehicle–tire model is first constructed and simplified into a linearized form. This model serves as the basis for the development of a Tube-based Robust Model Predictive Control (Tube-RMPC) strategy. The aim is to ensure that the actual system trajectory remains within a predefined robust tube surrounding the nominal prediction, despite the presence of external disturbances and parameter variations.

2.1. Dynamic Vehicle Model

The vehicle dynamics model is developed for model predictive control, prioritizing computational efficiency while retaining essential planar motion characteristics. Based on the prior knowledge of vehicle dynamics, a simplified three-degree-of-freedom vehicle model is developed under specific assumptions [31]. Key assumptions include: (1) planar motion constraints (longitudinal, lateral, yaw) under flat-road assumptions; (2) rigid-body suspension and chassis; (3) decoupled pure lateral tire slip properties; (4) single-track bicycle model eliminating load transfers; (5) quasi-static longitudinal dynamics; (6) neglected aerodynamic forces. These assumptions reduce the system to three degrees of freedom with front-wheel-drive actuation. The dynamic model of an autonomous vehicle is illustrated in Figure 1. Utilizing trigonometric relationships, the forces acting on the front and rear tires in the x- and y-directions can be expressed as follows:

$$\left\{\begin{array}{l}{F}_{xf}=F_{lf}\cos {\delta }_f-F_{cf}\sin {\delta }_f\hfill \\ F_{xr}=F_{lr}\cos {\delta }_r-F_{cr}\sin {\delta }_r\hfill \\ F_{yf}=F_{l_f}\sin {\delta }_f+F_{cf}\cos {\delta }_f\hfill \\ F_{yr}=F_{1r}\sin {\delta }_r+F_{cr}\cos {\delta }_r\hfill \end{array}\right.,$$

(1)

where $F_{lf}$, $F_{cf}$, and $F_{cr}$ denote the longitudinal forces acting on the front and rear tires, respectively; $F_{xf}$ and $F_{yr}$ represent the combined forces acting on the front and rear tires, decomposed into longitudinal and lateral components; and ${\delta }_f$ and ${\delta }_r$ describe the steering angles of the front and rear tires.

According to Newton’s second law in Figure 2, the equilibrium equations of vehicle dynamics are obtained as follows:

$$\left\{\begin{array}{l}m\ddot{y}=-m\dot{x}\dot{\phi }+2F_{xf}+2F_{yf}\hfill \\ m\ddot{x}=m\dot{y}\dot{\phi }+2F_{xf}+2F_{xr}\hfill \\ I_z\ddot{\phi }=2a{F}_{yf}-2b{F}_{yr}\hfill \end{array}\right.,$$

(2)

where $a$ and $b$ denote the distances from the center of mass to the front and rear axles, respectively; $m$ represents the mass of the autonomous vehicle; $I_z$ corresponds to the moment of inertia; $\phi$ describes the heading angle; and $\dot{x}$ and $\dot{y}$ indicate the center-of-mass velocities along the x-axis and y-axis, respectively.

Under the small-angle assumption derived from the Magic Tire model in [32], the lateral force is approximately linearly related to the sideslip angle of the tire, as shown below:

$$\left\{\begin{array}{l}{F}_l\approx C_{l}s,F_c\approx C_c{\alpha }_{(f/r)}\hfill \\ {\alpha }_f={\displaystyle \frac{\dot{y}+a\dot{\phi }}{\dot{x}}}-{\delta }_f,{\alpha }_r={\displaystyle \frac{\dot{y}-b\dot{\phi }}{\dot{x}}}\hfill \end{array}\right.,$$

(3)

where $C_l$ is the tire cornering stiffness, $C_c$ refers to the lateral stiffness, $s$ defines the slip ratio, and ${\alpha }_f$ and ${\alpha }_r$ are the front and rear wheel slip angles, respectively.

Using (1)–(3), a nonlinear model of a dynamic vehicle system based on a small front wheel deflection angle and tire model assumption is obtained as follows:

$$\left\{\begin{array}{l}m{\dot{v}}_y=-m{v}_x\dot{\phi }+2\left[C_{\mathrm{cf}}\left({\delta }_{\mathrm{f}}-{\displaystyle \frac{v_{\mathrm{y}}+a\dot{\phi }}{v_x}}\right)+C_{\mathrm{cr}}{\displaystyle \frac{b\dot{\phi }-v_{\mathrm{y}}}{v_x}}\right]\hfill \\ m{\dot{v}}_x=m{v}_y\dot{\phi }+2\left[C_{\mathrm{lf}}{s}_{\mathrm{f}}+C_{\mathrm{cf}}\left({\delta }_{\mathrm{f}}-{\displaystyle \frac{v_{\mathrm{y}}+a\dot{\phi }}{v_x}}\right){\delta }_{\mathrm{f}}+C_{\mathrm{lr}}{s}_{\mathrm{r}}\right]\hfill \\ I_z\ddot{\phi } = 2\left[ a{C}_{cf}\left({\delta }_f - {\displaystyle \frac{v_r + a\dot{\phi }}{v_x}}\right)-b{\overline{C}}_{cr} {\displaystyle \frac{b\dot{\phi } - v_y}{v_x}}\right]\hfill \\ \dot{Y}=\dot{x}\sin \phi +\dot{y}\cos \phi \hfill \\ \dot{X}=\dot{x}\cos \phi -\dot{y}\sin \phi \hfill \end{array}\right.,$$

(4)

Combining the above equations, the state-space equation of nonlinear dynamics is written as

$${\dot{\xi }}_{dyn}=A{\xi }_{dyn}+B{u}_{dyn}.$$

(5)

with $\left\{\begin{array}{c}{\xi }_{dyn}={\left[\begin{array}{c}\dot{y},\dot{x},\phi ,\dot{\phi },Y,X\end{array}\right]}^T\\ u_{dyn}={\delta }_f\end{array}\right.$.

2.2. Model Integration

Although nonlinear MPC can more accurately represent vehicle dynamics, its high online computational burden limits its applicability in high-frequency trajectory tracking [33]. Through dynamic modeling, a nonlinear system is formulated, which cannot be directly applied to linear time-varying model predictive control. Linear approximation is required to obtain a suitable linear time-varying representation. Taylor series expansion [34] is performed around specific operating points, retaining only the first-order terms and neglecting higher-order components, resulting in

$$\dot{\xi }=f({\xi }_{dyn},u_{dyn})+{\displaystyle \frac{\partial f}{\partial \xi }}{|}_{\begin{array}{c}\begin{array}{c}\xi ={\xi }_{dyn}\end{array}\\ \begin{array}{c}u=u_{dyn}\end{array}\end{array}}(\xi -{\xi }_{dyn})+{\displaystyle \frac{\partial f}{\partial u}}{|}_{\begin{array}{c}\begin{array}{c}\xi ={\xi }_{dyn}\end{array}\\ \begin{array}{c}u=u_{dyn}\end{array}\end{array}}(u-u_{dyn})$$

(6)

The nonlinear dynamic system is changed as follows:

$$\stackrel{·}{\overline{\xi }}=A(t)\overline{\xi }+B(t)\overline{u}$$

(7)

with $\overline{\xi }=\xi -{\xi }_{dyn}$, $A(t)={\displaystyle \frac{\partial f}{\partial \xi }}{|}_{({\xi }_r,u_r)},B(t)={\displaystyle \frac{\partial f}{\partial u}}{|}_{({\xi }_r,u_r)}.$

The derived equation is continuous, and continuous-time models are theoretically applicable to predictive control, but they often result in excessive computational effort in real-time scenarios. Therefore, it is a reasonable and effective approach to discretize the continuous linear system. The continuous linear system is converted into its discrete-time form using the Forward Euler method [35] as follows:

$$\overline{\xi }\left(k+1\right)=A_{k,t}\overline{\xi }\left(k\right)+B_{k,t}\overline{u}\left(k\right),$$

(8)

with $A_{k,t}=I+TA(k), B_{k,t}=TB(k)$.

$A_{k,t}=\left[\begin{array}{cccccc}{\widehat{A}}_{1,1}(k)& {\widehat{A}}_{1,2}(k)& 0& {\widehat{A}}_{1,4}(k)& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 1& T_s& 0& 0\\ {\widehat{A}}_{4,1}(k)& {\widehat{A}}_{4,2}(k)& 0& {\widehat{A}}_{4,4}(k)& 0& 0\\ {\widehat{A}}_{5,1}(k)& {\widehat{A}}_{5,2}(k)& {\widehat{A}}_{5,3}(k)& 0& 1& 0\\ {\widehat{A}}_{6,1}(k)& {\widehat{A}}_{6,2}(k)& {\widehat{A}}_{6,3}(k)& 0& 0& 1\end{array}\right]$, ${\widehat{A}}_{1,1}(k)=1-{\displaystyle \frac{T(2C_{cf}+2C_{cr})}{m\dot{x}}}$, ${\widehat{A}}_{1,2}(k)={\displaystyle \frac{T(2C_{cf}+2C_{cr})\dot{y}}{m{\dot{x}}^2}}-{\displaystyle \frac{T(2b{C}_{cf}-2a{C}_{cr})\dot{\phi }}{m{\dot{x}}^2}}$, ${\widehat{A}}_{1,4}(k)=T\left(-\dot{x}+{\displaystyle \frac{2b{C}_{cr}-2a{C}_{cf}}{m\dot{x}}}\right)$, ${\widehat{A}}_{4,1}(k)=T_s{\displaystyle \frac{2b{C}_{cr}-2a{C}_{cf}}{I_z{\dot{x}}_r(k)}}$, ${\widehat{A}}_{4,2}(k)=-{\displaystyle \frac{T(2b{C}_{cf}-2a{C}_{cr})}{I_z{\dot{x}}^2}}\dot{y}+{\displaystyle \frac{T(2a^2{C}_{cf}+2b^2{C}_{cr})}{I_z{\dot{x}}^2}}\dot{\phi }$, ${\widehat{A}}_{4,4}(k)=1-T{\displaystyle \frac{2a^2{C}_{cf}+2b^2{C}_{cr}}{I_z{\dot{x}}^2}}$, ${\widehat{A}}_{5,1}(k)=T\cos \phi$, ${\widehat{A}}_{5,2}(k)=T\sin \phi$, ${\widehat{A}}_{5,3}(k)=T\dot{x}\cos \phi -T\dot{y}\sin \phi$, ${\widehat{A}}_{6,1}(k)=-T\sin \phi$, ${\widehat{A}}_{6,2}(k)=T\cos \phi$, ${\widehat{A}}_{6,3}(k)=-T\dot{y}\sin \phi -T\dot{x}\cos \phi$, $B_{k,t}={\left[\begin{array}{cccccc}{\displaystyle \frac{2T{C}_{cf}}{m}}& 0& 0& {\displaystyle \frac{2a{C}_{cf}}{I_z}}& 0& 0\end{array}\right]}^T$.

3. Tube-RMPC Strategy

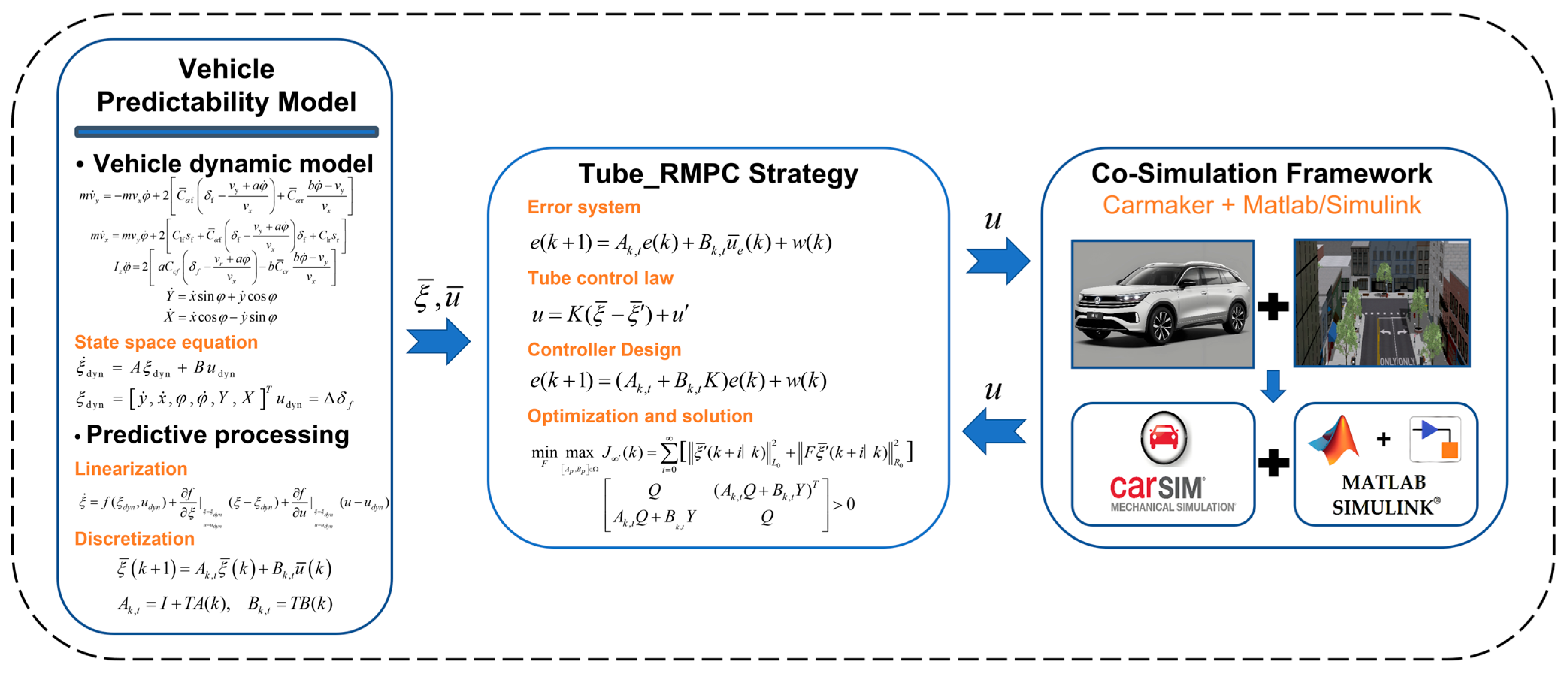
As shown in Figure 2, the proposed Tube-RMPC Strategy integrates a vehicle predictability model with a robust control strategy to enhance system stability and trajectory-tracking performance under uncertainties. The framework incorporates a dynamically fused vehicle model, leveraging state-space representation, linearization, and discretization to facilitate predictive processing. Employing robust control techniques, the approach effectively counteracts external disturbances and ensures system invariance within a predefined robust invariant set. Finally, the effectiveness of the proposed control scheme is validated through a high-fidelity experimental platform.

3.1. Tube-RMPC Controller Design

After model (5) is discretized, the influence of external bounded parameter interference is considered and expressed as follows:

$$\begin{array}{l}\overline{\xi }\left(k+1\right)=A_{k,t}\overline{\xi }\left(k\right)+B_{k,t}\overline{u}\left(k\right)+Dw(k)\\ y(k)=C\overline{\xi }\left(k+1\right)\end{array},$$

(9)

where $\overline{\xi }\left(k\right)\in R^6$ denotes the state variable, $\overline{u}\left(k\right)\in R^1$ presents the control input, $y(k)\in R$ describes the output, $D$ is the disturbance distribution matrix, and $w(k)\in R^6$ corresponds to a bounded parameter disturbance.

For comparison, the nominal dynamic model of the system, which is unaffected by external parameter disturbances, is given as follows:

$${\overline{\xi }}^{\prime }\left(k+1\right)=A_{k,t}{\overline{\xi }}^{\prime }\left(k\right)+B_{k,t}{\overline{u}}^{\prime }\left(k\right),$$

(10)

where ${\overline{\xi }}^{\prime }\left(k\right)\in R^6$ denotes the nominal state variable, and ${\overline{u}}^{\prime }\left(k\right)\in R^1$ represents the nominal control input.

Firstly, the error system is defined by taking the difference between Equations (9) and (10):

$$\begin{array}{l}\overline{\xi }\left(k+1\right)-{\overline{\xi }}^{\prime }\left(k+1\right)=A_{k,t}(\overline{\xi }\left(k\right)-{\overline{\xi }}^{\prime }\left(k\right))\\ +B_{k,t}(\overline{u}\left(k\right)-{\overline{u}}^{\prime }\left(k\right))+w(k)\end{array}$$

(11)

Let $e(k)=\overline{\xi }\left(k\right)-{\overline{\xi }}^{\prime }\left(k\right),{\overline{u}}_e(k)=\overline{u}\left(k\right)-{\overline{u}}^{\prime }\left(k\right)$.

The error system is reformulated as

$$e(k)=\overline{\xi }\left(k+1\right)-{\overline{\xi }}^{\prime }\left(k+1\right),{\overline{u}}_e(k)=\overline{u}\left(k\right)-{\overline{u}}^{\prime }\left(k\right),$$

(12)

Equation (11) is rewritten as

$$e(k+1)=A_{k,t}e(k)+B_{k,t}{\overline{u}}_{\mathrm{e}}(k)+w(k)$$

(13)

The Tube-RMPC controller is formulated to establish a specific control law for actual uncertainties while adhering to the input restrictions (9), ensuring that the trajectory of the perturbed system remains within the “Tube” centered on the nominal trajectory. Specifically, this relationship can be expressed as ${\overline{\xi }}_i\left(k\right)={{\overline{\xi }}^{\prime }}_i\left(k\right)\oplus Z$.

• where ${{\overline{\xi }}^{\prime }}_i\left(k\right)$ denotes the nominal state, ${\overline{\xi }}_i\left(k\right)$ represents the actual system state, and $Z$ describes the interference invariant set.

The Tube-RMPC control law, which constitutes the core of the proposed controller, is expressed as:

$$u=K(\overline{\xi }-{\overline{\xi }}^{\prime })+u^{\prime }$$

(14)

The control law consists of two components. The first component serves as an auxiliary feedback controller that ensures the actual system’s state (9) closely follows the nominal state. The second component $u^{\prime }$ is a control strategy tailored for the nominal system (10), which guides the nominal state toward the equilibrium point.

Since $u_e=u-u^{\prime }=K(\overline{\xi }-{\overline{\xi }}^{\prime })=Ke$, we can substitute it into (13) to obtain

$$e(k+1)=(A_{k,t}+B_{k,t}K)e(k)+w(k)$$

(15)

Secondly, it is necessary to determine the feedback control gain $K$. This gain plays a crucial role in mitigating the effects of bounded disturbances on the system, ensuring that the dynamic system (15) with the error $e(k)$ remains stable. Specifically, $K$ is configured to ensure the stability of $A_{k,t}+B_{k,t}K$. Additionally, as noted in [36], when $A_{k,t}+B_{k,t}K$ it is stable, a robust positively invariant set is guaranteed for the error system. The feedback gain matrix $K$ can be obtained by applying Theorem 1 presented below.

3.2. Theoretical Demonstration and Analysis

Theorem 1 ([37]).

For the error model (15), if there are matrices $Y$ and $Q>0$ that make the following linear matrix inequalities (16) true, then the controller $K=Y{Q}^{-1}$, and $e(k)$ is stable.

$$\left[\begin{array}{cc}Q& {(A_{k,t}Q+B_{k,t}Y)}^T\\ A_{k,t}Q+B_{k,t}Y& Q\end{array}\right]>0,A_{k,t},B_{k,t}\in \Omega$$

(16)

Proof. 

Since the error system (15) is linear and the disturbances are bounded, the effect of the disturbance on system stability has already been considered when defining the disturbance-invariant set. Given this, we can directly analyze the stability of the error system without the disturbance term (17).

$$e(k+1)=(A_{k,t}+B_{k,t}K)e(k)$$

(17)

Define the Lyapunov function as $V(k)=e{(k)}^T(k,t)e(k)$, where it is the Lyapunov matrix, and the feedback control gain satisfies $V((A_{k,t}+B_{k,t}K)e(k))-V(e(k))<0$ for any $e(k)\in R^n$, $A_{k,t},B_{k,t}\in \Omega$. Then, the stability condition is equivalent to

$$(k,t)-{(A_{k,t}+B_{k,t}K)}^T(k,t)(A_{k,t}+B_{k,t}K)>0$$

(18)

Let $(k,t)=Q^{-1},K=Y{Q}^{-1}$. Then, we have

$$Q^{-1}-{(A_{k,t}+B_{k,t}Y{Q}^{-1})}^T{Q}^{-1}(A_{k,t}+B_{k,t}Y{Q}^{-1})>0$$

(19)

Multiplying the left and right sides of (19) by Q results in

$$Q-{(A_{k,t}Q+B_{k,t}Y)}^T{Q}^{-1}(A_{k,t}Q+B_{k,t}Y)>0$$

(20)

Applying the Schur complement lemma to (20) yields

$$\left[\begin{array}{cc}Q& {(A_{k,t}Q+B_{k,t}Y)}^T\\ A_{k,t}Q+B_{k,t}Y& Q\end{array}\right]>0.$$

Next, we define $\overline{\xi }-{\overline{\xi }}^{\prime }$ by calculating the disturbance-invariant set $Z$, leading to Lemma 1. □

Lemma 1 ([38]).

Let $Z$ be the interference invariant set of the system (15), the actual uncertain system (9), and the corresponding nominal system (10). If, at time $k$, the state of the actual system $\overline{\xi }$ satisfies $\overline{\xi }(k)\in {\overline{\xi }}^{\prime }(k)\oplus Z$, which is the control input $u=K(\overline{\xi }-{\overline{\xi }}^{\prime })+u^{\prime }$, it can be guaranteed that for all $A_{k,t},B_{k,t}\in \Omega$ and $\forall w(k)\in W$, $\overline{\xi }(k+1)\in {\overline{\xi }}^{\prime }(k+1)\oplus Z$ is true.

From Lemma 1, to ensure the optimal control performance, the size of $Z$ should be minimized; here, we adopt the minimum robust positively invariant (RPI) set as $Z$.

In reference [39], the minimum RPI set is defined as $S_{\infty }={\oplus }_{i=0}^{\infty }{(A_{k,t}+B_{k,t}K)}^{i}W$, which involves the summation of Minkowski sets of infinite terms. However, computing such a set necessitates that the system dynamics exhibit nilpotency [40]. Therefore, to address this challenge, we simplify the expression of the invariant set by defining it in inequality form: $Z=\{x\in R^n:-z\le x\le z\},z>0$. With the help of the method proposed in the literature [41], the original optimization problem is cleverly converted into a linear programming problem.

Next, for the design of Tube-RMPC, the first and most crucial step is to determine a central trajectory, which is the optimal trajectory.

Based on this principle, we adopt the same control law for each vertex. We select Lyapunov functions $V^{\prime }(k+i|k)={\overline{\xi }}^{\prime }{(k+i|k)}^T(k_0,t_0){\overline{\xi }}^{\prime }(k+i|k)$, $(k_0,t_0)>0$ as a calm matrix, and ${\overline{\xi }}^{\prime }(k+i|k)$ on behalf of the nominal system forecast, and at time $k+i$, $u^{\prime }(k+i|k)$ is the $k+i$ moment of nominal control input.

The Lyapunov function at time $k$ is defined as $V^{\prime }(k|k)={\overline{\xi }}^{\prime }{(k|k)}^T(k_0,t_0){\overline{\xi }}^{\prime }(k|k)$ of the upper bound value of ${\gamma }_0$.

The objective function is defined as

$$J_{\infty }^{\prime }(k)={\displaystyle \sum _{i=0}^{\infty }(}{‖{\overline{\xi }}^{\prime }(k+i|k)‖}_{L_0}^2+{‖u^{\prime }(k+i|k)‖}_{R_0}^2),$$

where $L_0$ and $R_0$ are positive definite weighted matrices.

Referring to the MPC algorithm mentioned in reference [42], the feedback gain matrix for the nominal system can be derived by solving optimization problem 1.

Optimization problem 1:

$$\begin{array}{l}\underset{F}{\min }\underset{\left[A_p,B_p\right]\in \Omega }{\max }{J}_{{\infty }^{\prime }}(k)={\displaystyle \sum _{i=0}^{\infty }[}{‖{\overline{\xi }}^{\prime }(k+i\mid k)‖}_{L_0}^2+{‖F{\overline{\xi }}^{\prime }(k+i\mid k)‖}_{R_0}^2]\\ s.t.\\ {‖{\overline{\xi }}^{\prime }(\mathrm{k})‖}_{(k_0,t_0)}^2\le {\gamma }_0,{\overline{\xi }}^{\prime }(k)={\overline{\xi }}^{\prime }(k|k)\\ {‖{\overline{\xi }}^{\prime }(k+i+1\mid k)‖}_{(k_0,t_0)}^2-{‖{\overline{\xi }}^{\prime }(k+i\mid k)‖}_{(k_0,t_0)}^2\le -{‖{\overline{\xi }}^{\prime }(k+i\mid k)‖}_{L_0}^2-{‖F{\overline{\xi }}^{\prime }(k+i\mid k)‖}_{R_0}^2\\ u^{\prime }(k)\in U\Theta KZ\end{array}.$$

Consider constraints: $u\in U:=\left\{u\in R\left|u(k)\le u_{\max }\right|\right\}$ where $U\subset R$ is a compact set containing the origin.

To ensure that the actual perturbated system satisfies the input constraint $u\in U$, the constraints of the nominal system must be tightened through a constraint-tightening procedure, as formalized by $u^{\prime }(k)\in U\Theta KZ$ in the aforementioned optimization problem 1. Therefore, optimization problem 1 can be transformed into an LMI problem. For a given initial state ${\overline{\xi }}^{\prime }$ and all vertices of the vehicle dynamic model system, if there exist symmetric matrices and a constant $\gamma >0$ such that the following LMIs hold, then the state feedback control law $u^{\prime }=F{\overline{\xi }}^{\prime }$ ensures the stability of the nominal system.

Optimization problem 2:

$$\begin{array}{l}\underset{\gamma ,Y^{\prime },Q^{\prime }}{\min }\gamma \\ \mathrm{s}.\mathrm{t}\\ \left[\begin{array}{cc}1& *\\ {\overline{\xi }}^{\prime }(k)& Q^{\prime }\end{array}\right]\ge 0\\ \left[\begin{array}{cccc}{Q}^{\prime }& *& *& *\\ A_{k,t}{Q}^{\prime }+B_{k,t}{Y}^{\prime }& Q^{\prime }& *& *\\ L^{{\displaystyle \frac{1}{2}}}{Q}^{\prime }& 0& \gamma I& *\\ R^{{\displaystyle \frac{1}{2}}}{Y}^{\prime }& 0& 0& \gamma I\end{array}\right]\ge 0\\ \left[\begin{array}{cc}\chi & Y^{\prime }\\ Y^{\prime T}& Q^{\prime }\end{array}\right]\ge 0,\chi \le U\Theta KZ.\end{array}$$

with $\forall (A_{k,t},B_{k,t})\in \Omega , F=Y^{\prime }{Q}^{\prime -1}, P^{\prime }=\gamma Q^{\prime -1}$.

Based on the above analysis, the control law $u=K(\overline{\xi }-{\overline{\xi }}^{\prime })+u^{\prime }$ can be rewritten as $u=K(\overline{\xi }-{\overline{\xi }}^{\prime })+F{\overline{\xi }}^{\prime }$. It is evident that if $\overline{\xi }(k)\in {\overline{\xi }}^{\prime }(k)\oplus Z,u^{\prime }=F{\overline{\xi }}^{\prime }\in U\Theta KZ$, then for $\forall (A_{k,t},B_{k,t})\in \Omega$ and $w(k)\in W$, the actual uncertain system’s control input satisfies the constraint $u\in U$. Furthermore, if the local feedback gain $F$ can robustly stabilize the nominal system ${\overline{\xi }}^{\prime }$ and its nominal state, it can effectively track reference trajectories while ensuring that $\overline{\xi }(k)\in {\overline{\xi }}^{\prime }(k)\oplus Z$. Consequently, the actual system’s state $\overline{\xi }$ will converge to a tube centered around the nominal trajectory, thereby guaranteeing the robust stability of the actual system.

4. Simulation Result and Analysis

4.1. Co-Simulation Process

We conducted an in-depth study on the path-tracking performance of robust model predictive control (Tube-RMPC) under various typical vehicle conditions, focusing on model parameter uncertainty in road adhesion coefficients.

To comprehensively evaluate the performance of the Tube-RMPC controller, the experiments simulated various real-world driving conditions by varying two key parameters. The first is vehicle speed, set at 10 m/s, 20 m/s, and 30 m/s to represent urban driving, highway driving, and high-speed maneuvers, respectively. The second is the road adhesion coefficient, set at 0.4, 0.6, and 0.8, corresponding to wet/icy roads, mixed conditions, and dry asphalt.

These test conditions provide a rigorous evaluation of the controller’s robustness at varying speeds and road friction levels. Based on this foundation, two representative path scenarios were selected for simulation testing: a double lane change test requiring a high vehicle dynamic response and a complex S-curve test involving continuous steering. These scenarios encompass various typical driving conditions and effectively reflect the performance advantages and potential issues of the Tube-RMPC algorithm in dynamic path tracking. Moreover, the predefined reference trajectories, though not exact solutions of the nonlinear dynamics, are approximately feasible and serve as practical benchmarks for robustness evaluation under modeling errors and disturbances and provide detailed simulation and theoretical support for autonomous system design.

Furthermore, to thoroughly evaluate the control algorithm’s performance, this paper compares the results of Tube-RMPC with those of MPC and PID algorithms under identical experimental settings. To ensure a fair comparison, all three controllers—Tube-RMPC, MPC, and PID—were tuned using the same performance criterion: minimizing trajectory tracking error under identical simulation conditions. As noted in the literature, PID and MPC are widely used in vehicle trajectory tracking and serve as effective baselines for evaluating the proposed Tube-RMPC approach.

4.2. Co-Simulation Results

In this study, a specific subset of experimental conditions was analyzed to evaluate the system’s performance at varying road adhesion levels. The analysis focused on a constant vehicle speed of 20 m/s, whereas the road adhesion coefficient (μ) was varied across three levels: 0.4, 0.6, and 0.8. These conditions thoroughly represent a wide spectrum of road surfaces, ranging from low-adhesion to high-adhesion surfaces.

The parameters used in this study were $m$ = 1723 kg, $a$ = 1.232 m, $b$ = 1.468 m, $I_z$ = 4175 kg, $T$ = 0.02 s, $C_{cf}$ = 66.9 kN/rad, and $C_{cr}$ = 62.7 kN/rad.

According to Theorem 1, the feedback gain is given by

$$K=\left[\begin{array}{llllll}0.112\hfill & 0\hfill & -18.0\hfill & 0\hfill & -0.0297\hfill & -0.0297\hfill \end{array}\right]$$

To facilitate a comprehensive comparison of the experimental datasets, the analysis focused on two key metrics: the maximum value Y and yaw angle error, with the mean squared error (RMSE) compared to the original reference estimation.

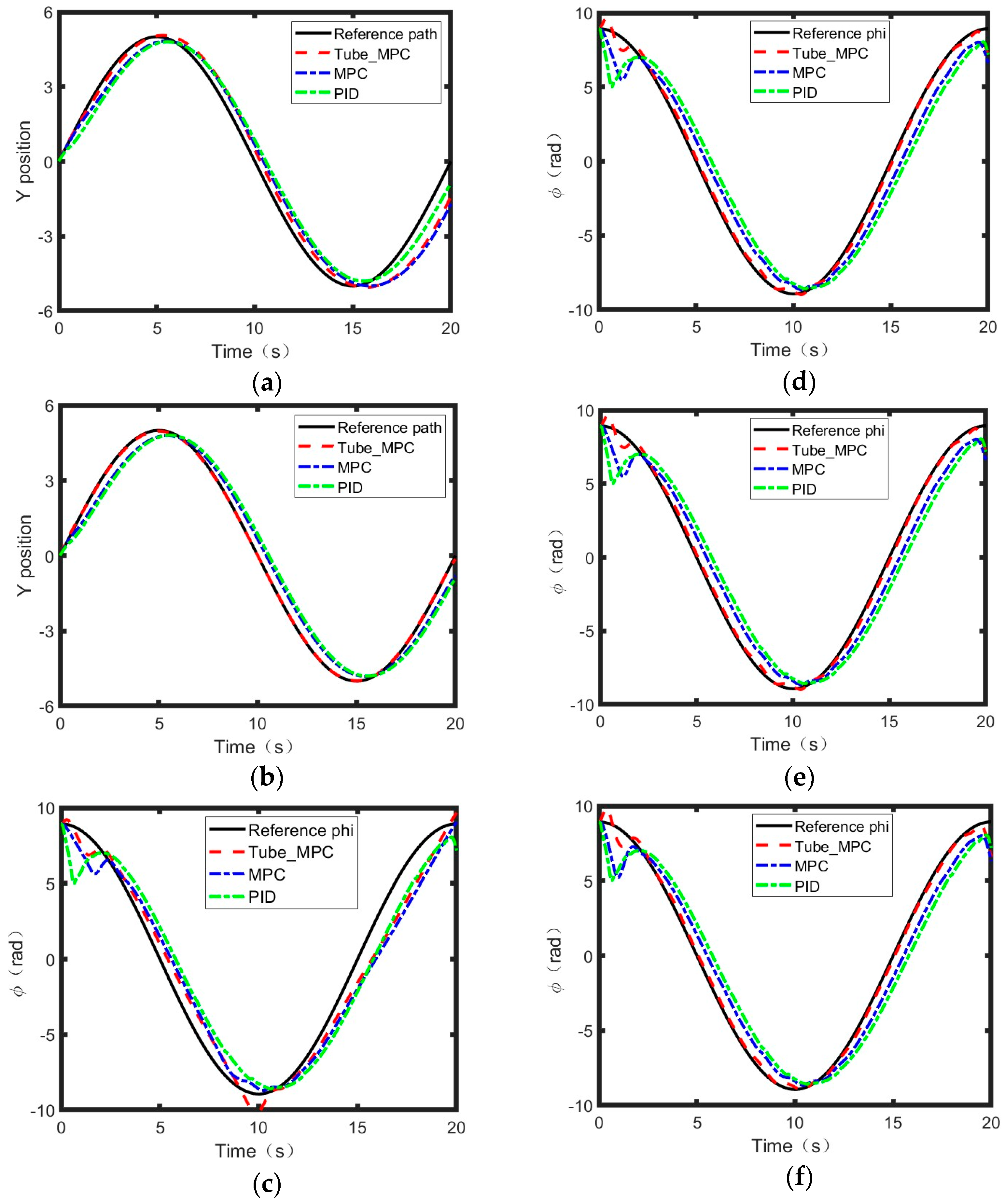
As shown in Figure 3 and

Table 1. S-curve result analysis.

Mean Tracking Error	Y	RMES
Tube-RMPC	7.6390	0.2482
MPC	8.4103	0.2885
PID	9.6074	0.3890
Yaw Angle Error	ϕ	RMES
Tube-RMPC	17.5866	4.4729
MPC	17.8978	4.7853
PID	18.5831	4.8950

, reduction in maximum tracking error in S-curve: Tube-RMPC achieves a 9.17% reduction in the peak deviation compared to MPC and a 20.5% improvement over PID; Lower mean squared error (RMSE): Tube-RMPC reduces MSE by 14.0% compared to MPC and leads to a 36.2% improvement over PID. Moreover, Reduction in Yaw angle error in S-curve: Tube-RMPC achieves a 1.77% reduction in the peak deviation compared to MPC and a 5.66% improvement over PID; Lower Yaw angle RMSE: Tube-RMPC achieves a 7.00% reduction in peak deviation compared to MPC and an 9.44% improvement over PID.

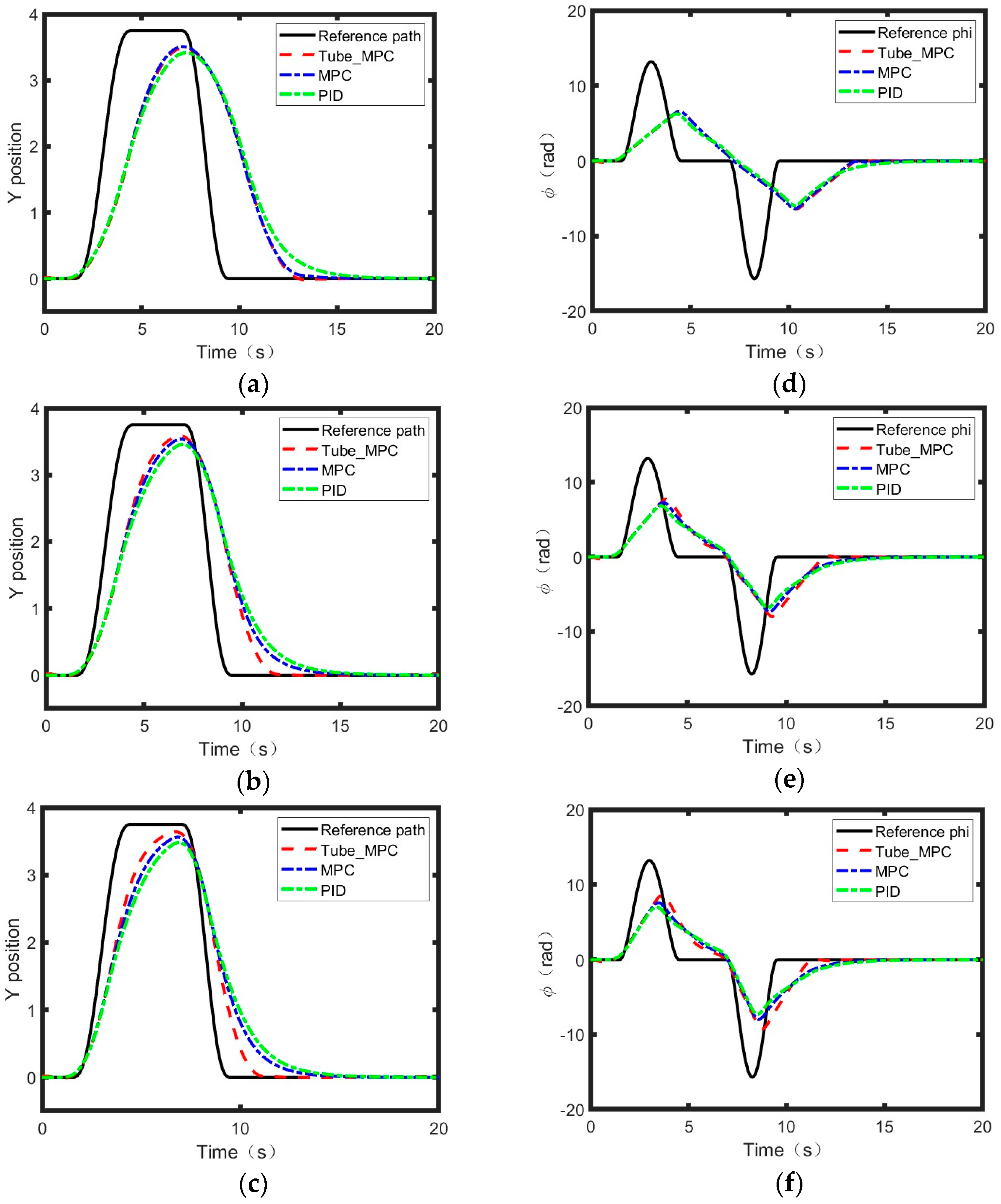
Similarly, as shown in Figure 4 and

Table 2. Double lane change result analysis.

Mean Tracking Error	Y	RMES
Tube-RMPC	3.4806	0.0986
MPC	3.5607	0.1396
PID	3.6477	0.3417
Yaw Angle Error	ϕ	RMES
Tube-RMPC	12.2372	1.8839
MPC	15.0593	1.8845
PID	15.6746	2.0125

, the following results were obtained for the double lane change. Reduction in maximum tracking error in double lane change: Tube-RMPC achieves a 2.25% reduction in the peak deviation compared to MPC and a 4.58% improvement over PID; Lower mean squared error (RMSE): Tube-RMPC reduces MSE by 29.38% compared to MPC and leads to a 71.17% improvement over PID. Moreover, Reduction in Yaw angle error in double lane change: Tube-RMPC achieves a 23.06% reduction in the peak deviation compared to MPC and a 28.10% improvement over PID; Lower Yaw angle RMSE: Tube-RMPC achieves a 0.03% reduction in the peak deviation compared to MPC and a 6.83% improvement over PID.

Tube-RMPC outperforms MPC and PID in both S-curve and double lane change scenarios, achieving up to 71.17% lower RMSE in tracking accuracy and superior yaw-angle stabilization, especially in dynamic maneuvers. Its robustness is evident in the near-identical yaw RMSE (0.03% difference) compared to MPC during double lane change, underscoring its precision and reliability for high-performance autonomous navigation. However, asymptotic tracking cannot be strictly guaranteed due to model simplifications and external disturbances, which aligns with the bounded tracking errors observed and discussed in the simulation analysis.

5. Conclusions

This study introduced a Tube-based Robust Model Predictive Control (Tube-RMPC) framework to enhance the trajectory-tracking performance of autonomous vehicles under complex road conditions. Integrating a unified vehicle–tire modeling approach, the proposed method effectively addresses model parameter uncertainties and variations in road adhesion, ensuring enhanced stability through a robust invariant tube mechanism.

Simulation results demonstrated that Tube-RMPC consistently outperforms conventional MPC and PID controllers across different velocities and road adhesion conditions. Notably, in the S-curve test, Tube-RMPC reduced the peak tracking error by 20.5% and RMSE by 36.2% compared to PID; meanwhile, in the double lane change scenario, its RMSE improvements reached 71.17%.

With its computational efficiency and robustness, Tube-RMPC offers a viable solution for real-world autonomous driving applications. Future research could explore the integration of learning-based adaptive mechanisms to further enhance control performance and extend the framework to cooperative vehicle control for multi-agent coordination in dynamic environments.