Abstract
Effective analysis of central bank communications is critical for anticipating monetary policy changes and guiding market expectations. However, traditional natural language processing models face significant challenges in processing lengthy and nuanced policy documents, which often exceed tens of thousands of tokens. This study addresses these challenges by proposing a novel integrated deep learning framework based on Hyena Hierarchy architectures, which utilize sub-quadratic convolution mechanisms to efficiently process ultra-long sequences. The framework employs Delta-LoRA (low-rank adaptation) for parameter-efficient fine-tuning, updating less than 1% of the total parameters without additional inference overhead. To ensure robust performance across institutions and policy cycles, domain-adversarial neural networks are incorporated to learn domain-invariant representations, and a multi-task learning approach integrates auxiliary hawkish/dovish sentiment signals. Evaluations conducted on a comprehensive dataset comprising Federal Open Market Committee statements and European Central Bank speeches from 1977 to 2024 demonstrate state-of-the-art performance, achieving over 6% improvement in macro-F1 score compared to baseline models while significantly reducing inference latency by 65%. This work offers a powerful and efficient new paradigm for handling ultra-long financial policy texts and demonstrates the effectiveness of integrating advanced sequence modeling, efficient fine-tuning, and domain adaptation techniques for extracting timely economic signals, with the aim to open new avenues for quantitative policy analysis and financial market forecasting.
1. Introduction
In today’s increasingly interconnected and complex global economy, the communication strategies of central banks have become central tools for executing monetary policy and managing market expectations [1,2]. Whether it is the policy statements and meeting minutes released by the U.S. Federal Open Market Committee (FOMC) or the speeches and press conference transcripts from the European Central Bank (ECB) President, these English-language texts convey critical information about future economic trends, inflation prospects, and interest rate paths [3]. Financial market participants, from large institutional investors to the general public, heavily rely on accurate interpretations of these communications to make investment decisions and assess risks. Therefore, conducting timely and in-depth quantitative analysis of central bank communication texts, particularly for nowcasting the short-term direction of interest rate changes following their release, holds significant theoretical importance and immense practical value. This can provide forward-looking insights before the release of official economic data, which is crucial for navigating rapidly changing market dynamics. However, leveraging natural language processing (NLP) techniques to extract reliable predictive signals from central bank communication texts presents a series of severe and unique challenges.
While traditional econometric models and classical machine learning approaches have been extensively applied to financial forecasting, they face fundamental limitations when confronted with the complexity of contemporary central bank communications. Conventional econometric models, such as Vector Autoregression (VAR) and linear regression frameworks, rely primarily on structured numerical data and predefined variables, making them inadequate for processing the rich, unstructured textual information embedded in policy statements and speeches. Similarly, classical machine learning techniques like Support Vector Machines or logistic regression with TF-IDF features can only capture shallow linguistic patterns, and fail to understand the nuanced, context-dependent meanings inherent in central bank language. These approaches are particularly challenged by the lengthy nature of policy documents, which often exceed 10,000 tokens and contain complex inter-sentence dependencies that require sophisticated sequential modeling capabilities that are beyond the scope of traditional methods.
First, the nature of the data itself poses a substantial obstacle. Official central bank documents, especially in-depth reports like FOMC meeting minutes, are exceptionally lengthy, often exceeding ten thousand tokens. This far surpasses the context length that current mainstream NLP models, particularly those based on the standard Transformer architecture [4], can effectively handle. The self-attention mechanism widely used in these models has computational and memory complexity quadratic in sequence length () [5], making direct processing of such long, complete documents computationally prohibitive or infeasible. The existing work often resorts to compromise strategies like truncating input, analyzing only summaries, or performing sentence-level processing [6,7], but this inevitably sacrifices document-level global context, long-range argumentative logic, and subtle tones that might permeate the entire text, thereby compromising information integrity and analytical depth.
Simultaneously, the language used by central banks is often highly specialized, cautiously worded, and filled with nuances [8]. Policymakers meticulously weigh every word, using precise economic terminology, complex conditional clauses, and subtle tonal variations to convey intricate policy intentions and risk assessments. This demands analytical models that can not only handle long-range dependencies, but also possess deep semantic understanding capabilities to discern subtle tonal differences (such as hawkish vs. dovish leanings), comprehend implicit policy signals, and accurately grasp the overall stance of the text. Simple keyword counting or shallow models are inadequate for this task.
Second, model efficiency and real-time requirements constitute another constraint. Even if long texts can be technically processed, if the model training and inference processes are too time-consuming, their value in a “nowcasting” scenario diminishes significantly. Financial markets react extremely rapidly to information, and the core utility of nowcasting lies in its immediacy. Therefore, not only must the model architecture itself be capable of efficiently processing long sequences, but model adaptation and deployment stages must also minimize computational overhead and inference latency as much as possible.
Third, model adaptation and generalization emerge as critical bottlenecks. Current state-of-the-art NLP models are typically large-scale models with billions or more parameters, pretrained on massive general-purpose corpora [9]. Making these general models accurately understand and analyze the highly specialized domain language of central banking necessitates downstream task fine-tuning. However, full parameter fine-tuning is computationally resource-intensive [10] and prone to overfitting, especially when domain-specific labeled data (such as central bank texts precisely labeled with subsequent interest rate changes) is relatively scarce. Parameter-efficient fine-tuning (PEFT) techniques [11,12] alleviate computational and storage pressures, but common methods like LoRA [10] (low-rank adaptation) might still lag behind full fine-tuning in performance [13,14]. Deciphering how to maximize model performance while maintaining high efficiency remains an urgent problem.
Finally, cross-domain robustness is a challenge that practical application must address. Different central banks exhibit variations in communication styles, policy frameworks, and areas of focus [15]. Even within the same central bank, communication strategies and linguistic patterns evolve across different historical periods [8]. A model trained in one scenario may suffer significant performance degradation when directly applied to another due to this domain drift. Consequently, building a model that can robustly adapt to different institutions and time periods requires strong domain adaptation capabilities.
Despite prior research advancements in long sequence modeling [16], parameter-efficient fine-tuning [10,14], and domain adaptation [17,18], a comprehensive framework that systematically integrates these cutting-edge technologies to synergistically address the core challenges of ultra-long text processing, high-performance economical fine-tuning, and strong cross-domain generalization for the complex task of central bank interest rate nowcasting, has been lacking.
To address this research gap, this paper proposes and implements a novel, integrated deep learning framework designed to overcome the limitations of existing methods by strategically combining complementary state-of-the-art techniques. The framework selects Hyena Hierarchy [19] as its foundational architecture, utilizing its gated long convolutional mechanism with sub-quadratic complexity () [20] to efficiently process complete central bank documents exceeding ten thousand tokens, thereby tackling the core challenge of long text processing. For high-performance and economical model adaptation, we employ Delta-LoRA [13] for parameter-efficient fine-tuning. This technique leverages the change in low-rank updates to drive adjustments in the pretrained weights, aiming to close the performance gap with full fine-tuning while maintaining an extremely low parameter count (<1%) and zero additional inference latency [13]. Concurrently, to enhance the model’s generalization capability across different central banks and time periods, the framework integrates domain-adversarial neural networks (DANN) [21], learning domain-invariant feature representations through adversarial training. Furthermore, a multi-task learning (MTL) mechanism [22] utilizes auxiliary signals, such as hawkish/dovish tendencies, to further refine representations. The uniqueness and core innovation of this paper lie in the integration of Hyena, Delta-LoRA, and DANN for the first time, which are applied to solve the complex problem of interest rate nowcasting from long central bank texts, overcoming multiple bottlenecks through technological synergy to achieve dual improvements in performance and efficiency.
In summary, the main contributions of this paper are manifested in several aspects:
- We propose and implement a novel framework integrating Hyena Hierarchy, Delta-LoRA, and DANN, offering a new and powerful solution for NLP tasks involving ultra-long sequences, high-performance parameter-efficient fine-tuning, and cross-domain generalization, particularly for central bank interest rate prediction.
- On a self-constructed large-scale cross-institutional dataset (FOMC and ECB, 1977–2024) for interest rate prediction, we demonstrate that the proposed framework achieves a significant improvement of over 5 percentage points on key metrics compared to strong baseline models, while substantially reducing the inference latency for long-text processing (>60%).
- Experimental validation confirms the effectiveness of the DANN component, showing that the framework generalizes better from a single source domain (e.g., FOMC) to a target domain (e.g., ECB), enhancing the model’s reliability in practical applications.
- Preliminary analysis of the model’s internal mechanisms reveals connections between model decisions and key financial policy terminology, providing perspectives for understanding model behavior.
The remainder of this paper is organized as follows: Section 2 reviews related work. Section 3 details the dataset construction and preprocessing. Section 4 elaborates on the proposed methodology. Section 5 presents comprehensive experimental results and in-depth analysis. Section 6 provides a discussion covering research implications, limitations, and the future outlook. Section 7 concludes the paper.
2. Related Work
This section reviews the key research areas that form the foundation of our study, organized into distinct subsections to provide comprehensive context for our proposed framework. We examine the evolution of central bank communication analysis, advances in long sequence modeling architectures, parameter-efficient fine-tuning techniques, and domain adaptation strategies. This structured review demonstrates how our integrated approach addresses limitations identified across these diverse but interconnected research domains.
2.1. Central Bank Communication Analysis
Official communications from central banks, like the U.S. Federal Reserve’s FOMC [23] and the European Central Bank [24], are crucial information sources for understanding monetary policy and predicting market movements. Research in this domain has evolved through several distinct phases, each characterized by increasingly sophisticated analytical approaches.
Early studies predominantly employed dictionary-based approaches and simple statistical methods to quantify policy sentiment and tone. For instance, Lucca and Trebbi [25] developed lexicon-based measures to capture hawkish and dovish language in FOMC statements, while Hansen et al. [26] constructed transparency indices using word counting techniques. However, these methods struggle with linguistic nuances, contextual dependencies, and the evolving nature of central bank language over time [24].
The second generation of research introduced machine learning techniques to enhance analytical flexibility and capture more complex patterns. Topic modeling approaches such as Latent Dirichlet Allocation (LDA) enabled researchers to identify thematic structures in central bank communications, while Support Vector Machines and ensemble methods improved classification performance for sentiment analysis tasks. Nonetheless, these approaches remained limited by their reliance on hand-crafted features and shallow architectural designs.
The contemporary phase has witnessed the adoption of deep learning methodologies, particularly pretrained language models based on Transformer architecture. Domain-specific models, like FinBERT [27], have demonstrated excellent performance in financial text analysis [28,29], successfully capturing subtle semantic relationships and policy implications. However, central bank texts present unique challenges that remain unresolved: their exceptional length often exceeds the context limits of standard Transformer models, and their specialized, diplomatically neutral language requires sophisticated processing capabilities. The need to truncate or oversimplify these documents for analysis continues to limit the effectiveness of current approaches.
2.2. Model Architecture Components
2.2.1. Long Sequence Processing Architectures
The standard Transformer architecture’s self-attention mechanism has quadratic complexity () [5], limiting its ability to process long sequences. This computational bottleneck has motivated extensive research into alternative architectures capable of handling extended contexts more efficiently. Researchers have explored sparse attention patterns [30], recurrence mechanisms, and sliding windows with global attention to address this limitation. However, these approaches still face efficiency-performance trade-offs with extremely long sequences.
Novel architectures like Hyena Hierarchy [19] use implicitly parameterized long convolutions and data-controlled gating [5] to achieve sub-quadratic complexity (). The Hyena architecture represents a significant departure from attention-based mechanisms, instead leveraging gated convolutions with learnable kernels to capture long-range dependencies. This approach demonstrates particular promise for processing financial documents, where maintaining complete contextual information across entire documents is crucial for accurate interpretation. These architectures effectively handle sequences far beyond traditional models’ limits while maintaining or surpassing Transformer performance [19,31]. This technological advancement enables the direct processing of lengthy central bank reports, motivating our choice of Hyena as the model’s backbone.
2.2.2. Parameter-Efficient Fine-Tuning Methods
Modern pretrained language models are extremely large [32], making full parameter fine-tuning computationally expensive [10]. Parameter-efficient fine-tuning (PEFT) techniques adapt models by adjusting only a small fraction of parameters (<1%), reducing computational and storage requirements [32,33]. PEFT approaches can be categorized into several methodological families: selective fine-tuning methods that update only specific model components, additive approaches that introduce trainable modules such as adapters, prompt-based techniques that optimize trainable prompts, and reparameterization methods that decompose weight updates using mathematical transformations.
Among these, low-rank adaptation (LoRA) [10] is popular for its effectiveness, simplicity, and zero inference latency. However, a performance gap between LoRA and full fine-tuning may exist [13]. This limitation has spurred the development of enhanced PEFT methods that seek to close the performance gap while maintaining computational efficiency. Delta-LoRA [13] represents a significant advancement in this direction, introducing mechanisms that allow frozen pretrained weights to be updated based on the trajectory of low-rank adaptations, thereby achieving performance levels much closer to full fine-tuning. These mature PEFT techniques allow for the economical adaptation of powerful models like Hyena to resource-constrained financial text analysis tasks.
2.2.3. Domain Adaptation and Cross-Domain Generalization
Models trained in one domain (e.g., FOMC texts) often experience performance degradation when applied to another related domain (e.g., ECB texts), a phenomenon known as domain shift [21]. This challenge is particularly pronounced in central banking research, where institutional differences, linguistic variations, and policy framework distinctions can significantly impact model transferability. Domain adaptation techniques aim to build models that are robust to such changes. Unsupervised domain adaptation is particularly important as it only requires unlabeled target domain data.
Domain-adversarial neural networks [21] use a domain classifier and gradient reversal layer to train the feature extractor to generate domain-invariant representations [21]. The adversarial training paradigm encourages the model to learn representations that are discriminative for the target task while being indistinguishable across different source domains. This approach has proven particularly effective in scenarios where labeled data is abundant in one domain but scarce in target domains. Other methods like AdapterFusion [34] learn to dynamically combine domain-specific knowledge modules. These approaches represent different adaptation paradigms: DANN seeks unified domain-invariant representations, while AdapterFusion combines domain-specific knowledge. For tasks requiring robust performance across different central banks or economic cycles, domain adaptation techniques are key for enhancing generalization capabilities.
While existing research has made significant strides in each of these individual areas, there remains substantial room for optimizing the integration of efficient long-sequence processing, parameter-efficient fine-tuning, and cross-domain generalization. The systematic combination of these technologies, specifically for the challenging task of nowcasting from lengthy central bank texts, represents a significant gap in the literature that our framework aims to address. The Methodology section details how these components are integrated into a cohesive and effective system.
3. Data and Preprocessing
This section details the collection and alignment of central bank texts and interest rate labels from multiple public sources (summarized in Table 1), demonstrates the process of cleaning, segmenting, and statistically splitting the raw data, and visually presents the distribution of FOMC statement lengths and the proportions of interest rate change labels through figures, thereby verifying the data quality and providing a solid foundation for model training.
3.1. Data Sources and Alignment
We constructed our dataset from multiple complementary sources to ensure comprehensive coverage of central bank communications and associated market reactions. The primary textual data comes from two key datasets that provide different, but complementary, perspectives on Federal Reserve communications.
We utilized the “FOMC Meeting Statements & Minutes” dataset curated by Vladtasca on Kaggle [35], covering over 900 official FOMC statements and meeting minutes texts from 1977 to 2024. This dataset represents the most comprehensive publicly available collection of Federal Reserve communications, encompassing both formal policy statements released immediately after FOMC meetings and detailed meeting minutes that provide deeper insights into policymaker deliberations. The dataset includes critical metadata such as exact publication timestamps, document types, and meeting identifiers, enabling precise temporal alignment with market data. The documents vary significantly in length, with policy statements typically containing 1000–3000 tokens, while meeting minutes often exceed 8000 tokens, highlighting the need for our long-sequence processing capabilities. Each text entry includes accurate publication dates and authoring body information, greatly facilitating subsequent temporal alignment and multi-task annotation.
To construct the primary nowcasting task labels, we simultaneously used the “Federal Reserve Interest Rates, 1954–Present” data published by the federalreserve team on Kaggle, which provides monthly records of the federal funds’ target rate and effective rate. We further sourced daily data from the “Effective Federal Funds Rate (FEDFUNDS)” from the St. Louis Fed website [36] to achieve high-resolution measurement of interest rate change within 7 days following the statement release date. The interest rate change labels were categorized as “Up” if bp, “Down” if bp, and “Stable” otherwise. The selection of this 5 bp threshold aligns with industry practices for measuring macroeconomic policy volatility.
To evaluate cross-institutional model generalization, we batch-downloaded speech texts from the European Central Bank (ECB) website, covering official speeches by the President and Executive Board members with complete metadata from 1999 to the 2025. We also incorporated the “Euro Area Communication Event-Study Database (EA-CED)” toolkit published by the Banque de France [37], which records immediate Euro Area market reactions triggered by 304 major policy announcements and over 4400 speeches, serving for subsequent inter-source performance comparison and domain adaptation validation.
Additionally, we integrated the “Trillion Dollar Words” dataset open-sourced by the Georgia Tech Financial Services Innovation Lab [38]. This dataset provides granular paragraph-level sentiment annotations for FOMC communications, with expert-labeled classifications of policy language as “hawkish”, “dovish”, or “neutral”. The dataset covers approximately 30,000 paragraphs spanning 1994–2023, offering rich sentiment supervision that complements our primary interest rate prediction task. The annotation methodology employed professional financial analysts who labeled content based on its implied policy stance regarding future monetary tightening or easing. This high-quality sentiment labeling enables our multi-task learning approach, where the auxiliary hawkish/dovish classification task provides additional supervisory signals to improve overall model performance. This dataset provides paragraph-level annotations of hawkish/dovish sentiment for FOMC texts, serving as auxiliary sentiment signal input for multi-task learning to enhance the model’s ability to capture fine-grained policy tones.

Table 1.
Overview of data sources used.
Table 1.
Overview of data sources used.
| Source | Period | Scale | Label Type | Source |
|---|---|---|---|---|
| FOMC Statements/Minutes | 1977–2024 | ≈900 documents | Date | Kaggle [35] |
| FOMC Annotations | 1994–2023 | ≈30k paragraphs | Hawkish/dovish | Trillion Dollar Words [38] |
| ECB Speeches Dataset | 1999–2024 | ≈1000 speeches | Date | ECB Website [39] |
| EA-CED Event Study | 1999–2024 | ≈4400 events | Market reaction | Banque de France [37] |
| FRED Interest Rates | 1954–2025 | Daily/monthly | Benchmark rates | St Louis Fed [36] |
3.2. Text Cleaning, Segmentation, and Structuring
After collecting multi-source texts and labels, we applied a unified cleaning pipeline to all statements and speeches. This included removing HTML tags, unifying Unicode encoding and full/half-width symbols, correcting common OCR errors, and standardizing punctuation. Subsequently, we used regular expression-based sentence splitting algorithms to segment documents into paragraph units delimited by periods or paragraph symbols. Meta-tags such as “Publication Date”, “Speaker/Body”, and “Crisis Period Indicator (Dummy)” were embedded before each segment to ensure that the model input could utilize temporal, source, and contextual prior information simultaneously. These steps referenced the preprocessing script details from the official example notebook for “FOMC Meeting Statements and Minutes” on Kaggle to ensure consistency with community practices and reproducibility.
Figure 1 illustrates the comprehensive text preprocessing pipeline employed in our study. The process begins with raw document ingestion from multiple sources, followed by systematic cleaning and standardization steps. HTML tags and metadata markers are stripped, Unicode characters are normalized, and common OCR errors are corrected using pattern matching and contextual replacement rules. The cleaned text undergoes sophisticated segmentation using linguistically-informed algorithms that preserve semantic boundaries while maintaining compatibility with our tokenization approach. Finally, domain-specific tags and temporal markers are embedded to enable the model to leverage contextual information during training and inference.
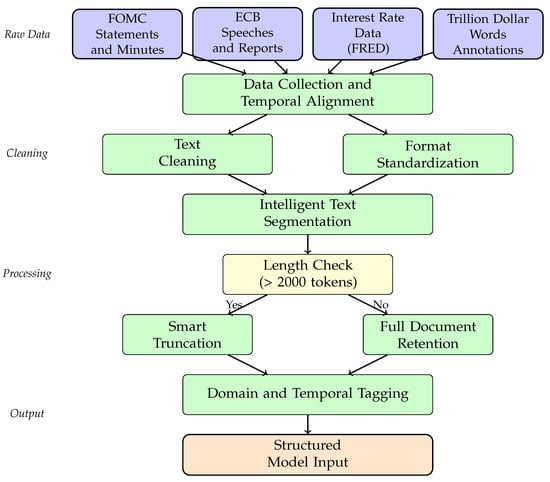
Figure 1.
Text preprocessing and structuring workflow. The diagram shows the sequential steps from raw document collection through cleaning, segmentation, and final structuring for model input.
3.3. Dataset Splitting and Statistical Visualization
To appropriately evaluate model performance in both within-source and cross-domain scenarios, we split the FOMC and ECB corpora chronologically. Specifically, within each dataset, documents from the most recent 12 months were reserved as the test set. The remaining corpus was randomly split into training and validation sets using an 80%:20% ratio. This temporal split ensures the novelty of the test data and prevents information leakage during training and validation. Within each subset, we maintained approximately the same distribution for “up/down/stable” and “hawkish/dovish” labels to ensure that the evaluation results were not biased by class imbalance.
To intuitively present the data’s underlying structure, we generated two important figures. The first is a histogram showing the token length distribution of FOMC statements (Figure 2), illustrating that most documents cluster between 1000 and 4000 tokens, with long-tail documents not exceeding 12,000 tokens. This validates the necessity of our long-text handling strategies. The second is a pie chart displaying the distribution of interest rate change labels (Figure 3), showing “stable” accounting for about 54%, “up” for about 25%, and “down” for about 21%. This aligns with the historically conservative adjustment strategy of the Federal Reserve and provides a non-trivial prior distribution for the multi-class task. These figures not only depict the raw data distribution, but also provide strong evidence for subsequent model architecture design choices, such as weighted loss for minority classes or data augmentation strategies.
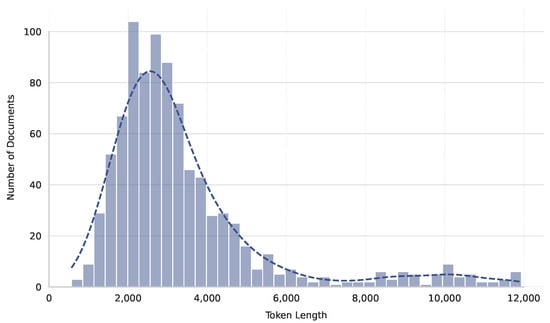
Figure 2.
Distribution of FOMC statement token lengths.
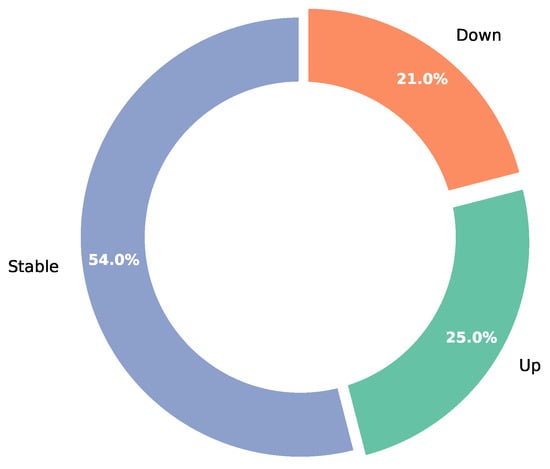
Figure 3.
Distribution of interest rate change labels (7-day window, 5 bp threshold) in the FOMC dataset.
4. Methodology
This chapter details the innovative deep learning framework constructed to address the task of interest rate nowcasting from central bank policy communication texts. Given that central bank policy statements often feature ultra-long sequences of thousands or even tens of thousands of tokens, and that significant domain differences exist between different central banks (e.g., Federal Reserve—FOMC and European Central Bank—ECB) as well as across different economic cycles (e.g., pre/post quantitative easing, hiking cycles), our proposed method aims to efficiently process long sequences, achieve parameter-efficient fine-tuning, and possess cross-domain adaptation capabilities.
Before detailing our methodology, we formally state the testable hypotheses that drive our research design and experimental validation:
Hypothesis 1 (Long-Sequence Processing).
Complete central bank documents contain more predictive information for interest rate changes than truncated or summarized versions. We hypothesize that models capable of processing entire documents without truncation will achieve superior predictive performance compared to those limited by sequence length constraints.
Hypothesis 2 (Architecture Efficiency).
Hyena Hierarchy architectures with sub-quadratic complexity will demonstrate both higher computational efficiency and superior or comparable predictive performance compared to standard Transformer-based approaches when processing ultra-long financial documents.
Hypothesis 3 (Parameter Efficiency).
Delta-LoRA fine-tuning will achieve performance levels comparable to full parameter fine-tuning while using less than 1% of the total parameters, demonstrating superior parameter efficiency for domain adaptation in financial text analysis.
Hypothesis 4 (Domain Generalization).
Models trained with domain-adversarial training will exhibit significantly better cross-institutional generalization (e.g., FOMC to ECB) compared to models trained without domain adaptation mechanisms.
Hypothesis 5 (Multi-Task Learning).
Incorporating auxiliary hawkish/dovish sentiment classification as a secondary task will improve primary interest rate prediction performance through shared representation learning and implicit regularization effects.
This chapter first defines the core research problem in Section 4.1. Subsequently, Section 4.2 details the model’s backbone network, Hyena Hierarchy, explaining its efficiency in handling ultra-long text sequences. Section 4.3 then elaborates on the parameter-efficient fine-tuning strategy, Delta-LoRA, illustrating how large pretrained models can be effectively adapted to downstream tasks with minimal parameters and explaining its improvements over standard LoRA. To address the domain shift issue in multi-source data, Section 4.4 introduces a multi-source domain adaptation mechanism based on domain-adversarial training of neural networks (DANN). Furthermore, to leverage implicit sentiment signals within the text, Section 4.5 presents a multi-task learning paradigm combining the main interest rate prediction task with an auxiliary hawkish/dovish classification task. Finally, Section 4.6 provides the complete model training procedure and inference stage implementation details.
It is important to emphasize that these three core technologies (Hyena, Delta-LoRA, DANN) are not simply stacked but deeply integrated through a unified loss function and a backpropagation path. Hyena provides powerful long-range contextual awareness; Delta-LoRA, under stringent computational and storage budgets, effectively injects task-specific knowledge by optimizing the pretrained weights themselves; domain-adversarial training and multi-task learning synergistically operate at the gradient level, jointly guiding the model to learn feature representations that are both discriminative and domain-invariant. The ultimate goal is to minimize the overall risk upper bound under a mixed domain distribution, thereby achieving robust interest rate prediction for real-world central bank communication texts across institutions and time periods. Figure 4 presents a comprehensive overview of our integrated architecture, illustrating how these components work together to process long sequences, adapt efficiently to domain-specific patterns, and generate robust predictions across different institutional contexts. Figures are included in Section 4.2, Section 4.3 and Section 4.4 to visually aid understanding of the backbone structure, Delta-LoRA update mechanism, and domain-adversarial module computation flow, respectively.
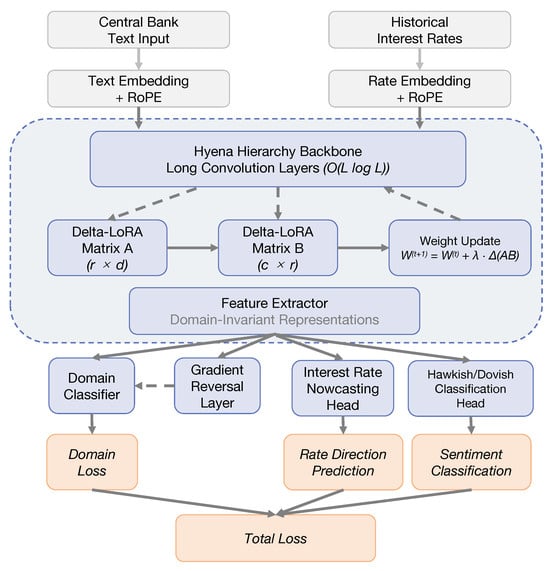
Figure 4.
Comprehensive overview of our integrated framework showing the interaction between Hyena Hierarchy backbone, Delta-LoRA fine-tuning, domain-adversarial neural networks (DANN), and multi-task learning (MTL) components.
4.1. Problem Definition
The core task of this research is to perform nowcasting of the short-term directional change in the benchmark interest rate following the release of official central bank policy communication texts (such as FOMC statements and ECB speeches), based on the text itself and the historical benchmark interest rate trend preceding the release.
Formally, given a policy communication text document x (with token sequence length potentially reaching 10,000 or higher) and a historical benchmark interest rate time series aligned with the document’s release date (where T is the lookback period, set to months in this study, with sequence length ), our objective is to train a model to predict the category y to which the future short-term interest rate change belongs. The prediction category y is defined as a three-class classification:
where is a predefined threshold (set to 5 basis points, 5 bp, in this study).
The model takes the text x and the rate sequence r as input. To enable the model to handle these two different modalities and leverage their sequential properties, we first apply positional encoding (PE) to both separately, then concatenate or otherwise fuse them before feeding them into the model. The mathematical representation of the model can be simplified as:
where is the predicted class probability distribution, denotes applying positional encoding to the input sequences, represents the core network structure composed of modules like Hyena Hierarchy, Delta-LoRA, DANN, etc., (with parameters ) detailed in subsequent sections, and is the final classification head (typically one or more fully connected layers).
The training objective is to minimize the difference between the model prediction and the true label y, typically using a weighted cross-entropy loss function . Additionally, to achieve domain adaptation and utilize auxiliary information, the total optimization objective will include extra loss terms, such as the domain-adversarial loss and the auxiliary task loss , as described in Section 4.4 and Section 4.5.
4.2. Model Backbone: Hyena Hierarchy
Processing ultra-long documents like central bank policy statements is one of the key challenges of this task. Traditional Transformer-based self-attention mechanisms have computational and memory complexity, making direct processing of sequences with tens of thousands of tokens impractical. To overcome this limitation, we employ Hyena Hierarchy [19] as the model’s backbone feature extractor. Hyena is a novel deep learning operator that, by cleverly alternating stacks of implicitly parameterized long convolutions and data-controlled gating, can effectively capture long-range dependencies within sub-quadratic complexity (specifically, , where N is the depth of the Hyena operator and L is the sequence length). It also demonstrates faster inference speeds on long sequences compared to highly optimized attention mechanisms, like FlashAttention. Figure 5 provides an illustration of the Hyena architecture and its core mechanism.
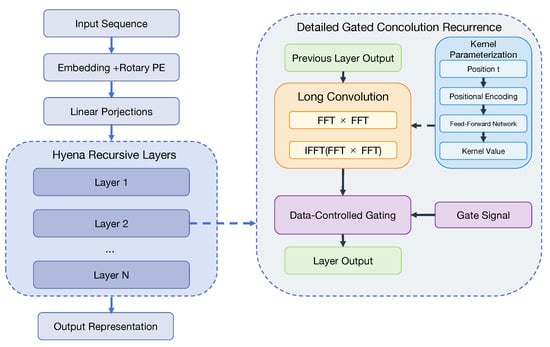
Figure 5.
Illustration of the Hyena backbone architecture and the gated convolution recurrence mechanism.
The core of the Hyena operator is a recursive process. For an input sequence u (after initial embedding and positional encoding), linear projections yield a set of sequences . Then, an N-step recursion is performed:
The final output is . In this recursion, is the n-th layer’s long convolution kernel. Its length can be as long as the input sequence L, providing a global receptive field. Crucially, is implicitly parameterized rather than having its weights learned directly. The ∗ symbol denotes convolution, implemented efficiently using Fast Fourier Transform (FFT)-based algorithms with complexity. is the n-th linear projection of the input sequence u, serving as a data-controlled gate. The ⊙ symbol represents element-wise multiplication (Hadamard product), allowing the convolution results to be modulated by the input data itself, introducing data dependency similar to attention mechanisms.
Hyena’s long convolution kernel is not learned directly, but dynamically generated by a small feed-forward network (FFN). Specifically, for time step t (or sequence position t), the kernel value is determined by:
Here, maps position t to an embedding vector. The FFN (e.g., a shallow MLP) maps the positional embedding to a basis for the filter response, often using periodic activation functions (like sin) to capture high-frequency information. is a window function (e.g., a parameterized exponential decay plus a bias term) that shapes the filter, enabling it to adaptively focus on information at different time scales (like macroeconomic cycles). This parameterization decouples the number of parameters from the sequence length L (sub-linear parameter scaling) and allows the effective filter length to be learned during training.
To make the model aware of sequence position information, we inject Rotary Positional Embeddings (RoPE) [40] after the input embedding layer for both the text sequence x and the interest rate sequence r. RoPEs have demonstrated excellent performance in various Transformer architectures by effectively encoding relative position information. The Hyena architecture is designed to be compatible with and benefit from modern positional encoding methods like RoPEs.
In this study, we adopt a variant of Hyena-Small (125M parameters). The specific configuration involves layers of Hyena recursion with a model hidden dimension . For the text input x and the historical interest rate sequence r, we first process them independently through separate RoPE layers and the initial few Hyena operator layers (e.g., the first 3 layers) to obtain their respective sequence representations. Then, at an intermediate layer (e.g., after the 3rd layer), the text representation sequence and the rate representation sequence are concatenated along the feature dimension. A convolution layer might be needed for linear transformation to unify dimensions. The concatenated sequence is then processed through the remaining shared Hyena recursive layers (e.g., the last 3 layers). This design allows the model to capture complex interactions and coupling between text content/tone (often high-frequency signals) and historical interest rate low-frequency trends within a unified vector space, providing high-quality fused features for subsequent prediction tasks, parameter fine-tuning, and domain adaptation.
4.3. Parameter-Efficient Fine-Tuning: Delta-LoRA
Directly applying full fine-tuning to large models like Hyena-Small (125M) might yield the best results, but is costly and prone to overfitting when labeled data (like specific domain central bank texts) is limited and computational resources are constrained. Therefore, we employ parameter-efficient fine-tuning (PEFT) techniques.
Low-rank adaptation (LoRA) [10] is a widely used PEFT method. Its core idea is to freeze most weights of the pretrained model during fine-tuning and introduce a parallel, trainable low-rank “bypass” structure for certain linear layers (e.g., in MHA or FFN layers). This bypass decomposes the original weight update into the product of two low-rank matrices: , where , , and the rank . During forward propagation, the output h is computed as:
where x is the input and is a scaling factor. Only the parameters of A and B are updated during training, significantly fewer than those in W. After training, can be merged back into W (), eliminating extra computational overhead during inference.
While LoRA significantly reduces fine-tuning costs, its performance often lags behind full fine-tuning because the frozen W cannot adapt. Delta-LoRA [13] proposes a novel improvement strategy aiming to bridge this gap while maintaining comparable memory and computational efficiency to LoRA. The core idea of Delta-LoRA is to not only update the low-rank matrices A and B, but also leverage the change in the low-rank update to drive the update of the pretrained weights W. The structure and update mechanism of Delta-LoRA are depicted in Figure 6.
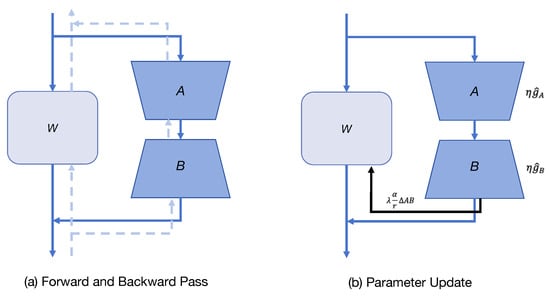
Figure 6.
Diagram illustrating the Delta-LoRA structure and its update mechanism. Shows the base model weight W, the low-rank matrices A and B, and the delta update influencing W.
Specifically, at each training step t, first compute gradients for A and B like in the standard LoRA, and obtain updated and via an optimizer (e.g., AdamW). Second, calculate the change (delta) in the low-rank adaptation matrix:
Third, use this change to update the pretrained weights W:
where is a new hyperparameter controlling the extent to which the “momentum” or “change trend” of the low-rank update is transferred to W. This parameter update typically starts after an initial number of training steps K (e.g., ).
Delta-LoRA allows the pretrained weights W to participate in the learning process, enabling better adaptation to the downstream task. Theoretically, under certain conditions (no dropout), , making an effective surrogate for the update direction of W, capturing the learning trajectory of the low-rank adaptation. Crucially, updating W does not require computing or storing the gradients of W itself or its optimizer states (like first and second moments in AdamW). The update of W depends solely on the already computed and their previous values . This keeps Delta-LoRA’s memory footprint and computational overhead nearly identical to standard LoRA. Standard LoRA implementations often include dropout before A or B. However, the derivation of Delta-LoRA suggests that dropout breaks the equality . Therefore, the Delta-LoRA structure removes dropout from the LoRA bypass to ensure that is a more accurate estimate of W’s update direction. This modification might also offer additional benefits like mitigating underfitting and saving minor activation memory.
In this study, we insert Delta-LoRA modules after key linear layers in the Hyena model (e.g., projection layers for gating signals and value v, and potentially linear layers within the FFN parameterizing the convolution kernel). We experimented with different ranks and selected the optimal configuration based on validation set performance. The scaling factor is typically set relative to r (e.g., for ), and is tuned experimentally (e.g., ). Using Delta-LoRA, we train less than 1% of the total parameters, yet achieve significant performance improvements, approaching the effectiveness of full parameter fine-tuning.
4.4. Multi-Source Domain Adaptation
Our dataset comprises texts from different central banks (FOMC and ECB) and various historical periods (e.g., spanning multiple economic cycles and policy paradigms like pre-QE, during QE, early hiking phase, late hiking phase). These different sources constitute distinct “domains” that may exhibit systematic differences in language style, focus areas, terminology usage, and even policy implications (i.e., domain shift). If a model trained solely on one domain (e.g., FOMC) is directly applied to another (e.g., ECB), performance might drop substantially. To enhance the model’s cross-domain generalization ability, we adopt an unsupervised domain adaptation strategy based on domain-adversarial training of neural networks (DANN) [21]. Figure 7 illustrates the DANN architecture.
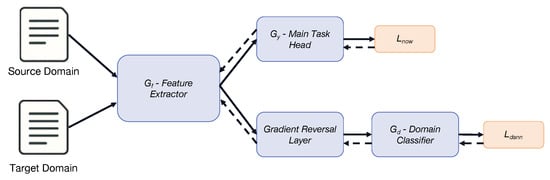
Figure 7.
Diagram illustrating the domain-adversarial training (DANN) module structure. Solid arrows represent the forward pass, while dashed arrows represent the gradient flow. The diagram shows the feature extractor (Gf), the main task classifier (Gy), the domain classifier (Gd), and the gradient reversal layer (GRL).
The core idea of DANN is to learn a feature representation that is discriminative for the main task (e.g., interest rate prediction) but indistinguishable concerning the domain source of the data. In other words, the model should learn to focus on the essential task-relevant features shared across domains while ignoring superficial domain-specific features irrelevant to the task.
To achieve this, we introduce a domain classifier (with parameters ) parallel to the main task classification head (parameters ), following the Hyena feature extractor (parameters ). The task of is to receive the features extracted by and predict the domain d from which the input sample x originated (e.g., for FOMC, for ECB).
The training involves an adversarial objective: first, minimize the main task loss. For samples from the source domain (labeled data, e.g., FOMC), minimize the main task (interest rate prediction) loss . This updates parameters , making extract useful features for the main task. Second, minimize the domain classification loss (for the domain classifier). For all samples (from source or target domains; target domain samples lack but have domain label ), train the domain classifier to minimize the loss between its predicted domain label and the true domain label (usually binary or multi-class cross-entropy loss). This updates , making it accurately distinguish features from different domains. Third, maximize the domain classification loss (for the feature extractor): This is the key to adversarial training. When updating the feature extractor parameters , we aim not only to minimize the main task loss , but also to maximize the domain classification loss . This means that we want to produce features z that confuse the domain classifier as much as possible, making it unable to determine the origin domain of z.
To implement step 3 (maximizing with respect to ) within a standard gradient descent framework, DANN introduces a gradient reversal layer (GRL). The GRL is placed between the feature extractor and the domain classifier . In forward propagation, GRL acts as an identity transform (). In backward propagation, when gradients from pass back through to the GRL, the GRL multiplies the gradient by a negative constant (or simply −1, with weighting the loss term) before passing it to . Thus, using standard backpropagation and gradient descent (or variants like AdamW) optimizes the entire network such that receives signals to minimize , while receives combined gradient signals to minimize and maximize , achieving the desired adversarial training objective.
In our implementation, we add a special domain token at the beginning of each input sequence to indicate its source (e.g., ‘<FOMC>’, ‘<ECB>’, ‘<QE_PERIOD>’, ‘<TIGHTENING_PERIOD>’). The domain classifier (e.g., an MLP with several fully connected layers) takes feature representations from an intermediate layer of Hyena (e.g., the 4th layer) and outputs a probability distribution predicting the input’s domain class. The domain adversarial loss typically uses cross-entropy:
where N is the batch size, is the number of domain classes, is a one-hot vector indicating the true domain of sample , and is the probability predicted by the domain classifier that belongs to the k-th domain. By minimizing an upper bound on the source domain risk and the H-divergence between domains [41], DANN encourages the model to learn more generalizable, domain-invariant feature representations, thereby improving prediction performance on unseen target domains (like ECB texts or texts from future economic cycles).
4.5. Multi-Task Learning
Beyond the primary task of nowcasting interest rate direction, central bank communication texts often contain subtle signals about future policy leanings, commonly interpreted by the market as “hawkish” (inclined towards tightening monetary policy, e.g., raising rates) or “dovish” (inclined towards easing, e.g., cutting rates or maintaining low rates). This policy “tone” or sentiment is crucial for understanding the deeper meaning of the text and predicting future rate movements.
To enable the model to capture and utilize these latent signals more effectively, we introduce an auxiliary task: hawkish/dovish classification of policy statement or speech paragraphs. We leverage the “Trillion Dollar Words” dataset, which offers paragraph-level hawkish/dovish annotations for FOMC texts. We employ this binary classification task as an auxiliary task, training it jointly with the main three-class interest rate prediction task.
In the multi-task learning framework, the primary interest rate prediction task and the auxiliary hawkish/dovish classification task share most of the underlying Hyena feature extractor network structure (including the parts fine-tuned via Delta-LoRA). At a higher level of (e.g., the output of the second-to-last Hyena block), the network structure branches into two independent task-specific heads: 1. Nowcasting head (): typically one or more fully connected layers followed by a Softmax layer, outputting probabilities for the three classes (up/down/stable). Its loss function is (e.g., weighted cross-entropy loss). 2. Hawkish/dovish head (): similarly, one or more fully connected layers followed by a Sigmoid or Softmax layer (binary classification here), outputting hawkish/dovish probabilities. Its loss function is (e.g., binary cross-entropy loss).
The model’s total loss function is a weighted sum of the main task loss, the auxiliary task loss, and the aforementioned domain adversarial loss:
where and are hyperparameters balancing the importance of different tasks. Based on our experiments and framework setup, we set . The weight employs a linear warm-up strategy, gradually increasing from 0 to 1 during the initial phase of training, then remaining constant. This warm-up strategy helps stabilize feature learning early in training and prevents the domain adversarial component from prematurely dominating the gradients.
By jointly training these related tasks, we expect to achieve implicit regularization, as the auxiliary task compels the shared feature extractor to learn more general and robust representations capable of reflecting policy tones alongside predicting the final rate decision. Learning to distinguish hawkish/dovish tendencies helps the model to gain a deeper understanding of the text’s semantic and sentiment nuances, potentially improving interest rate prediction accuracy indirectly. Our preliminary validation indicated that adding the hawkish/dovish auxiliary task yielded an approximate 0.6 pp improvement in AUC on the validation set. Furthermore, the trained auxiliary task head itself can provide valuable quantitative metrics on policy statement sentiment. In conclusion, the multi-task learning framework enriches the model’s learning objectives by introducing relevant auxiliary signals, contributing to improved performance on the core interest rate prediction task and enhancing the model’s overall generalization ability.
4.6. Training and Inference Details
To ensure experimental reproducibility, we present key parameters for model training and inference in Table 2, followed by additional implementation details.

Table 2.
Key training and inference parameters.
Our two-stage training approach stabilizes learning while maximizing the benefits of parameter-efficient fine-tuning and domain adaptation. We truncate documents to the final 2000 tokens based on the hypothesis that conclusions and forward guidance contain the most critical information for interest rate nowcasting.
The total loss is calculated as , with class weights applied to to address class imbalance.
During inference, auxiliary components ( and ) are removed, and Delta-LoRA matrices with accumulated updates are merged into W to obtain . This ensures no additional computational overhead compared to the original architecture, enabling real-time financial market analysis applications.
5. Results and Analysis
This chapter systematically evaluates the performance, efficiency, and robustness of our proposed Hyena Hierarchy + Delta-LoRA + DANN + multi-task learning framework on the task of central bank interest rate change nowcasting. We present direct comparisons with mainstream baseline models, ablation studies of key model components, analysis of cross-domain generalization capabilities, and explorations of model interpretability and error analysis. This serves to validate the research questions and hypotheses outlined earlier. Primary evaluation metrics include accuracy, macro F1-score, Area Under the Receiver Operating Characteristic Curve (ROC-AUC), directional accuracy, and model calibration (Brier score). The statistical significance of performance improvements is rigorously evaluated using the Diebold–Mariano (DM) test [42]. The DM test employs a quadratic loss function to compare forecast accuracy, with the test statistic computed as , where is the mean loss differential and is its estimated variance. Under the null hypothesis of equal predictive accuracy, the DM statistic follows a standard normal distribution. We report significance at p < 0.05 throughout our analysis. The significance of performance improvements is confirmed using the Diebold–Mariano test [42] (p < 0.05).
5.1. Overall Performance Comparison
We first compare our proposed full model, denoted as ours (Hyena + -LoRA + DANN + MTL), against several baseline models on the test sets of the core FOMC dataset (1977–2024) and the ECB dataset (1999–2024) used for evaluating cross-institutional generalization. The baselines include the following: logistic regression + TF-IDF: a classical econometric baseline using TF-IDF features with logistic regression to demonstrate the value-add of deep learning approaches. Transformer-XL + Full FT: a strong Transformer-based long sequence model with full parameter fine-tuning. Longformer + LoRA: a Transformer variant optimized for long texts, combined with standard LoRA for parameter-efficient fine-tuning. GPT-2 + AdapterFusion: a GPT-2-based model using AdapterFusion for multi-task and multi-domain adaptation. Ours (Hyena + LoRA): a variant of our model using standard LoRA instead of Delta-LoRA to assess the gain from Delta-LoRA. Ours (Hyena + -LoRA): our base model, removing DANN and multi-task components.
Table 3 shows that our proposed full model significantly outperforms all baseline models on all main metrics across both FOMC and ECB datasets. Notably, compared to the classical econometric baseline (logistic regression + TF-IDF), our full model demonstrates substantial improvements of 14.1 percentage points in macro F1 on FOMC (0.862 vs. 0.721) and 9.5 percentage points on ECB (0.780 vs. 0.685), clearly justifying the adoption of sophisticated deep learning architectures for this task. Compared to Longformer + LoRA, our full model improves macro F1 by 6.0 percentage points (pp) on FOMC (0.862 vs. 0.802) and 5.7 pp on ECB (0.780 vs. 0.723). Diebold–Mariano tests confirmed that these improvements are statistically significant with DM statistics of 3.42 (p < 0.001) for FOMC and 2.89 (p < 0.004) for ECB comparisons against Longformer + LoRA. The reported 95% confidence intervals were computed using bootstrap resampling with 1000 iterations, ensuring robust uncertainty quantification. Diebold–Mariano tests confirmed these improvements are statistically significant (p < 0.05). Comparing ours (Hyena + -LoRA) with Longformer + LoRA, even without DANN and multi-task learning, the Hyena and Delta-LoRA combination alone achieved a 4.8 pp macro F1 improvement (0.850 vs. 0.802) on the FOMC dataset. This strongly supports our hypothesis that the Hyena and Delta-LoRA-based method outperforms Transformer-based approaches with standard LoRA for the single-domain long-text task on FOMC data. Our model also demonstrates similar advantages in accuracy and AUC. These results indicate that the combination of Hyena Hierarchy’s long convolution mechanism and Delta-LoRA’s efficient fine-tuning strategy provides a superior foundation architecture for processing ultra-long financial policy texts.

Table 3.
Main performance metrics of models on FOMC and ECB test sets with 95% confidence intervals.
5.2. Efficiency and Latency Analysis
Besides prediction accuracy, the efficiency of processing long texts is crucial for practical applications, especially those with real-time requirements. We compare the average inference latency (measured on an NVIDIA A100 32 GB GPU) for processing a single sample of 2000 tokens and the parameter scales of different models.
As shown in Figure 8, our Hyena-based models (including the final model) demonstrate exceptional efficiency. When processing a 2000-token sequence, their inference latency is only 2.3 ms, significantly lower than Longformer+LoRA (6.5 ms) and Transformer-XL (25.0 ms). This corresponds to over 65% latency reduction compared to Longformer. This advantage stems from Hyena’s sub-quadratic complexity () and its efficient FFT convolution implementation. Although our model achieves the highest F1 score, its parameter count (dominated by Hyena-Small 125M, with PEFT parameters < 1%) is comparable to Longformer-base or GPT-2-base, and much smaller than Transformer-XL, which might require a larger scale to reach similar performance. This validates part of our research question regarding reducing computational cost while maintaining or improving accuracy for long policy text processing during inference.
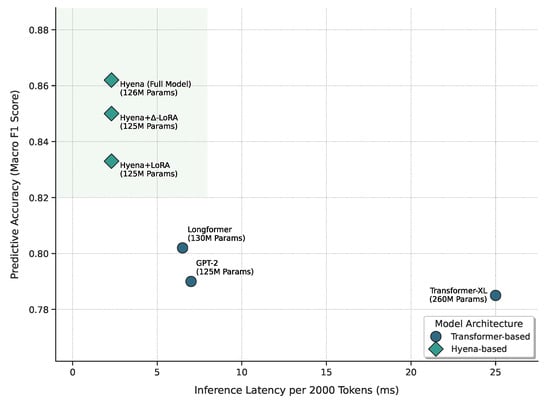
Figure 8.
Model accuracy (FOMC macro F1) vs. inference latency (per 2000-token sample).
5.3. Robustness Analysis: Subperiod Performance
To assess the robustness of our model across different economic conditions and policy regimes, we conduct a comprehensive subperiod analysis. This evaluation is crucial for understanding how model performance varies across distinct macroeconomic environments and policy frameworks, addressing concerns about temporal stability and economic regime dependence.
We partition our FOMC dataset into four economically meaningful subperiods: pre-crisis (1977–2006), financial crisis (2007–2009), post-crisis/QE era (2010–2015), and normalization period (2016–2024). Each period represents distinct monetary policy paradigms characterized by different communication strategies, policy tools, and economic contexts.
Table 4 demonstrates that our model maintains consistent performance advantages across all economic subperiods, with improvements ranging from 5.2 to 5.9 percentage points. Notably, the model shows particularly robust performance during the financial crisis period, achieving a 5.9 pp improvement when policy communication was most critical and markets were most volatile. This consistency across diverse economic regimes validates the generalizability of our approach and suggests that the learned representations capture fundamental relationships between central bank language and policy actions that transcend specific economic conditions.

Table 4.
Subperiod performance analysis: macro F1 scores across different economic regimes.
The slight performance degradation during the financial crisis period (compared to other periods) is expected and consistent across all models, reflecting the inherently challenging nature of predicting policy actions during periods of extreme uncertainty and unconventional policy measures. However, our model’s superior performance in this challenging period demonstrates its capacity to extract meaningful signals, even from highly complex and unprecedented policy communications.
5.4. Ablation Studies
To deeply understand the contribution of each key component, we conducted a series of ablation experiments, primarily evaluating the change in macro F1 score on the FOMC dataset.
Table 5 shows that replacing Delta-LoRA with standard LoRA (rank r = 16) results in a 1.7 pp drop in macro F1. This indicates that Delta-LoRA, through its mechanism of updating pretrained weights W, indeed adapts more effectively to the downstream task, enhancing the model’s expressive power. Regarding the rank (r) in Delta-LoRA, increasing it from 8 to 16 brings a 0.5 pp improvement, but further increasing it from 16 to 32 yields a very minor gain (0.1 pp). Considering the increase in parameters and computational cost with r, r = 16 appears to be a favorable trade-off point.

Table 5.
Impact of Delta-LoRA and its rank (r) on FOMC macro F1.
Table 6 shows that defining the interest rate change label based on the 7-day window following the statement release yields the best model performance. A window that is too short (3 days) might capture excessive market noise, while a window that is too long (14 days) might extend beyond the immediate impact scope of the text or be confounded by subsequent events.

Table 6.
Impact of prediction window length (defining the label) on FOMC macro F1.
The contributions of domain adaptation (DANN) and multi-task learning (MTL) are analyzed in detail in the following subsections, but briefly, ablation studies show that removing DANN leads to a decrease of approximately 1.8 pp in cross-domain (FOMC → ECB) macro F1, and removing MTL (the hawkish/dovish auxiliary task) results in a decrease of about 1.2 pp in the main task (FOMC nowcasting) Macro F1. These ablation results clearly demonstrate the positive contribution of Delta-LoRA, DANN, and MTL to the overall model performance.
5.5. Cross-Domain Generalization Analysis
To evaluate the model’s ability to transfer knowledge learned from FOMC data to ECB data (or different economic cycles), we focus on analyzing the effect of the domain-adversarial training (DANN) component. We compare the performance of the full model versus a model with the DANN component removed on the ECB test set (both trained on FOMC data and incorporating Delta-LoRA and MTL).
The results in Table 7 show that incorporating DANN improves the macro F1 score on the target ECB domain by 1.8 pp. This strongly supports the hypothesis that domain adaptation via DANN significantly enhances the model’s generalization performance on cross-central bank corpora.

Table 7.
Impact of DANN on cross-domain (FOMC → ECB) performance.
Figure 9 illustrates the typical loss dynamics during training. The domain classifier’s loss tends to decrease as it learns to distinguish domains, potentially oscillating due to the adversarial nature. Concurrently, the feature extractor, influenced by the gradient reversal layer, aims to maximize this domain loss, pushing it towards producing domain-agnostic features. The main task loss consistently decreases, indicating simultaneous learning of the prediction task and domain adaptation. This adversarial dynamic confirms the successful operation of the DANN mechanism, compelling the feature extractor to generate more domain-invariant representations and thereby enhancing cross-domain generalization.
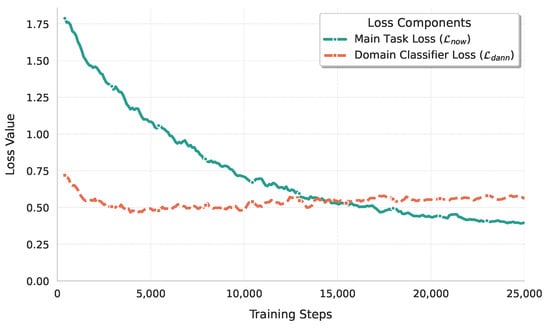
Figure 9.
Convergence of domain classifier Loss () and main task loss () during training.
5.6. Multi-Task Learning Benefits Analysis
We next assess the impact of adding the “hawkish/dovish classification” auxiliary task on the performance of the primary interest rate prediction task, aiming to validate our third hypothesis. We compare the macro F1 score of the full model against a model without the multi-task learning (MTL) component on the FOMC test set.
The results in Table 8 clearly show that adding the hawkish/dovish classification auxiliary task improves the main task’s macro F1 by 1.2 pp. This supports the hypothesis that jointly training the main task with a related auxiliary task (like policy tone classification) can enhance the main task’s performance. This improvement likely arises because the auxiliary task forces the shared Hyena layers to learn richer feature representations capable of capturing both semantic content and sentiment nuances, which are beneficial for accurately predicting interest rate decisions.

Table 8.
Impact of multi-task learning (MTL) on main task (FOMC nowcasting) performance.
5.7. Interpretability, Calibration, and Error Analysis
Beyond quantitative metrics, understanding the model’s internal working mechanisms, assessing the reliability of its predictions, and analyzing its failure cases are equally important.
Although Hyena uses long convolutions rather than self-attention, its implicitly parameterized convolution kernels can still be analyzed. By visualizing the weights of the trained kernels or their response to inputs (analogous to attention maps but along the time/sequence dimension), we can investigate which parts or patterns in the input text the model focuses on.
As in Figure 10, analysis of the model’s internal mechanisms (like kernel responses or equivalent contribution scores) suggests a tendency to focus on keywords and phrases directly related to monetary policy stance and economic conditions. For instance, terms like “inflation risks”, “tighter monetary policy”, “restrictive stance”, and “raise the target range” often receive higher contribution scores, particularly when predicting an “up” rate change. Conversely, words like “accommodative”, “patient”, or “softening labor market” are more frequently associated with “down” or “stable” predictions. This pattern indicates that the model is indeed learning to understand the economic meaning and policy signals within the text, rather than relying solely on superficial statistical features.
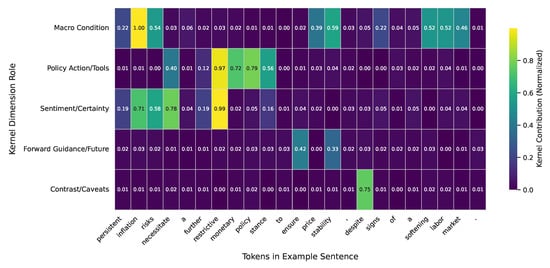
Figure 10.
Heatmap of Hyena convolution kernel contribution response to specific vocabulary in an example sentence. Higher scores indicate greater model focus.
A reliable predictive model should not only be accurate, but also produce probability scores that reflect true confidence levels. We use the Brier score to measure overall calibration error and visualize calibration using a reliability diagram.
Figure 11 shows the calibration curve for the model’s predicted probabilities for the “up” class. Ideally, the curve should closely follow the diagonal line (perfect calibration). Our model’s curve (blue line) is reasonably close to the diagonal, suggesting that its predicted probabilities are largely reliable. For example, when the model predicts an “up” probability around 0.8, the actual frequency of “up” events is also close to 80%. The calculated Brier score is relatively low, further confirming the model’s good overall calibration. This implies that the model’s output probabilities can be used with reasonable confidence for risk assessment or decision-making.
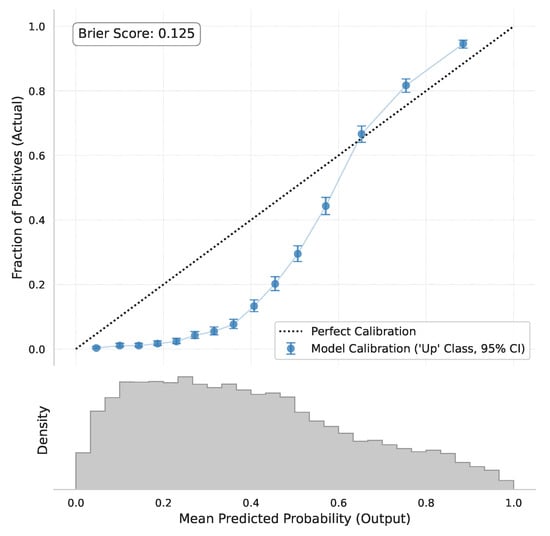
Figure 11.
Model prediction probability calibration curve (reliability diagram) for the ‘up’ class.
To evaluate the three-class classification performance in more detail, we plot ROC curves and precision–recall (PR) curves for each class.
Figure 12 presents the receiver operating characteristic (ROC, left) and precision–recall (PR, right) curves for the three output classes (‘up’, ‘down’, and ‘stable’) evaluated on the FOMC test set. The ROC curves indicate that the model performs significantly better than random chance for all classes. Notably, the area under the curve (AUC) scores for the directional change classes, ‘up’ (AUC = 0.86) and ‘down’ (AUC = 0.86), suggest a reasonable ability to distinguish these instances from others based on the model’s score rankings. However, the lower AUC for the ’stable’ class (AUC = 0.73) points to greater difficulty in uniquely identifying neutral or ambiguous policy stances from potentially directional ones.
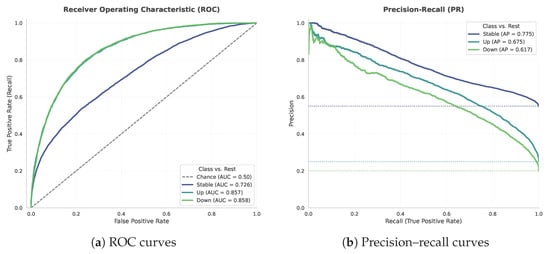
Figure 12.
Receiver operating characteristic (ROC) and precision–recall (PR) curves per class for the model on the FOMC test set. (a) ROC curves for all three classes (‘up’, ‘down’, and ‘stable’) are well above the diagonal, with high AUC values, indicating strong discriminative ability. (b) PR curves show high average precision (AP) scores for all classes, including the minority ‘up’ and ‘down’ classes.
6. Discussion
This section analyzes the superior performance achieved by our integrated framework and examines its practical implications and limitations.
6.1. Model Performance Analysis
Our framework’s exceptional performance stems from synergistic technological integration. The Hyena Hierarchy backbone’s sub-quadratic complexity () enables processing complete documents without truncation-induced information loss. Delta-LoRA’s innovative parameter updating mechanism allows pretrained weights to actively participate in adaptation, achieving near full fine-tuning performance while maintaining efficiency. DANN’s adversarial training produces domain-invariant representations that generalize across institutions and time periods. Multi-task learning with hawkish/dovish classification creates implicit regularization, enriching feature representations for policy tone understanding.
6.2. Practical Investment Applications
The framework offers significant value for financial market participants. With 87% accuracy and 65% latency reduction, it enables real-time policy analysis for high-frequency trading and risk management. Institutional investors can leverage the 86.2% macro F1 performance for asset allocation decisions, while fixed-income managers can use precise interest rate scenario classification for duration management. The cross-institutional generalization enables global macro strategies across different central bank jurisdictions.
These findings carry certain policy and market implications. The model demonstrates the potential to derive early signals regarding the short-term direction of future interest rate movements through in-depth analysis of central bank communication texts. If validated and optimized for practical application, this near real-time monitoring capability might offer financial market participants more timely informational input than traditional economic data releases.
6.3. Research Limitations
Several limitations warrant acknowledgment. The reliance solely on textual information excludes complementary macroeconomic data and market conditions that influence central bank decisions. The 2000-token truncation, while computationally necessary, may cause information loss in longer documents. The 5-basis point threshold introduces subjectivity in categorizing interest rate changes. Domain adaptation has been tested on limited institutional contexts, and the model assumes stable historical relationships between communication language and policy outcomes, which may not hold during unprecedented policy environments.
6.4. Future Directions
Based on current achievements, future research should explore multimodal approaches integrating textual and macroeconomic variables, extend the framework to multilingual central bank communications, and investigate adaptive truncation strategies for handling varying document lengths while maintaining computational efficiency.
7. Conclusions
In conclusion, this research contributes on three main fronts: methodological innovation, dataset construction, and empirical performance validation. We proposed and validated a novel integrated deep learning framework combining Hyena Hierarchy for long sequence modeling, Delta-LoRA for parameter-efficient fine-tuning, domain adaptation techniques, and multi-task learning. This framework systematically addresses the core challenges encountered in analyzing central bank communication texts, namely ultra-long sequence processing, efficient model adaptation, and cross-domain generalization. Concurrently, we constructed and annotated a large-scale, cross-institutional dataset covering decades of official communications from the U.S. Federal Open Market Committee and the European Central Bank.
The empirical results clearly demonstrate that our proposed complete model achieves state-of-the-art performance in the interest rate nowcasting task compared to strong baseline models, showing significant improvements in key metrics such as accuracy, macro F1 score, and AUC. Furthermore, it drastically reduces the inference time required for processing long texts. The combination of the Hyena architecture and the Delta-LoRA fine-tuning technique, in particular, showcases its superiority and significant potential for tackling tasks involving the analysis of lengthy, information-dense texts characteristic of the financial and macroeconomic policy domains.
We believe this work opens new possibilities for leveraging advanced natural language processing techniques to gain deeper insights from central bank communications, aiding economic forecasting and policy analysis. Future research should continue exploring more powerful model architectures, richer multimodal information fusion, and broader cross-lingual and cross-institutional applications. We also call for enhanced collaboration between academia and industry to jointly build and maintain more comprehensive, standardized, and open benchmark resources for central bank communication text analysis, fostering continued progress and knowledge sharing in this interdisciplinary field.
Author Contributions
Conceptualization, T.S., S.Y. and R.Z.; methodology, T.S. and S.Y.; software, T.S. and S.Y.; validation, T.S., S.Y. and R.Z.; formal analysis, T.S. and S.Y.; investigation, T.S. and S.Y.; resources, R.Z.; data curation, T.S. and S.Y.; writing—original draft preparation, T.S.; writing—review and editing, T.S., S.Y. and R.Z.; visualization, T.S. and S.Y.; supervision, R.Z.; project administration, R.Z.; funding acquisition, R.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets used in this study are available from the corresponding author upon reasonable request. Raw data sources are publicly available as cited in the manuscript.
Acknowledgments
The authors would like to thank the anonymous reviewers for their helpful and constructive comments which greatly contributed to the improvement of the final version of the paper.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Blinder, A.S.; Ehrmann, M.; Fratzscher, M.; De Haan, J.; Jansen, D.J. Central bank communication and monetary policy: A survey of theory and evidence. J. Econ. Lit. 2008, 46, 910–945. [Google Scholar] [CrossRef]
- Neuenkirch, M. Managing financial market expectations: The role of central bank transparency and central bank communication. Eur. J. Political Econ. 2012, 28, 1–13. [Google Scholar] [CrossRef]
- Fernández-Cruz, J.; Moreno-Ortiz, A. Tracking diachronic sentiment change of economic terms in times of crisis: Connotative fluctuations of ‘inflation’ in the news discourse. PLoS ONE 2023, 18, e0287688. [Google Scholar] [CrossRef] [PubMed]
- Arner, D.W.; Castellano, G.G.; Selga, E.K. Financial Data Governance: The Datafication of Finance, the Rise of Open Banking and the End of the Data Centralization Paradigm. In Proceedings of the “Data Governance in Banking and Finance: What role for the Industry?”—International Workshop on Data Governance in the Financial Industry, Tilburg, The Netherlands, 26 April 2023. [Google Scholar]
- Keles, F.D.; Wijewardena, P.M.; Hegde, C. On the computational complexity of self-attention. In Proceedings of the International Conference on Algorithmic Learning Theory, Singapore, 20–23 February 2023; pp. 597–619. [Google Scholar]
- Goyal, T.; Xu, J.; Li, J.J.; Durrett, G. Training Dynamics for Text Summarization Models. In Proceedings of the Findings of the Association for Computational Linguistics: ACL 2022, Dublin, Ireland, 22–27 May 2022; pp. 2061–2073. [Google Scholar]
- Woźniak, S.; Kocoń, J. From big to small without losing it all: Text augmentation with chatgpt for efficient sentiment analysis. In Proceedings of the 2023 IEEE International Conference on Data Mining Workshops (ICDMW), Shanghai, China, 1–4 December 2023; pp. 799–808. [Google Scholar]
- Holmes, D.R. Economy of Words: Communicative Imperatives in Central Banks; University of Chicago Press: Chicago, IL, USA, 2013. [Google Scholar]
- Min, B.; Ross, H.; Sulem, E.; Veyseh, A.P.B.; Nguyen, T.H.; Sainz, O.; Agirre, E.; Heintz, I.; Roth, D. Recent advances in natural language processing via large pre-trained language models: A survey. ACM Comput. Surv. 2023, 56, 1–40. [Google Scholar] [CrossRef]
- Hu, E.J.; Shen, Y.; Wallis, P.; Allen-Zhu, Z.; Li, Y.; Wang, S.; Wang, L.; Chen, W. LoRA: Low-Rank Adaptation of Large Language Models. In Proceedings of the International Conference on Learning Representations, Virtual, 25 April 2022. [Google Scholar]
- Xu, L.; Xie, H.; Qin, S.Z.J.; Tao, X.; Wang, F.L. Parameter-efficient fine-tuning methods for pretrained language models: A critical review and assessment. arXiv 2023, arXiv:2312.12148. [Google Scholar]
- Xin, Y.; Luo, S.; Zhou, H.; Du, J.; Liu, X.; Fan, Y.; Li, Q.; Du, Y. Parameter-efficient fine-tuning for pre-trained vision models: A survey. arXiv 2024, arXiv:2402.02242. [Google Scholar]
- Zi, B.; Qi, X.; Wang, L.; Wang, J.; Wong, K.F.; Zhang, L. Delta-lora: Fine-tuning high-rank parameters with the delta of low-rank matrices. arXiv 2023, arXiv:2309.02411. [Google Scholar]
- Hayou, S.; Ghosh, N.; Yu, B. LoRA+: Efficient Low Rank Adaptation of Large Models. In Proceedings of the International Conference on Machine Learning, Vienna, Austria, 21–27 July 2024; pp. 17783–17806. [Google Scholar]
- Zhu, R.; Guo, D.; Qi, D.; Chu, Z.; Yu, X.; Li, S. Trustworthy representation learning across domains. arXiv 2023, arXiv:2308.12315. [Google Scholar] [CrossRef]
- Yang, S.; Wang, Y.; Chen, H. Mambamil: Enhancing long sequence modeling with sequence reordering in computational pathology. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Marrakesh, Morocco, 6–10 October 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 296–306. [Google Scholar]
- Li, J.; Yu, Z.; Du, Z.; Zhu, L.; Shen, H.T. A comprehensive survey on source-free domain adaptation. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 5743–5762. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.; Lu, J.; Li, K.; Fang, Z.; Zhang, G. Source-free unsupervised domain adaptation: Current research and future directions. Neurocomputing 2024, 564, 126921. [Google Scholar] [CrossRef]
- Poli, M.; Massaroli, S.; Nguyen, E.; Fu, D.Y.; Dao, T.; Baccus, S.; Bengio, Y.; Ermon, S.; Ré, C. Hyena hierarchy: Towards larger convolutional language models. In Proceedings of the International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; pp. 28043–28078. [Google Scholar]
- Gaido, M.; Papi, S.; Negri, M.; Bentivogli, L. How Do Hyenas Deal with Human Speech? Speech Recognition and Translation with ConfHyena. In Proceedings of the 2024 Joint International Conference on Computational Linguistics, Language Resources and Evaluation (LREC-COLING 2024), Torino, Italy, 20–25 May 2024; pp. 8184–8191. [Google Scholar]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; March, M.; Lempitsky, V. Domain-adversarial training of neural networks. J. Mach. Learn. Res. 2016, 17, 1–35. [Google Scholar]
- Wang, Y.; Lin, Y.; Zeng, X.; Zhang, G. Multilora: Democratizing lora for better multi-task learning. arXiv 2023, arXiv:2311.11501. [Google Scholar]
- Rosa, C. The financial market effect of FOMC minutes. Econ. Policy Rev. 2013, 19, 1–15. [Google Scholar]
- Nardelli, S.; Martens, D.; Tobback, E. Between hawks and doves: Measuring Central Bank Communication. egional S 2017, 101, 1–42. [Google Scholar]
- Lucca, D.O.; Trebbi, F. Measuring Central Bank Communication: An Automated Approach with Application to FOMC Statements; Technical Report; National Bureau of Economic Research: Cambridge, MA, USA, 2009. [Google Scholar]
- Hansen, S.; McMahon, M.; Prat, A. Transparency and deliberation within the FOMC: A computational linguistics approach. Q. J. Econ. 2018, 133, 801–870. [Google Scholar] [CrossRef]
- Huang, A.H.; Wang, H.; Yang, Y. FinBERT: A large language model for extracting information from financial text. Contemp. Account. Res. 2023, 40, 806–841. [Google Scholar] [CrossRef]
- Gambacorta, L.; Kwon, B.; Park, T.; Patelli, P.; Zhu, S. CB-LMs: Language Models for Central Banking; Bank for International Settlements, Monetary and Economic Department: Basel, Switzerland, 2024. [Google Scholar]
- Doh, T.; Song, D.; Yang, S.K. Deciphering Federal Reserve Communication via Text Analysis of Alternative Fomc Statements; Federal Research Bank of Kansas City: Kansas City, MO, USA, 2020. [Google Scholar]
- Beltagy, I.; Peters, M.E.; Cohan, A. Longformer: The long-document transformer. arXiv 2020, arXiv:2004.05150. [Google Scholar]
- Ralambomihanta, T.R.; Mohammadzadeh, S.; Islam, M.S.N.; Jabbour, W.; Liang, L. Scavenging hyena: Distilling transformers into long convolution models. arXiv 2024, arXiv:2401.17574. [Google Scholar]
- Han, Z.; Gao, C.; Liu, J.; Zhang, J.; Zhang, S.Q. Parameter-efficient fine-tuning for large models: A comprehensive survey. arXiv 2024, arXiv:2403.14608. [Google Scholar]
- He, R.; Liu, L.; Ye, H.; Tan, Q.; Ding, B.; Cheng, L.; Low, J.W.; Bing, L.; Si, L. On the effectiveness of adapter-based tuning for pretrained language model adaptation. arXiv 2021, arXiv:2106.03164. [Google Scholar]
- Pfeiffer, J.; Kamath, A.; Rücklé, A.; Cho, K.; Gurevych, I. Adapterfusion: Non-destructive task composition for transfer learning. arXiv 2020, arXiv:2005.00247. [Google Scholar]
- Tasca, V. FOMC Meeting Statements & Minutes. Kaggle Dataset. 2022. Available online: https://www.kaggle.com/datasets/vladtasca/fomc-meeting-statements-and-minutes (accessed on 26 April 2025).
- Federal Reserve (Kaggle Team). Federal Reserve Interest Rates, 1954–Present. Kaggle Dataset, 2024. Version 2.1. Available online: https://www.kaggle.com/datasets/federalreserve/interest-rates (accessed on 26 April 2025).
- Istrefi, K.; Odendahl, F.; Sestieri, G. Introduces the Euro Area Communication Event-Study Database (EA-CED). In ECB Communication and Its Impact on Financial Markets; Working Paper 859; Banque de France: Paris, France, 2022. [Google Scholar]
- Shah, A.; Paturi, S.; Chava, S. Trillion Dollar Words: A New Financial Dataset, Task & Market Analysis. In Proceedings of the 61st Annual Meeting of the Association for Computational Linguistics (ACL 2023), Toronto, ON, Canada, 9–14 July 2023; pp. 6664–6679. [Google Scholar]
- Bank, E.C. All ECB Speeches Dataset. CSV Export from the ECB Website, 2025. Snapshot Downloaded. Available online: https://www.ecb.europa.eu/press/key/html/index.en.html (accessed on 26 April 2025).
- Heo, B.; Park, S.; Han, D.; Yun, S. Rotary position embedding for vision transformer. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 289–305. [Google Scholar]
- Kashyap, A.R.; Hazarika, D.; Kan, M.Y.; Zimmermann, R. Domain divergences: A survey and empirical analysis. arXiv 2020, arXiv:2010.12198. [Google Scholar]
- Diebold, F.X. Comparing predictive accuracy, twenty years later: A personal perspective on the use and abuse of Diebold–Mariano tests. J. Bus. Econ. Stat. 2015, 33, 1. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).