A Machine Learning Approach for Predicting Particle Spatial, Velocity, and Temperature Distributions in Cold Spray Additive Manufacturing
Abstract
1. Introduction
2. Methodology
2.1. Sampling
2.2. The 1st ML Model to Predict the Spatial Distribution of Particles on the Substrate
2.2.1. KNN-KDE-Based Prediction Module
- Random Sampling: With a predetermined probability prand, points are directly selected at random from the KDE output, focusing primarily on regions corresponding to the peaks of the probability density.
- Farthest Sampling: For the remaining proportion (1-prand), within a batch of sampled points, the point that is farthest from the local mean (calculated as the mean of the neighbors obtained via KNN) is selected, simulating potential extreme deposition points.
2.2.2. ChatGPT Assisted Optimization
2.2.3. Projection Algorithm
2.3. The 2nd ML Model to Predict the Velocity and Temperature of Each Particle upon Impact on the Substrate
2.3.1. Interpolation
2.3.2. Mathematical Transformation—Symbolic Regression
2.3.3. Model Optimization—Weighted Random Forest
3. Results and Discussion
3.1. Results of the 1st Model (Evaluating the 1st Model Independently)
3.2. Results of the 2nd Model Using CFD Inputs (Evaluating the 2nd Model Independently)
3.3. Results from the Integration of the 1st and 2nd Models
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| CFD | Computational Fluid Dynamics |
| KDE | kernel density estimation |
| KD-Tree | k-Dimensional Tree |
| KL | Kullback–Leibler Divergence |
| KNN | k-Nearest Neighbors |
| ML | Machine Learning |
| MSE | Mean Squared Error |
| OOB | Out-of-bag |
| Variables | |
| The boundary between the (k–1)-th and k-th bins for a feature | |
| Number of intervals (bins) used for feature partitioning | |
| A sample point drawn | |
| The i-th feature value of a sample in the current sample set | |
| The current set of selected (or accepted) samples | |
| The dimensionality of the feature space (i.e., number of features) | |
| The OBB sample set for the i-th tree | |
| Gaussian random variable (zero-mean unless otherwise specified) | |
| Bandwidth parameter used in kernel density estimation (KDE) | |
| The prediction of i-th tree | |
| (⋅) | Kernel function |
| The region corresponding to the i-th multidimensional feature combination | |
| MSE for the i-th tree in the OBB sample set | |
| Mean of the feature | |
| Total count; used to denote the number of layers, datasets, candidate points, or invalid points depending on the context | |
| Nbatch | The total number of points sampled in the current batch |
| Nrejected | The number of points that fall within the dead zone |
| k-th quantile of a feature distribution | |
| Current rejection rate during sampling | |
| The target rejection rate | |
| The radial distance from the substrate center | |
| The maximum radial distance | |
| Set of all candidate points under consideration | |
| Standard deviation | |
| Variance | |
| T | Particle temperature on the substrate |
| The coordinates of the i-th particle at the substrate | |
| u, v, w | Particle velocity components on the substrate |
| Variance of the feature | |
| Variance of the original data for feature | |
| Variance of the sampled data for feature | |
| The wire diameter | |
| Weight of i-th tree | |
| A candidate point | |
| The i-th feature value of a candidate point (i.e., its coordinate in the i-th dimension of the feature space) | |
| The input feature value at the interpolation point i | |
| ,y, z | Particle coordinates on the substrate |
| The interpolated output feature value at that point | |
| The interpolated data after adding noise | |
| The prediction of the i-th tree on the OBB sample |
Appendix A
Projection Algorithm for Physically Constrained Particle-Distribution Prediction
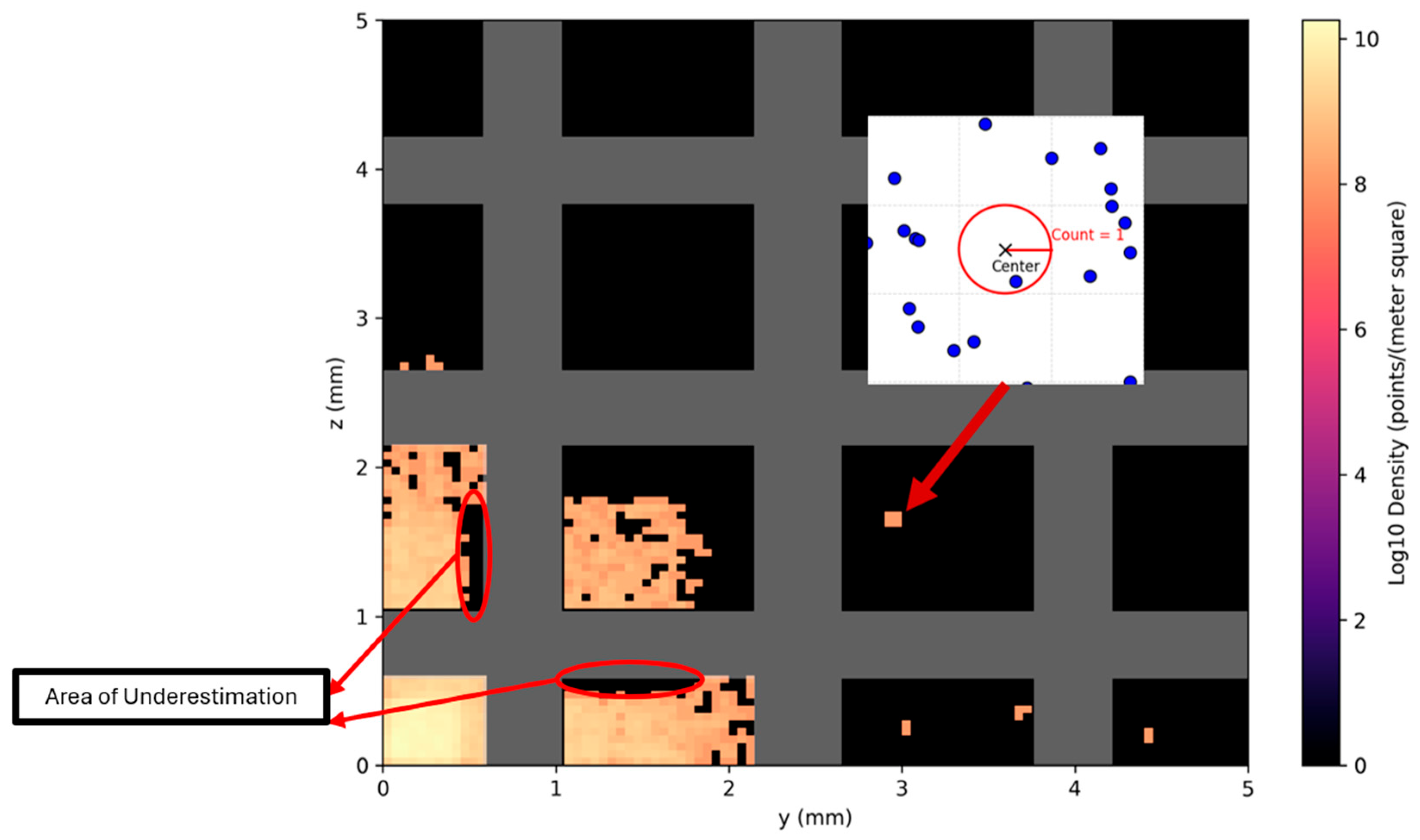
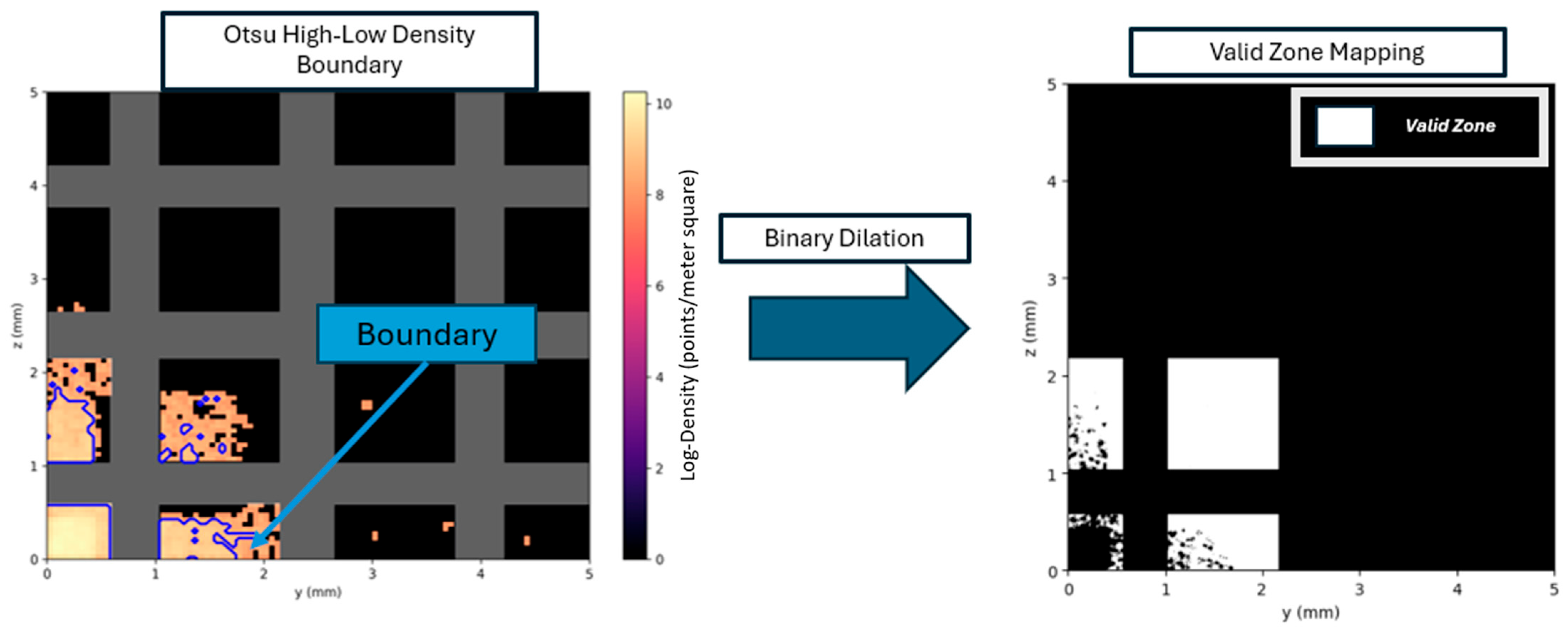
Appendix B
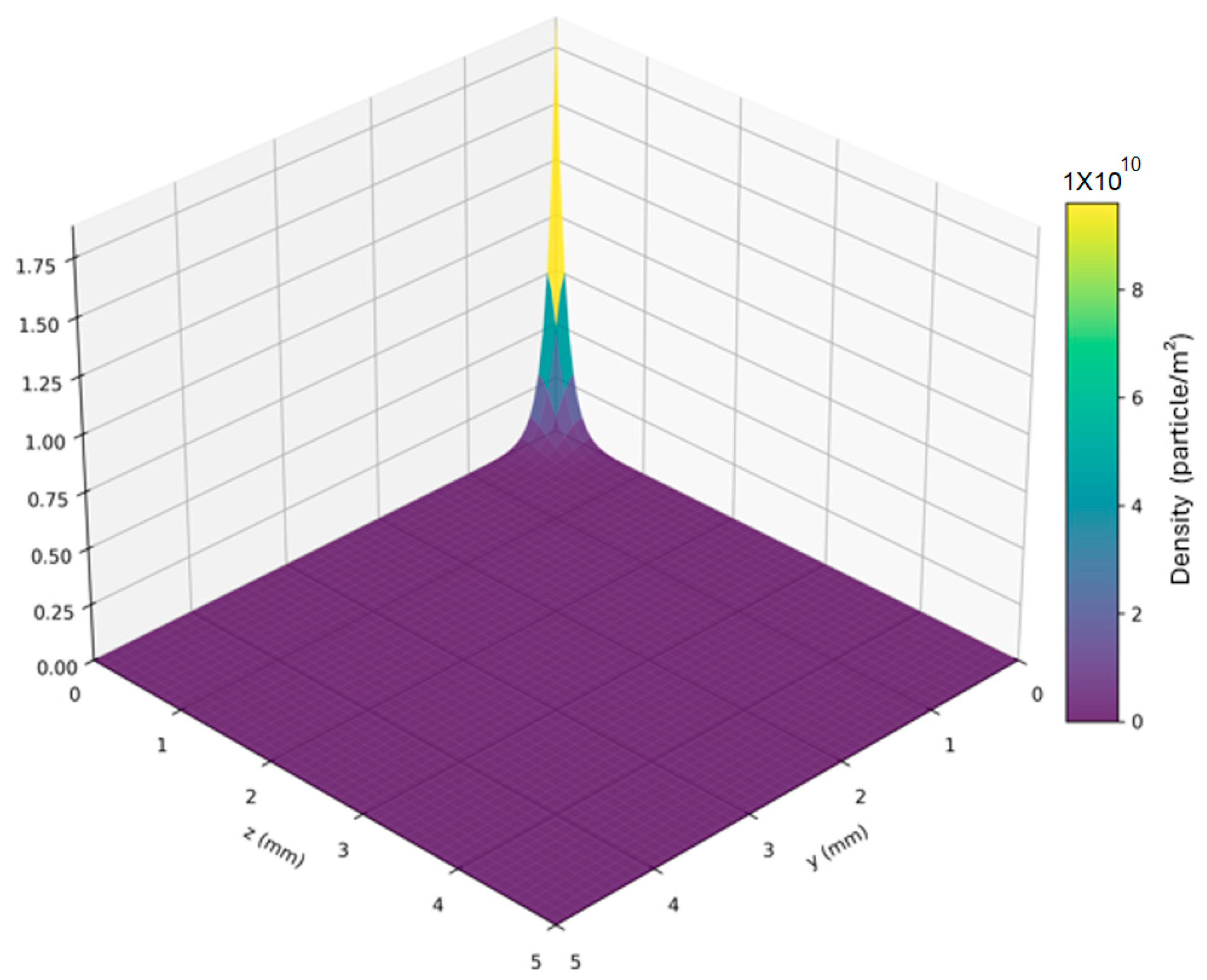
Interpolation-Based Data-Augmentation Protocol for Expanding Sparse Process Parameters
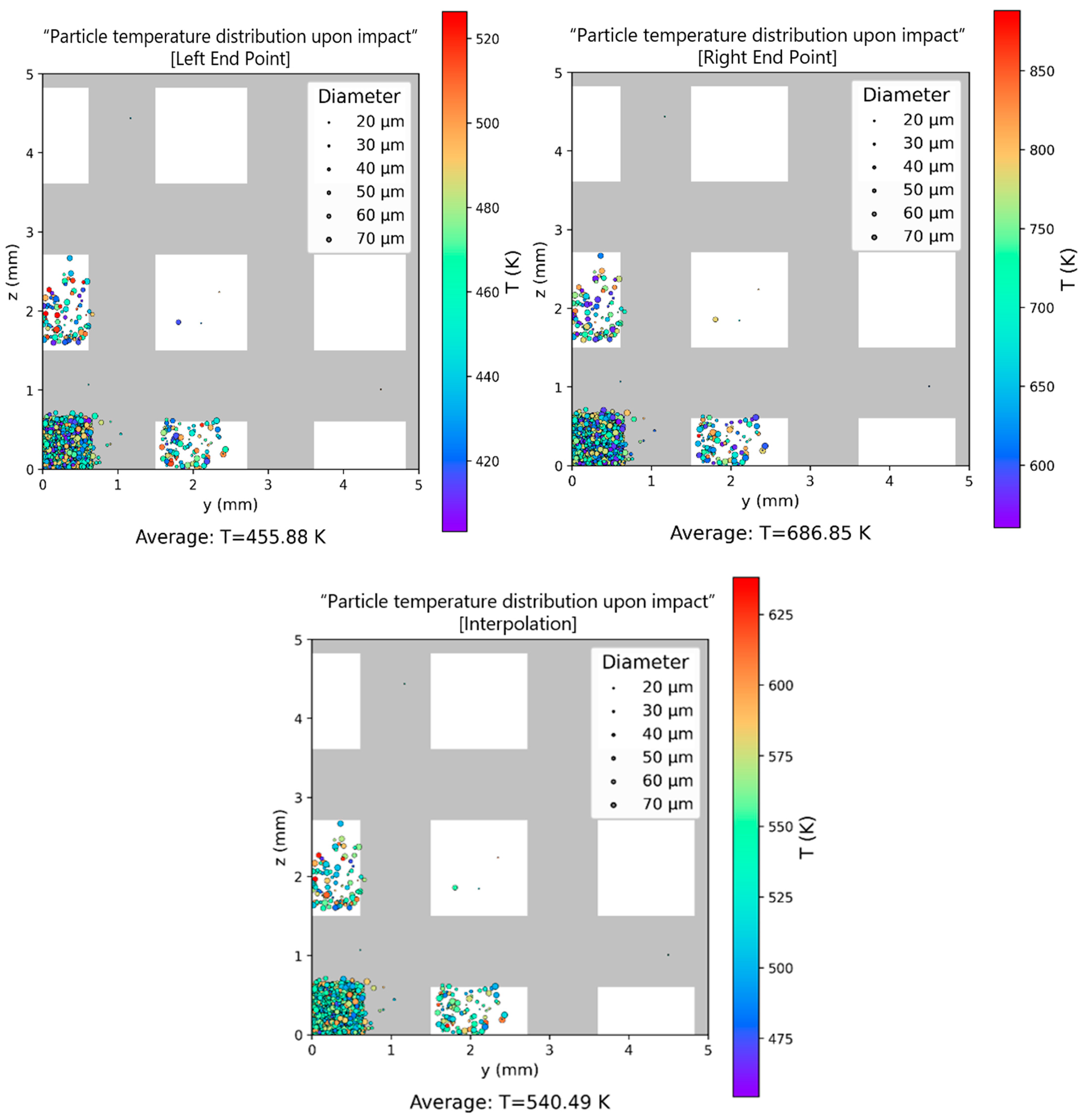

References
- Grujicic, M.; Zhao, C.L.; DeRosset, W.S.; Helfritch, D. Adiabatic Shear Instability Based Mechanism for Particles/Substrate Bonding in the Cold-Gas Dynamic-Spray Process. Mater. Des. 2004, 25, 681–688. [Google Scholar] [CrossRef]
- Yin, S.; Cavaliere, P.; Aldwell, B.; Jenkins, R.; Liao, H.; Li, W.; Lupoi, R. Cold Spray Additive Manufacturing and Repair: Fundamentals and Applications. Addit. Manuf. 2018, 21, 628–650. [Google Scholar] [CrossRef]
- Ashokkumar, M.; Thirumalaikumarasamy, D.; Sonar, T.; Deepak, S.; Vignesh, P.; Anbarasu, M. An Overview of Cold Spray Coating in Additive Manufacturing, Component Repairing and Other Engineering Applications. J. Mech. Behav. Mater. 2022, 31, 514–534. [Google Scholar] [CrossRef]
- Vo, P.; Martin, M. Layer-by-Layer Buildup Strategy for Cold Spray Additive Manufacturing. In Proceedings of the Proceedings of the International Thermal Spray Conference, Dusseldorf, Germany, 7–9 June 2017. [Google Scholar]
- Raoelison, R.N.; Verdy, C.; Liao, H. Cold Gas Dynamic Spray Additive Manufacturing Today: Deposit Possibilities, Technological Solutions and Viable Applications. Mater. Des. 2017, 133, 266–287. [Google Scholar] [CrossRef]
- Rahmati, S.; Jodoin, B. Physically Based Finite Element Modeling Method to Predict Metallic Bonding in Cold Spray. J. Therm. Spray Technol. 2020, 29, 611–629. [Google Scholar] [CrossRef]
- Smith, M.F. Introduction to Cold Spray. In High Pressure Cold Spray; Springer International Publishing: Cham, Switzerland, 2016; pp. 1–16. [Google Scholar]
- Papyrin, A.; Kosarev, V.; Klinkov, S.; Alkimov, A.; Fomin, V. Cold Spray Technology; Elsevier: Amsterdam, The Netherlands, 2007; ISBN 9780080451558. [Google Scholar]
- Wang, S.; Lu, A.; Zhong, C.-J. Hydrogen Production from Water Electrolysis: Role of Catalysts. Nano Converg. 2021, 8, 4. [Google Scholar] [CrossRef]
- Aghasibeig, M.; Dolatabadi, A.; Wuthrich, R.; Moreau, C. Three-Dimensional Electrode Coatings for Hydrogen Production Manufactured by Combined Atmospheric and Suspension Plasma Spray. Surf. Coat. Technol. 2016, 291, 348–355. [Google Scholar] [CrossRef]
- Aghasibeig, M.; Monajatizadeh, H.; Bocher, P.; Dolatabadi, A.; Wuthrich, R.; Moreau, C. Cold Spray as a Novel Method for Development of Nickel Electrode Coatings for Hydrogen Production. Int. J. Hydrogen Energy 2016, 41, 227–238. [Google Scholar] [CrossRef]
- Aghasibeig, M.; Moreau, C.; Dolatabadi, A.; Wuthrich, R. Engineered Three-Dimensional Electrodes by HVOF Process for Hydrogen Production. J. Therm. Spray Technol. 2016, 25, 1561–1569. [Google Scholar] [CrossRef]
- Nasire, N.; Jadidi, M.; Dolatabadi, A. Numerical Analysis of Cold Spray Process for Creation of Pin Fin Geometries. Appl. Sci. 2024, 14, 11147. [Google Scholar] [CrossRef]
- Bobzin, K.; Wietheger, W.; Heinemann, H.; Dokhanchi, S.R.; Rom, M.; Visconti, G. Prediction of Particle Properties in Plasma Spraying Based on Machine Learning. J. Therm. Spray Technol. 2021, 30, 1751–1764. [Google Scholar] [CrossRef]
- Canales, H.; Cano, I.G.; Dosta, S. Window of Deposition Description and Prediction of Deposition Efficiency via Machine Learning Techniques in Cold Spraying. Surf. Coat. Technol. 2020, 401, 126143. [Google Scholar] [CrossRef]
- Eberle, M.; Pinches, S.; Guzman, P.; King, H.; Zhou, H.; Ang, A. Application of Machine Learning for the Prediction of Particle Velocity Distribution and Deposition Efficiency for Cold Spraying Titanium Powder. Comput. Mater. Sci. 2024, 244, 113224. [Google Scholar] [CrossRef]
- Malamousi, K.; Delibasis, K.; Allcock, B.; Kamnis, S. Digital Transformation of Thermal and Cold Spray Processes with Emphasis on Machine Learning. Surf. Coat. Technol. 2022, 433, 128138. [Google Scholar] [CrossRef]
- Samareh, B.; Dolatabadi, A. A Three-Dimensional Analysis of the Cold Spray Process: The Effects of Substrate Location and Shape. J. Therm. Spray Technol. 2007, 16, 634–642. [Google Scholar] [CrossRef]
- Sheather, S.J.; Jones, M.C. A Reliable Data-Based Bandwidth Selection Method for Kernel Density Estimation. J. R. Stat. Soc. Ser. B Stat. Methodol. 1991, 53, 683–690. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational Inference: A Review for Statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Alonso, L.; Garrido-Maneiro, M.A.; Poza, P. A Study of the Parameters Affecting the Particle Velocity in Cold-Spray: Theoretical Results and Comparison with Experimental Data. Addit. Manuf. 2023, 67, 103479. [Google Scholar] [CrossRef]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine Learning for Fluid Mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation Learning: A Review and New Perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routledge: New York, NY, USA, 2017; ISBN 9781315139470. [Google Scholar]
- Box, G.E.P.; Cox, D.R. An Analysis of Transformations. J. R. Stat. Soc. Ser. B Stat. Methodol. 1964, 26, 211–243. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Schmidt, T.; Gärtner, F.; Assadi, H.; Kreye, H. Development of a Generalized Parameter Window for Cold Spray Deposition. Acta Mater. 2006, 54, 729–742. [Google Scholar] [CrossRef]
- Garmeh, S.; Jadidi, M.; Lamarre, J.-M.; Dolatabadi, A. Cold Spray Gas Flow Dynamics for On and Off-Axis Nozzle/Substrate Hole Geometries. J. Therm. Spray Technol. 2023, 32, 208–225. [Google Scholar] [CrossRef]
- Rahmati, S.; Zúñiga, A.; Jodoin, B.; Veiga, R.G.A. Deformation of Copper Particles upon Impact: A Molecular Dynamics Study of Cold Spray. Comput. Mater. Sci. 2020, 171, 109219. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, X.; Zhou, W.; Cheng, T.; Chen, L.; Guo, Z.; Han, B.; Lu, L. Digital Twins for Additive Manufacturing: A State-of-the-art Review. Appl. Sci. 2020, 10, 8350. [Google Scholar] [CrossRef]
- Bergs, T.; Gierlings, S.; Auerbach, T.; Klink, A.; Schraknepper, D.; Augspurger, T. The Concept of Digital Twin and Digital Shadow in Manufacturing. Procedia CIRP 2021, 101, 81–84. [Google Scholar] [CrossRef]
- Mukherjee, T.; DebRoy, T. A Digital Twin for Rapid Qualification of 3D Printed Metallic Components. Appl. Mater. Today 2019, 14, 59–65. [Google Scholar] [CrossRef]
- Tao, F.; Qi, Q.; Wang, L.; Nee, A.Y.C. Digital Twins and Cyber–Physical Systems toward Smart Manufacturing and Industry 4.0: Correlation and Comparison. Engineering 2019, 5, 653–661. [Google Scholar] [CrossRef]
- Petrovskiy, A.; Arifeen, M.; Petrovski, S. The Use of Machine Learning for Digital Shadowing in Thermal Spray Coating. In Proceedings of the Seventh International Scientific Conference “Intelligent Information Technologies for Industry” (IITI’23); Lecture Notes in Networks and Systems. Springer Science and Business Media Deutschland GmbH: Cham, Switzerland, 2023; Volume 776, pp. 343–352, ISBN 9783031437885. [Google Scholar]
- Ikeuchi, D.; Vargas-Uscategui, A.; Wu, X.; King, P.C. Neural Network Modelling of Track Profile in Cold Spray Additive Manufacturing. Materials 2019, 12, 2827. [Google Scholar] [CrossRef] [PubMed]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Ramani, S.; Thevenaz, P.; Unser, M. Regularized Interpolation For Noisy Data. In Proceedings of the 2007 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Arlington, VA, USA, 12–15 April 2007; pp. 612–615. [Google Scholar]
- Lehmann, T.M.; Gonner, C.; Spitzer, K. Survey: Interpolation Methods in Medical Image Processing. IEEE Trans. Med. Imaging 1999, 18, 1049–1075. [Google Scholar] [CrossRef] [PubMed]
- Achilleos, G. Errors within the Inverse Distance Weighted (IDW) Interpolation Procedure. Geocarto Int. 2008, 23, 429–449. [Google Scholar] [CrossRef]




















| Hyperparameter | Value |
|---|---|
| Max generations | 20 |
| Population size | 30 |
| Mutation rate | 0.1 |
| Feature Name | Global Var Ratio | Global Mean Ratio |
|---|---|---|
| y | 1.01994 | 1.00214 |
| z | 1.0287 | 1.01776 |
| Diameter | 0.98584 | 1.00052 |
| u | 0.98206 | 0.99928 |
| v | 1.13894 | 0.99796 |
| w | 1.149002 | 1.1052 |
| T | 0.98838 | 1.0006 |
| Feature | Math Transformation |
|---|---|
| Diameter | x |
| y-Coordinate | |
| z-Coordinate | sqrt(cos(x)) |
| Wire Diameter | |
| Opening Size | |
| Open Area Percent | |
| Pressure | |
| Temperature | |
| Substrate Standoff Distance | |
| Mask Standoff Distance |
| Hyperparameters | Values |
|---|---|
| Initial Population | 500 |
| End Population | 50 |
| Max Generation | 5 |
| Cross over Rate | 0.7 |
| Mutate Rate | 0.3 |
| Max Depth | 4 |
| Hyperparameters | Values |
|---|---|
| N estimators | 200 |
| Max depth | None (Unlimited) |
| Min samples split | 2 |
| Min samples leaf | 1 |
| Max features | None (Unlimited) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Jadidi, M.; Dolatabadi, A. A Machine Learning Approach for Predicting Particle Spatial, Velocity, and Temperature Distributions in Cold Spray Additive Manufacturing. Appl. Sci. 2025, 15, 6418. https://doi.org/10.3390/app15126418
Wang L, Jadidi M, Dolatabadi A. A Machine Learning Approach for Predicting Particle Spatial, Velocity, and Temperature Distributions in Cold Spray Additive Manufacturing. Applied Sciences. 2025; 15(12):6418. https://doi.org/10.3390/app15126418
Chicago/Turabian StyleWang, Lurui, Mehdi Jadidi, and Ali Dolatabadi. 2025. "A Machine Learning Approach for Predicting Particle Spatial, Velocity, and Temperature Distributions in Cold Spray Additive Manufacturing" Applied Sciences 15, no. 12: 6418. https://doi.org/10.3390/app15126418
APA StyleWang, L., Jadidi, M., & Dolatabadi, A. (2025). A Machine Learning Approach for Predicting Particle Spatial, Velocity, and Temperature Distributions in Cold Spray Additive Manufacturing. Applied Sciences, 15(12), 6418. https://doi.org/10.3390/app15126418







