Balancing Efficiency and Efficacy: A Contextual Bandit-Driven Framework for Multi-Tier Cyber Threat Detection

Abstract

In response to the rising volume and sophistication of cyber intrusions, data-oriented methods have emerged as critical defensive measures. While machine learning—including neural network-based solutions—has demonstrated strong capabilities in identifying malicious activities, several fundamental challenges remain. Chief among these difficulties are the substantial resource demands related to data preprocessing and inference procedures, limited scalability beyond centralized environments, and the necessity of deploying multiple specialized detection models to address diverse stages of the cyber kill chain. This paper introduces a contextual bandit-based reinforcement learning approach, designed to reduce operational expenditures and enhance detection cost-efficiency by introducing an adaptive decision boundary within a layered detection scheme. The proposed framework continually measures the confidence of each participating detection model, applying a reward-driven mechanism to balance cost and accuracy. Specifically, each potential action, representing a particular decision boundary, earns a reward reflecting its overall cost-to-effectiveness ratio, thereby prioritizing reduced overheads. We validated our method using two highly representative datasets that capture prevalent modern-day threats: phishing and malware. Our findings show that this contextual bandit-based strategy adeptly regulates the frequency of resource-intensive detection tasks, significantly lowering both inference and processing expenses. Remarkably, it achieves this reduction with minimal compromise to overall detection accuracy and efficacy.

1. Introduction

In today’s cyber arena, phishing has overtaken malware as the foremost hazard on the Web [1,2]. Since the onset of the conflict in Ukraine, adversaries have increased their use of credential-harvesting phishing strategies to compromise targeted email accounts [3,4]. Meanwhile, malicious code, whether in the form of binaries or scripts, remains a persistent and dangerous element. Traditionally, malware detection has relied on static and dynamic analyses of executables present in local storage. In response, cybercriminals have increasingly turned to fileless malware techniques [5,6], a shift that makes detection more resource-intensive. Advanced methods, such as sandbox-based dynamic analysis, have consequently become more prevalent and costly.

Furthermore, the rise of AI-generated phishing emails, polymorphic malware, and living-off-the-land attacks has complicated traditional detection practices [1,2,3]. These techniques are increasingly designed to evade signature-based detection, often leveraging legitimate system tools or continuously mutating their code structure [4,5]. Additionally, the rapid proliferation of Internet of Things (IoT) devices and edge computing has expanded the attack surface, creating new challenges for maintaining visibility and control across distributed environments [6,7].

Protecting against these evolving threats continues to be an active focus of research. Notably, machine learning approaches have started employing richer, more expansive, and more intricate datasets and models [7,8]. Unlike static detection methods such as denial lists, machine learning does not rely solely on current indicators of compromise (IoCs) to maintain effectiveness. Instead, it leverages its capacity to generalize from known samples to recognize never-before-seen threats. However, this adaptability comes at a price: machine learning-driven solutions are inherently computationally intensive. This complexity facilitates the uncovering of nuanced and highly sophisticated attack patterns.

Simultaneously, cyber defenders face multiple difficulties stemming from the complex and layered data ecosystems embedded within their infrastructure. Certain segments of this environment are considerably more diverse than others—take, for example, the disparity between processing email attachments versus handling custom application logs. Consequently, detection solutions tailored to specific attack surfaces must accommodate the inherent intricacy of those environments. Although prior research, e.g., [9,10], has explored the feasibility of compiling numerous attack strategies into robust datasets, only limited attention has been given to the practical costs associated with rolling out such elaborate detection frameworks. Moreover, as infrastructure sizes grow and additional devices are introduced, data movement, computational overheads, and storage demands escalate. All of these factors add time and expense before any model inference occurs, thus increasing latency and expenditure.

While prior works have proposed “multi-layered” detection architectures as a way to manage these obstacles, the logic guiding progression through each layer has not been finely tuned [9,11]. For instance, a recent study [12] sought to split detection from attribution steps to streamline processing and boost detection quality. Nevertheless, one might argue that the commonly employed default classifier threshold of 0.5, as observed in the literature (e.g., [13,14]), is insufficient. In scenarios where model retraining is infrequent, adapting a flexible decision threshold could help sustain overall detection effectiveness.

Against this backdrop, we introduce a contextual bandit-based reinforcement learning approach, a solution that brings flexible decision boundaries into multi-tier attack detection systems. Conceived as a framework for decision optimization, our approach implements a value estimation strategy that is intended to lower the operational costs linked to identifying malicious activities. To achieve this, it continuously fine-tunes its decision thresholds based on the statistical likelihoods generated by various detection models, as well as on historical context drawn from the surrounding environment.

This approach is designed to be broadly compatible, allowing for seamless integration into established data workflows and analytical engines that may incorporate additional, and often more resource-intensive, detection capabilities. More specifically, it consolidates outputs from different detection tools—whether these operate in batch mode or deliver results in real time—serving as a coordinator to streamline decision-making and cut down expenses. Consider, for instance, a cloud-based security solution comparable to Microsoft Defender. In such a layered detection setting, the cloud-driven detection functions would represent costlier tiers of the proposed architecture, supplementing on-device scanning and analysis. By doing so, our contextual bandit-based approach ensures that organizations can strategically allocate their budget, incurring higher costs only when more sophisticated and, thus, more expensive cloud-based detection services are genuinely needed.

This paper offers several key contributions. First, it introduces a contextual bandit-based reinforcement learning framework: a supervised machine learning-driven, cost-sensitive solution designed for detecting cyber threats. By employing a layered detection structure, our approach identifies and adjusts an optimal set of decision thresholds, dynamically adapting them to reflect varying environmental factors, such as shifts in model confidence, across different datasets.

Second, this approach leverages multi-armed bandit algorithms along with newly devised reward mechanisms that quantify the decision certainty of the chosen detection models. These mechanisms were purposefully crafted to implicitly maintain an effective balance between exploration and exploitation, all while minimizing expenses and enhancing detection accuracy. When benchmarked against existing cutting-edge solutions, these reward strategies delivered superior results in terms of both cost reduction and threat detection capabilities.

Third, our approach is tested using two representative datasets that capture today’s most common threat vectors: phishing and malware attacks. By examining how the framework’s decision boundaries respond to variations in parameters, reward configurations, and selection methods, we identify the optimal operational settings of our contextual bandit-based solution with respect to cost-efficiency and detection effectiveness.

The remainder of this paper is structured as follows: Section 2 reviews related work. Section 3 introduces our contextual bandit-based reinforcement learning approach. Section 4 presents the evaluation process and results. Section 5 discusses and interprets the findings. Finally, Section 6 concludes the paper and outlines directions for future research.

2. Related Work

This subsection provides an overview of pertinent research, examining efforts in threat detection methods and limitations observed within production system environments.

2.1. Threat Detection

Contemporary threat detection tasks have become increasingly intricate and resource-intensive. For example, Zhu et al. [15] introduced a specialized framework to uncover collusion-oriented attacks exploiting inter-application communication. Their method employs a three-phase procedure encompassing metadata extraction, static assessment, and a novel taint analysis. Although this strategy imposes higher operational costs, it delivers a five-percent improvement in detection accuracy over previously established benchmarks.

Similarly, Ullah et al. [16] addressed the rapidly evolving landscape of Android malware by constructing a detection mechanism that incorporates features such as API calls and permissions into a convolutional neural network (CNN). Their approach also integrates genetic evolutionary techniques with existing malware instances, ultimately surpassing classical classifiers (e.g., Support Vector Machine (SVM), Random Forest (RF)). Nawshin et al. [17] adopted a different tactic, leveraging API semantics and clustering algorithms to isolate malware similarities. Meanwhile, Belenguer et al. [18] suggested processing APIs and their parameters as sequential inputs, yielding superior performance compared to conventional sequence-based methodologies. The utility of byte sequence analysis has also been demonstrated, as Imamverdiyev et al. [19] successfully utilized byte-level signatures to identify malicious software. In addition, Almazroi et al. [20] proposed an ensemble classification approach utilizing API and system call information to address dynamic behaviors such as code loading at runtime, which are often overlooked by conventional static analysis methods.

Building on prior work, Bertrand van Ouytsel et al. [21] orchestrated a comprehensive set of malware packing detection experiments involving 119 distinct features across nine classification algorithms. Their analysis revealed that static attributes, such as API invocation patterns, exerted a particularly strong influence on detection outcomes while also maintaining a favorable cost-effectiveness ratio.

In a related study, Gu et al. [22] proposed a framework that introduced innovative features aimed at identifying malware that employs anonymization services for communication. Each executable was characterized by extracting behavioral cues derived from network-level indicators. Although the costs associated with computing these aggregate connection-based statistics were not explicitly quantified—despite Perez et al.’s [23] recognition that such feature extraction is often resource-intensive—the method nonetheless demonstrated strong detection capabilities.

Centralized threat detection architectures, long considered to be standard, have faced persistent challenges regarding data storage, processing overheads, and transmission demands [24]. To address these issues, the authors developed a lightweight client-side distributed APT detection mechanism. Similarly, Nobakht et al. [25] implemented a federated learning paradigm, allowing each client to train a localized model and periodically contribute updates to a centralized global model, thereby enhancing computational efficiency.

Meanwhile, Song et al. [26] acknowledged the considerable expense involved in deploying multiple classifiers. To mitigate this, they introduced a reinforcement learning strategy wherein a neural network, informed by the classifiers’ confidence distributions and associated computational costs, determines when to activate each model. However, this approach encounters limitations due to the absence of a predefined detection sequence. Consequently, the model risks selecting redundant detectors multiple times. Although the authors attempted to counteract such repetition through severe penalization, this tactic only deters the currently evaluated sequence, leaving an effectively unlimited number of possible sequences. In contrast, the methodology presented here addresses this complexity by employing a multi-layered architectural design. This structure eliminates the need for the model to learn an indefinite sequence of detectors under varying conditions, thereby simplifying the decision-making process.

Aljabri et al. [27] introduced a detection strategy composed of two classification layers, wherein each layer functions as an independent classifier. Their system employed a predetermined threshold mechanism that enabled the second classifier to operate only when the initial classifier’s probability estimate fell within a specified boundary. However, one drawback of this design was the use of a fixed decision threshold, limiting its flexibility and adaptiveness. A related initiative by Altwaijry et al. [28] also adopted a two-tier classification scheme. In their framework, the first layer could produce a “hybrid” classification category, which, when encountered, activated a secondary classification process aimed explicitly at addressing class imbalance issues. Similarly, van Khan et al. [29] proposed a hybridized detection model that integrates the outputs of multiple individual classifiers via a stacking function. Their extensive evaluation of various stacking approaches identified logistic regression as the most effective method.

Another critical research focus in threat detection involves optimizing feature sets to retain or enhance prediction capabilities while minimizing dimensionality. By selecting only the most informative features, it becomes possible to preserve detection accuracy without inflating computational costs. Studies such as those conducted by Truong et al. [30] and Sarker [31] have examined multiple feature-selection techniques, including the reinforcement learning-based strategies explored by Maniriho et al. [32].

Additionally, multi-armed bandit (MAB) algorithms have been employed in prior research as adaptive optimization tools under uncertainty. For instance, Heidari et al. [33] applied MABs to refine decision thresholds within an unsupervised anomaly detection setting. Through iterative trials, their method dynamically explored and rewarded the selection of an optimal hyperparameter, referred to as a contamination value, to converge upon a suitable threshold. The principal advantage of employing MABs in this context lies in their capacity to iteratively adjust to evolving conditions, thereby optimizing detection performance in fluid and changing threat landscapes.

Barik et al. [34] introduced an MAB framework to advance automated threat-hunting operations. In their approach, each investigative action retrieves certain attack-related artifacts, at an associated cost. This process relies on a curated repository of known attacks and their corresponding artifacts, serving as a defined search space. By enforcing a budgetary limit on the number of iterations, each investigative step can be optimized, effectively reducing the complexity and expense that analysts typically confront.

Karagiannis et al. [35] presented a defensive architecture designed to prevent adversarial entities from deducing the detection model’s underlying strategy. Their solution employs an MAB to identify an optimal subset of classifiers when predicting malicious network traffic flows, prioritizing those that maximize accuracy. Although the precise nature of the reward mechanism remains ambiguous, they leverage the Thompson sampling algorithm to gradually refine the probability distributions associated with each classifier. Complementing this perspective, Elhanashi et al. [36] argue that diversifying the set of classifiers used in a model can mitigate various challenges in machine learning, including class imbalance, concept drift, and the burdens posed by high-dimensional data.

Shen et al. [37] proposed an MAB-driven methodology to counter multistage Advanced Persistent Threat (APT) attacks, which infiltrate systems through complex chains of running processes. Their approach uses a provenance graph to represent inter-process relationships, thereby enabling selective oversight under limited resources. Notably, they adapt the Upper Confidence Bound (UCB) algorithm by substituting the standard exploration term, typically the mean reward value, with a newly defined measure of malevolence. This metric is derived from historical temporal patterns modeled by a Long Short-Term Memory (LSTM) network. An elevated malevolence score increases the likelihood of selecting and, in turn, closely monitoring a particular process path.

2.2. Production Environment Constraints

Contemporary studies endeavor to elucidate the complexity and operational hurdles associated with machine learning (ML) applications in production settings [23]. For example, Perez et al. [23] conducted a comprehensive investigation into Google’s ML pipelines. Their analysis revealed that approximately 22% of total computational expense is attributable to data ingestion, which is notably high when juxtaposed with the roughly 23% devoted to model training, commonly regarded as the most resource-intensive phase. Meanwhile, research carried out by Achouch et al. [38] highlights the difficulties of implementing ML models in environments constrained by scarce computational resources, thereby underscoring the importance of considering limited power supplies, memory, and data bandwidth when deploying deep learning models on networked infrastructures. Both Perez et al. [23] and Achouch et al. [38] call attention to the multifaceted obstacles encountered when integrating ML solutions into practical systems. Nonetheless, few previous investigations adequately address all of these interconnected issues.

Although enterprise-level network deployments often face various model integration constraints, similar limitations also permeate mobile platforms. The widespread use of ML techniques, particularly Deep Neural Networks (DNNs), on mobile devices has encouraged hardware-focused optimizations, including specialized GPU components and enhanced battery management. Deng et al. [39] examined 62,583 applications available in an app store, identifying a total of 960 on-device DNN models deployed across 568 apps. The presence of these models raises security concerns, as they present lucrative opportunities for adversaries interested in exfiltrating trained model parameters to reduce their own costs. To mitigate such vulnerabilities, Liu et al. [40] proposed a federated learning architecture aimed at expediting both model training and updates while safeguarding the confidentiality of the underlying data. While the present work emphasizes cost containment, a complementary strategy could involve offloading computationally demanding inference tasks to edge nodes, thereby alleviating both cost and security pressures on the user’s device.

Addressing concept drift is another critical matter that profoundly influences the effectiveness of deployed models over time [38]. Any cost-centric decision-making framework should remain cognizant of an overreliance on model outputs such as probability distributions when adjusting the operational parameters. Broadening the range of detection methods can help mitigate typical ML drawbacks by introducing algorithmic diversity and varied feature representations, thus minimizing the negative consequences of imbalanced datasets, concept drift, and high-dimensional feature spaces [39,41]. However, integrating multiple detection mechanisms typically escalates computational demands, since the number of models directly influences the training time and memory consumption. Nonetheless, employing a greater variety of models can enhance the overall detection accuracy [12,42]. For instance, Yogesh [43] demonstrated that implementing multiple binary classifiers was more effective than relying solely on a single multi-class classifier. These interrelated difficulties and potential benefits fundamentally inform the decision-making strategies detailed in Section 3.

Fu et al. [41] expressed concern regarding the inherently opaque nature of certain decision-making models, which constrains their interpretability for analysts. In response, they introduced a decision framework aimed at enhancing the transparency of models designed to detect intricate network patterns. Their conception of model complexity, largely influenced by the size of the underlying decision tree, aligns well with the notion that segmenting features into more manageable subsets may facilitate improved explainability.

In the domain of threat detection, considerations related to computational expense, encompassing factors such as energy consumption, execution time, and memory usage, often receive insufficient attention. Although highly effective detection systems can deliver strong performance, they may also impose substantial computational burdens as training times and memory demands escalate with an increasing number of classifiers.

Addressing this challenge, Catal et al. [44] investigated the processing costs of mobile phishing detection through an exclusive reliance on URL-based features. Their approach achieved an average detection time of approximately 621 milliseconds. Moreover, their measurements indicated that the real-time extraction of lexical and content features took 5.85 times longer to process legitimate pages relative to phishing ones. Nonetheless, their methodology did not account for page loading times, which can add additional seconds to the overall latency. Subsequently, Aljabri et al. [27] and Shahin et al. [11] found that DNS-based feature collection imposes higher computational overheads compared to static features, given its dependence on network-level data capture. In a similar vein, more expensive feature sets, such as those derived from Public Key Infrastructure (PKI) components [45,46], can also enrich phishing detection capabilities while increasing operational costs.

In an alternative line of inquiry, Rosenberg et al. [47] evaluated the throughput associated with different detection models. Their findings revealed that LSTM networks required more time to evaluate URLs—roughly 280 URLs per second—compared to the 942 URLs per second achieved by Random Forest (RF) models. Although the LSTM model demanded approximately eighty-times-longer training periods, it maintained considerably lower memory usage (581 KB) than the Random Forest approach (288 MB).

Furthermore, Mtukushe et al. [48] underscored the necessity of factoring in both feature processing and extraction times when scaling threat detection to accommodate billions of users. By employing transfer learning, they demonstrated the potential to curtail computational costs while simultaneously enhancing the model’s generalization capabilities.

3. A Contextual Bandit-Based Reinforcement Learning Approach

This section introduces a contextual bandit-based reinforcement learning approach, which builds upon concepts presented in studies such as that of Shahin et al. [11]. Our approach contributes a novel mechanism for real-time decision optimization in a multi-layered detection pipeline. Concretely, it formalizes the real-time positioning of a decision threshold aimed at (a) limiting excessive resource usage triggered by unnecessarily activating subsequent classification modules ($cj$), and (b) preserving robust classification effectiveness.

The framework consists of two key components: a detection engine and a decision module. The detection engine processes incoming sensor data through multiple classification models, producing probabilistic outputs. These outputs are then evaluated by the decision module, which employs a contextual bandit mechanism to determine optimal actions. By leveraging learned reward signals, the system adaptively fine-tunes decision boundaries to improve detection efficiency while minimizing operational costs.

The following sections provide a detailed breakdown of the core elements: the decision boundary adaptation, the reward mechanism, and the action selection strategy.

3.1. Model Formulation

This subsection models the pursuit of an optimal decision boundary for attack detection as a multi-armed bandit (MAB) optimization task. The overarching objectives of an attack detection system are twofold: to correctly recognize malicious behavior based on observable traits, and to remain practical and cost-conscious in real-world operational settings, for instance, by minimizing network delays. To achieve these goals, a collection of detection models must be thoroughly trained on high-quality datasets that capture recent and plausible attack scenarios.

Relying on a single detection model is often insufficient due to difficulties in generalizing across multifaceted attack patterns. Thus, we adopt an ensemble detection paradigm. By leveraging multiple specialized detection models simultaneously, ensemble methods have shown improved odds of achieving high performance [49,50,51,52]. However, this work does not address multi-classifying detectors intended to pinpoint specific attack categories. Instead, we define the detection mechanism as a sequence of binary classifiers ${\left(c_i\right)}_{i=2}^n$for $i$ ranging from 2 to $n$, where n denotes the total number of distinct classifiers designed for a given feature set and classification algorithm. In this context, the detection process partitions the attack space into various types using distinct subsets of the global feature set $F$. Let $Fi \subset F$ represent the subset of features applicable to the classifier $ci$, and let $yi,t$ denote $ci$’s predicted class at time $t$.

Feature extraction costs can differ substantially. Some feature sets require continuous real-time capture, such as those relying on network traffic data, while others, such as standardized log files, demand fewer resources. As a result, the solution can be conceptualized by grouping features into subsets ordered according to their computational expense. At each time step t, the system receives an observation $Xt$ and utilizes one or more classifiers to infer $Xt$’s class. This inference produces a probability vector $Ot$ = ($P1, P2, \dots , Pn$), where $Pi$ is $ci$’s probability estimate at time $t$.

To conserve computational effort, higher-level (and more resource-intensive) classifiers $ci+1, \dots , cn$ are only triggered if $Pi$ resides within an uncertainty region defined by the lower and upper thresholds $Li$ and $Ui$, respectively. This conditional activation process, referred to as “triaging”, helps avoid unnecessary evaluation. Specifically, if $Pi$ falls between $Li$ and $Ui (\mathrm{i}.\mathrm{e}., Li<Pi<Ui)$, $Xt$ is escalated to the next classifier $ci+1$ for further scrutiny; otherwise, $ci$’s decision stands as the final output. Although reducing the number of subsequent classifications yields cost savings, it may also diminish the overall detection effectiveness, given that some nuanced attacks might require deeper analysis.

To enhance flexibility in deciding when to trigger the next classifier, the traditional single, symmetric decision boundary is replaced with a dual-threshold mechanism. Because each classifier’s uncertainty distribution is modeled independently with respect to $Pi$, the class-specific probability distributions of $ci$ guide the selection of boundary values $Li$ and $Ui$ for each $i$, where $i<n-1$. This approach enables the dynamic adjustment of the decision environment and aims to balance computational cost against detection accuracy.

3.2. Multi-Armed Bandits: Balancing Exploration and Exploitation

Multi-armed bandits (MABs) represent a foundational paradigm in reinforcement learning that equips decision-making algorithms to handle uncertainty [53,54]. The overarching challenge within MAB scenarios is to negotiate the trade-off between choosing known options that yield consistently good results (“exploitation”) and experimenting with less familiar alternatives in pursuit of even better outcomes (“exploration”).

MAB problems typically involve three main elements: (1) a selection mechanism that identifies which action to take next, (2) a reward function that quantifies the outcome, and (3) a set of available options (the “arms” of the bandit).

To illustrate how MABs can be applied, imagine a router tasked with directing network traffic along multiple possible paths. Because Internet latency can vary over time, sometimes periodically or unpredictably, selecting a route that provides the best performance at a given moment becomes non-trivial. With an MAB, the router repeatedly picks one route (an action) from its collection of options. In return, it observes a reward reflecting the overall latency. The algorithm must intelligently alternate between relying on routes known to be fast and attempting less frequently used routes in case they have recently become better. By doing so, it strives to find the top-performing route under the current conditions, even if that condition is characterized by generally high latency.

This work explores three selection strategies commonly employed in MAB contexts, as outlined below:

• Boltzmann Exploration (Softmax): Boltzmann exploration, or Softmax action selection [55], relies on probabilistic decision-making. Each available action is associated with an expected return, and these values are transformed into a probability distribution:

$$P(a_i)={\displaystyle \frac{e^{V\left(a_i\right)/\tau }}{{\sum }_{j=1}^{n}1e^{v\left(a_j\right)/\tau }}}$$

where $P\left(a_i\right)$ is the likelihood of choosing action $a_i$, and $\tau$ (the temperature parameter) determines how evenly spread these probabilities are. A lower $\tau$ makes the algorithm more strongly favor the highest-valued actions, while a higher $\tau$ encourages the algorithm to sample more evenly, effectively promoting exploration. An action is then selected by sampling according to these probabilities, ensuring that even actions with lower values can still occasionally be tested. To mitigate overfitting during this process, the Softmax strategy is executed over multiple randomized iterations and leverages exploration dynamics to avoid convergence on a narrow subset of boundaries too early in the learning cycle.

• Upper Confidence Bound (UCB): UCB is a deterministic selection approach that balances the known performance of actions with the uncertainty associated with them. At each decision point, the algorithm calculates an uncertainty factor for each action based on how frequently it has been chosen relative to the total number of trials. Specifically, if $t$ is the current trial count and $nt\left(a\right)$ is how many times an action a has been chosen, the uncertainty term is given by

  $$r_t(a)=\sqrt{{\displaystyle \frac{2\log t}{n_t\left(a\right)}}}$$

• Combining the action’s average reward with this uncertainty measure yields a final score. Actions that have been selected less often carry higher uncertainty values, making them more appealing to try. Over time, all actions are tested, and the strategy hones in on the subset of actions that yield the best results. Importantly, UCB’s built-in confidence bounds function as a natural regularizer, helping to prevent overfitting by encouraging the exploration of less frequently selected boundaries
• Thompson Sampling: Thompson sampling leverages Bayesian updating to determine which action to select. The algorithm models the reward distribution of each action (often using a beta distribution in the case of binary rewards) and, at each decision step, samples from these distributions to choose the action that seems most promising. The parameters α and $\beta$ represent the cumulative counts of positive and negative outcomes, respectively. After selecting an action based on the sampled expected values, the parameters are updated to reflect the newly observed reward. Over time, this Bayesian approach naturally balances exploration and exploitation by favoring actions with better underlying reward distributions while still allowing for the possibility that less favored actions might improve. Additionally, the posterior sampling mechanism in Thompson sampling provides intrinsic variance control, limiting overfitting by factoring uncertainty into each decision update

3.3. Action Selection

As discussed earlier, the classification threshold is defined by two boundaries: a lower boundary $Li$ and an upper boundary $Ui$. Since each category (benign or malicious) is associated with distinct levels of prediction confidence, each class naturally follows its own probability distribution. We initially set the central decision boundary at $Z=0.5$, corresponding to the midpoint between the high-confidence regions of both classes. Here, prediction scores closer to zero indicate strong negative (benign) certainty, whereas those nearer to one signify robust positive (malicious) certainty.

In a continuously learning system, each newly processed data instance $\mathrm{X}\mathrm{t}$ may necessitate an adjustment of these boundaries based on prediction accuracy. Let $yt\in \left\{\mathrm{0,1}\right\}$ denote the true label of the observation $Xt$ at time $t$, where $yt=0y$ denotes a benign instance and $yt=1y$ a malicious one. Given a particular classifier $ci$ producing a prediction $yi,ty\_\{i,t\}$ at time t, we define an action $a$ that responds accordingly. If $yt=0$, the action affects the lower boundary Li; if $yt=1y$, it influences the upper boundary $Ui$.

In this work, three well-established MAB algorithms are evaluated for selecting the appropriate action: Softmax, Upper Confidence Bound (UCB), and Thompson sampling, as introduced in Section 2.1. Furthermore, we propose an extended variant of UCB, denoted as UCBe, which employs the update rule in Equation (1) instead of a running average for its value estimates.

Each algorithm leverages historical data collected through interactions with the environment to determine which action to choose. We conducted a preliminary parameter-tuning experiment on a small scale (50 iterations) before performing a more comprehensive assessment over 10,000 iterations. These evaluations were carried out under multiple proposed reward policies. Since all three algorithms depend on a defined reward policy, we assign both a reward value and a corresponding value estimate to each action.

Let $Rt\left(a\right)$ denote the reward obtained by selecting action $a$ at time t, as determined by the reward function discussed in Section 4.3. This function measures the impact of each action on the decision environment, guiding the classification boundaries toward an optimal setting that enhances cost-effectiveness. The action selection strategy utilizes expected values derived from historical rewards to establish the decision boundary.

To represent the anticipated outcome of choosing a particular action $a$ for a given classifier $ci$, we define the value estimate $Va$. Initially, $Va$ is updated using performance feedback from the boundary’s behavior at time $t$. As new observations accumulate, these value estimates adjust to better reflect environmental responses, thereby improving future action selections. More accurate estimates lead to the more effective triage of incoming observations.

To address this, we compute the expected value for each action using the following recursive update:

$$V_{a,c_i,t+1}=V_{a,c_i,t}+\gamma \left[R_t\left(a,c_i\right)-V_{a,c_i,t}\right]$$

(1)

where γ$\in \left(\mathrm{0,1}\right]$ is a decay factor determining the relative emphasis placed on recent rewards. A higher γ value grants greater importance to immediate feedback, while a lower value places more emphasis on historical averages. Empirical methods are employed to select this parameter.

We measure the performance of the selection algorithms using two metrics: cumulative regret, and the total number of observations that undergo subsequent inference (triaged observations). Cumulative regret quantifies the cost of not always choosing the best possible action, while the frequency of triaged observations reveals how often boundaries are shifted away from regions where correct classifications are already stable. By minimizing boundary adjustments in high-confidence zones where predictions are frequently accurate, we prevent unnecessary resource expenditure on repeated inference steps.

3.4. Reward Policy

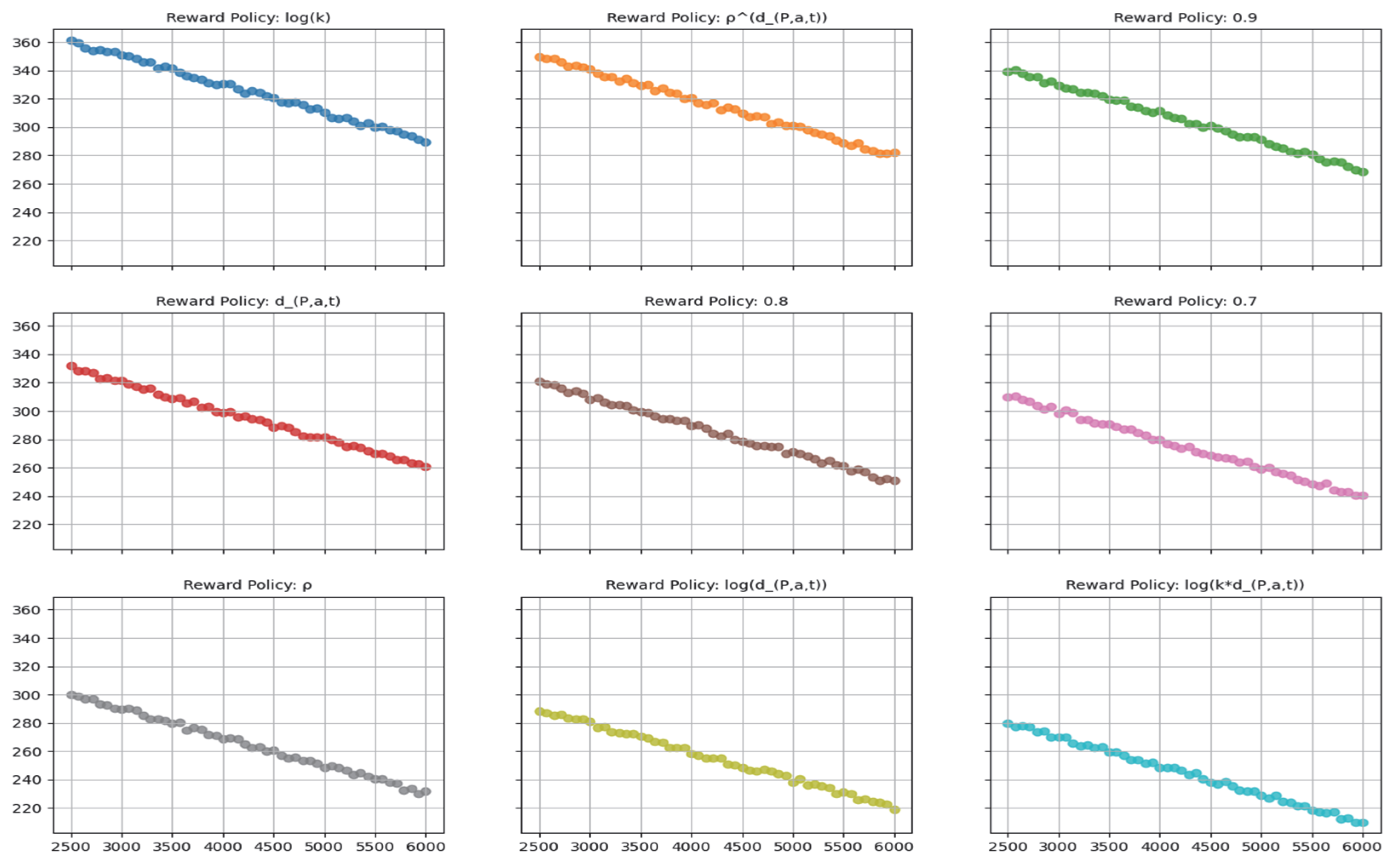
We examined our contextual bandit-based reinforcement learning approach across several reward configuration strategies to determine which approach would yield the highest performance under the previously outlined decision environment and selection functions. In reinforcement learning contexts, a reward provides either favorable or unfavorable environmental feedback, thereby guiding the selection mechanism toward optimal actions. In our approach, assigning a reward at each time step t involves two distinct steps: (a) selecting the reward’s magnitude, $R$, and (b) determining its polarity (positive or negative). We evaluated four categories of reward policies: ($\mathrm{i}$) static cost, ($\mathrm{i}\mathrm{i}$) imbalanced cost, ($\mathrm{i}\mathrm{i}\mathrm{i}$) contextual index, and ($\mathrm{i}\mathrm{v}$) distance.

Static Cost Reward Function: Under the static cost framework, the reward is consistently assigned as either 1 or −1. While this simplicity is appealing, it does not distinguish between scenarios that narrowly miss a positive outcome and those that are decidedly negative. Thus, all unfavorable results receive an equivalent penalty, regardless of proximity to a more favorable outcome. Implementing a static cost scheme requires the careful calibration of the cost value. In this study, we explored several fixed reward signals, i.e., 0.9, 0.8, 0.7, and 0.6, to determine their effectiveness.

Contextual Index: As indicated earlier, relying solely on binary rewards (1 or −1) treats every instance uniformly, which may not be ideal. To address this issue, we introduce a contextual index mechanism. Let $ak$ represent the $k-th$ action from the set of candidate actions $A$, with $1 \le k \le \nu$. We arrange these actions in ascending order based on their values, making ak’s position within the set a contextual factor. Actions with $k$ closer to $\nu$ correspond to higher-confidence predictions. The primary objective is to establish a boundary selection strategy that minimizes reliance on actions near regions of high-confidence predictions, since additional inference might be unnecessarily costly. To achieve this, we employ a logarithmic transformation, defining $Rt(ak, ci)=log\left(k\right)$. This approach introduces reward scaling based on relative boundary certainty, reducing the risk of overfitting by avoiding overly aggressive reward gradients in highly confident zones.

Imbalanced Cost: Training classifiers for cyber-attack detection often involves datasets with inherent class imbalances, generally with fewer malicious instances than benign ones. This imbalance can skew the reward function, making it disproportionately responsive to the majority class. To mitigate this effect, we draw on a reward function component proposed by Al-Saegh et al. [56], which incorporates class distribution ratios. Specifically, we define an imbalance ratio $\rho =\left|DP\right| / \left|DN\right|$, where $DP$ represents the minority class subset and $DN$ the majority class subset. Adjusting rewards according to $\rho$ can improve the detection performance by ensuring that both true positives and true negatives are appropriately weighted. By integrating class imbalance into reward estimation, the model avoids skewed updates that could lead to overfitting on the dominant class.

Distance: An alternative contextual strategy involves tying the reward to the distance between the predicted probability and the selected action. For each classifier $ci$ and chosen action $a$ at time $t$, we define $Rt(a, ci)=dP,a,t$, where $dP,a,t=|Pi-a|$ denotes the magnitude of the discrepancy between the prediction $Pi$ and action $a$. This difference can be viewed as an error metric, restricted to the range 0.5 ≤ $dP,a,t$ ≤ 1, reflecting that the initial decision threshold $Z=0.5$, and that ideal predictions approach 1 for benign and 0 for malicious classes. Since this method focuses solely on $Pi$ and $a$, it constrains the reward assessment to the local context rather than the broader operating environment.

Determining the Reward Sign: Determining the sign of the reward involves evaluating two conditions: (1) whether the classifier’s predicted label aligns with the true label, and (2) whether the chosen decision boundary adjustment has influenced the final outcome. Equation (2) illustrates these conditions. If the classifier’s prediction is accurate and the decision boundary has prevented unnecessary escalation, the reward is positive; otherwise, it is negative.

$$R_t(a,c_i)=\{\begin{array}{c}r,\left({\mathrm{P}}_i\in \left({\mathrm{L}}_{\mathrm{i}},{\mathrm{U}}_{\mathrm{i}}\right) and y_{i,t}\ne y_t\right) or (P_i\notin \left({\mathrm{L}}_{\mathrm{i}},{\mathrm{U}}_{\mathrm{i}}\right) and y_{i,t}=y_t)\\ -r,\left({\mathrm{P}}_i\in \left({\mathrm{L}}_{\mathrm{i}},{\mathrm{U}}_{\mathrm{i}}\right) and y_{i,t}=y_t\right) or (P_i\notin \left({\mathrm{L}}_{\mathrm{i}},{\mathrm{U}}_{\mathrm{i}}\right) and{ y}_{i,t}\ne y_t)\end{array}$$

(2)

3.5. Operational Workflow of the Contextual Bandit Framework

This provides an overview of the core operational flow for our contextual bandit-based reinforcement learning approach. The principal steps are as follows:

• Each classifier ci configures its upper and lower boundaries (L_i and U_i) and initializes a pool of possible actions as increments of $\mu$.
• For each incoming data point, ci generates a prediction $Pi$.
• The selection function, guided by $Pi$, determines which decision boundary to apply from the available action set.
• Based on the selection function’s parameters, the algorithm may either leverage known successful actions or explore alternative actions.
• The chosen boundary is then applied. If the boundary suggests that further refinement is needed, the data instance is passed on the subsequent classifier $ci+1$; otherwise, the prediction stands.
• The executed action is assessed against a specified set of criteria, producing a computed reward. This feedback updates the action value estimates, informing future decision-making processes.
• This classification-and-evaluation cycle continues until $i<n-1$, ensuring that each instance progresses through the chain of classifiers as necessary.

4. Evaluation

To assess the effectiveness of our contextual bandit-based reinforcement learning approach, we begin by establishing several baseline detection models employing standard supervised machine learning techniques. We then investigate various parameters related to cost-efficiency and attack detection accuracy, subsequently evaluating this new framework with respect to different exploratory algorithms and reward allocation strategies.

4.1. Datasets

The capabilities of our contextual bandit-based reinforcement learning approach are demonstrated using the CSE-CIC-IDS2018 dataset [36,57,58], a well-regarded intrusion detection benchmark that captures a broad spectrum of modern network attack scenarios (e.g., DDoS, infiltration, and Web-based threats). Chosen for its authenticity and relevance, CSE-CIC-IDS2018 conditions observations in contemporary cyber environments, offering a wealth of features that can be selectively partitioned for cost-sensitive analyses.

Since the classifiers in our contextual bandit-based reinforcement learning approach are arranged in a cost-sensitive hierarchy, we divided the CSE-CIC-IDS2018 dataset into two distinct feature subsets, enabling the training of two classifiers per layer. This division ensures that differences in data acquisition and processing overheads are explicitly represented. For layer 1, we employed low-cost, flow-oriented features—such as basic packet statistics and connection metadata—while layer 2 utilized resource-intensive attributes (e.g., deeper packet inspection metrics or additional protocol-specific details). This structured, tiered approach to feature selection underscores our approach’s emphasis on balancing operational efficiency with robust detection performance.

4.2. Experimental Configuration

Computational Environment: To enable concurrent experiments on the two distinct datasets, the infrastructure was arranged into two virtual machines running Ubuntu Desktop 22.0. Each virtual machine drew on an evenly distributed subset of the hardware resources, operating atop an ESXi hypervisor (Version 8). Neural network model training tasks were subsequently performed on a separate Apple M2 2022 system equipped with 16 GB of memory. The models leveraged TensorFlow 2.0 for the neural network approach and Scikit-learn for the Random Forest method.

Modeling Approaches: Two core detection methodologies were employed: a Random Forest classifier, representing a decision-tree-based ensemble technique, and a feedforward neural network, embodying a more flexible representation-learning paradigm. Random Forests, consisting of 150 integrated decision trees, are known for their accuracy [59,60], yet they may fail to generalize effectively when dealing with highly intricate data distributions. To address this limitation, a sequential feedforward neural network architecture was implemented, designed to produce a more generalizable solution. This neural network began with an input layer sized according to the dimensionality of each dataset. A subsequent dense layer with 256 neurons employed a ReLU activation function, followed by a dropout layer with a 0.3 probability to mitigate overfitting risks. Another dense layer containing 128 ReLU-activated neurons was then introduced. The final output layer utilized a sigmoid activation function, enabling probability-based classification outcomes. All neural network hyperparameters, including a batch size of 50 and a training duration capped at 120 epochs, were selected through a comprehensive grid search procedure (see

Table 1. Experimental parameters and datasets.

Neural Network	Parameters
Optimizer	Adam
Batch size	50
Epochs	120
Neurons	256, 128
Random Forest	Parameters
n_estimators	150
Datasets	Description

), and an early stopping callback was integrated to prevent unnecessary training epochs. Although these parameter settings may vary depending on factors such as data volume, the chosen configuration proved effective in the context of the present experiments. To explore synergies between different detection models, we also implemented a stacked architecture in which outputs from one model (e.g., Random Forest) are used as input features for the subsequent neural network. This design aims to capitalize on the strengths of both models—leveraging the robustness of Random Forests for structured decision boundaries and the expressive capacity of neural networks to model nonlinear interactions. The performance of this synergistic configuration was benchmarked against standalone models across both datasets

To evaluate the proposed methodology relative to established detection strategies, we employed several baseline models. Specifically, we considered a comprehensive single-model approach trained with the full set of available features to maximize detection capabilities, along with a two-tier, stacked design in which distinct classifiers were trained and integrated, with each utilizing a different subset of the feature space (refer to Section 4.1). For each dataset, we benchmarked our technique against these baselines, applying both neural networks and Random Forests as learning algorithms.

Detection Metrics: We assessed detection quality through standard classification metrics, as follows:

• Accuracy: This metric quantifies a model’s overall effectiveness in distinguishing malicious inputs from benign ones. Formally,

$$ACC={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

where $TP$ represents true positives (malicious instances correctly detected), $FP$ indicates false positives (benign cases incorrectly labeled as malicious), $TN$ denotes true negatives (benign instances correctly classified), and $FN$ corresponds to false negatives (malicious cases misclassified as benign).

• Precision: Precision gauges the proportion of correct positive predictions among all instances classified as positive. Formally,

$${\displaystyle \frac{TP}{TP+FP}}$$

• Recall: Recall measures the fraction of actual malicious instances that are correctly identified. Higher recall values indicate more effective recognition of malicious inputs:

$${\displaystyle \frac{TP}{TP+FN}}$$

• F1-Score: The F1-score synthesizes both precision and recall into a single statistic, offering a balanced view of performance:

$${\displaystyle \frac{2\times Precision\times Recall}{Precision+Recall}}$$

MAB Metrics: To determine the efficacy of optimizing the decision boundary within our attack detection framework, we introduce additional evaluation criteria:

• Total Triaged: This measures how frequently an observation is subjected to further inference based on its initial classification and the decision boundary at a given time step t. Since our goal is to reduce computational costs, counting how often the more resource-intensive model is utilized provides an indication of cost savings.
• Remaining False Predictions: Another critical performance indicator involves quantifying residual classification errors (i.e., false positives and false negatives) after applying the decision boundary. While a lower number of false predictions generally signifies improved performance, this metric is closely tied to the total number of triaged instances. A clear trade-off emerges: reducing the number of triaged observations may come at the cost of increased classification errors, and vice versa. 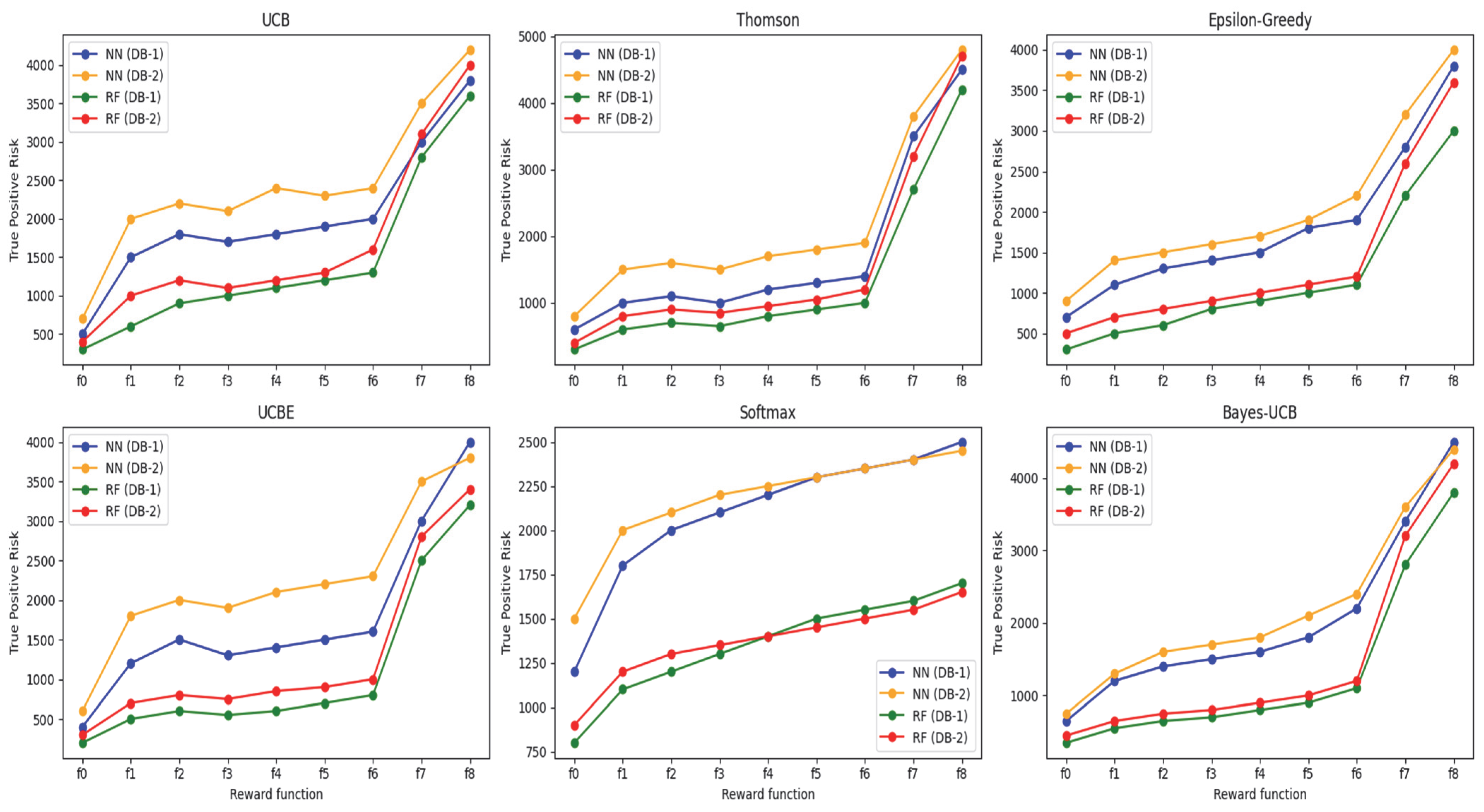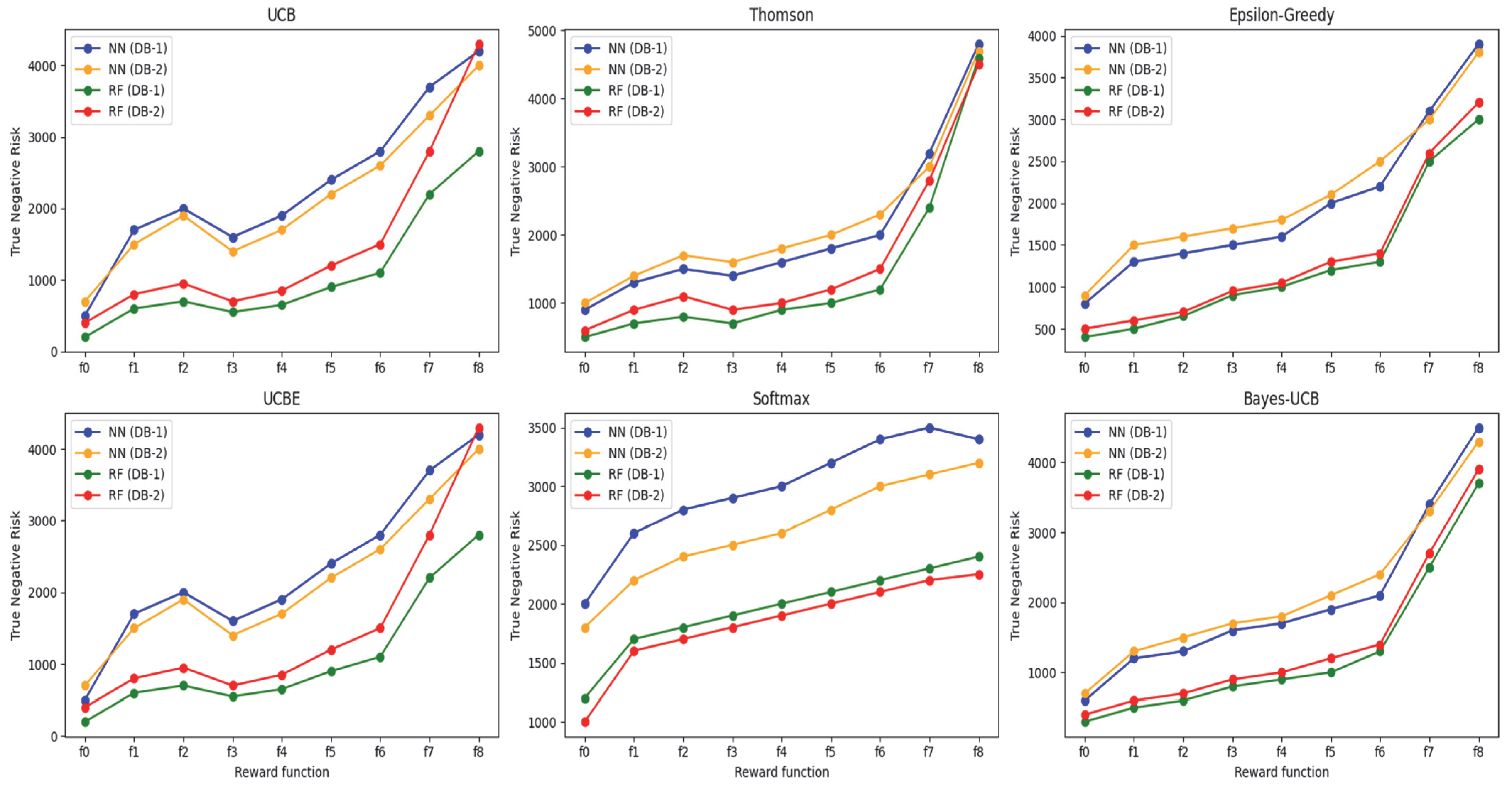As illustrated in Figure 1 and Figure 2, different reward policies exhibit varying degrees of correlation between the numbers of triaged observations and false predictions. In this study, our primary objective is to minimize the number of triaged inputs. However, the remaining false predictions provide valuable insight into optimizing the system parameters for a balanced decision-making process.

4.3. Parameter Selection

As the decision boundary may assume any real value between 0 and 1, it is pragmatic to restrict the available actions to incremental steps $\left(\mu \right)$ of 0.03. Accordingly, the range 0 < a < 0.5 applies for $Li$, and 0.5 < $a$ < 1 applies for $Ui$, ensuring a suitable number of possible actions without overcomplicating the search space.

To assess our contextual bandit-based reinforcement learning approach’s proficiency in minimizing detection costs, we employed nine distinct reward policies. Each policy operates on a unique reward scale, thus complicating direct comparisons using metrics such as mean reward and cumulative regret. We used a grid search strategy to tune key parameters across these policies. Specifically, for each policy, we ran a systematic exploration of parameter combinations, using 50 iterations per configuration.

Initially, we explored various parameter settings over 50 iterations for each policy. This phase focused on two key metrics: (a) the total count of triaged observations, and (b) the residual number of erroneous predictions. Each configuration was evaluated using a hold-out validation subset (20% of the dataset), and tuning was performed independently for each dataset–model pair.

Our approach further examines the hypothesis that combining reward policies can exploit their individual strengths, thereby enhancing overall performance. For instance, we first integrated the contextual index with distance, aiming to interpret the relevance of each action relative to the cumulative probability distribution of model predictions. We also investigated the combination of imbalanced cost with distance, as reflected in policies such as ${\rho }^{d_{P,a,t}}, d_{P,a,t}^{\rho }$, and $\log \left({\rho }^{d_{P,a,t}}\right)$.

The parameter tuning involved varying both the decay constant $\left(\gamma \right)$ and the exploration term $\left(\tau \right)$. The Softmax and UCB strategies were implemented following the update rules outlined in Section 3. For τ, we tested values {0.1, 0.2, 0.4, 0.8, 1.0} in the Softmax function to explore trade-offs between exploration and exploitation. For the UCB family, γ was tuned across {0.1, 0.2, 0.4, 0.8, 1.0}, determining the aggressiveness of exploration. The optimal configuration can be chosen based on the following priorities: (a) higher detection rates, (b) greater cost savings, or (c) a balanced trade-off. This study emphasizes configurations that favor cost-efficiency. Parameter selection was finalized based on the configuration that achieved the best F1-score under the lowest triage cost.

Although the UCB-based variants exhibited the most comprehensive cost-effectiveness, we found that two of our proposed reward policies offer notable versatility when utilizing Softmax. To support robust selection, correlation heatmaps between false predictions and triage rates were analyzed per configuration. Correlation analyses indicated a strong relationship between residual false predictions and triage rates across various parameters and reward policies. In particular, for the parameters $log\left(k\right)$ and $log(d_{P,a,t}\times k)$, it is possible to select points along the correlation curve that cater to specific contextual requirements, rather than focusing exclusively on maximizing cost savings.

4.4. Cost-Saving Results

This section examines the extent of cost reductions achieved by each reward policy. Specifically, we concentrate on the five most effective reward policies, applying them to the two datasets and the two model configurations introduced in Section 4.2. A concise summary of these findings is provided in

Table 2. Triage rates across different reward policies and selection strategies for neural network and Random Forest models on subsets A and B.

Dataset (Subset)	Detection Model	Reward Description	Selection Strategy	Triage Rate (Requests)
Subset A	Neural Network	$log\left(k\right)$	UCB	1350.62
		$log\left(k\right)$	Thompson	2100.34
		$log\left(k\right)$	UCBE	2156.18
		${\rho }^{d_{P,a,t}}$	Thompson	3000.12
		0.9	Thompson	3200.78
	Random Forest	$log\left(k\right)$	UCBE	700.42
		$log\left(k\right)$	UCB	800.55
		$log\left(k\right)$	Thompson	1250.34
		${\rho }^{d_{P,a,t}}$	Thompson	1400.67
		0.9	Thompson	1550.12
Subset B	Neural Network	$log\left(k\right)$	UCB	3700.18
		$log\left(k\right)$	UCBE	4000.25
		$log\left(k\right)$	Thompson	4500.11
		$d_{P,a,t}^{\rho }$	Thompson	5000.32
		${\rho }^{d_{P,a,t}}$	Thompson	5500.45
	Random Forest	$log\left(k\right)$	UCBE	1900.62
		$log\left(k\right)$	UCB	2000.1
		$log\left(k\right)$	Thompson	2800.4
		$d_{P,a,t}^{\rho }$	Thompson	3200.18
		${\rho }^{d_{P,a,t}}$	Thompson	3500.22

Reward description note: The “Reward Description” column specifies the reward policies used in the experiments, such as “$log\left(k\right)$ or “$d_{P,a,t}^{\rho }$”, which define the criteria for reward allocation in the reinforcement learning framework.

.

Overall, the highest-performing reward policies yield notably reduced triage frequencies. In particular, the $log\left(k\right)$ policy stands out, as it consistently records the lowest triage rate across both datasets, surpassing policies that incorporate alternative exploration mechanisms. This indicates that the $log\left(k\right)$ policy fosters stable, cost-effective operation regardless of the underlying dataset or detection model.

Within this study, “cost” corresponds to the proportion of instances processed by the more resource-intensive layer. Hence, cost savings can be quantified as follows:

$${\displaystyle \frac{totalobservations-totaltriaged}{totalobservations}}$$

When applied to subset A of the CSE-CIC-IDS2018 dataset using the Random Forest model, our contextual bandit-based reinforcement learning approach incurs only 5.69% of the full operational cost (734.78 out of 12,904), thus achieving a 94.31% reduction. In comparison, the neural network-based approach involves 13.16% of the full cost (1697.62 out of 12,904), translating to an 86.84% cost-saving advantage over a scenario utilizing all detection resources. A similar trend emerges with subset B of the CSE-CIC-IDS2018 dataset, where the neural network configuration expends 23.91% (3834.04 out of 16,032) for a 76.08% saving, while the Random Forest variant uses 11.99% (1922.68 out of 16,032), yielding an 88% reduction.

Among the four evaluated selection functions, those employing UCB, UCBe, and Thompson sampling achieve greater cost savings than the Softmax-based strategies. The UCB variants, in particular, aggressively reduce the volume of triaged items, although the relative effectiveness of UCB versus UCBe varies depending on the dataset. Softmax, on the other hand, offers a prudent compromise, balancing cost reduction and detection quality. This balance makes Softmax an appealing candidate for scenarios that demand heightened detection accuracy, as evidenced by the observed relationship between triage volume and classification performance across different parameter settings, as seen in Figure 2 and Figure 3.

4.5. Classification Risk

To assess the risks associated with triage, we consider how often items require a subsequent classification step. The underlying concept is that while the initial classification (layer 1) provides a preliminary decision, the subsequent classification stage (layer 2) can potentially alter that decision. This means that an observation initially deemed to be benign (a true negative) might later be identified as malicious (a false positive), thus altering the final classification outcome.

Figure 3 and Figure 4 present comparative results for various reward policies and selection strategies across both datasets and model types. Notably, the $log\left(k\right)$ policy consistently demonstrates the lowest classification risk, irrespective of dataset, model type, or selection approach. Minimizing disturbances to the correct prediction space is generally desirable. Nonetheless, the degree of overlap between true and false prediction distributions can influence outcomes, as some datasets produce probability distributions that make it more challenging to avoid unnecessary reclassifications.

To further quantify the impact of triage decisions on prediction quality, we examined the false positive rate (FPR)—the proportion of benign instances incorrectly flagged as malicious. Our findings indicate that contextual bandit configurations with aggressive triage reductions (e.g., high-confidence thresholds) may slightly increase the FPR. However, policies such as $log\left(k\right)$, which restrict interference with correct predictions, effectively shift the focus toward the primary model’s accuracy. Recognizing that probability distributions often overlap, practitioners seeking to optimize detection performance with modest cost reductions might consider $log(d_{P,a,t}\times k)$. Although $log\left(d_{P,a,t}\times k\right)$endeavors to encapsulate as many negative observations as possible, the inevitable overlap between true and false prediction confidences can trigger avoidable second-stage classifications, inflating the cost for true predictions that would not have required re-evaluation (see

Table 3. F1-score comparison of contextual bandit reward policies across selection strategies and detection models on subsets A and B.

Dataset	Detection Model	Reward Description	Selection Strategy	Accuracy	Precision	Recall	F1-Score
Subset A	Neural Network	$log\left(k\right)$	UCB	0.891	0.881	0.902	0.891
		$log\left(k\right)$	Thompson	0.892	0.882	0.903	0.892
		$log\left(k\right)$	UCBE	0.89	0.88	0.901	0.89
		${\rho }^{d_{P,a,t}}$	Thompson	0.889	0.879	0.9	0.889
		0.9	Thompson	0.885	0.875	0.896	0.885
	Random Forest	$log\left(k\right)$	UCBE	0.901	0.891	0.911	0.901
		$log\left(k\right)$	UCB	0.902	0.892	0.912	0.902
		$log\left(k\right)$	Thompson	0.9	0.89	0.91	0.9
		${\rho }^{d_{P,a,t}}$	Thompson	0.899	0.889	0.909	0.899
		0.9	Thompson	0.895	0.885	0.905	0.895
Subset B	Neural Network	$log\left(k\right)$	UCB	0.971	0.961	0.981	0.971
		$log\left(k\right)$	UCBE	0.972	0.962	0.982	0.972
		$log\left(k\right)$	Thompson	0.971	0.961	0.981	0.971
		$d_{P,a,t}^{\rho }$	Thompson	0.97	0.96	0.98	0.97
		${\rho }^{d_{P,a,t}}$	Thompson	0.969	0.959	0.979	0.969
	Random Forest	$log\left(k\right)$	UCBE	0.994	0.984	0.995	0.994
		$log\left(k\right)$	UCB	0.993	0.983	0.994	0.993
		$log\left(k\right)$	Thompson	0.993	0.983	0.994	0.993
		$d_{P,a,t}^{\rho }$	Thompson	0.992	0.982	0.993	0.992
		${\rho }^{d_{P,a,t}}$	Thompson	0.991	0.981	0.992	0.991

Reward description note: The “Reward Description” column specifies the reward policies used in the experiments, such as “$log\left(k\right)$ or “$d_{P,a,t}^{\rho }$”, which define the criteria for reward allocation in the reinforcement learning framework.

).

4.6. Attack Detection Results

This section assesses the detection capabilities of our contextual bandit-based reinforcement learning approach through standard evaluation metrics, namely, accuracy, precision, recall, and F1-score. The findings, ordered by F1-score, are presented in Table 3.

These outcomes show that, within the top five policies employed by our approach on subset A of the CSE-CIC-IDS2018 dataset, the accuracy remains above 86%, while for subset B it surpasses 95%. In particular, when using Thompson sampling on subset A, 0.9 achieves the highest detection effectiveness among all considered reward strategies. Nevertheless, as indicated in Table 2, 0.9’s cost-effectiveness lags behind that of the top five policies, showing an approximately 52% increase in cost relative to $log\left(k\right)$. Notably, $log\left(k\right)$consistently ranks among the top five best-performing policies across all four evaluations (i.e., both subsets combined with both models), regardless of the selection strategy (Thompson, UCB, or UCBE). The Thompson-driven ${\rho }^{d_{P,a,t}}$ policy attains the second-best accuracy in three out of the four scenarios. Overall, the experiments demonstrate that detection efficacy remains relatively stable across the two CSE-CIC-IDS2018 subsets for all tested policies, exhibiting only about a 1% fluctuation in accuracy. Lastly, although the Softmax selection approach does not secure a place in the top five, it still provides some degree of adaptability, as evidenced by the relationship between triage rate and false predictions across different parameter settings.

4.7. Comparison with Baseline Architectures

For further validation, the detection performance of our contextual bandit-based reinforcement learning approach was benchmarked against several baseline configurations, as summarized in

Table 4. Comparison of detection model architectures on subsets A and B, including traditional and contextual bandit-based models.

Dataset	Detection Model	Architecture	Accuracy	Precision	Recall	F1-Score	Triage Rate
Subset A	Neural Network	Large	0.91	0.92	0.88	0.9	N/A
		Stacked	0.9	0.93	0.87	0.89	N/A
		Light (L1)	0.78	0.81	0.74	0.77	N/A
		Light (L2)	0.96	0.88	0.9	0.91	N/A
	$\mathrm{Contextual} \mathrm{Bandit} \left(log\right(k)$, UCB)	Cost-Sensitive	0.9	0.89	0.91	0.9	1650.0
	$\mathrm{Contextual} \mathrm{Bandit} ({\rho }^{d_{P,a,t}}$, Thompson)	Cost-Sensitive	0.91	0.9	0.92	0.91	3450.0
	Random Forest	Large	0.97	0.96	0.97	0.96	N/A
Subset B	Random Forest	Stacked	0.96	0.96	0.95	0.95	N/A
		Light (L1)	0.89	0.87	0.86	0.86	N/A
		Light (L2)	0.96	0.94	0.95	0.95	N/A
	Contextual Bandit (0.9, Thompson)	Cost-Sensitive	0.92	0.9	0.93	0.91	1750.4
	$\mathrm{Contextual} \mathrm{Bandit} \left(log\right(k)$, UCBe)	Cost-Sensitive	0.93	0.91	0.94	0.92	720.3
	Neural Network	Large	0.98	0.99	0.97	0.98	N/A
		Stacked	0.99	0.99	0.99	0.99	N/A
		Light (L1)	0.79	0.81	0.78	0.79	N/A
		Light (L2)	0.99	0.99	0.99	0.99	N/A
	$\mathrm{Contextual} \mathrm{Bandit} \left(log\right(k)$, Thompson)	Cost-Sensitive	0.97	0.98	0.96	0.97	5200.38
	$\mathrm{Contextual} \mathrm{Bandit} \left(log\right(k)$, UCB)	Cost-Sensitive	0.97	0.98	0.96	0.97	3800.18
	Random Forest	Large	0.99	0.98	0.99	0.99	N/A
		Stacked	0.98	0.97	0.98	0.98	N/A

. Our contextual bandit-based reinforcement learning approach can be compared to modern cloud-based phishing and malware detection services, such as Microsoft Defender, which incorporate a local, low-cost detection mechanism and an auxiliary cloud-based inference engine that is triggered only if the host-based component is unable to yield a definitive decision. Analogous configurations have thus been adopted as baseline architectures for evaluating our approach.

In Table 4, the “Large” model trains on all features available in subset A and subset B of the CSE-CIC-IDS2018 dataset, whereas the “Light” variants, L1 and L2, operate using only subsets of these features (see Section 4.2 for details). The “Stacked” model combines L1 and L2 by averaging their predictive probabilities, with a cost similar to that of the Large model. We compared these approaches with two configurations in our contextual bandit-based reinforcement learning approach, selected for having either the best performance or the lowest triage rate, according to the results in Table 2 and Table 3.

As expected, the Large and Stacked models yielded the highest detection rates overall. Similarly, L2 outperformed L1 due to its utilization of more complex and resource-intensive features. Although the variants of our approach demonstrate minor reductions in detection metrics, they compensate with substantial cost savings. Among the strategies in our contextual bandit-based reinforcement learning approach, those employing UCB and Thompson sampling often achieve either superior performance or more pronounced cost reductions, qualifying them for inclusion in Table 3.

Focusing on the Bell dataset with the neural network (NN) model, we observed that $log\left(k\right)$ (UCB) and ${\rho }^{d_{P,a,t}}$ (Thompson) differ by only about 1% in performance, while $log\left(k\right)$ achieves a 50.4% cost reduction compared to ${\rho }^{d_{P,a,t}}$. Against the Large model, both $log\left(k\right)$ and ${\rho }^{d_{P,a,t}}$ exhibit an approximately 1% decrease in accuracy and a reduction in precision of approximately 4% and 3%, respectively. Interestingly, the L2 model surpasses the Large model in terms of accuracy, with a 7% improvement, reaching 95%. When using Random Forests on the Bell dataset, $log\left(k\right)$ (UCBe) achieves a 42.8% higher cost saving. In comparison, 0.9 (Thompson) trails by only 1% in terms of accuracy (88% versus 89%), while the Large model attains the best accuracy at 96%. Thus, employing our approach in these instances trades an approximate 8% decrease in detection performance for noteworthy cost benefits.

For subset B of the CSE-CIC-IDS2018 dataset, both the RF and NN models demonstrate robust detection capabilities, likely due to the dataset’s nature. With NN, two configurations in our contextual bandit-based reinforcement learning approach ($log\left(k\right)$ with Thompson and $log\left(k\right)$ with UCB) deliver nearly identical detection outcomes, although $log\left(k\right)$ (UCB) offers a 74.5% greater cost reduction than $log\left(k\right)$ (Thompson). Similarly, when RF is applied, $log\left(k\right)$ (UCBe) achieves both top-tier detection performance and cost savings, exceeding the Stacked model and performing comparably to the Large model.

5. Discussion

Our evaluation findings demonstrate that the configuration of the exploration algorithm’s parameters markedly shapes the balance between cost and detection quality. In essence, any attempt to reduce computational expense may risk impairing detection accuracy. Among the parameter selection strategies explored here, the Softmax approach displayed noteworthy adaptability over a broad parameter space, making it particularly suitable for stakeholders whose risk tolerance may vary.

Unsurprisingly, our trials indicated that approaches engaging in more extensive triage operations, thus incurring greater computational overheads, attained superior detection metrics. This result aligns with the principle that assembling multiple predictive models, rather than relying on a single model limited to a reduced set of features, enhances overall performance. Nevertheless, as discussed in Section 4, our introduction of the contextual index reward function $log\left(k\right)$ in our contextual bandit-based reinforcement learning approach enables a more economical balance. By adopting $log\left(k\right)$, our contextual bandit-based reinforcement learning approach achieves cost savings while maintaining detection results that are not far removed from those of the optimal architecture described in Table 4. System administrators retain the option to select reward functions that emphasize either computational thrift or enhanced detection rigor, according to their priorities. However, when practical considerations such as human oversight significantly inflate operational costs, the importance of cost trade-offs intensifies. Our comparison of reward policies across various selection algorithms and both classifier/dataset settings revealed that the contextual index reward consistently delivered superior cost reductions in three out of four cases, underscoring its dependability.

Our results further suggest that a model’s detection performance, shaped by the particular dataset, influences the degree of achievable cost mitigation. Realistically, not all models cleanly partition their predictions into confidently correct versus uncertain classifications. Some degree of overlap is inevitable, and not every dataset will be comprehensive enough to ensure that all incorrect classifications register as low-confidence and, thus, become targets for our decision optimization process. Consequently, ongoing improvements in the underlying detection models remain essential. By enhancing a model’s baseline accuracy, our contextual bandit-based reinforcement learning approach can more effectively leverage confidence-based cost savings, focusing resource reductions primarily on the high-confidence prediction domain.

In addition, our experiments confirm that a model’s intrinsic strength has a direct bearing on how confidently it assigns probabilities to its predictions. The pairwise variations introduced by using two distinct datasets and two classifier types provided ample opportunity to observe differences in confidence levels. Ideally, the training process should encourage a model to assign lower confidence values to incorrect predictions than to correct ones, thereby facilitating the more precise implementation of cost-saving strategies.

Our evaluation utilized a two-tier detection structure for identifying malware and phishing threats, mirroring the architectures employed by certain commercial cloud-based services (e.g., Microsoft Defender, Version: 1.429.356.0). In a similar fashion to our contextual bandit-based reinforcement learning approach, Microsoft Defender uses a cost-efficient local detection component supported by a more resource-intensive cloud-based system that is only invoked when the local module cannot produce a definitive decision. Although our contextual bandit-based reinforcement learning approach could theoretically be scaled to incorporate additional models, or even human analysts, such expansion increases the complexity of determining their optimal cost-performance ordering.

Extensibility to Multi-Layered Architectures: Our contextual bandit-based reinforcement learning framework is intentionally modular, allowing it to be integrated into more complex, multi-layered detection environments. In such systems, each detection layer—ranging from signature-based filters to advanced behavioral analysis engines—can be associated with different computational costs and detection strengths. The reward function in our framework can be adapted to reflect these varying cost–accuracy trade-offs, enabling the system to dynamically adjust decision thresholds across layers. This makes it feasible to design pipelines where lightweight models filter the majority of traffic, while more resource-intensive models are invoked only when required. Such an approach mirrors real-world architectures, like those found in security operation centers (SOCs) and cloud-native security platforms, which often incorporate multiple detection stages before escalating alerts. Future work will explore how this dynamic allocation strategy can be extended to include additional layers, including human-in-the-loop verification stages.

While our study focuses on contextual bandits, which are particularly suited for real-time, low-latency decision-making with limited feedback, we acknowledge the broader reinforcement learning landscape. Compared to hierarchical reinforcement learning methods that address large state–action spaces [59] and transfer reinforcement learning frameworks that leverage previously learned knowledge for improved performance on new tasks [60], contextual bandits offer faster convergence and lower computational requirements. These qualities make them especially effective for adaptive threshold tuning in time-sensitive, cost-constrained environments such as cyber threat detection. Future work may explore hybrid models that combine contextual bandits’ efficiency with the generalization power of hierarchical and transfer-based methods.

Finally, it is important to note that the sign and magnitude of the reward signal (positive or negative) hinge on the availability of supervisory labels. If the model encounters evolving data distributions without corresponding new labels, it may face concept drift, a well-known challenge that affects many model-driven approaches. Since a deployed detection model might lack a continuous stream of fresh labels, it must rely on intermittent labeling or probabilistic estimates. It is generally presumed that, through retraining or adaptive online methods, the model will undergo periodic refinement as newly labeled samples become available, possibly sourced through human expertise.

6. Conclusions

This study introduces our contextual bandit-based reinforcement learning approach, an innovative decision optimization methodology for multi-layered threat detection systems. By employing a novel value estimation mechanism, our approach aims to both accurately distinguish malicious activities and limit the computational overheads associated with data processing and model inference. Central to this framework is the dynamic adjustment of decision boundaries through a multi-armed bandit strategy, enabling our contextual bandit-based reinforcement learning approach to refine its actions as new observations are encountered.

A comprehensive evaluation of our contextual bandit-based reinforcement learning approach was conducted within a two-tier detection pipeline designed to address the two most common cyber threats: phishing and malware attacks. The first (lower-cost) tier managed the bulk of the classification workload, while the second (more resource-intensive) tier was employed selectively, i.e., only when the initial layer’s classification confidence was insufficient. This approach parallels the operational structure of commercial security services such as Microsoft Defender, where local, less costly classification models are supplemented by a more computationally demanding, remote detection engine on an as-needed basis.

To validate this proposed framework, experiments were performed using subsets A and B of the CSE-CIC-IDS2018 dataset, training models within a two-layer architecture. The outcomes confirm that our contextual bandit-based reinforcement learning approach delivers robust detection capabilities and economic efficiency, effectively mitigating inference and processing costs without compromising overall performance across diverse network threat scenarios.

Future work should focus on examining this method’s adaptability in greater depth. In particular, more extensive research into the set of available actions, especially within a multi-classification context, is warranted. Additionally, the systematic exploration of action selection frequency is necessary to ensure that value estimation updates do not introduce unnecessary computational burdens. In this way, our contextual bandit-based reinforcement learning approach can continue to evolve, maintaining its balance between cost-effectiveness and detection efficacy.