1. Introduction
Multimodal sentiment analysis (MSA) involves integrating and synergistically parsing diverse heterogeneous data modalities [
1,
2,
3], encompassing many information forms such as text, visual, auditory, and even biometric markers [
4]. With the evolution of social media ecosystems and the proliferation of multimedia content, information presentation has evolved from pure text to richly illustrated content, culminating in today’s prevalent video-based information [
5,
6].
Traditional unimodal sentiment analysis is confined mainly to the textual domain [
7]. In contrast, MSA encompasses a comprehensive interpretation of multiple perceptual channels, including visual cues (e.g., facial expressions, scene color, and body movement) and audio characteristics (e.g., pitch amplitude, frequency distribution, and speech tempo) [
8,
9]. MSA has garnered significant attention in recent research. On the one hand, human emotional expression inherently possesses cross-modal properties, with text, speech, and even haptic cues intricately interwoven to form sentiments, rendering a single modality insufficient to fully unveil the complexity of these sentiments [
10,
11]. On the other hand, through their deep fusion of multiple signal sources, MSA technologies significantly enhance the accuracy of sentiment recognition and understanding, fulfilling the high-precision sentiment intelligence demands in domains such as intelligent customer service, VR/AR experience optimization, and mental health assessment [
12,
13].
Existing deep learning-based MSA models typically consist of three core components: a single-modality feature extraction module, a multimodal feature fusion module, and a classification head [
14]. The use of pre-trained models as the single-modality feature extraction module has been widely recognized as an effective strategy. Consequently, current researchers often focus on optimizing multimodal feature fusion methods and model training processes to further enhance the overall performance of the models.
Multimodal fusion has emerged as a core technique for understanding video contexts, demonstrating its value across numerous downstream tasks [
15,
16,
17]. Prior research has proposed a series of fusion techniques for MSA. For instance, Yu et al. [
18] employed a self-supervised joint learning strategy called Self-MM, which integrates discriminative information learned from individual unimodal tasks with shared similarity information from the multimodal task during the late fusion stage, thereby enhancing model performance.
While multimodal fusion techniques are crucial for models [
19,
20], setting optimization objectives is equally indispensable in model construction [
5]. Suitable optimization objectives effectively guide the model toward continuous performance optimization throughout training [
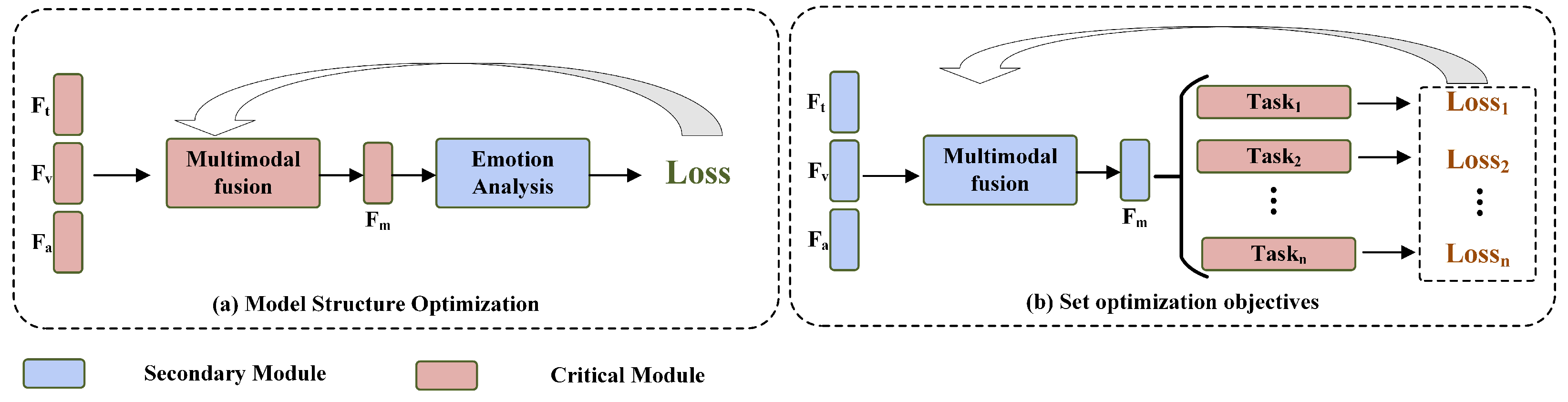
5]. Moreover, as shown in
Figure 1, the setting of optimization objectives and model structure optimization focus on different modules, complementing each other. Early researchers typically used only the cross-entropy loss function to supervise the training of MSA models [
14]. However, relying solely on single-task training makes it difficult to fully exploit the correlations between different modalities [
5]. Therefore, subsequent researchers attempted to use multi-task learning methods, allowing MSA models to complete multiple related tasks simultaneously during training, thereby enhancing the utilization of different modality information. In this approach, the selection of related tasks is crucial, as different tasks can influence each other. Only by choosing the right combination of tasks can the model achieve better performance in multi-task training.
As shown in
Figure 2, the sentiment intensity derived solely from analyzing text data is +1. When analyzing audio data alone, the sentiment intensity is −0.2. Similarly, when considering only visual information, the sentiment intensity is −1. However, when taking into account these three modalities of data comprehensively, the overall sentiment intensity of the information is 0. If we ignore the text information, we might conclude that the sentiment is negative. Conversely, if we overlook the visual information, we might infer that the sentiment is positive. In any case, it is impossible to accurately analyze the overall sentiment of the entire piece of information. Therefore, in the MSA task, single-modality sentiment has a direct impact on the overall sentiment [
12,
21,
22]. Nevertheless, many existing methods tend to overlook the significance of unimodal sentiment [
18,
23]. Thus, enabling MSA models to focus on both uni- and multimodal sentiments concurrently has emerged as a formidable challenge in this field. Another challenge faced by MSA tasks lies in their broad range of sentiment ratings. For example, the MOSI dataset requires models to accurately map samples to a sentiment intensity scale of [−3, +3], which increases the prediction difficulty.
Given these challenges, we propose DMMSA, a Dynamic Tuning and Multi-Task Learning-Based MSA model. DMMSA ensures that the model can capture unimodal signals in detail and integrate multimodal information through the collaborative optimization of unimodal and multimodal tasks. The model is equipped with a text-oriented contrastive learning module to promote feature decoupling and enhance the depth and accuracy of sentiment understanding. Furthermore, incorporating coarse-grained sentiment classification tasks to converge the prediction range improves the accuracy of sentiment intensity determination. We implement Global Dynamic Weight Generation (GDWG) to avoid negative transfer effects and achieve the joint adjustment of model parameters, thereby maximizing overall performance.
The main contributions of this paper can be summarized as follows:
We propose the Multi-NT-Xent loss to guide the model in decomposing unimodal features and establishing text-centered contrastive relations.
By employing coarse-grained sentiment analysis tasks, we effectively converge the prediction range, reducing the complexity of modeling sentiment intensity.
To address the issue of unequal convergence rates among different tasks during multi-task training, we propose the GDWG strategy, effectively mitigating the negative transfer effects arising from such mismatches.
Our model is evaluated on three benchmark datasets: CH-SIMS [
18], MOSI [
24], and MOSEI [
23]. The results show that DMMSA outperforms the baseline method in classification and regression tasks when the model structure remains unchanged and only the optimization objectives are replaced. Additionally, we conduct comprehensive ablation studies, substantiating the efficacy of each component within our proposed architecture.
3. Methodology
In this section, we first provide a brief introduction to the task definition. We then describe the overall operational process of the DMMSA model, and finally, we detail our proposed model training method based on multi-task learning and dynamic tuning.
3.1. Task Definition
MSA aims to decipher sample sentiment states by harnessing multiple signals, encompassing text (), visual (), and audio () modalities. Task types within this domain are typically categorized into two broad classes: classification and regression. Focusing on the latter, the proposed DMMSA model takes , , and as inputs, yielding an output sentiment intensity value , constrained within the actual interval , where R defines the upper and lower bounds of the sentiment score.
3.2. Model Architecture
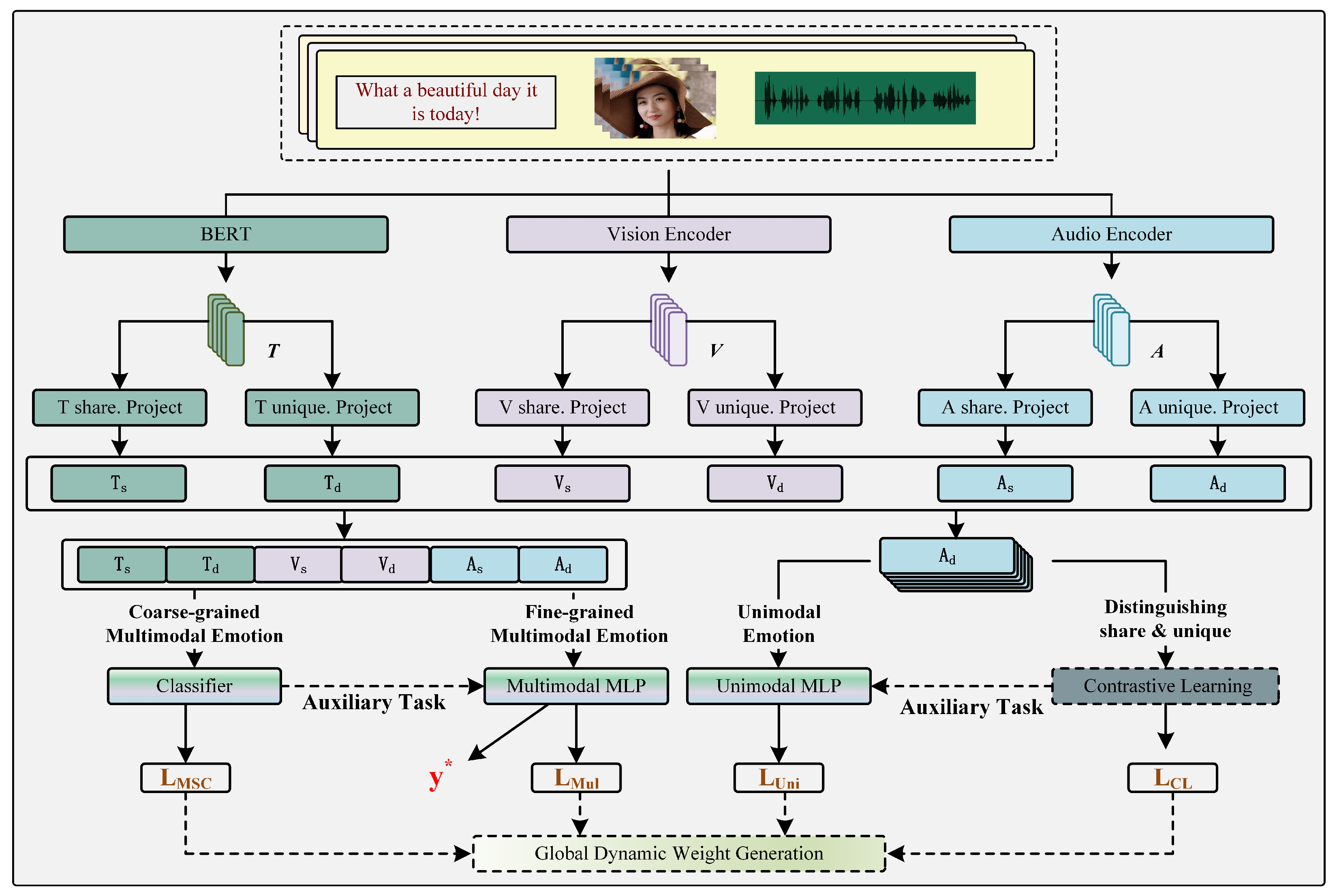
This section primarily introduces the overall architecture of the DMMSA model to facilitate the reader’s understanding. The overall architecture of the DMMSA model is depicted in
Figure 3.
In the single-modality feature extraction stage, we employ the pre-trained
model to extract text features.
is a pre-trained language model based on the transformer architecture. During pre-training, it leverages a vast amount of unsupervised text data to learn rich linguistic knowledge and semantic information. Therefore, compared to models such as RNN, LSTM, and GRU, it can encode text more effectively. For processing visual and audio modality data, we use the transformer model as the visual encoder and audio encoder in DMMSA. The overall formula is as follows:
where
T,
V, and
A represent the text, visual, and audio features extracted by the encoders, respectively.
represents the encoder for visual information, and
represents the encoder for audio information.
Next, we input the features from different modalities into the feature decomposition module to obtain modality-similar features and modality-dissimilar features. The feature decomposition module consists of six parallel project modules, each of which includes a fully connected layer with a Tanh activation function and layer normalization [
5]. The formulas are as follows:
where
,
, and
represent the modality-similar features extracted by the mapping modules;
,
, and
represent the modality-dissimilar features;
represents the Tanh activation function; and
represents the fully connected layer. The feature decomposition module decomposes features from different modalities into modality-similar and modality-dissimilar features. This is attributed to the incorporation of two tasks, single-modality sentiment classification and contrastive learning, in the training process, which helps the model effectively perform feature decomposition. The details are discussed in the section on multi-task learning.
Finally, we concatenate the extracted modality-similar and modality-dissimilar features and input them into a multi-layer perceptron (MLP) network to obtain the final sentiment prediction result. The formula is as follows:
where
represents the predicted result and “;” represents concatenation.
3.3. Multi-Task Learning
In this section, we focus on the setup of multi-task learning and how we mitigate negative transfer through dynamic tuning.
As shown in
Figure 3, we employ a hard parameter sharing method for multi-task learning. In this approach, all tasks share the hidden layer parameters of the neural network, and each task has its own output layer. This method not only reduces the risk of overfitting but also encourages the model to find a general representation that covers all tasks.
In terms of task setup, we first draw inspiration from previous studies and introduce a unimodal sentiment classification task to help the model better analyze the sentiment of the information [
5]. Given that the MSA task requires the model to predict a value from a wide range, which is quite challenging, we further add a coarse-grained sentiment analysis task to help the model narrow down the prediction range and thus improve prediction accuracy. Moreover, to assist the model in better distinguishing between similarity and dissimilarity features, we also incorporate a contrastive learning task. Additionally, by leveraging the collaborative effect of the unimodal sentiment analysis and contrastive learning tasks, we enable the model to accurately extract similarity and dissimilarity features from the three information modalities. This, in turn, enhances the model’s effective utilization of the intrinsic relevance and distinctive emotional inclinations embedded in the sentiment signals of different modalities. The final multi-task learning objective function is given by
where
represents the weights generated by the GDWG method,
is the multimodal sentiment regression loss,
is the loss related to multimodal sentiment classification,
is the unimodal sentiment analysis loss, and
is the contrastive learning loss.
—
Multimodal Sentiment Regression Loss. The purpose of this task is to guide the model in integrating signals from different modalities to estimate the sentiment intensity of samples accurately. Herein, we feed the fused decomposed similarity and dissimilarity features into a multimodal MLP for sentiment intensity prediction, associating its output with the given multimodal sentiment intensity labels via a smooth L1 loss function to derive this loss. The formulaic expression is as follows:
where
represents the predicted result, “;” represents concatenation,
y represents the multimodal sentiment label, and
controls the smoothness.
—
Multimodal Sentiment Classification Loss. The purpose of this task is to direct the model toward the coarse-grained classification of sentiment, thus narrowing down the prediction scope. Unlike the fine-grained sentiment analysis task, this task does not require the model to precisely predict the exact intensity of sentiment, but rather to predict the range interval to which the sentiment intensity belongs. Initially, we map the sentiment intensity labels of samples to preset sentiment polarity classifications (such as positive, negative, and neutral) in accordance with predefined regulations, thereby creating a sentiment polarity label collection. Next, the disassembled multimodal features are efficiently combined and fed into a sentiment classifier as input, generating the probability distribution of each sample among different sentiment polarities. Eventually, the predicted probability distribution of the classifier is compared with the actual assigned sentiment polarity labels, and the cross-entropy loss function is utilized to measure the loss between the two. The specific formulaic expression is as follows:
where
N denotes the number of samples and
C represents the number of categories.
—
Unimodal Sentiment Analysis Loss. The purpose of this task is to guide the model in delving into the sentiment information embedded within each modality. Here, to ensure consistent treatment of modal features, we feed the similarity features (
,
, and
) and dissimilarity features (
,
, and
) of each modality separately into a weight-sharing MLP layer. The MLP layer outputs six sentiment predictions,
, with the similarity features used to infer the multimodal sentiment label
y and the dissimilarity features used to predict the corresponding unimodal sentiment labels
. In the absence of unimodal labels, the dissimilarity feature prediction task adjusts to instead predict the multimodal label
y, maintaining the coherence of model training. Finally, a smooth L1 loss function is employed for each prediction to measure the loss between the prediction and the respective ground-truth label
. The specific formulaic expression is as follows:
—
Contrastive Learning Loss. Contrastive learning tasks help models learn the commonalities among positive examples and the differences from negative examples by comparing positive and negative samples. Through this task, models can extract high-quality similarity and dissimilarity features, thereby paying attention to both unimodal and multimodal sentiment information. Here, considering that text modality data often assume a dominant role in MSA tasks, with other modalities providing auxiliary information to enhance prediction accuracy, we opt to use text data as the reference anchor for constructing positive and negative sample pairs [
12]. The specific configuration is as follows:
Subsequently, we employ our proposed Multi-NT-Xent loss to guide the model in maximizing the similarity between positive sample pairs while minimizing the similarity between negative sample pairs. The calculation formula for the Multi-NT-Xent loss is as follows:
where
is the temperature coefficient that controls the similarity distribution;
and
denote positive and negative sample pairs, respectively;
N represents the set of negative pairs; and
P signifies the set of positive pairs.
3.4. Global Dynamic Weight Generation
In multi-task learning scenarios, distinct tasks often exhibit asynchronous convergence patterns, leading specific tasks to stabilize either prematurely or tardily [
22,
24,
33,
34]. This inconsistency in convergence rates can engender negative transfer, where the learning process of one task adversarially impacts the performance of other tasks, thereby compromising overall model effectiveness [
35]. To address this challenge, we introduce the GDWG mechanism. This mechanism aims to adaptively adjust the relative weights of individual tasks during training. Specifically, it assesses the descent rate of each task’s loss function at every training stage and, based on these assessments, generates weight values for each task. The specific mathematical expression is as follows:
where
denotes the relative decay rate of task
k at the t-th training stage,
represents the weight value assigned to task
k at stage
t, and
signifies the loss incurred by task
k at stage
t.
J signifies the total number of tasks subject to adjustment, and
is a temperature coefficient that governs the magnitude of weight updates, with smaller values indicating greater amplitudes of weight updates. All tasks under consideration are initially assigned equal weights during the model’s initialization phase. Subsequently, their actual loss values at the first training stage,
, serve as the respective baseline loss references.
4. Experiments
4.1. Experimental Settings
All experiments in this study were conducted on a 3090 GPU. For the CH-SIMS dataset, the “bert-base-chinese” model was employed, while for the MOSI and MOSEI datasets, the “bert-base-uncased” model was selected for fine-tuning. During fine-tuning, the learning rate was set at 0.00001, with a batch size of 64 and a total of 150 training epochs. In terms of modality information extraction, for the CH-SIMS and MOSI datasets, two single-layer transformers were used to extract audio and visual information. However, for the MOSEI dataset, considering its data characteristics and complexity, a three-layer transformer was adopted to extract information from the visual and audio modalities. Throughout the entire training process, the learning rate was uniformly set at 0.0001, with a batch size of 128 and a total of 300 training epochs.
4.2. Datasets and Baseline Models
To evaluate the performance of the DMMSA model, we selected three representative MSA datasets: CH-SIMS [
18], MOSI [
24], and MOSEI [
23]. CH-SIMS, a resource for MSA in Chinese, comprises 2281 video samples, with sentiment labels expressed as scores within the continuous interval [−1, +1]. MOSI, an English dataset, includes 2199 video clips and employs a [−3, +3] sentiment intensity rating system. MOSEI, an extended English MSA collection derived from MOSI, significantly expands the scale to 22,856 video segments, maintaining the [−3, +3] sentiment intensity scoring range. The specific details of the dataset division are presented in
Table 1.
4.3. Baseline Models
LF-DNN: This model concatenates unimodal features and analyzes sentiment [
18].
MFN: This model first employs LSTM for view-specific interaction, then utilizes the attention mechanism for cross-view interaction, and finally summarizes through time with a multi-view gated memory [
23].
LMF: By decomposing in parallel tensors and weights, this model utilizes modality-specific low-rank factors to perform multimodal fusion [
36].
TFN: This model learns end-to-end dynamics within and across modalities. It utilizes a new multimodal fusion method (tensor fusion) to model the dynamics across modalities [
26].
MulT: The core of MulT lies in its cross-modal attention mechanism, which offers a potential cross-modal adaptation by directly attending to low-level features in other modalities to fuse multimodal information [
37].
MISA: This model learns modality-invariant and modality-specific representation spaces for each modality to obtain better representations for the fused input [
38].
MAG-BERT: This model enhances performance by applying multimodal adaptation gates at different layers of the BERT backbone [
14].
Self-MM: This model first utilizes a self-supervised label generation module to obtain unimodal labels and then jointly learns multimodal and unimodal representations based on multimodal labels [
39].
ConFEDE: This model first decomposes unimodal features into modality-invariant and modality-specific features through feature decomposition. Subsequently, it utilizes multi-task learning to jointly optimize multimodal sentiment analysis, unimodal sentiment analysis, and contrastive learning tasks [
5].
4.4. Evaluation Metrics
We report the model’s performance in classification and regression tasks following prior work. For classification, we computed the accuracy of three-class prediction (Accuracy-3) and five-class prediction (Accuracy-5) on CH-SIMS, as well as the accuracy of two-class prediction (Accuracy-2) and seven-class prediction (Accuracy-7) on MOSI and MOSEI. Here, Accuracy-2 and the F1-score for MOSI and MOSEI are reported in two forms: “negative/non-negative” and “negative/positive” (excluding 0). We present Mean Absolute Error (MAE) and Pearson correlation (Corr) regarding regression. All metrics, except for MAE, are better when higher. Since the output of the model is a specific value, in the context of classification tasks, we primarily determined whether the classification was accurate by checking if this value fell within the correct interval. For example, in the three-class classification task of the CH-SIMS dataset, the accuracy (ACC-3) was divided into the following intervals: [−1, −0.1], (−0.1, 0.1], and (0.1, 1]. For example, suppose the ground truth of an input sample was −0.5, and the model predicted a value of −0.3. In this case, we consider that the model has made a correct classification in the three-class classification task, as it successfully predicted the interval in which the sample’s sentiment lies.
4.5. Comparative Experiments
Table 2 and
Table 3 summarize the results of the comparative experiments with various methods. The listed results are based on the average of five runs with different random seeds, with the performance data for all baseline models, except for ConFEDE, sourced from published studies.
On the CH-SIMS dataset, DMMSA outperformed all baseline models in classification and regression tasks. Compared to ConFEDE, it achieved increases of 1.27% and 3.20% in Acc-3 and Acc-5, respectively. This is mainly due to the integrated coarse-grained sentiment analysis task, which boosts classification performance. DMMSA also showed significant progress in the MAE and Corr metrics. It effectively captured the interdependencies of uni- and multimodal sentiment analysis and embedded a coarse-grained task that constrained the prediction scope and simplified the analysis. As shown in
Figure 4, DMMSA exhibited smaller MAE fluctuations and faster convergence during training than models without coarse-grained analysis, confirming its positive role in optimization.
To further validate our approach, experiments were conducted on the MOSI and MOSEI datasets without unimodal sentiment labels.
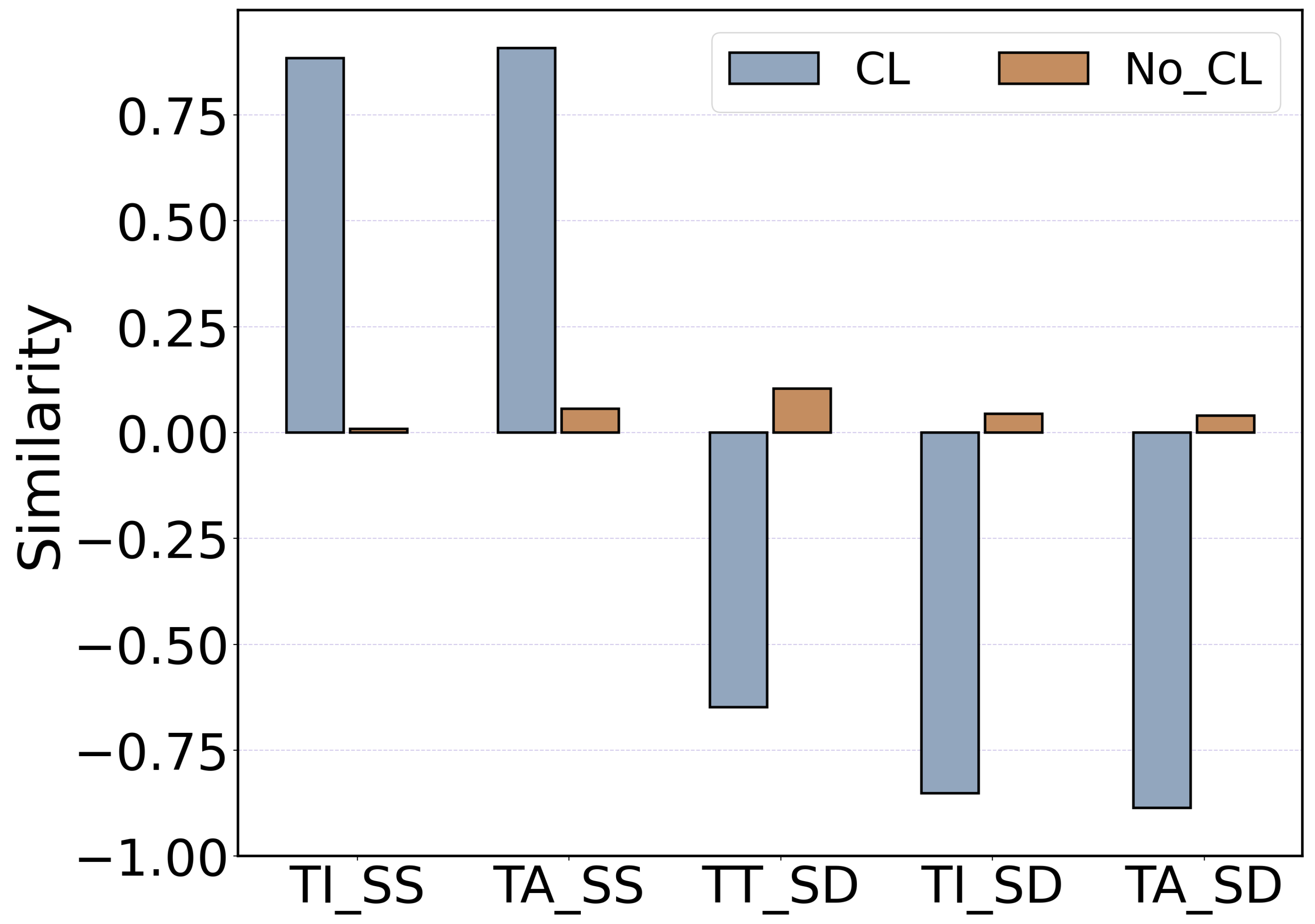
Table 3 shows that DMMSA surpassed all baselines, demonstrating excellent performance even without unimodal labels. This is mainly due to the design of the contrastive learning task. As shown in
Figure 5, the model was still able to identify and separate uni- and multimodal features effectively under the guidance of this task. Notably, DMMSA’s improvements in Acc-5, MAE, and Corr were more significant than those in Acc-2 and Acc-3. This is because complex tasks require higher model performance and feature quality. Simple tasks can yield good results with lower-level features, while DMMSA’s advantage lies in extracting higher-quality features, making its performance gain more prominent as the task difficulty increases.
To confirm this hypothesis, we designed an incremental experiment.
Table 4 shows that DMMSA’s performance in Acc-2 converged when trained with 60% of the data and did not improve with more data. In contrast, its performance in Acc-7 and regression tasks continuously improved as the amount of training data increased.
4.6. Ablation Study and Analysis
We carried out an ablation study on the proposed method to explore the individual contributions of each module to model performance. The results are presented in
Table 5.
We can observe that the model’s performance decreased to varying degrees under the three ablation strategies. The “w/o MSC” strategy resulted in decreases across all performance metrics. The decline can primarily be attributed to the loss of practical constraints on the sentiment prediction range after removing the MSC task. Under the “w/o CL” configuration, the model’s MAE and Corr. indicators significantly decreased. This is mainly because the core objective of CL tasks is to assist the model in effectively distinguishing and extracting similarity and dissimilarity features from single modalities. Once the CL task was removed, the model lost the feature discrimination ability promoted by this mechanism, making it difficult to accurately distinguish and utilize these critical sentiment features; so, its performance was weakened in regression tasks.
In the “w/o GDWG” setting, the model showed a slight upward trend in performance in regression tasks but a significant decline in classification tasks. The reason for this phenomenon is that the model lost the effective regulatory mechanism for gradient convergence rates and magnitude differences among the various tasks during training. As a result, the model tended to over-optimize a single task at the cost of neglecting the learning needs of other tasks, leading to an obvious imbalance in overall performance.
6. Discussion
The DMMSA model has achieved remarkable performance across multiple datasets, which can be attributed to several key factors. First, its multi-task learning strategy incorporates single-modality sentiment classification tasks and contrastive learning tasks, enabling the model to gain a more comprehensive understanding and analysis of sentiment signals. This strategy not only enhances the model’s comprehension of single-modality sentiment but also optimizes the feature extraction and decomposition process through the contrastive learning mechanism. Second, the Global Dynamic Weight Generation (GDWG) strategy dynamically adjusts task weights based on the convergence speed of tasks, effectively avoiding the negative transfer issues in multi-task learning. This mechanism ensures that the model balances the learning progress of different tasks during training, thereby improving overall performance. Additionally, by introducing coarse-grained sentiment classification tasks, the DMMSA model more accurately predicts sentiment intensity. This task simplifies the complexity of sentiment analysis by restricting the prediction range, thereby enhancing the model’s prediction accuracy. Compared with existing baseline models, the DMMSA model has achieved significant improvements in multiple key metrics. For instance, on the CH-SIMS dataset, the DMMSA model’s Acc-3 and Acc-5 values were 1.27% and 3.20% higher than those of the ConFEDE model. On the MOSI and MOSEI datasets, the DMMSA model outperformed all baseline models in metrics such as Acc-2, Acc-7, MAE, and Corr. These results indicate that while optimizing the model structure is important, optimizing the training objectives can also effectively enhance model performance.