Abstract
The article focuses on the issue of the sliding mode control of a vehicle platoon with matched and mismatched disturbances. A novel finite-time disturbance observer-based sliding mode control scheme is developed to effectively mitigate the adverse impact of disturbances and achieve the control goals of a platoon. As matched and mismatched disturbances might decrease the control performance or even cause the instability of a vehicle platoon, a finite-time disturbance observer (FTDO) is designed to effectively reduce the effects of both types of disturbances. Unlike previous studies, the proposed FTDO in this article has the capability to directly estimate disturbances without the need to know the precise upper bounds of the disturbances. A feedforward compensation term, derived from disturbance estimation, is incorporated into the FTDO-based sliding mode control scheme to solve the issue of the degradation of control performance. The controlled vehicle platoon’s stability is proven through the Lyapunov approach, which means that the control goals of the platoon can be achieved under the developed FTDO-based sliding mode control scheme. Finally, a numerical example is conducted to confirm the efficacy of the developed control scheme.
1. Introduction
A variety of issues, such as traffic jams, traffic collisions, and air pollution, are becoming more and more serious in modern transport systems [1,2,3,4,5]. Vehicle platoon control refers to coordinating and regulating the movement of a group of vehicles in a transportation network to guarantee that the transport system operates efficiently and safely [6]. Vehicle platoon control has shown significant advantages in increasing the traffic volume of roads, reducing traffic congestion, and improving the efficiency of traveling [7,8,9]. To address traffic problems, the field of vehicle platoon control has attracted growing attention [10,11]. Fundamental issues in the vehicle platoon field which have been studied include homogeneous or heterogeneous dynamics [12], stability analysis [13], spacing policies [14], and others.
Maintaining consistent spacing between adjacent vehicles and achieving velocity synchronization of followers with the leader are the primary control goals of use of a platoon [15]. Issues such as the degradation of control performance and instability of a vehicle platoon in practice are usually caused by unknown external disturbances [16,17]. Disturbances that appear in the control input channel are usually classified as matched disturbances, such as those involving model uncertainty, rolling resistance, and gusts of wind [18]. Disturbances which do not appear in the control input channel are usually classified as mismatched disturbances, such as unmodeled dynamics, dynamic friction, and velocity uncertainty [19]. Numerous studies have been carried out to reduce the impact of unknown external disturbances on vehicle platoons [20,21,22,23]. In [20], the article considers the robust control problem confronted by a vehicle platoon when subjected to matched disturbances, and presents a distributed control strategy designed to effectively accomplish the control goals of the platoon. Ref. [21] integrates a disturbance observer and a multi-power convergence method into a coupled sliding mode controller, aiming to counteract the adverse effects induced by matched disturbances. An investigation of platoon control issues, particularly those arising from matched disturbances, is presented in [22], which proposes a distributed adaptive sliding mode control approach to effectively handle disturbances and ensure that a vehicle platoon achieves the predetermined tracking performance. The authors of [23] present an adaptive event-triggered control strategy that can effectively deal with matched disturbances and synchronize a vehicle platoon. It is to be noted that only the matched disturbances of a vehicle platoon are considered in the control methods mentioned above. However, in practice, mismatched disturbances may also degrade control performance and even cause instability of the platoon control system [19].
In recent studies, several control schemes have been presented for systems under mismatched disturbances to solve the issues caused by such disturbances [24,25]. In [25], a nonsingular dynamic terminal sliding mode control method is developed, where both matched and mismatched disturbances are effectively compensated, thereby guaranteeing the stability of the vehicle platoon under intermittent communication conditions. Ref. [26] develops a disturbance observer-based nonsingular terminal sliding mode control scheme to effectively mitigate both matched and mismatched disturbances of a vehicle platoon, ensuring system stability while optimizing platoon control performance. Ref. [27] investigates a distributed adaptive singularity-free fixed-time neural network tracking control problem for a vehicle platoon with mismatched disturbance, where a novel backstepping control architecture synergistically integrating a neural network is developed to effectively address mismatched disturbance. It is to be noted that nearly all the aforementioned works assume that the precise upper bounds of mismatched disturbances are known. However, due to the uncertainty of systems in practice, it is difficult or impossible to obtain these precise upper bounds and achieve good control results using the abovementioned methods. Consequently, this presents a challenge and the need to devise a novel control scheme to both achieve the control goals of the platoon and mitigate the influence of disturbances under the condition that the precise upper bounds of disturbances are unknown.
According to the above analysis, we investigate the sliding mode control issue of a vehicle platoon affected by matched and mismatched disturbances in this article. A novel FTDO-based sliding mode control strategy is developed to improve platoon control performance and achieve its control goals. The proposed FTDO, which is designed to solve the issue of degraded control performance and enhance the vehicle platoon’s stability, can directly estimate disturbances without the need to know the precise upper bounds of the disturbances. A feedforward compensation term based on disturbance estimation is incorporated into the FTDO-based sliding mode controller to effectively reduce the influence of disturbances. The primary contributions of this article are as follows:
- Unlike existing studies which focus on vehicle platoons with matched disturbances [20,21,22,23], this work investigates the control issues of a vehicle platoon influenced by matched and mismatched disturbances.
- In contrast to [28,29,30], in which the assumptions regarding the known precise upper bounds of disturbances are made, this work presents a novel FTDO capable of directly estimating matched and mismatched disturbances without the need to know the precise upper bounds of both types of disturbances, which makes this approach more general and extends applicability to a broader range of practical systems.
- For a vehicle platoon affected by matched and mismatched disturbances, a novel FTDO-based sliding mode control approach is developed to achieve the control goals. Moreover, a feedforward compensation term is constructed by utilizing disturbance estimation to effectively reduce the negative effects of disturbances and guarantee the platoon’s stability.
The rest of the article is organized as follows: A dynamics model of the vehicle and the problem formulation are described in Section 2. Section 3 illustrates the development process of the FTDO-based sliding mode control strategy. A numerical example is outlined in Section 4 to confirm the efficacy of the developed FTDO-based sliding mode control approach. The conclusions are outlined in Section 5.
2. Problem Formulation
2.1. Vehicle Dynamics Modeling
A vehicle platoon is considered to contain one leader vehicle, represented by 0, and N follower vehicles, identified by . Then, the dynamics of the ith follower vehicle is considered as [31]
where represents the position; , , and represent the mass, tire radius, and driving torque; represents the velocity; and represent the transmission efficiency and drag coefficient, respectively; and g denote the rolling resistance and gravitational acceleration; denotes mismatched disturbances caused by unmodeled dynamics, dynamic friction, and velocity uncertainty [19]; represents matched disturbances.
Consider the following feedback linearization law [31]
where represents the control input. Substituting (3) into (2) yields
Consider a (virtual) leader [32]
where denotes the position; and represent the velocity and unknown nonlinear function, respectively.
2.2. Platoon Control Problem Formulation
In this paper, the information flow topology of predecessor following is considered as shown in Figure 1. Each vehicle adjusts its driving status according to its predecessor to accomplish the goals of the platoon. This paper utilizes the CTH (constant time headway) spacing policy, and the configuration of the vehicle platoon system under this policy is depicted in Figure 2.

Figure 1.
Information flow topology.
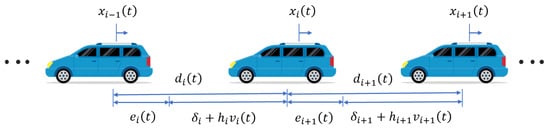
Figure 2.
Configuration of the vehicle platoon system under CTH spacing policy.
The spacing error is defined as
where represents the relative spacing between the ith vehicle and its predecessor. The desired spacing is specified by , where and denote the standstill spacing and time headway, respectively. The velocity error of the ith vehicle is
To ensure that the vehicle keeps a desired spacing from the preceding vehicle and achieves velocity synchronization with the leader, the control goals can be formally described as follows:
- Each vehicle keeps the predetermined inter-vehicle spacing and achieves velocity synchronization with the leader vehicle;
- The matched and mismatched disturbances of the vehicle platoon are estimated by utilizing the developed FTDO without requiring to know the exact upper bounds of the disturbances;
- An FTDO-based sliding mode control scheme is proposed to compensate for the adverse influences caused by matched and mismatched disturbances and to ensure the vehicle platoon’s stability.
2.3. Definitions and Lemmas
Definition 1
([33]). If for any , there exists such that , the origins of (6) with vehicle dynamics (4) are said to be string stable.
Definition 2
([34]). Consider
where is a continuous bounded function. The origin is a finite-time convergent equilibrium of (8) if an open neighborhood of the origin and a function exist, such that for every initial point , the solution trajectory is well defined for all and . The function is known as the convergence-time function. The origin is considered as a finite-time equilibrium if it is both finite-time convergent and Lyapunov stable. If , the origin is a globally finite-time stable equilibrium.
Definition 3
([35]). The origins of (6) with vehicle dynamics (4) are regarded as strong string stable, if such that the error transfer function is satisfied, where is the Laplace transform of .
Lemma 1
([36]). Consider the following differentiator
where are the state variables; and ; The disturbance term satisfies , where , for . Then, the differentiator converges to a bounded neighborhood of zero for .
Lemma 2
([30]). There are and , if and , then
Lemma 3
([37]). The super-twisting algorithm (STA) is described as
where , ; and are the state variables. The trajectories of (11) converge to the origin at , where is the initial state, , and with
3. Finite-Time Disturbance Observer and Controller Design
In this part, a novel FTDO-based sliding mode control approach for a vehicle platoon affected by matched and mismatched disturbances is developed to accomplish platoon control goals, with the FTDO designed to directly estimate both types of disturbances.
Assumption 1
([32]). The disturbance in (4) is twice differentiable, and there exists such that , for and .
Remark 1.
Assumption 1 is employed only for stability analysis and not for controller design, so there is no need to know the exact values of the bounds.
Remark 2.
The bounds involved in Assumption 1 will only be used in stability analysis, and will not be applied in control protocol design, which means that the precise values of these bounds do not need to be known.
3.1. Finite-Time Disturbance Observer Design
Design the novel FTDO for ith vehicle as
where , , and , for ; represents the estimate of the position; is the estimate of ; is the estimate of ; and represent the estimates of the velocity and , respectively. Define the estimation errors of states and disturbances as follows: , , , and , for .
To provide a detailed explanation of the FTDO design process, we present its design block diagram as shown in Figure 3.
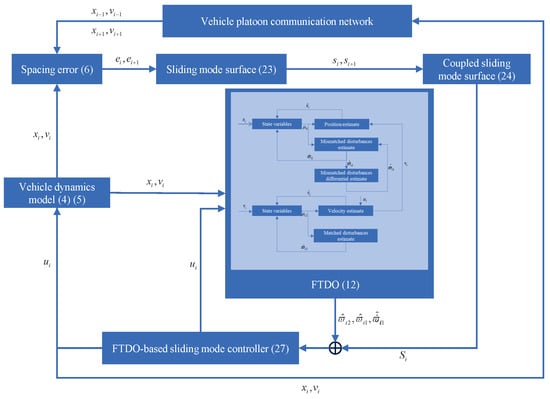
Figure 3.
FTDO-base sliding mode controller design block diagram.
Theorem 1.
Consider the vehicle dynamics (4) under Assumption 1. The proposed FTDO in (12) is finite-time stable in the sense that there exists a time such that , and converge to a bounded neighborhood of zero, .
Proof of Theorem 1.
Taking the derivative of according to (4) and (12), we can obtain
By (4) and (12), the derivative of is
Using (12), we can obtain
Substituting (15) into (14),
Calculating the derivative of from (12) yields
Differentiating , one has
And, the time derivative of is
According to (12), one can obtain
Substituting (20) into (19), we have
Then, the observation error can be expressed as
According to Lemma 1, by designing observer gains , the observation error (22) is finite-time stable, which means that , and converge to a bounded neighborhood of zero for [30]. The proof of Theorem 1 is complete. □
3.2. FTDO-Based Sliding Mode Controller Design and Stability Analysis
A novel FTDO-based sliding mode controller for a vehicle platoon affected by matched and mismatched disturbances is developed in this section to accomplish the platoon control goals. Define the sliding mode surface as
where .
To ensure string stability, a coupled sliding mode surface is designed as [16]
where .
Then, from (24), we have
where , and
As , is an invertible matrix. According to (24), converges to a bounded neighborhood of zero if, and only if, converges to a bounded neighborhood of zero at the same time, and vice versa [35].
Differentiating , one can obtain
where , .
The novel FTDO-based sliding mode controller is designed as
where and ; and are the feedforward compensation terms, constructed by utilizing the estimation of mismatched and matched disturbances.
To provide a clearer explanation of the structure of the controller (27), we present its design block diagram as shown in Figure 3.
Theorem 2.
Consider the vehicle dynamics (4), the leader (5), and the FTDO (12) under Assumption 1. The FTDO-based sliding mode controller (27) can guarantee that for converges to a bounded neighborhood of zero, while the string stability of the entire vehicle platoon can also be ensured when .
Proof of Theorem 2.
The proof procedure first analyzes the state boundedness of for , and then addresses the global stabilization of in the second part.
Part 1 (State boundedness for ): According to (4) and (6), the differential of is
Substituting (27) into (28), one can obtain
where
According to Theorem 1, is bounded for . Based on (27), (26) becomes
Define the Lyapunov function as , and its time derivative is
By Lemma 2, we can obtain
where max and max. As is bounded for , both and are bounded. From (32), we can get that and are also bounded for [30].
Define . Then, (29) can be rewritten as
For , define , and its differential is
As is bounded for , and are also bounded for [30].
For , let , which is bounded for . Then, we have . Similar to the derivation of which is bounded, we can obtain that and are bounded for , and is also bounded for .
Part 2 (Global stabilization): As converges to a bounded neighborhood of zero according to Theorem 1 for , (30) is rewritten as
According to Lemma 3, (35) is finite-time stable, which means that converges to a bounded neighborhood of zero for . From (24), as and exhibit the same convergence, also converges to a bounded neighborhood of zero for . Then, (33) is rewritten as
Choose the Lyapunov function , and its derivative is
The above analysis indicates that converges to a bounded neighborhood of zero, which means that the string stability of the vehicle platoon is guaranteed.
An approach similar to [35] is utilized to demonstrate strong string stability of the entire platoon. As converges to a bounded neighborhood of zero, we have
Substituting (23) into (38), we have
The Laplace transform of (39) yields
where is the design parameter. Assume such that . Then, if holds, is satisfied, which indicates that strong string stability is ensured for the vehicle platoon. The proof of Theorem 2 is complete. □
4. Performance Results
The accuracy of the developed FTDO (12) and controller (27) is validated for a vehicle platoon subject to matched and mismatched disturbances through a numerical example in this section. The proposed FTDO-based sliding mode controller is applied to a vehicle platoon that includes a leader vehicle (5) and six follower vehicles (4). The disturbances are given by and , with . The acceleration profile of the leader vehicle is given by [16]
The parameters of the FTDO and controller are , , , s, m, for [16,36].
By utilizing the proposed FTDO (12) and FTDO-based sliding mode controller (27), a numerical example is executed on the vehicle platoon (4) and (5) under the topology shown in Figure 1. The results are illustrated in Figure 4 and Figure 5. As shown in Figure 4a, the mismatched disturbance error exhibits significant fluctuations around the 5 s mark, but rapidly converges to zero after 21 s, indicating that the method proposed in this paper can effectively estimate mismatched disturbances. From Figure 4b, we observe that exhibits minor fluctuations at 5 s but rapidly converges to zero, which implies that the matched disturbance is accurately estimated within finite time. The profiles of the position are given in Figure 5a. As there are no crossed and overlapped profiles in Figure 5b, collisions between neighboring vehicles are avoided. The curves of the velocity and velocity error are given in Figure 5b and Figure 5c, respectively. It is evident that velocity synchronization is realized among all follower vehicles and the leader. As shown in Figure 5d, the amplitude of does not increase along the platoon, indicating that strong string stability is achieved. The numerical example results demonstrate that the vehicle platoon can achieve the control goals by the designed FTDO-based sliding mode controller. The efficacy of the proposed FTDO and controller is verified.
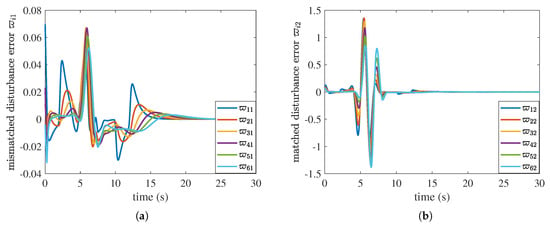
Figure 4.
The estimation results of the proposed FTDO. (a) Estimation error of mismatched disturbances . (b) Estimation error of matched disturbances .
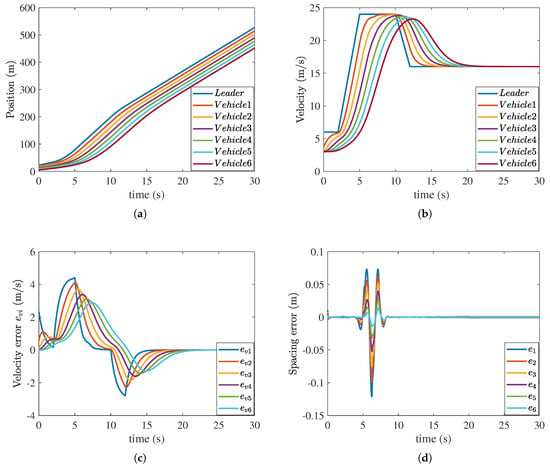
Figure 5.
The control results of the proposed FTDO-based sliding mode controller. (a) Position of ith vehicle. (b) Velocity of ith vehicle. (c) Velocity error . (d) Spacing error .
To demonstrate the superior performance of the proposed FTDO-based sliding mode controller, the results of the disturbance observer (DO)-based sliding mode controller in [38] are presented in Figure 6 and Figure 7 for comparison. From Figure 6a, we can see that fluctuates slightly at 5 s, but quickly converges to zero after 24 s, indicating that mismatched disturbances are effectively estimated. As shown in Figure 6b, fluctuates slightly but converges to zero quickly, which illustrates matched disturbances are effectively estimated by DO. From Figure 7a, we can obtain that the collisions between neighboring vehicles are avoided. The velocity and velocity error curves in Figure 7b,c show that the vehicle platoon achieves velocity synchronization. Figure 7d shows that decreases along the platoon, which indicates that strong string stability is achieved.
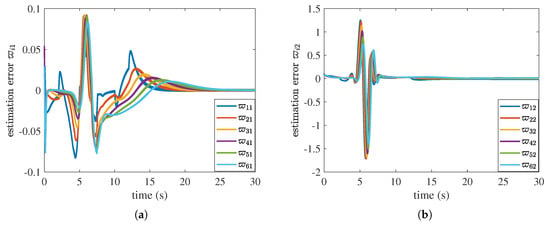
Figure 6.
The estimation results of the DO. (a) Estimation error of mismatched disturbances . (b) Estimation error of matched disturbances .
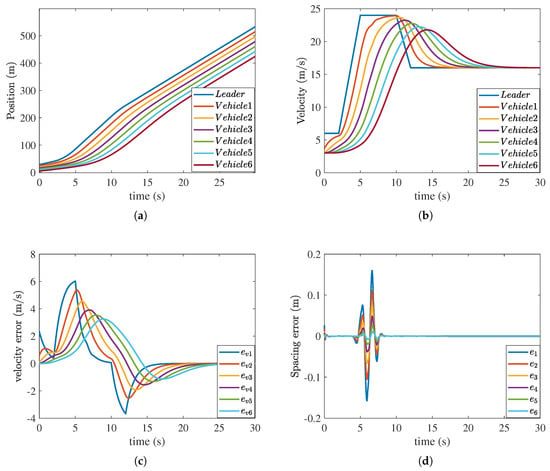
Figure 7.
The control results of the DO-based controller. (a) Position of ith vehicle. (b) Velocity of ith vehicle. (c) Velocity error . (d) Spacing error .
To achieve a quantitative comparison of the performance between the proposed method and the DO-based sliding mode control strategy, the overshoot and integral of the time-weighted absolute error (ITAE) index of are incorporated as shown in Table 1. According to Table 1, we can observe that compared to the DO-based sliding mode controller in [38], the FTDO-based controller can reduce the overshoot of by and improve the tracking accuracy by . A quantitative comparison of the performance between FTDO and DO is presented in Table 2. According to Table 2, compared to the DO in [38], FTDO can improve the estimation accuracy of the mismatched disturbance by and that of the matched disturbance by .

Table 1.
Comparative results under different controllers.

Table 2.
Comparative results under different DOs.
By analyzing the results, we can conclude that the proposed control strategy enhances the tracking accuracy and reduces the overshoot of , thereby enabling the vehicle platoon to achieve better control performance. Moreover, the proposed FTDO can effectively improve the estimation accuracy of the disturbances.
5. Conclusions
This study proposes a novel FTDO-based sliding mode control scheme for a vehicle platoon affected by matched and mismatched disturbances to accomplish control goals. The novel FTDO is designed to estimate the two types of disturbances directly without the need to know the precise upper bounds of the disturbances. To mitigate the adverse impact of disturbances, a feedforward compensation term derived from the disturbance estimation is incorporated into the FTDO-based sliding mode control scheme to address the control performance degradation caused by disturbances and to ensure the vehicle platoon’s stability. The example results validate the efficacy of the proposed FTDO-based sliding mode control scheme. Note that we study the control problem of vehicle platoons with mismatched disturbances under the assumption of ideal communication conditions, while neglecting the impact of time-varying communication delays. In future work, it will be of value to investigate control strategies for vehicle platoons with communication delays.
Author Contributions
Conceptualization, Y.W. (Yiguang Wang) and Y.J.; methodology, X.Z.; software, X.Z. and X.L.; validation, X.Z. and Y.W. (Yaxuan Wang); formal analysis, Y.J.; investigation, Y.W. (Yiguang Wang) and X.Z.; resources, X.T.; data curation, X.Z.; writing—original draft preparation, X.Z.; writing—review and editing, Y.J.; visualization, X.Z.; supervision, X.L.; project administration, X.T. and X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Fund of Guangxi Science and Technology Key Research and Development Program under Grant 2024AB33219, in part by the Fund of Guilin Science Research and Technology Development Program under Grant 20230105-3 and Grant 20230110-4, and in part by the Fund of Innovation Project of Guangxi Graduate Education under Grant JGY2023151.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FTDO | Finite time disturbance observer |
| CTH | Constant time headway |
References
- Wang, Y.; Dong, H.; Li, X. Distributed Cooperative Neural Control for Nonlinear Heterogeneous Platoon Systems with Unknown Uncertainties. Arab. J. Sci. Eng. 2024, 49, 15957–15970. [Google Scholar] [CrossRef]
- Xu, L.; Zhuang, W.; Yin, G.; Bian, C. Energy-oriented cruising strategy design of vehicle platoon considering communication delay and disturbance. Transp. Res. Part C Emerg. Technol. 2019, 107, 34–53. [Google Scholar] [CrossRef]
- Deng, Z.; Fan, J.; Shi, Y.; Shen, W. A coevolutionary algorithm for cooperative platoon formation of connected and automated vehicles. IEEE Trans. Veh. Technol. 2022, 71, 12461–12474. [Google Scholar] [CrossRef]
- Zhai, C.; Chen, C.; Zheng, X.; Han, Z.; Gao, Y.; Yan, C.; Luo, F.; Xu, J. Ecological cooperative adaptive cruise control for heterogenous vehicle platoons subject to time delays and input saturations. IEEE Trans. Intell. Transp. Syst. 2022, 24, 2862–2873. [Google Scholar] [CrossRef]
- Zhou, A.; Peeta, S.; Wang, J. Cooperative control of a platoon of connected autonomous vehicles and unconnected human-driven vehicles. Comput.-Aided Civ. Infrastruct. Eng. 2023, 38, 2513–2536. [Google Scholar] [CrossRef]
- Hu, J.; Bhowmick, P.; Arvin, F.; Lanzon, A.; Lennox, B. Cooperative control of heterogeneous connected vehicle platoons: An adaptive leader-following approach. IEEE Robot. Autom. Lett. 2020, 5, 977–984. [Google Scholar] [CrossRef]
- Xue, Y.; Wang, C.; Ding, C.; Yu, B.; Cui, S. Observer-based event-triggered adaptive platooning control for autonomous vehicles with motion uncertainties. Transp. Res. Part C Emerg. Technol. 2024, 159, 104462. [Google Scholar] [CrossRef]
- Xu, L.; Ma, J.; Zhang, S.; Wang, Y. Car following models for alleviating the degeneration of CACC function of CAVs in weak platoon intensity. Transp. Lett. 2023, 16, 599–611. [Google Scholar] [CrossRef]
- Gao, H.; Ren, X.; You, Z.; Li, X.; Xiao, Y.; Guo, M.; Ma, X. Determination of the optimal connected and automated vehicles platoon size based on the merging success rate. Transp. Lett. 2023, 16, 857–871. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, X.; Jiang, Y.; Li, X.; Zhan, X. Adaptive integral sliding mode control strategy for vehicular platoon with prescribed performance. Sci. Rep. 2025, 15, 14156. [Google Scholar] [CrossRef]
- Di Bernardo, M.; Salvi, A.; Santini, S. Distributed consensus strategy for platooning of vehicles in the presence of time-varying heterogeneous communication delays. IEEE Trans. Intell. Transp. Syst. 2014, 16, 102–112. [Google Scholar] [CrossRef]
- Yu, G.; Wong, P.K.; Huang, W.; Zhao, J.; Wang, X.B.; Yang, Z.X. Distributed adaptive consensus protocol for connected vehicle platoon with heterogeneous time-varying delays and switching topologies. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17620–17631. [Google Scholar] [CrossRef]
- Mattas, K.; Albano, G.; Donà, R.; He, Y.; Ciuffo, B. On the relationship between traffic hysteresis and string stability of vehicle platoons. Transp. Res. Part B Methodol. 2023, 174, 102785. [Google Scholar] [CrossRef]
- Chen, J.; Liang, H.; Li, J.; Lv, Z. Connected automated vehicle platoon control with input saturation and variable time headway strategy. IEEE Trans. Intell. Transp. Syst. 2020, 22, 4929–4940. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, J.; Wang, Z.; Yan, H.; Zhang, C. Distributed adaptive event-triggered control and stability analysis for vehicular platoon. IEEE Trans. Intell. Transp. Syst. 2020, 22, 1627–1638. [Google Scholar] [CrossRef]
- Guo, X.; Wang, J.; Liao, F.; Teo, R.S.H. Distributed adaptive sliding mode control strategy for vehicle-following systems with nonlinear acceleration uncertainties. IEEE Trans. Veh. Technol. 2016, 66, 981–991. [Google Scholar] [CrossRef]
- Li, X.; Shi, P.; Wang, Y.; Wang, S. Cooperative tracking control of heterogeneous mixed-order multiagent systems with higher-order nonlinear dynamics. IEEE Trans. Cybern. 2020, 52, 5498–5507. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, X.; Xia, Y.; Zuo, Z.; Wang, Y. Disturbance observer-based integral sliding-mode control for systems with mismatched disturbances. IEEE Trans. Ind. Electron. 2016, 63, 7040–7048. [Google Scholar] [CrossRef]
- Fang, X.; Liu, F.; Wang, Z.; Dong, N. Novel disturbance-observer-based control for systems with high-order mismatched disturbances. Int. J. Syst. Sci. 2018, 49, 371–382. [Google Scholar] [CrossRef]
- Li, S.E.; Gao, F.; Li, K.; Wang, L.Y.; You, K.; Cao, D. Robust longitudinal control of multi-vehicle systems—A distributed H-infinity method. IEEE Trans. Intell. Transp. Syst. 2017, 19, 2779–2788. [Google Scholar] [CrossRef]
- Wang, J.; Luo, X.; Yan, J.; Guan, X. Distributed integrated sliding mode control for vehicle platoons based on disturbance observer and multi power reaching law. IEEE Trans. Intell. Transp. Syst. 2020, 23, 3366–3376. [Google Scholar] [CrossRef]
- Guo, G.; Li, D. Adaptive sliding mode control of vehicular platoons with prescribed tracking performance. IEEE Trans. Veh. Technol. 2019, 68, 7511–7520. [Google Scholar] [CrossRef]
- Wu, Z.; Sun, J.; Hong, S. RBFNN-based adaptive event-triggered control for heterogeneous vehicle platoon consensus. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18761–18773. [Google Scholar] [CrossRef]
- Xiao, W.; Ren, H.; Zhou, Q.; Li, H.; Lu, R. Distributed finite-time containment control for nonlinear multiagent systems with mismatched disturbances. IEEE Trans. Cybern. 2021, 52, 6939–6948. [Google Scholar] [CrossRef]
- Lei, H.; Sun, J.; Zeng, Y.; Yi, L.; Wang, F. Sliding-mode control for heterogeneous vehicular platoons with unknown matched and mismatched disturbances under intermittent communications. Veh. Commun. 2024, 45, 100718. [Google Scholar] [CrossRef]
- Shafei, H.R.; Bahrami, M.; Talebi, H.A. Disturbance observer-based two-Layer control strategy design to deal with both matched and mismatched uncertainties. Int. J. Robust Nonlinear Control 2021, 31, 1640–1656. [Google Scholar] [CrossRef]
- An, J.; Liu, Y.; Sun, J.; Wang, L.; Xue, H. Distributed fixed-time NN tracking control of vehicular platoon systems with singularity-free. Neural Comput. Appl. 2023, 35, 2527–2540. [Google Scholar] [CrossRef]
- Wei, X.; Guo, L. Composite disturbance-observer-based control and H∞ control for complex continuous models. Int. J. Robust Nonlinear Control 2010, 20, 106–118. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Chen, W.H. Nonlinear disturbance observer-based control for multi-input multi-output nonlinear systems subject to mismatching condition. Int. J. Control 2012, 85, 1071–1082. [Google Scholar] [CrossRef]
- Wang, X.; Li, S.; Lam, J. Distributed active anti-disturbance output consensus algorithms for higher-order multi-agent systems with mismatched disturbances. Automatica 2016, 74, 30–37. [Google Scholar] [CrossRef]
- Bian, Y.; Li, S.E.; Ren, W.; Wang, J.; Li, K.; Liu, H.X. Cooperation of multiple connected vehicles at unsignalized intersections: Distributed observation, optimization, and control. IEEE Trans. Ind. Electron. 2019, 67, 10744–10754. [Google Scholar] [CrossRef]
- Li, X.; Shi, P. Cooperative fault-tolerant tracking control of heterogeneous hybrid-order mechanical systems with actuator and amplifier faults. Nonlinear Dyn. 2019, 98, 447–462. [Google Scholar] [CrossRef]
- Swaroop, D.; Hedrick, J.K.; Choi, S.B. Direct adaptive longitudinal control of vehicle platoons. IEEE Trans. Veh. Technol. 2001, 50, 150–161. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Continuous finite-time stabilization of the translational and rotational double integrators. IEEE Trans. Autom. Control 1998, 43, 678–682. [Google Scholar] [CrossRef]
- Kwon, J.; Chwa, D. Adaptive bidirectional platoon control using a coupled sliding mode control method. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2040–2048. [Google Scholar] [CrossRef]
- Levant, A.; Livne, M. Globally convergent differentiators with variable gains. Int. J. Control 2018, 91, 1994–2008. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. A Lyapunov approach to second-order sliding mode controllers and observers. In Proceedings of the 2008 47th IEEE Conference on Decision and Control 2008, Cancun, Mexico, 9–11 December 2008; pp. 2856–2861. [Google Scholar]
- Wang, Y.; Liu, Y.; Li, X.; Liang, Y. Distributed consensus tracking control based on state and disturbance observations for mixed-order multi-agent mechanical systems. J. Frankl. Inst. 2023, 360, 943–963. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).