Enhancing Predictive Accuracy of Landslide Susceptibility via Machine Learning Optimization

Abstract

The present study examines the application of four machine learning models—Multi-Layer Perceptron, Naive Bayes, Credal Decision Trees, and Random Forests—to assess landslide susceptibility using Mei County, China, as a case study. Aerial photographs and field survey data were integrated into a GIS system to develop a landslide inventory map. Additionally, 16 landslide conditioning factors were collected and processed, including elevation, Normalized Difference Vegetation Index, precipitation, terrain, land use, lithology, slope, aspect, stream power index, topographic wetness index, sediment transport index, plan curvature, profile curvature, and distance to roads. From the landslide inventory, 87 landslides were identified, along with an equal number of randomly selected non-landslide locations. These data points, combined with the conditioning factors, formed a spatial dataset for our landslide analysis. To implement the proposed methodological approach, the dataset was divided into two subsets: 70% formed the training subset and 30% formed the testing subset. A correlation analysis was conducted to examine the relationship between the conditioning factors and landslide occurrence, and the certainty factor method was applied to assess their influence. Beyond model comparison, the central focus of this research is the optimization of machine learning parameters to enhance prediction reliability and spatial accuracy. The results show that the Random Forests and Multi-Layer Perceptron models provided superior predictive capability, offering detailed and actionable landslide susceptibility maps. Specifically, the area under the receiver operating characteristic curve and other statistical indicators were calculated to assess the models’ predictive accuracy. By producing high-resolution susceptibility maps tailored to local geomorphological conditions, this work supports more informed land-use planning, infrastructure development, and early warning systems in landslide-prone areas. The findings also contribute to the growing body of research on artificial intelligence-driven natural hazard assessment, offering a replicable framework for integrating machine learning in geospatial risk analysis and environmental decision-making.

1. Introduction

Landslides can be described as a natural phenomenon in which slope materials collapse and move downhill along the slope under the action of gravity, triggered by both natural factors and human activities [1]. Landslides have become one of the most significant natural disasters and seriously affect human life, the safety of properties, and infrastructure development [2]. According to statistics, developing countries have suffered the most losses due to landslide disasters (e.g., China and Iran), with 95% of landslide disasters occurring in developing countries [3]. Consequently, mitigating landslide-related damage has become an urgent and indispensable area of research. Furthermore, the mechanism of landslide occurrence is highly complex and influenced by numerous natural and anthropogenic factors [4]. As a result, the spatial prediction of landslide occurrence is a critical area of research. Effective analyses require the use of relevant data and software to identify the factors contributing to landslides. Studies have shown that the slope angle, lithology, slope aspect, and land use are strongly correlated with landslide occurrences [5]. Additionally, human activities and infrastructure development play significant roles in triggering landslides.

A review of previous research on landslide management indicates that areas with a high probability of landslide occurrence can be proactively managed to mitigate risks [6]. Studies consistently emphasize that understanding the mechanisms behind landslide occurrences and accurately delineating landslide-prone areas are essential for effective land use planning and management. In this context, landslide susceptibility maps are widely recognized as a crucial tool for natural disaster management [7,8].

When creating landslide susceptibility maps, two factors are considered extremely important: (a) high-quality and sufficiently available data and (b) the application of appropriate predictive models [4]. Currently, there are a multitude of research methods which present a variety, in terms of the approach followed, and are constantly updated. Landslide susceptibility mapping is a complex nonlinear problem; therefore, in most cases, traditional statistical methods are considered inadequate for this task [9]. Methods such as the statistical index (SI), frequency ratio (FR), evidence-based belief functions (EBFs), and certainty factors (CFs) tend to yield less accurate predictions compared with the more advanced machine learning and hybrid models that have been introduced in recent years [10,11,12]. In this context, machine learning methods are playing an increasingly important role in the study of natural hazards, not just for landslide susceptibility assessments, but also in broader domains where predictive modeling and risk evaluation are critical [13]. Recent advances in performance-based hazard analysis have underscored the importance of selecting optimal intensity measures to enhance the resilience of underground infrastructure under seismic conditions. For example, a recent study by Shen et al. (2025) [14] demonstrated that sustained maximum acceleration is the most effective indicator for probabilistic seismic demand analysis of shield tunnels in both liquefiable and non-liquefiable soils, outperforming traditional measures such as peak ground acceleration and Housner spectral intensity. This insight aligns with our emphasis on identifying key conditioning factors in landslide-prone regions, where precise hazard quantification is essential for improving infrastructure resilience and disaster preparedness strategies [14].

Using machine learning algorithms, the probability of the occurrence of potential landslides in the study area can be determined by analyzing the spatial relationship between the landslide hazards that have occurred and the conditioning factors that induced landslides. In recent years, several machine learning methods have achieved remarkable results in landslide susceptibility research, such as artificial neural networks (ANNs), J48 decision trees (JDTs), bagging, and Logistic Model Trees (LMTs) [13,14,15,16,17,18]. Furthermore, the four machine learning algorithms used in this article are also widely used. For instance, Pham et al. used different machine learning models, namely, Naive Bayes (NB), Multi-Layer Perceptron (MLP), and Functional Trees (FTs), to map the susceptibility of landslides in Uttarakhand Area, India [19]. Similarly, Wang et al. used Credal Decision Tree (CDT) and Radial Basis Function Network (RBFN) models and their hybrid models to conduct a comparative study on the susceptibility to landslides in Nanchuan County, China [20]. In another study, Trigila et al. applied the Random Forest (RF) method to the evaluation of the susceptibility to shallow landslides in Giampilieri (in the northeast of Sicily, Italy) and conducted a comparative study with Logistic Regression (LR) [21]. Additionally, Lee et al. applied NB and Bayesian network models to landslide prediction research [22].

Each machine learning model has distinct characteristics, and its performance is often influenced by the specific attributes of the study area and the reliability of the data input [13,23]. This study aimed to advance landslide susceptibility assessment by applying four machine learning models—MLP, NB, CDT, and RF—to Mei County. These models span a range of complexities, from probabilistic (NB) and tree-based (CDT and RF), to neural network-based (MLP), allowing us to explore how different algorithmic approaches handle spatial and geomorphological variability. Our choice was further guided by findings in existing literature where these models have demonstrated reliable performance in complex terrain and data-limited contexts. Although no formal preliminary benchmarking was conducted in this specific area prior to full modeling, the diversity of the algorithms allowed us to compare their performance and robustness under the same conditions.

While machine learning models are widely used in landslide prediction, their accuracy and effectiveness are significantly affected by the modeling parameters, data quality, and regional characteristics [24]. Many prior studies have employed single-model approaches; however, comparatively few have systematically optimized and evaluated multiple algorithms within the context of a specific, hazard-prone area. Additionally, the influence of classification strategies on the interpretation of LSI values remains underexplored, despite its critical role in final zoning outputs. To address these gaps, the present study was designed to: (a) conduct a comparative evaluation of four machine learning models (MLP, NB, CDT, and RF) for landslide susceptibility mapping in Mei County; (b) optimize each model’s parameters to improve predictive performance; and (c) assess the effectiveness of four LSI classification techniques to identify the most reliable zoning method. The novelty of this research lies not only in its integrated comparative framework but also in its context-specific application to a mountainous, data-limited region. By combining model calibration, certainty factor analysis, and comprehensive validation using ROC curves and statistical indicators, this work presents a refined and transferable methodology for landslide susceptibility assessment. The results are intended to support regional disaster preparedness strategies and inform spatial planning in similarly vulnerable environments.

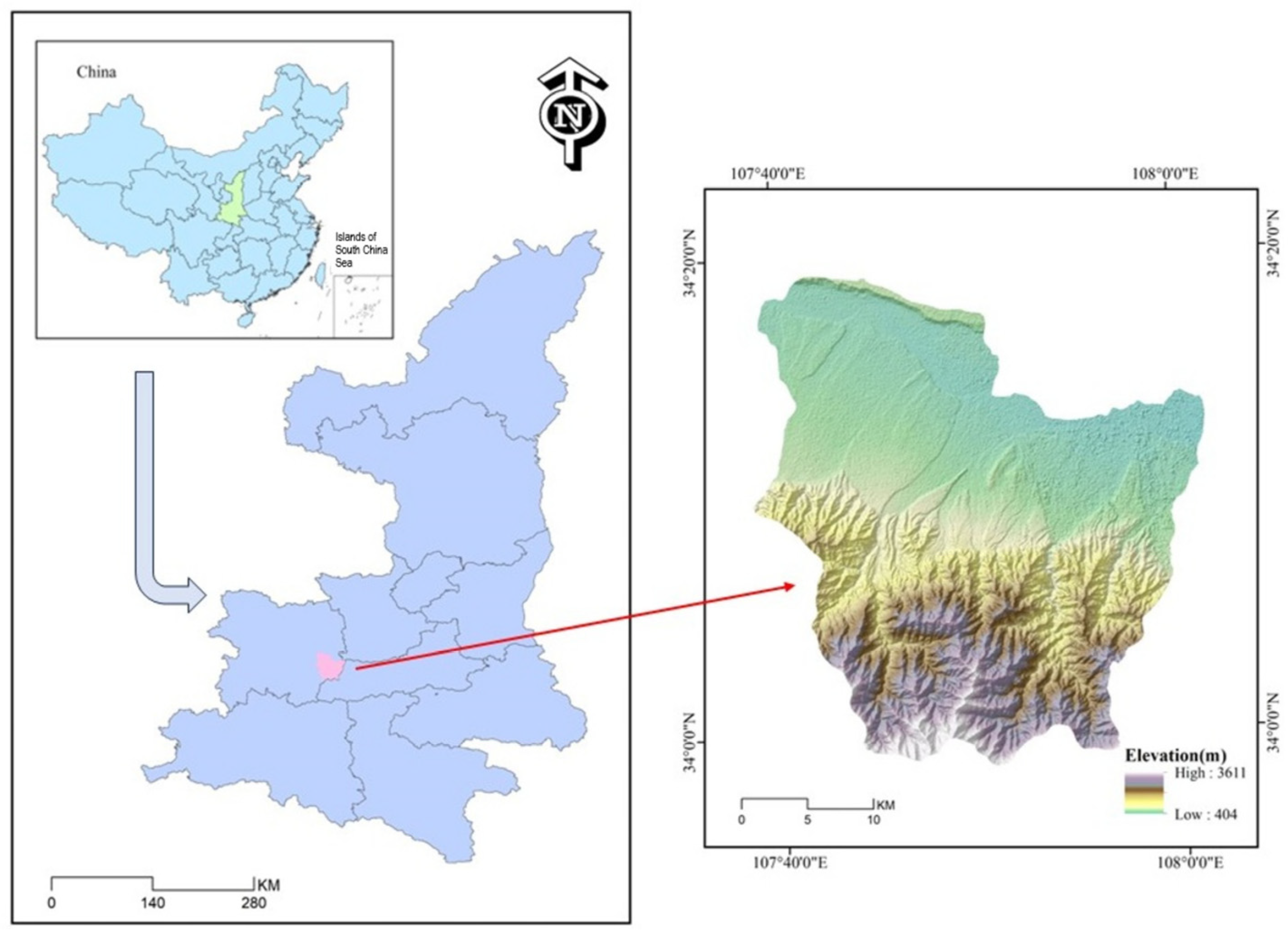
2. Study Area

Mei County, a subdivision of Baoji City, is geographically located between 33°59′ and 34°19′ N latitude and 107°39′ and 108°00′ E longitude (Figure 1), covering a total area of 863 km², which represents 4.74% of the total area of Baoji City District. Situated at the foot of the Taibai Mountains in the Qinling range, Mei County lies on the north bank of the Wei River and is part of the semi-hilly region on the northern slopes of the Qinling Mountains. Geologically, Mei County is part of the Mei County Shallow Depression, a secondary tectonic unit characterized by complex lithological formations and significant structural variation. The southern portion, particularly around Yingtou and Tangyu towns, lies within the North Qinling Fold Belt, an active orogenic zone with intense tectonic deformation. The region’s lithology, as shown in, comprises five distinct groups: unconsolidated deposits such as gravel, sand, and clay (Group 1); loess and loess-like soils (Group 2); granitic and gneissic rocks (Group 3); metamorphic sequences including marble and volcanic clastic rocks (Group 4); and highly foliated schists and quartzites (Group 5). These diverse lithological units exhibit varying mechanical properties and weathering behaviors, directly influencing slope stability and the development of landslide-prone areas. Mei County’s hydrogeological setting is strongly influenced by its diverse soil types, including Regosols, Luvisols, Leptosols, Fluvisols, Cambisols, and Anthrosols. These soils vary in permeability and water retention, affecting how rainwater moves through the landscape. Less cohesive soils like Regosols and Fluvisols are more prone to erosion and saturation, which can trigger landslides, especially during heavy rainfall. In contrast, soils like Cambisols and Leptosols offer better drainage, reducing slope failure risk. Combined with the region’s steep terrain and seasonal rains, these conditions contribute significantly to landslide susceptibility across the area.

The region experiences a temperate continental monsoon climate, characterized by altitudes ranging from 442 to 3767 m, an annual frost-free period of 218 days, an average annual temperature of 12.9 °C, and mean annual precipitation of 609.5 mm. The terrain is elevated in the north and south, with a lower central area, featuring loess ridges and the northern Weinan loess tableland. The landscape is relatively flat, with fertile soils that are rich in organic matter, while the climate offers ample sunlight, abundant rainfall, and significant temperature variations between day and night.

3. Methodology

The methodology developed in the present study involves three phases of analysis: data collection and preprocessing, model selection and parameter optimization, and performance evaluation. The first phase involved collecting all the necessary data, which included landslides, non-landslide areas, and landslide-related variables, along with preprocessing, which involved classification based on standard classification schemes and weighting of the classes using their degrees of influence. For the weighing process, this study utilized the certainty factor method. The first phase also included the preparation of the training and testing subsets. The second phase involved the implementation of the four models (MLP, NB, CDT, and RF), along with a parameter optimization process. Finally, a comparative analysis was carried out in the third phase, evaluating the model’s accuracy using ROC curve analysis and landslide density calculations to validate the models’ predictive reliability. The following section provides a brief description of the models and techniques used (Figure 2).

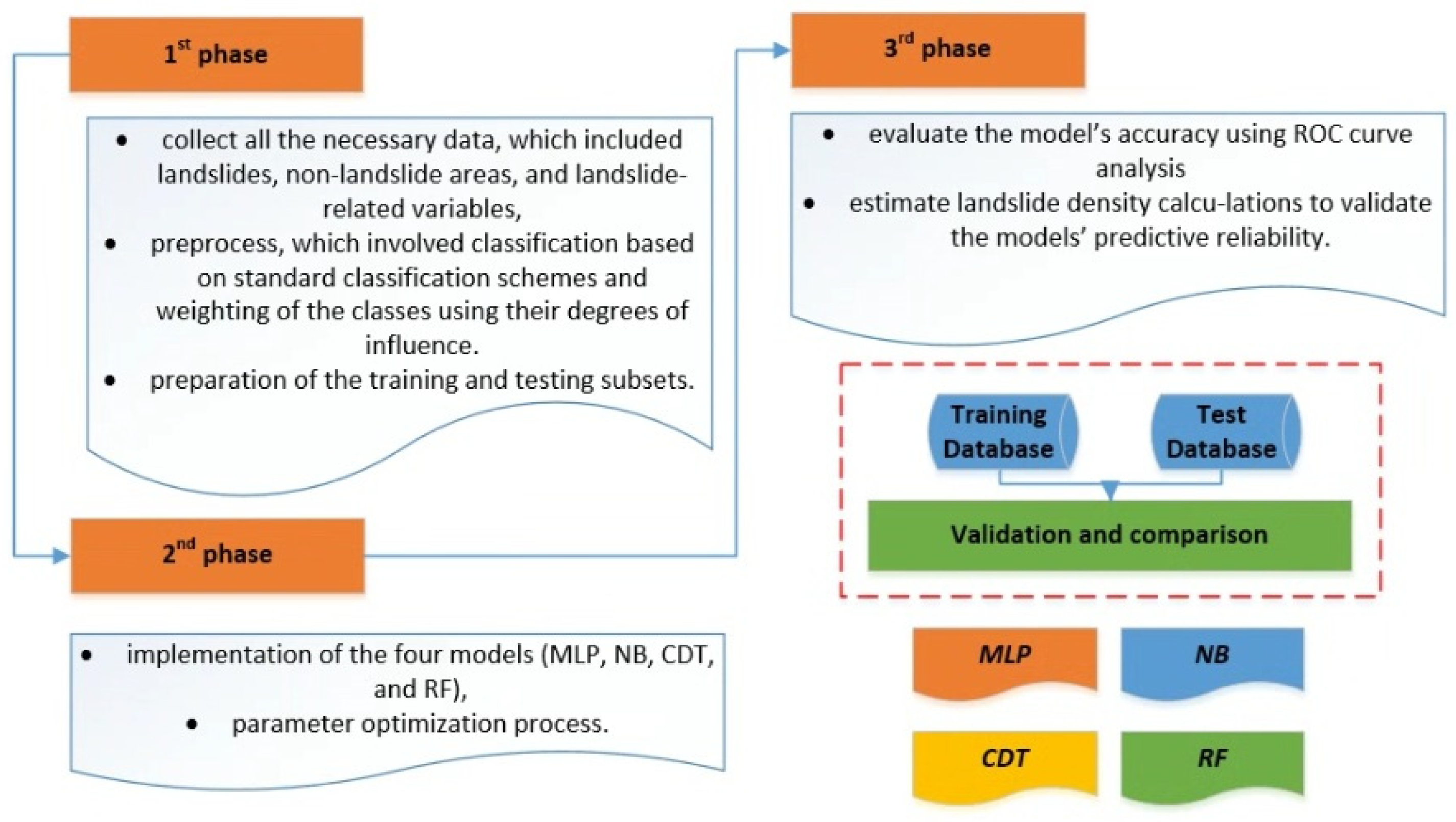
3.1. First Phase: Data Collection and Preprocessing

An accurate and reliable landslide inventory map is essential for landslide susceptibility evaluations [25,26,27]. In most cases, its construction relies on geological survey reports, remote sensing imagery, and field surveys, providing a comprehensive record of past landslides. Beyond identifying the locations and types of landslides, the inventory map also serves as a valuable tool for predicting future landslide occurrences, aiding in risk assessment and mitigation efforts [28,29,30]. In the present study, 87 landslides were identified based on the landslide inventory map of the study area. Since the landslides that have been identified in the study area have different shapes and sizes, the centroid of each landslide polygon was used for the landslide susceptibility assessments. To create a balanced landslide database, the same number of non-landslide points were randomly selected from the areas that were free of landslides within the study area. The next step included the division of the original dataset into training and testing datasets, using a ratio of 70:30. A total of 16 landslide conditioning factors were selected for the landslide susceptibility assessment in the study area: elevation, NDVI, rainfall, soil type, land use, lithology, slope, aspect, sediment transport index (STI), stream power index (SPI), topographic wetness index (TWI), plan curvature, profile curvature, and distances to faults, roads, and rivers (

Table 1. Sixteen landslide conditioning factors.

Factor Category	Factor	Classifications/Ranges
Topographic	Slope (°)	0.00–8.72, 8.72–19.19, 19.19–30.82, 30.82–43.32, 43.32–74.13
	Aspect	North, Northeast, East, Southeast, South, Southwest, West, Northwest
	Elevation (m)	422–798, 798–1281, 1281–1818, 1818–2399, 2399–3648
Hydrological/Terrain Indices	STI	<18.25, 18.25–66.91, 66.91–164.22, 164.22–352.78, >352.78
	SPI	<20.47, 20.47–88.80, 88.80–232.30, 232.30–573.93, >573.93
	TWI	<1.73, 1.73–2.66, 2.66–6.44, 6.44–10.22, >10.22
	Plan Curvature	−28.23 to −0.05, −0.05 to 0.05, 0.05 to 25.33
	Profile Curvature	−34.05 to −0.05, −0.05 to 0.05, 0.05 to 32.55
Proximity Factors	Distance to Faults (m)	0–500, 500–1000, 1000–1500, 1500–2000, >2000
	Distance to Roads (m)	0–300, 300–600, 600–900, 900–1200, >1200
Climatic	Rainfall (mm/year)	463.58–484.42, 484.42–500.94, 500.94–518.63, 518.63–537.50, 537.50–563.85
Land Use	Type	Farmland, Forest land, Grassland, Water bodies, Residential areas, Others
Soil Type	Soil Class	Eutric Regosol, Calcic Luvisol, Mollic Leptosol, Calcaric Fluvisol, Eutric Cambisol, Calcaric Cambisol, Fimic Anthrosol, Cumulic Anthrosol
Geological	Lithology Group	Group 1: Gravel/sand/clayey silt, Group 2: Loess, Group 3: Granite/gneiss, Group 4: Marble/volcanic rocks, Group 5: Schist/quartzite

). The selection of these factors was guided by the geological and environmental characteristics of the study area, combined with insights from previous research to ensure a comprehensive assessment. Moreover, in the case of numerical conditioning factors, we applied the Natural Breaks (Jenks) classification method to ensure that the grouping reflected local variability and data structure [31].

The Normalized Difference Vegetation Index (NDVI) reflects the vegetation coverage, with higher values indicating denser vegetation, which can influence the landslide susceptibility [32]. Vegetation plays a crucial role in slope stability by reinforcing the soil and reducing surface erosion, while areas with low NDVI values (indicating sparse or absent vegetation) are generally more prone to landslides. The NDVI map (Figure 3a), derived from Landsat 8 Operational Land Imager data, helps identify regions where reduced vegetation cover may contribute to an increased likelihood of landslide occurrences. Landslides are strongly influenced by the rainfall intensity and total precipitation, although their impact is highly dependent on the topography [33]. Steep slopes and the soil composition affect how rainfall infiltrates or accumulates, potentially triggering slope failures. The rainfall map (Figure 3b) was created using annual average precipitation data, with the highest recorded rainfall reaching 563.85 mm/year, providing insight into regions where excessive rainfall may contribute to increased landslide susceptibility. Different soil types vary in permeability, directly influencing the landslide susceptibility, as soils with low permeability can lead to water accumulation and slope instability, while more permeable soils achieve better drainage, reducing the likelihood of failure. The soil map (Figure 3c) was compiled from a 1:1,000,000-scale soil type map, providing essential information for assessing the role of soil characteristics in landslide occurrence. Land use is closely linked to human activities, which can either increase or decrease landslide susceptibility. Urbanization, deforestation, and agricultural practices can destabilize slopes, while vegetation-covered areas may help reinforce the soil and prevent erosion. The land use map (Figure 3d) was extracted from a 1:100,000-scale land use plan, providing insight into how different land use types influence the slope stability and landslide risk. Lithology is closely linked to geomorphological and surface characteristics [34] and plays a crucial role in landslide susceptibility, as different rock types exhibit varying degrees of weathering, strength, and permeability. The lithology map (Figure 3e) was compiled from a 1:500,000-scale geological map, providing essential insights into the geological conditions influencing the slope stability.

Additionally, other topographic factors were extracted from ASTER GDEM at a 30 × 30 m resolution, ensuring consistency in data processing. In this study, all 16 landslide conditioning factors were standardized to the same spatial resolution (30 × 30 m) to facilitate accurate susceptibility analysis and modeling.

3.2. Certainty Factor Method

The certainty factor (CF) method is a probabilistic approach that is used to evaluate the contribution of different landslide conditioning factors to the landslide susceptibility. It is widely employed due to its ability to measure the degree of certainty regarding the occurrence of landslides based on statistical relationships between observed landslide events and contributing factors [35]. A notable example of the usage of CF in advance modeling approaches is the work by Ma et al., who used CF for feature weighting in combination with a deep neural network (DNN) to evaluate landslide susceptibility [36]. The CF can be obtained using the following formula:

$$f\left(x\right)=\left\{\begin{array}{c}{\displaystyle \frac{PPa-PPs}{PPa\left(1-PPs\right)}}, if PPa\ge PPs\\ {\displaystyle \frac{PPa-PPs}{PPs\left(1-PPa\right)}}, if PPa<PPs\end{array}\right.$$

where PPa is the conditional probability of landslides in the a-th category, and PPs is the prior probability of the total number of landslides in the study area. The value of the CF is proportional to the probability of landslide occurrence, with values ranging between −1 and 1. A positive CF value indicates a higher likelihood of landslides, while a negative value suggests a lower probability. If the CF value is close to 0, it implies a weak or no correlation, making the certainty of landslide occurrence statistically insignificant.

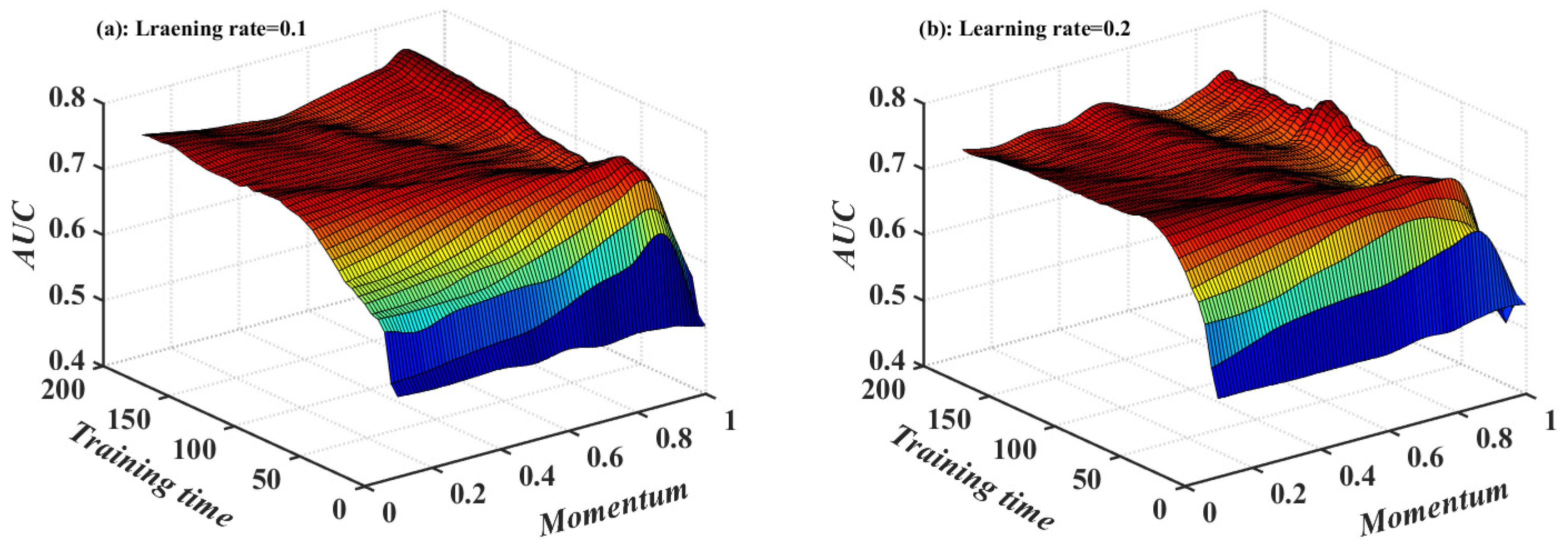
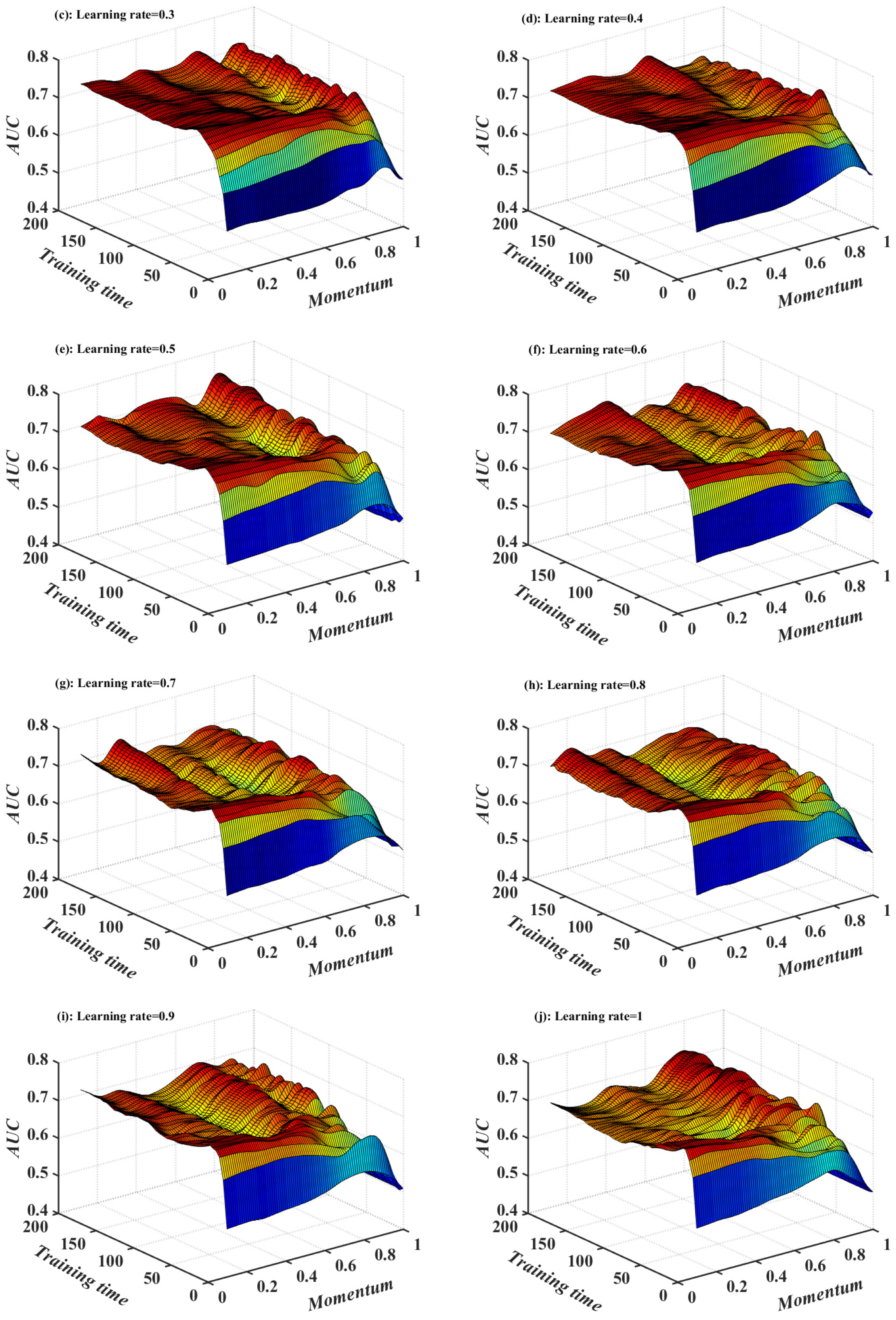
3.3. Multilayer Perceptron

The Multi-Layer Perceptron (MLP) is a type of artificial neural network (ANN) and widely used in artificial intelligence (AI) applications [37]. It is particularly effective for binary classification tasks involving nonlinear data [38]. The MLP model consists of three layers: an input layer, a hidden layer, and an output layer [39]. The layers are interconnected through weighted connections, which are adjusted during the training process to enhance the model’s stability and performance [40]. Research has also demonstrated the significant impact of weight optimization on MLP outcomes in various applications [41]. Compared with traditional classification methods, MLP offers superior predictive capability due to its ability to model complex, nonlinear relationships [38]. However, it also has certain limitations, such as a tendency to become trapped in local minima and slow learning speeds. Given that a landslide occurrence is a highly nonlinear process, MLP’s nonlinear mapping capabilities make it a suitable choice for landslide susceptibility prediction (LSP).

In the present study, the MLP model was applied for landslide susceptibility mapping, with the model architecture consisting of three layers: an input layer with 16 landslide conditioning factors, a hidden layer that served as the classification tool, and an output layer, which assigned a binary classification (1 for landslide, 0 for non-landslide) to each data point. The MLP neural network, in general, follows a unidirectional signal flow, where data are processed sequentially from the input layer to the output layer. Within this three-layer structure, weighted connections link the input layer to the hidden layer and the hidden layer to the output layer. These weights are iteratively adjusted during the training phase to refine the model’s predictive accuracy. The MLP model was developed using Weka software v3.8.6, where its parameters were fine-tuned to optimize its performance. Using the training dataset, the model was iteratively trained and validated to identify the optimal parameter configuration, ensuring stable and reliable susceptibility predictions.

3.4. Naive Bayes

Naive Bayes (NB) is a simple, yet effective, machine learning algorithm and commonly used for classification tasks [42]. While decision trees are also widely applied in classification problems [43,44,45,46], the NB model is rooted in classical probability theory [47,48,49,50,51], providing a strong mathematical foundation and consistent classification efficiency [52,53]. One of the key advantages of the NB model is its ability to handle small-scale datasets efficiently, making it particularly useful for multi-class classification problems. It is also computationally efficient and easy to implement and requires fewer estimated parameters than other machine learning models. Additionally, NB is less sensitive to missing data, which enhances its robustness in real-world applications [54]. However, NB has limitations—its classification performance is highly dependent on the input data representation, and it does not always outperform other models, particularly on complex datasets. Furthermore, the model operates under the strong assumption of attribute independence, meaning that it assumes that all input features contribute independently to the classification outcome, which may not always hold true in real-world scenarios [55]. Despite this, the NB model remains a widely used and reliable classification method due to its simplicity and efficiency. The implementation of NB in landslide susceptibility assessments can be expressed as follows:

$$y_{NB}=p\left(y_i\right){\displaystyle \prod _{i=1}^{n}P\left(x_i|y_i\right)}$$

(1)

where $p\left(y_i\right)$ and $P\left(x_i|y_i\right)$ represent the prior probability and conditional probability, respectively. $P\left(x_i|y_i\right)$ can be expressed as follows:

$$P\left(x_i|y_i\right)={\displaystyle \frac{1}{\sqrt{2\pi \beta }}}{e}^{{\displaystyle \frac{-{\left(x_i-\alpha \right)}^2}{2{\beta }^2}}}$$

(2)

where $\alpha$ represents the mean, and $\beta$ represents the standard deviation.

3.5. Credal Decision Trees

Credal Decision Trees (CDTs) is a classifier that was originally developed to solve classification problems [55,56,57]. To address the issue of the increasing uncertainty caused by the development of overly complex decision trees, the blocking classification process was introduced. This approach prevents excessive tree growth by implementing a stopping criterion during the generation of credal decision trees (CDTs). Specifically, if a tree split leads to increased uncertainty, the algorithm immediately halts further splitting, ensuring a more balanced and interpretable model [58,59]. The uncertainty of the trusted dataset is calculated as follows:

$$Eu\left(x\right)=NG\left(x\right)+RG\left(x\right)$$

(3)

where Eu represents the overall uncertainty value of the credal set, NG represents a non-specific function, and RG represents a general random function in the credal set. Furthermore, X is the framework of the entire credal set [57,60]. The probability interval of each variable can be calculated and determined using an imprecise probability model. Let Z be a variable, with zj representing its value; then, p(zj) represents the zj probability distribution:

$$p\left(Z_j\right)\in \left[{\displaystyle \frac{n_{zj}}{N+s}},{\displaystyle \frac{n_{zj}+s}{N+s}}\right],j=1,\dots ,k$$

(4)

where N represents the size of the sample dataset, while n_zj represents the frequency of an event occurring (Z = zj); s is a hyperparameter, and its value is selected from 1 or 2 [60,61].

3.6. Random Forest

The Random Forest (RF) algorithm was first introduced by Leo Breiman [62,63] and belongs to the category of ensemble machine learning methods. RF operates by generating a large number of classification trees and then aggregating their predictions to enhance the classification accuracy and reduce variance [62,63]. It is a nonparametric model that is widely applied in landslide susceptibility assessment due to its robustness in handling complex datasets and nonlinear relationships [18,64]. The RF algorithm primarily depends on two key parameters: t, the number of decision trees that are constructed, and m, the number of input features that are considered when splitting each node of a tree [65]. A major advantage of RF over other machine learning models is its ability to prevent overfitting by constructing multiple trees while maintaining its generalization capability. Unlike many other models, RF does not require cross-validation to assess its classification accuracy, as it inherently provides out-of-bag (OOB) error estimates [66]. The OOB error serves as an unbiased estimate of the generalization error, which stabilizes as the number of trees (t) increases. Therefore, selecting a sufficiently high t-value is crucial for achieving model convergence and optimal performance.

4. Results

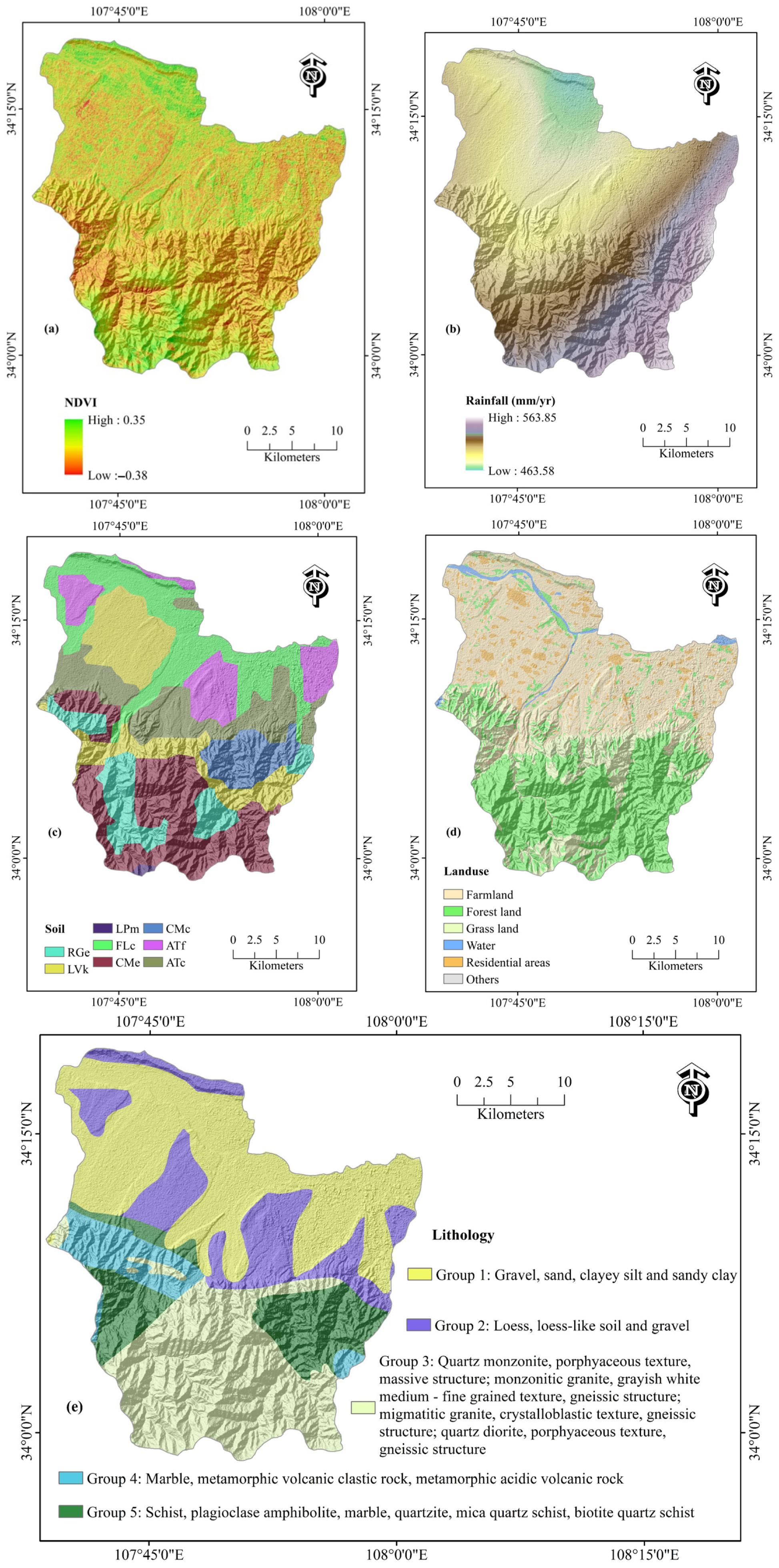
4.1. Landslide Conditioning Factor Analysis

As previously discussed, landslide susceptibility assessments typically involve analyzing a wide range of landslide-related factors. It is common practice to apply various selection methods to identify the most relevant and influential factors that best align with the specific characteristics of the study area, ensuring accurate and reliable model performance [66]. In order to analyze the spatial relationship between landslides and various conditioning factors in this study, we applied the CF method [67]. As illustrated in Table S1 in Supplementary File, the analysis revealed that the slope aspect has the highest correlation with landslide occurrence, with the south-west slopes achieving the highest CF value (0.625). Additionally, the statistical data confirmed that this category contains the highest number of recorded landslides. Regarding the slope steepness, among the five classified slope categories, the 8.82–19.19° and 19.19–30.82° ranges showed a positive correlation with landslide occurrence. Elevation is important when analyzing the spatial relationship between factors and landslides. Within our study area, which spans elevations from 422 m to 3648 m, landslides were positively correlated with two specific elevation ranges: 422–798 m and 2399–3648 m. In contrast, certain terrain indices showed no relationship with landslide activity. For instance, the last two classes of the STI had CF values of −1, indicating no recorded landslides in these categories. Similarly, when the SPI was greater than 573.93, the CF value was −1, confirming zero landslide occurrences. The TWI also showed an inverse relationship with the landslide probability, where increasing TWI values corresponded with a decreasing certainty of landslide occurrence, with the last two categories reaching CF = −1. Regarding the curvature, the plan curvature range of −0.05 to 0.05 showed a negative CF value of −0.213, while profile curvatures in the range of −34.05 to −0.05 had a slight positive correlation (CF = 0.089), with half of the recorded landslides falling within this category. Concerning the distance to faults, for areas greater than 2000 m, the correlation between this classification and the occurrence of landslides decreased (CF value of −0.24). On the other hand, when examining the distance to roads and when the area in question was within the range 0-300 m, there was a higher certainty regarding the occurrence of landslides. When examining the distance to rivers, we found that the 400–600 m (−0.77) and 600–800 m (0.49) ranges showed the lowest and highest correlations, respectively, with the occurrence of landslides. When the NDVI value rose in the negative range, the certainty of the occurrence of landslides also increased. When the NDVI value was −0.01–0.35 (−0.03), the correlation with the occurrence of landslides decreased. Regarding the certainty of rainfall and landslide occurrence, when the rainfall was in the range of 463.58–484.42 mm/year (0.45), it was highly correlated with landslides, while other ranges were not significantly correlated with the landslide occurrence. Among the six different land use categories, grassland (0.553) exhibited the highest correlation with the occurrence of landslides. Different soil types had different correlations with landslides. Except for Cumulic Anthrosol (ATC) and Calcaric Fluvisol (FLC), the other soil types showed negative certainties regarding the occurrence of landslides in this study. For lithology, the highest correlation was found in group 2 (0.37), with groups 1 (−0.21) and 5 (−0.27) achieving the lowest correlations with the occurrence of landslides.

4.2. Model Application

Research indicates that as landslide susceptibility assessment advances, machine learning models are playing an increasingly crucial role in predictive analysis. A key challenge in this process is optimizing model parameters to ensure maximum predictive accuracy and efficiency. This study focuses on enhancing the performance and reliability of three machine learning models, MLP, RF, and CDT, for landslide susceptibility assessment by systematically reconfiguring and fine-tuning their parameters using a grid search optimization technique.

For the RF model, two important parameters were selected: the number of iterations to be performed (numIterations), ranging from 1 to 200, and the random number seed, ranging from 1 to 30. After the parameter optimization process was completed, the optimal parameters (numIterations:16; seed:15) were used to improve the performance of the RF model (Figure 4). For the CDT model, two internal parameters were selected: numFold, which determines the amount of data used for pruning (ranging from 2 to 9), and seed, which is used for data randomization (ranging from 1 to 300). Combined with the training dataset, the optimal numFold value (8) and seed value (230) were obtained using the Weka software by comparing the AUC values of the model under different numFold and seed parameter values (Figure 5). The AUC is often used to quantitatively verify and compare the predictive power of models [68]. For the optimization of the MLP model in this study, the three parameters were applied to the parameter adjustment and optimization process: learning rate (the learning rate of the weight), training time (the number of epochs in training), and momentum (the momentum applied to the weight update). The learning rate values ranged from 0.1 to 1, with an interval of 0.1. Regarding the learning time value, we adjusted the momentum to within the range of 0.1 to 1 and the training time to within the range of 1 to 200, with intervals of 0.1 and 1, respectively. There were clear differences in the performance of the MLP model under different parameters, which was discovered after a large number of parameter adjustments (Figure 6). In the model optimization process, it could be seen that the performances of the three machine learning models were significantly affected by different parameters. After optimizing the selection of model parameters, the performance of the model was improved.

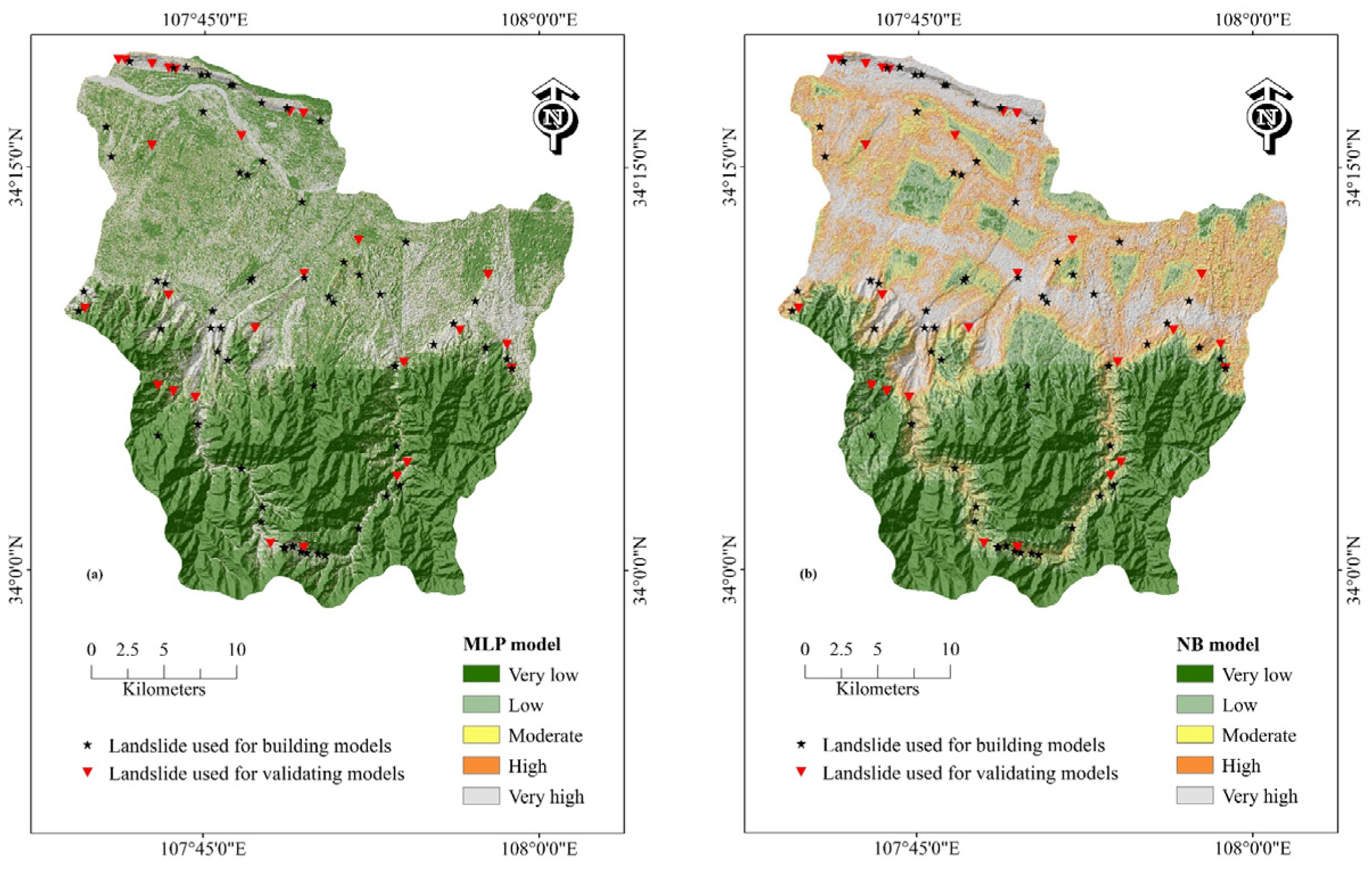
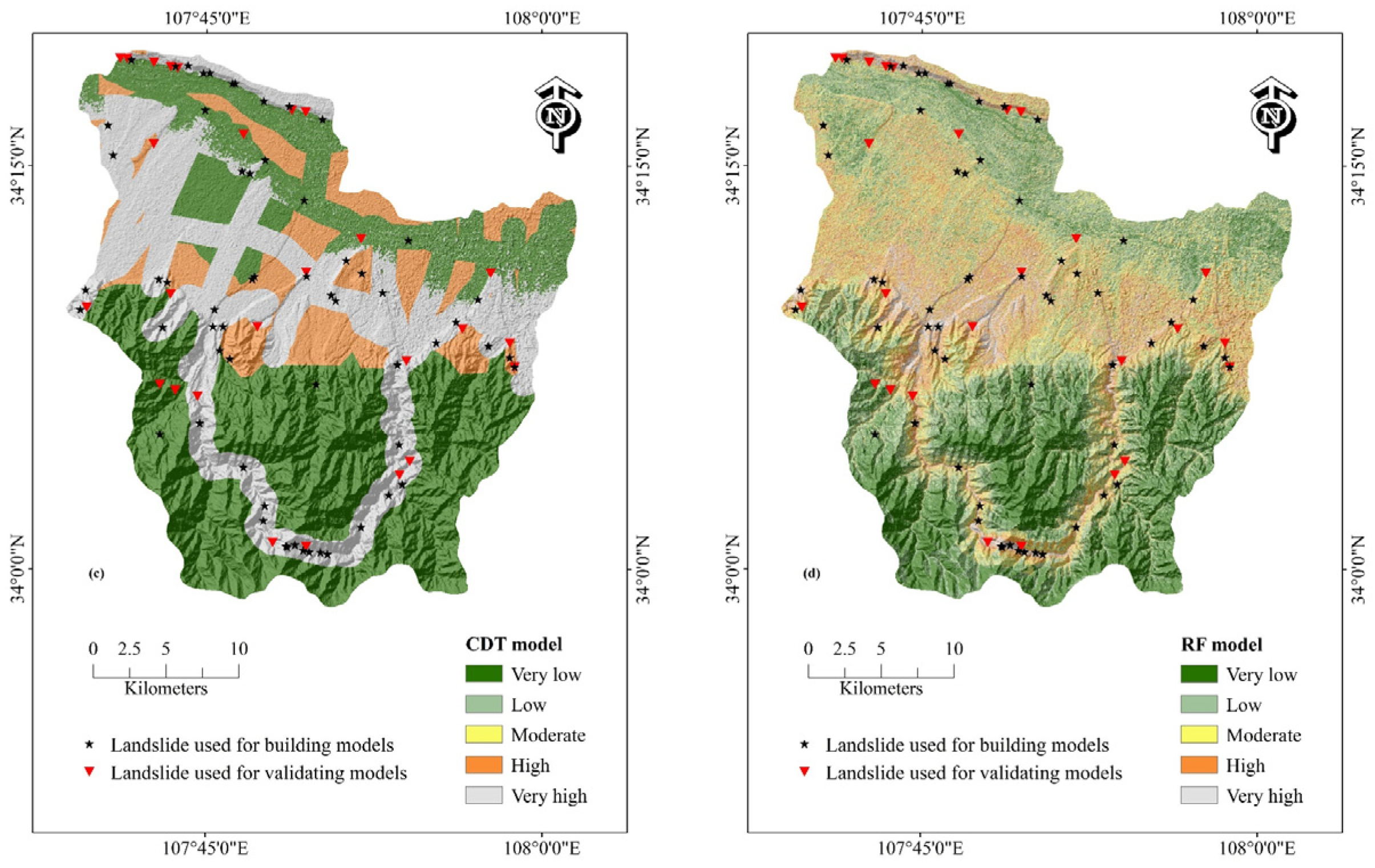
4.3. Generating Landslide Susceptibility Maps

For each of the optimized models, the next step of analysis was to calculate the landslide susceptibility index (LSI) for the study area. The range of LSI values is between 0 and 1, which corresponds to the susceptibility of an area to landslides. The available classification methods that could be applied to the produced landslide susceptibility map to divide the LSI value were the equal interval method, quantile method, natural break method, and geometric interval method [69,70,71]. After evaluating all the classification methods, the geometric interval method was determined to be the most suitable for this study. This method, along with the other three classification techniques, was applied to all four models to divide the LSI values into five susceptibility levels: very low, low, medium, high, and very high. The classification was conducted using ArcGIS 10.5 software (Figure 6, Figure 7, Figure 8 and Figure 9). In previous studies, researchers have primarily used the natural break method for landslide susceptibility zoning [72,73,74].

The CDT model exhibited a serious blocking phenomenon across the four classification schemes. After partitioning using the quantile and natural interval methods, the resultant maps of the LSI, calculated using the CDT model, differed too much from the results of the remaining three models (Figure 7 and Figure 9). Most of the lower half of the study area was shown to have low landslide susceptibility in the results of the RF, MLP, and NB models, while most of this part was classified as medium landslide susceptibility in the CDT model. Due to these inconsistencies, the natural break and quantile methods were deemed unsuitable for this study. In response to the results obtained by applying the equal interval method, the CDT model, due to its characteristics of splitting to reduce the uncertainty and using the equal interval method, led to the generation of three categories (very high, medium, and very low landslide susceptibility), which demonstrated a clear phenomenon of chunking, as shown in Figure 9. The geometric interval method effectively classified the LSI into five distinct levels across all four models. When compared with the 87 recorded landslide locations, the overall spatial distributions of the landslide susceptibility that were predicted by the four models closely aligned with real-world conditions, demonstrating the reliability and applicability of this classification approach (Figure 10).

Additionally, landslide density maps were generated for both classification methods to compare their effectiveness. The geometric interval method produced more accurate landslide density distributions across different susceptibility classes compared with the equal interval method. In the equal interval classification, the NB and CDT models exhibited lower landslide densities in the very high and high susceptibility classes, reducing their classification reliability. Furthermore, the equal interval method showed minimal variation in landslide densities across different susceptibility levels, making it less effective for capturing the actual distribution of landslide occurrences (Figure 11).

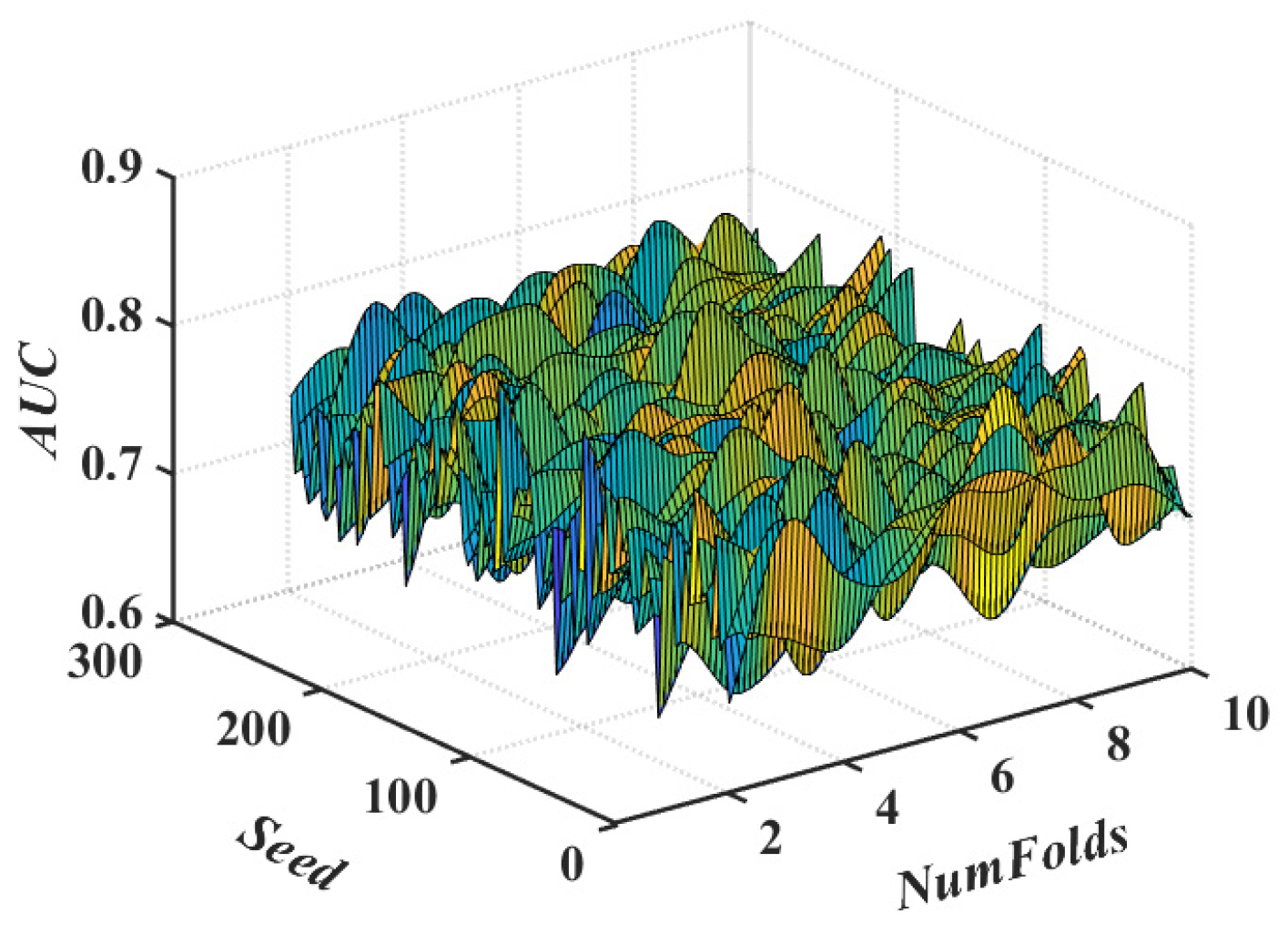
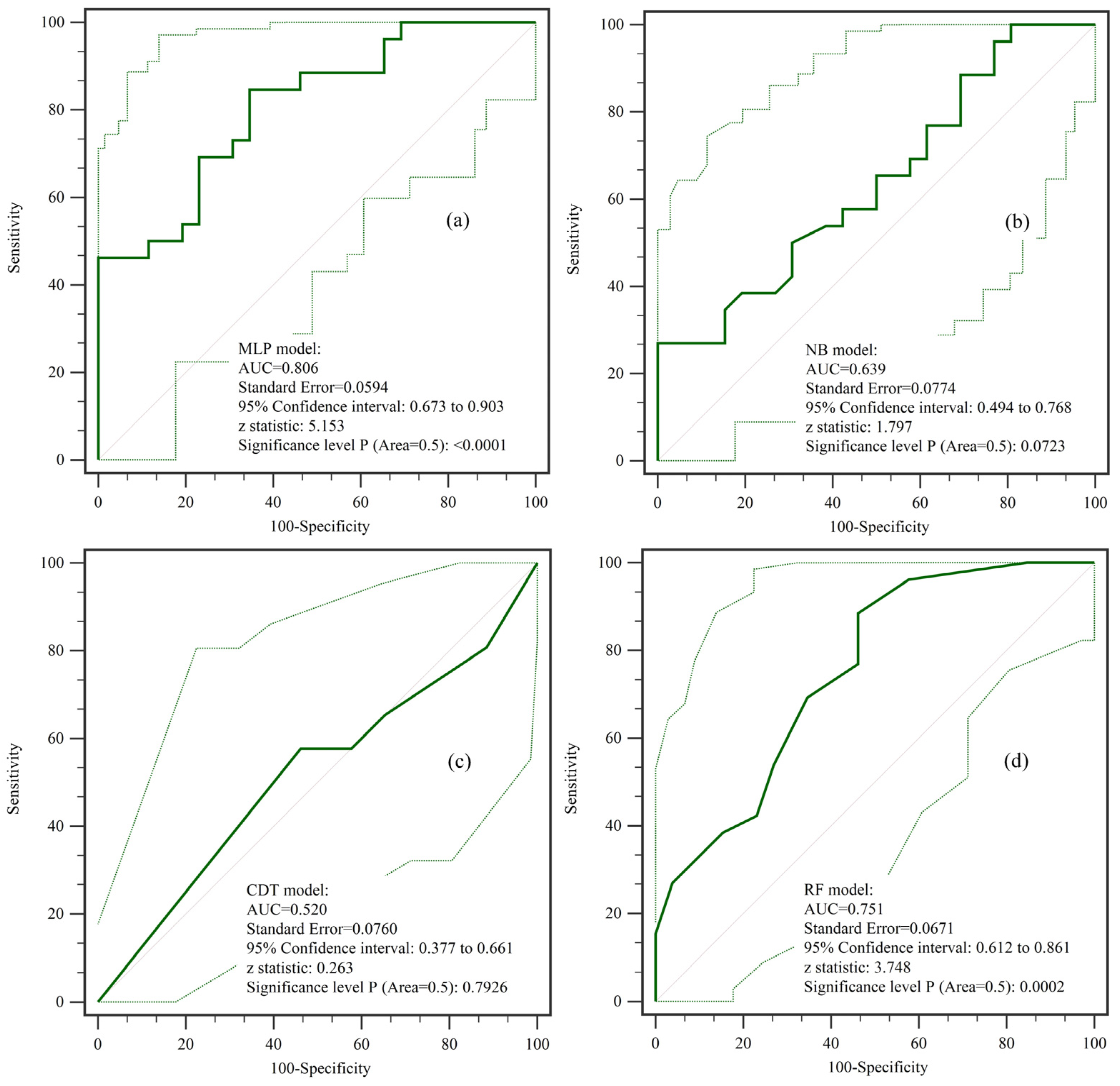
4.4. Validation and Comparison of Models

The success rate curve (SRC) under the training dataset and the prediction rate curve (PRC) under the validation dataset were used to complete the model comparison and validation process in this study. As a quantitative indicator, the AUC can reflect the goodness-of-fit and accuracy of the landslide susceptibility model. In the training dataset, the AUC values of the four landslide susceptibility models were 0.746 for MLP, 0.648 for NB, 0.839 for the CDT, and 0.868 for the RF (Figure 12). In the validation dataset, the corresponding AUC values of the four landslide susceptibility models MLP, NB, CDT, and RF were 0.806, 0.639, 0.520, and 0.751, respectively (Figure 13).

At the same time, some statistical indicators (standard error, 95% confidence interval, z statistic, and significance level P) were introduced to compare and verify the performances of the models. The standard error values corresponding to the MLP, NB, CDT, and RF models under the training dataset were 0.0444, 0.0498, 0.0354, and 0.0351, respectively. For the validation dataset, the corresponding standard deviation values of the MLP, NB, CDT, and RF models were 0.0594, 0.0774, 0.0760, and 0.0671, respectively.

The 95% CIs of the MLP, NB, CDT, and RF models were 0.659–0.820, 0.556–0.732, 0.762–0.899, and 0.795–0.923, respectively, under the training dataset. In the validation dataset, the 95% CIs of the MLP, NB, CDT, and RF models were 0.673–0.903, 0.494–0.768, 0.337–0.661, and 0.612–0.861, respectively.

In the training dataset, the Z-values of the MLP, NB, CDT, and RF models were 5.532, 2.966, 9.570, and 10.503, respectively. Meanwhile, the Z-values of the MLP, NB, CDT, and RF models were 5.135, 1.797, 0.263, and 3.748, respectively, under the validation dataset.

Except for the NB model, the p-values (significance level p) of the other three models (MLP, CDT, and RF) were all below 0.0001 under the training dataset. In the validation dataset, only the MLP model showed a small p-value (p < 0.0001).

5. Discussion

This study demonstrated that the highest correlation with the occurrence of landslides among a number of factors is the classification of the southwest slope direction (0.62), and that the certainty of landslides occurring is high at distances from the road in the range of 0–300 (0.60), with this certainty decreasing as the distance increases. The probability of landslides in calcareous Calcaric Fluvisol (0.44) and grasslands (0.55) is much higher than in other soil types and land use types, respectively. The certainty of landslides was 0.45 when the rainfall was in the range of 463.58–484.42, with other precipitation ranges having lower levels of correlation with landslides. Of the five categories delineated by the slope, the range of 19.19–30.82 had the highest certainty (0.40) associated with the occurrence of a landslide event. The remaining influence factors, such as the STI, SPI, TWI, planar curvature, and profile curvature, were all related to landslides to varying degrees depending on the type or range of values. There were also a few cases in which the CF value was −1 and no landslides occurred.

These patterns suggest that both topographic orientation and proximity to anthropogenic features play crucial roles in slope instability within the study area. The strong association with southwest-facing slopes may reflect prevailing climatic or geomorphic processes, such as sun exposure, prevailing wind directions, and differential moisture retention [75]. However, it is important to note that slope aspect may also be indirectly correlated with other geo-environmental variables that influence landslide development, relationships that are often not fully captured in purely statistical analyses. Previous studies have emphasized the statistical coupling between slope aspect and other landslide-predisposing factors [76], while others [77,78] suggest that local geological, hydrological, and morphological conditions can further modulate or even reshape slope aspect over time. These insights underscore the complexity of interpreting aspect-related correlations and highlight the need for multidimensional approaches that integrate both surface patterns and underlying geomorphic controls. Concerning the influence of road network, road construction frequently involves slope cutting, blasting, and vegetation removal, which significantly alter local terrain stability. As noted by Ghosh et al. [77], roadside sections are particularly prone to failure due to mechanical disturbance and concentrated runoff and that poorly designed drainage and slope modifications near roads can significantly amplify landslide susceptibility.

To optimize models’ performance in landslide susceptibility assessment, the MLP, CDT, and RF models were fine-tuned by selecting the most effective parameters. The MLP model was tested with learning rate values between 0.1 and 1, along with varying momentum factors, to identify the optimal configuration. The RF model was optimized by adjusting the number of decision trees (iterations) and random seed values, ensuring stability and accuracy in the LSI computation. Similarly, the CDT model was reconfigured by modifying iteration counts and random seed values to enhance the classification accuracy and minimize uncertainty. Through this parameter tuning process, the most suitable settings for each model were determined, improving their predictive reliability and overall performance.

In the present study, four partitioning methods were applied to classify the LSI values that were generated by different models. The CDT model exhibited severe chunking effects across the entire study area, while the NB model displayed notable chunking patterns, primarily in the upper half of the image. Most of the recorded landslides were concentrated in forest park regions, such as Taibai Mountain and Red River Valley, as well as surrounding mountainous areas, including exposed loess cropland, semi-exposed “V”-shaped gullies, and regions along the Tangyu River watershed, particularly in Qizhen, Hengqu, and Yingtou. The landslide susceptibility maps generated by the MLP, NB, and RF models closely aligned with the actual landslide distribution, whereas the CDT model, when classified using the quantile and natural break methods, produced results that significantly deviated from the other models. A comparison of the landslide density maps derived from the remaining two classification methods confirmed that the geometric interval method produced the most reliable and accurate zoning results. This could be attributed to its ability to accommodate skewed LSI distributions and enhance the spatial distinction between susceptibility classes, leading to more realistic zoning patterns that better reflected observed landslide occurrences. This is not always the case, as mentioned by other researchers that prefer other classification schemes, mostly Natural Breaks [17]. However, the observed consistency of higher accuracy among the MLP, NB, and RF models in our case underscores the importance of choosing an appropriate classification method.

Overall, the MLP achieved the most pronounced delineation of the study area, with AUC values of 0.746 and 0.868 for the MLP and RF models in the training dataset and 0.806 and 0.751 in the validation dataset, respectively. Compared with the NB and CDT models, the accuracies of their calculation results were better. Meanwhile, in the validation dataset, the 95% CIs of the MLP and RF model were 0.673–0.903 and 0.612–0.861, respectively, with a more concentrated distribution. However, the MLP model’s P-value was relatively small for both the training and validation samples. Since it is the most complex of the four models, combining the selected parameters, specific noise or details are recognized during the learning process, and the MLP model may have overfitted. The optimal iteration parameter chosen for the RF model was not too high, which would make the number of trees smaller, the depth of each tree correspondingly larger, and the complexity higher, while the p-value was not small enough to run the risk of underfitting. Similarly, the training dataset was larger than the validation dataset, meaning that the complexity of the model needed to be higher to compute the training dataset than the complexity of the validation dataset, and the corresponding risk of overfitting was larger. This meant that the p-value in the validation dataset of the four models was a little larger. Combining the selected model parameters and the computational results of the model, the RF model is more suitable for landslide susceptibility assessment in this area, and the MLP model is more prone to overfitting problems. The CDT and NB models are relatively ineffective in the assessment of landslide susceptibility.

The observed differences in model performance likely stem from their underlying learning architectures and assumptions. The MLP model, while highly flexible in capturing nonlinear relationships, is particularly sensitive to noise and parameter settings, which may explain its tendency toward overfitting—especially when trained on a relatively small and balanced dataset. As Pham et al. [19] noted, MLP does not require pre-assumptions about data distribution, and it adjusts input-variable weights dynamically during training, enabling greater adaptability to complex spatial patterns. The use of the back-propagation algorithm further minimizes errors between actual and predicted outcomes, enhancing predictive precision. These attributes have enabled MLP to achieve high accuracy in previous LSM studies [19,79,80], a trend also supported by the present results, where it achieved the highest PR and SR values (86.68% and 90.08%, respectively).

In contrast, the RF model’s ensemble-based structure ensures greater robustness and generalization by reducing variance through the aggregation of numerous decision trees trained on bootstrapped datasets. This characteristic makes RF particularly effective in modeling complex nonlinear relationships while avoiding overfitting, even when handling high-dimensional geospatial data [17]. However, this strength in generalization may limit the model’s ability to capture localized terrain variations and subtle feature interactions critical for high-resolution landslide delineation. As RF relies on majority voting from multiple shallow or randomly split trees, it may underrepresent small-scale spatial heterogeneity—especially in terrains with highly variable lithological or hydrological conditions [80]. The weaker performance of the NB model likely results from its assumption of conditional independence between features—an unrealistic premise in heterogeneous geospatial datasets. Similarly, CDT’s conservative approach to splitting under uncertainty appears to underrepresent true spatial variability. These results highlight that model suitability is context-dependent and must account for not only accuracy metrics but also algorithmic behavior, data structure, and the trade-off between generalization and detail capture. Despite its simplicity and computational efficiency, the NB model’s strong assumption of feature independence limits its ability to capture complex spatial interactions, which may contribute to its weaker performance in this study [55,81]. Nevertheless, its robustness with small datasets and low sensitivity to missing values makes it a viable tool for rapid, preliminary susceptibility assessments. CDTs, while effective in managing uncertainty through imprecise probabilities, tend to underperform in highly variable terrain due to their conservative splitting mechanism. Their strength lies in interpretability and reduced risk of overfitting, yet this comes at the expense of spatial granularity in complex geohazard contexts [58].

In the present study, ASTER GDEM at 30 m resolution was utilized for deriving topographic factors due to its consistent spatial coverage, compatibility with other datasets, and proven effectiveness in regional-scale landslide studies. While this resolution was sufficient for identifying susceptibility patterns at a broader scale, we acknowledge that finer-resolution datasets, such as LiDAR-derived DEMs, could provide more detailed terrain representation and enhance the precision of susceptibility zoning, particularly in localized or highly variable terrain. Recent studies [82,83] have demonstrated that DEM resolution significantly impacts the accuracy of slope-related hazard modeling. Similarly, Mahalingam et al. [84] emphasized the importance of high-resolution terrain data for extracting conditioning factors and validating results. Our methodology complements existing research by integrating a probabilistic framework with machine learning models, and we align with internationally endorsed protocols for landslide risk analysis [85]. However, future studies should explore the integration of high-resolution DSMs generated from UAV or LiDAR sources to improve terrain detail, particularly in micro-topographic features critical to slope instability. Additionally, coupling object-oriented image analysis techniques [86] with spectral and morphometric data could further refine landslide inventory generation and enhance model training. To advance the field, future work should also include time-series analysis of dynamic conditioning factors such as rainfall, vegetation changes (NDVI), and anthropogenic activity to capture temporal variability in susceptibility. Expanding the inventory with post-disaster UAV surveys and implementing more robust cross-validation strategies across multiple regions could further validate the generalizability of the proposed models.

In this study, the contribution of each conditioning factor to landslide occurrence was assessed using the certainty factor (CF) method, which enables range-based interpretation of variable influence. This approach allowed for a more nuanced understanding of how specific categories, such as slope aspect or lithology type, affect landslide probability—offering interpretable, domain-relevant insights essential for hazard planning. While alternative techniques like partial dependence plots (PDPs) or SHAP values could further improve model transparency, especially from a machine learning interpretability perspective, future research may benefit from integrating such tools to complement CF-based geomorphological reasoning [87]. Moreover, while this study employed a structured grid search approach for model optimization due to its transparency and computational feasibility, especially in resource-limited contexts, we acknowledge the growing value of advanced hyperparameter tuning methods. Techniques such as Bayesian Optimization, Genetic Algorithms, and Particle Swarm Optimization have shown promise in recent studies for enhancing model performance in complex geohazard applications [87]. Although not adopted here due to practical constraints, integrating these metaheuristic algorithms could be a valuable direction for future research—particularly when working with larger datasets or in multi-objective scenarios demanding greater computational precision and efficiency. Another point that should be mentioned is the possibility of the risk of autocorrelation concerning the distribution and selection of training and validation landslides. To minimize data leakage, each landslide sample in this study was derived from the centroid of a unique landslide polygon, ensuring no spatial overlap between training and validation datasets. This approach reduces the risk of autocorrelation and maintains dataset independence. However, we recognize that applying spatial cross-validation methods, such as k-fold blocking or buffer-zone partitioning, could further improve model robustness and will be considered in future research.

6. Conclusions

In this study, using Mei County as our study area, we screened and identified 16 landslide conditioning factors in conjunction with 87 landslides and analyzed their relationships with the landslides. We also explored the effectiveness of four machine learning models, namely, Multi-Layer Perceptron, Naive Bayes, Credible Decision Trees, and Random Forests, in assessing landslide susceptibility, selected the optimal parameters for computation, and mapped the landslide susceptibility based on the computed LSI values. The main conclusions are as follows:

• Among the many influencing factors, the slope orientation, distance from roads, and land use type are strongly associated with the occurrence of landslides in the study area. This is likely due to geomorphological controls on slope stability and the impact of human activities near road networks. In contrast, the STI, SPI, TWI, and NDVI showed weaker correlations, possibly due to low variability or indirect influence on slope failure mechanisms.
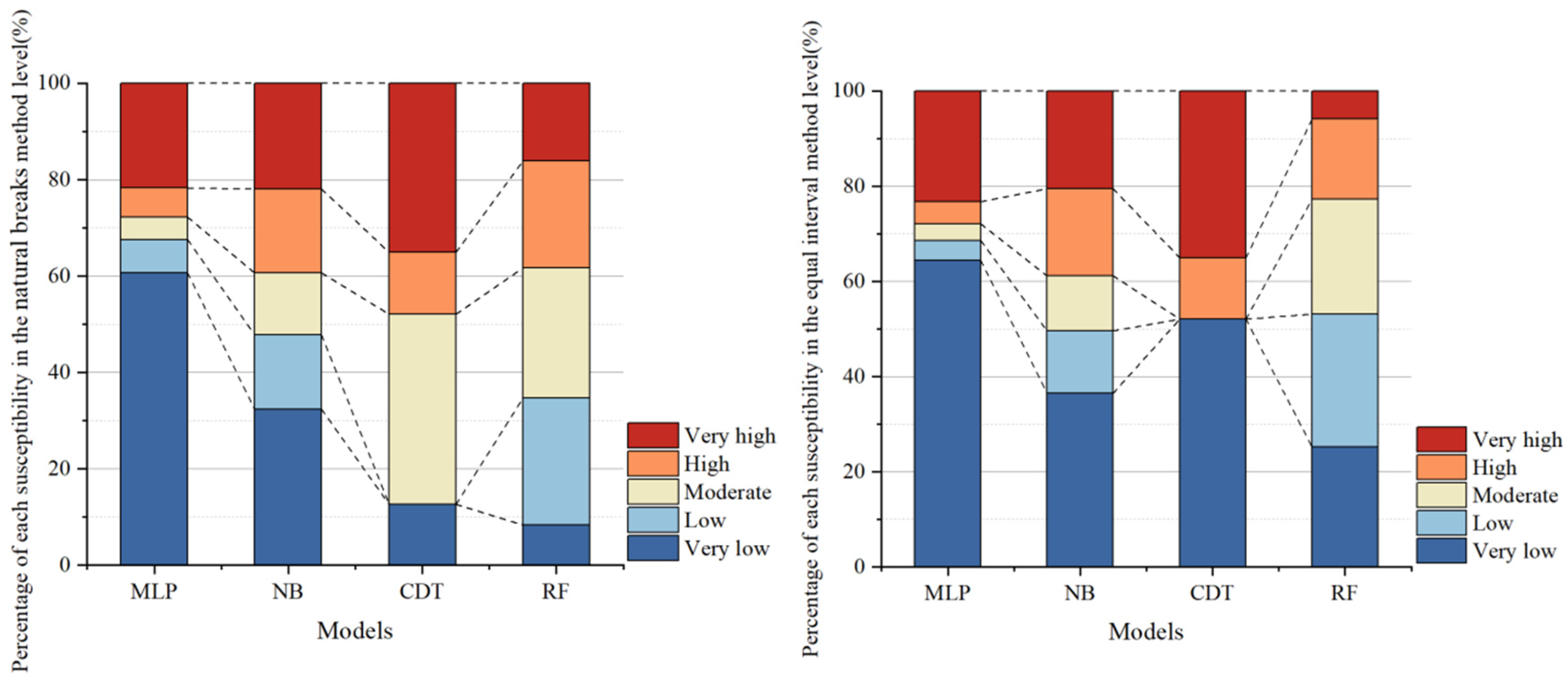
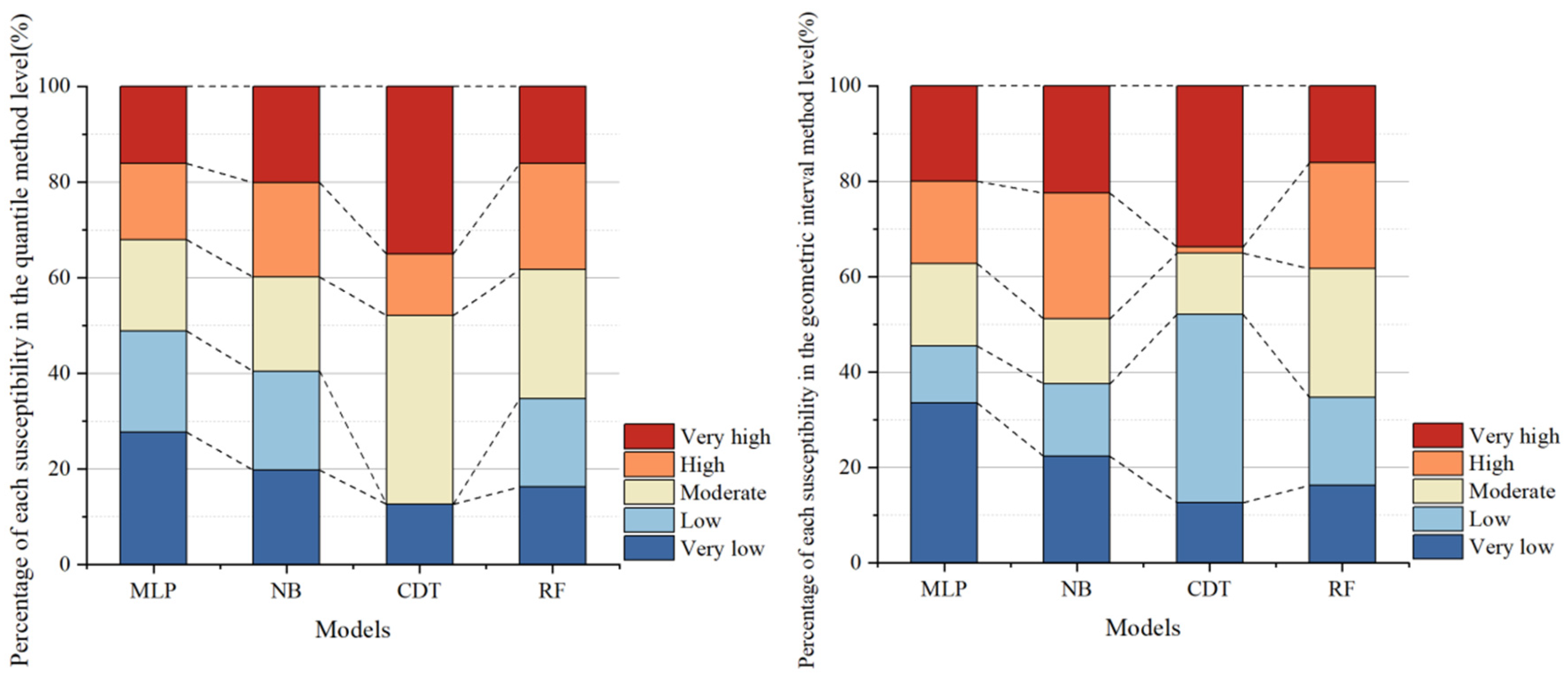
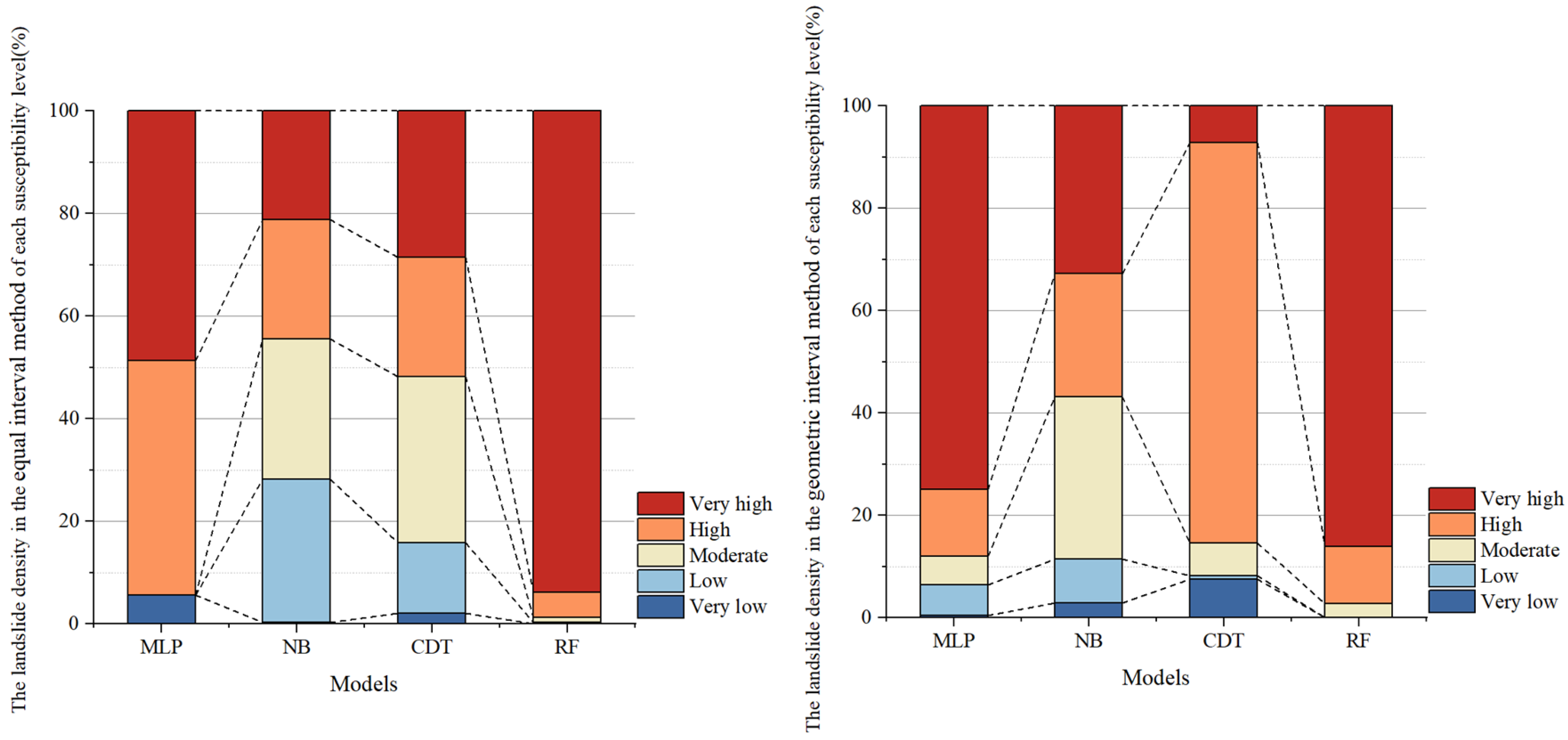
• Four partitioning methods were used to partition the results for each of the four model calculations, and the best results were obtained by using the geometric interval model. This method outperformed others because it effectively handled skewed distributions and enhanced the spatial contrast between susceptibility levels, aligning well with actual landslide occurrences.
• The CDT model displayed significant segmentation issues in its landslide susceptibility analysis, leading to overly generalized classification results and lower accuracy. This probably stems from its conservative splitting mechanism, which underrepresents spatial heterogeneity. The NB model also showed limitations in its predictive performance, possibly due to its strong independence assumptions among features which rarely hold true in complex terrain. In contrast, the MLP and RF models demonstrated higher reliability and accuracy, making them better suited for landslide susceptibility assessments.
• Based on the LSI distribution, the RF model exhibited the best overall performance, providing well-defined susceptibility zones, due to its ensemble learning structure and robustness to noise. The MLP model effectively highlighted areas of very low and very high landslide susceptibility, offering a more detailed delineation of landslide-prone regions, benefiting from its flexible architecture. The models, ranked from best to worst in terms of performance, are as follows: RF, MLP, NB, and CDT.