Abstract
Soil temperature is a critical environmental factor that affects plant development, physiological processes, and overall productivity. This study compares two modeling approaches for predicting soil temperature at various depths: (i) fuzzy logic-based systems, including the Mamdani fuzzy inference system (MFIS) and the adaptive neuro-fuzzy inference system (ANFIS); (ii) supervised machine learning algorithms, such as multilayer perceptron (MLP), support vector regression (SVR), random forest (RF), extreme gradient boosting (XGB), and k-nearest neighbors (KNN), along with multiple Linear regression (MLR) as a statistical benchmark. Soil temperature data were collected from Tokat, Türkiye, between 2016 and 2024 at depths of 5, 10, 20, 50, and 100 cm. The dataset was split into training (2016–2021) and testing (2022–2024) periods. Performance was evaluated using the root mean square error (RMSE), the mean absolute error (MAE), and the coefficient of determination (R2). The ANFIS achieved the best prediction accuracy (MAE = 1.46 °C, RMSE = 1.89 °C, R2 = 0.95), followed by RF, XGB, MLP, KNN, SVR, MLR, and MFIS. This study underscores the potential of integrating machine learning and fuzzy logic techniques for more accurate soil temperature modeling, contributing to precision agriculture and better resource management.
1. Introduction
Soil temperature is an important environmental parameter that controls numerous biological, chemical, and physical processes within the soil system [1,2]. It has a direct influence on plant growth, seed germination, microbial activity, and the uptake of water and nutrients. A reliable estimation of soil temperature is therefore crucial not only for improving agricultural productivity and optimizing irrigation scheduling, but to support environmental assessments. Conventional methods—especially in situ sensors—provide accurate measurements, but are often expensive and limited in their spatial and temporal coverage. This has led to a growing interest in predictive models as practical and cost-effective alternatives [3].
Soil temperature also serves as a valuable indicator for understanding broader ecosystem dynamics that are closely linked to agricultural, hydrological, and ecological processes. A variety of modeling approaches have been developed to estimate it, including those based on heat flux equations [4], coupled heat and moisture transfer models [5], and models that account for topographic and vegetative features [6]. However, in regions with limited observational data, or when measurements at multiple depths are required, conventional methods may become impractical due to logistical and financial constraints [7]. In such cases, artificial intelligence (AI)-based models offer a promising alternative, as they are able to capture complex, nonlinear interactions between multiple environmental variables, and thus improve the accuracy and efficiency of soil temperature predictions [8,9,10].
AI-based models have been increasingly and successfully used in a wide range of agricultural applications in recent years [11,12,13,14], and their use has become particularly prominent in the prediction of soil temperature. Among these, fuzzy logic-based approaches—especially the Mamdani fuzzy inference system (MFIS) and the adaptive neuro-fuzzy inference system (ANFIS)—offer interpretable modeling frameworks capable of capturing imprecise and uncertain relationships between variables, making them well-suited for modeling soil temperature dynamics. For instance, Kim and Singh [15] developed the multilayer perceptron (MLP) and ANFIS models to estimate daily soil temperature at the Champaign and Springfield stations in Illinois. Similarly, Sabziparvar et al. [16] employed the ANFIS model to estimate soil temperature at six different depths across three climatically diverse regions. The performance of the ANFIS was systematically evaluated against conventional regression-based methods, with results indicating superior predictive accuracy and robustness across varying climatic conditions.
In addition, various machine learning methods, including artificial neural networks (ANNs), deep learning (DL), kernel-based models, and hybrid techniques, have demonstrated their performance in modeling soil temperature dynamics under different environmental conditions. ANNs, especially in the prediction of soil temperature within hydrological and meteorological modeling, are among the most widely used machine learning techniques due to their proven superior performance in numerous studies. For instance, Yang et al. [17] developed an ANN model using five years of meteorological data collected from a weather station in Canada. The model used daily rainfall, potential evapotranspiration, and the day of the year as inputs to estimate daily soil temperatures at depths of 10, 50, and 150 cm. Napagoda and Tilakaratne [18] proposed an improved method for predicting morning and evening soil temperatures at depths of 5 cm and 10 cm, using minimum historical soil temperature data. Tabari et al. [19] estimated daily soil temperatures at six depths (5, 10, 20, 30, 50, and 100 cm) in an arid region of Iran using both ANN and multivariate linear regression models, driven by mean daily meteorological inputs, such as air temperature, solar radiation, relative humidity, and precipitation. In another study [20], monthly soil temperature in Adana, Türkiye, was modeled using linear regression (LR), nonlinear regression (NLR), and ANN methods.
Furthermore, several studies have conducted comparative analyses of fuzzy logic and neural network models for soil temperature estimation [21,22,23,24,25,26,27,28]. For instance, Kisi et al. [29] compared radial basis function neural networks (RBFNNs), generalized regression neural networks (GRNNs), MLP, and MLR, revealing that RBFNN achieved the highest accuracy at shallow soil depths, whereas MLR and GRNN performed better at greater depths. Bayatvarkeshi et al. [30] evaluated the performance of both standalone models—ANN and CANFIS—as well as hybrid models that combine wavelet transformation with these algorithms (WANN and WCANFIS) for predicting soil temperature in Iran. Similarly, Hosseinzadeh Talaee [31] employed the CANFIS model to estimate daily soil temperatures at depths ranging from 5 to 100 cm in arid and semi-arid regions of Iran, using meteorological variables, such as mean, maximum, and minimum air temperatures, relative humidity, sunshine duration, and solar radiation, as model inputs selected through correlation analysis. Zare Abyaneh et al. [32] used two intelligent models—ANN and CANFIS—to estimate soil temperatures at six depths (5, 10, 20, 30, 50, and 100 cm), relying solely on mean air temperature as input.
Recent research has investigated a range of machine learning techniques for soil temperature prediction, including random forest (RF) [33], support vector regression (SVR) [34,35], extreme gradient boosting (XGB) [36], and k-nearest neighbors (KNN) [37], among several others [38,39,40,41,42].
Despite the progress that has been made in predicting soil temperature using machine learning and fuzzy logic techniques, there are still some gaps in the existing literature. Most previous studies focus on individual modeling approaches without performing a systematic comparison between fuzzy logic models and conventional regression techniques across multiple soil depths. Moreover, many models require extensive input data sets, which limits their practical application in data-scarce regions.
To address these gaps, the present study aims to perform the following:
- Conduct a comparative evaluation of fuzzy logic-based models (MFIS and ANFIS) and supervised machine learning algorithms (MLP, SVR, RF, XGB, KNN, and MLR) for predicting soil temperature at different depths (5, 10, 20, 50 and 100 cm).
- Develop models with minimal and easily accessible input variables, such as average air temperature and soil depth, to enhance usability in regions with limited observational data.
Through this integrated approach, this study contributes to advancing soil temperature modeling methods and supports the development of practical decision support tools, especially for environments with limited data availability.
2. Materials and Methods
2.1. Site Description and Data
The province of Tokat (40°55′ N latitude and 37°39′ E longitude) is situated in the Black Sea region of Türkiye (Figure 1), covering an area of 9958 km2 with an average elevation of 623 m above sea level. Meteorological data for the province were obtained from the General Directorate of State Meteorological Services. The dataset includes daily air temperature measured at a height of 2 m, as well as soil temperature recorded at depths of 10, 20, 50, and 100 cm. These observations span the period from 2016 to 2024. For model development, data from 2016 to 2021 were used for training, while data from 2022 to 2024 were reserved for testing.
Figure 1.
Location of Tokat province on Türkiye.
2.2. Machine Learning and Fuzzy Logic Models for Soil Temperature Estimation
In this study, two approaches for predicting soil temperature at different depths (5, 10, 20, 50, and 100 cm) using air temperature and soil depth were tested: (i) fuzzy logic systems (MFIS and ANFIS); (ii) supervised machine learning algorithms (MLP, SVR, RF, KNN, and XGB). For comparative purposes, an MLR model was also included in the analysis.
2.2.1. Mamdani Fuzzy Inference System (MFIS)
Fuzzy logic was introduced by Zadeh [43], and has since been used in many scientific studies. Fuzzy logic divides data into classes and assigns them degrees of membership between 0 and 1. There are different types of fuzzy membership functions (MFs) (triangular, trapezoidal, Gaussian, etc.). However, Gaussian MFs are generally preferred [44].The FIS is a rule-based computational framework designed to model complex systems using approximate reasoning. It comprises four fundamental components: fuzzification, knowledge base, inference engine, and defuzzifier [45]. During the fuzzification process, input data are transformed into linguistic variables—such as low, high, small, or large—and assigned corresponding membership degrees within predefined fuzzy sets. Subsequently, a set of IF–THEN rules is applied to infer outputs based on the fuzzy inputs. An example of such a rule set is presented below.
Rule 1: IF x1 is low and x2 is low THEN y is low
Rule 2: IF x1 is low and x2 is high THEN y is medium
Rule 3: IF x1 is high and x2 is high THEN y is high
With these rules, x1 and x2 are the inputs, while y is the output. Defuzzification is applied to obtain crisp values from the fuzzified set and to determine the output values of the model.
2.2.2. Adaptive Neuro-Fuzzy Inference System (ANFIS)
The ANFIS is an artificial intelligence method developed by Jang [46] that combines the strengths of ANNs and fuzzy logic systems. The ANFIS automatically optimizes the parameters of the fuzzy inference system through its ability to learn from data. This system is usually based on a Takagi–Sugeno type fuzzy inference structure, and can successfully model linear and non-linear relationships between inputs and outputs. In this study, the ANFIS model is used to model the relationship between the input variables and the target variable (output). Hyperparameters such as the type of MFs (e.g., Gaussian, triangular), the number of MFs, and the learning algorithm were optimized. ANFIS models offer high accuracy and a strong generalization capability, especially for small- and medium-sized data sets. However, the computational effort can increase with increasing model complexity. Detailed information about the ANFIS can be obtained from related reference [47].
2.2.3. Multilayer Perceptron (MLP)
In this study, an MLP neural network with a feedforward structure and backpropagation learning algorithm was employed for modeling purposes. The MLP model comprises an input layer, one or more hidden layers, and an output layer. Although an MLP can include multiple hidden layers, theoretical studies have demonstrated that a single hidden layer is sufficient for approximating complex nonlinear functions [48,49]. Therefore, a one-hidden-layer MLP was used. The network architecture and the number of neurons in the hidden layer were determined through a trial-and-error approach. The Levenberg–Marquardt (LM) algorithm was selectively employed for training, as it is known for effective learning performance. MLP networks are widely preferred due to their strong capability for arbitrary input–output mapping. A detailed explanation about MLP neural networks can be found in the study of [50].
2.2.4. Random Forest (RF)
RF is an ensemble learning algorithm introduced by Breiman [51], which constructs a multitude of decision trees to enhance predictive performance. Each tree in the ensemble is trained on a distinct bootstrap sample of the data, and further randomness is introduced by selecting a random subset of features at each split, thereby promoting model diversity. In regression tasks, the final prediction is obtained by averaging the output of all trees; whereas, in classification tasks, a majority voting scheme is applied. In the present study, key hyperparameters—such as the number of trees, the maximum number of features considered at each split, and the maximum tree depth—were tuned to optimize model performance. RF models offer several advantages, including robust handling of complex, non-linear relationships, resistance to overfitting, and the ability to rank variable importance. However, they may require substantial computational resources in terms of training time and memory, particularly when applied to large-scale datasets.
2.2.5. K-Nearest Neighbors (KNN)
KNN is a non-parametric, instance-based learning algorithm introduced by Cover and Hart [52], widely used for both classification and regression tasks. The core principle of KNN is that the class or predicted value of a given data point is determined by the properties of its k nearest neighbors, which are usually calculated using a distance metric, such as Euclidean distance. The performance of the model depends heavily on the hyperparameters, including the number of neighbors (k), the weighting scheme applied to the neighbors, and the choice of distance metric. In this study, these hyperparameters—particularly the optimal k value and the most appropriate distance metric—were systematically selected to improve model accuracy. While KNN is appreciated for its simplicity and ability to effectively capture local data structures, it also faces limitations, such as increased computational costs for large datasets and sensitivity to feature scaling, which can affect performance if not properly addressed.
2.2.6. Extreme Gradient Boosting (XGB)
XGB is a powerful machine learning algorithm based on the gradient-boosted decision trees (GBDT) framework, originally introduced by Chen and Guestrin [53]. XGB constructs tree-based models in a sequential manner, where each new tree is trained to correct the residual errors of the previous ensemble, reducing both bias and variance to improve the overall accuracy of the model. In this study, the key hyperparameters—including learning rate, maximum tree depth, minimum child weight, and number of boosting rounds (trees)—were systematically optimized. XGB is known for its superior prediction accuracy and computational efficiency, which is facilitated by advanced features, such as built-in handling of missing values, regularization to control overfitting, and support for parallel processing. Despite these advantages, the performance of the model is very sensitive to the configuration of the hyperparameters, which makes the tuning process relatively complex.
2.2.7. Support Vector Regression (SVR)
SVR is a supervised learning algorithm derived from support vector machines (SVM), and is widely employed for regression tasks involving nonlinear and high-dimensional data. SVR aims to identify a function that deviates from the actual target values by no more than a specified margin (ε) while maintaining model complexity as low as possible. It utilizes kernel functions—such as radial basis function (RBF), polynomial, or linear kernels—to transform the input space into a higher-dimensional feature space, allowing for the modeling of complex nonlinear relationships. In this study, key hyperparameters of the SVR model, including the penalty parameter (C), the kernel type, the ε-insensitive loss function width, and the kernel-specific parameters (e.g., γ for the RBF kernel), were optimized to enhance model accuracy. SVR offers advantages in terms of robustness to overfitting and strong generalization performance, particularly with appropriately tuned kernels. However, its computational cost can be high for large datasets, and model performance is highly sensitive to the choice of hyperparameters and kernel function [54].
2.2.8. Multiple Linear Regression (MLR)
MLR is a widely used statistical modeling technique for establishing the relationship between a dependent variable and multiple independent variables. When the relationship between the dependent variable and two or more predictors is assumed to be linear, the method is referred to as multiple linear regression. The general form of an MLR model can be expressed as follows:
where y is the dependent variable, x1, x2, … xn are the independent variables, β1, β2, and βn are the slope coefficients, β0 is a constant term, and ε is the error term.
2.3. Model Performance Criteria
In this study, the root mean square error (RMSE), the mean absolute error (MAE), and the coefficient of determination (R2) were employed, as they have been widely used in the previous studies in different areas of agricultural science to assess model performance [55,56,57].
where zmea denotes the actual value, zpre symbolizes the predicted value, zavg is the average actual value, and n is the total data number.
3. Results
The descriptive statistics of air and soil temperature at different soil depths (5, 10, 20, 50, and 100 cm) were analyzed comparatively over the periods 2016–2021 (training) and 2022–2024 (testing) (Table 1). The results show that the soil temperature is higher than the air temperature at all depths, although this difference is more pronounced in the near-surface layers. The standard deviation and standard error values showed that temperature variability was high in the 5–20 cm range, while thermal variability decreased significantly at depths of 50 and 100 cm. Negative skewness values indicate that the data distribution is skewed to the left and dominated by low temperatures, while positive kurtosis values indicate that the temperature distribution deviates from normality and narrows, especially during the testing period. However, while minimum temperatures increased with depth, maximum temperatures remained higher in the near-surface layers. The temperature increase observed in all layers during the test period indicates that regional warming effects are reflected in the soil profile and that this change can be felt from the surface to depth.

Table 1.
Descriptive statistics of input and output variables.
3.1. Statistical Outcomes Derived from MLR Analysis
The MLR model demonstrated satisfactory performance in predicting soil temperature, exhibiting both statistical significance and adequate explanatory power. The detailed model parameters and results are presented in Table 2.

Table 2.
Summary of MLR for soil temperature Tokat, Türkiye.
All variables in the model are statistically significant (at the 1% significance level). With a coefficient value of 1.224 and a t-value of 57.597, the average air temperature is the most important determining variable in the model. While the variable depth contributes positively to soil temperature with a positive coefficient (0.097), the negative coefficient (−0.007) of the interaction term depth–temperature indicates that the temperature increase slows down with depth. This situation shows that the effect of air temperature decreases, especially in deep layers.
The general significance of the model was confirmed with F = 1563.45 and p < 0.01. The explanatory power of the model is quite high with an R2 value of 0.931 and an adjusted R2 value (R2adj) of 0.93. These results show that about 93% of the total change in soil temperature is explained by the model. The error measurements of the model for the training and test periods are shown in Table 3. In the training set, the MAE is 1.54 °C, the RMSE is 2.00 °C, and the R2 value is 0.93. In the testing set, these values are 1.89 °C (MAE), 2.33 °C (RMSE), and 0.94 (R2), respectively. No significant loss of performance was observed between the training and testing periods, indicating that the generalization ability of the model is strong and that there is no overfitting problem.

Table 3.
Evaluation metrics of the MLR model on training and testing dataset.
This MLR model, developed for the province of Tokat, is able to provide very accurate predictions of soil temperature, especially considering key variables such as air temperature and depth. The successful performance of the model in both the training and testing period shows that MLR is a viable and reliable method for predicting soil temperature.
3.2. Performance Evaluation of the MFIS Model
The MFs and fuzzy inference rules were determined through a comprehensive analysis and interpretation of the relationships between soil temperature and air temperature data. In the fuzzy logic system, the air temperature and soil depth were employed as input variables, while the output variable was defined as the soil temperature at various depths. For the fuzzy sets, the input and output variable ranges were as follows: soil depth ranged from 5 to 100 cm, air temperature from −15 to 35 °C, and soil temperature from −5 to 35 °C. As a result of the data-driven analysis, a total of sixteen fuzzy rules were formulated to represent the underlying patterns and relationships in the dataset (Table 4). The corresponding fuzzy sets and MFs are illustrated in Figure 2.

Table 4.
Rules for soil temperature (°C) at average air temperature (°C) and soil depth (cm).
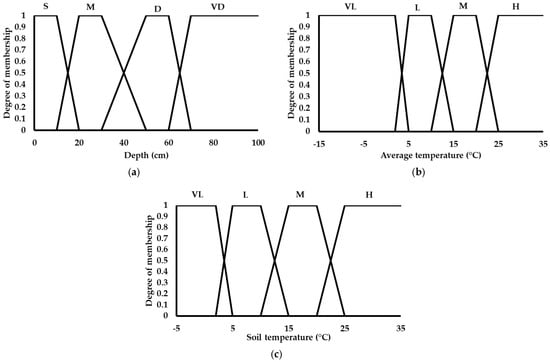
Figure 2.
MFIS model setup: (a) depth (input); (b) air temperature (input); (c) soil temperature (output).
Five different defuzzification methods were employed to convert the fuzzy output of the model into a crisp value: centroid, Bisector, mean of maximum (MOM), largest of maximum (LOM), and smallest of maximum (SOM). The predictive performance of the fuzzy inference system was assessed using statistical metrics including MAE, RMSE, and R2, applied to both training and testing datasets, as presented in Table 5. Among the methods evaluated, the centroid defuzzification approach yielded the most accurate results. Specifically, in the training dataset, the centroid method achieved an MAE of 2.58 °C, an RMSE of 3.29 °C, and an R2 value of 0.83. In the testing dataset, the corresponding values were 2.83 °C for MAE, 3.45 °C for RMSE, and 0.85 for R2, indicating strong generalization capability. By contrast, the remaining defuzzification methods demonstrated comparatively lower predictive accuracy, with the LOM method exhibiting the weakest performance, attaining an R2 value of only 0.70 in the testing dataset.

Table 5.
Evaluation metrics of the MFIS models on training and testing dataset.
The MFIS presents a viable approach for soil temperature prediction, primarily due to its high level of interpretability and adaptable framework. Nevertheless, in the context of this study, the MFIS model demonstrated inferior predictive performance when compared to the MLR model. Although the centroid defuzzification method yielded the most favorable results among the techniques evaluated, it is advisable to prioritize statistical or data-driven models in applications where high predictive accuracy is essential.
3.3. Performance Evaluation of the ANFIS Model
In an ANFIS analysis, a linear output function was employed in conjunction with different types of MFs for the inputs, including triangular, trapezoidal, and Gaussian shapes. Each input variable was divided into three fuzzy classes to facilitate rule generation and to improve model resolution. As an example, the fuzzy rules generated by the ANFIS model using the triangular membership (Trimf) function and the corresponding linear model parameters are listed in Table 6.

Table 6.
ANFIS rules and parameters.
Table 7 summarizes the performance metrics of the fuzzy logic models developed using different types and configurations of MFs based on input variables, including soil depth and average air temperature. For the 3 × 3 MF configurations, all three MF types—Triangular (Trimf), Trapezoidal (Trapmf), and Gaussian (Gaussmf)—performed comparably. On the testing dataset, these models yielded consistent MAE values ranging from 1.49 to 1.55 °C, an RMSE of approximately 1.97 °C, and an R2 of 0.95, reflecting a high degree of accuracy and model fit. By contrast, the 4 × 4 MF configurations demonstrated slightly improved performance on the training set. Among them, the Trimf (4 × 4) configuration achieved the lowest MAE (1.35 °C) and RMSE (1.88 °C), while maintaining a high R2 of 0.94. In testing, this configuration continued to perform well with an MAE of 1.46 °C, an RMSE of 1.89 °C, and an R2 of 0.95. Other 4 × 4 MF types produced similar results, suggesting that increasing the number of fuzzy sets did not significantly enhance accuracy, but may improve generalization under certain conditions. In summary, the Trimf (4 × 4) configuration provided the most favorable balance between model accuracy and complexity, and was therefore the most effective approach among the tested alternatives.

Table 7.
Evaluation metrics of the ANFIS models on training and testing dataset.
3.4. Performance Evaluation of the Machine Learning Models
Data pre-processing constitutes a critical step in developing robust and accurate machine learning models. In this phase, important issues such as noise, missing values, and inconsistencies within the dataset are addressed. The pre-processing workflow included standard procedures, such as data cleansing, transformation, and stratified partitioning. To eliminate the effects of different units of measurement and to mitigate the influence of outliers, all feature values were normalized to a range of 0–1. The data set was temporally split into a training set (2016–2021) and a testing set (2022–2024). For model calibration, 90% of the training data was used and hyperparameter tuning was performed on a randomly selected 90% subset of this training pool. This process was repeated with ten-fold cross-validation to ensure statistical rigor and to enhance the reliability of the model performance evaluation. The final hyperparameter configurations of the machine learning models employed in this study are summarized in Table 8.

Table 8.
Hyperparameter values used in machine learning models.
The performance outcomes of the machine learning models are comprehensively summarized in Table 9, which presents the MAE, RMSE, and R2 values for both training and testing stages. The MLP architecture, a compact network configuration was adopted to balance model complexity and generalization ability. The selected structure comprised a single hidden layer with three neurons, resulting in a (2-3-1) topology. This configuration was deemed sufficient to capture the fundamental relationships within the dataset while mitigating the risk of overfitting. The Levenberg–Marquardt (LM) optimization algorithm was employed for training, owing to its proven efficiency and speed in handling nonlinear regression tasks. The activation functions used were hyperbolic tangent sigmoid (tansig) in the hidden layer and linear (purelin) in the output layer. The model was trained for 200 epochs to ensure convergence without overtraining.

Table 9.
Evaluation metrics of machine learning models on training and testing dataset.
For the KNN algorithm, the number of neighbors was set to 9, with a uniform weighting scheme, and Euclidean distance was set as the distance metric. This configuration allows the model to be sensitive to local variations in the data space while assuming equal influence from each of the neighboring points.
In the SVR model, the penalty coefficient (C = 14.05), error tolerance (ε = 0.763), and kernel coefficient (γ = 0.001) were selected. A high C value was used to reduce bias and tightly fit the data, whereas a low γ value was preferred to avoid excessive model complexity and to preserve the generalization capability.
The RF model was configured with 78 decision trees, a maximum tree depth of five, sqrt as the maximum number of features considered at each split, and parameters for minimum samples per leaf and per split set to two and five, respectively. The restricted tree depth was implemented to prevent overfitting and to promote diversity among the trees.
In the XGB model, the number of boosting iterations was set to 91 and the learning rate to 0.06. The relatively low learning rate allowed the model to learn in a more stable and gradual manner, while the number of iterations was sufficient to achieve high predictive accuracy without overfitting.
These hyperparameter selections reflect a strategic balance between model complexity and generalization capacity. The configuration of the SVR model, combining a high C with a small γ, was based on established best practices for producing accurate yet generalizable models [58]. Similarly, ensemble models, such as RF and XGB, were optimized for both diversity and learning stability [59].
The soil temperature prediction performance of the machine learning models is summarized in Table 9. The XGB model demonstrated the highest accuracy on the training data, with an R2 of 0.97, an MAE of 1.06 °C, and an RMSE of 1.43 °C. The RF model followed closely, achieving an R2 of 0.96, an MAE of 1.09 °C, and an RMSE of 1.49 °C. In terms of generalization to the testing dataset, RF outperformed the other models with the highest R2 value of 0.94, indicating superior generalization capability. Although XGB had slightly higher error metrics on the testing data (MAE = 1.82 °C, RMSE = 2.30 °C), its overall performance remained robust (R2 = 0.92). By contrast, the SVR, KNN, and MLP models exhibited relatively lower accuracy, with higher error values across both datasets. Among these, the KNN model showed the weakest generalization performance with an R2 of 0.92 on the testing set. These results suggest that ensemble-based models, particularly RF and XGB, are more effective in capturing the complex relationships governing soil temperature variation. Therefore, they represent promising tools for predictive modeling in agricultural and environmental applications.
3.5. Comparative Evaluation of Prediction Models for Soil Temperature
The comparative scatterplots of the predicted versus measured soil temperatures for each model are illustrated in Figure 3, providing a visual representation of the prediction accuracy across models.
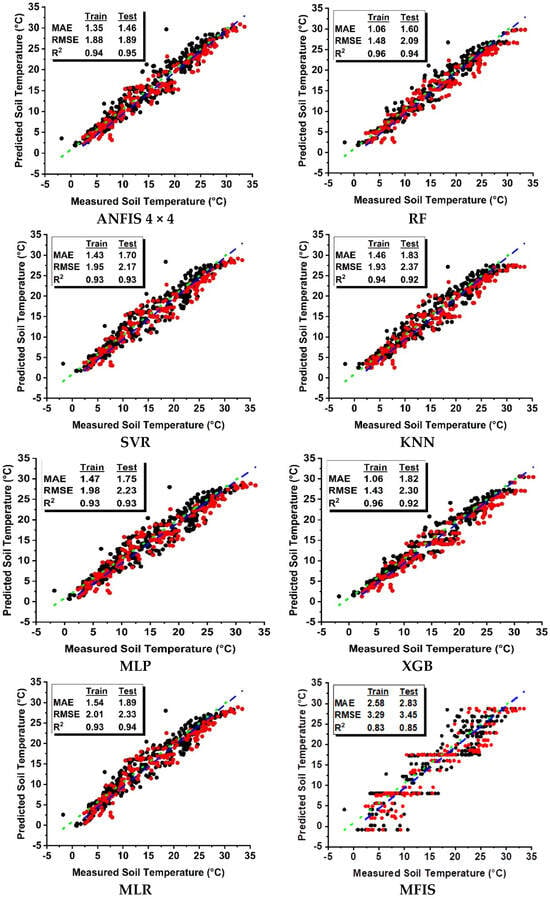
Figure 3.
Comparison of soil temperature prediction with scatter plots using fuzzy logic, machine learning, and MLR models (black dots represent training data, while red dots indicate testing data).
The ANFIS model was developed using Trimf (4 × 4) along with a linear output function. The model demonstrated excellent performance, achieving an MAE of 1.35 °C, an RMSE of 1.88 °C, and an R2 of 0.94 on the training dataset. On the testing dataset, the model’s performance remained strong, with an MAE of 1.46 °C, an RMSE of 1.89 °C, and an R2 of 0.95. These results highlight the ANFIS model’s high learning capacity and generalization ability, making it a statistically robust approach for soil temperature prediction.
By contrast, the MFIS, while providing significant advantages in terms of model interpretability, exhibited relatively lower accuracy. It yielded higher error values, with an MAE of 2.58 °C, an RMSE of 3.29 °C, and an R2 of 0.83 on the training dataset. The performance on the testing data was similarly suboptimal, with an MAE of 2.83 °C, an RMSE of 3.45 °C, and an R2 of 0.85. These results suggest that, while the MFIS is useful for interpretable models, it is less effective in predictive accuracy compared to the ANFIS.
Among the machine learning algorithms, XGB and RF distinguished themselves with their low error rates and high R2 values. In particular, XGB achieved the lowest error values, with an MAE of 1.06 °C and an RMSE of 1.43 °C on the training dataset, while also demonstrating the highest explanatory power, with an R2 of 0.97. The model maintained its strong performance on the testing dataset, achieving an MAE of 1.82 °C, an RMSE of 2.30 °C, and an R2 of 0.92. RF produced consistent and well-balanced results across both training and testing datasets. On the other hand, methods such as SVR, KNN, and MLP exhibited moderate success, with relatively higher error rates compared to XGB and RF.
The MLR model exhibited an average performance on the training dataset, with an MAE of 1.54 °C, an RMSE of 2.00 °C, and an R2 of 0.93. Although its performance on the testing dataset was relatively comparable to some machine learning methods, achieving an MAE of 1.89 °C, an RMSE of 2.33 °C, and an R2 of 0.94, it failed to effectively capture the complex relationships present in the data due to its inherently linear structure. Despite the seemingly high R2 value on the testing set, the limitations of the linear model become particularly evident in the deeper layers, where the nonlinearity of the soil temperature dynamics becomes more pronounced.
4. Discussion
One notable strength of this study lies in the comprehensive comparative evaluation of fuzzy logic-based models (MFIS and ANFIS) and various supervised machine learning algorithms (MLP, SVR, RF, XGB, KNN, and MLR) for predicting soil temperature. Among these models, the ANFIS showed superior prediction accuracy and consistent error performance on both the training and testing datasets. This robustness is attributed to the hybrid architecture of the ANFIS, which synergistically combines the adaptive learning capabilities of neural networks with the rule-based reasoning of fuzzy logic. Such integration enables the effective modeling of uncertainties and complex nonlinear relationships typical of environmental processes [46]. The stability of the model across different data sets underlines its reliability in predicting soil temperature.
By contrast, the MFIS, although offering advantages in terms of interpretability due to its rule-based framework, demonstrated limited predictive accuracy. Its inability to adequately handle extreme values resulted in relatively high MAE and RMSE values, limiting its suitability for high-precision prediction applications.
Machine learning algorithms, especially when applied to large data sets, also demonstrated strong predictive capabilities. Among them, ensemble-based models, such as RF and XGB, were consistently better than others due to their ability to capture complex patterns, reduce model variance and mitigate overfitting. These models excelled in scenarios with high-dimensional and complex data, and were among the most accurate and generalizable approaches [60,61].
From a practical point of view, the choice of a suitable modeling approach should be based on the specific requirements of the planned application. The ANFIS is recommended when best prediction accuracy is required. For applications where transparency and ease of use are important—such as operational decision-making in the field—the MLR remains a viable option. In environments with large data sets that require a balance between scalability and performance, RF and XGB are highly effective solutions.
Another particular strength of this study is its minimal data requirements. Unlike the many previous studies [22,28,33] that relied on extensive meteorological data sets—including variables such as humidity, solar radiation, and wind speed—this study used only two readily available data sets: air temperature and soil depth. This parsimonious modeling strategy significantly improves the practical applicability and scalability of the models, especially in regions with limited access to comprehensive weather data. By achieving high predictive performance with limited inputs, this study contributes to the development of efficient and accessible decision support systems for precision agriculture and environmental monitoring.
Furthermore, the inclusion of a rarely studied soil depth of 20 cm introduces a new dimension to the modeling effort and extends the applicability of the results. Another methodological innovation is the temporal separation of the training and testing datasets by year. This approach allows for a more rigorous assessment of model generalization and addresses a common limitation of the previous studies that did not account for temporal dependencies, potentially inflating model performance.
5. Conclusions and Limitations
The accuracy of the prediction of environmental variables, such as soil temperature, can vary considerably depending on the modeling approach used. An accurate prediction of the soil temperature is crucial for agricultural productivity, as it directly affects crop growth and development. By using reliable forecasting methods, farmers can optimize key agricultural operations, such as planting schedules, irrigation timing, and fertilizer application, making resource use more efficient and maximizing crop yields. As a result, predicting soil temperature is a fundamental part of precision agriculture and an essential element of modern farming practices.
In this study, the ANFIS demonstrated particularly strong performance, achieving low error rates and high prediction accuracy. Other machine learning algorithms, including RF, XGB, KNN, SVR, and MLP, also delivered robust results. By contrast, the MFIS showed limitations in capturing nonlinear relationships in the data. The MLR model provided a performance comparable to some machine learning methods. This can be explained by the statistical results: when the soil depth and the average air temperature were considered as independent variables, the average air temperature had a positive and statistically significant effect on the soil temperature, while the effect of depth alone was not significant (p = 0.423). The introduction of an interaction term between depth and average temperature as an additional predictor improved the model, with all coefficients reaching statistical significance, and the coefficient of determination approaching that of the machine learning models.
The choice of modeling technique should be based on the specific application requirements, data availability, and system complexity. Predicting the soil temperature at different depths using accessible data, such as soil depth and air temperature, offers considerable practical benefits for agricultural management. Predictions derived from fuzzy logic, machine learning, and regression-based models can inform and optimize key field activities, such as planting, irrigation, fertilization, tillage, and drainage. Ultimately, these tools provide valuable support to farmers and agricultural practitioners by facilitating the development of smart farming systems that improve decision-making and operational efficiency.
Nevertheless, some limitations of this study must be acknowledged. The analysis was limited to only two input variables—air temperature and soil depth—which, while practical, may limit the ability of the models to fully capture the complex atmospheric interactions that influence soil temperature dynamics. In addition, this study was conducted in a specific climatic and geographic context, which may limit the generalizability of the results. Future research should aim to evaluate the performance of the model incorporating weather forecasts and a wider range of meteorological variables in different climatic regions. Such studies would help to improve the robustness, adaptability, and broader applicability of soil temperature prediction models in different agro-ecological zones.
Author Contributions
Conceptualization, B.C., Y.K. and E.C.; methodology, B.C., Y.K., E.C., E.K. and H.S.; software, B.C. and E.K.; validation, B.C., E.C. and H.S.; formal analysis, B.C., E.C. and E.K.; investigation, B.C., Y.K. and E.C.; resources, B.C., Y.K. and E.C.; data curation, B.C., E.C. and H.S.; writing—original draft preparation, B.C., Y.K. and E.C.; writing—review and editing, B.C., E.K. and H.S.; visualization, B.C., Y.K. and E.K.; supervision, B.C. and H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| MFIS | Mamdani Fuzzy Inference System |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| MLP | Multilayer Perceptron |
| SVR | Support Vector Regression |
| RF | Random Forest |
| XGB | Extreme Gradient Boosting |
| KNN | K-Nearest Neighbors |
| MLR | Multiple Linear Regression |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
| R2 | Coefficient of Determination |
| ANNs | Artificial Neural Networks |
| GBDTs | Gradient-Boosted Decision Trees |
| MOM | Mean of Maximum |
| LOM | Largest of Maximum |
| SOM | Smallest of Maximum |
References
- Hu, G.; Zhao, L.; Wu, X.; Li, R.; Wu, T.; Xie, C.; Qiao, Y.; Shi, J.; Cheng, G. An analytical model for estimating soil temperature profiles on the Qinghai-Tibet Plateau of China. J. Arid Land 2016, 8, 232–240. [Google Scholar] [CrossRef]
- Yan, Y.; Yan, R.; Chen, J.; Xin, X.; Eldridge, D.J.; Shao, C.; Wang, X.; Lv, S.; Jin, D.; Chen, J. Grazing modulates soil temperature and moisture in a Eurasian steppe. Agric. For. Meteorol. 2018, 262, 157–165. [Google Scholar] [CrossRef]
- Taheri, M.; Schreiner, H.K.; Mohammadian, A.; Shirkhani, H.; Payeur, P.; Imanian, H.; Cobo, J.H. A review of machine learning approaches to soil temperature estimation. Sustainability 2023, 15, 7677. [Google Scholar] [CrossRef]
- Gupta, S.C.; Radke, J.; Swan, J.; Moncrief, J. Predicting soil temperatures under a ridge-furrow system in the US Corn Belt. Soil Tillage Res. 1990, 18, 145–165. [Google Scholar] [CrossRef]
- Flerchinger, G.; Pierson, F. Modeling plant canopy effects on variability of soil temperature and water. Agric. For. Meteorol. 1991, 56, 227–246. [Google Scholar] [CrossRef]
- Kang, S.; Kim, S.; Oh, S.; Lee, D. Predicting spatial and temporal patterns of soil temperature based on topography, surface cover and air temperature. For. Ecol. Manag. 2000, 136, 173–184. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, G. Estimation of soil moisture from optical and thermal remote sensing: A review. Sensors 2016, 16, 1308. [Google Scholar] [CrossRef]
- Liu, X.; Luo, T. Spatiotemporal variability of soil temperature and moisture across two contrasting timberline ecotones in the Sergyemla Mountains, Southeast Tibet. Arct. Antarct. Alp. Res. 2011, 43, 229–238. [Google Scholar] [CrossRef]
- Wang, X.; Li, W.; Li, Q. A new embedded estimation model for soil temperature prediction. Sci. Program. 2021, 2021, 5881018. [Google Scholar] [CrossRef]
- Mehdizadeh, S.; Fathian, F.; Safari, M.J.S.; Khosravi, A. Developing novel hybrid models for estimation of daily soil temperature at various depths. Soil Tillage Res. 2020, 197, 104513. [Google Scholar] [CrossRef]
- Tunca, E.; Köksal, E.; Akay, H.; Öztürk, E.; Taner, S.Ç. Novel machine learning framework for high-resolution sorghum biomass estimation using multi-temporal UAV imagery. Int. J. Environ. Sci. Technol. 2025, 1–16. [Google Scholar] [CrossRef]
- Demirsoy, H.; Küçüktopçu, E.; Dogan, D.E. Novel Machine Learning Approaches for Accurate Leaf Area Estimation in Apples. Appl. Fruit Sci. 2025, 67, 68. [Google Scholar] [CrossRef]
- Cemek, B.; Arslan, H.; Küçüktopcu, E.; Simsek, H. Comparative analysis of machine learning techniques for estimating groundwater deuterium and oxygen-18 isotopes. Stoch. Environ. Res. Risk Assess. 2022, 36, 4271–4285. [Google Scholar] [CrossRef]
- Tunca, E.; Köksal, E.S.; Öztürk, E.; Akay, H.; Taner, S.Ç. Accurate leaf area index estimation in sorghum using high-resolution UAV data and machine learning models. Phys. Chem. Earth Parts A/B/C 2024, 133, 103537. [Google Scholar] [CrossRef]
- Kim, S.; Singh, V.P. Modeling daily soil temperature using data-driven models and spatial distribution. Theor. Appl. Climatol. 2014, 118, 465–479. [Google Scholar] [CrossRef]
- Sabziparvar, A.; Zreabyaneh, H.; Bayat, M. A model comparison between predicted soil temperatures using ANFIS model and regression methods in three different climates. Water Soil 2010, 24, 274–285. [Google Scholar]
- Yang, C.-C.; Prasher, S.O.; Mehuys, G.R. An artificial neural network to estimate soil temperature. Can. J. Soil Sci. 1997, 77, 421–429. [Google Scholar] [CrossRef]
- Napagoda, N.; Tilakaratne, C. Artificial neural network approach for modeling of soil temperature: A case study for Bathalagoda area. Sri Lankan J. Appl. Stat. 2013, 13, 39–59. [Google Scholar] [CrossRef]
- Tabari, H.; Sabziparvar, A.-A.; Ahmadi, M. Comparison of artificial neural network and multivariate linear regression methods for estimation of daily soil temperature in an arid region. Meteorol. Atmos. Phys. 2011, 110, 135–142. [Google Scholar] [CrossRef]
- Bilgili, M. Prediction of soil temperature using regression and artificial neural network models. Meteorol. Atmos. Phys. 2010, 110, 59–70. [Google Scholar] [CrossRef]
- Citakoglu, H. Comparison of artificial intelligence techniques for prediction of soil temperatures in Turkey. Theor. Appl. Climatol. 2017, 130, 545–556. [Google Scholar] [CrossRef]
- Kisi, O.; Sanikhani, H.; Cobaner, M. Soil temperature modeling at different depths using neuro-fuzzy, neural network, and genetic programming techniques. Theor. Appl. Climatol. 2017, 129, 833–848. [Google Scholar] [CrossRef]
- Mehdizadeh, S.; Ahmadi, F.; Kozekalani Sales, A. Modelling daily soil temperature at different depths via the classical and hybrid models. Meteorol. Appl. 2020, 27, e1941. [Google Scholar] [CrossRef]
- Penghui, L.; Ewees, A.A.; Beyaztas, B.H.; Qi, C.; Salih, S.Q.; Al-Ansari, N.; Bhagat, S.K.; Yaseen, Z.M.; Singh, V.P. Metaheuristic optimization algorithms hybridized with artificial intelligence model for soil temperature prediction: Novel model. IEEE Access 2020, 8, 51884–51904. [Google Scholar] [CrossRef]
- Behnia, M.; Valani, H.A.; Bameri, M.; Jabalbarezi, B.; Eskandari, H. Potential Assessment of ANNs and Adaptative Neuro Fuzzy Inference systems (ANFIS) for Simulating Soil Temperature at diffrent Soil Profile Depths. Int. J. Adv. Biol. Biomed. Res. 2017, 5, 52–59. [Google Scholar]
- Malik, A.; Tikhamarine, Y.; Sihag, P.; Shahid, S.; Jamei, M.; Karbasi, M. Predicting daily soil temperature at multiple depths using hybrid machine learning models for a semi-arid region in Punjab, India. Environ. Sci. Pollut. Res. 2022, 29, 71270–71289. [Google Scholar] [CrossRef] [PubMed]
- Parsafar, N.; Marofi, S. Estimation of soil temperature from air temperature using regression models, artificial neural network and adaptive neuro-fuzzy inference system (Case Study: Kermanshah Region). Water Soil Sci. 2011, 21, 139–152. [Google Scholar]
- Samadianfard, S.; Ghorbani, M.A.; Mohammadi, B. Forecasting soil temperature at multiple-depth with a hybrid artificial neural network model coupled-hybrid firefly optimizer algorithm. Inf. Process. Agric. 2018, 5, 465–476. [Google Scholar] [CrossRef]
- Kisi, O.; Tombul, M.; Kermani, M.Z. Modeling soil temperatures at different depths by using three different neural computing techniques. Theor. Appl. Climatol. 2015, 121, 377–387. [Google Scholar] [CrossRef]
- Bayatvarkeshi, M.; Bhagat, S.K.; Mohammadi, K.; Kisi, O.; Farahani, M.; Hasani, A.; Deo, R.; Yaseen, Z.M. Modeling soil temperature using air temperature features in diverse climatic conditions with complementary machine learning models. Comput. Electron. Agric. 2021, 185, 106158. [Google Scholar] [CrossRef]
- Hosseinzadeh Talaee, P. Daily soil temperature modeling using neuro-fuzzy approach. Theor. Appl. Climatol. 2014, 118, 481–489. [Google Scholar] [CrossRef]
- Zare Abyaneh, H.; Bayat Varkeshi, M.; Golmohammadi, G.; Mohammadi, K. Soil temperature estimation using an artificial neural network and co-active neuro-fuzzy inference system in two different climates. Arab. J. Geosci. 2016, 9, 1–10. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Hao, W.; Gao, L.; Gong, D. Estimation of soil temperature from meteorological data using different machine learning models. Geoderma 2019, 338, 67–77. [Google Scholar] [CrossRef]
- Delbari, M.; Sharifazari, S.; Mohammadi, E. Modeling daily soil temperature over diverse climate conditions in Iran—A comparison of multiple linear regression and support vector regression techniques. Theor. Appl. Climatol. 2019, 135, 991–1001. [Google Scholar] [CrossRef]
- Guleryuz, D. Estimation of soil temperatures with machine learning algorithms—Giresun and Bayburt stations in Turkey. Theor. Appl. Climatol. 2022, 147, 109–125. [Google Scholar] [CrossRef]
- Dong, J.; Huang, G.; Wu, L.; Liu, F.; Li, S.; Cui, Y.; Wang, Y.; Leng, M.; Wu, J.; Wu, S. Modelling Soil Temperature by Tree-Based Machine Learning Methods in Different Climatic Regions of China. Appl. Sci. 2022, 12, 5088. [Google Scholar] [CrossRef]
- Küçük, C.; Birant, D.; Taşer, P.Y. A novel machine learning approach: Soil temperature ordinal classification (STOC). J. Agric. Sci. 2022, 28, 635–649. [Google Scholar] [CrossRef]
- Geng, Q.; Wang, L.; Li, Q. Soil temperature prediction based on explainable artificial intelligence and LSTM. Front. Environ. Sci. 2024, 12, 1426942. [Google Scholar] [CrossRef]
- Farhangmehr, V.; Imanian, H.; Mohammadian, A.; Cobo, J.H.; Shirkhani, H.; Payeur, P. A spatiotemporal CNN-LSTM deep learning model for predicting soil temperature in diverse large-scale regional climates. Sci. Total Environ. 2025, 968, 178901. [Google Scholar] [CrossRef]
- Imanian, H.; Mohammadian, A.; Farhangmehr, V.; Payeur, P.; Goodarzi, D.; Hiedra Cobo, J.; Shirkhani, H. A comparative analysis of deep learning models for soil temperature prediction in cold climates. Theor. Appl. Climatol. 2024, 155, 2571–2587. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Ren, X. Modeling hourly soil temperature using deep BiLSTM neural network. Algorithms 2020, 13, 173. [Google Scholar] [CrossRef]
- Alizamir, M.; Kim, S.; Zounemat-Kermani, M.; Heddam, S.; Shahrabadi, A.H.; Gharabaghi, B. Modelling daily soil temperature by hydro-meteorological data at different depths using a novel data-intelligence model: Deep echo state network model. Artif. Intell. Rev. 2021, 54, 2863–2890. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Russell, S.O.; Campbell, P.F. Reservoir operating rules with fuzzy programming. J. Water Resour. Plan. Manag. 1996, 122, 165–170. [Google Scholar] [CrossRef]
- Küçüktopçu, E.; Cemek, B.; Simsek, H. Application of Mamdani fuzzy inference system in poultry weight estimation. Animals 2023, 13, 2471. [Google Scholar] [CrossRef]
- Jang, J.-S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Daneshmand, H.; Tavousi, T.; Khosravi, M.; Tavakoli, S. Modeling minimum temperature using adaptive neuro-fuzzy inference system based on spectral analysis of climate indices: A case study in Iran. J. Saudi Soc. Agric. Sci. 2015, 14, 33–40. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Tatnall, A.R. Introduction neural networks in remote sensing. Int. J. Remote Sens. 1997, 18, 699–709. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1996, 9, 155–161. [Google Scholar]
- Tunca, E. Evaluating the performance of the TSEB model for sorghum evapotranspiration estimation using time series UAV imagery. Irrig. Sci. 2024, 42, 977–994. [Google Scholar]
- Banda, P.; Cemek, B.; Küçüktopcu, E. Estimation of daily reference evapotranspiration by neuro computing techniques using limited data in a semi-arid environment. Arch. Agron. Soil Sci. 2018, 64, 916–929. [Google Scholar]
- Imanian, H.; Hiedra Cobo, J.; Payeur, P.; Shirkhani, H.; Mohammadian, A. A comprehensive study of artificial intelligence applications for soil temperature prediction in ordinary climate conditions and extremely hot events. Sustainability 2022, 14, 8065. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar]
- Khan, A.A.; Chaudhari, O.; Chandra, R. A review of ensemble learning and data augmentation models for class imbalanced problems: Combination, implementation and evaluation. Expert Syst. Appl. 2024, 244, 122778. [Google Scholar] [CrossRef]
- Antoniadis, A.; Lambert-Lacroix, S.; Poggi, J.-M. Random forests for global sensitivity analysis: A selective review. Reliab. Eng. Syst. Saf. 2021, 206, 107312. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).