Abstract
This study proposes the use of Physics-Informed Neural Networks (PINNs) to further advance the curvature interference analysis method. The nonlinear equation system encountered in determining the curvature interference limit line is embedded into the PINN loss function, thereby enabling the solution of high-dimensional, nonlinear equations. Computational results demonstrate that the PINN model achieves a solution accuracy on the order of 10−13 when solving multidimensional nonlinear systems, which is comparable to the classical Fsolve algorithm. The curvature interference analysis reveals the presence of two curvature interference boundary lines, although they rarely extend to the worm gear tooth surface. A study on the influence of design parameters on the interference boundaries indicates that the axial installation distance has the greatest impact. Inadequate axial spacing causes the interference limit line to shift toward the inner end of the worm gear, significantly increasing the risk of interference in that region. The proposed curvature interference analysis method based on PINNs can be extended to other types of gear drives. It also lays the foundation for future work on establishing both forward and inverse mappings between design parameters and curvature interference using PINNs.
1. Introduction
The meshing process in face worm gear drives essentially represents the enveloping process of the worm gear tooth surface by the worm helical surface. The existence of singular points on tooth surfaces may lead to curvature interference, resulting in undercutting. These singular points generally create a continuous curve across the enveloping surface. This singular trajectory constitutes the envelope curve of the contact lines. The singular trajectory bifurcates the envelope surface into two distinct domains: an interference zone and a non-interference zone. To avoid undercutting, the tooth surfaces should be strictly confined to the non-interference area. Due to this characteristic, the singular trajectory is referred to as the curvature interference limit line [1].
At singular points of the enveloping surface, the normal vector, the tangent vector, and the velocity vector all equal zero [2,3,4]. From these singularity conditions, further singularity conditions with clear physical interpretation and computational efficiency have since been derived [5,6,7]. Although mathematically distinct in these singularity conditions, these conditions have been proven equivalent [8]. Applying these singularity conditions, the curvature interference mechanisms of spiral bevel gears, hypoid gears, and worm gear drives have been investigated [9,10,11,12,13].
Building upon these studies, this work establishes the mechanism of the curvature interference for this face worm gear drive. The mathematical model is derived using elimination techniques and geometric synthesis methods to handle the associated nonlinear equation systems [14]. However, the applicability of these methods depends on the specific geometry of tooth surfaces. Moreover, the effectiveness of these approaches is inherently limited by the selection of initial iteration values. Notably, initial values exhibit high sensitivity to design parameter variations. Thus, any parameter modification necessitates re-establishing the initial values through geometric construction. Moreover, the lack of sufficient experimental data in the initial design phase makes it difficult to directly apply traditional machine learning approaches [15,16], artificial neural networks (ANNs) [17], and other methods to predict design parameters for avoiding curvature interference.
To address this issue and build upon existing curvature interference theory, this study advances the integration of the PINN technique into curvature interference analysis. The classical PINN technique was first proposed by Raissi et al. [18]. This technique establishes a supervised learning framework that incorporates physical laws as training constraints. Through encoding residual terms of nonlinear partial differential equations, the technique has demonstrated particular success in solving fundamental fluid dynamics problems including the Naiver–Stokes equations. In recent years, PINN techniques and their improved variants have found widespread applications in solving nonlinear partial differential equations across multiple domains, including computational fluid dynamics, structural vibrations, and material degradation problems. Gu [19] investigated quadrotor inverse dynamics through PINN modeling, while Zheng [20] developed a homotopy-based PINN approach for addressing multi-solution nonlinear differential equations. Dong et al. [21] successfully embedded measured pressure fluctuation data and fundamental hydraulic principles into a PINN framework for pump flow prediction. Söyleyici et al. [22] implemented a PINN model for Euler–Bernoulli beam vibration analysis and damping parameter estimation. Wang et al. [23] established an empirical degradation-based PINN model integrating state–space equations for robust battery health monitoring. Shahvandi et al. [24] utilized PINN ensembles trained on geophysical measurement data to characterize polar motion patterns.
In summary, compared with conventional deep neural networks (DNNs), PINNs demonstrate significant advantages and broad application prospects in the design of novel worm drive, particularly under conditions where experimental and simulation data are limited but comprehensive theoretical support from meshing theory is available. Consequently, the employment of PINN methodology is proposed to advance curvature interference theory. Through the application of PINNs, the initial-value issues inherent in the system of nonlinear equations are reformulated as a physical boundary-value problem. The approach facilitates solutions for the system of nonlinear equations. By adjusting boundary conditions within the neural network loss function during training, solutions for multiple key points along the curvature interference limit line are obtained. Multi-solution domains and residual connections [25] are incorporated into the enhanced PINN architecture, thereby enabling issues of gradient vanishing and local optima entrapment to be mitigated, with reliable convergence to globally optimal solutions ensured.
Compared with conventional curvature interference analysis methods [14], the proposed PINN-based analysis method embeds the governing nonlinear equations into the loss function architecture, enabling equation resolution through the minimization of the loss function. Secondly, the method can integrate the nonlinear curvature interference boundary equations as boundary constraints for parametric optimization, achieving the simultaneous realization of global design optimization and curvature interference avoidance [26].
This study presents an advanced approach to curvature interference analysis through the application of Physics-Informed Neural Networks (PINN). Traditional curvature interference analysis involves determining the curvature interference limit line by solving curvature interference equations post-design. However, a critical research gap remains in ensuring both interference-free operation and optimal meshing performance in the contact zone during the initial design phase, particularly concerning the inverse determination of design parameters.
Given that experimental and simulation data are limited during the initial design phase but the meshing principles are well established, this study transforms the curvature interference conditions into physical constraints within the PINN framework, constructing a loss function that incorporates the curvature interference limit function. This method overcomes the limitations of traditional forward solution analysis for curvature interference boundaries and lays the groundwork for the subsequent inverse determination of design parameters using PINN technology. The derivation strategy for the formulas in this manuscript is as shown in Figure 1.
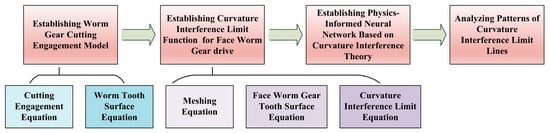
Figure 1.
A global flowchart of derivation strategy.
2. Cutting Engagement of Worm
2.1. Generating Surface Equation of Grinding Wheel
Worm-cutting engagement is demonstrated via a right-handed worm in this section. To ensure meshing quality, both helical surfaces of the worm are ground using conical grinding wheels with specific taper angles [27,28]. The working surfaces of the conical grinding wheel are designated as . The worm helicoids can be mathematically represented as . The subscript S (where S ∈ {1, 2}) identifies the two flanks of the worm. For S = 1, the corresponding flank engages with the convex surface of the face worm gear, hereafter termed the i-flank. For S = 2, it characterizes the opposing flank, designated as the e-flank, as depicted in Figure 2.
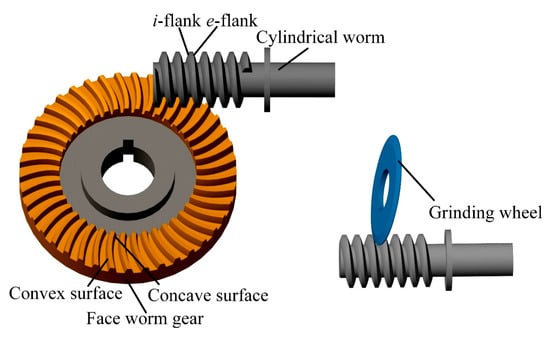
Figure 2.
Schematic of cutting engagement of worm and meshing of face worm gear drive.
To characterize the cutting engagement, a right-handed, fixed reference frame and a rotating reference frame are established on the worm. Two additional coordinate systems, and , are established on the grinding wheel to describe its orientation after two sequential deflections for proper installation, as shown in Figure 3a. The angle between and the plane is designated as the first tilt angle. The symbol represents the secondary tilt angle, which is the worm lead angle, as shown in Figure 3b. A local coordinate system, , is defined on the conical grinding wheel to characterize its geometric profile. The parameter denotes the semi-cone angle of the grinding wheel, while indicates the radius at its larger end. Figure 4 presents the complete configuration of these coordinate systems, as shown in Figure 4.
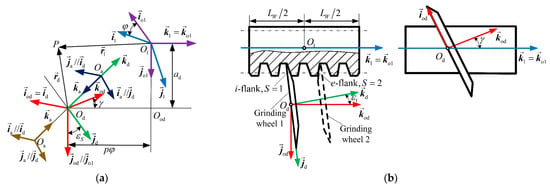
Figure 3.
Setting of coordinate system for cutting engagement. (a) Coordinate systems for worm grinding process; (b) first tilt angle and second tilt angle of the grinding wheel.
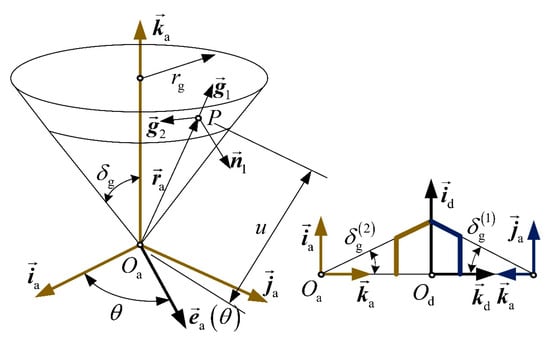
Figure 4.
Relative positions of coordinate systems during grinding i- and e-flanks.
Using the geometrical relationship in Figure 4, the equation of can be expressed in as:
where and are the two variables of , whose normal vector and its direction points from the entity to space.
Therefore, the fundamental quantities of are and [29]. Thus, the directions of the parametric curves on the conical surface are two primary directions. Using Equation (1), the primary directions of are derived in as:
whose principal curvatures are and . The symbols and represent the spherical vector functions [30].
2.2. Equation of Worm Tooth Surface
From Figure 4, different coordinate system settings of yield distinct equations of . Therefore, the equations of can be uniformly expressed within as:
Then, through coordinate rotation , the radius vector can be acquired in as:
whose normal vector is . The symbols and represent the rotating matrix [3]. After deduction, the components of and are , , , and , , and . The coefficients are , , , , , and .
Significantly, the aforementioned coefficients , , , , , and are functions of . In contrast, the coefficients , , and are all constants.
Generally, the angular velocity for the worm can be taken as . Moreover, as the grinding wheel constitutes a rigid rotor, its high angular velocity does not govern the grinding engagement. Therefore, the angular velocity can be ignored to obtain the relatively angular velocity vector . Accordingly, the relative velocity vector for cutting engagement can be determined in as
Therefore, using in Equation (4) and in Equation (5), the worm-cutting engagement function for the machining worm can be expressed as:
where , and .
According to the meshing theory [3], it can be derived from Equation (16) that the function representing the meshing limit function is identically equal to zero. Therefore, during cutting engagement, the meshing limit line coincides with the instantaneous contact line.
When cutting , the grinding wheel turns around while simultaneously translating along . This kinematic combination generates the action surface by . Using Equation (6), the equation of the action surface is acquired in as:
From Equation (7), the equation for can be obtained in via the rotating transformation as:
whose coefficients are and .
When S = 1, it corresponds to the i-flank helical surface of the worm. When S = 2, it represents the equation of the e-flank. From Equation (18), it can be seen that of the three variables, only two parameters are independent. Therefore, once the motion parameters are determined, the instantaneous contact line for cutting engagement can be obtained.
2.3. Function of Curvature Interference Limit Line
Then, using the principal frame, the normal vector of the contact line in cutting engagement can be determined as:
where the coefficient is . The principal direction vectors and on can be represented in from Equation (2) as and by using the coordinate rotation , whose components are , , and .
Using Equations (5) and (9), the curvature interference limit function [3] of cutting engagement can be obtained as:
where , and .
3. Curvature Interference Limit Function of Meshing
To enhance meshing efficiency, the worm gear is supposed to be configured with a left-hand rotational direction when paired with a right-hand worm. As the mesh of the right-hand worm gears with left-hand worms follows an analogous meshing theory, this configuration will not be further discussed. In this section, the portion of the face worm gear proximal to the inner diameter is designated as the inner end, while the opposite side is termed the outer end, as illustrated in Figure 5. The tooth surface of the face worm gear is denoted as .
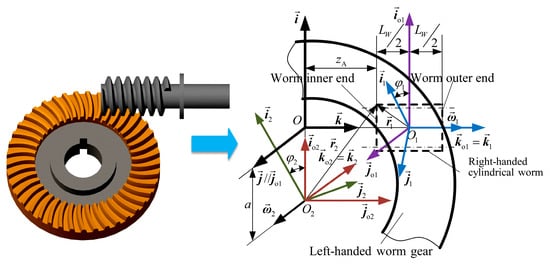
Figure 5.
Coordinate system settings while machining face worm gear.
During machining , a stationary frame and a rotating frame reflecting the original and present positions of the face worm gear are created. is the center distance. While the worm turns around via a certain angle , the turning angle of the worm gear is , where and indicate the gear ratio. Detailed steps for creating and are given in ref. [31].
When the worm turns around , the worm helicoid can form a family of one-parameter surfaces in . Thereupon, the equation for can be obtained in from Equation (8) as:
whose normal vector is , and coefficients are , , , and .
During face worm gear machining operations, the worm angular velocity is conventionally designated as [3]. Accordingly, the angular velocity of the worm gear can be given as , where represents the transmission ratio. As the face worm gear is left handed, the orientation of is along the negative direction of . Hence, the angular velocity vector and the relative velocity vector can be attained in as:
where , , and .
From Equations (11) and (12), the meshing function can be obtained as:
where the components can be obtained after calculation as , , and .
Using the coordinate transformation , the equation for can be determined in from Equations (11) and (13) as:
whose components are , , and .
When S = 1, Equation (14) denotes the convex flank of the face worm gear, while for S = 2, it represents the concave flank.
Through the computation of the partial derivative of with , the meshing limit function can be determined as:
A moving orthogonal frame is built at an arbitrary contact point of during meshing. and are arbitrarily two orthogonal directions on . According to Equation (9), and can be obtained as:
where , , , and .
Based on this, using Equation (16), the normal vector of the contact line can be acquired in as:
where , and .
From in Equation (12), in Equation (17), and in Equation (15), the curvature interference limit function can be attained as:
where , and .
As can be seen from Equation (18), there are four variables involved in the expression. Therefore, it is necessary to further simplify the curvature interference boundary function in Equation (18) by eliminating variables based on the boundary conditions of the tooth surface. The resulting expression will yield the curvature interference boundary of the worm gear tooth surface. The detailed calculation process will be discussed in the subsequent section.
4. Curvature Interference Characteristic Analysis Based on PINN Technology
In this section, a Physics-Informed Neural Network (PINN) model driven by curvature interference mechanisms is established to further develop the curvature interference characteristic analysis. Firstly, the curvature interference boundary function derived from Equation (20), together with the boundary conditions of the tooth surface, is used to construct the loss function. Subsequently, the variables to be solved are determined. A deep neural network is then established, comprising the initialization of the network, forward propagation of outputs, loss computation, and backpropagation for optimization. During the training process, if the loss does not meet the prescribed accuracy threshold, the model continues to iterate and update. Once the loss has converged, the numerical results of the key points on the curvature interference boundary are obtained. Finally, these results are employed to perform curvature interference analysis. The flowchart of the proposed tooth surface contact analysis method based on PINNs is illustrated in Figure 6. The detailed derivation of the loss function will be presented in the subsequent subsection.
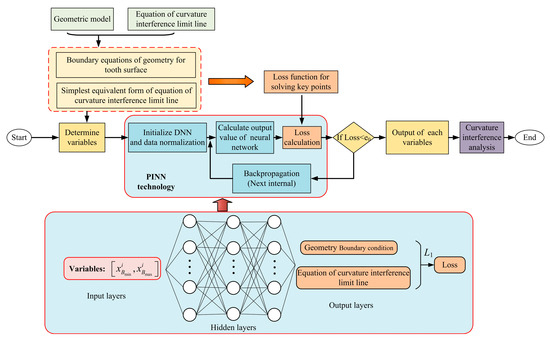
Figure 6.
Flowchart of curvature interference characteristic analysis using PINN based on curvature interference theory.
The calculation of curvature interference limit lines can be reduced to determining key points on the curvature interference limit lines. Based on this, a loss function can be established.
To determine the geometric boundary conditions of the tooth surface, the worm and face gear tooth surfaces are projected onto their axial cross-sections, as illustrated in Figure 7a,b. As illustrated in Figure 7, within the axial section coordinate system of the face worm gear, the vertical coordinates and of the dedendum AD and addendum BC define the upper and lower boundaries of the relevant region. Within this range, the vertical coordinate of the key point Pj can be expressed as . Subsequently, by combining with in Equation (6), in Equation (13), and in Equation (18), a system of four nonlinear equations is derived for solving the key point Pj on the curvature interference limit line. This system is expressed as:
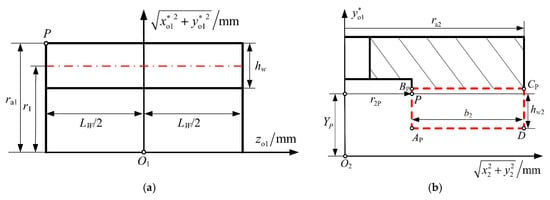
Figure 7.
Projection in axial section: (a) projection of worm helical surface in the axial coordinate system; (b) projection of worm gear tooth surface in its axial coordinate system.
To solve Equation (19), the elimination method is initially employed to eliminate variables of Equation (19).
Therefore, from Equation (7), when , can be rewritten as
By simultaneously considering and in Equation (19), it is possible to derive it as:
Consequently, the trigonometric functions and can be derived using Equation (21) as
By employing trigonometric identities, it is possible to obtain as
where the coefficients are , , , , and .
By utilizing Equation (23), the curvilinear coordinate of key points Pj on the curvature interference limit line can be expressed as
The meshing equation in Equation (19) can be rephrased as concerning . Consequently, within one meshing cycle, by utilizing this trigonometric equation , one of the solutions for can be expressed as a function of and as
where , and .
Finally, through elimination, the function from Equation (22), in Equation (24), and in Equation (25) are substituted into the curvature interference limit function in Equation (19). As a result, a univariate equation with can be derived.
The necessary and sufficient condition for the equation to possess valid solutions within a given solving region is the existence of intersections between the curve of and the abscissa axis within the solving interval. Therefore, by employing geometric construction methods [31], both the existence of solutions and appropriate initial values for numerical iteration can be determined through graphical inspection. By observing the number of intersections between the curve of and the abscissa axis within the solving interval, the number of equation solutions of can be determined, which directly corresponds to the number of curvature interference limit lines. After determining the number of solutions, the curvature interference function is combined with boundary conditions to yield the loss function as
where are boundary conditions, and dynamically adjusting the weights , , and in can ensure that each condition can be satisfied in a balanced way during the model training process.
Then, a deep neural network is constructed. A ReLU activation function is introduced through each hidden layer to enhance the non-linear mapping capability and, thus, alleviate the gradient vanishing problem. Based on this, the affine translation of the nonlinear activation network is depicted as:
where and are the weight matrices and offset vectors of the l + 1th layer. and refer to the weight and offset terms.
The network is trained via the L-BFGS optimization algorithm. Automatic differentiation technology and the cosine annealing learning rate scheduling strategy are employed. These techniques not only simplify the gradient computation process but also improve the stability and convergence rate of training.
The trained PINN can accept capable input from any contact point in the Ω-domain and instantly output an exact numerical solution for the variables in Equation (24). Based on this, the of the key points on the curvature interference limit line can be obtained.
Upon acquiring the value of , it is sequentially substituted into the function from Equation (22), in Equation (24), and in Equation (25) to solve for the values of other pertinent parameters. Subsequently, the positions of these key points can be ascertained using equations of and in Equations (8) and (14). By interpolating the respective key points, the curvature interference limit line can be plotted. Finally, an investigation into the curvature interference characteristics can be conducted based on the distribution of the curvature interference limit line.
5. Numerical Examples
5.1. Numerical Results of Curvature Interference Limit Lines
The basic parameters of the face worm gear drive can be determined based on the gear manual [32], as summarized in Table 1. The process parameters of the worm are shown in Table 2.

Table 1.
Design parameters of face worm gear drive.

Table 2.
Operating parameters for machining worm.
The existence of two contact lines was first determined using the geometric construction method, and the procedure is described in ref. [26]. To calculate the curvature interference limit line, five key points are uniformly selected within the coordinate system , with their coordinate values listed in Table 3. The variable L values at these five key points are then substituted into the function in Equation (19).

Table 3.
Numerical results of key point Pj (j = 1 to 5) for i-flank.
The neural network architecture consists of 20 hidden layers, each containing 26 neurons. For the L-BFGS optimization algorithm, the initial learning rate was set to 0.01, with a cosine annealing learning rate scheduler employing a minimum learning rate of 0.01. The training process was terminated once the loss function within a subdomain reached the desired accuracy. The loss function converged to the expected accuracy within 500 epochs and exhibited stable performance throughout the training, as illustrated in Figure 8. The training was conducted on an Intel(R) Core(TM) i7-8700 CPU with 16 GB of RAM, with a memory footprint of approximately 528.7 MB. The PINN model required approximately 1.95 s to reach the desired precision. In contrast, the Fsolve method achieved the same level of accuracy in approximately 0.02 s. While the Fsolve method remains an ideal method for solving nonlinear systems in traditional curvature interference boundary analyses, the PINN model is more suitable when inverse design parameter estimation is required.
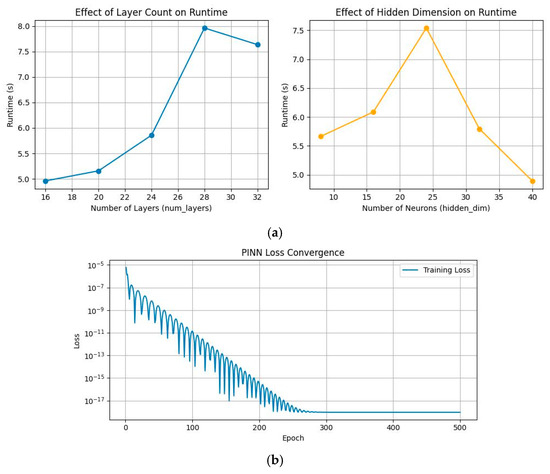
Figure 8.
Performance evaluation of the developed PINN model: (a) effect of the number of layers and neurons on the training time; (b) training loss curve.
Figure 8a illustrates the convergence behavior of the loss function during the training process of the PINN model. Initially, the loss is relatively high, but it gradually decreases as training progresses. Although some fluctuations are observed in the early stages, the loss eventually stabilizes at a very low value, indicating an extremely small model error and near-optimal performance. Figure 8b illustrates the impact of the number of layers and neurons on the training time and inference speed. According to the observed trends, increasing the number of layers significantly raises the runtime. However, further increases in the number of neurons lead to a decrease in the runtime.
From the obtained numerical results, the values of other variables and the positional coordinates of the key points can be calculated. These numerical outcomes are summarized in Table 3 and Table 4. The numerical results demonstrate that the convergence accuracy achieved with the established PINN model for the specified case is comparable to that of the iterative method (e.g., Fsolve), as shown in Table 3 and Table 4.

Table 4.
Numerical results of key point Pj (j = 1 to 5) for e-flank.
After determining the key point positions, three-dimensional plots of both the curvature interference limit lines and their conjugate lines can be generated separately for the face worm gear tooth surface and the worm helicoid, as shown in Figure 9 and Figure 10. For clarity, Figure 11 also shows projections of these curvature interference limit lines and their conjugate lines onto the axial sections of the worm helicoid and face worm gear tooth surface, respectively. Case studies demonstrate that with proper parameter selection and matching, neither the curvature interference limit lines nor their conjugate lines intrude into the tooth surfaces. Moreover, the curvature interference limit lines are located closer to the inner circle of the face worm gear tooth surface. Consequently, this location is at risk of curvature interference.
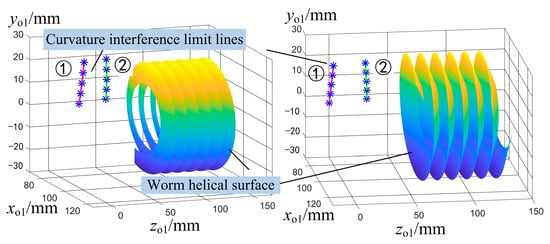
Figure 9.
Curvature interference limit lines on the worm helical surface .
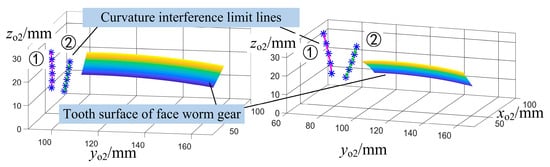
Figure 10.
Curvature interference limit lines on the face worm gear tooth surface .
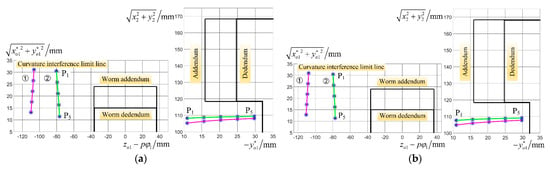
Figure 11.
Curvature interference limit lines on cross-sections of and : (a) i-flank; (b) e-flank.
5.2. Influence of Design Parameters on Curvature Limit Lines
Previous studies indicate that the meshing performance in face worm gear drives can be controlled by adjusting the grinding wheel deflection angle, semi-cone angle, and worm axial installation distance. Therefore, this section investigates the influence of these parameters on curvature interference limit lines through three numerical cases. The selected cases are listed in Table 5, and their corresponding curvature interference limit lines are illustrated in Figure 12, Figure 13 and Figure 14.

Table 5.
Operating parameters for machining worm.
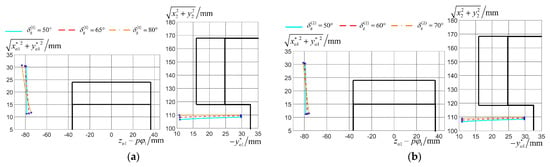
Figure 12.
Influence of grinding wheel half taper angle , (S = 1, 2) on curvature interference limit lines: (a) i-flank; (b) e-flank.
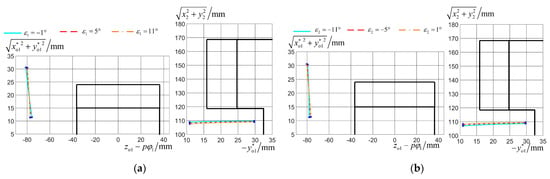
Figure 13.
Influence of grinding wheel secondary tilt angle , (S = 1, 2) on curvature interference limit lines: (a) i-flank; (b) e-flank.
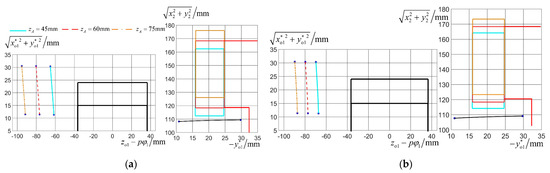
Figure 14.
Influence of worm axial mounting distance on curvature interference limit lines: (a) i-flank; (b) e-flank.
The influence of the grinding wheel semi-cone angle on the curvature interference limit line is illustrated in Figure 12. The effect of the grinding wheel secondary inclination angle on the curvature interference limit line is shown in Figure 13. The analysis of Figure 12 and Figure 13 reveals that curvature interference limit lines exhibit minimal sensitivity to the grinding wheel deflection angle and semi-cone angle. Alterations to the grinding wheel parameters displace the curvature interference limit lines toward the tooth surfaces, yet these limit lines remain sufficiently distant from the tooth surface. This prevents the occurrence of curvature interference.
However, the curvature interference limit lines exhibit significant sensitivity to the worm axial installation distance, as shown in Figure 14. Reducing the worm axial installation distance can cause the limit lines to progressively migrate toward the tooth surfaces. An excessive reduction in the axial installation distance may allow the limit lines to penetrate the tooth surfaces. Consequently, this may lead to curvature interference.
In conclusion, this study demonstrates that the geometric parameters of the grinding wheel utilize negligible influence on the curvature interference limit lines within appropriate process parameter ranges. However, the axial installation distance requires stringent control to prevent interference.
6. Conclusions
Within the theoretical framework of curvature interference limit lines for conical surface enveloping cylindrical worm–face worm gear drives, this study develops a Physics-Informed Neural Network (PINN) model that integrates the underlying mechanism of curvature interference. By incorporating tooth surface geometric equations, meshing functions, and critical curvature interference functions, a comprehensive deep learning architecture is constructed, embedding spatial boundary constraints, kinematic coupling conditions, and mechanism-driven loss functions.
The model employs a loss function minimization strategy to implicitly solve the nonlinear system of equations. Numerical experiments demonstrate that it achieves a computational accuracy on the order of 10-13, which is comparable to that of classical iterative methods.
Characteristic analysis reveals that dual curvature interference limit lines are located at the inner end of the face worm gear tooth surface. This implies that penetration of the curvature interference limit lines into the tooth surface may occur from the inner end, thereby inducing curvature interference phenomena. The analysis of process parameter influences demonstrates that variations in the grinding wheel’s geometric parameters exhibit no significant impact on curvature interference boundaries under both drive conditions. However, a reduction in the worm axial mounting distance may result in penetration of the curvature interference limit lines into the tooth flank, thereby giving rise to interference phenomena.
The proposed PINN model, constrained by curvature interference mechanisms, demonstrates promising generalizability and can be extended to interference analysis in other types of worm drive systems. This research lays a foundation for the development of a physics-constrained intelligent design of the worm drive and offers scope for further exploration in the inverse optimization of design parameters.
Author Contributions
Conceptualization, S.M. and Y.Z.; methodology, S.M.; software, H.Y.; validation, S.Q. and H.Z.; formal analysis, W.Z.; resources, Y.L.; writing—original draft preparation, S.M.; writing—review and editing, X.S. and Z.D.; project administration, X.S.; funding acquisition, Z.D. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the National Natural Science Foundation of China (52075083, 52005346, and 52005347), Project of the Science and Technology Innovation Team of Liaoning Provincial Department of Education (LJ222410142011), Basic Research Projects of Higher Colleges and Universities of Liaoning Provincial Department of Education (LJ212410142040 and JYTMS2023190), Liaoning Province Natural Science Foundation (2024-BS-103), Liaoning Province Science and Technology Plan Joint Program (2024-MSLH-161, 2024-MSLH-203, and 2024-MSLH-367), Support Program for Young and Middle-aged Talents in Science and Technology Innovation in Shenyang (RC220066), and Liaoning Huanghai Laboratory Open Innovation Fund (2024LHLKC0300).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in this article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Litvin, F.L.; Fuentes, A. Gear Geometry and Applied Theory, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Wu, D.; Luo, J. Theory of Gearing; Science Press: Beijing, China, 1985. [Google Scholar]
- Dong, X. Foundation of Meshing Theory for Gear Drives; China Machine Press: Beijing, China, 1989. [Google Scholar]
- Wu, X. Meshing Theory of Gear, 2nd ed.; Xi’an Jiaotong University Press: Xi’an, China, 2009. [Google Scholar]
- Argyris, J.; Litvin, F.L.; Lian, Q.M.; Lagutin, S.A. Determination of envelope to family of planar parametric curves and envelope singularities. Comput. Methods Appl. Mech. Eng. 1999, 175, 175–187. [Google Scholar] [CrossRef]
- Litvin, F.L.; Demenego, A.; Vecchiato, D. Formation by branches of envelope to parametric families of surfaces and curves. Comput. Methods Appl. Mech. Eng. 2001, 190, 4587–4608. [Google Scholar] [CrossRef]
- Dong, X. Design and Modification of Hourglass Worm Drives; China Machine Press: Beijing, China, 2004. [Google Scholar]
- Mu, S.B.; Zhao, Y.P.; Wang, T.F.; Meng, Q.X.; Li, G.F. New method for determining singularities on enveloped surface and its application to study curvature interference theory of involute worm drive. Adv. Mech. Eng. 2021, 13, 16878140211038086. [Google Scholar] [CrossRef]
- Litvin, F.L.; Yukishima, K.; Hayasaka, K.; Gonzalez-Perez, I.; Fuentes, A. Geometry and investigation of Klingelnberg-type worm gear drive. ASME. J. Mech. Des. 2007, 129, 17–22. [Google Scholar] [CrossRef]
- Sohn, J.; Park, N. Study on the influence of gear hobbing and shaft misalignments on the geometric interference of cylindrical worm gear set. Proc. Inst. Mech. Eng. C–J. Mech. Eng. Sci. 2017, 231, 4646–4654. [Google Scholar] [CrossRef]
- Wang, D.Y.; Zhang, L.H.; Tian, C.; Miao, J.C.; An, L.Q.; Shi, J.; Chen, B.K. Mathematical model and analysis of novel bevel gear with high load-capacity based on the geometric elements. Mathematics 2024, 12, 1373. [Google Scholar] [CrossRef]
- Sheng, W.; Li, Z.M.Q.; Yu, X.F.; Xi, R.S. Active design method and performance prediction of internal gear pairs with low sliding ratio. Meccanica 2025, 59, 1121–1137. [Google Scholar] [CrossRef]
- Han, X.H.; Wang, Y.H.; Hua, L.; Zhuang, W.H.; Zheng, F.Y.; Feng, W. A new multi-DOF envelope forming process for fabricating spiral bevel gears with back taper tooth. Chin. J. Aeronaut. 2025, 38, 103239. [Google Scholar] [CrossRef]
- Meng, Q.X.; Jiao, Y.G.; Zhao, Y.P.; Mu, S.B.; Cui, J.; Zhang, M.H. Undercutting mechanism of worm wheel in offsetting normal arc-toothed cylindrical worm drive. J. Cent. South Univ. 2023, 32, 495–508. [Google Scholar] [CrossRef]
- Tošić, M.; Marian, M.; Habchi, W.; Lohner, T.; Stahl, K. Application of machine learning for film thickness prediction in elliptical EHL contact with varying entrainment angle. Tribol. Int. 2024, 199, 109940. [Google Scholar] [CrossRef]
- Skulić, A.; Bukvić, M.; Gajević, S.; Miladinović, S.; Stojanović, B. The influence of worm gear material and lubricant on the efficiency and coefficient of friction. Tribol Mater. 2024, 3, 15–23. [Google Scholar] [CrossRef]
- Tuninetti, V.; Forcael, D.; Valenzuela, M.; Martínez, A.; Ávila, A.; Medina, C.; Pincheira, G.; Salas, A.; Oñate, A.; Duchêne, L. Assessing Feed-Forward Backpropagation Artificial Neural Networks for Strain-Rate-Sensitive Mechanical Modeling. Materials 2024, 17, 317. [Google Scholar] [CrossRef] [PubMed]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Gu, W.B.; Primatesta, S.; Rizzo, A. Physics-informed neural network for quadrotor dynamical modeling. Robot. Auton. Syst. 2024, 171, 104569. [Google Scholar] [CrossRef]
- Zheng, H.Y.; Huang, Y.; Huang, Z.Y.; Hao, W.R.; Lin, G. HomPINNs: Homotopy physics-informed neural networks for solving the inverse problems of nonlinear differential equations with multiple solutions. J. Comput. Phys. 2024, 500, 112751. [Google Scholar] [CrossRef]
- Dong, C.; Tao, J.F.; Sun, H.; Wei, Q.; Tan, H.Y.; Liu, C.L. Innovative fault diagnosis for axial piston pumps: A physics-informed neural network framework predicting pump flow ripple. Mech. Syst. Signal Process. 2025, 225, 112274. [Google Scholar] [CrossRef]
- Söyleyici, C.; Ünver, H.Ö. A physics-informed deep neural network based beam vibration framework for simulation and parameter identification. Eng. Appl. Artif. Intell. 2025, 141, 109804. [Google Scholar] [CrossRef]
- Wang, F.J.; Zhai, Z.; Zhao, Z.B.; Di, Y.; Chen, X.F. Physics-informed neural network for lithium-ion battery degradation stable modeling and prognosis. Nat. Commun. 2024, 15, 4332. [Google Scholar] [CrossRef]
- Shahvandi, M.K.; Adhikari, S.; Dumberry, M.; Modiri, S.; Heinkelmann, R.; Schuh, H.; Mishra, S.; Soja, B. Contributions of core, mantle and climatological processes to Earth’s polar motion. Nat. Geosci. 2024, 17, 705–710. [Google Scholar] [CrossRef]
- Tian, R.Z.; Kou, P.; Zhang, Y.H.; Mei, M.Y.; Zhang, Z.H.; Liang, D.L. Residual-connected physics-informed neural network for anti-noise wind field reconstruction. Appl. Energy 2024, 357, 122439. [Google Scholar] [CrossRef]
- Mu, S.B.; Sun, X.W.; Dong, Z.X.; Yang, H.R.; Liu, Y.; Zhang, W.F.; Meng, Q.X.; Zhao, Y.P. Meshing theory of point-contact conical-envelope cylindrical worm-face worm gear drive. Mech. Mach. Theory 2025, 205, 105870. [Google Scholar] [CrossRef]
- Chen, Y.; Pu, Y.; Chen, Y.H. Study on the Wear Performance of Spiroid Worm Drive with Steel-Steel Meshing. Machines 2025, 13, 205. [Google Scholar] [CrossRef]
- Xu, Z.K.; Li, H.T.; Ren, W.; Ma, M. Investigation of non-linear dynamic characteristics of a point-contact spiroid worm drive generated by two-generating-surface method. J. Sound Vib. 2025, 597, 118805. [Google Scholar] [CrossRef]
- Chen, W. Differential Geometry, 2nd ed.; Peking University Press: Beijing, China, 2018. [Google Scholar]
- Zhao, Y. Engineering Differential Geometry of Curves and Surfaces; Science Press: Beijing, China, 2023. [Google Scholar]
- Meng, Q.X.; Zhao, Y.P.; Cui, J.; Mu, S.B.; Li, G.F. Meshing theory of offsetting Archimedes cylindrical worm drive. Mech. Based Des. Struct. Mach. 2024, 52, 152–168. [Google Scholar] [CrossRef]
- Editorial Committee of Gear Handbook. Gear Handbook; Machine Press: Beijing, China, 2004. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).