A Cox Model-Based Workflow for Increased Accuracy in Activity-Travel Patterns Generation
Abstract
1. Introduction
2. Literature Review
2.1. Data Sources
2.2. Modeling Travel Activity Patterns
2.3. Cox Proportional Hazards and Hazard-Based Models in Transport Research
2.4. Modeling Activity Durations
- Development of an activity-based method integrating hazard-based models to enhance the accuracy of synthetic activity-travel pattern generation,
- Evaluation and comparison of Cox-based modeling approaches, including models with and without unobserved heterogeneity, to improve activity duration estimation.
- Assessment of the realism of the generated synthetic datasets through statistical testing against real-world data from Athens, demonstrating improved behavioral fidelity.
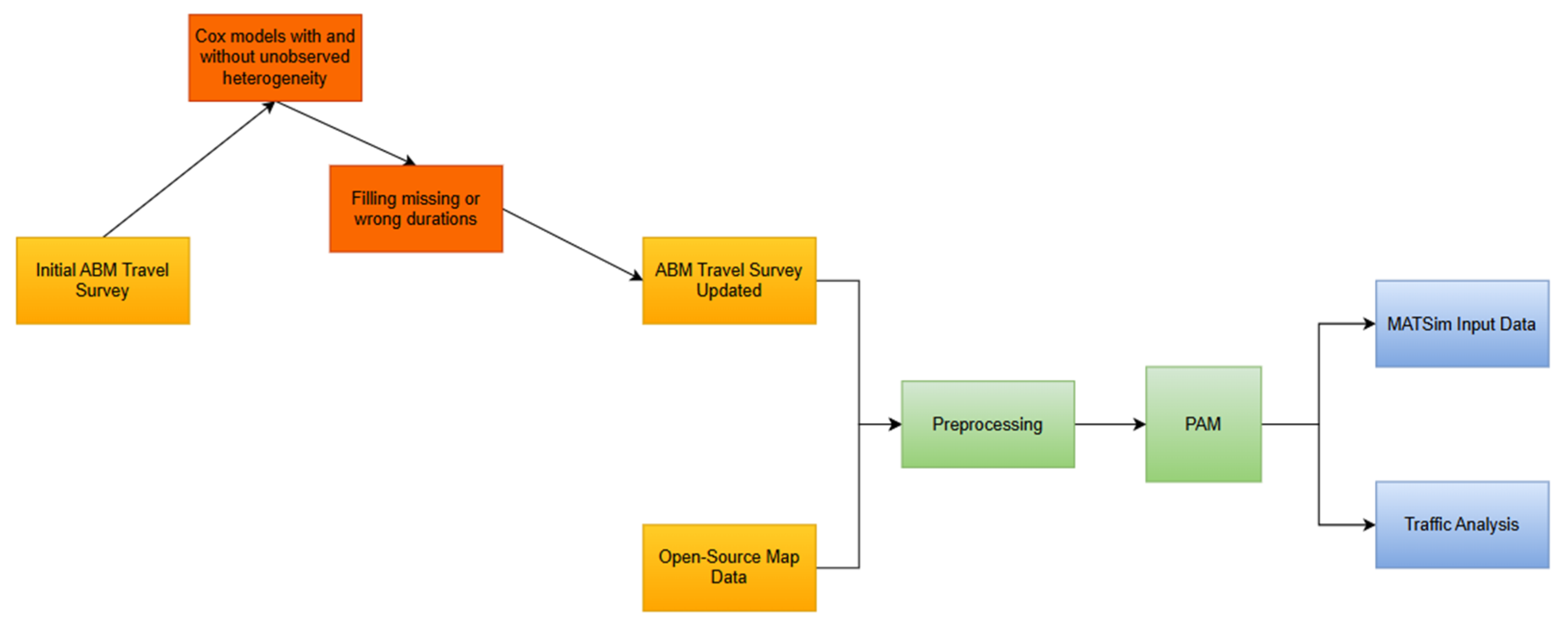
3. Methodology
3.1. Modeling Unobserved Heterogeneity and Non-Linear Relationships in Source Data by Using the Cox-Based Model
- A simple Cox model without unobserved heterogeneity considerations,
- A Cox model that accounts for unobserved heterogeneity in the source dataset by including two latent classes,
- A Cox-based machine learning model, which leverages a neural network to learn complex, non-linear relationships in the data while maintaining the proportional hazards structure of the traditional Cox model.
- The hazard function for individual i at time t,
- : The non-parametric baseline hazard function,
- : The probability that individual i belongs to latent class c,
- : The vector of predictor variables for individual i,
- : The vector of coefficients for latent class c,
- : The frailty term for class c, calculated as:
- is an uncentered random factor ranging from 0 to 1,
- is the standard deviation.
- Latent Class Membership Probabilities
- classprobsc is the prior probability of belonging to latent class
- likelihoodc represents how well the data fit the parameters of latent class c, defined as:
- Survival Function for Each Latent Class
- : The non-parametric baseline hazard function
- : the inner product of the coefficients βc and the covariates for individual
- : The frailty term for each latent class
- Overall Survival Function
- (probability of belonging to latent class 1)
- (probability of belonging to latent class 2)
- The Cox-based machine learning model
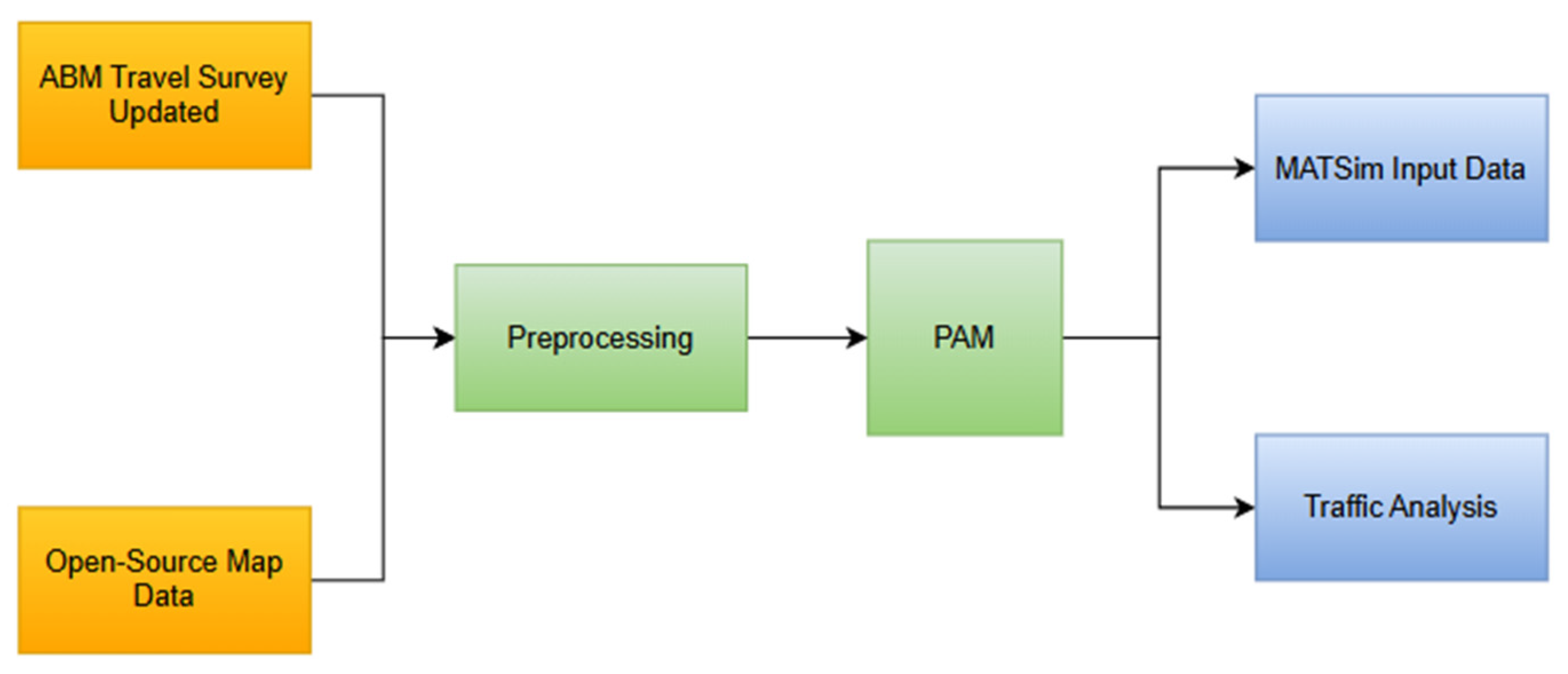
3.2. Activity-Based Model Structure and Integration with Cox-Based Models
- Missing activity durations,
- Invalid activity durations (Negative values occurred when durations were calculated from inconsistent trip start times, requiring correction through estimation),
- Missing the “return-to-home” activity.
3.3. Model Performance Evaluation
3.3.1. Cox Models Comparison According to Metrics
3.3.2. Comparison of Synthetic Data vs. Real Data
4. Results
4.1. Cox and Cox-Based Models Comparison
| Trip Purpose | Model Type | C-index | MAE | RMSE |
|---|---|---|---|---|
| Work | 80/20 Split | 0.6746 | 5.9995 | 6.6242 |
| 5-Fold CV | 0.6788 | 5.9963 | 6.7622 | |
| Market | 80/20 Split | 0.45 | 3.72 | 4.8572 |
| 5-Fold CV | 0.393 | 3.0232 | 3.8979 | |
| Education | 80/20 Split | 0.4545 | 3.7411 | 4.7305 |
| 5-Fold CV | 0.6718 | 4.5595 | 5.3528 | |
| Other | 80/20 Split | 0.8421 | 3.4673 | 4.5029 |
| 5-Fold CV | 0.7071 | 7.3472 | 12.9006 |
| Trip Purpose | Model Type | C-index | MAE | RMSE |
|---|---|---|---|---|
| Work | 80/20 Split | 0.4319 | 4.5439 | 5.2035 |
| 5-Fold CV | 0.4753 | 4.6526 | 5.2832 | |
| Market | 80/20 Split | 0.5 | 3.4341 | 3.7552 |
| 5-Fold CV | 0.5164 | 3.2440 | 3.5082 | |
| Education | 80/20 Split | 0.7879 | 4.1424 | 4.8065 |
| 5-Fold CV | 0.507 | 3.4398 | 4.0277 | |
| Other | 80/20 Split | 0.2632 | 6.2377 | 6.7870 |
| 5-Fold CV | 0.4907 | 5.5641 | 6.3158 |
| Trip Purpose | Model Type | C-index | MAE | RMSE |
|---|---|---|---|---|
| Work | 80/20 Split | 0.7005 | 2.2353 | 3.1947 |
| 5-Fold CV | 0.6814 | 2.2546 | 3.2137 | |
| Market | 80/20 Split | 0.15 | 1.4444 | 1.7321 |
| 5-Fold CV | 0.404 | 2.3028 | 2.9354 | |
| Education | 80/20 Split | 0.4848 | 3.2857 | 4.0883 |
| 5-Fold CV | 0.6707 | 2.2667 | 2.9981 | |
| Other | 80/20 Split | 0.6842 | 1.8571 | 2.2361 |
| 5-Fold CV | 0.651 | 2.4238 | 3.1286 |
| Trip Purpose | Model Type | Criterion | Value |
|---|---|---|---|
| Work | Cox without frailty | AIC | 3162.45 |
| Cox with frailty | WAIC | 1590.6 | |
| Other | Cox without frailty | AIC | 171.83 |
| Cox with frailty | WAIC | 166.17 | |
| Market | Cox without frailty | AIC | 285.44 |
| Cox with frailty | WAIC | 103.1 | |
| Education | Cox without frailty | AIC | 257.65 |
| Cox with frailty | WAIC | 229.44 |
4.2. Comparison of Synthetically Generated Data with Real-World
| Metrics | Synth. Data 1 | Synth. Data 2 | Synth. Data 3 | Synth. Data 4 |
|---|---|---|---|---|
| K–S test (D/p-value) | 0.2939/ <2.2 × 10−16 | 0.25486/ <2.2 × 10−16 | 0.20822/ 3.46 × 10−11 | 0.16116/ 6.885 × 10−8 |
| MAE | 4.572079 | 3.707881 | 3.664099 | 4.195042 |
| RMSE | 5.609498 | 4.739945 | 4.723046 | 5.323675 |
| Metrics | Synth. Data 1 | Synth. Data 2 | Synth. Data 3 | Synth. Data 4 |
|---|---|---|---|---|
| K–S test (D/p-value) | 0.8619/ 2.2 × 10−16 | 0.62409/ 1.73 × 10−14 | 0.4235/ 3.71 × 10−7 | 0.4213/ 2.033 × 10−7 |
| MAE | 2.685109 | 2.3248 | 2.407971 | 2.841279 |
| RMSE | 3.932881 | 3.943628 | 3.591605 | 4.174001 |
| Metrics | Synth. Data 1 | Synth. Data 2 | Synth. Data 3 | Synth. Data 4 |
|---|---|---|---|---|
| K–S test (D/p-value) | 0.25078/ 0.000972 | 0.2253/ 0.02735 | 0.18736/ 0.1031 | 0.24032/ 0.01534 |
| MAE | 4.047721 | 3.91789 | 3.951568 | 3.971024 |
| RMSE | 5.132352 | 5.062376 | 5.040041 | 4.999081 |
| Metrics | Synth. Data 1 | Synth. Data 2 | Synth. Data 3 | Synth. Data 4 |
|---|---|---|---|---|
| K–S test (D/p-value) | 0.47753/ 8.42 × 10−8 | 0.2801/ 0.005868 | 0.35482/ 0.0001707 | 0.31586/ 0.001193 |
| MAE | 4.755 | 4.5188 | 4.3898 | 4.45858 |
| RMSE | 6.1339 | 5.9359 | 5.8461 | 5.921535 |
4.3. ABM’s Outputs and Traffic Analysis Results



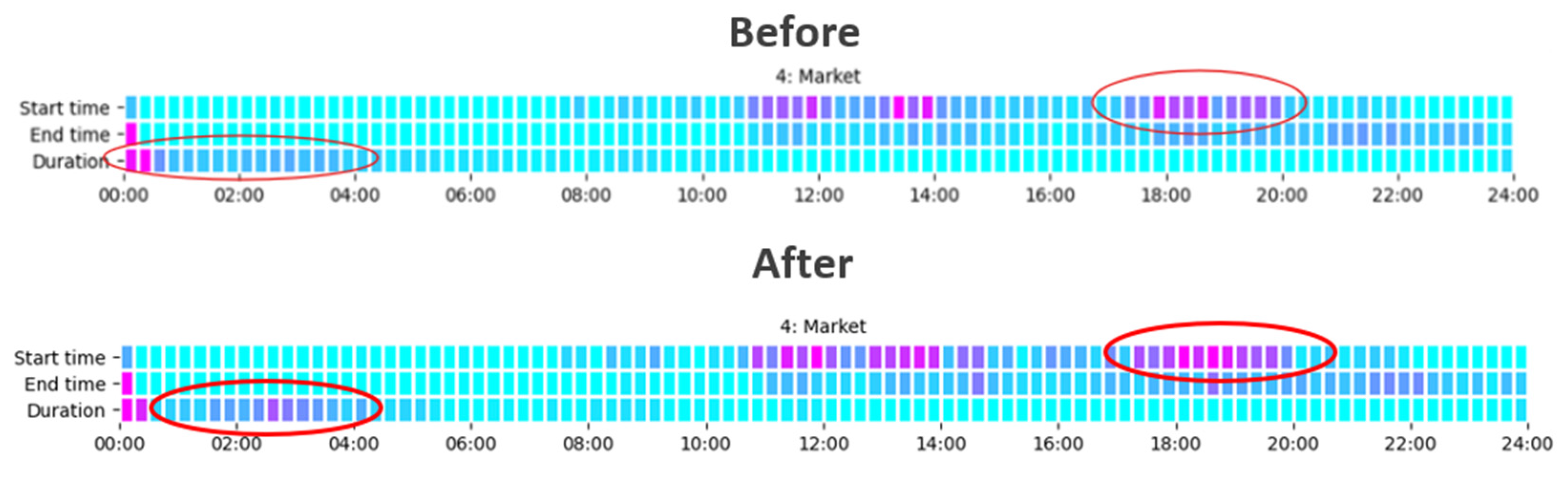
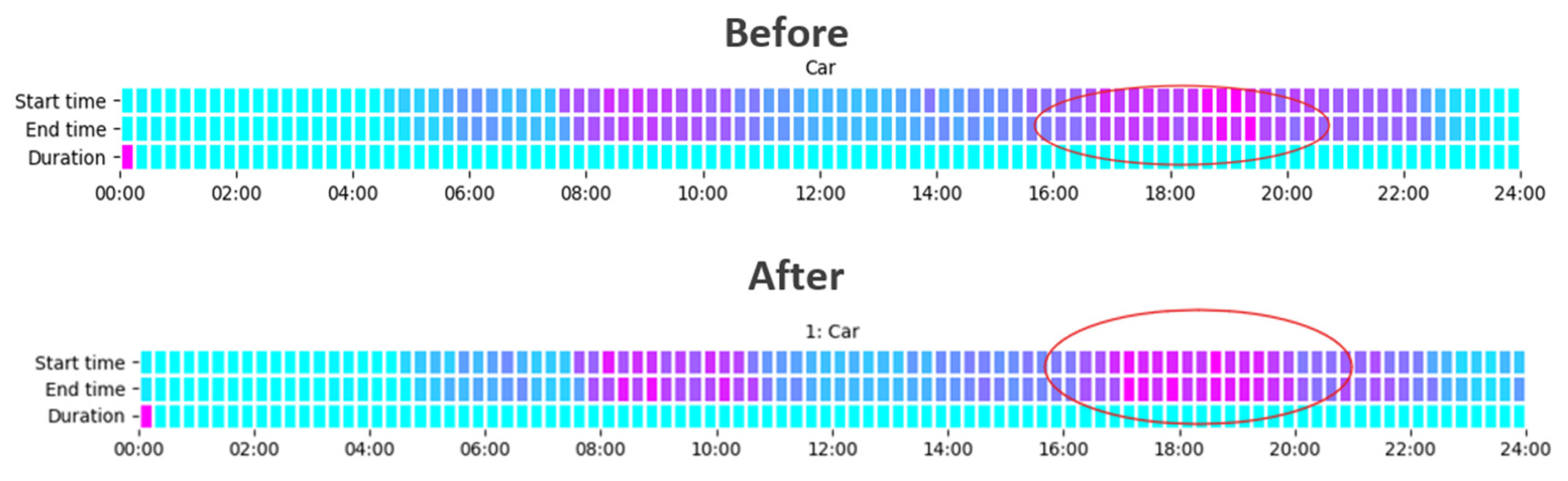
5. Discussion
- In shopping-related trips, an increase in duration range is observed, with several trips lasting 2–3 h, which is expected. Higher activity is noted in the afternoon, particularly between 18:00 and 19:30.
- Work-related trips show greater variability in duration and end times, unlike the unprocessed data, where trip endings concentrate in the afternoon.
- Other and service-related trips display a previously absent duration range, with more trips lasting 1.5–3 h. While most occur in the afternoon, service-related trips show increased morning activity.
- Educational trips remain largely unchanged, likely due to minimal intervention. Their start and end times, as well as durations, follow a pattern that can be considered more irregular than other types of purpose trips.
- Increased percentage of use of cars and trains/metro during peak afternoon hours.
- Slightly reduced percentage of use of motorcycles and buses in the afternoon.
- Higher usage percentage of e-scooters and bicycles at night.
- Greater walking activity in the afternoon.
- Rise in both percentage and absolute number of trips during peak hours (17:00–20:00, 22:00–00:00), with a relative decline at 16:00 and 20:00.
- The high-income category aligns with typical working hours, showing peak trip percentages in both morning and afternoon. The low-income category exhibits a midday peak, absent in other groups.
- Fewer trips are associated with the high-income category, while the remaining groups follow similar patterns.
- Older age groups correspond to fewer trips, while younger groups travel more in the synthetic data produced by the updated workflow.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABM | Activity-based Modeling |
| AIC | Akaike Information Criterion |
| C-index | Concordance Index |
| DOAJ | Directory of open access journals |
| GPS | Global Positioning System |
| HOH | Home-Other-Home |
| HWH | Home-Work-Home |
| IBS | Integrated Brier Score |
| K–S | Kolmogorov–Smirnov |
| MAE | Mean Absolute Error |
| MDPI | Multidisciplinary Digital Publishing Institute |
| NTUA | National Technical University of Athens |
| OD | Origin-Destination |
| PAM | Population Activity Modeler |
| WAIC | Watanabe-Akaike Information Criterion |
| RMSE | Root Mean Square Error |
Appendix A

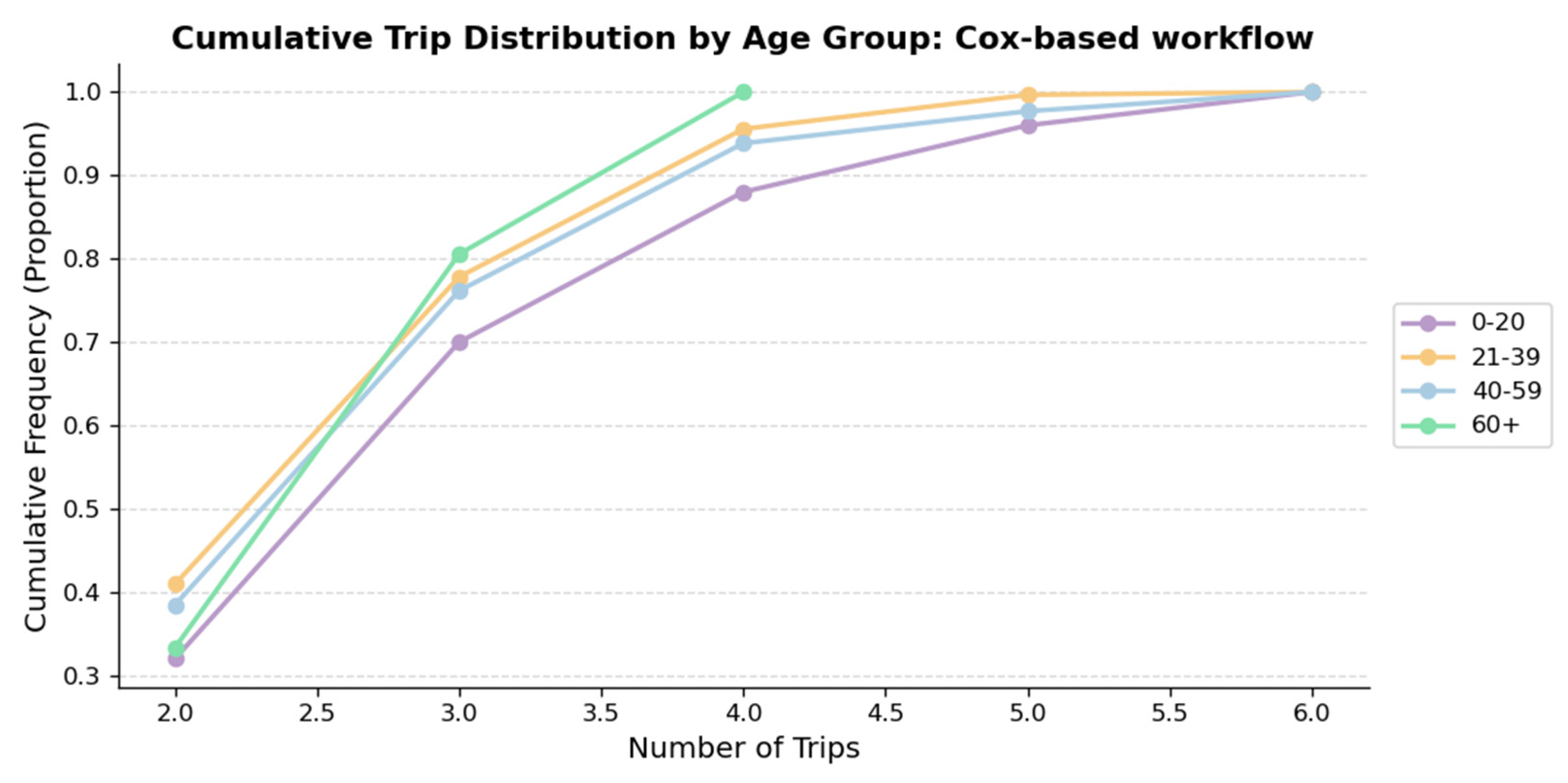
References
- Fina, S.; Joshi, J.; Wittowsky, D. Monitoring travel patterns in German city regions with the help of mobile phone network data. Int. J. Digit. Earth 2021, 14, 379–399. [Google Scholar] [CrossRef]
- Shen, S.; Koech, W.; Feng, J.; Rice, T.M.; Zhu, M. A cross-sectional study of travel patterns of older adults in the USA during 2015: Implications for mobility and traffic safety. BMJ Open 2017, 7, e015780. [Google Scholar] [CrossRef]
- Barmpounakis, E.; Geroliminis, N. On the new era of urban traffic monitoring with massive drone data: The pNEUMA large-scale field experiment. Transp. Res. Part C Emerg. Technol. 2020, 111, 50–71. [Google Scholar] [CrossRef]
- Hörl, S.; Balac, M. Synthetic population and travel demand for Paris and Île-de-France based on open and publicly available data. Transp. Res. Part C Emerg. Technol. 2021, 130, 103291. [Google Scholar] [CrossRef]
- Yee, J.L.; Niemeier, D.A. Analysis of activity duration using the Puget sound transportation panel. Transp. Res. Part A Policy Pract. 2000, 34, 607–624. [Google Scholar] [CrossRef]
- TomTom. 2024. Available online: https://www.tomtom.com/traffic-index/ranking/ (accessed on 31 March 2025).
- Canalys. Available online: https://www.canalys.com/newsroom/europe-smartphone-market-Q1-2024 (accessed on 31 March 2025).
- PewResearch. 2024. Available online: https://www.pewresearch.org/internet/2012/05/11/three-quarters-of-smartphone-owners-use-location-based-services/ (accessed on 31 March 2025).
- DataReportal. 2024. Available online: https://datareportal.com/reports/digital-2024-deep-dive-5-billion-social-media-users (accessed on 31 March 2025).
- Gkiotsalitis, K.; Stathopoulos, A. A utility-maximization model for retrieving users’ willingness to travel for participating in activities from big-data. Transp. Res. Part C Emerg. Technol. 2015, 58, 265–277. [Google Scholar] [CrossRef]
- Li, J.; Rombaut, E.; Vanhaverbeke, L. A Stepwise Approach of Generating Agent-based Simulation Model for Brussels Using Ubiquitous Big Data. Transp. Res. Procedia 2023, 72, 2261–2268. [Google Scholar] [CrossRef]
- Chen, C.; Ma, J.; Susilo, Y.; Liu, Y.; Wang, M. The promises of big data and small data for travel behavior (aka human mobility) analysis. Transp. Res. Part C Emerg. Technol. 2016, 68, 285–299. [Google Scholar] [CrossRef] [PubMed]
- Munizaga, M.A.; Palma, C. Estimation of a disaggregate multimodal public transport Origin–Destination matrix from passive smartcard data from Santiago, Chile. Transp. Res. Part C Emerg. Technol. 2012, 24, 9–18. [Google Scholar] [CrossRef]
- Ahmed, B. The Traditional Four Steps Transportation Modeling Using Simplified Transport Network: A Case Study of Dhaka City, Bangladesh. Int. J. Adv. Sci. Eng. Technol. Res. 2012, 1, 19–40. [Google Scholar]
- Ziemke, D.; Kaddoura, I.; Nagel, K. The MATSim Open Berlin Scenario: A multimodal agent-based transport simulation scenario based on synthetic demand modeling and open data. Procedia Comput. Sci. 2019, 151, 870–877. [Google Scholar] [CrossRef]
- Tozluoğlu, Ç.; Dhamal, S.; Yeh, S.; Sprei, F.; Liao, Y.; Marathe, M.; Barrett, C.L.; Dubhashi, D. A synthetic population of Sweden: Datasets of agents, households, and activity-travel patterns. Data Brief 2023, 48, 109209. [Google Scholar] [CrossRef] [PubMed]
- Joubert, J.W. Synthetic populations of South African urban areas. Data Brief 2018, 19, 1012–1020. [Google Scholar] [CrossRef]
- Aljoufie, M.; Zuidgeest, M.; Brussel, M.; van Vliet, J.; van Maarseveen, M. A cellular automata-based land use and transport interaction model applied to Jeddah, Saudi Arabia. Landsc. Urban. Plan. 2013, 112, 89–99. [Google Scholar] [CrossRef]
- Wang, Y.; Monzon, A.; Di Ciommo, F. Assessing the accessibility impact of transport policy by a land-use and transport interaction model—The case of Madrid. Comput. Environ. Urban. Syst. 2015, 49, 126–135. [Google Scholar] [CrossRef]
- Guzman, L.A.; Gomez, A.M.; Rivera, C. A Strategic Tour Generation Modeling within a Dynamic Land-Use and Transport Framework: A Case Study of Bogota, Colombia. Transp. Res. Procedia 2017, 25, 2536–2551. [Google Scholar] [CrossRef]
- Ortega, J.; Hamadneh, J.; Esztergár-Kiss, D.; Tóth, J. Simulation of the Daily Activity Plans of Travelers Using the Park-and-Ride System and Autonomous Vehicles: Work and Shopping Trip Purposes. Appl. Sci. 2020, 10, 2912. [Google Scholar] [CrossRef]
- Gkiotsalitis, K.; Stathopoulos, A. Predicting Traveling Distances and Unveiling Mobility and Activity Patterns of Individuals from Multisource Data. J. Transp. Eng. A Syst. 2020, 146, 04020025. [Google Scholar] [CrossRef]
- Sallard, A.; Balac, M. Travel demand generation using Bayesian Networks: An application to Switzerland. Procedia Comput. Sci. 2023, 220, 267–274. [Google Scholar] [CrossRef]
- He, B.Y.; Zhou, J.; Ma, Z.; Chow, J.Y.J.; Ozbay, K. Evaluation of city-scale built environment policies in New York City with an emerging-mobility-accessible synthetic population. Transp. Res. Part A Policy Pract. 2020, 141, 444–467. [Google Scholar] [CrossRef]
- Jovicic, G.; Hansen, C.O. A passenger travel demand model for Copenhagen. Transp. Res. Part A Policy Pract. 2003, 37, 333–349. [Google Scholar] [CrossRef]
- Rizopoulos, D.; Esztergár-Kiss, D. A modal share scenario evaluation framework including electric vehicles. Res. Transp. Bus. Manag. 2024, 56, 101201. [Google Scholar] [CrossRef]
- Gong, L.; Han, P.; Lei, T.; Li, B.; Luo, Q.; Zhu, C. Analyzing the transfer duration of public transport passengers using classification and regression tree-multiple-Cox proportional hazards (CART-Multi-Cox) model. Transp. Lett. 2024, 1–16. [Google Scholar] [CrossRef]
- Raux, C.; Ma, T.-Y.; Joly, I.; Kaufmann, V.; Cornelis, E.; Ovtracht, N. Travel and activity time allocation: An empirical comparison between eight cities in Europe. Transp. Policy 2011, 18, 401–412. [Google Scholar] [CrossRef]
- Kalatian, A.; Farooq, B. DeepWait: Pedestrian Wait Time Estimation in Mixed Traffic Conditions Using Deep Survival Analysis. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019. [Google Scholar]
- Bhat, C.R. A generalized multiple durations proportional hazard model with an application to activity behavior during the evening work-to-home commute. Transp. Res. Part B Methodol. 1996, 30, 465–480. [Google Scholar] [CrossRef]
- Nishiuchi, H.; Chikaraishi, M. Identifying Passengers Who Are at Risk of Reducing Public Transport Use: A Survival Time Analysis Using Smart Card Data. Transp. Res. Procedia 2018, 34, 291–298. [Google Scholar] [CrossRef]
- Mbotwa, J.; de Kamps, M.; Baxter, P.D.; Gilthorpe, M.S. Application of Cox Model to predict the survival of patients with Chronic Heart Failure: A latent class regression approach. arXiv 2019, arXiv:1907.07957. [Google Scholar]
- Sinha, P.M.; Calfee, C.S.M.; Delucchi, K.L. Practitioner’s Guide to Latent Class Analysis: Methodological Considerations and Common Pitfalls. Crit. Care Med. 2021, 49, e63–e79. [Google Scholar] [CrossRef]
- Sreela, P.K.; Melayil, S.; Anjaneyulu, M.V.L.R. Modeling of Shopping Participation and Duration of Workers in Calicut. Procedia Soc. Behav. Sci. 2013, 104, 543–552. [Google Scholar] [CrossRef][Green Version]
- Bhat, C.R. A hazard-based duration model of shopping activity with nonparametric baseline specification and nonparametric control for unobserved heterogeneity. Transp. Res. Part B Methodol. 1996, 30, 189–207. [Google Scholar] [CrossRef]
- Hamed, M.M.; Easa, S.M. Integrated Modeling of Urban Shopping Activities. J. Urban. Plan. Dev. 1998, 124, 115–131. [Google Scholar] [CrossRef]
- Enam, A.; Auld, J. Hazard-Based Model of Activity Generation Using Vehicle Trajectory Data. Procedia Comput. Sci. 2020, 170, 764–770. [Google Scholar] [CrossRef]
- Liu, C.; Zuo, X.; Gu, X.; Shao, M.; Chen, C. Activity Duration under the COVID-19 Pandemic: A Comparative Analysis among Different Urbanized Areas Using a Hazard-Based Duration Model. Sustainability 2023, 15, 9537. [Google Scholar] [CrossRef]
- Van den Berg, P.; Arentze, T.; Timmermans, H. A latent class accelerated hazard model of social activity duration. Transp. Res. Part A Policy Pract. 2012, 46, 12–21. [Google Scholar] [CrossRef]
- Li, Y.; Dai, Z.; Zhu, L.; Liu, X. Analysis of spatial and temporal characteristics of citizens’ mobility based on e-bike GPS trajectory data in Tengzhou City, China. Sustainability 2019, 11, 5003. [Google Scholar] [CrossRef]
- Tilahun, N.; Levinson, D. Contacts and Meetings: Location, Duration and Distance Traveled. 2009. Available online: https://ideas.repec.org/p/nex/wpaper/contactsandmeetings.html (accessed on 15 May 2025).
- Moeckel, R.; Huang, W.-C.; Ji, J.; Llorca, C.; Moreno, A.T.; Staves, C.; Zhang, Q.; Erhardt, G.D. The Activity-based model ABIT: Modeling 24 hours, 7 days a week. Transp. Res. Procedia 2024, 78, 499–506. [Google Scholar] [CrossRef]
- Liao, X.; Jiang, Q.; He, B.Y.; Liu, Y.; Kuai, C.; Ma, J. Deep Activity Model: A Generative Approach for Human Mobility Pattern Synthesis. arXiv 2024, arXiv:2405.17468. [Google Scholar]
- Alsger, A.; Tavassoli, A.; Mesbah, M.; Ferreira, L.; Hickman, M. Public transport trip purpose inference using smart card fare data. Transp. Res. Part C Emerg. Technol. 2018, 87, 123–137. [Google Scholar] [CrossRef]
- Kharoufeh, J.P.; Goulias, K.G. Nonparametric identification of daily activity durations using kernel density estimators. Transp. Res. Part B Methodol. 2002, 36, 59–82. [Google Scholar] [CrossRef]
- Golshani, N.; Shabanpour, R.; Auld, J.; (Kouros) Mohammadian, A. Activity start time and duration: Incorporating regret theory into joint discrete–continuous models. Transp. A Transp. Sci. 2018, 14, 809–827. [Google Scholar] [CrossRef]
- He, B.Y.; Zhou, J.; Ma, Z.; Wang, D.; Sha, D.; Lee, M.; Chow, J.Y.; Ozbay, K. A validated multi-agent simulation test bed to evaluate congestion pricing policies on population segments by time-of-day in New York City. Transp. Policy 2021, 101, 145–161. [Google Scholar] [CrossRef]
- Shone, F.; Chatziioannou, T.; Pickering, B.; Kozlowska, K.; Fitzmaurice, M. PAM: Population Activity Modeller. J. Open Source Softw. 2024, 9, 6097. [Google Scholar] [CrossRef]
- Therneau, T.M.; Grambsch, P.M. The Cox Model. In Modeling Survival Data: Extending the Cox Model; Springer: New York, NY, USA, 2000; pp. 39–77. [Google Scholar] [CrossRef]
- Faraggi, D.; Simon, R. A neural network model for survival data. Stat. Med. 1995, 14, 73–82. [Google Scholar] [CrossRef] [PubMed]
- Katzman, J.L.; Shaham, U.; Cloninger, A.; Bates, J.; Jiang, T.; Kluger, Y. DeepSurv: Personalized treatment recommender system using a Cox proportional hazards deep neural network. BMC Med. Res. Methodol. 2018, 18, 24. [Google Scholar] [CrossRef]

| Authors | Year | Decision Variables | Study Purpose | Type of Model | |
|---|---|---|---|---|---|
| Travel Demand Modeling and Forecasting | J.L. Yee et al. [5] | 2000 | Socioeconomic Characteristics and Trip Characteristics | Estimating activity durations per purpose based on socioeconomic and trip characteristics | Non-Linear Model (Cox parametric hazard-based) |
| Munizaga et al. [13] | 2012 | Location and Duration between consecutive payments | Recording OD matrices from public transport data | Discrete Non-Linear Model (Τrip-based model) | |
| Bayes Ahmed [14] | 2012 | Population, Income, Land Cost, Unemployment | Forecasting OD matrices in 10 years | Linear Model | |
| Hörl et al. [4] | 2021 | Trip Characteristics | Creation of synthetic travel demand using open data to facilitate methodology replication | Discrete Non-Linear Model (Agent-based model) | |
| Aljoufie et al. [18] | 2013 | Land Use, availability, Trip cost | OD matrices and accessibility estimation | Discrete non-Linear Model (LUTI model) | |
| Gkiotsalitis et al. [22] | 2020 | Location, Type of Activity, Travel Distance | Retrieve information for trip characteristics based on social media data | Hybrid Activity-Mobility Model with Machine Learning | |
| Enam et al. [37] | 2020 | Socioeconomic Characteristics and Trip Characteristics | Activity generation modeling from vehicle trajectory data to improve travel behavior prediction | Non-Linear Model (Weibull parametric hazard-based) | |
| Chunguang Liu et al. [38] | 2023 | Socioeconomic characteristics, Land Use, travel distances | Estimating activity duration based on socioeconomic characteristics and land use | Semi-parametric model (Cox) | |
| Tilahun et al. [41] | 2009 | Socioeconomic Characteristics and Trip Characteristics | Estimating locations, trip distance, and duration based on social characteristics | Non-Linear Model (path model) | |
| Rolf Moeckel et al. [42] | 2024 | Socioeconomic Characteristics and Trip Characteristics | Creation of a simulation environment, retrieving and forecasting trip characteristics information | Activity-based model | |
| Liao et al. [43] | 2024 | Socioeconomic Characteristics and Trip Characteristics | Generating accurate activity chains through a deep learning process | Activity-based model | |
| Alsger et al. [44] | 2018 | Spatial and Temporal variables, socioeconomic characteristics, Land Use | Estimation of travel purposes | Discrete Non-Linear Model (rule-based model) | |
| Activity Duration estimation research | Tozluoglu et al. [16] | 2023 | Socioeconomic and spatial characteristics | Estimation of travel activity patterns and their Spatial-Temporal Distribution | Discrete Non-Linear Model (rule-based model) |
| Dominik Ziemke et al. [15] | 2019 | Socioeconomic and trip characteristics | Population Synthesis and creation of a MATSim environment | Discrete Non-Linear Model (Agent-based model) | |
| Sallarda et al. [23] | 2023 | Socioeconomic characteristics and trip purposes | Estimation of travel activity patterns | Discrete Non-Linear Model (machine learning) | |
| He, B.Y., et al. [24] | 2020 | Mode choice, Trip cost, trip duration | Spatial and Temporal Distribution of trips and Mode choice based on specific scenarios | Discrete Non-Linear Model (Tour-based model) | |
| Jovicic et al. [25] | 2003 | Population, Land Use, Car Ownership | Estimation of the number of trips and purposes for toll policy examination | Discrete Non-Linear Model (Tour-based model) | |
| Sreela P. et al. [34] | 2013 | Socioeconomic Characteristics and Trip Characteristics | Estimating workers’ shopping duration based on socioeconomic characteristics | Non-Linear Model (Weibull parametric) | |
| Chandra R. Bhat [35] | 1996 | Socioeconomic Characteristics and Trip Characteristics | Estimating shopping durations based on trip characteristics and by taking into consideration heterogeneity | Non-Linear Model (Weibull parametric vs. non parametric) | |
| M. Hamed [36] | 1998 | Socioeconomic and Trip Characteristics | Disaggregate modeling of shopping urban activities based on social characteristics and household | Non-Linear Model (Weibull parametric hazard) | |
| Kharoufeh et al. [45] | 2002 | Socioeconomic characteristics/gender | Examining non-parametric pattern recognition tool for the purpose of investigating covariate effects and heterogeneity in duration models | Non-Linear Model (Kernel density estimator) | |
| N. Golshani et al. [46] | 2018 | Socioeconomic characteristics and Start trip time | Estimating activity duration based on socioeconomic characteristics and travel time | Non-Linear Model (copula joint-based model) | |
| Activity-Based Modeling and Simulation | Li, J., et al. [11] | 2023 | Population, Location, Start trip time | Estimation of chain activities through ABM simulation | Discrete non-Linear Model (Agent-based model) |
| Chen et al. [12] | 2016 | Location, Start Trip time, Duration, | Estimation of OD Matrix and trip purposes | Discrete Choice non-Linear Model | |
| Yixiao Li et al. [40] | 2019 | Location, Start trip time and travel speed | Estimation of travel activity patterns | Discrete non-Linear Model (spatial statistic model) | |
| Pauline Van den Berg et al. [39] | 2012 | Socioeconomic Characteristics and Trip Characteristics | Estimating social activity durations by latent class based on social characteristics | Non-Linear Model (Weibull parametric) | |
| Scenario Analysis and Policy Evaluation | Gkiotsalitis et al. [10] | 2015 | Start trip time and type of trip | Forecasting traveled distances and travel patterns | Discrete Non-Linear Model (machine learning) |
| He, B.Y., et al. [47] | 2021 | Mode choice, Spatial Distribution | Examination of toll policy scenarios based on different pricing policies | Discrete Non-Linear Model (Agent-based model) | |
| Joubert J. [17] | 2018 | Socioeconomic Characteristics | Population Synthesis in order to be input for MATSim | Discrete Non-Linear Model (Agent-based model) | |
| Y. Wang et al. [19] | 2015 | Socioeconomic characteristics and accessibility, land use | Exploration of scenarios and their evaluation based on financial conclusions. | Discrete Non-Linear Model (LUTI model) |
| Sets | |
| Set of covariates included as predictive factors in the model | |
| Set of Latent Classes | |
| Set of Observations | |
| Parameters | |
| Coefficients for each characteristic k and latent class c | |
| Latent frailty variables for each class | |
| Standard deviation of frailty terms | |
| The probabilities of belonging to each latent class | |
| Variables | |
| The duration of activity (survival time) for each observation i | |
| The vector of predictor variables k for each observation i | |
| The censoring variable (1 = event occurred, 0 = censored) | |
| Category | Variable Name | Type | Vaue Mappings |
|---|---|---|---|
| Demographic | Gender | Categorical | (1: male, 0: female) |
| Age | Continuous | Age in years | |
| Education | Categorical | 1: Primary School, 2: High School, 3: Bachelor, 4: Master or PhD | |
| Employment | Categorical | 1: Inactive, 2: Unemployed, 3: Student, 4: Active | |
| Income | Categorical | 0: No income, 1: ≤750, 2: 750–1500, 3: 1500–2500, 4: ≥2500 | |
| Car_own | Categorical | 0: No, 1: Yes | |
| Spatial Variables | Dest | Categorical | 1: Central Athens, 2: West Athens, 3: East Attica, 4: South Athens, 5: North Athens, 6: Piraeus |
| Home | Categorical | Same as Dest | |
| Mode Choice | Mode | Categorical | 1: car, 2: taxi,3: bus, 4: train, 5: motorcycle, 6: bicycle, 7: walk, 8: E-scooter |
| Temporal Variables | Time | Continuous | Start trip time (24-h format) |
| Distance | Dist | Continuous | Distance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katsaitis, D.; Rizopoulos, D.; Gkiotsalitis, K. A Cox Model-Based Workflow for Increased Accuracy in Activity-Travel Patterns Generation. Appl. Sci. 2025, 15, 6237. https://doi.org/10.3390/app15116237
Katsaitis D, Rizopoulos D, Gkiotsalitis K. A Cox Model-Based Workflow for Increased Accuracy in Activity-Travel Patterns Generation. Applied Sciences. 2025; 15(11):6237. https://doi.org/10.3390/app15116237
Chicago/Turabian StyleKatsaitis, Dionysios, Dimitrios Rizopoulos, and Konstantinos Gkiotsalitis. 2025. "A Cox Model-Based Workflow for Increased Accuracy in Activity-Travel Patterns Generation" Applied Sciences 15, no. 11: 6237. https://doi.org/10.3390/app15116237
APA StyleKatsaitis, D., Rizopoulos, D., & Gkiotsalitis, K. (2025). A Cox Model-Based Workflow for Increased Accuracy in Activity-Travel Patterns Generation. Applied Sciences, 15(11), 6237. https://doi.org/10.3390/app15116237









